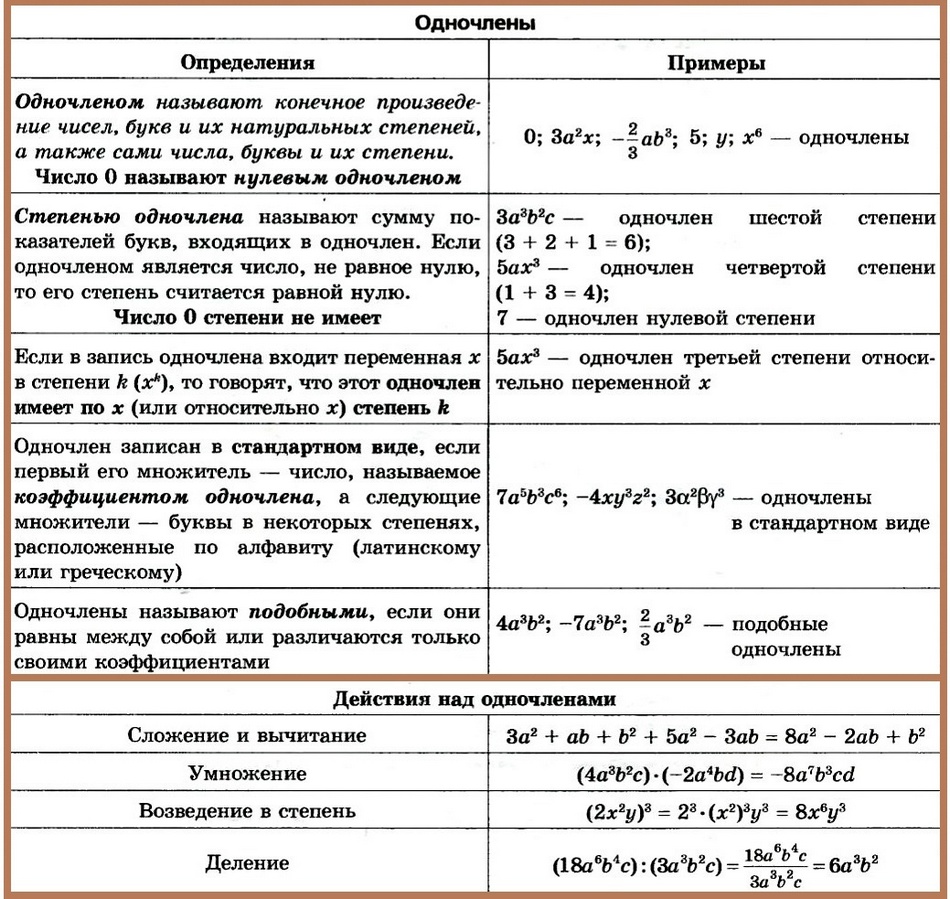
Многочлен и его стандартный вид
Ключевые слова конспекта: Многочлен, стандартный вид многочлена, члены многочлена, полиномы, нуль-многочлен, степень многочлена, приведение подобных слагаемых, старший коэффициент, свободный член многочлена.
Выражение 5a2b – 3ab – 4а3 + 7 представляет собой сумму одночленов 5a2b, –5ab, –4а3 и 7. Такие выражения называют многочленами.
Определение. Многочленом называется сумма одночленов.
Одночлены, из которых составлен многочлен, называют членами многочлена. Например, членами многочлена х3у – 4х2 + 9 являются одночлены х3у, –4х2 и 9.
Многочлен, состоящий из двух членов, называется двучленом, а многочлен, состоящий из трёх членов, — трёхчленом. Одночлен считают многочленом, состоящим из одного члена. Многочлены иногда называют полиномами, а двучлены — биномами (от греческих слов «поли» — «много», «номос» — «член, часть» и латинского «би» — «два, дважды»).
Зная значения переменных, входящих в многочлен, можно вычислить значение многочлена.
Пример 1. Найдём значение многочлена –0,3х2у – х3 + 7у при х = –0,2, у = –1.Имеем:–0,3х2у – х3+7у = –0,3 • (–0,2)2 • (–1) – (–0,2)3 + 7 • (–1) = 0,012 + 0,008 – 7 = –6,98.
Стандартный вид многочлена
В многочлене 13х2у + 4 + 8ху – 6х2у — 9 первый и четвёртый члены имеют одинаковую буквенную часть. Члены многочлена, имеющие одинаковую буквенную часть, называются подобными членами. Подобными членами считаются и слагаемые, не имеющие буквенной части.
Сумму подобных членов многочлена можно заменить одночленом. Такое тождественное преобразование называют приведением подобных членов или приведением подобных слагаемых. Приведение подобных членов основано на переместительном и сочетательном свойствах сложения и распределительном свойстве умножения.
Пример 2. Приведём подобные члены многочлена 13х2у + 4 + 8ху – 6х2у — 9. Имеем: 13х2у + 4 + 8ху – 6х2у – 9 = (13х2у – 6х2у) + 8ху + (4 – 9) = (13 – 6)х2у + 8ху – 5 = 7х2у + 8ху – 5.
В многочлене 7х2у + 8ху – 5 каждый член является одночленом стандартного вида, причём среди них нет подобных членов. Такие многочлены называются многочленами стандартного вида.
Рассмотрим многочлен стандартного вида За3 – 5а3b2 + 7. Его членами являются одночлены третьей, пятой и нулевой степени. Наибольшую из этих степеней называют степенью многочлена. Таким образом, этот многочлен является многочленом пятой степени.
Степенью многочлена стандартного вида называют наибольшую из степеней входящих в него одночленов. Степенью произвольного многочлена называют степень тождественно равного ему многочлена стандартного вида.
Пример 3. Определим степень многочлена а6 + 2а2b – а6 + 1. Для этого приведём многочлен к стандартному виду: а6 + 2а2b – а6 + 1 = 2a2b + 1. Степень полученного многочлена равна трём. Значит, и степень заданного многочлена равна трём.
Если многочлен является числом, отличным от нуля, то степень такого многочлена равна 0. Число нуль называют нуль-многочленом. Его степень считается не определённой.
Среди многочленов выделяют многочлены с одной переменной. Многочлен n-й степени с одной переменной в стандартном виде записывается так: ахn + а1хn-1 + а2хn-2 + … + аn-2х2 + аn-1х + аn, где х — переменная, а, a1 а2, …, аn-1, аn — произвольные числа, n ∈ N или n = 0. Коэффициент при хn называют старшим коэффициентом (в нашем случае это а). Слагаемое, не содержащее переменной х, называют свободным членом многочлена (в нашем случае это аn). Например, старший коэффициент многочлена х4 + 2х3– х2 + 3х равен 1, а свободный член равен нулю.
Заметим, что значение многочлена с переменной х при х = 0 равно свободному члену этого многочлена, а при х = 1 — сумме его коэффициентов.
Это конспект по математике на тему «Многочлен и его стандартный вид». Выберите дальнейшие действия:
- Перейти к следующему конспекту:
- Вернуться к списку конспектов по Математике.
- Проверить знания по Математике.
Одночлены и действия над ними
Ключевые слова конспекта: Одночлены, стандартный вид одночлена, коэффициент и степень одночлена, умножение одночленов,
Выражения 15а2b, 3ху • 2у, –3с7 представляют собой произведения чисел, переменных и их степеней. Такие выражения называют одночленами. Числа, переменные и их степени также считаются одночленами. Например, выражения –11, а, а6 — одночлены.
Одночлен 5а2b • 2аb3 можно упростить, если воспользоваться свойствами умножения и правилом умножения степеней с одинаковыми основаниями. Тогда получим: 5а2b • 2аb3 = 5 • 2а2 • а • b • b3 = 10а3b4.
Мы представили данный одночлен в виде произведения числового множителя, записанного на первом месте, и степеней различных переменных. Такой вид одночлена называют стандартным видом. Числа, переменные, их степени также считаются одночленами стандартного вида.
Коэффициент и степень одночлена
Любой одночлен можно преобразовать так, чтобы получился одночлен стандартного вида. Если одночлен записан в стандартном виде, то числовой множитель называют коэффициентом одночлена. Например, в одночлене –10а2b4 коэффициент равен –10. Если коэффициент одночлена равен 1 или –1, то его обычно не пишут.
Степенью одночлена стандартного вида называют сумму показателей степеней входящих в него переменных. Если одночлен представляет собой число, отличное от нуля, то его степень считается равной нулю.
Например, степень одночлена 12х2у3равна 5, степень одночлена –6аb равна 2. Выражение 2,32 является одночленом нулевой степени.
Число нуль — это одночлен, степень которого не определена.
Умножение одночленов
При умножении одночленов снова получается одночлен, который обычно записывают в стандартном виде, используя для этого свойства умножения и правило умножения степеней с одинаковыми основаниями.
Пример. Умножим одночлен 12а6b4 на одночлен –2а3b. Для этого составим произведение одночленов и преобразуем его в одночлен стандартного вида:12а6b4 • (–2а3b) = 12 • (–2) • (а6 • а3) • (b4 • b) = –24а9b5.
Возведение одночлена в степень
Рассмотрим сначала правила возведения в степень произведения и степени. Преобразуем четвёртую степень произведения ab:(ab)4 = (ab)(ab)(ab)(ab) = (aaaa)(bbbb) = а4b4, т.е. (аb)4 = а4b4.Четвёртая степень произведения равна произведению четвёртых степеней множителей. Аналогичным свойством обладает любая натуральная степень произведения двух множителей.
Если а и b — произвольные числа и n — любое натуральное число, то(аb)n = аnbn.
Докажем это, воспользовавшись определением степени и свойствами умножения:
Доказанное свойство распространяется на произведение трёх и более множителей. Например, (abc)n = anbncn; (abcd)n = anbncndn.
Отсюда следует правило:
чтобы возвести в степень произведение, нужно возвести в эту степень каждый множитель и результаты перемножить.
Рассмотрим теперь, как можно возвести степень в степень. Преобразуем, например, выражение (а5)4: (а5)4 = а5 • а5 • а5 • а5 = а5+5+5+5 = а20, то есть (а5)4 = а5•4
Аналогичное свойство выполняется для произвольных степеней с натуральными показателями.
Если а — произвольное число, m и n — любые натуральные числа, то(аm)n = аm • n
Из этого свойства следует правило:
чтобы возвести степень в степень, нужно основание оставить тем же, а показатели степеней перемножить.
Аналогично тому, как было доказано свойство степени произведения, можно доказать свойство степени дроби: (a/b)n = an/bn, где b ≠ 0. Из этого свойства следует правило:
чтобы возвести в степень дробь, нужно возвести в эту степень числитель и знаменатель, первое выражение записать в числитель, а второе — в знаменатель.
Правила возведения в степень произведения и степени используются при возведении одночленов в степень.
Это конспект по математике на тему «Одночлены и действия над ними». Выберите дальнейшие действия:
- Перейти к следующему конспекту: Многочлен и его стандартный вид
- Вернуться к списку конспектов по Математике.
- Проверить знания по Математике.
Степень одночлена
Для одночлена существует понятие его степени. Разберемся, что это такое.
Определение.
Степень одночлена стандартного вида – это сумма показателей степеней всех переменных, входящих в его запись; если в записи одночлена нет переменных, и он отличен от нуля, то его степень считается равной нулю; число нуль считается одночленом, степень которого не определена.
Определение степени одночлена позволяет привести примеры. Степень одночлена a равна единице, так как a это есть a1. Степень одночлена 5 есть нуль, так как он отличен от нуля, и его запись не содержит переменных. А произведение 7·a2·x·y3·a2 является одночленом восьмой степени, так как сумма показателей степеней всех переменных a, x и y равна 2+1+3+2=8.
Кстати, степень одночлена, записанного не в стандартном виде, равна степени соответствующего одночлена стандартного вида. Для иллюстрации сказанного вычислим степень одночлена 3·x2·y3·x·(−2)·x5·y. Этот одночлен в стандартном виде имеет вид −6·x8·y4, его степень равна 8+4=12. Таким образом, степень исходного одночлена равна 12.
Что такое одночлен? Определение, примеры
Первое запланированное знакомство с одночленами происходит в 7 классе средней школы. Там дается следующее определение одночлена:
Определение.
Одночлены – это числа, переменные, их , а также всевозможные составленные из них произведения.
Озвученное определение позволяет привести примеры одночленов. Каждое из чисел 1, 7, 1 002, , −1, −7, 0,8, 1/4, — это одночлен. Любая переменная, к примеру, a, b, p, q, t, x, y, z – это тоже одночлены по определению. Одночленами являются и степени чисел и переменных, например, 23, (−3,41)7, x2 и t115. Но наиболее яркими представителями одночленов являются произведения чисел, переменных и их степеней: 5·x, 7·(−3)·x·y3·6, x·x·y3·x·y2·z и т.п. Из приведенных примеров видно, что в составе одночлена может быть как одно, так и несколько чисел, как одна, так и несколько переменных и их степеней, причем они могут повторяться.
До 7 класса в школе были изучены натуральные, целые и рациональные числа, они и фигурируют в приведенных выше примерах одночленов. Однако нужно заметить, что определение одночлена в указанной формулировке остается в силе после знакомства с действительными числами и комплексными числами. Так , 2·π·x3 и — это тоже одночлены.
Сложение одночленов
Чтобы сложить одночлены, надо:
- Составить сумму, записав все слагаемые одно за другим.
- Привести все одночлены к стандартному виду.
- Раскрыть скобки, если они есть в выражении.
- Привести подобные слагаемые. Для этого нужно:
- сложить их численные множители;
- после получившегося коэффициента дописать буквенные множители без изменений.
Пример 1. Сложить одночлены 12ab, -4a2b и -5ab.
Решение: Составим сумму одночленов:
12ab + (-4a2b) + (-5ab).
Все одночлены находятся в стандартном виде. Значит, можно приступить к раскрытию скобок. Правила раскрытия скобок смотрите тут.
12ab — 4a2b — 5ab.
Теперь надо определить, есть ли среди слагаемых подобные одночлены и, если они есть, сделать приведение:
12ab — 4a2b — 5ab = (12 + (-5))ab — 4a2b = 7ab — 4a2b.
Пример 2. Сложить одночлены 5a2bc и -5a2bc.
Решение: Составим сумму одночленов:
5a2bc + (-5a2bc).
Раскроем скобки:
5a2bc — 5a2bc.
Эти два одночлена являются противоположными, то есть, отличаются только знаком. Значит, если мы сложим их численные множители, то получим нуль:
5a2bc — 5a2bc = (5 — 5)a2bc = 0a2bc = 0.
Следовательно, при сложении противоположных одночленов в результате получается нуль.
Общее правило сложения одночленов:
Чтобы сложить несколько одночленов, следует записать все слагаемые одно за другим с сохранением их знаков, отрицательные одночлены надо заключить в скобки и сделать приведение подобных слагаемых (подобных одночленов).
Стандартный вид одночлена
Стандартный вид одночлена — это запись одночлена, представляющая собой число, степень переменной или произведение, в котором только один числовой множитель, записанный на первом месте, а каждая его буква участвует в его записи лишь один раз, при этом буквы записаны в алфавитном порядке.
Пример. 7, a, -3xy2, 1abс — одночлены стандартного вида.
А вот следующие одночлены записаны не в стандартном виде:
12aa3b и 4cb(−2)y,
так как первый содержит одинаковые буквы, а во втором два числовых множителя и буквенные множители записаны не в алфавитном порядке.
Стандартный вид нулевого одночлена есть 0.
Коэффициент одночлена
Коэффициент одночлена — это числовой множитель в одночлене стандартного вида, который содержит хотя бы одну переменную. Понятие коэффициент также относят к одночленам стандартного вида, представляющим собой числа без буквенных множителей. Коэффициентами таких одночленов считаются сами числа.
Пример. Одночлены
-7ab3, , -1x, 15
записаны в стандартном виде. Их коэффициенты соответственно равны числам -7, , -1, 15.
Коэффициент одночлена, равный 1 или -1 обычно не пишут.
Если одночлен имеет только буквенные множители, то условились считать, что его коэффициент равен +1 или -1, в зависимости от знака, который стоит (или подразумевается) перед одночленом.
Пример. Одночлены
a, —xy
записаны в стандартном виде. Коэффициент первого из них равен 1, второго -1, так как
a = 1 · a, —xy = -1 · xy.
Целый положительный коэффициент означает, сколько раз повторяется слагаемым буквенное выражение, перед которым он стоит.
Пример.
3ab = (ab) · 3 = ab + ab + ab.
Дробный положительный коэффициент означает, какая часть берётся от буквенного выражения, к которому он относится.
Пример. В одночлене коэффициент означает, что от x2 берётся , потому что , а умножить на значит взять от множимого.
Отрицательный коэффициент означает, что буквенное выражение, перед которым он стоит, умножается на абсолютную величину этого коэффициента и результат берётся с противоположным знаком.
Пример.
-4mn = -4 · mn = -(mn + mn + mn + mn).
Задания для самостоятельного решения
Задание 1. Приведите одночлен −2aba к стандартному виду.
Решение:
−2aba = −2a2b
Задание 2. Приведите одночлен 0,5m × 2n к стандартному виду.
Решение:
0,5m × 2n = (0,5 × 2)(mn) = 1mn = mn
Задание 3. Приведите одночлен −8ab(−2,5)b2 к стандартному виду.
Решение:
−8ab(−2,5)b2 = −8 × (−2,5) × a × (b × b2) = 20ab3
Задание 4. Приведите одночлен 0,15pq × 4pq2 к стандартному виду.
Решение:
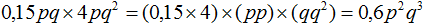
Задание 5. Приведите одночлен −2×3 × 0,5xy2 к стандартному виду.
Решение:
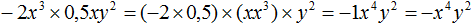
Задание 6. Приведите одночлен 2m3n × 0,4mn к стандартному виду.
Решение:
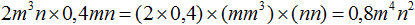
Задание 7. Приведите одночлен к стандартному виду.
Решение:
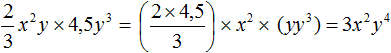
Задание 8. Приведите одночлен к стандартному виду.
Решение:
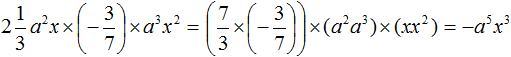
Задание 9. Перемножьте одночлены 2x и 2y
Решение:
2x × 2y = 4xy
Задание 10. Перемножьте одночлены 6x, 5x и y
Решение:
6x × 5x × y = 30x2y
Задание 11. Перемножьте одночлены 2×2, 2×3 и y2
Решение:
2×2 × 2×3 × y2 = (2 × 2) × (x2x3) × y2 = 4x5y2
Задание 12. Перемножьте одночлены −8x и 5×3
Решение:
−8x × 5×3 = (−8 × 5)×(xx3) = −40×4
Задание 13. Перемножьте одночлены x2y5 и (−6xy2)
Решение:
x2y5 × (−6xy2) = −6 × (x2x) × (y5y2) = −6x3y7
Задание 14. Выполните умножение:
Решение:
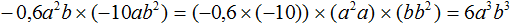
Задание 15. Выполните умножение:
Решение:
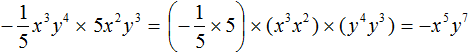
Задание 16. Возведите одночлен x2y2z2 в третью степень
Решение:
(x2y2z2)3 = (x2)3 × (y2)3 × (z2)3 = x6y6z6
Задание 17. Возведите одночлен xy2z3 в пятую степень.
Решение:
(xy2z3)5 = x5 × (y2)5 × (z3)5 = x5y10z15
Задание 18. Возведите одночлен 4x во вторую степень.
Решение:
(4x)2 = 42 × x2 = 16×2
Задание 19. Возведите одночлен 2y3 в третью степень.
Решение:
(2y3)3 = 23 × (y3)3 = 8y9
Задание 20. Возведите одночлен −0,6x3y2 в третью степень.
Решение:
(−0,6x3y2)3 = (−0,6)3 × (x3)3 × (y2)3= −0,216x9y6
Задание 21. Возведите одночлен −x2yz3 в пятую степень.
Решение:
(−x2yz3)5 = (−x2)5 × y5 × (z3)5= −x10y5z15
Задание 22. Возведите одночлен −x3y2z во вторую степень.
Решение:
(−x3y2z)2 = (−x3)2 × (y2)2 × z2 = x6y4z2
Задание 23. Представьте одночлен −27x6y9 в виде одночлена, возведённого в куб.
Решение:
−27x6y9 = (−3x2y3)3
Задание 24. Представьте одночлен −a3b6в виде одночлена, возведённого в куб.
Решение:
−a3b6 = (−ab2)3
Задание 25. Выполните деление
Решение:
Задание 26. Выполните деление
Решение:
Задание 27. Выполните деление
Решение:
Задание 28. Выполните деление
Решение:
Задание 29. Выполните деление
Решение:
Задание 30. Выполните деление
Решение:
Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Разложение одночлена на множители
Поскольку одночлен является произведением чисел, переменных и степеней, то он может быть , из которых состоит.
Пример 1. Разложить одночлен 3a3b2 на множители
Данный одночлен можно разложить на множители 3, a, a, a, b, b
3a3b2 = 3aaabb
Либо степень b2 можно не раскладывать на множители b и b
3a3b2 = 3aaab2
Либо степень b2 разложить на множители b и b, а степень a3 оставить без изменений
3a3b2 = 3a3bb
В каком виде представлять одночлен зависит от решаемой задачи. Главное, чтобы разложение было тождественно равно исходному одночлену.
Пример 2. Разложить одночлен 10a2b3c4 на множители.
Разложим коэффициент 10 на множители 2 и 5, степень a2 разложим на множители aa, степень b3 — на множители bbb, степень c4 — на множители cccc
10a2b3c4 = 2 × 5 × aabbbcccc
Одночлены и многочлены от нескольких переменных
Одночленом (мономом) от переменных x1 , x2 , … , xn называют выражение вида:
где c – произвольное число, называемое коэффициентом одночлена, а символами
i1 , i2 , … in
обозначены целые неотрицательные числа.
Таким образом, одночлен от нескольких переменных является произведением числа на несколько букв, каждая из которых входит в одночлен .
Степенью одночлена называют сумму степеней всех входящих в него букв, т.е. сумму целых неотрицательных чисел:
i1 + i2 + … + in .
Число c называют коэффициентом одночлена.
Пример. Степень одночлена
равна 3, а коэффициент равен – 0,83 .
Два одночлена равны, если, во-первых, у них равны коэффициенты, а во-вторых, одночлены состоят из одних и тех же букв, которые входят в них с соответственно равными показателями степеней.
Алгебраическая сумма одночленов от нескольких переменных носит название многочлена или полинома от нескольких переменных. Например,
Степенью многочлена от нескольких переменных называют наивысшую степень входящих в него одночленов.
В частности, степень многочлена
равна 8.
Многочлен от нескольких переменных называют однородным многочленом, если степени всех входящих в него одночленов равны. В этом случае степень многочлена равна степени каждого входящего в него одночлена.
Например, многочлен
является однородным многочленом степени 3.

На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Деление одночленов
Одночлен можно разделить на другой одночлен. Для этого нужно коэффициент первого одночлена разделить на коэффициент второго одночлена, а буквенную часть первого одночлена разделить на буквенную часть второго одночлена. При этом используется правило .
Например, разделим одночлен 8a2b2 на одночлен 4ab. Запишем это деление в виде дроби:
Первый одночлен 8a2b2 будем называть делимым, а второй 4ab — делителем. А одночлен, который получится в результате, назовём частным.
Разделим коэффициент делимого на коэффициент делителя, получим 8 : 4 = 2. В исходном выражении ставим знак равенства и записываем этот коэффициент частного:
Теперь делим буквенную часть. В делимом содержится a2, в делителе — просто a. Делим a2 на a, получаем a, поскольку a2 : a = a2 − 1 = a. Записываем в частном a после 2
Далее в делимом содержится b2, в делителе — просто b. Делим b2 на b, получаем b, поскольку b2 : b = b2 − 1 = b. Записываем в частном b после a
Значит, при делении одночлена 8a2b2 на одночлен 4ab получается одночлен 2ab.
Сразу можно выполнить проверку. При умножении частного на делитель должно получаться делимое. В нашем случае, если 2ab умножить на 4ab, должно получиться 8a2b2
2ab × 4ab = (2 × 4) × (aa) × (bb) = 8a2b2
Не всегда можно первый одночлен разделить на второй одночлен. Например, если в делителе окажется переменная, которой нет в делимом, то говорят, что деление невозможно.
К примеру, одночлен 6xy2 нельзя разделить на одночлен 3xyz. В делителе 3xyz содержится переменная z, которая не содержится в делимом 6xy2.
Проще говоря, мы не сможем найти частное, которое при умножении на делитель 3xyz дало бы делимое 6xy2, поскольку такое умножение обязательно будет содержать переменную z, которой нет в 6xy2.
Но если в делимом содержится переменная, которая не содержится в делителе, то деление будет возможным. В этом случае переменная, которая отсутствовала в делителе, будет перенесена в частное без изменений.
Например, при делении одночлена 4x2y2z на 2xy, получается 2xyz. Сначала разделили 4 на 2 получили 2, затем x2 разделили на x, получили x, затем y2 разделили на y, получили y. Затем приступили к делению переменной z на такую же переменную в делителе, но обнаружили, что такой переменной в делителе нет. Поэтому перенесли переменную z в частное без изменений:
Для проверки умножим частное 2xyz на делитель 2xy. В результате должен получиться одночлен 4x2y2z
2xyz × 2xy = (2 × 2) × (xx) × (yy) × z = 4x2y2z
Но в некоторых дробях, если невозможно выполнить деление, бывает возможным выполнить . Делается это с целью упростить выражение.
Так, в предыдущем примере нельзя было разделить одночлен 6xy2 на одночлен 3xyz. Но можно сократить эту дробь на одночлен 3xy. Напомним, что сокращение дроби это деление числителя и знаменателя на одно и то же число (в нашем случае на одночлен 3xy). В результате сокращения дробь становится проще, но её значение не меняется:
В числителе и знаменателе мы пришли к делению одночленов, которое можно выполнить:
Процесс деления обычно выполняется в уме, записывая над числителем и знаменателем получившийся результат:
Пример 2. Разделить одночлен 12a2b3c3 на одночлен 4a2bc
Пример 3. Разделить одночлен x2y3z на одночлен xy2
Дополнительно упомянем, что деление одночлена на одночлен также невозможно, если одна из степеней, входящая в делимое, имеет показатель меньший, чем показатель той же степени из делителя.
Например, разделить одночлен 2x на одночлен x2 нельзя, поскольку степень x, входящая в делимое, имеет показатель 1, тогда как степень x2, входящая в делитель, имеет показатель 2. Мы не сможем найти частное, которое при перемножении с делителем x2 даст в результате делимое 2x.
Конечно, мы можем выполнить деление x на x2, воспользовавшись свойством степени с целым показателем:
и такое частное при перемножении с делителем x2 будет давать в результате делимое 2x
Но нас пока интересуют только те частные, которые являются так называемыми целыми выражениями. Целые выражения это те выражения, которые не являются дробями, в знаменателе которых содержится буквенное выражение. А частное целым выражением не является. Это дробное выражение, в знаменателе которого содержится буквенное выражение.
Стандартный вид одночлена
С одночленами удобно работать, когда они приведены к так называемому стандартному виду.
Определение.
Стандартный вид одночлена — это такой вид одночлена, в котором он представлен как произведение числового множителя (который обычно записывают перед остальными множителями слева и называют ) и натуральных степеней различных переменных.
Для пояснения приведем примеры нескольких одночленов стандартного вида: 5 (этот одночлен не содержит переменных), 2·a, −7·x2·y3, , x·y (здесь коэффициент равен единице), −x3 (здесь коэффициент равен −1). А вот одночлены 4·a·a2·a3 и 5·x·(−1)·3·y2 записаны не в стандартном виде, так как первый из них содержит одинаковые переменные, а второй – несколько числовых множителей.
Отметим, что в одночленах стандартного вида принято буквенные множители записывать в алфавитном порядке. Например, одночлен b4·6·a·z2·c предпочтительнее записать как 6·a·b4·c·z2. Давайте договоримся в дальнейшем везде записывать переменные в составе одночлена в алфавитном порядке. Записывать переменные не в алфавитном порядке мы будем только тогда, когда будем преследовать какую-то определенную цель.
Любой одночлен путем тождественных преобразований может быть представлен в стандартном виде. Иными словами, можно любой одночлен привести к стандартному виду.
Приведение одночлена к стандартному виду
С одночленами удобнее работать, когда они записаны в стандартном виде. Любой одночлен можно привести к стандартному виду путём тождественных преобразований. Процесс таких преобразований называют приведением одночлена к стандартному виду.
Привести одночлен к стандартному виду — значит выполнить с ним такие , чтобы он принял стандартный вид.
Чтобы привести одночлен к стандартному виду надо:
- Выполнить группировку числовых множителей (если их несколько), а также одинаковых буквенных множителей и их степеней.
- Вычислить произведение числовых множителей и по свойству степеней с одинаковыми основаниями перемножить буквенные множители.
- Поставить на первое место числовой множитель, а после него расположить буквенные множители в алфавитном порядке.
Пример 1. Запишите одночлен -2b(-3)x34ab2x2 в стандартном виде.
Решение:
Используя переместительное и сочетательное свойства умножения, сгруппируем по отдельности числовые и одинаковые буквенные множители. В результате исходный одночлен примет вид:
((-2) · (-3) · 4) · (b · b2) · (x3 · x2) · a.
Перемножаем числовые множители и степени с одинаковыми основаниями. Произведение числовых множителей равно 24. Произведение степеней b равно b · b2 = b3. Произведение степеней x равно x3 · x2 = x5:
24 · b3 · x5 · a.
Записываем на первом месте числовой множитель, а после него располагаем буквенные множители в алфавитном порядке. В итоге получаем одночлен стандартного вида:
24ab3x5.
Следовательно:
-2b(-3)x34ab2x2 = ((-2) · (-3) · 4) · (b · b2) · (x3 · x2) · a = 24 · b3 · x5 · a = 24ab3x5.
Пример 2. Представить одночлен -2a4c0b в стандартном виде.
Решение:
Среди своих множителей, данный одночлен имеет множитель 0, значит всё произведение в результате будет равно 0. Стандартный вид нулевого одночлена есть 0:
-2a4c0b = 0.
Подобные одночлены
Подобные одночлены — одночлены, которые состоят из одних и тех же букв, но могут иметь разные или одинаковые коэффициенты (числовые множители). Одинаковые буквы в подобных одночленах должны иметь одинаковые показатели степени. Если у одной и той же буквы в разных одночленах степени не совпадают, то такие одночлены нельзя назвать подобными:
5ab2 и -7ab2 — подобные одночлены;
5a2b и 5ab — не подобные одночлены.
Обратите внимание, что последовательность букв в подобных одночленах может не совпадать. Также одночлены могут быть представлены в виде выражения, которое можно упростить
Поэтому, прежде чем приступать к определению, подобны ли данные одночлены, или нет, стоит привести одночлены к . Например, возьмём два одночлена:
5abb и -7b2a.
Оба одночлена находятся в нестандартном виде, поэтому будет нелегко определить, являются ли они подобными. Чтобы это узнать, приведём одночлены к стандартному виду:
5ab2 и -7ab2.
Теперь сразу видно, что данные одночлены являются подобными.
Два подобных одночлена, отличающиеся только знаком, называются противоположными. Например:
5a2bc и -5a2bc — противоположные одночлены.
Приведение подобных одночленов — это упрощение выражения, содержащего подобные одночлены, путём их сложения. Сложение подобных одночленов производится по правилам приведения подобных слагаемых.
Умножение одночленов
Одночлены можно перемножать. Чтобы перемножить одночлены, нужно перемножить их числовые и буквенные части.
Пример 1. Перемножить одночлены 5x и 8y
Перемножим числовые и буквенные части по отдельности. Для удобства перемножаемые сомножители будем заключать в скобки:
5x × 8y = (5 × 8) × (x × y) = 40xy
Пример 2. Перемножить одночлены 5x2y3 и 7x3y2c
Перемножим числовые и буквенные части по отдельности. В процессе умножения будем применять правило перемножения степеней с одинаковыми основаниями. Перемножаемые сомножители будем заключать в скобки:
5x2y3 × 7x3y2c = (5 × 7) × (x2x3) × (y3y2) × c = 35x5y5c
Пример 3. Перемножить одночлены −5a2bc и 2a2b4
−5a2bc × 2a2b4 = (−5 × 2) × (a2a2) × (bb4) × c = −10a4b5c
Пример 4. Перемножить одночлены x2y5 и (−6xy2)
x2y5 × (−6xy2) = −6 × (x2x) × (y5y2) = −6x3y7
Пример 5. Найти значение выражения
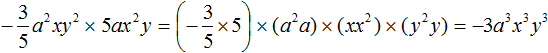

![Одночлены, многочлены [wiki.eduvdom.com]](https://rusinfo.info/wp-content/uploads/b/8/5/b8588502a60c44a2a8d9a2e59a0029df.png)








![Одночлены, многочлены [wiki.eduvdom.com]](https://rusinfo.info/wp-content/uploads/5/0/7/507e08d849ed9551a8d53a2aa397a77b.jpg)









![Одночлены, многочлены [wiki.eduvdom.com]](https://rusinfo.info/wp-content/uploads/f/2/9/f293552887004d5463c2cc22f79509ed.jpg)









![Одночлены, многочлены [wiki.eduvdom.com]](https://rusinfo.info/wp-content/uploads/0/1/d/01dd9d9e75ab7ad448067f9585bb938f.jpg)








![Одночлены, многочлены [wiki.eduvdom.com]](https://rusinfo.info/wp-content/uploads/e/a/e/eaef71f96b64aeee40c5585e4c586e30.jpg)

















