Парабола

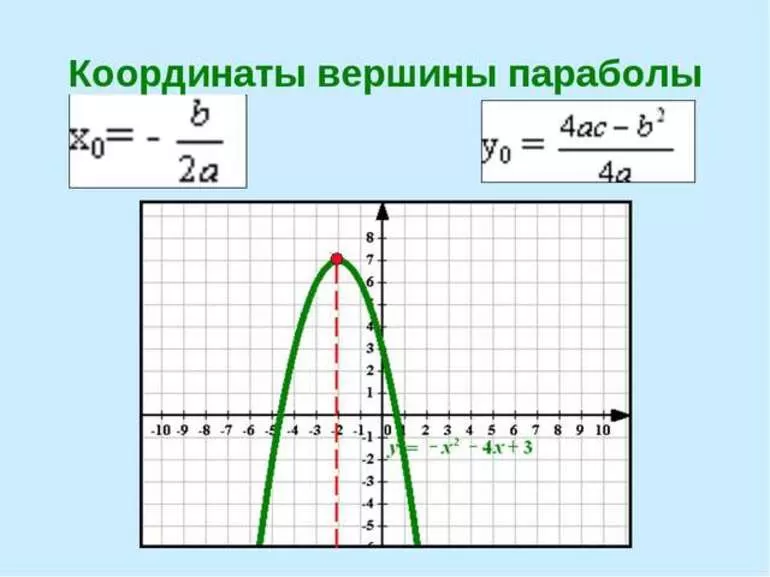
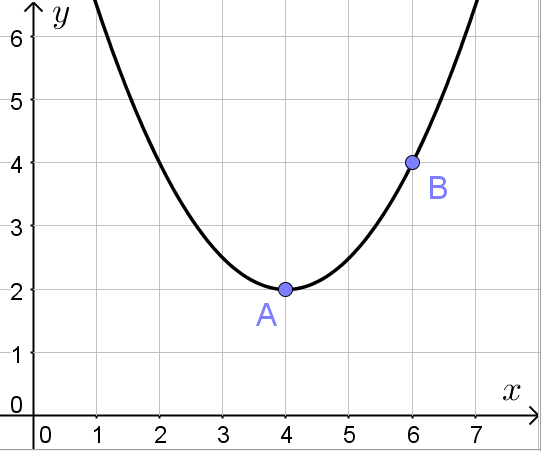
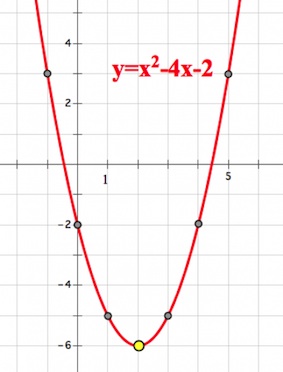
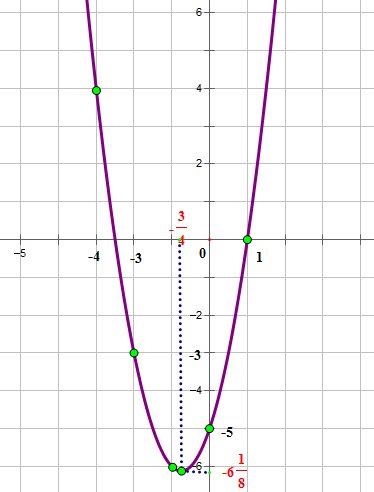
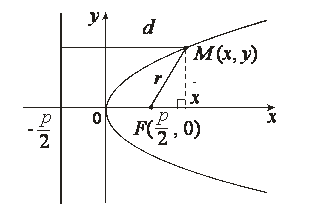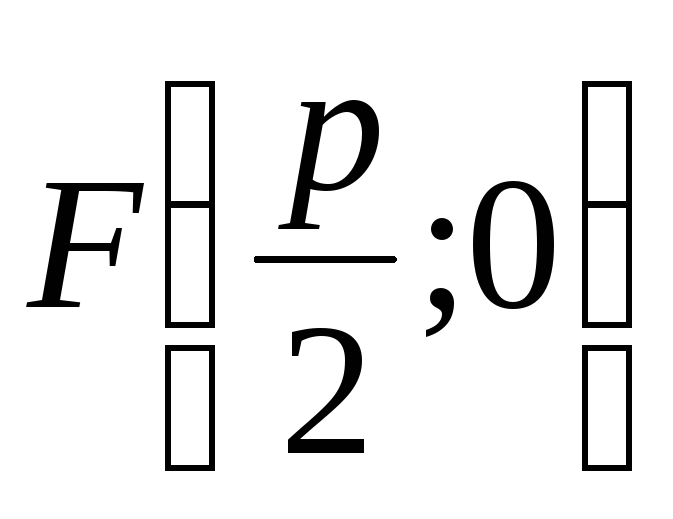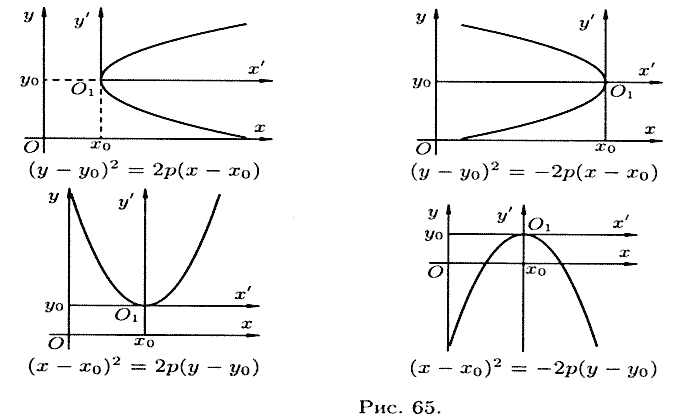Уравнение касательной к параболе.

Выведем уравнение касательной к параболе в точке \(M_{0}(x_{0}, y_{0})\), лежащей на ней. Пусть \(y_{0} \neq 0\). Через точку \(M_{0}\) проходит график функции \(y=f(x)\), целиком лежащий на параболе. (Это \(y=\sqrt{2px}\) или же \(y=-\sqrt{2px}\), смотря по знаку \(y_{0}\).) Для функции \(f(x)\) выполнено тождество \((f(x))^{2}=2px\), дифференцируя которое имеем \(2f(x)f'(x)=2p\). Подставляя \(x=x_{0}\) и \(f(x_{0})=y_{0}\), находим \(f'(x_{0})=p/y_{0}\) Теперь мы можем написать уравнение касательной к параболе
$$
y-y_{0}=\frac{p}{y_{0}}(x-x_{0}).\nonumber
$$
Упростим его. Для этого раскроем скобки и вспомним, что \(y_{0}^{2}=2px_{0}\). Теперь уравнение касательной принимает окончательный вид
$$
yy_{0}=p(x+x_{0}).\label{ref17}
$$

Заметим, что для вершины параболы, которую мы исключили, положив \(y_{0} \neq 0\), уравнение \eqref{ref17} превращается в уравнение \(x=0\), то есть в уравнение касательной в вершине. Поэтому уравнение \eqref{ref17} справедливо для любой точки на параболе.

Утверждение.

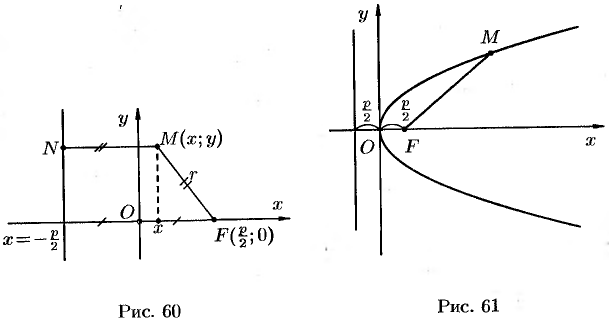
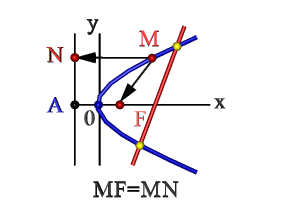
Касательная к параболе в точке \(M_{0}\) есть биссектриса угла, смежного с углом между отрезком, который соединяет \(M_{0}\) с фокусом, и лучом., выходящим из этой точки в направлении оси параболы (рис. 8.12).

Рис. 8.12. Касательная к параболе.

Рассмотрим касательную в точке \(M_{0}(x_{0}, y_{0})\). Из уравнения \eqref{ref17} получаем ее направляющий вектор \(\boldsymbol{v}(y_{0}, p)\). Значит, \((\boldsymbol{v}, \boldsymbol{e}_{1})=y_{0}\) и \(\cos \varphi_{1}=y_{0}/\boldsymbol{v}\). Вектор \(\overrightarrow{FM_{0}}\) имеет компоненты \(x_{0}=p/2\) и \(y_{0}\), а потому
$$
(\overrightarrow{FM_{0}}, \boldsymbol{v})=x_{0}y_{0}-\frac{p}{2}y_{0}+py_{0}=y_{0}(x_{0}+\frac{p}{2}).\nonumber
$$
Но \(|\overrightarrow{FM_{0}}|=x_{0}+p/2\). Следовательно, \(\cos \varphi_{2}=y_{0}/|\boldsymbol{v}|\). Утверждение доказано.

Заметим, что \(|FN|=|FM_{0}|\) (см. рис. 8.12).

Примеры решения

Пример 1

Задача

Найти координаты фокуса и составить уравнение директрисы параболы

.

Решение

Сравнивая каноническое уравнение

и данное
, получим
,
, тогда
. Так как уравнение директрисы
, тогда в данном случае
.

Ответ

координаты фокуса:

, а уравнение директрисы параболы:
.

Пример 2

Задача

Составить каноническое уравнение параболы:

а) с фокусом в точке

;

б) с фокусом в точке

.

Решение

а). Так как фокус 

на положительной полуоси
, тогда парабола симметрична относительно
с вершиной в точке
и
, поэтому
и согласно формуле (1)
.

б). Фокус 

лежит на отрицательной полуоси
с вершиной в точке
, ветви направлены вниз, каноническое уравнение следует искать в виде
. Фокусное расстояние параболы
и уравнение запишется
.

Ответ

а) каноническое уравнение параболы с фокусом в точке 

:  
;

б) каноническое уравнение с фокусом в точке 

Пример 3

Задача

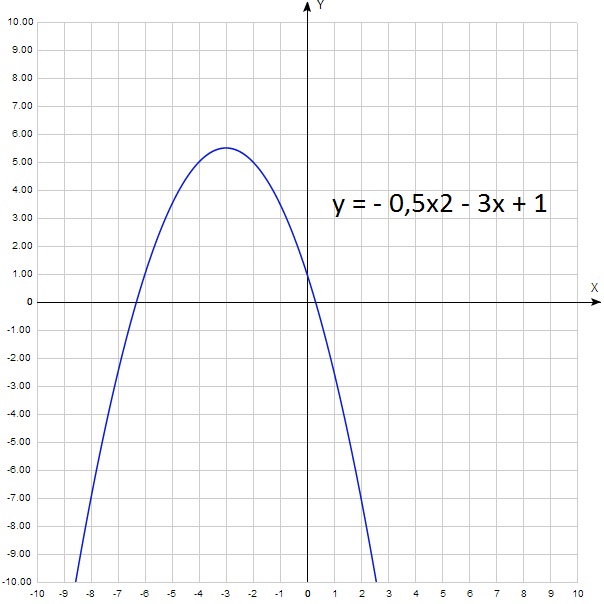
Показать путём выделения полного квадрата, что уравнение

– это уравнение параболы. Привести его к каноническому виду. Найти вершину, фокус, ось и директрису этой параболы.

Решение

Выделим относительно переменной

полный квадрат

=
=
=
=
=
=
.

Обозначим

,
.  Тогда в результате параллельного переноса координатных осей в новое начало, то есть в точку
, получим каноническое уравнение параболы
.

Ветви этой параболы направлены вниз симметрично относительно оси

,
,
– фокусное расстояние. В новой системе координат фокус находится в точке
, уравнение директрисы в новой системе
.

Повернёмся к старым координатам при помощи замены

,
. Уравнение оси в новой системе
, а в старой
– уравнение оси параболы.

Уравнение директрисы в новой системе координат

, а в старой
.

В новой системе

для фокуса
,
, а в старой системе
,
, то есть
.

Ответ

Каноническое уравнение параболы – 

;

вершина – ветви параболы направлены вниз;

,
,
– фокусное расстояние, а фокус находится в точке
;

уравнение оси

;

уравнение директрисы

.

Квадратичная функция и как построить график параболы

Квадратичная функция выглядит следующим образом:

y = ax² + bx + c, где a≠0

(a — старший коэффициент; b — второй коэффициент; с — свободный член).

1. Как определить, куда направлены ветви параболы

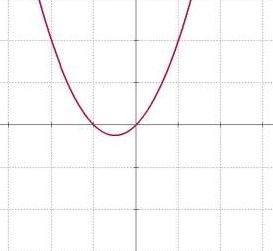
Таким образом выглядит функция y = x².

Т. е. a (старший коэффициент) в данном случае равен 1, b (второй коэффициент) и c (свободный член) оба равны 0.

Ветви параболы будут направлены вверх, когда a > 0.

Таким образом выглядит функция y = -x².

А в данном случае a = –1 (b = 0, с = 0).

Ветви параболы будут направлены вниз, когда a < 0.

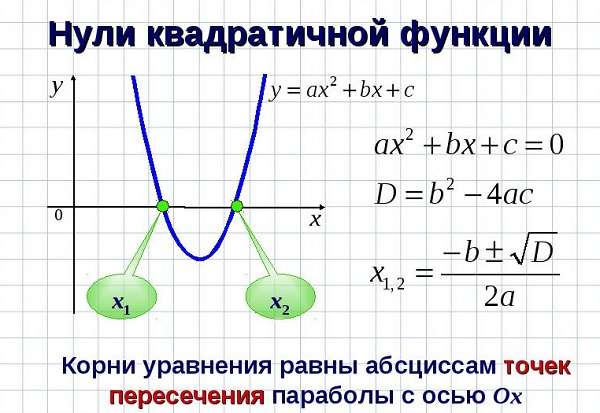
2. Как определить нули функции (значения х, где функция равна нулю)

Так как ордината (у) любой точки, лежащей на оси ОХ, равна нулю, значит нужно решить уравнение f (x) = 0. Т. е. ax² + bx + c = 0

Для этого нужно найти дискриминант по этой формуле: D = b² – 4ac, который определит количество корней квадратного уравнения.

• Если D < 0, то у квадратичной параболы нет точек пересечения с осью ОХ (она расположена выше или ниже оси ОХ и не дотрагивается до неё);
• Если D = 0, то квадратичная парабола имеет только одну точку пересечения с осью ОХ;
• Если D > 0, то у квадратичной параболы будут две точки пересечения с осью ОХ, которые можно найти по этим формулам:

Формулы для их вычисления:

4. Как посчитать точку пересечения параболы с осью OY

Точка пересечения параболы с осью OY имеет координаты (0;c). Так как абсцисса любой точки, лежащей на оси OY, равна нулю.

Чтобы найти точку пересечения параболы с осью OY, нужно всего лишь в вашу формулу вида ax² + bx + c вместо х подставить ноль.

Пример построения графика квадратичной функции

Например, нужно построить график квадратичной функции y = x² − 7x + 10.

1) Если квадратичная функция выглядит как y = ax² + bx + c, получается, в нашем случае: a = 1, b = −7, c = 10.

a = 1, а это a > 0, следовательно ветви параболы будут направлены вверх

2) Определяем нули функции, это значит ax² + bx + c = 0, в нашем случае: x² − 7x + 10 = 0

Ищем дискриминант по формуле: D = b² − 4ac, это D = (−7)² − 4*1*10 = 49 − 40 = 9

Потом вычисляем х1 и х2:

х1 = (−b + ²√D) / 2a = (7 + ²√9) / (2*1) = 5

х2 = (−b − ²√D) / 2а = (7 − ²√9) / (2*1) = 2

3) Вычисляем координаты вершины параболы:

х0 = −b / 2a = 7 / (2*1) = 3,5

y0 = −D / 4а = −9 / (4*1) = −2,25

4) Точка пересечения параболы с осью OY имеет координаты (0;c), следовательно, если c = 10, она пересекает её на (0;10).

Таким образом, получилась парабола такого вида:

Анализ уравнения и описание параболы

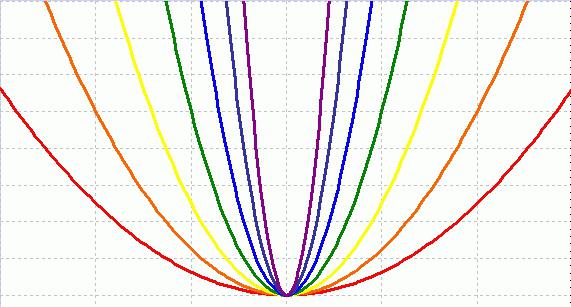
Сначала необходимо обратить внимание на коэффициент $a$ при $x^2$. Если он отрицательный, то парабола перевёрнутая по отношению к обычной и её ветви смотрят вниз, а если положительный – то её ветви смотрят вверх.
Также модуль коэффициента $a$ влияет на степень пологости (ширину) параболы, чем меньше модуль $a$, тем парабола более широкая (пологая), и чем больше модуль $a$, тем она более узкая (крутая)

Далее необходимо посмотреть на коэффициент $c$. Коэффициент $c$ обозначает смещение по оси $OY$ относительно пересечения осей координат.
Это легко проверить, если приравнять $x$ к нулю в имеющемся уравнении.
Если коэффициент $c$ — положительный, то парабола смещена вверх относительно точки $(0;0)$, а если отрицательный – то вниз.
В случае если $c=0$ — парабола проходит через точку начала координат.

Теперь можно найти вершину параболы, её координаты вычисляются по формуле:

$x = — \frac{b}{2a}$ (1).

Чтобы найти $y$, нужно подставить полученный по формуле $x$ в уравнение.

Пример 1

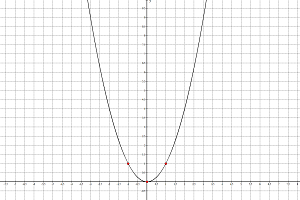
Рассмотрим уравнение параболы $y = x^2 + 2x + 3$

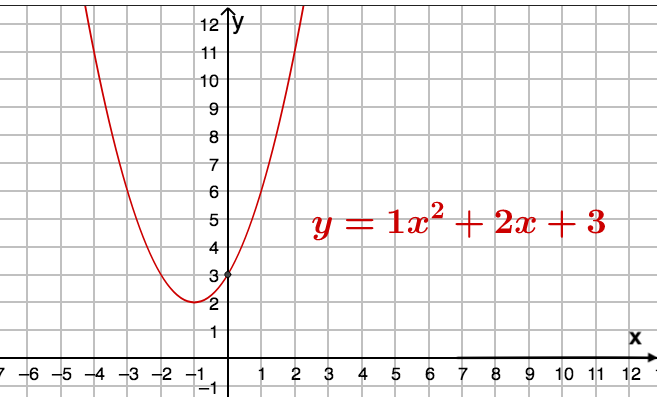Рисунок 2. Анализ уравнения параболы, график и примеры решения

1. Коэффициент при $a$ положительный, значит, ветви параболы смотрят вверх.
2. Теперь смотрим на коэффициент $c$, он равен 3, значит, парабола пересекается с осью ординат в точке $(0; 3)$.
3. Найдём координату $x$ вершины параболы по формуле (1), она равна $x = — \frac{2}{2} = -1$. Теперь найдём значение $y$, подставив значение $x$ в уравнение:
   $y = 1^2 +(-1) \cdot 2 + 3 = 2$. Координаты вершины равны $(-1; 2)$.

Основные понятия

Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.

Задать функцию означает определить правило в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

• Табличный способ. Помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
• Графический способ: наглядно.

• Аналитический способ, через формулы. Компактно и можно посчитать функцию при произвольном значении аргумента из области определения.
• Словесный способ.

График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.

Параболы в физическом пространстве

Параболический компас Леонардо да Винчи

Траектории некоторых космических тел (комет, астероидов и других), проходящих вблизи звезды или другого массивного объекта (звезды или планеты) на достаточно большой скорости, имеют форму параболы (или гиперболы). Эти тела, вследствие своей большой скорости, не захватываются гравитационным полем звезды и продолжают свободный полёт. Это явление используется для гравитационных манёвров космических кораблей (в частности, аппаратов Вояджер).

Для создания невесомости в земных условиях проводятся полёты самолётов по параболической траектории, так называемой параболе Кеплера.

При отсутствии сопротивления воздуха траектория полёта тела в приближении однородного гравитационного поля представляет собой параболу.

Также параболические зеркала используются в любительских переносных телескопах систем Кассергена, Шмидта — Кассергена, Ньютона, а в фокусе параболы устанавливают вспомогательные зеркала, подающие изображение на окуляр.

При вращении сосуда с жидкостью вокруг вертикальной оси поверхность жидкости в сосуде и вертикальная плоскость пересекаются по параболе.

Свойство параболы фокусировать пучок лучей, параллельных оси параболы, используется в конструкциях прожекторов, фонарей, фар, а также телескопов-рефлекторов (оптических, инфракрасных, радио- …), в конструкции узконаправленных (спутниковых и других) антенн, необходимых для передачи данных на большие расстояния, солнечных электростанций и в других областях.

Форма параболы иногда используется в архитектуре для строительства крыш и куполов.

Свойства квадратичной функции y = x²

График функции y = x² выглядит следующим образом:

Свойства

1) Область определения функции y = x² — множество всех действительных чисел, т. е. D(y) = R = (−∞; +∞).

2) Множество значений функции — положительная полупрямая: E(y) = [0; +∞).

3) В точке x = 0 (и y = 0) функция принимает минимальные значения (наибольшего значения у функции нет).

Эта точка (с координатами (0;0)) является вершиной параболы; одновременно точка (0;0) является единственной общей точкой параболы с осями координат (начало координат).

4) Функция у = x² чётная, график симметричен относительно оси Оу, т. е. f(−x) = (−x)² = x² = f(x).

5) Функция непрерывна на всей области определения. На (−∞; 0) функция монотонно убывает, а на (0; + ∞) функция монотонно возрастает.

6) Функция у = x² непериодическая.

7) Единственный нуль функции — значение аргумента x = 0.

8) Функция у = x² не имеет асимптот.

9) Функция принимает положительные значения на всех точках параболы, кроме начала координат, т. е. в: (−∞;0) ∪ (0;+∞).

Узнайте также, что такое Экспонента, Аксиома, Корреляция и Логарифм.

Построение квадратичной функции

Квадратичная функция задается формулой y = ax2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0. В уравнении существует следующее распределение:

a — старший коэффициент, который отвечает за ширину параболы. Большое значение a — парабола узкая, небольшое — парабола широкая. b — второй коэффициент, который отвечает за смещение параболы от центра координат. с — свободный член, который соответствует координате пересечения параболы с осью ординат.

График квадратичной функции — парабола, которая имеет следующий вид для y = x2:

Точки, обозначенные зелеными кружками называют базовыми точками. Чтобы найти их координаты для функции y = x2, нужно составить таблицу:

x	-2	-1	1	2
y	4	1	1	4

Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x2 при любых значениях остальных коэффициентов.

График функции y = –x2 выглядит, как перевернутая парабола:

Зафиксируем координаты базовых точек в таблице:

x	-2	-1	1	2
y	-4	-1	-1	-4

Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:

• Если старший коэффициент больше нуля a > 0, то ветви параболы напрaвлены вверх.
• Если старший коэффициент меньше нуля a < 0, то ветви параболы напрaвлены вниз.

Как строить график квадратичной функции — учитывать значения х, в которых функция равна нулю. Иначе это можно назвать нулями функции. На графике нули функции f(x) — это точки пересечения у = f(x) с осью ОХ.

Так как ордината (у) любой точки на оси ОХ равна нулю, поэтому для поиска координат точек пересечения графика функции у = f(x) с осью ОХ, нужно решить уравнение f(x) = 0.

Для наглядности возьмем функцию y = ax2 + bx + c, для построения которой нужно решить квадратное уравнение ax2 + bx + c = 0. В процессе найдем дискриминант D = b2 — 4ac, который даст нам информацию о количестве корней квадратного уравнения.

Рассмотрим три случая:

1.  Если D < 0, то уравнение не имеет решений и парабола не имеет точек пересечения с осью ОХ. Если a > 0,то график выглядит так:

1. Если D = 0, то уравнение имеет одно решение, а парабола пересекает ось ОХ в одной точке. Если a > 0, то график имеет такой вид:

1. Если D > 0, то уравнение имеет два решения, а парабола пересекает ось ОХ в двух точках, которые можно найти следующим образом:



Если a > 0, то график выглядит как-то так:

На основе вышеизложенного ясно, что зная направление ветвей параболы и знак дискриминанта, у нас есть понимание, как будет выглядеть график конкретной функции.

Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:

Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.

Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).

На изображении отмечены основные параметры графика квадратичной функции: