Задача на построение
Построим треугольник со сторонами 3, 5 и 4. Каждая из сторон это отрезок заданной величины. Это еще одно из свойств отрезков. По трем отрезкам заданной величины всегда можно построить треугольник.
Для начала проведем отрезок АВ=3. Можно выбрать и любую другую величину из заданных.
Конкретно в этой задаче такой подбор чисел выполнен для возможности дальнейшей проверки.
Примем точку А за центр окружности с радиусом 4 и проведем ее. Затем примем точку В за центр окружности с радиусом 5. В точке пересечения двух окружностей мы получим точку С – третью точку треугольника.
Треугольник со сторонами 3, 4 и 5 – это классический прямоугольный треугольник. Соответственно с катетами 3, 4 и гипотенузой 5. Эти пропорции были выведены еще в Древней Греции и сегодня очень часто применяются в простых задачах на решение прямоугольных треугольников.
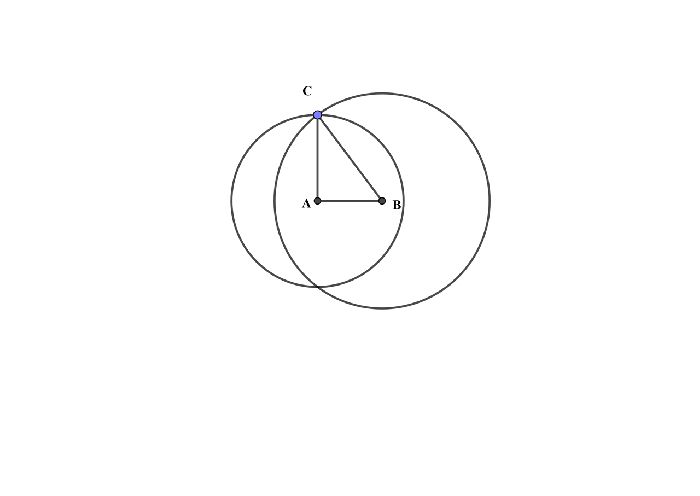
Рис. 2. Построение треугольника.
Конкретно в нашем случае это означает, что получившийся треугольник должен быть прямоугольным по теореме, обратной теореме Пифагора.
Проверим:
$$5^2=3^2+4^2$$
$$25=9+16$$
25=25 – все верно, условие выполняется. И на рисунке визуально понятно, что треугольник построен правильно. В случае построения произвольного треугольника по трем заданным отрезкам, убедитесь заранее, что выполняются условия неравенства в треугольнике: сторона всегда меньше суммы двух других сторон.
Задача с числовым лучом
Необходимо сравнить пять чисел: ${5\over6}; {7\over15}; {18\over4}; {25\over7}$
Нанесем значения на числовой луч. Каждой дроби будет соответствовать свое значение.
$${5\over6}$$ обозначим отрезком ОА. Он будет меньше единичного отрезка
$${7\over15}$$ обозначим отрезком ОВ. Он так же меньше единичного отрезка
$${18\over4}$$ обозначим отрезком ОС. Он будет больше значения 4, нанесенного на числовом луче.
$${25\over7}$$ обозначим отрезком ОD, который будет расположен между 3 и 4.
Значит, вместо сравнения 4 дробей, нам необходимо сравнить только две: ${5\over6}$ и ${7\over15}$.
Разложим 6 и 15 на простые числа и найдем НОК.
$$6=2*3$$
$$15=5*3$$
$$НОК=2*3*5=30$$
$${5\over6}={{5*5}\over{6*5}}={25\over30}$$
$${7\over15}={{7*2}\over{15*2}}={14\over30}$$
$${25\over30}>{14\over30}$$
Значит:
${5\over6}>{7\over15}$ – теперь можно обозначить точное положение этих чисел. Сравнение выполнено, задача решена.

Рис. 3. Числовой луч.
Что мы узнали?
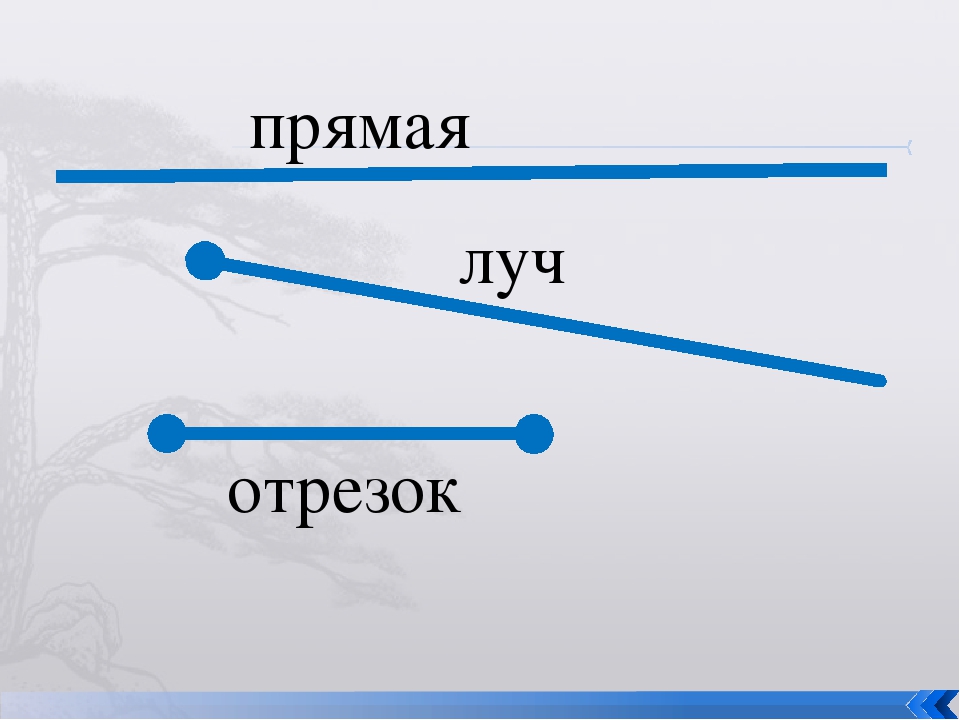
Мы разобрались, что такое отрезок в математике, выделили отличие от луча и прямой. Определили возможность применения его в геометрии для построения треугольников по значениям сторон и в математике для сравнения ряда дробей.
Определение
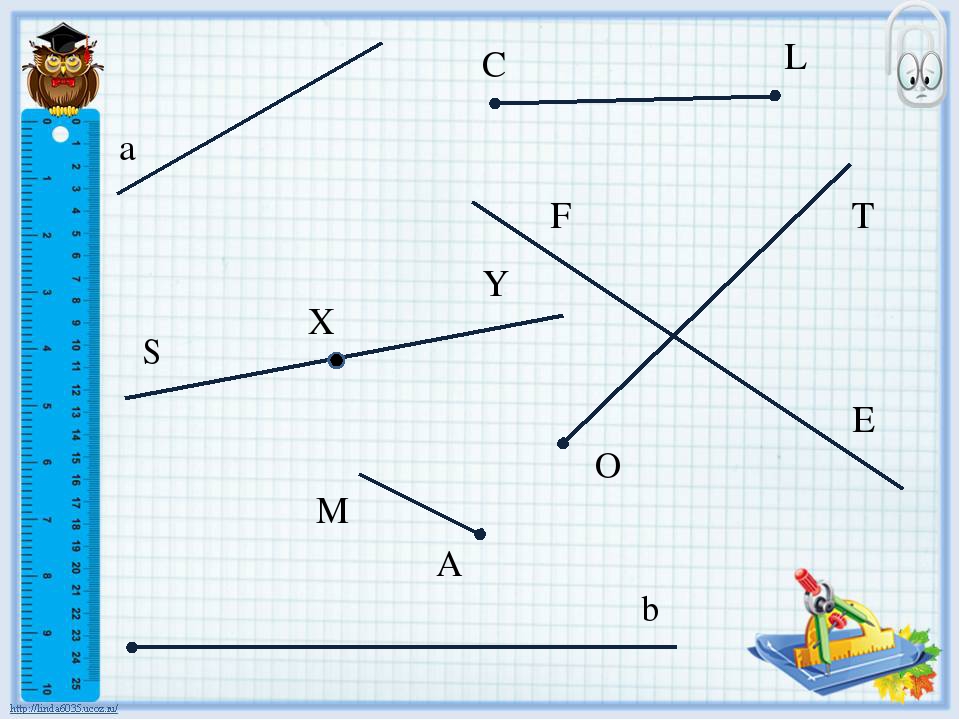
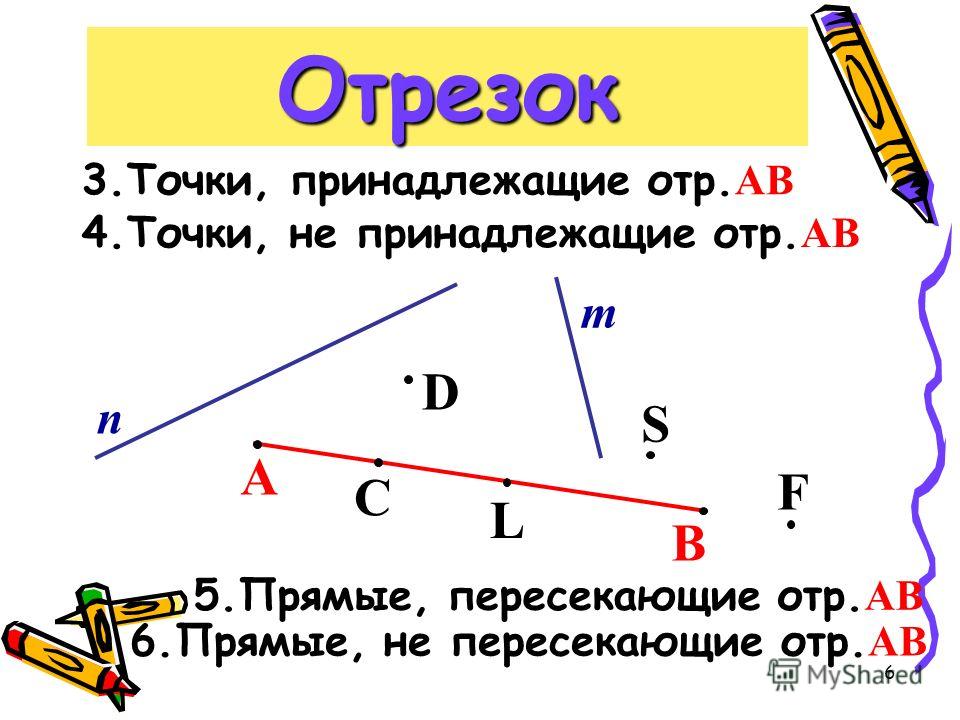
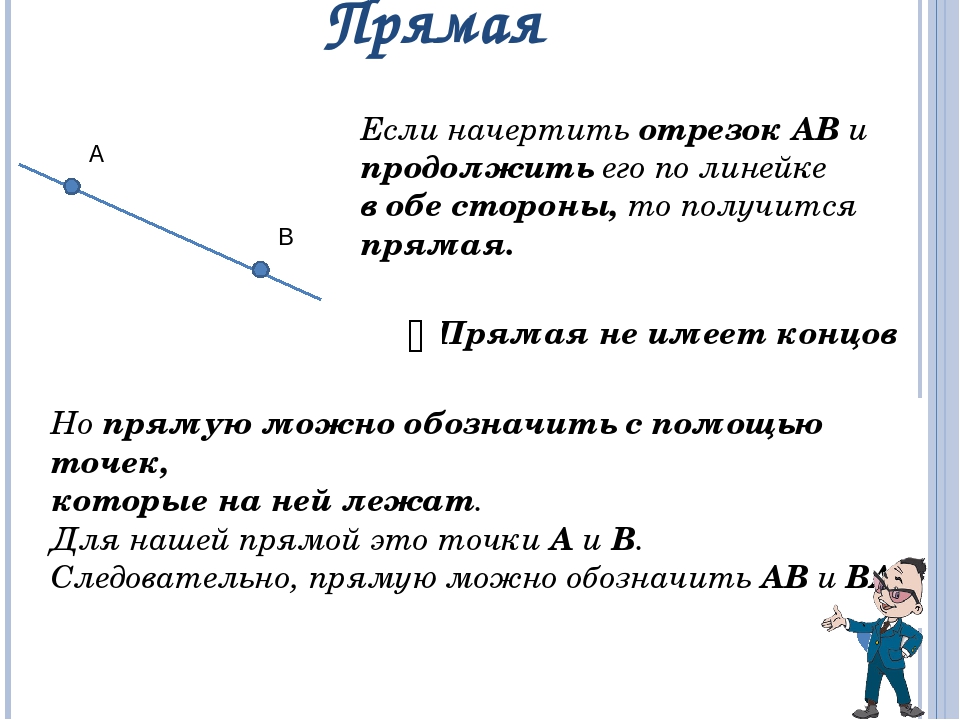
Отрезок – это часть прямой, ограниченный двумя точками. Это значит, что в отличие от прямой или луча, отрезок конечен и не имеет направления. Числовой отрезок на числовом луче или числовой прямой означает конкретное число. С помощью числовых отрезков можно выполнять сравнение чисел.

Рис. 1. Отрезок, прямая и луч.
Числовой луч обычно принимается для сравнения положительных чисел. Если среди ряда чисел, которые необходимо сравнить, есть отрицательные значения – правильнее будет воспользоваться числовой прямой.
Отрезок всегда имеет определенное значение. Прямую или луч нельзя определить конечным числом в метрах или сантиметрах, поэтому во всех современных подсчетах, как теоретических, так и практических, используются отрезки.