Введение в архитектуры нейронных сетей

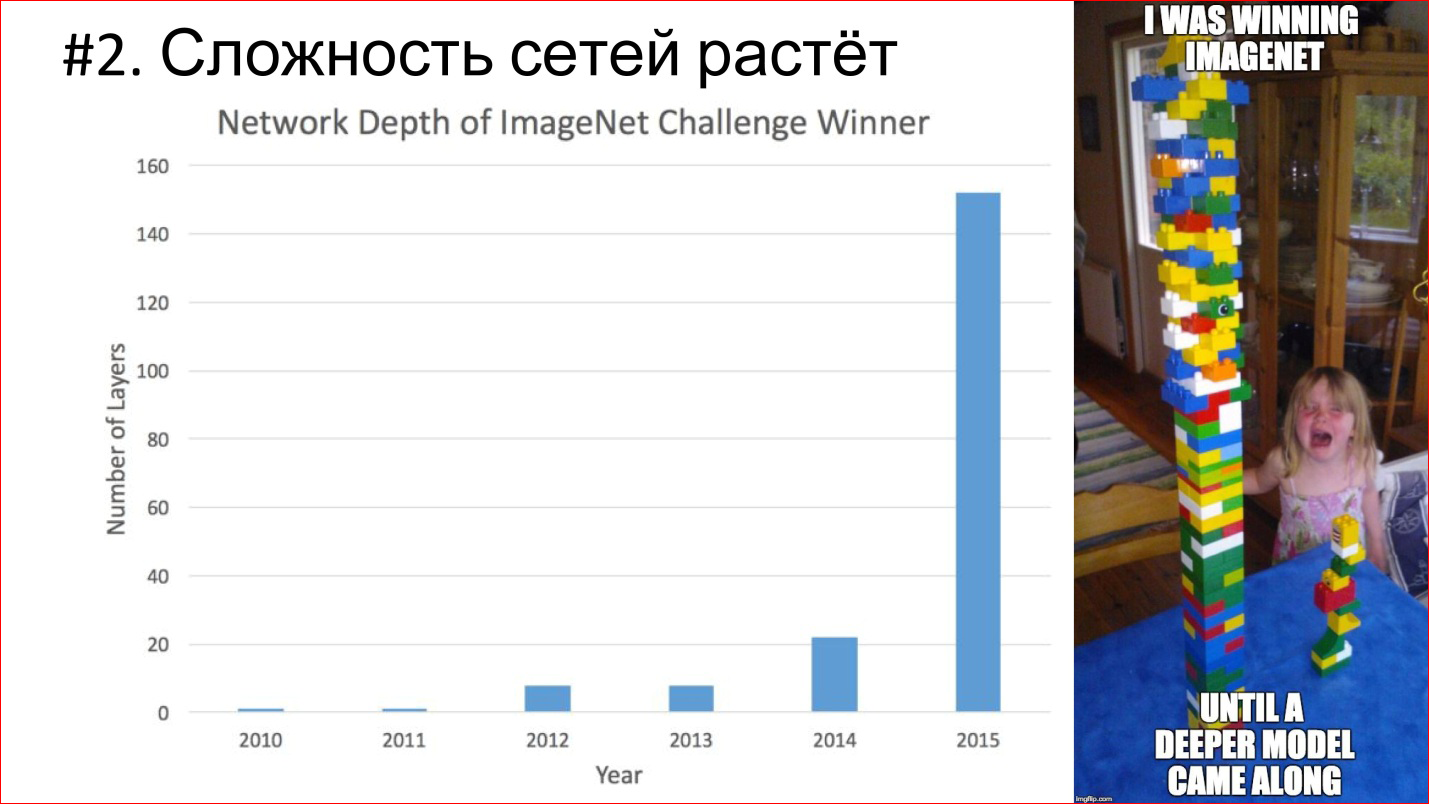
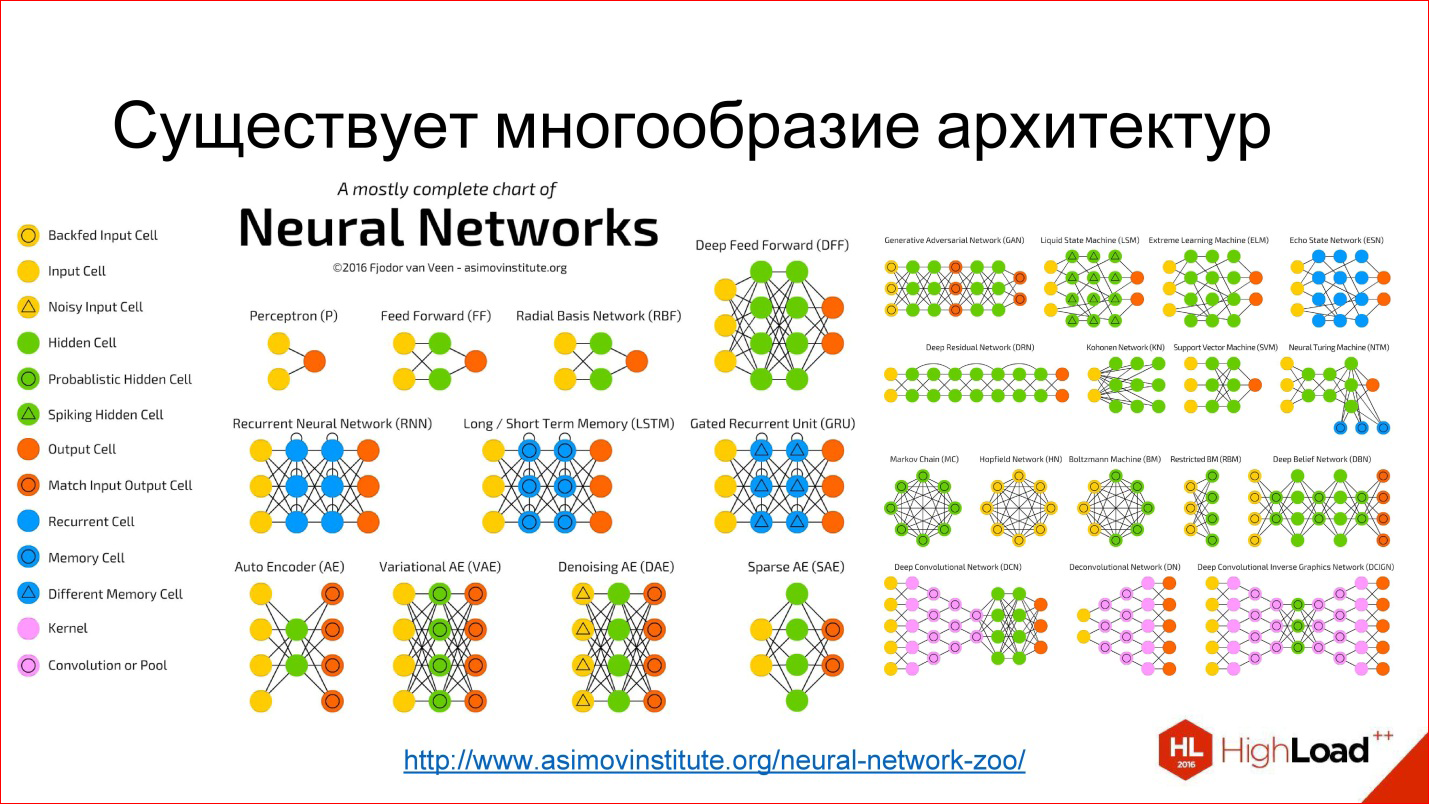
Нейронная сеть

Не бывает однозначно симпатичных и однозначно общительных дам. Да и влюблённость влюблённости рознь, кто бы что ни говорил. Потому давайте вместо брутальных и бескомпромиссных “0” и “1”, будем использовать проценты. Тогда можно сказать — “я сильно влюблён (80%), или “эта дама не особо разговорчива (20%)”.

Наш примитивный “нейрон-максималист” из первой части уже нам не подходит. Ему на смену приходит “нейрон-мудрец”, результатом работы которого будет число от 0 до 1, в зависимости от входных данных.

“Нейрон-мудрец” может нам сказать: “эта дама достаточно красива, но я не знаю о чём с ней говорить, поэтому я не очень-то ей и восхищён”

Поехали дальше. Сделаем по этим двум фактам другую оценку: насколько хорошо с такой девушкой работать (сотрудничать)? Будем действовать абсолютно аналогичным образом — добавим мудрый нейрон и настроим веса комфортным для нас образом.

Но, судить девушку по двум характеристикам — это очень грубо. Давайте судить её по трём! Добавим ещё один факт – деньги. Который будет варьироваться от нуля (абсолютно бедная) до единицы (дочь Рокфеллера). Посмотрим, как с приходом денег изменятся наши суждения….

Для себя я решил, что, в плане очарования, деньги не очень важны, но шикарный вид всё же может на меня повлиять, потому вес денег я сделаю маленьким, но положительным.

В работе мне абсолютно всё равно, сколько денег у девушки, поэтому вес сделаю равным нулю.

Оценивать девушку только для работы и влюблённости — очень глупо. Давайте добавим, насколько с ней будет приятно путешествовать:

• Харизма в этой задаче нейтральна (нулевой или малый вес).
• Разговорчивость нам поможет (положительный вес).
• Когда в настоящих путешествиях заканчиваются деньги, начинается самый драйв, поэтому вес денег я сделаю слегка отрицательным.

Соединим все эти три схемы в одну и обнаружим, что мы перешли на более глубокий уровень суждений, а именно: от харизмы, денег и разговорчивости — к восхищению, сотрудничеству и комфортности совместного путешествия. И заметьте — это тоже сигналы от нуля до единицы. А значит, теперь я могу добавить финальный “нейрон-максималист”, и пускай он однозначно ответит на вопрос — “жениться или нет”?

Ладно, конечно же, не всё так просто (в плане женщин). Привнесём немного драматизма и реальности в наш простой и радужный мир. Во-первых, сделаем нейрон «женюсь — не женюсь» — мудрым. Сомнения же присущи всем, так или иначе. И ещё — добавим нейрон «хочу от неё детей» и, чтобы совсем по правде, нейрон “держись от неё подальше».

Я ничего не понимаю в женщинах, и поэтому моя примитивная сеть теперь выглядит как картинка в начале статьи.

Входные суждения называются “входной слой”, итоговые — “выходной слой”, а тот, что скрывается посередине, называется «скрытым». Скрытый слой — это мои суждения, полуфабрикаты, мысли, о которых никто не знает. Скрытых слоёв может быть несколько, а может быть и ни одного.

Softmax (функция мягкого максимума)

L_jL_j

L₁L₂L₃L₄оригинале статьиL₄L₄L₄L₄L₄L₄

L₄L_jL_j

Упражнения

• Монотонность Softmax. Покажите, что ∂aL_j / ∂zL_k положительна, если j=k, и отрицательна, если j≠k. Как следствие, увеличение zL_j гарантированно увеличивает соответствующую выходную активацию aL_j, и уменьшает все остальные выходные активации. Мы уже видели это эмпирически на примере ползунков, однако данное доказательство будет строгим.
• Нелокальность Softmax. Приятной особенностью сигмоидных слоёв является то, что выход aL_j — функция соответствующего взвешенного входа, aL_j = σ(zL_j). Поясните, почему с Softmax-слоем это не так: любая выходная активация aL_j зависит от всех взвешенных входов.

Функция потери (loss function)

Функция потерь находится в центре нейронной сети. Она используется для расчета ошибки между  реальными и полученными ответами. Наша глобальная цель — минимизировать эту ошибку. Таким образом, функция потерь эффективно приближает обучение нейронной сети к этой цели.

Функция потерь измеряет «насколько хороша» нейронная сеть в отношении данной обучающей выборки и ожидаемых ответов. Она также может зависеть от таких переменных, как веса и смещения.

Функция потерь одномерна и не является вектором, поскольку она оценивает, насколько хорошо нейронная сеть работает в целом.

Некоторые известные функции потерь:

• Квадратичная (среднеквадратичное отклонение);
• Кросс-энтропия;
• Экспоненциальная (AdaBoost);
• Расстояние Кульбака — Лейблера или прирост информации.

Cреднеквадратичное отклонение – самая простая фукция потерь и наиболее часто используемая. Она задается следующим образом:

Функция потерь в нейронной сети должна удовлетворять двум условиям:

• Функция потерь должна быть записана как среднее;
• Функция потерь не должна зависеть от каких-либо активационных значений нейронной сети, кроме значений, выдаваемых на выходе.

Долой максимализм.

Помните, я говорил об отрицательном влияние денег на моё желание путешествовать с человеком? Так вот — я слукавил. Для путешествий лучше всего подходит персона, у которой денег не мало, и не много. Мне так интереснее и не буду объяснять почему.

Но тут я сталкиваюсь с проблемой:

Если я ставлю вес денег отрицательным, то чем меньше денег — тем лучше для путешествий.
Если положительным, то чем богаче — тем лучше,
Если ноль — тогда деньги “побоку”.

Не получается мне вот так, одним весом, заставить нейрон распознать ситуацию “ни много -ни мало”!

Чтобы это обойти, я сделаю два нейрона — “денег много” и “денег мало”, и подам им на вход денежный поток от нашей дамы.

Теперь у меня есть два суждения: “много” и “мало”. Если оба вывода незначительны, то буквально получится “ни много — ни мало”. То есть, добавим на выход ещё один нейрон, с отрицательными весами:

“Нимногонимало”. Красные стрелки — положительные связи, синие — отрицательные

Вообще, это значит, что нейроны подобны элементам конструктора. Подобно тому, как процессор делают из транзисторов, мы можем собрать из нейронов мозг. Например, суждение “Или богата, или умна” можно сделать так:

Или-или. Красные стрелки — положительные связи, синие – отрицательные

Или так:

можно заменить “мудрые” нейроны на “максималистов” и тогда получим логический оператор XOR. Главное — не забыть настроить пороги возбуждения.

В отличие от транзисторов и бескомпромиссной логики типичного программиста “если — то”, нейронная сеть умеет принимать взвешенные решения. Их результаты будут плавно меняться, при плавном изменение входных параметров. Вот она мудрость!

Обращу ваше внимание, что добавление слоя из двух нейронов, позволило нейрону “ни много — ни мало” делать более сложное и взвешенное суждение, перейти на новый уровень логики. От “много” или “мало” — к компромиссному решению, к более глубокому, с философской точки зрения, суждению

А что если добавить скрытых слоёв ещё? Мы способны охватить разумом ту простую сеть, но как насчёт сети, у которой есть 7 слоёв? Способны ли мы осознать глубину её суждений? А если в каждом из них, включая входной, около тысячи нейронов? Как вы думаете, на что она способна?

Представьте, что я и дальше усложнял свой пример с женитьбой и влюблённостью, и пришёл к такой сети. Где-то там в ней скрыты все наши девять нейрончиков, и это уже больше похоже на правду. При всём желании, понять все зависимости и глубину суждений такой сети — попросту невозможно. Для меня переход от сети 3х3 к 7х1000 — сравним с осознанием масштабов, если не вселенной, то галактики — относительно моего роста. Попросту говоря, у меня это не получится. Решение такой сети, загоревшийся выход одного из её нейронов — будет необъясним логикой. Это то, что в быту мы можем назвать “интуицией” (по крайней мере – “одно из..”). Непонятное желание системы или её подсказка.

Но, в отличие от нашего синтетического примера 3х3, где каждый нейрон скрытого слоя достаточно чётко формализован, в настоящей сети это не обязательно так. В хорошо настроенной сети, чей размер не избыточен для решения поставленной задачи — каждый нейрон будет детектировать какой-то признак, но это абсолютно не значит, что в нашем языке найдётся слово или предложение, которое сможет его описать. Если проецировать на человека, то это — какая-то его характеристика, которую ты чувствуешь, но словами объяснить не можешь.

Многослойный перцептрон с сигмоидной функцией активации (итерация модели 2)

слойдругого

Пример 1: распознавание паттерна лестницы

1. Построим модель, которая срабатывает при распознавании «левых лестниц», $inline$\widehat y_{left}$inline$
2. Построим модель, которая срабатывает при распознавании «правых лестниц», $inline$\widehat y_{right}$inline$
3. Добавим базовым моделям оценку, чтобы конечная сигмоида срабатывала только если оба значения ($inline$\widehat y_{left}$inline$, $inline$\widehat y_{right}$inline$) велики

Другой вариант

1. Построим модель, срабатывающую, когда нижний ряд тёмный, $inline$\widehat y_1$inline$
2. Построим модель, срабатывающую, когда верхний левый пиксель тёмный и верхний правый пиксель светлый, $inline$\widehat y_2$inline$
3. Построим модель, срабатывающую, когда верхний левый пиксель светлый и верхний правый пиксель тёмный, $inline$\widehat y_3$inline$
4. Добавим базовые модели так, что конечная сигмоидная функция срабатывала только когда $inline$\widehat y_1$inline$и $inline$\widehat y_2$inline$ велики, или когда $inline$\widehat y_1$inline$и $inline$\widehat y_3$inline$ велики. (Заметьте, что $inline$\widehat y_2$inline$ и $inline$\widehat y_3$inline$ не могут быть большими одновременно.)

Пример 2: распознать лестницы светлого оттенка

1. Построим модели, срабатывающие при «затенённом нижнем ряде», «затенённом x1 и белом x2», «затенённом x2 и белом x1», $inline$\widehat y_1$inline$, $inline$\widehat y_2$inline$ и $inline$\widehat y_3$inline$
2. Построим модели, срабатывающие при «тёмном нижнем ряде», «тёмном x1 и белом x2», «тёмном x2 и белом x», $inline$\widehat y_4$inline$, $inline$\widehat y_5$inline$ и $inline$\widehat y_6$inline$
3. Соединим модели таким образом, чтобы «тёмные» идентификаторы вычитались из «затенённых» идентификаторов перед сжиманием результата сигмоидой

Одноодин выходной слойдвутри

Чему мы можем поучиться друг у друга?

Теперь, после того, как мы установили связь между трансформерами и графовыми нейронными сетями, давайте обсудим несколько идей.

Как работать с дистантными зависимостями (long-term dependencies)?

С представлением в виде полных графов есть ещё одна проблема: так сложно работать с сильно удалёнными друг от друга связями между словами. Дело в том, что количество рёбер в полных графах квадратично зависит от числа вершин, и с ростом числа последних увеличивается очень быстро, то есть в предложении с словами трансформер или GNN будут совершать вычисления для пар слов. Всё летит в просто выходит из-под контроля для очень больших значений .

И, вероятно, разные головы в многоголовом внимании смотрят на разные «синтаксические свойства».

Почему голов внимания несколько? Зачем вообще нужно внимание?

Вопреки ожиданиям, GNN с куда более простыми функциями агрегации (например, сумма или максимум) не нуждаются в нескольких головах для стабильного обучения. Вот бы трансформерам не нужно было вычислять «величины совместимости» для каждой пары слов в предложении!

Почему так трудно обучать трансформеры?

Читая свежие статьи о трансформерах, не могу отделаться от ощущения, что обучение этих моделей требует навыков, близких к чёрной магии, когда дело доходит до определения лучшего расписания скорости обучения (learning rate schedule), способа «разогрева» (warmup strategy) и настроек затухания (decay settings). Возможно, это от того, что модели — гигантские, а рассматриваемые задачи — не из числа простых.

В твите я, конечно, просто ворчу, но вот что вызывает мой скепсис: неужели нам и правда так нужны все эти головы вычислительно дорогого попарного внимания, наделённые чрезмерно большим числом параметров «перцептронные подслои» и хитроумные расписания обучения?

Однослойный перцептрон (итерация модели 0)

перцептрона

$$display$$f(x)={\begin{cases} 1 &{\text{if }}\ w_1x_1 + w_2x_2 + w_3x_3 + w_4x_4 > threshold\\ 0 & {\text{otherwise}} \end{cases}}$$display$$

$$display$$\widehat y = \mathbf w \cdot \mathbf x + b$$display$$

$$display$$f(x)={\begin{cases} 1 &{\text{if }}\ \widehat{y} > 0\\ 0 & {\text{otherwise}} \end{cases}}$$display$$

$inline$\hat{y}$inline$оценка прогноза

$$display$$\hat{y}=-0.0019x_{1}+0.0016x_{2}+0.0020x_{3}+0.0023x_{4}+0.0003$$display$$

$inline$x_{3}$inline$$inline$x_{4}$inline$

1. Модель выдаёт на выходе действительное число, значение которого коррелирует с концепцией похожести (чем больше значение, тем выше вероятность того, что на изображении есть лестница), но нет никакой основы для интерпретации этих значений как вероятностей, потому что они могут находиться вне интервала .
2. Модель не может ухватить нелинейные взаимосвязи между переменными и целевым значением. Чтобы убедиться в этом, рассмотрим следующие гипотетические сценарии:

Случай B

$inline$x_{3}$inline$
случай A$inline$\hat{y}$inline$случай B$inline$x_{3}$inline$$inline$\hat{y}$inline$

Что такое ИНС?

Давайте начнем с Вашего представления о ИНС. Исходя из общепринятых знаний, многие думают что ИНС представляют собой копию человеческой НС в коре головного мозга. Некий набор алгоритмов и накопленных знаний, благодаря которым сеть принимает дальнейшие решения. Это суждение верно, но не стоит переоценивать ее возможности. Если наша ИНС умеет варить Вам кофе с утра, то вряд ли она сможет приготовить Вам завтрак, если Вы сами ее этому не научите. Из этого можно сделать вывод, что ИНС выполняет лишь те функции, которым она обучена. Самообучающиеся нейронные сети это не миф, но пока еще не удалось разработать стабильную сеть, которая самостоятельно генерировала бы алгоритмы для решения различных задач.

Для понимания устройства нейронной сети давайте немного окунемся в биологию и устройство человеческого мозга и проведем некоторые параллели с устройством ИНС. Это не так сложно, как может показаться! 

Давайте более подробно разберем это определение. Из него следует что нейронная сеть представляет собой некоторое количество нейронов, связанных между собой. Сколько нейронов в мозге человека? По подсчетам многих ученых, мозг человека состоит из порядка 100 миллиардов нейронов (плюс-минус пара миллиардов). Именно эта цифра долгие годы приводилась в учебниках по нейробиологии и психологии. Каждый из нейронов является вычислительной единицей, которая обрабатывает входящую информацию и передает ее дальше. Для получения информации у нейрона есть входные каналы, которые называются синапсы. Синапсы это каналы, по которым в нейрон поступает информация из других нейронов. На рисунке синапсы обозначены буквой W, а другие нейроны буквой X. Каждый синапс обладает весом, чем больше вес синапса, тем больше результат работы нейрона будет преобладать в дальнейших вычислениях. Рассмотрим работу синапсов на примере изображения:

Разноцветные круги слева — нейроны. Линиями изображены синапсы. Как видно, каждый синапс обладает весом. Этот вес проставляется случайным образом в диапазоне от 0 до 1. На изображении справа изображена работа сумматора. Сумматор — это функция, которая рассчитывает вес входных сигналов и передает их дальше в функцию активации, об этом чуть позже. Давайте попробуем рассчитать вес входных сигналов, если результаты работы нейронов были следующие:

• 1 — 0.35
• 2 — 0.12
• 3 — 0.6

Важно понимать что ИНС оперирует данными в диапазоне от 0 до 1. Вычисление веса в сумматоре производится пос следующей формуле:. Функция совершенно линейна, из этого мы получаем следующую формулу:

Функция совершенно линейна, из этого мы получаем следующую формулу:

Таким образом мы получили некую единицу, вес который будет передан в функцию активации. 

Функций активации достаточно много поэтому мы рассмотрим самые основные: Линейная, Сигмоид (Логистическая) и Гиперболический тангенс. Главные их отличия — это диапазон значений.

Линейная функция

Эта функция почти никогда не используется, за исключением случаев, когда нужно протестировать нейронную сеть или передать значение без преобразований.Сигмоид

Это самая распространенная функция активации, ее диапазон значений . Именно на ней показано большинство примеров в сети, также ее иногда называют логистической функцией. Соответственно, если в вашем случае присутствуют отрицательные значения (например, акции могут идти не только вверх, но и вниз), то вам понадобиться функция которая захватывает и отрицательные значения.Гиперболический тангенс

Имеет смысл использовать гиперболический тангенс, только тогда, когда ваши значения могут быть и отрицательными, и положительными, так как диапазон функции . Использовать эту функцию только с положительными значениями нецелесообразно так как это значительно ухудшит результаты вашей нейросети.

Подведем итоги. Что мы узнали про ИНС?

У нейрона есть входы. На них подаются сигналы в виде чисел. Каждый вход имеет свой вес (тоже число). Сигналы на входе умножаются на соответствующие веса. Получаем набор «взвешенных» входных сигналов.

Далее этот набор попадает в сумматор, которой просто складывает все входные сигналы, помноженные на веса. Получившееся число называют взвешенной суммой.

Затем взвешенная сумма преобразуется функцией активации и мы получаем выход нейрона.

SpineNet

SpineNet применяется для обнаружения объектов на изображении. Исследователи из Google Research достигли хороших результатов, которые превышают имеющиеся state-of-the-art (SOTA) подходы.

Предложенная модель SpineNet позволяет выучивать разномасштабные признаки из-за сверточных слоев смешанных размеров (смотрите рисунок ниже). Размеры слоев подбирались с помощью нейронного поиска архитектур (Neural Architecture Search, NAS). Использование SpineNet в качестве базовой модели дает прирост в точности (Average Precision, AP). При этом на обучение модели требуется меньше вычислительных ресурсов.

Рисунок – Построение моделей со смешанным масштабом с помощью перестановок слоев архитектуры ResNet (ResNet-50-FPN крайняя слева)

Оценка качества модели

• TP (True Positive) — истиноположительный. Классификатор решил, что клиент купит, и он купил.
• FP (False Positive) — ложноположительный. Классификатор решил, что клиент купит, но он не купил. Это так называемая ошибка первого рода. Она не так страшна, как ошибка второго рода, особенно в тех случаях, когда классификатор — тест на какое-нибудь заболевание.
• FN (False Negative) — ложноотрицательный. Классификатор решил, что клиент не купит, а он мог купить (или уже купил). Это так называемая ошибка второго рода. Обычно при создании модели желательно минимизировать ошибку второго, даже увеличив тем самым ошибку первого рода.
• TN (True Negative) — истиноотрицательный. Классификатор решил, что клиент не купит, и он не купил.

Рис. 13 — Сравнение результатов классификации разных моделей

Косвенное кодирование

О’Нил и Брабазон

<g> ::=
"<bitstring> ::=" <reps>
"<bbk4> ::=" <bbk4t>
"<bbk2> ::=" <bbk2t>

"<bbk1> ::=" <bbk1t>
"<bit> ::=" <val>
<bbk4t> ::= <bit><bit><bit><bit>

<bbk2t> ::= <bit><bit>
<bbk1t> ::= <bit>
<reps> ::= <rept>
| <rept> "|" <reps>

<rept> ::= "<bbk4><bbk4>"
| "<bbk2><bbk2><bbk2><bbk2>"
| "<bbk1><bbk1><bbk1><bbk1><bbk1><bbk1><bbk1><bbk1>"

<bit> ::= "<bit>"
| 1
| 0
<val> ::= <valt>
| <valt> "|" <val>

<valt> ::= 1 | 0

<bitstring> ::= <bit>11<bit>00<bit><bit>

| <bbk2><bbk2><bbk2><bbk2>
| 11011101
| <bbk4><bbk4>
| <bbk4><bbk4>
<bbk4> ::= <bit>11<bit>

<bbk2> ::= 11
<bbk1> ::= 1
<bit> ::= 1 | 0 | 0 | 1

Прочие методики

• Боерс и Куйпер (Boers and Kuiper) — использование контексто-зависимых L-систем
• Дилаерт и Бир (Dellaert and Beer) — подход, аналогичный Кангелосси и Элману, но с использованием случайных булевых нейросетей (random boolean networks)
• Харп, Самад и Гуха (Harp, Samad, and Guha) — позонное прямое кодирование структуры
• Груау (Gruau) — использование грамматического дерева для задания инструкций при делении клеток (чем-то похоже на Кангелосси, Париси и Нолфи)
• Ваарио (Vaario) — рост клеток задается L-системами

CenterNet

CenterNet моделирует объект, как одну точку, которая находится в центре ограничительной рамки. Размер объекта, его ориентация, 3D-форма, направление, поза и т.д. извлекаются в последствии через характеристики изображения (image features) около полученной точки. Авторы подают входное изображение в полносвязную сверточную сеть, которая генерирует тепловую карту (heatmap). Пики на этой тепловой карте соответствуют центрам объектов. Характеристики изображения в каждом пике тепловой карты предсказывают размеры ограничительной рамки вокруг объекта. С помощью CenterNet авторы статьи экспериментируют с определением 3D размеров объектов и оценкой позы человека по двумерному изображению.

Рисунок – Диаграмма CenterNet

CornerNet является предшественником CenterNet. CornerNet обнаруживает объект, как пару точек: верхний левый и правый нижний углы ограничительной рамки (bounding box). Таким образом распознавание по набору фиксированных рамкок (anchor box), как у нейросетей SSD и YOLO, заменяется на определение пары точек верхнего левого и правого нижнего углов ограничительной рамки вокруг объекта. Также авторы предлагают архитектуру на основе последовательности нескольких нейросетей типа «песочные часы», которые до этого не использовались для определения объектов.

В CornerNet применяется механизм «corner pooling» для определения углов ограничительной рамки вокруг объектов. В CenterNet добавляется механизм «center pooling» для определения центра рамки.

Рисунок – Механизм «corner pooling» для верхнего левого угла. Сканирование проходит справа налево для горизонтального «max-pooling» и снизу вверх для вертикального «max-pooling». Затем две карты характеристик (feature maps) слаживаются.

Топология сверточной нейросети

• определить решаемую задачу нейросетью (классификация, прогнозирование, модификация);
• определить ограничения в решаемой задаче (скорость, точность ответа);
• определить входные (тип: изображение, звук, размер: 100×100, 30×30, формат: RGB, в градациях серого) и выходных данные (количество классов).

Рисунок 2 — Топология сверточной нейросети

Сверточный слой

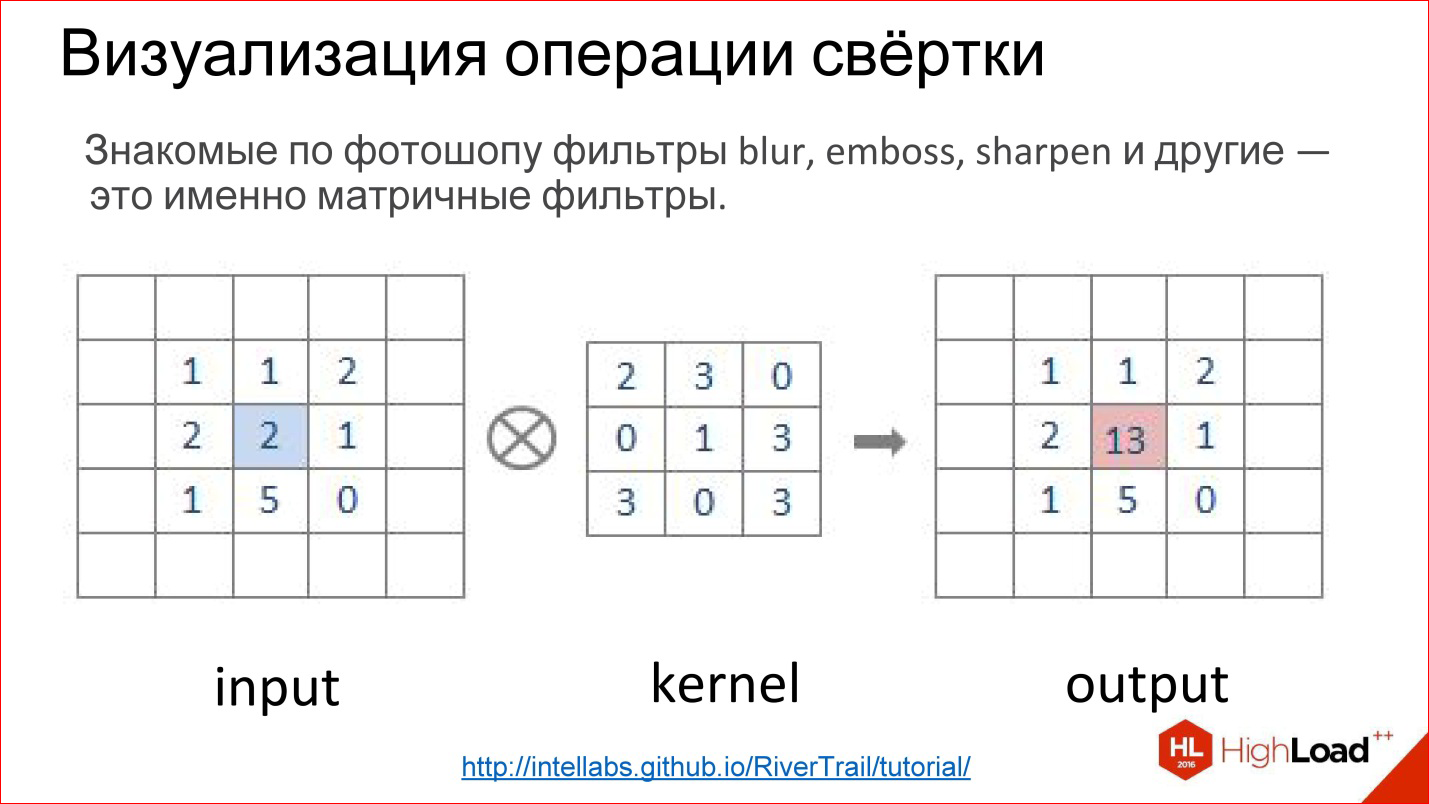
Рисунок 3 — Организация связей между картами сверточного слоя и предыдущегоРисунок 4 — Операция свертки и получение значений сверточной карты (valid)Операция свертки и получение значений сверточной карты. Ядро смещено, новая карта получается того же размера, что и предыдущая (same)Рисунок 5 — Три вида свертки исходной матрицы

Подвыборочный слой

Рисунок 6 — Формирование новой карты подвыборочного слоя на основе предыдущей карты сверточного слоя. Операция подвыборки (Max Pooling)

Выбор функции активации

• непрерывной;
• монотонно возрастающей;
• дифференцируемой.

Функция активации гиперболический тангенс

• симметричные активационные функции, типа гиперболического тангенса обеспечивают более быструю сходимость, чем стандартная логистическая функция;
• функция имеет непрерывную первую производную;
• функция имеет простую производную, которая может быть вычислена через ее значение, что дает экономию вычислений.

Функция активации ReLU

• ее производная равна либо единице, либо нулю, и поэтому не может произойти разрастания или затухания градиентов, т.к. умножив единицу на дельту ошибки мы получим дельту ошибки, если же мы бы использовали другую функцию, например, гиперболический тангенс, то дельта ошибки могла, либо уменьшиться, либо возрасти, либо остаться такой же, то есть, производная гиперболического тангенса возвращает число с разным знаком и величиной, что можно сильно повлиять на затухание или разрастание градиента. Более того, использование данной функции приводит к прореживанию весов;
• вычисление сигмоиды и гиперболического тангенса требует выполнения ресурсоемких операций, таких как возведение в степень, в то время как ReLU может быть реализован с помощью простого порогового преобразования матрицы активаций в нуле;
• отсекает ненужные детали в канале при отрицательном выходе.

Финансы

34 сотрудников японской компании заменит система IBM Watson Explorer AI.помогает распознавать потенциальные случаи мошенничества в различных сферах жизни.

Коммерция

существенно улучшил механизмы рекомендаций в онлайн-магазинах и сервисах.Механизм рекомендаций обеспечивает Amazon 35% продаж. Алгоритм Brain, используемый YouTube для рекомендации контента, позволил добиться того, что практически 70% видео, просматриваемых на сайте, люди нашли благодаря рекомендациям (а не по ссылкам или подпискам). WSJ сообщало о том, что использование искусственного интеллекта для рекомендаций является одним из факторов, повлиявших на 10-кратный рост аудитории за последние пять лет.способен предсказывать влияние промоакциймогут использоваться для создания чат-ботовмаркетинговая платформа полного цикла, самостоятельно осуществляющая практически все операции.

Развлечения и искусство

обработки фото и видеораскрашиваетнейронные сети компании уже записали два альбома:Nirvana“Гражданской обороны”написаннаявдохновляласьЯпонский алгоритм написал книгуГарри ПоттеруИгре Престоловгопрограмма обыграла сильнейшего игрока в го в мире

Безопасность

поиск акул в прибрежных водах и предупреждение людей на пляжахАвстралия занимает второе место в мире после США по количеству случаев нападения акул на людей. В 2016 году в этой стране были зафиксированы 26 случаев нападения акул, два из которых закончились смертью людей.определять зараженные файлыНейросети также способны искать определенные закономерности в том, как хранится информация в облачных сервисах, и сообщать об обнаруженных аномалиях, способных привести к бреши в безопасности.

Препроцессинг

1. Создание векторного пространства признаков, где будут жить примеры обучающей выборки. По сути, это процесс приведения всех данных в числовую форму. Это избавляет нас от категорийных, булевых и прочих не числовых типов.
2. Нормализация данных. Процесс, при котором мы добиваемся, например того, чтобы среднее значение каждого признака по всем данным было нулевым, а дисперсия — единичной. Вот самый классический пример нормализации данных: X = (X — μ)/σ
3. Изменение размерности векторного пространства. Если векторное пространство признаков слишком велико (миллионы признаков) или мало (менее десятка), то можно применить методы повышения или понижения размерности пространства:
   • Для повышения размерности можно использовать часть обучающей выборки как опорные точки, добавив в вектор признаков расстояние до этих точек. Этот метод часто приводит к тому, что в пространствах более высокой размерности множества становятся линейно разделимыми, и это упрощает задачу классификации.
   • Для понижения размерности чаще всего используют PCA. Основная задача метода главных компонент — поиск новых линейных комбинаций признаков, вдоль которых максимизируется дисперсия значений проекций элементов обучающей выборки.

One-Hotстатьей о вкусовой сенсорной системе

class:	red:	green:	blue:	bitter:	sweet:	salti:	sour:	weight:	solid:
1	1	0.23	1
1	1	-0.85
1	1	1	0.14	1
1	1	1	0.38
1	1	-0.48

Таблица 2 — Пример данных обучающей выборки после препроцессинга_kk

Представляем функцию стоимости с перекрёстной энтропией

_1212jjj

−z

интерактивная формапосмотримраньше нейрон застревал₁₂L₁L₂

_jjjjL_jjjj

Упражнения

• Один подвох перекрёстной энтропии состоит в том, что сначала может быть трудно запомнить соответствующие роли y и a. Легко запутаться, как будет правильно, − или −. Что будет со вторым выражением, когда y=0 или 1? Влияет ли эта проблема на первое выражение? Почему?
• В обсуждении единственного нейрона в начале раздела, я говорил, что перекрёстная энтропия мала, если σ(z)≈y для всех обучающих входящих данных. Аргумент основывался на том, что y равен 0 или 1. Обычно в задачах классификации так и есть, но в других задачах (например, регрессии) y иногда может принмать значения между 0 и 1. Покажите, что перекрёстная энтропия всё равно минимизируется, когда σ(z)=y для всех обучающих входов. Когда так происходит, значение перекрёстной энтропии равно
  . Величину − иногда называют бинарной энтропией.

Задачи

• Многослойные сети с многими нейронами. В записи из последнего раздела покажите, что для квадратичной стоимости частная производная по весам в выходном слое равна
  Член σ'(zL_j) заставляет обучение замедляться, когда нейрон склоняется к неверному значению. Покажите, что для функции стоимости с перекрёстной энтропией выходная ошибка δL для одного обучающего примера x задаётся уравнением
  Используйте это выражение, чтобы показать, что частная производная по весам в выходном слое задаётся уравнением
  Член σ'(zL_j) исчез, поэтому перекрёстная энтропия избегает проблемы замедления обучения, не только при использовании с одним нейроном, но и в сетях с многими слоями и многими нейронами. С небольшим изменением этот анализ подходит и для смещений. Если это неочевидно для вас, вам лучше проделать и этот анализ также.
• Использование квадратичной стоимости с линейными нейронами во внешнем слое. Допустим, у нас многослойная сеть с многими нейронами. Допустим, в финальном слое все нейроны линейные, то есть сигмоидная функция активации не применяется, а их выход просто определяется, как aL_j = zL_j. Покажите, что при использовании квадратичной функции стоимости выходная ошибка δL для одного обучающего примера x задаётся
  Как и в прошлой задаче, используйте это выражение, чтобы показать, что частные производные по весам и смещениям во внешнем слое определяются, как

  Это показывает, что если выходные нейроны линейные, тогда квадратичная стоимость не вызовет никаких проблем с замедлением обучения. В этом случае квадратичная стоимость вполне подходит для использования.