III. Операции и свойства операций над множествами
Опр.1.Пересечением множеств А и В называется операция, результатом которой является множество, состоящее из тех и только тех элементов, которые принадлежат и А и В одновременно.
A∩B={x|x∈A∧x∈B}
Опр.2. Объединением множеств А и В называется операция, результатом которой является множество, состоящее из тех и только тех элементов, которые принадлежат множеству А или множеству В (т.е. хотя бы одному из этих множеств).
A∪B={x|x∈A∨x∈B}
Опр.3. Разностью множеств А и В называется операция, результатом которой является множество, состоящее из тех и только тех элементов, которые принадлежат А и не принадлежат В одновременно.
А\ В ={x∈A∧x∉B}
Опр.4. Дополнением множества А до универсального множества называется множество, каждый элемент которого принадлежит универсальному и не принадлежит А.
Выражения с множествами
Из множеств, знаков операций над ними и, может быть, скобок можно составлять выражения. Например, А∩В\С.
Необходимо знать порядок выполнения операций в таких выражениях и уметь их читать.
Порядок выполнения операций
-
если нет скобок, то в первую очередь выполняется дополнение до универсального множества простого множества, затем пересечение и объединение (они равноправны между собой), в последнюю очередь — разность;
-
если в выражении есть скобки, то сначала выполняют операции в скобках по порядку, приведенному в пункте 1), а затем все операции за скобками.
Например, а) А∩В\С; б) А∩(В\С); в) А∩(В\С)’ .
Чтение выражения начинается с результата последней операции. Например, выражение а) читается так: разность двух множеств, первое из которых пересечение множеств А и В, а второе — множество С.
Круги Эйлера
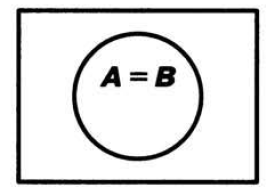
Операции над множествами и отношения между ними можно изобразить с помощью кругов Эйлера. Это специальные чертежи, на которых обычные множества изображаются кругами, универсальное множество — прямоугольником
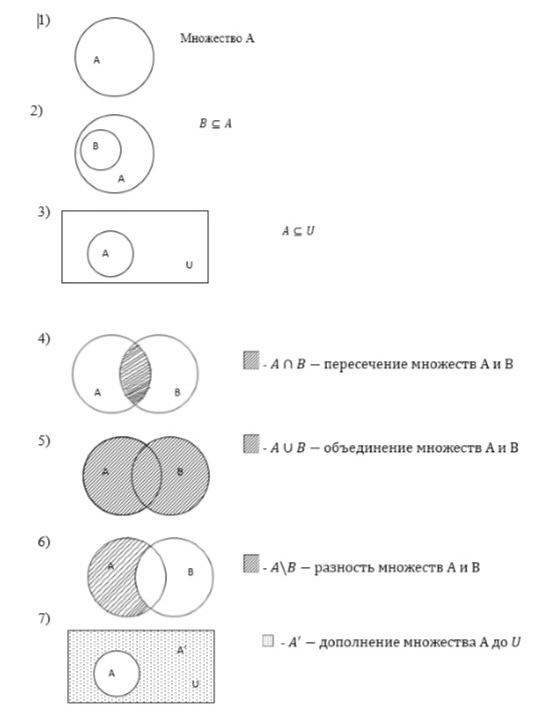
Задача. Изобразить с помощью кругов Эйлера множество (А∪В)’∩С.
Решение. Расставим порядок выполнения операций в данном выражении: (А∪В)’∩С. Заштрихуем результаты операций согласно порядку их выполнения
Свойства операции над множествами (рис.5)
Свойства I — 8 и 1 — 8 связаны между собой гак называемым принципом двойственности:
если в любом из двух столбиков свойств поменять знаки ∩→∪, ∪→∩, ∅→U, U→∅, то получится другой столбик свойств.

Множество чисел
Множеством называется совокупность определенных и различных между собой объектов, воспринимаемых как единое целое.
Например, совокупность учеников класса, совокупность целых положительных чисел.
Множества могут быть конечными и бесконечными. Количество учеников в классе — это конечное множество, можно четко назвать конкретное число учеников. Количество целых положительных чисел — бесконечное множество оно может быть бесконечно большим.
В математике множество обозначают прописными латинскими буквами.
Например, множество А={1,5,12,6,7} и множество В={2,4,12,3,7} конечные множества целых положительных чисел
С множествами можно выполнять различные действия. Одним из таких действий является пересечение множеств чисел.
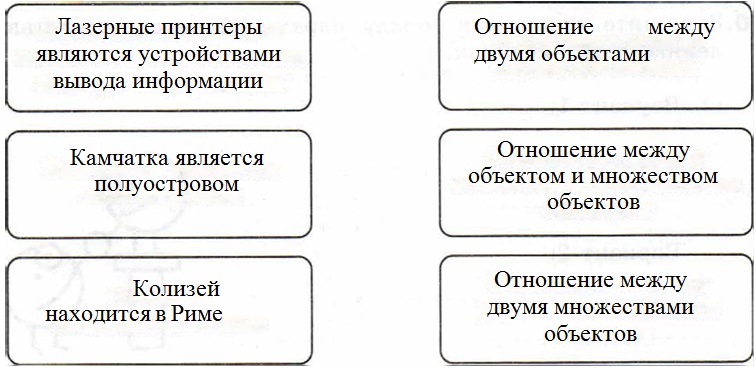
Объекты и множества — что это? свойства и совокупность
Мир, который нас окружает, — это мир предметов, явлений и процессов. С самого рождения человек познаёт окружающий его мир. Растения и животные, горы и реки, материки и страны, планеты и звёзды, полёт птицы или строительство дома – всё это становится для нас объектами познания.
Объект – это любая часть окружающей действительности, которую человек воспринимает как единое целое
Другими словами, объект – это то, на что обращено наше внимание: предметы, процессы и явления. Например, компьютерный стол, учебник, окно, попугай – это объекты-предметы; гроза, дождь, град, лунное затмение – объекты-явления; отпуск, прослушивание музыкальной композиции, высаживание рассады – это объекты-процессы
Например, компьютерный стол, учебник, окно, попугай – это объекты-предметы; гроза, дождь, град, лунное затмение – объекты-явления; отпуск, прослушивание музыкальной композиции, высаживание рассады – это объекты-процессы.
Задание. Назовите предметы, явления и процессы, с которыми имеет дело человек, когда:
- пишет и отправляет письмо;
- сдаёт ЕГЭ;
- загорает на пляже;
- разводит костёр;
- наблюдает за звёздами в телескоп.
Совокупность объектов, объединённых каким-либо общим признаком, называется множеством, а каждый из этих объектов – элементом множества.
Так, грибы – это множество объектов, а подберёзовик – это один из элементов этого множества. У множества месяцев его элементами являются январь, февраль, март, апрель и т. д.
Вопрос. Если врач – это множество, то каковы элементы этого множества?
Множество может быть конечным и бесконечным (множество страниц книги и множество действительных чисел), упорядоченным и неупорядоченным (то есть элементы которого выстроены по какому-либо порядку или выстроены беспорядочно), пустым и непустым.
Пустое множество – множество, не содержащее ни одного элемента: например, множество сиамских кошек, множество решений уравнения x2 – 5x + 6 = 0. Говорят, что пустое множество является своим подмножеством, но не является своим элементом.
Задание.Распределите данные примеры множеств таким образом, чтобы в каждой группе множеств находилось по два примера.
| Конечное множество | Бесконечное множество | Непустое множество | Пустое множество |
Множество звёзд во Вселенной; множество двоечников в классе; множество букв английского алфавита; фруктовых деревьев; множество чисел, которые делятся на нуль; множество съедобных грибов; множество натуральных чисел; множество домашних животных.
1 вариант
1. Выберите верное утверждение. Объект — это
1) любой предмет вокруг нас
2) любое явление вокруг нас
3) любой процесс вокруг нас
4) все перечисленные утверждения верны
2. Примером какого объекта является снегопад?
1) объект-предмет
2) объект-явление
3) объект-процесс
4) объект-утверждение
3. Выберите верное утверждение. Что такое множество?
1) множество — это коллекция объектов
2) множество — это набор объектов
3) оба утверждения верны
4) ни одно утверждение не верно
4. Как называются объекты, составляющие множество?
1) субъекты
2) подмножество
3) элементы
4) детали
5. Может ли множество состоять из одного объекта?
1) да
2) нет
6. Может ли в множестве быть бесконечное количество элементов?
1) да
2) нет
7. Какие два типа имен бывают у объекта?
1) общие и частные
2) общие и единичные
3) глобальные и локальные
4) множественные и единичные
8. Как называется тип имени элемента, который отражает свойства всего множества?
1) глобальное имя
2) множественное имя
3) общее имя
4) частное имя
9. Какими свойствами обладает единичное имя?
1) отражает свойство объекта
2) отражает общее свойство объектов всего множества
3) отражает отличительное свойство объекта
10. Выберите общее имя в словосочетании город России Новгород.
1) город
2) город России
3) город России Новгород
4) Новгород
Часть 4. Функции.
функциях
Функцияобластью определенияаргументамикообластьюобразомзаданияописывать
Инъекции, сюръекции и биекции
инъекциясюръекциябиекция
- Функция является инъективной (или «один к одному»), если каждый элемент в кообласти отображается не более чем на один элемент в области определения.
- Функция является сюръективной, если каждый элемент в кообласти отображается не менее чем на один элемент в области определения. (то есть образ и кообласть функции эквивалентны.)
- Функция является биективной, если каждый элемент кообласти отображается ровно на один элемент области определения.
описанияидентифицироватьинъекциейсюръекциейбиекциейобоимиБиекция (инъекция + сюръекция), инъекция (инъекция + не-сюръекция), сюръекция (не-инъекция + сюръеция), без классификации (не-инъекция + не-сюръекция)систему аксиом Цермело-Френкеля
Имена объектов
Человек может сообщить самые разнообразные сведения о том или ином объекте. Но чтобы сделать это, нужно сначала как-то обозначить, выделить объект из ряда других объектов – дать ему имя.
Имя объекта люди называют, отвечая на вопрос что это такое? или кто это такой? Например, так: это – град, это – тетрадь, это – труд и т. д. Но в разных ситуациях один и тот же объект мы обозначаем разными именами. Например, собаку можно назвать Тузиком, пёсиком, щенком, другом человека или просто животным. Чем отличаются эти имена и от чего зависит выбор имени объекта в каждом случае?
Прежде всего, существуют имена общие и единичные. Общее имя обозначает множество объектов (страна, прозвище, планета), а единичное имя обозначает один конкретный объект в некотором множестве объектов (столица России, Александр Сергеевич Пушкин).
Имена также могут быть собственными и нарицательными. Собственные имена даются объектам только некоторых видов, например, людям (Александр Сергеевич Пушкин), домашним животным (Пушок), географическим объектам (Москва), планетам (Юпитер) и т. д. Нарицательные имена используются для называния целой группы объектов, например, человек, книга, лицо, буква. Вспомните, что в соответствии с правилами русского языка собственные имена вы пишете с прописной (заглавной) буквы, а нарицательные – со строчной.
Задания
1. Какие из нижеперечисленных имён объектов относятся к собственным именам, какие – к нарицательным?
Дуб, Византия, Урал, река, колодец, улица Почтовая, мультфильм «В стране невыученных уроков», Мухтар, облако, информатика.
2. Выделите на помещённом ниже рисунке два множества объектов. Дайте общее имя каждому множеству и единичное имя каждому объекту. Какие из выбранных вами имён будут являться собственными?
Знакомые структуры данных
С некоторыми структурами данных вы уже знакомы. Например, на уроках математики вы изучали множество — некоторый набор элементов. Чтобы определить множество, мы должны перечислить все его элементы (например, множество, состоящее из Васи, Пети и Коли) или определить характерный признак, по которому элементы включаются в это множество (например, множество драконов с пятью зелёными хвостами или множество точек, в которых функция принимает положительные значения).
Множество может состоять из конечного числа элементов (множество букв русского алфавита), бесконечного числа элементов (множество натуральных чисел) или вообще быть пустым (множество слонов, живущих на Северном полюсе). Множества, с которыми работает компьютер, не могут быть бесконечными, потому что его память конечна.
В документах множество часто оформляют в виде маркированного списка, например:• процессор;
• память;
• устройства ввода;
• устройства вывода.
В таком списке порядок элементов не важен, от перестановки элементов множество не меняется (рис. 1.9).

Рис. 1.9
Линейный список состоит из конечного числа элементов, которые должны быть расположены в строго определённом порядке.
В отличие от множества элементы в списке могут повторяться
Список обычно упорядочен (отсортирован) по какому-то правилу, например по алфавиту, по важности, по последовательности действий и т. д
В тексте он часто оформляется как нумерованный список, например:1) надеть носки;
2) надеть ботинки;
3) выйти из дома.
Переставить местами элементы такого списка нельзя (это будет уже другой список). Список можно задать перечислением элементов, с первого до последнего:
(надеть носки, надеть ботинки, выйти из дома), а также представить в виде цепочки связанных элементов (рис. 1.10).

Рис. 1.10
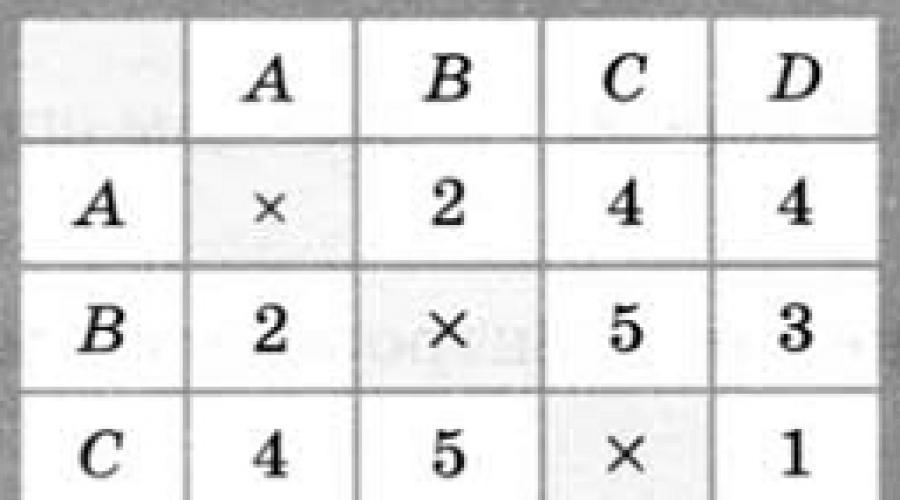
Ещё одна знакомая вам структура — таблица. С помощью таблиц устанавливается связь между несколькими элементами. Например, в табл. 1.2 элементы в каждой строке связаны между собой — это свойства некоторого объекта (человека).

Именно так хранится информация в базах данных: строка таблицы, содержащая информацию об одном объекте, называется записью, а столбец (название свойства) — полем.
Возможен и другой вариант таблицы, когда роли строк и столбцов меняются. В первом столбце записываются названия свойств, а данные в каждом из следующих столбцов описывают свойства какого-то объекта. Например, табл. 1.3 содержит характеристики разных марок автомашин.

Следующая страница Иерархия (дерево)
Cкачать материалы урока
Признаки объектов
Признаком любого объекта может быть его свойство, действие, поведение или состояние.
Свойства объекта помогают описать его характеристики и возможности, то есть назвать отличительные признаки этого объекта. Например, в сообщении о черёмухе, взятом из ботанической энциклопедии, сказано: «Черёмуха обыкновенная – дерево или крупный кустарник высотой 0,6-10 м; крона удлинённая, густая, кора матовая, чёрно-серая, с беловатыми чечевичками; молодые ветви оливковые или вишнёво-красные; листья простые, очерёдные, яйцевидно-ланцетные или продолговато-эллиптические, длиной 3-15 см, тонкие, на коротких черешках, заострённые; цветки белые (реже розоватые), собраны в длинные густые поникающие кисти длиной 8-12 см, с сильным запахом, на цветоножках». Такое подробное описание свойств объекта помогает отличить объект «черёмуха» от других деревьев и кустарников.
Каждое свойство определяется некоторой величиной и её значением. Например, в описании черёмухи обыкновенной присутствуют такие величины, как высота, длина, цвет и форма. Значениями данных величин будут являться: 0,6-10 м, чёрно-серая, розоватые, матовая, удлинённая, продолговато-эллиптические и др.
Признаки (свойства) могут быть существенными – необходимыми, крайне важными для выделения данного объекта из множества других, похожих на него. Так, существенными признаки, которые помогают отличить карликовую берёзу от других видов берёз, являются малая высота (до 1,2 м), маленький размер листьев (от 5 мм до 1,5 см), кустарниковая форма, стелящиеся по земле побеги.
В таблице приведены характеристики объектов и величины, которыми эти свойства могут быть обозначены:
| Объект | Характеристика | Величина | Значение величины |
| Стол | Деревянный | Материал | Дерево |
| Стол | С тремя выдвижными ящиками | Количество выдвижных ящиков | 3 |
| Человек | Темноволосый | Цвет волос | Тёмный (чёрный) |
| Кошка | Породистая | Порода | Сиамская, египетская и т. д. |
| Монитор | Широкоформатный, с диагональю 23″ | Диагональ экрана монитора (дюймов) | 23 дюйма |
Имена действий обозначают процессы, которые могут происходить с объектом: «самолёт летает», «мяч отскакивает», «в записной книжке можно хранить номера телефонов». Имена действий также помогают подробно описать какой-либо объект.
Задание
Попробуйте обозначить характеристики приведённых ниже объектов, воспользовавшись школьными учебниками:
- стебель растения;
- цветок растения;
- растение семейства розоцветных;
- имя существительное;
- глагол;
- прямоугольник;
- десятичная дробь;
- физическое тело;
- молекула.
Отображение множеств
Отображение множества во множество – это правило, по которому каждому элементу множества ставится в соответствие элемент (или элементы) множества . В том случае если в соответствие ставится единственный элемент, то данное правило называется однозначно определённой функцией или просто функцией.
Функцию, как многие знают, чаще всего обозначают буквой – она ставит в соответствие каждому элементу единственное значение , принадлежащее множеству .
Ну а сейчас я снова побеспокою множество студентов 1-го ряда и предложу им 6 тем для рефератов (множество ):
Векторы Матрицы Определители Комплексные числа (о, да!) Теория пределов Что такое производная?
Установленное (добровольно или принудительно =)) правило ставит в соответствие каждому студенту множества единственную тему реферата множества .
…а вы, наверное, и представить себе не могли, что сыграете роль аргумента функции =) =)
Элементы множества образуют область определения функции (обозначается через ), а элементы множества – область значений функции (обозначается через ).
Построенное отображение множеств имеет очень важную характеристику: оно является взаимно-однозначным или биективным (биекцией). В данном примере это означает, что каждому студенту поставлена в соответствие одна уникальная тема реферата, и обратно – за каждой темой реферата закреплён один и только один студент.
Однако не следует думать, что всякое отображение биективно. Если на 1-й ряд (к множеству ) добавить 7-го студента, то взаимно-однозначное соответствие пропадёт – либо один из студентов останется без темы (отображения не будет вообще), либо какая-то тема достанется сразу двум студентам. Обратная ситуация: если к множеству добавить седьмую тему, то взаимнооднозначность отображения тоже будет утрачена – одна из тем останется невостребованной.
Уважаемые студенты на 1-м ряду, не расстраивайтесь – остальные 20 человек после пар пойдут прибирать территорию университета от осенней листвы. Завхоз выдаст двадцать голиков, после чего будет установлено взаимно-однозначное соответствие между основной частью группы и мётлами…, а Вольдемар ещё и в магазин сбегать успеет =)
Теперь разберёмся со «школьной» функцией одной переменной. Пожалуйста, загляните на страницу Функции и графики (отроется на соседней вкладке), и в Примере 1 найдите график линейной функции .
Задумаемся, что это такое? Это правило , которое каждому элементу области определения (в данном случае это все значения «икс») ставит в соответствие единственное значение . С теоретико-множественной точки зрения, здесь происходит отображение множества действительных чисел во множество действительных чисел:
Первое множество мы по-обывательски называем «иксами» (независимая переменная или аргумент), а второе – «игреками» (зависимая переменная или функция).
Далее взглянем на старую знакомую параболу . Здесь правило каждому значению «икс» ставит в соответствие его квадрат, и имеет место отображение:
Итак, что же такое функция одной переменной? Функция одной переменной – это правило , которое каждому значению независимой переменной из области определения ставит в соответствие одно и только одно значение .
Как уже отмечалось в примере со студентами, не всякая функция является взаимно-однозначной. Так, например, у функции каждому «иксу» области определения соответствует свой уникальный «игрек», и наоборот – по любому значению «игрек» мы сможем однозначно восстановить «икс». Таким образом, это биективная функция.
! На всякий случай ликвидирую возможное недопонимание: моя постоянная оговорка об области определения не случайна! Функция может быть определена далеко не при всех «икс», и, кроме того, может быть взаимно-однозначной и в этом случае. Типичный пример:
А вот у квадратичной функции не наблюдается ничего подобного, во-первых: – то есть, различные значения «икс» отобразились в одно и то же значение «игрек»; и во-вторых: если кто-то вычислил значение функции и сообщил нам, что , то не понятно – этот «игрек» получен при или при ? Что и говорить, взаимной однозначностью здесь даже не пахнет.
Задание 2: просмотреть графики основных элементарных функций и выписать на листок биективные функции. Список для сверки в конце этого урока.
Действия над множествами. Диаграммы Венна
Диаграммы Венна (по аналогии с кругами Эйлера) – это схематическое изображение действий с множествами. Опять же предупреждаю, что я рассмотрю не все операции:
1) Пересечение множеств характеризуется логической связкой И и обозначается значком
Пересечением множеств и называется множество , каждый элемент которого принадлежит и множеству , и множеству . Грубо говоря, пересечение – это общая часть множеств:
Так, например, для множеств :
Если у множеств нет одинаковых элементов, то их пересечение пусто. Такой пример нам только что встретился при рассмотрении числовых множеств:
Множества рациональных и иррациональных чисел можно схематически изобразить двумя непересекающимися кругами.
Операция пересечения применима и для бОльшего количества множеств, в частности в Википедии есть хороший .
2) Объединение множеств характеризуется логической связкой ИЛИ и обозначается значком
Объединением множеств и называется множество , каждый элемент которого принадлежит множеству или множеству :
Запишем объединение множеств : – грубо говоря, тут нужно перечислить все элементы множеств и , причём одинаковые элементы (в данном случае единица на пересечении множеств) следует указать один раз.
Но множества, разумеется, могут и не пересекаться, как это имеет место быть с рациональными и иррациональными числами:
В этом случае можно изобразить два непересекающихся заштрихованных круга.
Операция объединения применима и для бОльшего количества множеств, например, если , то:
, при этом числа вовсе не обязательно располагать в порядке возрастания (это я сделал исключительно из эстетических соображений). Не мудрствуя лукаво, результат можно записать и так:
3) Разностью множеств и называют множество , каждый элемент которого принадлежит множеству и не принадлежит множеству :
Разность читаются следующим образом: «а без бэ». И рассуждать можно точно так же: рассмотрим множества . Чтобы записать разность , нужно из множества «выбросить» все элементы, которые есть во множестве :
Пример с числовыми множествами: – здесь из множества целых чисел исключены все натуральные, да и сама запись так и читается: «множество целых чисел без множества натуральных».
Зеркально: разностью множеств и называют множество , каждый элемент которого принадлежит множеству и не принадлежит множеству :
Для тех же множеств – из множества «выброшено» то, что есть во множестве .
А вот эта разность оказывается пуста: . И в самом деле – если из множества натуральных чисел исключить целые числа, то, собственно, ничего и не останется 🙂
Кроме того, иногда рассматривают симметрическую разность , которая объединяет оба «полумесяца»: – иными словами, это «всё, кроме пересечения множеств».
4) Декартовым (прямым) произведением множеств и называется множество всех упорядоченных пар , в которых элемент , а элемент
Запишем декартово произведение множеств :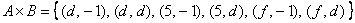 – перечисление пар удобно осуществлять по следующему алгоритму: «сначала к 1-му элементу множества последовательно присоединяем каждый элемент множества , затем ко 2-му элементу множества присоединяем каждый элемент множества , затем к 3-му элементу множества присоединяем каждый элемент множества »:
– перечисление пар удобно осуществлять по следующему алгоритму: «сначала к 1-му элементу множества последовательно присоединяем каждый элемент множества , затем ко 2-му элементу множества присоединяем каждый элемент множества , затем к 3-му элементу множества присоединяем каждый элемент множества »: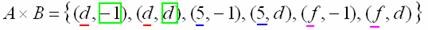
Зеркально: декартовым произведением множеств и называется множество всех упорядоченных пар , в которых . В нашем примере: – здесь схема записи аналогична: сначала к «минус единице» последовательно присоединяем все элементы множества , затем к «дэ» – те же самые элементы:
– здесь схема записи аналогична: сначала к «минус единице» последовательно присоединяем все элементы множества , затем к «дэ» – те же самые элементы: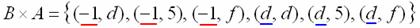
Но это чисто для удобства – и в том, и в другом случае пары можно перечислить в каком угодно порядке – здесь важно записать все возможные пары. А теперь гвоздь программы: декартово произведение – это есть не что иное, как множество точек нашей родной декартовой системы координат
А теперь гвоздь программы: декартово произведение – это есть не что иное, как множество точек нашей родной декартовой системы координат .
Задание для самостоятельного закрепления материала:
Выполнить операции 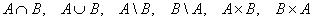 , если:
, если:
1) ;
2)
Множество удобно расписать перечислением его элементов.
И пунктик с промежутками действительных чисел:
3)
Напоминаю, что квадратная скобка означает включение числа в промежуток, а круглая – его невключение, то есть «минус единица» принадлежит множеству , а «тройка» не принадлежит множеству . Постарайтесь разобраться, что представляет собой декартово произведение данных множеств. Если возникнут затруднения, выполните чертёж 😉
Краткое решение задачи в конце урока.
2 вариант
1. Выберите верное утверждение. Объект — это
1) любая часть окружающей действительности
2) только окружающие нас предметы
3) оба утверждения верны
4) ни одно из перечисленных утверждений не верно
2. Примером какого объекта является праздник?
1) объект-предмет
2) объект-явление
3) объект-процесс
4) объект-утверждение
3. Выберите верное утверждение. Как можно назвать совокупность объектов?
1) множество
2) коллекция
3) оба утверждения верны
4) ни одно утверждение не верно
4. Чем являются элементы множества?
1) субъектами
2) подмножествами
3) объектами
4) деталями
5. Может ли в множестве не быть ни одного объекта?
1) да
2) нет
6. Всегда ли в множестве можно подсчитать количество элементов?
1) да
2) нет
7. Какими свойствами обладает общее имя объекта?
1) отражает свойство объекта
2) отражает свойство множества
3) отражает отличительное свойство объекта
8. Как называется тип имени объекта, который отражает свойства элемента множества?
1) элементарное
2) единичное
3) частное
9. Выберите единичное имя в словосочетании «река Сибири Ангара».
1) река
2) река Сибири
3) река Сибири Ангара
4) Ангара
10. Выберите собственное имя в словосочетании рассказ Тургенева «Муму»
1) рассказ
2) рассказ Тургенева
3) рассказ Тургенева «Муму»
4) «Муму»
Ответы на тест по информатике Объекты и множества для 6 класса1 вариант
1-4
2-2
3-3
4-3
5-1
6-1
7-2
8-3
9-3
10-22 вариант
1-1
2-3
3-1
4-3
5-1
6-2
7-2
8-2
9-4
10-4