Механическое движение

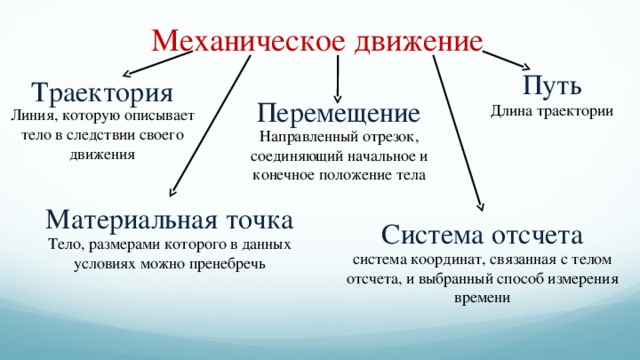
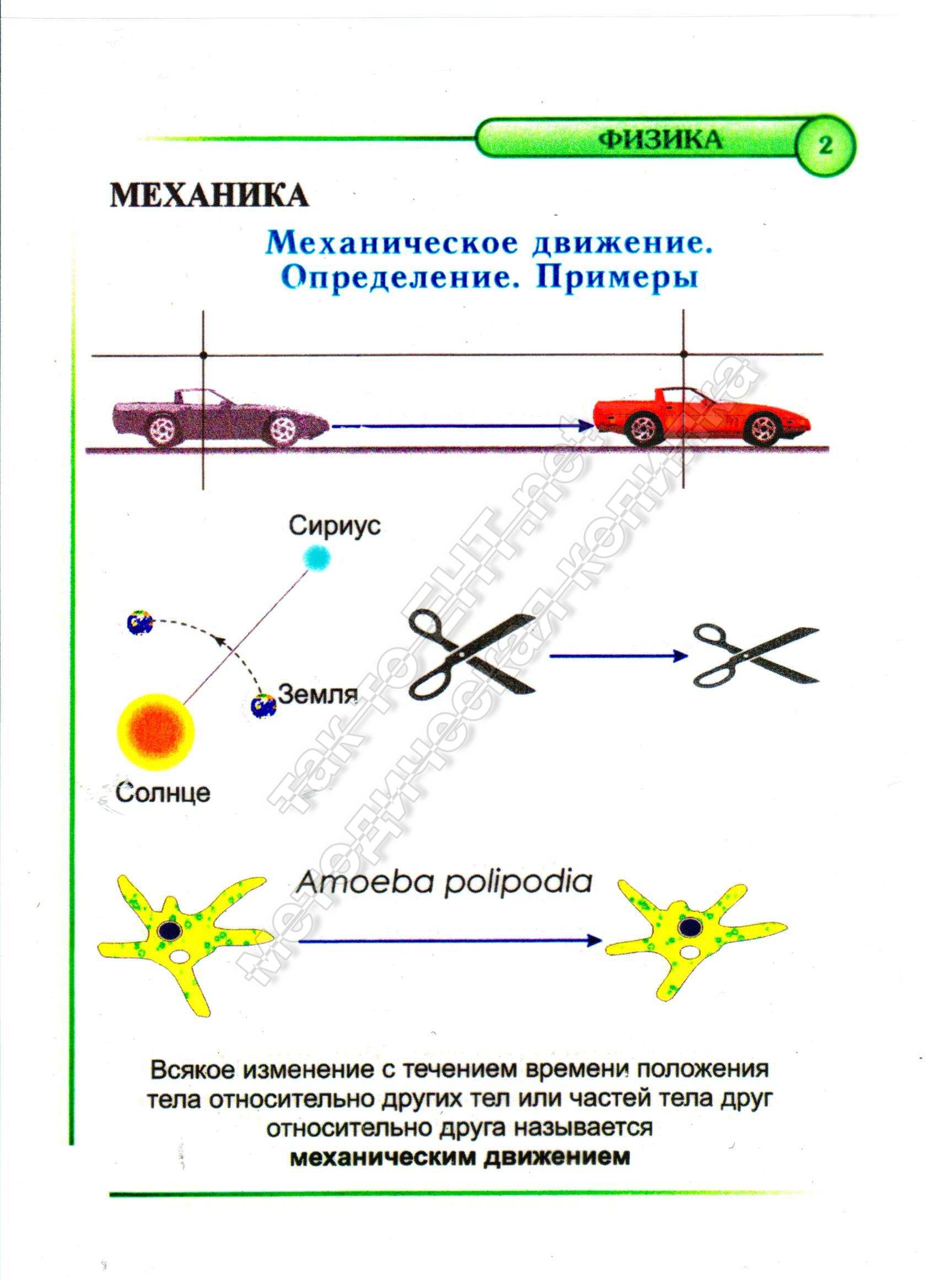
Что называется механическим движением

Это изменение положения какого-либо тела в пространстве, относительно других тел с течением времени. Материальные точки при этом взаимодействуют по законам механики.

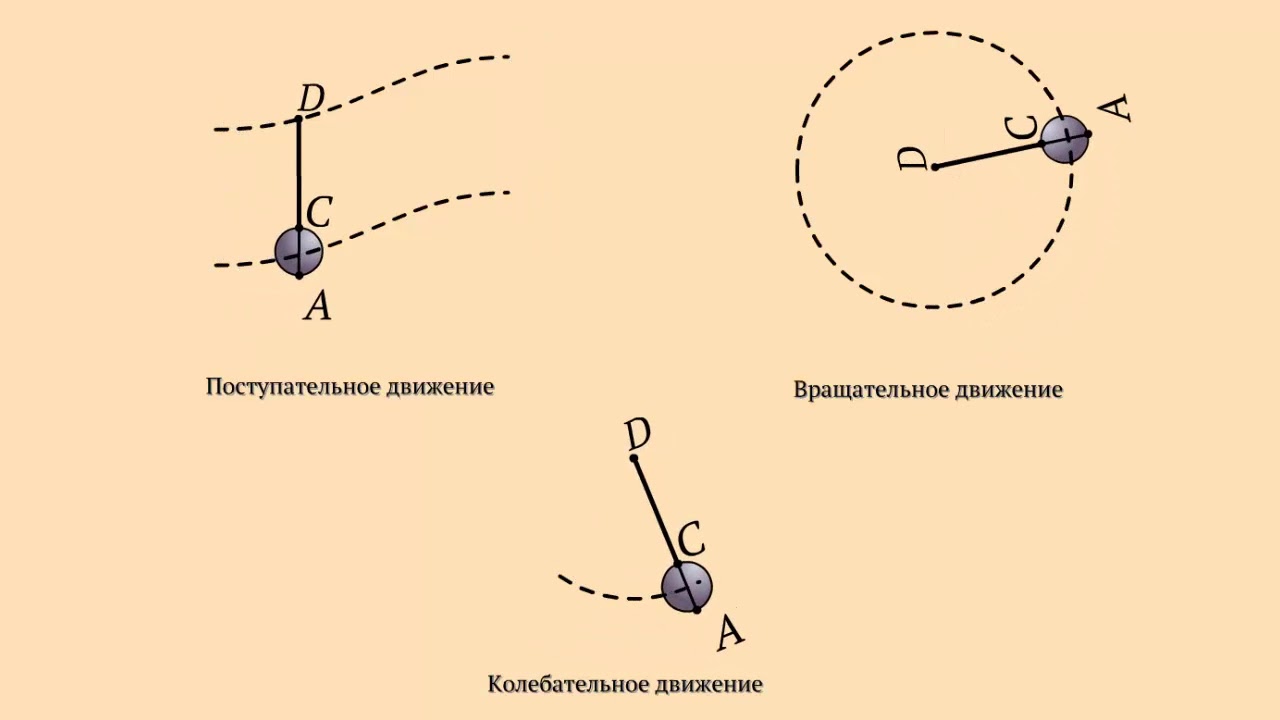
Подразделяется на несколько видов:

• Движение материальной точки измеряется с помощью нахождения ее координат и отслеживания изменений координат со временем. Найти эти показатели, значит вычислить значения по осям абсцисс и ординат. Изучением этого занимается кинематика точки, которая оперирует такими понятиями, как траектория, перемещение, ускорение, скорость. Движение объекта при этом может быть прямолинейное и криволинейное.
• Движение твердого тела складывается из перемещения какой-то точки, взятой за основу, и вращательного движения вокруг нее. Изучается кинематикой твердых тел. Перемещение может быть поступательным, то есть вращения вокруг заданной точки не происходит, и все тело движется равномерно, а также плоским — если все тело перемещается параллельно плоскости.
• Существует так же движение сплошной среды. Это перемещение большого количества точек, связанных только каким-либо полем или областью. Ввиду множества движущихся тел (или материальных точек) одной системы координат здесь недостаточно. Поэтому сколько тел, столько и систем координат. Примером тому может служить волна на море. Она — непрерывна, но состоит из большого количества отдельно взятых точек на множестве систем координат. Вот и получается, что движение волны — перемещение сплошной среды.

Свободное падение (ускорение свободного падения)

Свободное падение – это движение тела в безвоздушном пространстве под действием только силы тяжести.

Все тела при свободном падении независимо от массы падают с одинаковым ускорением, называемым ускорением свободного падения.
Ускорение свободного падения всегда направлено к центру Земли (вертикально вниз).

Обозначение – ​\( g \)​, единицы измерения – м/с2.

Важно! \( g \) = 9,8 м/с2, но при решении задач считается, что \( g \) = 10 м/с2

Движение тела по вертикали

Тело падает вниз, вектор скорости направлен в одну сторону с вектором ускорения свободного падения:

Если тело падает вниз без начальной скорости, то ​\( v_0 \)​ = 0.
Время падения рассчитывается по формуле:

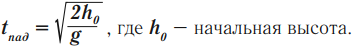
Тело брошено вверх:

Если брошенное вверх тело достигло максимальной высоты, то ​\( v \)​ = 0.
Время подъема рассчитывается по формуле:

Движение тела, брошенного горизонтально

Движение тела, брошенного горизонтально, можно представить как суперпозицию двух движений:

1. равномерного движения по горизонтали со скоростью ​\( v_0=v_{0x} \)​;
2. равноускоренного движения по вертикали с ускорением свободного падения ​\( g \)​ и без начальной скорости ​\( v_{0y}=0 \)​.

Уравнение скорости:

Уравнение координаты:

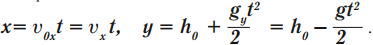
Скорость тела в любой момент времени:

Дальность полета:

Угол между вектором скорости и осью ОХ:

Движение тела, брошенного под углом к горизонту (баллистическое движение)

Движение тела, брошенного под углом к горизонту, можно представить как суперпозицию двух движений:

1. равномерного движения по горизонтали;
2. равноускоренного движения по вертикали с ускорением свободного падения.

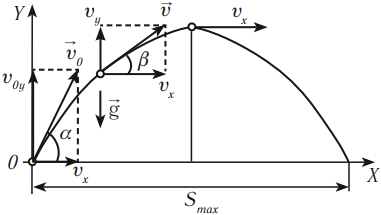
Уравнение скорости:

Уравнение координаты:

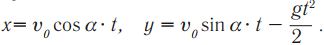
Скорость тела в любой момент времени:

Угол между вектором скорости и осью ОХ:

Время подъема на максимальную высоту:

Максимальная высота подъема:

Время полета:

Максимальная дальность полета:

Важно!
При движении вверх вертикальная составляющая скорости будет уменьшаться, т. е

тело вдоль вертикальной оси движется равнозамедленно.
При движении вниз вертикальная составляющая скорости будет увеличиваться, т. е. тело вдоль вертикальной оси движется равноускоренно.
Скорость ​\( v_0 \)​, с которой тело брошено с Земли, будет равна скорости, с которой оно упадет на Землю. Угол ​\( \alpha \)​, под которым тело брошено, будет равен углу, под которым оно упадет.

При решении задач на движение тела, брошенного под углом к горизонту, важно помнить, что в точке максимального подъема проекция скорости на ось ОУ равна нулю:

Это облегчает решение задач:

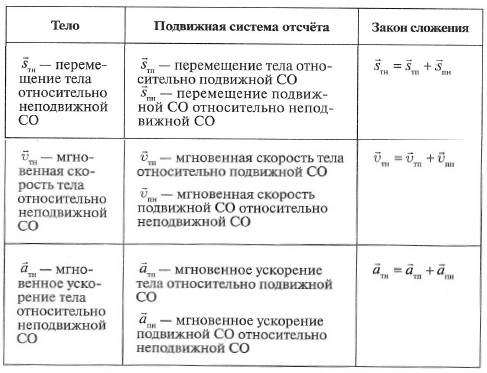
Система отсчёта

Материальная точка перемещается сравнительно инерции иных тел. Тело, согласно отношению к какому рассматривается это автоматическое перемещение, именуется телом отсчёта. Тело отсчета выбирают свободно в зависимости с поставленными заданиями.

С телом отсчёта вяжется система местоположение, что предполагает из себя точку отсчёта (основание координат). Концепция местоположение обладает 1, 2 либо 3 оси в связи с условием перемещения. Состояние точки на линии (1 ось), плоскости (2 оси) либо в месте (3 оси) устанавливают в соответствии с этим одной, 2-мя либо 3-мя координатами.

С целью установления положения тела в пространственной области в любой период времени необходимо установить старт отсчета времени. Устройство для замера времени, система координат, точка отсчета, с которым соединена система координат — это и есть система отсчёта.

Относительно этой системы рассматривается передвижение тела. У одной и той же точки в сравнении с различными телами отсчёта в различных концепциях координат имеют все шансы быть совершенно другие координаты. Система отсчёта также зависит от выбора траектория движения

Разновидности систем отсчёта могут быть разнообразными, например: недвижимая система отсчёта, подвижная система отсчета, инерциальная система отсчета, неинерциальная система отсчёта.

9 класс

01. Законы взаимодействия и движения тел

• 01. Материальная точка. Система отсчета
• 02. Перемещение
• 03. Определение координаты движущегося тела
• 04. Перемещение при прямолинейном равномерном движении
• 05. Прямолинейное равноускоренное движение. Ускорение
• 06. Скорость прямолинейного равноускоренного движения. График скорости
• 07. Перемещение при прямолинейном равноускоренном движении
• 08. Перемещение тела при прямолинейном равноускоренном движении без начальной скорости
• 09. Лабораторная работа 1. Исследование равноускоренного движения без начальной скорости
• 10. Решение задач на определение ускорения, мгновенной скорости и перемещения при равноускоренном прямолинейном движении
• 11. Решение задач по теме Прямолинейное равномерное и неравномерное движение
• 12. Относительность движения
• 13. Инерциальные системы отсчета. Первый закон Ньютона
• 14. Второй закон Ньютона
• 15. Третий закон Ньютона
• 16. Свободное падение тел
• 17. Движение тела, брошенного вертикально вверх
• 18. Лабораторная работа 2 Исследование свободного падения тел
• 19. Законы всемирного тяготения
• 20. Ускорение свободного падения на Земле и других небесных телах
• 21. Прямолинейное и криволинейное движение. Движение тела по окружности с постоянной по модулю скоростью
• 22. Решение задач
• 23. Искусственные спутники Земли
• 24. Импульс. Закон сохранения импульса
• 25. Реактивное движение. Значение работ К.Э. Циолковского
• 26. Решение задач
• 27. Решение задач на тему Законы взаимодействия и движения тел

02. Механические колебания и волны. Звук

• 01. Колебательное движение и его характеристики. Свободные и вынужденные колебания
• 02. Колебательное движение. Свободные колебания. Колебательные системы
• 03. Динамика колебательного движения
• 04. Лабораторная работа по теме Измерение ускорения свободного падения с помощью математического маятника
• 05. Длина волны. Скорость распространения волны
• 06. Звуковые волны
• 07. Отражение волн. Звуковой резонанс
• 08. Величины, характеризующие колебательное движение
• 09. Лабораторная работа 3. Исследование зависимости периода и частоты свободных колебаний математического маятника от его длины
• 10. Кинетическая энергия. Потенциальная энергия. Примеры решения задач
• 11. Закон сохранения механической энергии
• 12. Превращение энергии при колебательном движении. Затухающие колебания. Вынужденные колебания
• 13. Распространение колебаний в упругой среде. Продольные и поперечные волны
• 14. Длина волны. Скорость распространения волн
• 15. Источники звука. Звуковые колебания. Высота, тембр, громкость
• 16. Скорость звука. Отражение звука. Эхо
• 17. Решение задач по теме Механические колебания и волны. Звук

03. Электромагнитные явления

• 01. Магнитное поле и его графическое изображение. Неоднородное и однородное магнитное поле
• 02. Направление тока и направление линий его магнитного поля
• 03. Обнаружение магнитного поля по его действию на электрический ток. Правило левой руки
• 04. Индукция магнитного поля
• 05. Магнитный поток
• 06. Явление электромагнитной индукции
• 07. Лабораторная работа 4. Изучение явления электромагнитной индукции
• 08. Получение переменного электрического тока
• 09. Электромагнитное поле
• 10. Электромагнитные волны
• 11. Электромагнитная природа света
• 12. Вариант контрольной работы по теме Электромагнитные явления

04. Строение атома и атомного ядра. Использование энергии атомных ядер

• 01. Радиоактивность как свидетельство сложного строения атомов
• 02. Модели атомов. Опыт Резерфорда
• 03. Радиоактивные превращения атомных ядер
• 04. Экспериментальные методы исследования частиц
• 05. Открытие протона. Открытие нейтрона.
• 06. Состав атомного ядра. Массовое число.Зарядовое число. Ядерные силы
• 07. Энергия связи. Дефект масс
• 08. Деление ядер урана. Цепная реакция
• 09. Ядерный реактор
• 10. Атомная энергетика
• 11. Биологическое действие радиации
• 12. Термоядерная реакция
• 13. Контрольная работа по теме Строение атома и атомного ядра. Использование энергии атомных ядер
• 14. Обобщение темы

Основные понятия

Еще со школьной скамьи нас учат тому, что механическое движение представляет собой изменение положения тела в любой момент времени относительно других тел системы. На самом деле все так и есть. Давайте примем обыкновенный дом, в котором мы находимся, за ноль координатной системы. Представьте визуально, что дом будет началом координат, а из него в любых направлениях будет выходить ось абсцисс и ось ординат.

В таком случае наше движение в пределах дома, а также за его пределами будет наглядно демонстрировать механическое движение тела в системе отсчета. Представьте, будто точка перемещается по системе координат, в каждый момент времени изменяя свою координату относительно как оси абсцисс, так и относительно оси ординат. Все будет просто и понятно.

Облекаем векторы в числа

Векторы удобно представлять в виде стрелок, но это не всегда самый точный способ работы с ними. Векторы гораздо точнее можно характеризовать числами. Рассмотрим пример сложения векторов А + В, показанных на рис. 4.6.

Предположим, что измерения на рис. 4.6 даны в метрах. Это значит, что вектор А направлен на 1 метр вверх и на 5 метров вправо, а вектор В направлен на 1 метр вправо и на 4 метра вверх. Для получения параметров результирующего вектора С нужно сложить горизонтальные измерения обоих векторов и отдельно сложить вертикальные измерения обоих векторов.

Результирующий вектор С направлен на 6 метров вправо и на 5 метров вверх. Как видите, для получения вертикального измерения вектора С нужно сложить вертикальное измерение вектора А и вертикальное измерение вектора В. А для получения горизонтального измерения вектора С нужно сложить горизонтальное измерение вектора А и горизонтальное измерение вектора В.

С помощью такой системы обозначений сложение векторов существенно упрощается. Итак, для сложения двух векторов достаточно сложить их координаты по осям X и Y, чтобы получить координаты результирующего вектора по осям X и Y:

Получается, что весь секрет сложения векторов заключается в разбиении каждого вектора на координаты по осям X и Y с последующим их сложением, чтобы соответственно получить координаты X и Y результирующего вектора? Конечно, работа с этими числами для получения координат X и Y результирующего вектора требует некоторых усилий, но они достаточно просты, чтобы с успехом их выполнить.

Допустим, что нужный вам отель находится на расстоянии 20 миль к северу и на расстоянии 20 миль на восток. Как будет выглядеть вектор, направленный из исходной точки к этому отелю? С помощью координатного представления эта задача решается очень легко. Допустим, что положительное направление оси X направлено на восток, а положительное направление оси Y — на север. На первом этапе нужно проехать 20 миль на север, а на втором этапе — 20 миль на восток. В векторном представлении эта задача формулируется следующим образом (восток ; север ):

Чтобы сложить эти два вектора, нужно сложить их координаты по соответствующим осям:

Результирующий вектор, который указывает на отель, имеет вид (20; 20).

Теперь вы уже не едете, а почти “летите” со скоростью 300 миль в час, но в том же направлении. Итак, в этой задаче демонстрируется процедура умножения вектора на скаляр.

Главная особенность механического движения

Раздел физики, который называется механикой, изучает движение, описывает и характеризует его, выясняет причины движения и покоя.

                                                           

Изменение положения одних тел относительно других механическим движением называется. Дети перемещались относительно жилых домов, школы, деревьев. А вот одежда школьников как была на них, так и осталась. А если дети добирались до стадиона на автобусе? Они перемещались относительно домов, столбов, пешеходов, но не двигались по отношению к  водителю, креслам, самому автобусу.

Главная особенность механического движения состоит в том, что оно относительно. Какое расстояние проходит ученик седьмого класса, пока длится урок в школе? «Никакое», — скажут те, кто отсчитывает расстояние от школьной парты. «81 000 км», — ответят другие, кто учитывает, что ученик вместе со школой и Землей движется вокруг Солнца со скоростью 108 000 км/ч. Значит, относительно парты школьник в течение урока не движется, а относительно Солнца преодолевает большое расстояние.

()

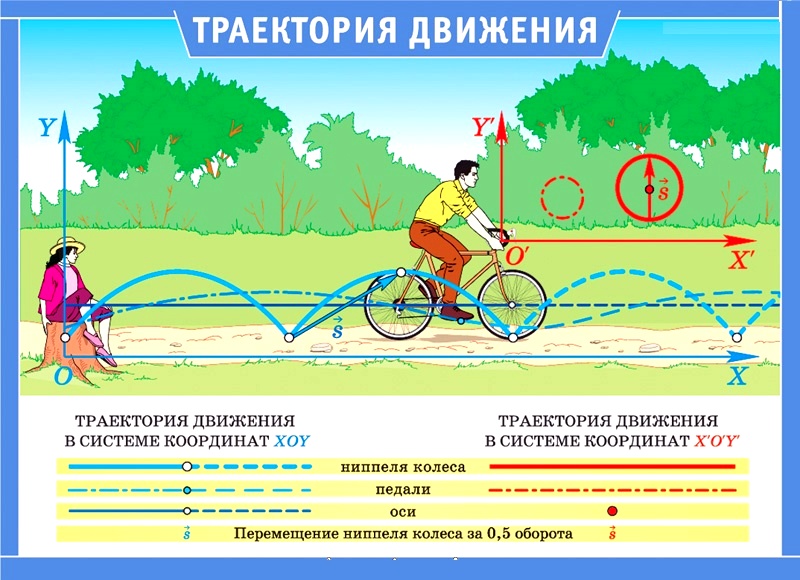
Тело движется, оставляет след, или этот след можно мысленно представить. В физике линия, вдоль которой тело движется, называется траекторией. Когда баскетболист отдает пас напарнику, мяч летит по прямой – траектория прямолинейная. Когда вратарь бросает в поле мяч, то он летит по кривой линии – криволинейная траектория.

                                              

Самую сложную траекторию для изучения разбивают на прямолинейные и криволинейные участки.

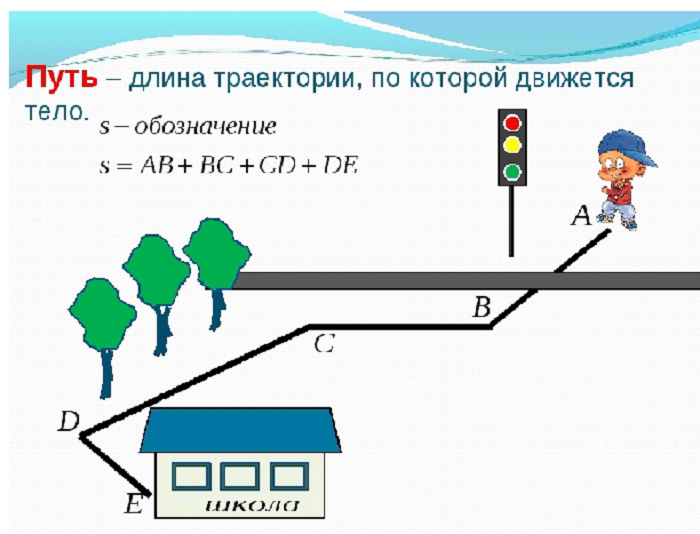
Движение характеризуется пройденным путем или длиной траектории. Лыжня – это траектория, а длина лыжни – дистанция или пройденный лыжником путь. Траектория кончика часовой стрелки – это окружность, пройденный путь – длина окружности.

Пройденный путь обозначают буквой s. Это расстояние или длина, поэтому измеряется в метрах.

()

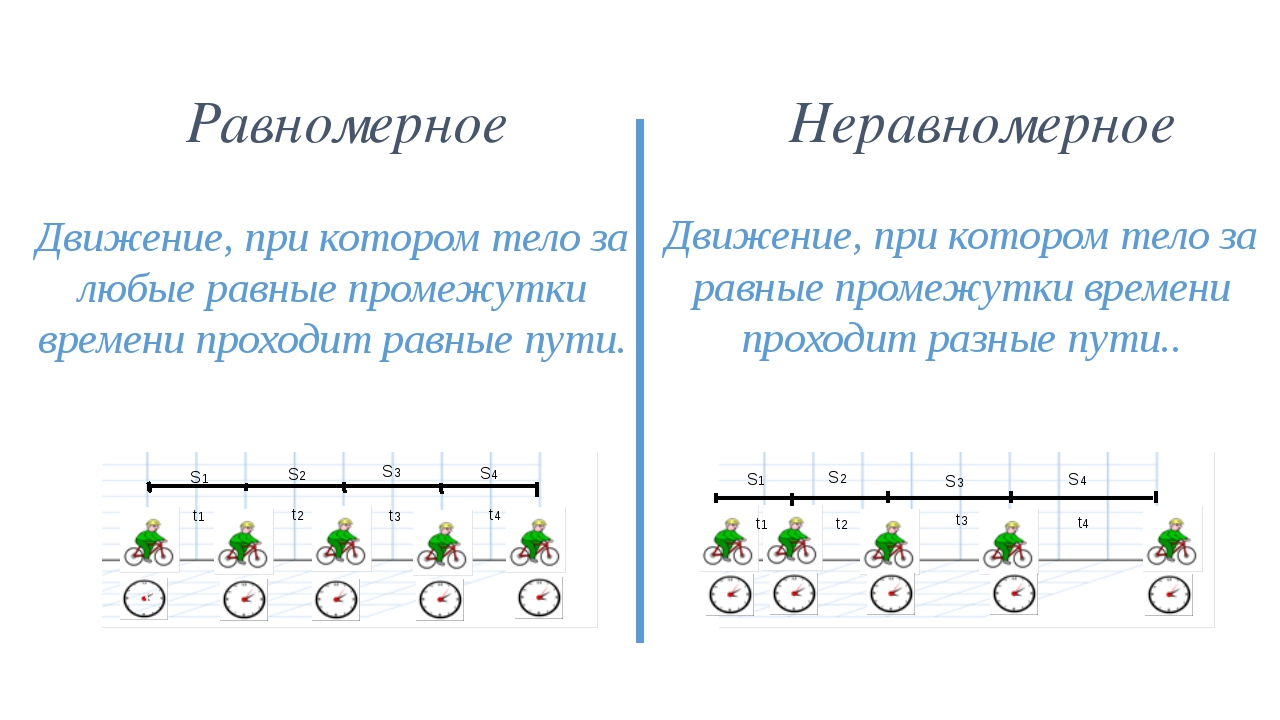
Движение, кроме траектории, описывается путем за единицу времени, т.е. за одну секунду. Если этот путь остается неизменным, то движение равномерное (за одну секунду одинаково), в противном случае – неравномерным (неодинаково за одну секунду).

Из большого количества различных видов движений самое простое – прямолинейное движение. В действительности такие движения крайне редки. Автомобиль, спортсмен, мотоцикл, самолет и другие движущиеся тела лишь небольшие промежутки времени участвуют в прямолинейном равномерном движении.

Итак, для запоминания:

Основная задача механики

Это строки из замечательного произведения Марка Твена «Приключения Тома Сойера»

Том целый день копался в земле то у дерева, то на холме, но клада так и не нашел. Прежде, чем отправиться за кладом, надо знать, где он находится.

Умение найти положение любого тела в данный момент времени и есть основная задача механики. Эту задачу решают диспетчеры, отправляющие поезд в путь. Они должны знать, как двигаются поезда, иначе – авария. Отправляя самолет в рейс, ракету в полет, специальные службы просчитывают траектории их движения. Космический корабль в огромных просторах космоса должен встретиться и состыковаться со станцией. Для этого надо произвести точнейшие расчеты, чтобы избежать ошибок, приводящих к неудаче.

Почему Том Сойер не мог решить основную задачу механики? Чтобы определить положение тела, надо знать еще какое-то тело, от которого вести отсчет расстояния, и направление, куда это расстояние отмерять. Герои «Острова сокровищ» (автор книги Роберт Стивенсон) смогли найти место, где лежал клад, так как у них была информация о направлении поиска и о дереве, от которого надо вести отсчет расстояния.

Так было написано на карте, которая вела к кладу на острове Сокровищ.

()

Стоит разобраться в записке на карте. Итак, высокое дерево – это тело, от которого надо вести отсчет расстояния в указанном направлении. Дано и расстояние — «в десяти саженях». Основная задача механики здесь решается.

Чтобы определить, где находится тело на прямой, на плоскости, в пространстве, нужно знать:

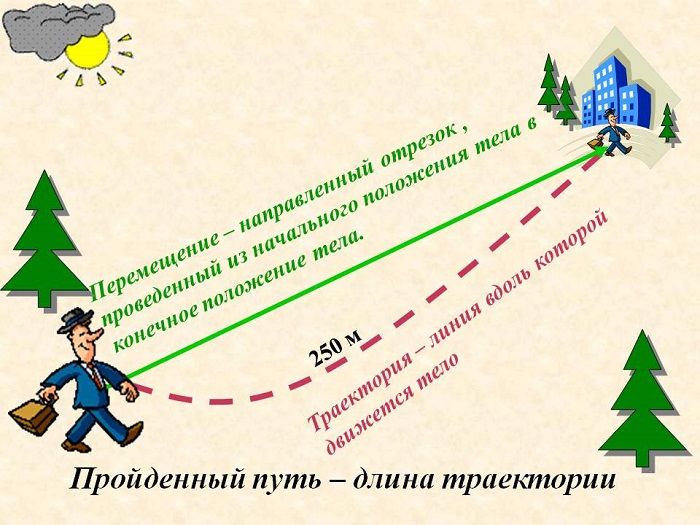
Если соединить по прямой тело отсчета с местом, где оказалось движущееся тело, получится отрезок, имеющий длину и направление (в сторону от тела отсчета до нового положения). Этот отрезок называется перемещением. Для обозначения используется буква s, но в отличие от пройденного пути над буквой ставится стрелка, так как перемещение есть векторная величина. Пройденный путь – это скаляр, он имеет только длину.

Итак, перемещение  — это вектор, соединяющий начальное и конечное положение тела.

()

Имея тело отсчета и перемещение, легко можно справиться с основной задачей механики.

При движении тела по прямой численные значения перемещения и пройденного пути совпадают и находятся по формуле s = v ∙ t. А если движение криволинейно? Вот три различных примера.

1. На соревнованиях по ориентированию, двигаясь от старта строго по компасу на северо-восток, Миша прошел 670 м. В этом случае 670м – это и пройденный мальчиком путь, и модуль вектора перемещения, направление которого задано.
2. Дима с Сережей отправились в лес за грибами. В лес они зашли от столба с пометкой 5 км. Набрав по корзинке грибов, друзья через 2 ч вышли на шоссе у столба с пометкой 6 км. Разве ребята прошагали по лесу 1 км? В этом случае перемещение мальчиков направлено от первого столба ко второму и по модулю равно 1 км. А вот пройденный путь, который прошли мальчики за 2 ч, двигаясь по сложной траектории, составляет несколько километров.
3. Братья Чук и Гек после прогулки вернулись домой. Начало совпадает с концом пути. Перемещение братьев получается равным нулю. За время прогулки дети прошли несколько метров, значит пройденный путь, в отличие от перемещения, нулю не равен.

Итак:

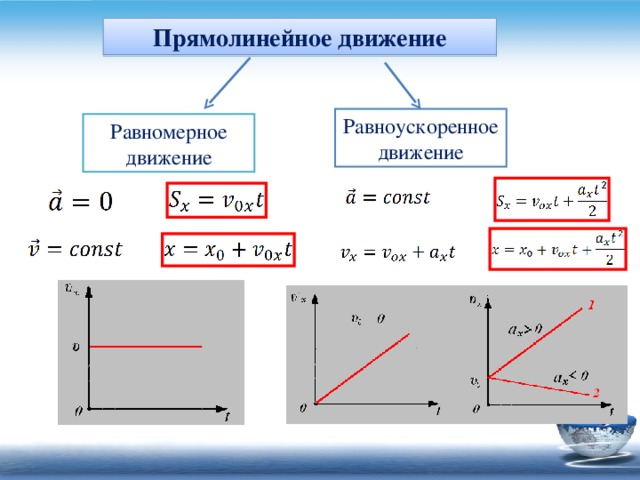
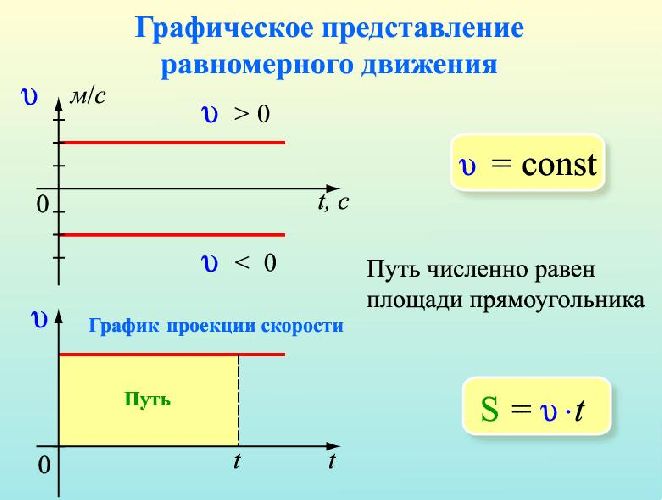
Формула равномерного движения

Если же мы будем говорить о равномерном движении, то вспомним, что при этом ускорение равно нулю (a = 0). Подставим ноль в формулу и получим: S = V0t. Но ведь скорость на всем участке пути у нас постоянна, если говорить грубо, то есть придется пренебречь силами, действующими на тело. Что, кстати, в кинематике практикуется повсеместно, поскольку кинематика не изучает причины возникновения движения, этим занимается динамика. Так вот, если скорость на всем участке пути у нас постоянна, то ее начальное значение совпадает с любым промежуточным, а также конечным. Поэтому формула расстояния будет выглядеть следующим образом: S = Vt. Вот и все.

Колебательное движение

Движение в двух противоположных направлениях, колебательное. Раскачивания, которые проходят в замкнутых концепциях называют независимыми или собственными колебаниями. Колыхания, которые происходят под действием внешних сил, называют вынужденными.

Если анализировать раскачивание согласно характеристик, которые изменяются (амплитуда, частота, период и др.), тогда их можно поделить на затухающие, гармонические, нарастающие (а также прямоугольные, сложные, пилообразные).

При свободных колебаниях в настоящих системах всегда происходят утраты энергии. Энергия тратится на работу по преодолению силы сопротивления воздуха. Сила трения уменьшает амплитуды колебаний, и они прекращаются через некоторое время.

Вынужденные раскачивания незатухающие. Поэтому надо пополнять потери энергии за каждый час колебаний. Для этого необходимо действовать на тело время от времени, изменяющейся силой. Вынужденные колыхания происходят с частотой, равной изменениям внешней силы.

Амплитуда принужденных колебаний достигает самого большого значения тогда, когда данный коэффициент такой же, как и частота колебательной системы. Это называется резонансом.

Например, если периодически дергать канат в такт его колебаниям, то мы увидим увеличение амплитуды его раскачивания.

Определение 3

Материальная точка – это тело, величиной которого в определенных условиях можно пренебрегать.

Часто вспоминаемый нами автомобиль возможно принимать за материальную точку сравнительно Земли. Но если люди перемещаются внутри этой машины, то уже нельзя пренебрегать размерами автомобиля.

Когда вы решаете задачи по физике, расценивают движение тела как движение материальной точки, и пользуются такими понятиями, как скорость точки, ускорение материального тела, инерция материальной точки и т.п.

Из истории

Само понятие «классической механики» появилось еще в древности, и подтолкнуло к этому развивающееся быстрыми темпами строительство. Архимед сформулировал и описал правило рычага, теорему о сложении параллельных сил, ввел понятие «центр тяжести». Так зачиналась статика.

Благодаря Галилею, в 17 веке стала развиваться «Динамика». Закон инерции и принцип относительности — это его заслуга.

Исаак Ньютон, как уже говорилось выше, ввел три закона, которые легли в основу ньютоновой механики. Также он открыл закон всемирного тяготения. Так были заложены основы классической механики.

Скорость движения. Первые задачи по физике

Урок физкультуры. Идут школьные соревнования по бегу. Как ни старался Артем (он пробежал 60 м за 12 секунд), место победителя досталось Денису, пробежавшему дистанцию за 10 секунд. Значит, Денис бежал быстрее соперника. На прохождение того же пути ему понадобилось меньше времени.

Что же характеризует быстроту движения? Семиклассникам знакомо слово «скорость», которое как раз и определяет быстроту движения. Скорость самолета больше скорости автомобиля, но меньше скорости ракеты.

()

Самая большая скорость в природе у света (300 000 км/с), ничто не может двигаться быстрее, чем свет.

Как найти скорость? В приведенном примере Денис 60 м пробежал за 10 с., значит, за секунду он пробегал по 6 м, а Артем на 60 м затратил 12 с времени, т. е. за 1 с он пробегал по 5 м. Денис опережал Артема на 1 м в течение одной секунды, а значит, бежал быстрее.

()

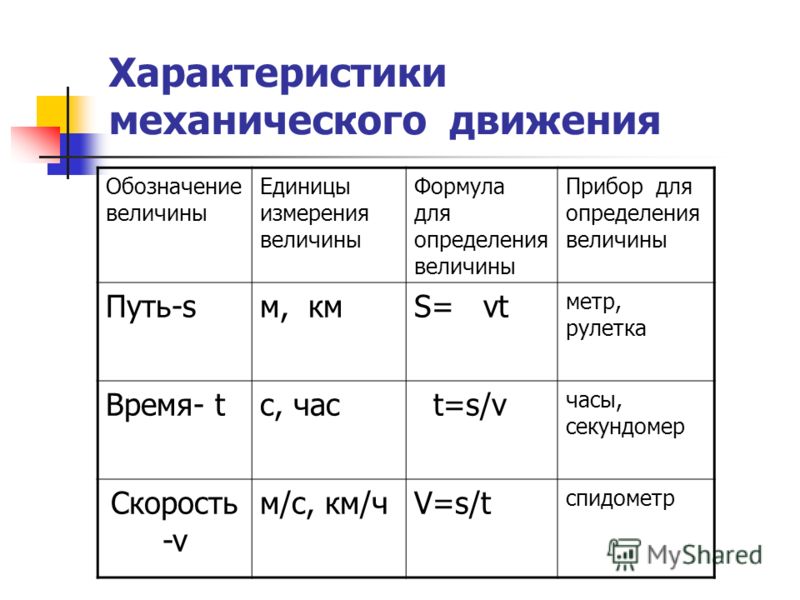
Скорость – это путь, проходимый телом за единицу времени. При решении задач нерационально каждый раз записывать правило, показывающее, как найти нужную величину, например, «Для вычисления скорости, надо пройденный путь разделить на время этого пути», затем составлять числовое выражение и считать. Поэтому в физике и других науках используется понятие «формула». Формула – это правило, записанное с помощью букв.

 Если ввести условные буквенные обозначения: скорость – v, пройденный путь – s, время – t, то правило вычисления скорости запишется коротко и ясно:

v = s / t

Это самая первая формула физики седьмого класса. Она называется формула скорости

Формулы важно запоминать и уметь применять для конкретных задач

Измеряется скорость в м/с (СИ), т. е. единица пути делится на единицу времени, следуя формуле. Используются разные единицы. Например, движение транспорта чаще измеряется в км/ч.

 Например, нарушает ли водитель правила, если легковой автомобиль движется со скоростью 20 м/с, а на обочине стоит знак с ограничением скорости «60»? На дорожных знаках скорость берется в км/ч. Значит, скорость автомобиля тоже надо перевести в км/ч. 1 м = 0,001 км, 1 ч = 3600с.

20 м/с = 20 ∙ 0, 001 ∙ 3600 км/ч = 72 км/ч.

()

Следует вывод: водитель нарушил правила дорожного движения.

А теперь нужно научиться правильно решать и оформлять физические задачи. Существует определенный порядок решения:

1. Условие задачи записать в сокращенном виде;
2. Выразить заданные величины в СИ;
3. Записать нужную формулу;
4. Проделать математические вычисления;
5. Получившийся результат записать в ответе.

Задача первая: Попрыгунья стрекоза летает со скоростью 36 км/ч, а скворец – 12 м/с. Догонит ли скворец стрекозу?

     Образец оформления задачи:

Задача вторая: Гепард считается самым быстрым животным в мире. В погоне за добычей 36 км он пробегает за 20 минут. Чему равна скорость гепарда?

     Образец оформления задачи:

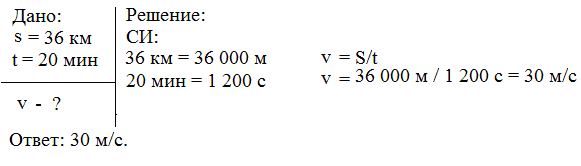
Зная скорость, легко определить и пройденный путь. Например, акула имеет скорость 10 м/с, значит, за 1 с она проплывет 10 м, за 2 с – 20 м, за 3 с – 30 м и т.д. А за 15 с? Надо скорость умножить на время. Получится 150 м. Для пройденного пути также есть правило, записать которое можно в виде формулы пути:

s = v ∙ t

а формула времени имеет вид:

t = s / v

Задача третья: Старик Хоттабыч с Волькой и Мишкой на машине «Волга», двигающейся со скоростью 108 км/ч, отправились за город. До привала они ехали 2 часа. На каком расстоянии от города был сделан привал?

     Решение:

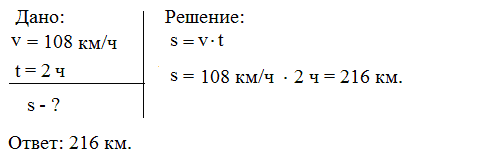
В случае этой задачи единицы в СИ переводить не надо. Они соответствуют друг другу (время дано в часах и скорость в километрах в час, а не в метрах в секунду) и дают реальное представление о времени и расстоянии.

В приведенных примерах считалось, скорость не менялась на всем пути, т. е. движение было прямолинейным и равномерным. А как быть с неравномерным движением? Из его определения получается, что скорость тела различна на отдельных участках пути.

Неравномерное движение характеризуется другой величиной – средней скоростью. Чтобы ее найти надо путь (пусть он даже состоит из отдельных участков) разделить на полное время движения.

v_ср = s / t

Средняя скорость волка при беге 16 м/с, это вовсе не значит, что он все время бежит с этой скоростью. Один участок пути он бежит со скоростью 18 м/с, другой – со скоростью 14 м/с, а в среднем – 16 м/с.

()

Иногда среднюю скорость считают скоростью равномерного движения. Например, автобус движется со скоростью 60 км/ч. Но ведь это его средняя скорость. У остановок автобус тормозит, а потом набирает скорость, на гладких участках дороги едет чуть быстрее, на неровностях медленнее. Вот и берется скорость, которая получается в среднем.

Скорость – значит быстро или медленно.

Равноускоренное движение

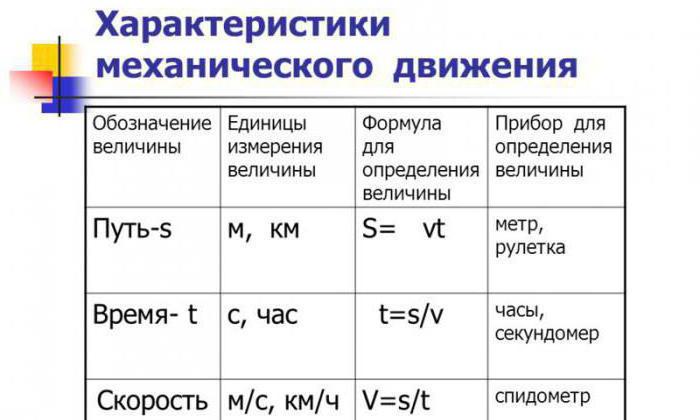
В физике такой вид движения встречается достаточно часто. Даже в задачах части “А” как 9-ого, так и 11-ого класса встречаются задания, в которых нужно уметь производить операции с ускорением. Например, “А-1”, где нарисован график движения тела в координатных осях и требуется вычислить, какое расстояние автомобиль прошел за тот или иной промежуток времени. Причем один из промежутков может демонстрировать равномерное движение, в то время как на втором необходимо вычислить сначала ускорение и только потом считать пройденное расстояние.

Как же узнать, что движение равноускоренное? Обычно в задачах информация об этом подается напрямую. То есть имеется либо численное указание ускорения, либо даются параметры (время, изменение скорости, дистанция), которые позволяют нам определить ускорение. Следует отметить, что ускорение – векторная величина. А значит она может быть не только положительной, но и отрицательной. В первом случае мы будем наблюдать ускорение тела, во втором – его торможение.

Но бывает, что информация о типе движения ученику преподается в несколько скрытной, если ее можно так назвать, форме. Например, говорится, что на тело ничего не действует или сумма всех сил равна нулю. Ну что же, в этом случае нужно четко понимать, что речь идет о равномерном движении либо о покое тела в определенной системе координат. Если вы вспомните второй закон Ньютона (в котором говорится о том, что сумма всех сил есть не что иное, как произведение массы тела на ускорение, сообщаемое под действием соответствующих сил), то легко заметите одну интересную вещь: если сумма сил равна нулю, то произведение массы на ускорение также будет равно нулю.

Что такое точка отсчета? Что такое механическое движение?

Andreus-папа-ndrey

Механи́ческим движе́нием тела называется изменение его положения в пространстве относительно других тел с течением времени. При этом тела взаимодействуют по законам механики. Раздел механики, описывающий геометрические свойства движения без учёта причин, его вызывающих, называется кинематикой
В более общем значении движением называется любое пространственное или временное изменение состояния физической системы. Например, можно говорить о движении волны в среде.
Механическое движение можно рассматривать для разных механических объектов:
* Движение материальной точки полностью определяется изменением её координат во времени (например, двух на плоскости) . Изучением этого занимается кинематика точки.
o Прямолинейное движение точки (когда она всегда находится на прямой, скорость параллельна эта прямой)
o Криволинейное движение это движение точки по траектории, не представляющей собою прямую, с произвольным ускорением и произвольной скоростью в любой момент времени (например, движение по окружности) .
* Движение твёрдого тела складывается из движения какой-либо его точки (например, центра масс) и вращательного движения вокруг этой точки. Изучается кинематикой твёрдого тела.
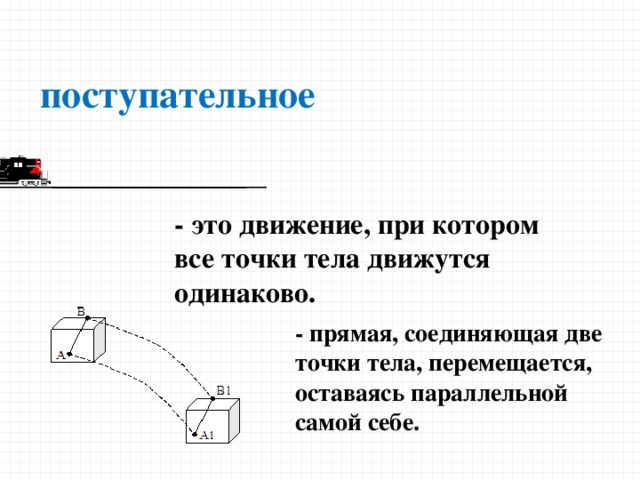
o Если вращение отсутствует, то движение называется поступательным и полностью определяется движением выбранной точки. Заметим, что при этом оно не обязательно является прямолинейным.
o Для описания вращательного движения — движения тела относительно выбранной точки, например закреплённого в точке, используют Углы Эйлера. Их количество в случае трёхмерного пространства равно трём.
o Также для твёрдого тела выделяют плоское движение — движение, при котором траектории всех точек лежат в параллельных плоскостях, при этом оно полностью определяется одним из сечений тела, а сечение тела положением любых двух точек.
* Движение сплошной среды. Здесь предполагается, что движение отдельных частиц среды довольно независимо друг от друга (обычно ограничено лишь условиями непрерывности полей скорости) , поэтому число определяющих координат бесконечно (неизестными становятся функции) .
Относительность — зависимость механического движения тела от системы отсчёта, не указав систему отсчёта — не имеет смысла говорить о движении.

Даниил юрьев

Виды механического движения
Механическое движение можно рассматривать для разных механических объектов:
Движение материальной точки полностью определяется изменением её координат во времени (например, для плоскости — изменением абсциссы и ординаты). Изучением этого занимается кинематика точки. В частности, важными характеристиками движения являются траектория материальной точки, перемещение, скорость и ускорение.
Прямолинейное движение точки (когда она всегда находится на прямой, скорость параллельна этой прямой)
Криволинейное движение — движение точки по траектории, не представляющей собою прямую, с произвольным ускорением и произвольной скоростью в любой момент времени (например, движение по окружности).
Движение твёрдого тела складывается из движения какой-либо его точки (например, центра масс) и вращательного движения вокруг этой точки. Изучается кинематикой твёрдого тела.
Если вращение отсутствует, то движение называется поступательным и полностью определяется движением выбранной точки. Движение при этом не обязательно является прямолинейным.
Для описания вращательного движения — движения тела относительно выбранной точки, например закреплённого в точке, — используют Углы Эйлера. Их количество в случае трёхмерного пространства равно трём.
Также для твёрдого тела выделяют плоское движение — движение, при котором траектории всех точек лежат в параллельных плоскостях, при этом оно полностью определяется одним из сечений тела, а сечение тела — положением любых двух точек.
Движение сплошной среды. Здесь предполагается, что движение отдельных частиц среды довольно независимо друг от друга (обычно ограничено лишь условиями непрерывности полей скорости), поэтому число определяющих координат бесконечно (неизвестными становятся функции).

Вектор – число и направление

Если где-то используется знак стрелки, то ясно, что она показывает направление, в котором следует двигаться. А скорость имеет направление? Где будет находиться автобус, если он движется от остановки со скоростью 70 км/ч? Местоположение автобуса не назвать, так как неизвестно, куда автобус едет от остановки, в каком направлении. Скорость имеет и численное значение. Она бывает маленькая и большая. Медленно движется черепаха, но быстро бежит гепард.

Получается, у скорости есть численное значение и направление. Такие величины называются векторными (просто векторами).

Обозначается векторная величина стрелкой над буквой, например, . Численное значение векторной величины записывается с двумя вертикальными палочками и называется модулем вектора. Например, модуль вектора скорости автобуса | | = 70 км/ч. Зная модуль вектора скорости, можно вычислить какой путь автобус прошел от остановки, а при известном направлении вектора (т.е. в какую сторону от остановки) уже определяется местоположением автобуса.                          

Величины, не имеющие направления, называются скалярами. Примеры скалярных величин: температура, время, объем, площадь, длина.

Вектор изображают в виде направленного отрезка, т. е. имеющего начало и конец. Конец отрезка отмечают стрелкой.

Основные свойства векторов

Два или несколько векторов с одинаковым модулем и направлением и равны.

Векторы, различающиеся по направлению не равны, если даже равны их численные значения.

Сумма одинаково направленных векторов по модулю равна сумме модулей этих векторов и имеет то же направление.

По этому правилу находят скорость по течению. Теплоход имеет собственную скорость, которую могут создать двигатели теплохода. У течения реки есть своя скорость. При движении по течению река будто помогает теплоходу. Скорости складываются. Числовой результат получается больше. Например, собственная скорость теплохода 60 км/ч, а скорость течения реки 2 км/ч. Результирующая скорость по модулю равна 62 км/ч, а направление остается тем же.

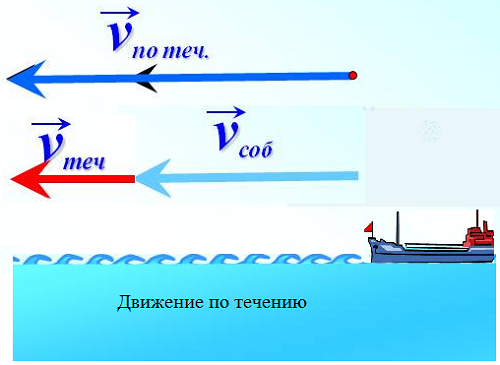
Если векторы направлены в противоположные стороны, то результирующий вектор направлен в сторону большего из них, а его численное значение равно разности численных значений этих векторов.

По этому правилу находят скорость против течения. При движении против течения река будто мешает движению теплохода, толкает течением назад. Значит, из модуля скорости теплохода надо вычесть модуль скорости течения

Здесь важно, чтобы вектор собственной скорости был больше, чем вектор скорости течения, иначе теплоход будет двигаться назад, даже при постоянной работе двигателей. Например, теплоход с собственной скоростью 60 км/ч движется в обратном направлении против течения реки, скорость которой 2 км/ч

Теплоход в результате будет иметь численное значение скорости 58 км/ч, направление вектора скорости – против течения.

Векторы можно умножать, делить, складывать. Как это делается, изучают на уроках математики.

Физикой свойства векторов используются при изучении величин, имеющих модуль и направление. Первой из них и является скорость.