Многоугольники
Многоугольник — это геометрическая фигура, которая характеризуется количеством углов и звеньев. Углы составлены парами звеньев замкнутой ломаной, сходящимися в одной точке. Звенья называются еще сторонами многоугольника. Общие точки двух отрезков называют вершинами многоугольника.

треугольникомчетырехугольникапятиугольник
Часть плоскости, которая ограничена замкнутой ломаной, называется плоским многоугольником. Другое ее название — многоугольная область.
Свойства
Ниже приведены основные свойства, общие для всех многоугольников:
- Если вершины многоугольника служат концами одной стороны, их называют соседними. Если же вершины не прилежат к одной стороне, они несоседние.
- Наименьшее количество сторон у многоугольника равняется трем. Однако треугольники, находясь рядом друг с другом, могут образовывать новые фигуры.
- Если отрезок соединяет между собой несоседние вершины, он носит название диагонали.
- Если фигура лежит относительно одной прямой в любой полуплоскости, она называется выпуклой. При этом прямая содержит в себе одну сторону фигуры и сама принадлежит полуплоскости.
- Угол, смежный внутреннему углу многоугольника при некоторой вершине, называется внешним.
- Если все стороны и углы многоугольника равны, он называется правильным.
Треугольники
Треугольником в математике принято называть плоскую геометрическую фигуру, которая состоит из трех точек, не располагающихся на одной прямой. Эти точки соединены тремя отрезками.
Точки представляют собой вершины или треугольника, а отрезки — его стороны. Возле каждой из вершин образуется угол треугольника. Таким образом эта фигура имеет три угла, что видно из ее названия.
Различают следующие виды треугольников:
- Равносторонние — все стороны их равны по длине.
- Разносторонние — все стороны различаются по длине.
- Равнобедренные — две стороны из трех имеют одинаковую длину.
- Остроугольные — если все углы острые.
- Прямоугольные — если имеется прямой угол.
- Тупоугольные — если есть один тупой угол.
Четырехугольники
Плоская геометрическая фигура, имеющая четыре угла и четыре стороны, называется четырехугольником.
Если все углы у четырехугольника прямые — это прямоугольник.
Правильный четырехугольник носит название квадрата.
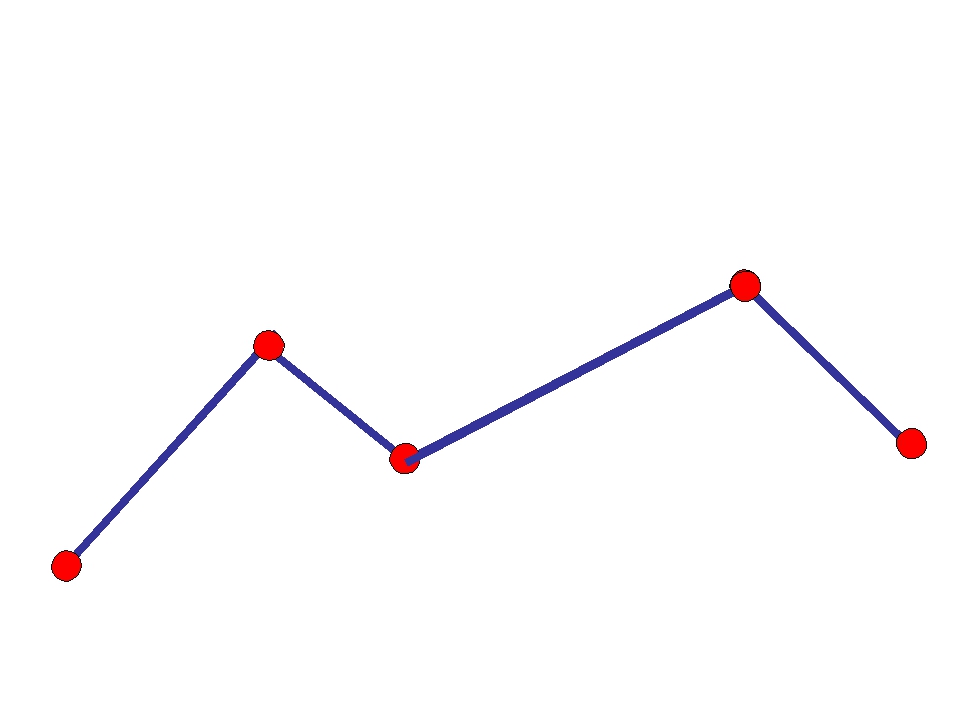
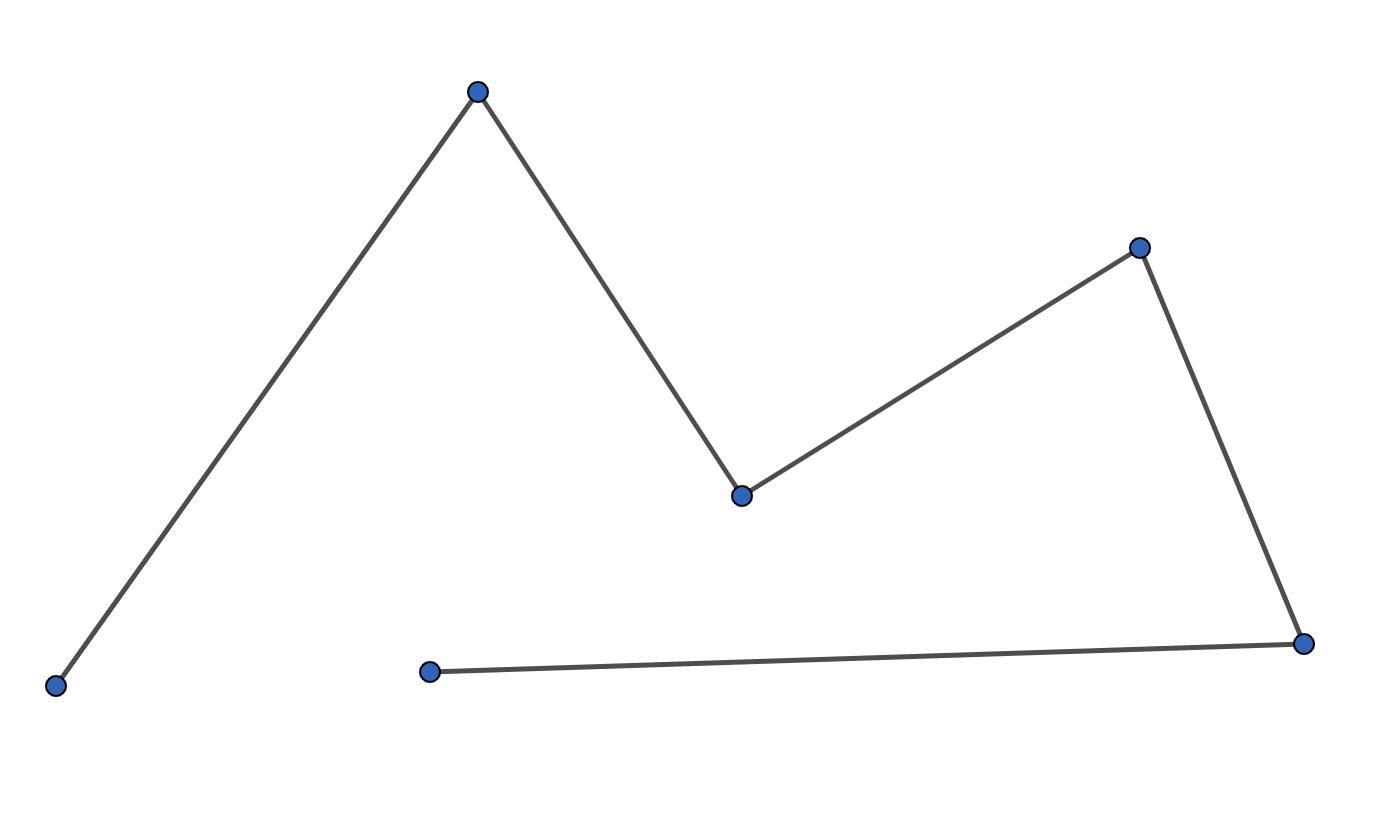
Типы ломаных линий
Рассматриваемые геометрические фигуры могут быть выстроены самыми разнообразными способами — они могут быть незамкнутыми и замкнутыми, пересекающимися и непересекающимися.
Замкнутая ломаная соответствует определенной геометрической фигуре — многоугольнику.
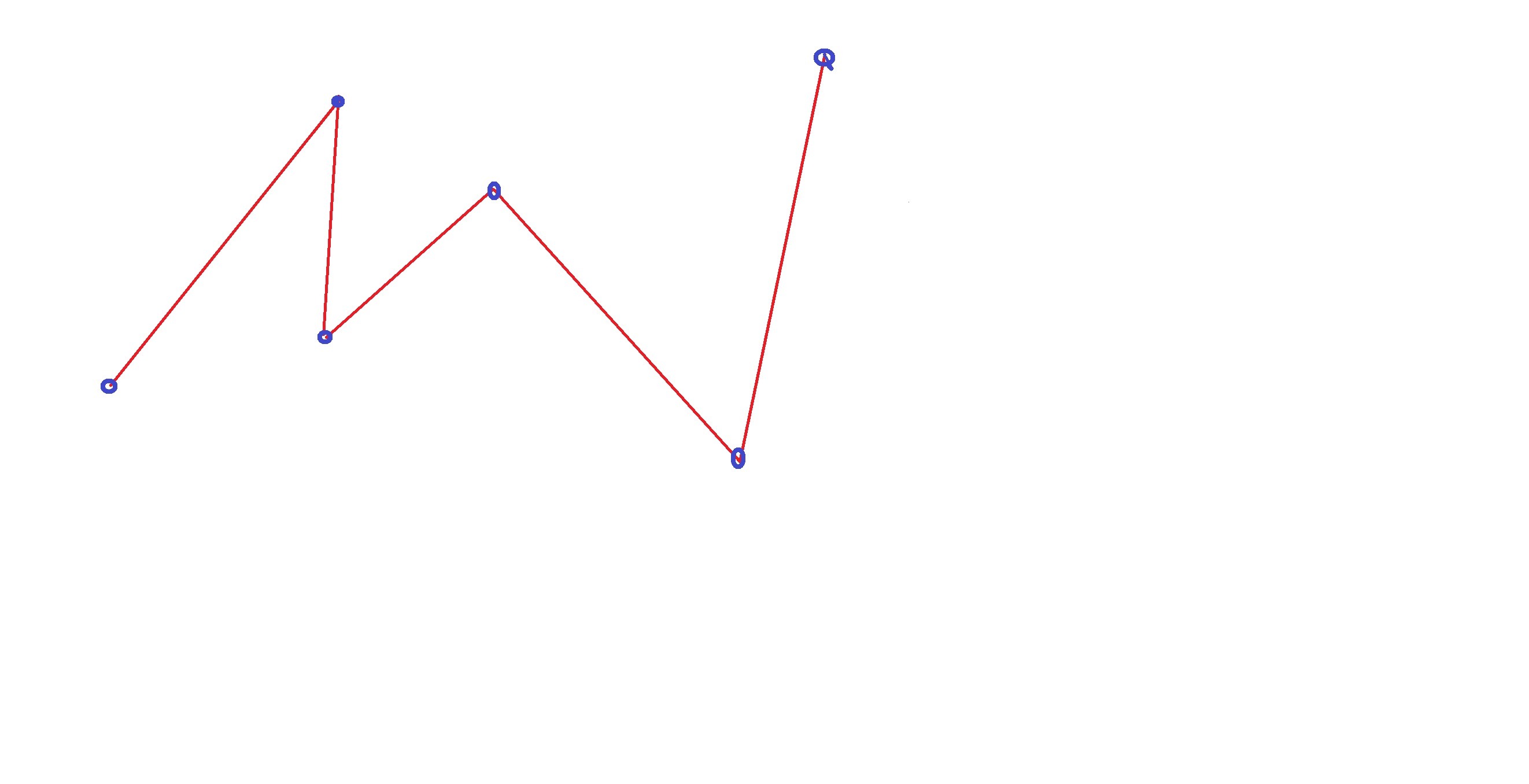
Если отрезки одной такой фигуры имеют точки пересечения друг с другом — эта линия называется самопересекающейся.
Всего существует 4 типа подобных линий по своей структуре:
- Замкнутые, которые не имеют пересечений.
- Незамкнутые, которые не имеют пересечений.
- Незамкнутые самопересекающиеся.
- Замкнутые, имеющие самопересечения.

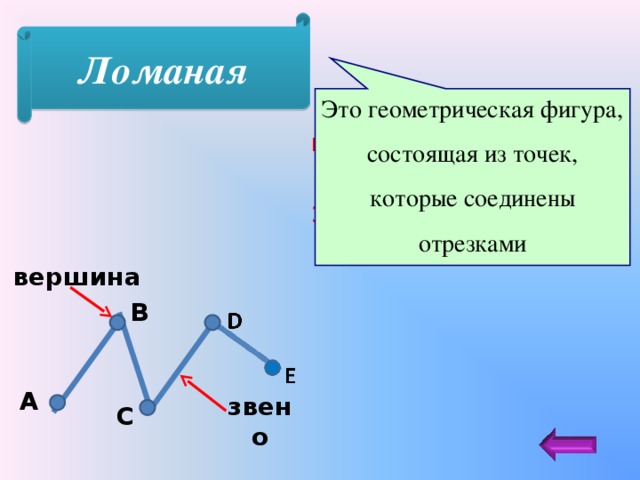
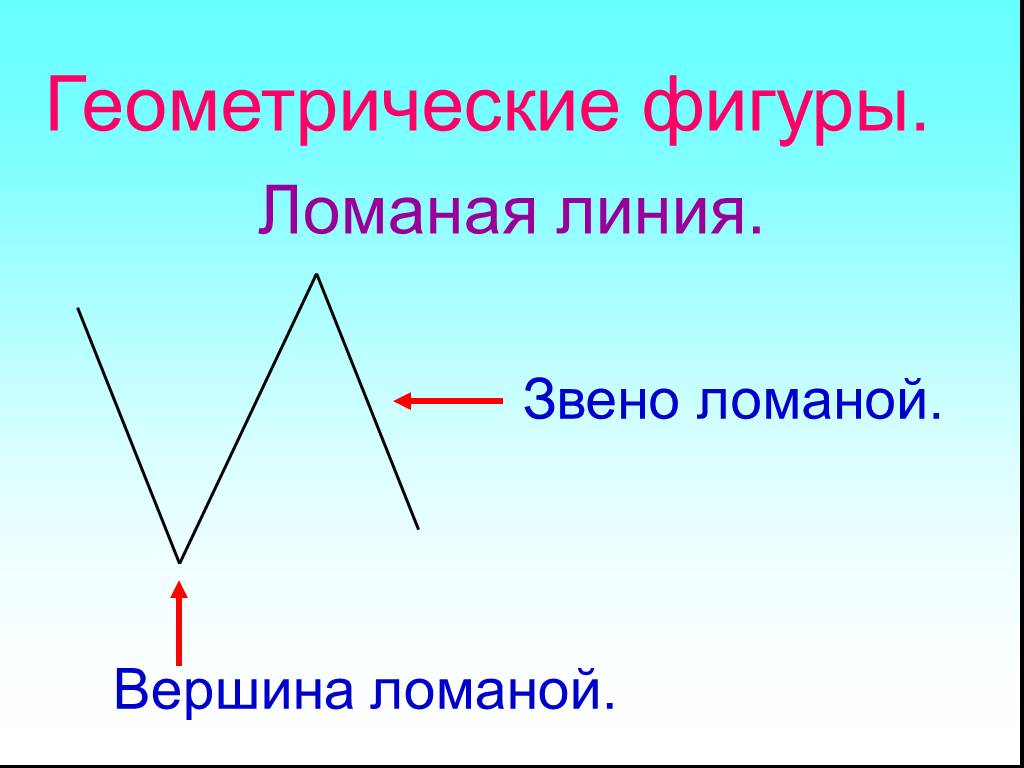
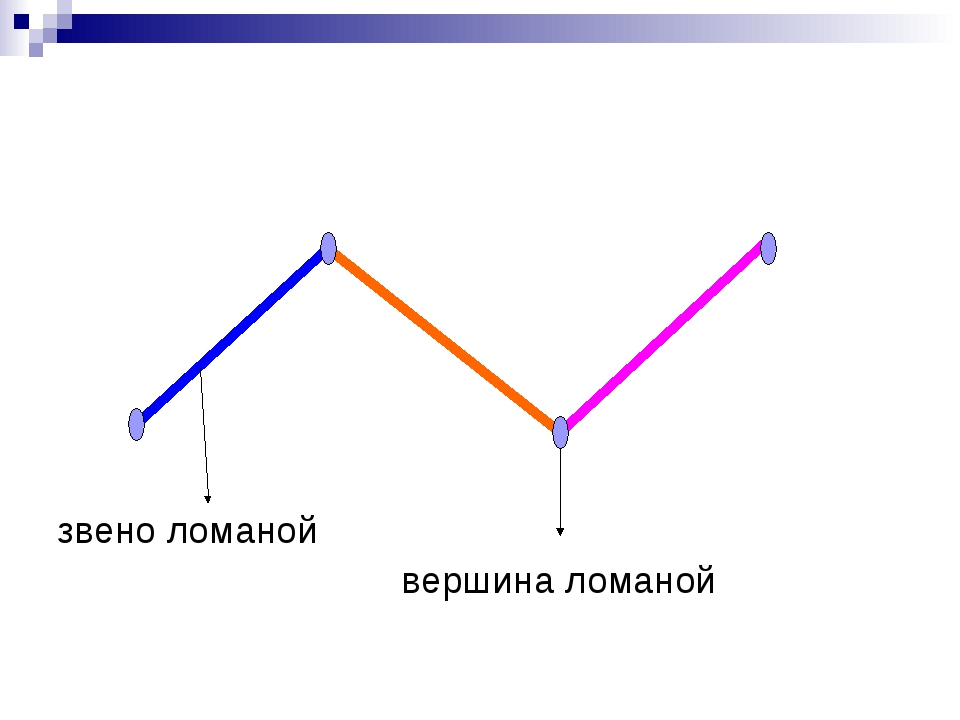
Звенья, вершины и длина
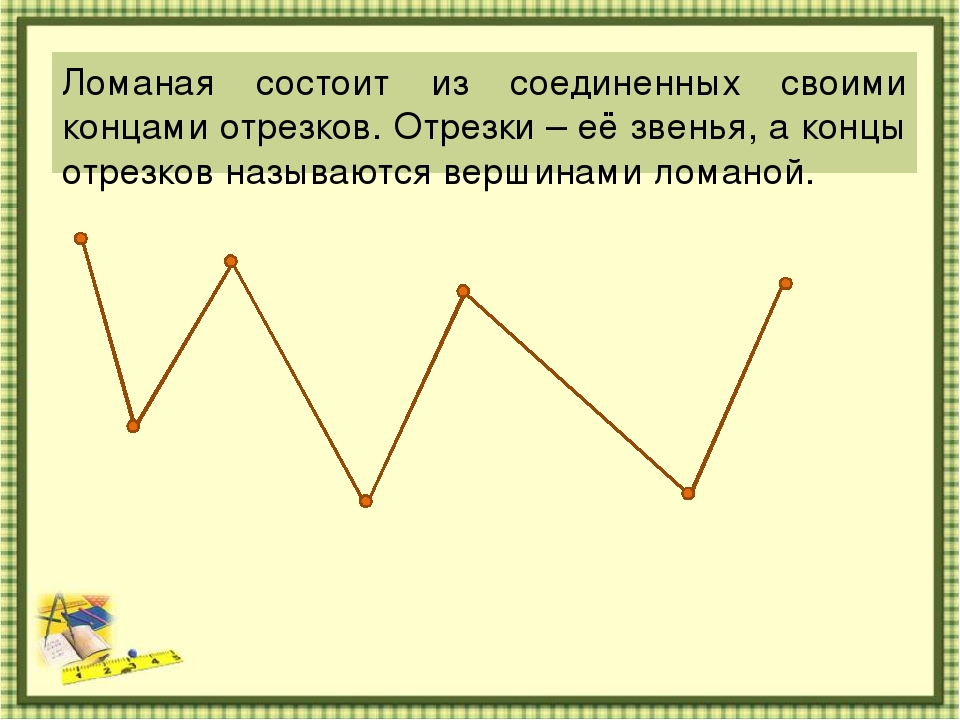
Чтобы полностью усвоить сущность и свойства этого понятия, рассмотрим, что такое звенья ломаной линии в математике, а также что представляют собой ее вершины и длина:
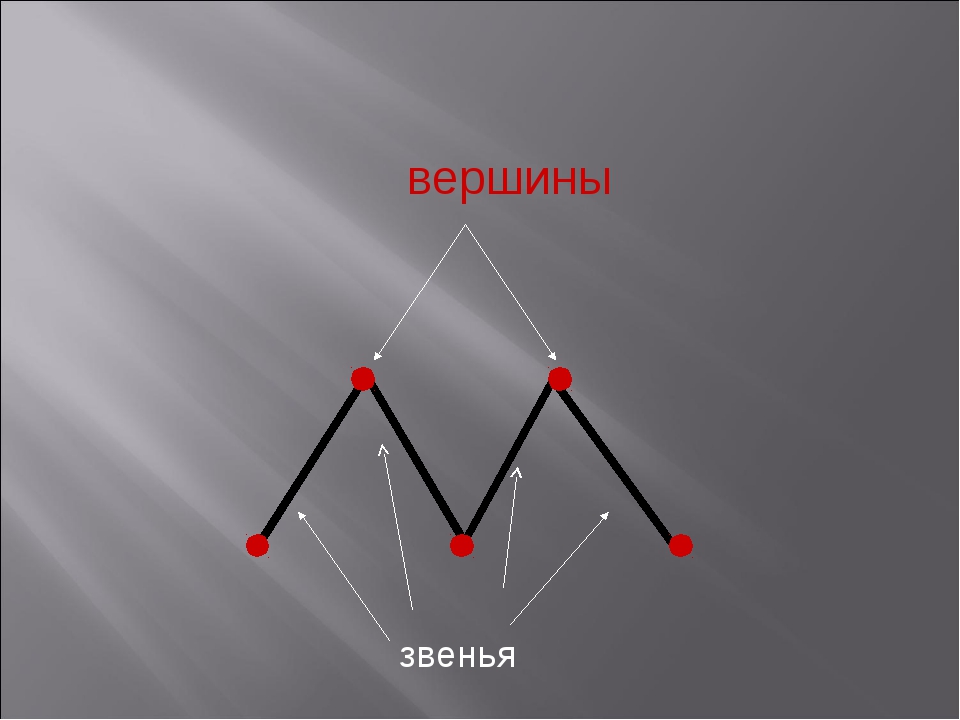
- Отдельные отрезки, составляющие такую линию, называются ее звеньями. Каждая такая линия может состоять как минимум из двух звеньев. Максимальное количество звеньев при этом не ограничено.
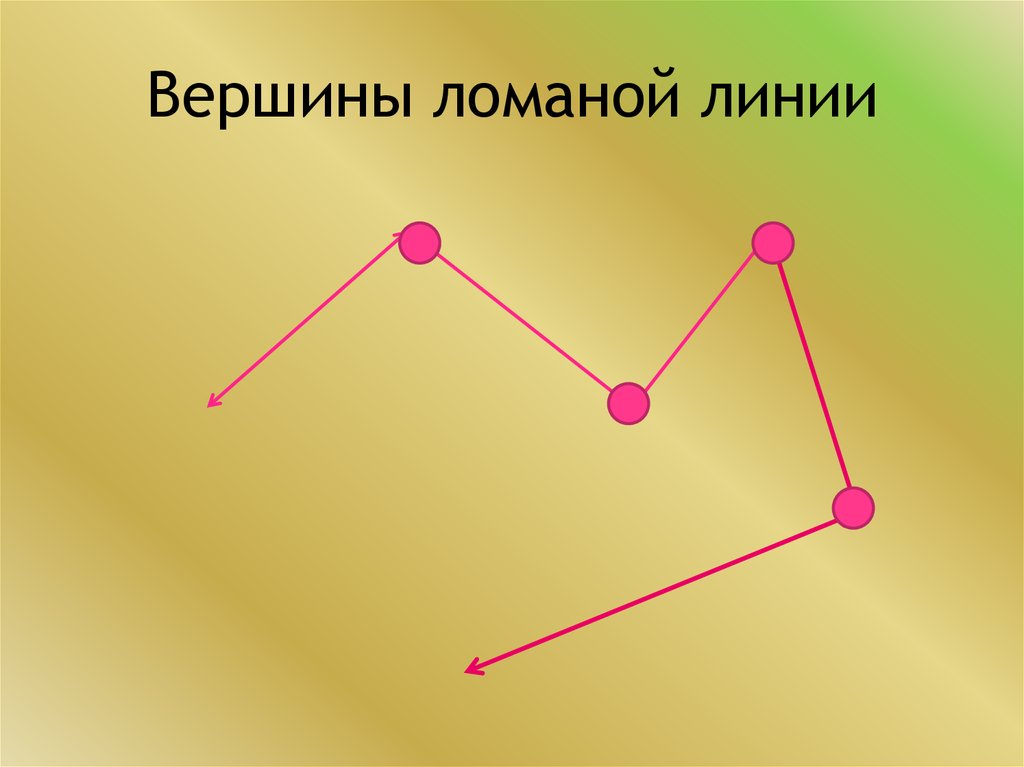
- Точки соединения концов этих отрезков называются вершинами.
- Если концы ломаной соединяются в одной точке, такая фигура носит название замкнутой. Ее звенья могут иметь взаимные пересечения.
- Если же звенья одной замкнутой линии не пересекаются между собой, она называется многоугольником.
- Геометрическое понятие длины ломаной включает в себя сумму длин всех ее звеньев.
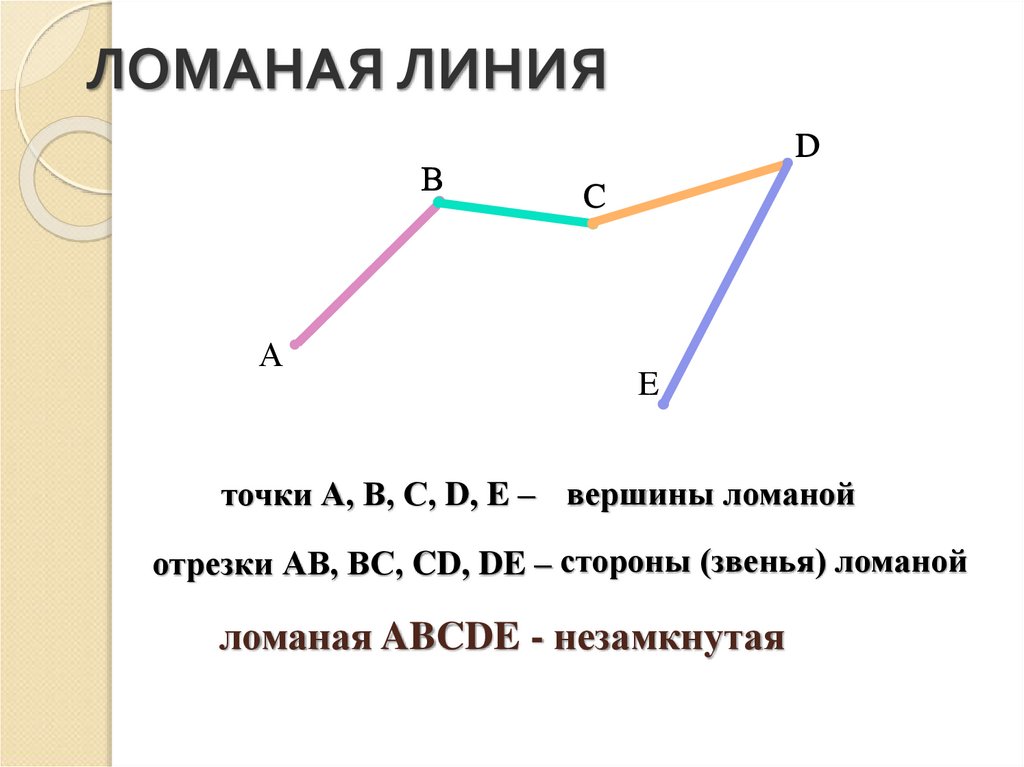
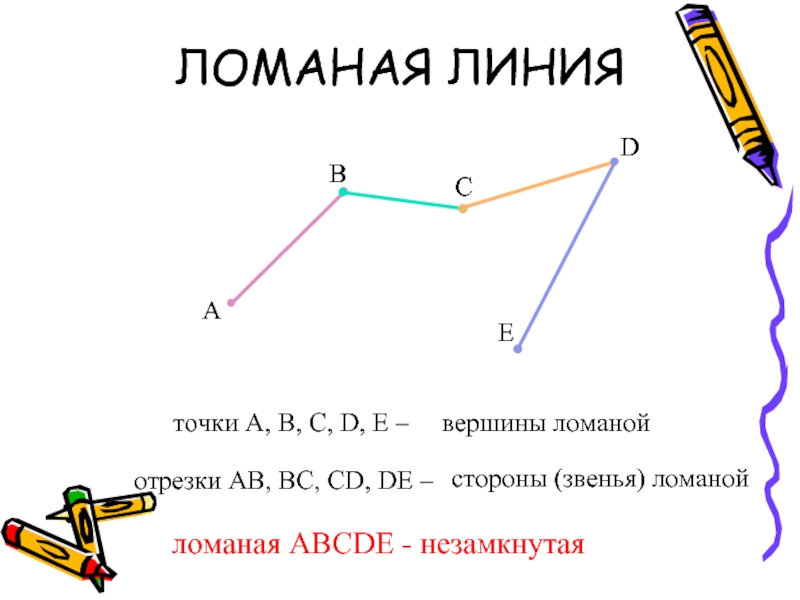
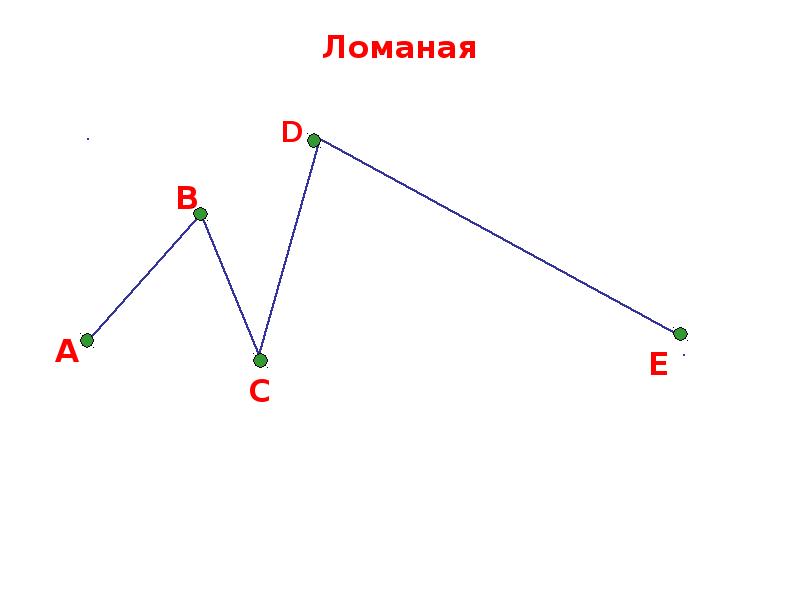
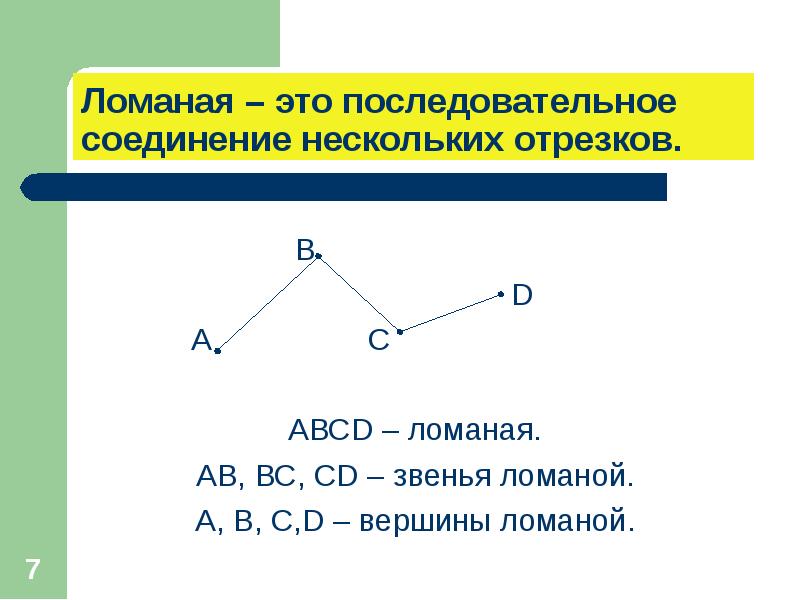
Обозначение ее составляется из заглавных латинских букв, которые стоят на вершинах:
- Каждая вершина на рисунке обозначается одной буквой (например: A, B, C, D или E).
- Звено принято обозначать двумя буквами (концы соответствующего отрезка, например: AB, BC, CD, DE).
В целом такую совокупность принято называть ABCDE или EDCBA.