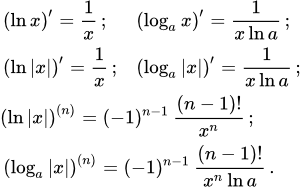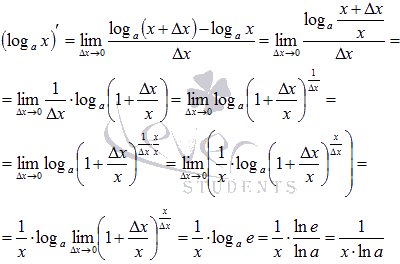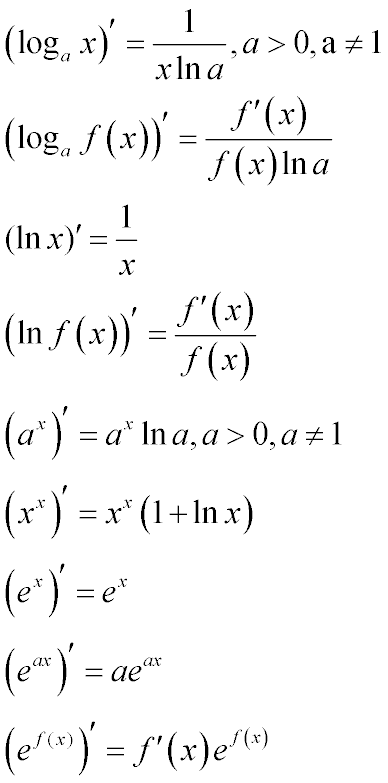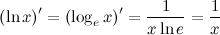Производная натурального логарифма

Численное значение

Методы вычисления

Для расчета численного значения натурального логарифма числа можно использовать разложение его в ряд Тейлора в виде:

ln⁡(1+x)=x(11−x(12−x(13−x(14−x(15−…)))))for|x|<1.{\displaystyle \ln(1+x)=x\,\left({\frac {1}{1}}-x\,\left({\frac {1}{2}}-x\,\left({\frac {1}{3}}-x\,\left({\frac {1}{4}}-x\,\left({\frac {1}{5}}-\dots \right)\right)\right)\right)\right)\quad {\rm {for}}\quad \left|x\right|<1.}

Чтобы получить лучшую скорость сходимости, можно воспользоваться следующим тождеством:

ln⁡(x)=ln⁡(1+y1−y){\displaystyle \ln(x)=\ln \left({\frac {1+y}{1-y}}\right)}	=2y(11+13y2+15y4+17y6+19y8+…){\displaystyle =2\,y\,\left({\frac {1}{1}}+{\frac {1}{3}}y^{2}+{\frac {1}{5}}y^{4}+{\frac {1}{7}}y^{6}+{\frac {1}{9}}y^{8}+\dots \right)}
	=2y(11+y2(13+y2(15+y2(17+y2(19+…))))){\displaystyle =2\,y\,\left({\frac {1}{1}}+y^{2}\,\left({\frac {1}{3}}+y^{2}\,\left({\frac {1}{5}}+y^{2}\,\left({\frac {1}{7}}+y^{2}\,\left({\frac {1}{9}}+\dots \right)\right)\right)\right)\right)}

при условии, что y = (x−1)/(x+1) и x > 0.

Для ln(x), где x > 1, чем ближе значение x к 1, тем быстрее скорость сходимости. Тождества, связанные с логарифмом, можно использовать для достижения цели:

ln⁡(123,456){\displaystyle \ln(123{,}456)}	=ln⁡(1,23456×102){\displaystyle =\ln(1{,}23456\times 10^{2})}
	=ln⁡(1,23456)+ln⁡(102){\displaystyle =\ln(1{,}23456)+\ln(10^{2})}
	=ln⁡(1,23456)+2×ln⁡(10){\displaystyle =\ln(1{,}23456)+2\times \ln(10)}
	≈ln⁡(1,23456)+2×2,3025851{\displaystyle \approx \ln(1{,}23456)+2\times 2{,}3025851}

Эти методы применялись ещё до появления калькуляторов, для чего использовались числовые таблицы и выполнялись манипуляции, аналогичные вышеописанным.

Высокая точность

Для вычисления натурального логарифма с большим количеством цифр точности ряд Тейлора не является эффективным, поскольку его сходимость медленная. Альтернативой является использование метода Ньютона, чтобы инвертировать в экспоненциальную функцию, ряд которой сходится быстрее.

Альтернативой для очень высокой точности расчёта является формула:

ln⁡x≈π2M(1,4s)−mln⁡2{\displaystyle \ln x\approx {\frac {\pi }{2M(1,4/s)}}-m\ln 2}

где M обозначает арифметико-геометрическое среднее 1 и 4/s, и

s=x2m>2p2,{\displaystyle s=x\,2^{m}>2^{p/2},}

m выбрано так, что p знаков точности достигается. (В большинстве случаев значение 8 для m вполне достаточно.) В самом деле, если используется этот метод, может быть применена инверсия Ньютона натурального логарифма для эффективного вычисления экспоненциальной функции. (Константы ln 2 и пи могут быть предварительно вычислены до желаемой точности, используя любой из известных быстро сходящихся рядов.)

Трансцендентность

Из теоремы Линдемана-Вейерштрасса (1885) вытекает следующее следствие: если аргумент x{\displaystyle x} есть алгебраическое число, отличное от единицы, то значение ln⁡x{\displaystyle \ln x} есть не только иррациональное, но и трансцендентное число.

Вычислительная сложность

Вычислительная сложность натуральных логарифмов (с помощью арифметико-геометрического среднего) равна O(M(n) ln n). Здесь n — число цифр точности, для которой натуральный логарифм должен быть оценен, а M(n) — вычислительная сложность умножения двух n-значных чисел.

Непрерывные дроби

Хотя для представления логарифма отсутствуют простые непрерывные дроби, но можно использовать несколько обобщённых непрерывных дробей, в том числе:

log⁡(1+x)=x11−x22+x33−x44+x55−⋯=x1−x+12×2−1x+22×3−2x+32×4−3x+42×5−4x+⋱{\displaystyle \log(1+x)={\frac {x^{1}}{1}}-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-{\frac {x^{4}}{4}}+{\frac {x^{5}}{5}}-\dots ={\cfrac {x}{1-0x+{\cfrac {1^{2}x}{2-1x+{\cfrac {2^{2}x}{3-2x+{\cfrac {3^{2}x}{4-3x+{\cfrac {4^{2}x}{5-4x+\ddots }}}}}}}}}}}

log⁡(1+2xy)=2xy+x1+x3y+2×1+2x5y+3×1+⋱=2xy+x−(1x)23(y+x)−(2x)25(y+x)−(3x)27(y+x)−⋱{\displaystyle \log \left(1+{\frac {2x}{y}}\right)={\cfrac {2x}{y+{\cfrac {x}{1+{\cfrac {x}{3y+{\cfrac {2x}{1+{\cfrac {2x}{5y+{\cfrac {3x}{1+\ddots }}}}}}}}}}}}={\cfrac {2x}{y+x-{\cfrac {(1x)^{2}}{3(y+x)-{\cfrac {(2x)^{2}}{5(y+x)-{\cfrac {(3x)^{2}}{7(y+x)-\ddots }}}}}}}}}

Примечания

Алгебра и начала анализа. Учебник для 10-11 классов. 12-е издание, М.: Просвещение, 2002. Стр. 233.
, с. 187.
, с. 34.
, с. 189..
↑
, Том I, стр. 159-160.
, Том I, стр. 164.
Рудио Ф. О квадратуре круга (Архимед, Гюйгенс, Ламберт, Лежандр). — Изд. 3-е. — М.-Л.: ОГИЗ, 1936. — С. 89. — 237 с. — (Классики естествознания).
Flashman, Martin. . Дата обращения 30 июня 2011.
J J O’Connor and E F Robertson. . The MacTutor History of Mathematics archive (сентябрь 2001). Дата обращения 30 июня 2011.
↑ , с. 325-328..
Рыбников К. А. История математики. В двух томах. — М.: Изд. МГУ, 1963. — Т. II. — С. 27, 230—231..
↑ , с. 623..
, с. 45-46, 99-100..
Дербишир, Джон. Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике. — Астрель, 2010. — 464 с. — ISBN 978-5-271-25422-2.
Weisstein, Eric W. (англ.). MathWorld. Дата обращения 26 апреля 2012.
Иванов М. Г. Размер и размерность // «Потенциал», август 2006.
Головин С. Ю. . Дата обращения 17 апреля 2012.
. Дата обращения 17 апреля 2012.
Welford, A. T. Fundamentals of skill. — London: Methuen, 1968. — P. 61. — ISBN 978-0-416-03000-6.

Происхождение термина

Сначала может показаться, что поскольку наша система счисления имеет основание 10, то это основание является более «натуральным», чем основание e. Но математически число 10 не является особо значимым. Его использование скорее связано с культурой, оно является общим для многих систем счисления, и связано это, вероятно, с числом пальцев у людей. Некоторые культуры основывали свои системы счисления на других основаниях: 5, 8, 12, 20 и 60.

log_e является «натуральным» логарифмом, поскольку он возникает автоматически и появляется в математике очень часто. Например, рассмотрим проблему производной логарифмической функции:

(loga⁡x)′=(1ln⁡a⋅ln⁡x)′=1ln⁡a(ln⁡x)′=1xln⁡a{\displaystyle (\log _{a}x)’=\left({\frac {1}{\ln a}}\cdot \ln {x}\right)’={\frac {1}{\ln a}}(\ln {x})’={\frac {1}{x\ln a}}}

Если основание a{\displaystyle a} равно e{\displaystyle e}, то производная равна просто 1x{\displaystyle {\frac {1}{x}}}, а при x = 1 эта производная равна 1. Другим обоснованием, по которому основание e логарифма является наиболее натуральным, является то, что он может быть довольно просто определён в терминах простого интеграла или ряда Тейлора, чего нельзя сказать о других логарифмах.

Дальнейшие обоснования натуральности не связаны со счислением. Так, например, есть несколько простых рядов с натуральными логарифмами. Пьетро Менголи и Николас Меркатор называли их логарифмус натуралис за несколько десятилетий до того, как Ньютон и Лейбниц разработали дифференциальное и интегральное исчисление.

Натуральный логарифм в интегрировании

Натуральный логарифм даёт простую интегральную функцию вида g(x) = f ‘(x)/f(x): первообразная функции g(x) имеет вид ln(|f(x)|). Это подтверждается цепным правилом и следующим фактом:

ddx(ln⁡|x|)=1x.{\displaystyle \ {d \over dx}\left(\ln \left|x\right|\right)={1 \over x}.}

В другом виде:

∫1xdx=ln⁡|x|+C{\displaystyle \int {1 \over x}dx=\ln |x|+C}

∫f′(x)f(x)dx=ln⁡|f(x)|+C.{\displaystyle \int {{\frac {f'(x)}{f(x)}}\,dx}=\ln |f(x)|+C.}

Ниже дан пример для g(x) = tan(x):

∫tan⁡(x)dx=∫sin⁡(x)cos⁡(x)dx{\displaystyle \int \tan(x)\,dx=\int {\sin(x) \over \cos(x)}\,dx}

∫tan⁡(x)dx=∫−ddxcos⁡(x)cos⁡(x)dx.{\displaystyle \int \tan(x)\,dx=\int {-{d \over dx}\cos(x) \over {\cos(x)}}\,dx.}

Пусть f(x) = cos(x) и f’(x)= — sin(x):

∫tan⁡(x)dx=−ln⁡|cos⁡(x)|+C{\displaystyle \int \tan(x)\,dx=-\ln {\left|\cos(x)\right|}+C}

∫tan⁡(x)dx=ln⁡|sec⁡(x)|+C{\displaystyle \int \tan(x)\,dx=\ln {\left|\sec(x)\right|}+C}

где C — произвольная константа.

Натуральный логарифм можно проинтегрировать с помощью интегрирования по частям:

∫ln⁡(x)dx=xln⁡(x)−x+C.{\displaystyle \int \ln(x)\,dx=x\ln(x)-x+C.}

Еще раз выпишем формулу производной логарифма по основанию . Эта формула имеет наиболее простой вид для натурального логарифма, для которого , . Тогда(1) .

Из-за такой простоты, натуральный логарифм очень широко используется в математическом анализе и в других разделах математики, связанных с дифференциальным исчислением. Логарифмические функции с другими основаниями можно выразить через натуральный логарифм, используя свойство (6):.

Производную логарифма по основанию можно найти из формулы (1), если вынести постоянную за знак дифференцирования:.

Другие способы доказательство производной логарифма

Здесь мы предполагаем, что нам известна формула производной экспоненты:(9) . Тогда мы можем вывести формулу производной натурального логарифма, учитывая, что логарифм является обратной функцией к экспоненте.

Докажем формулу производной натурального логарифма, применив формулу производной обратной функции:. В нашем случае . Обратной функцией к натуральному логарифму является экспонента:. Ее производная определяется по формуле (9). Переменные можно обозначить любой буквой. В формуле (9), заменим переменную x на y:. Поскольку , то. Тогда. Формула доказана.

Теперь докажем формулу производной натурального логарифма с помощью правила дифференцирования сложной функции. Поскольку функции и являются обратными друг к другу, то. Дифференцируем это уравнение по переменной (10) . Производная от икса равна единице:. Применяем правило дифференцирования сложной функции:. Здесь . Подставим в (10):. Отсюда.

Пример

Найти производные от ln 2x, ln 3x и ln nx.

Решение

Исходные функции имеют похожий вид. Поэтому мы найдем производную от функции y = ln nx. Затем подставим n = 2 и n = 3. И, тем самым, получим формулы для производных от ln 2x и ln 3x.

Итак, ищем производную от функцииy = ln nx. Представим эту функцию как сложную функцию, состоящую из двух функций:1) Функции , зависящей от переменной ;2) Функции , зависящей от переменной . Тогда исходная функция составлена из функций и .

Найдем производную от функции по переменной x:. Найдем производную от функции по переменной . Применяем формулу производной сложной функции.. Здесь мы подставили .

Итак, мы нашли:(11) . Мы видим, что производная не зависит от . Этот результат вполне естественен, если преобразовать исходную функцию, применяя формулу логарифма от произведения:. – это постоянная. Ее производная равна нулю. Тогда по правилу дифференцирования суммы имеем:.

Ответ

; ; .

См. также Все примеры вычисления производных с решениями > > >

Использование натурального логарифма при произвольном росте

— Ну конечно, — скажете вы, — это всё хорошо, если рост 100%-ный, а что в случае 5%, которые я получаю?»

Нет проблем. «Время», которое мы рассчитываем с помощью ln(), на самом деле является комбинацией процентной ставки и времени, тот самый Х из уравнения ex. Мы всего лишь решили задать процент как 100% для простоты, но мы вольны использовать любые числа.

Допустим, мы хотим достичь 30-кратного роста: берём ln(30) и получаем 3.4 Это означает:

ex = рост
e3.4 = 30

Очевидно, это уравнение означает «100%-ная доходность на протяжении 3.4 лет даёт рост в 30 раз». Мы можем записать это уравнение в таком виде:

ex = eставка*время
e100% * 3.4 года = 30

Мы можем менять значения «ставки» и «времени», лишь бы ставка * время оставалось 3.4. Например, если нас интересует 30-кратный рост — сколько нам придётся ждать при процентной ставке 5%?

ln(30) = 3.4
ставка * время = 3.4
0.05 * время = 3.4
время = 3.4 / 0.05 = 68 лет

Я рассуждаю так: «ln(30) = 3.4, значит, при 100%-ном росте это займёт 3.4 года. Если я удвою скорость роста, необходимое время уменьшится вдвое».

100% за 3.4 года = 1.0 * 3.4 = 3.4
200% за 1.7 года = 2.0 * 1.7 = 3.4
50% за 6.8 года = 0.5 * 6.8 = 3.4
5% за 68 года = .05 * 68 = 3.4 .

Здорово, правда? Натуральный логарифм может использоваться с любыми значениями процентной ставки и времени, поскольку их произведение остаётся постоянным. Можете перемещать значения переменных сколько душе угодно.

Логарифмы со специальным обозначением

Для некоторых логарифмов в математике введены специальные обозначения. Это связано с тем, что такие логарифмы встречаются особенно часто. К таким логарифмам относятся десятичный логарифм и натуральный логарифм. Для этих логарифмов справедливы все правила, что и для обычных логарифмов.

Десятичный логарифм

Десятичный логарифм обозначается lg и имеет основание 10, т.е.

Чтобы вычислить десятичный логарифм, нужно 10 возвести в степень X.

Например, вычислим lg100

Натуральный логарифм

Натуральный логарифм обозначается ln и имеет основание e, то есть

Чтобы вычислить данный логарифм нужно число е возвести в степень x. Некоторые из вас спросят, что это за число такое е? Число е – это иррациональное число, т.е. точное его значение вычислить невозможно. е = 2,718281…

Сейчас не будем подробно разбирать, зачем это число нужно, просто запомним, что

И вычислить его можно таким образом:

Основные свойства логарифмов

Логарифмы можно преобразовывать, но для этого необходимо знать правила, которые называются основными свойствами логарифмов. Данные свойства обязательно нужно знать каждому ученику! Без знания этих свойств невозможно решить ни одну серьезную логарифмическую задачу. Вот эти свойства:

Совет – тренируйтесь применять эти свойства в обе стороны, то есть как слева направо, так и справа налево!

Рассмотрим свойства логарифмов на примерах.

Логарифмический ноль и логарифмическая единица

Это следствия из определения логарифма. И их нужно обязательно запомнить. Эти простейшие свойства нередко вводят учеников в ступор.

Запомните, что логарифм от a по основанию а всегда равен единице:

log_a a = 1 – это логарифмическая единица.

Если же в аргументе стоит единица, то такой логарифм всегда равен нулю независимо от основания, так как a = 1:

log_a 1 = 0 – логарифмический ноль.

Основное логарифмическое тождество

В первой формуле число m становится степенью, которая стоит в аргументе. Данное число может быть любым. Некоторые выражения могут быть решены только с помощью этого тождества.

Вторая формула по сути является просто переформулированным определением логарифма

Разберем применение тождества на примере:

Необходимо найти значение выраженияСначала преобразуем логарифм

Вернемся к исходному выражению и применим правило умножения степеней с одинаковым основанием:Теперь применим основное логарифмическое тождество и получим:

Сумма логарифмов. Разница логарифмов

Логарифмы с одинаковыми основаниями можно складывать:Логарифмы с одинаковыми основаниями можно вычитать:Мы видим, что исходные выражения состояли из логарифмов, которые по отдельности не вычисляются, а при применении свойств логарифмов у нас получились нормальные числа. Поэтому повторим, что основные свойства логарифмов нужно знать обязательно!

Обратите внимание, что формулы суммы и разности логарифмов верны только для логарифмов с одинаковыми основаниями! Если основания разные, то данные свойства применять нельзя!

Вынесение показателя степени из логарифма:

Переход к новому основанию

Когда мы разбирали формулы суммы и разности логарифмов, то обращали внимание на то, что основания логарифмов должны быть при этом одинаковыми. А что же делать, если основания логарифмов разные? Воспользоваться свойством перехода к новому основанию

Такие формулы чаще всего нужны при решении логарифмических уравнений и неравенств.

Разберем на примере.

Необходимо найти значение такого выраженияДля начала преобразуем каждый логарифм с помощью свойства вынесения показателя степени из логарифма:

Теперь применим переход к новому основанию для второго логарифма:Подставим полученные результаты в исходное выражение:

Определение

ln(a) определяется как площадь под кривой f(x) = 1/x от 1 до a.

Формально ln(a) может быть определён как площадь, заключённая под кривой графика 1/x на участке от 1 до a, т. е. как интеграл:

ln⁡a=∫1a1xdx.{\displaystyle \ln a=\int _{1}^{a}{\frac {1}{x}}\,dx.}

Это действительно логарифм, поскольку он удовлетворяет фундаментальному свойству логарифма:

ln⁡ab=ln⁡a+ln⁡b{\displaystyle \ln ab=\ln a+\ln b}.

Это можно продемонстрировать, допуская t=xa{\displaystyle t={\frac {x}{a}}} следующим образом:

ln⁡ab=∫1ab1xdx=∫1a1xdx+∫aab1xdx=∫1a1xdx+∫1b1tdt=ln⁡a+ln⁡b{\displaystyle \ln ab=\int _{1}^{ab}{\frac {1}{x}}\;dx=\int _{1}^{a}{\frac {1}{x}}\;dx\;+\int _{a}^{ab}{\frac {1}{x}}\;dx=\int _{1}^{a}{\frac {1}{x}}\;dx\;+\int _{1}^{b}{\frac {1}{t}}\;dt=\ln a+\ln b}

Число e может быть определено как единственное действительное число a такое, что ln(a) = 1.

Или же, если показательная функция была определена раньше с использованием бесконечных рядов, натуральный логарифм может быть определён как обратная к ней функция, т. е. ln — это функция, такая что eln⁡(x)=x{\displaystyle e^{\ln(x)}=x}. Так как диапазон значений экспоненциальной функции от реальных аргументов есть все положительные вещественные числа, а экспоненциальная функция строго возрастает, то это хорошо определённая функция для всех положительных x.

Отпадный пример: Правило семидесяти двух

Правило семидесяти двух — математический приём, позволяющий оценить, сколько времени понадобится, чтобы ваши деньги удвоились. Сейчас мы его выведем (да!), и более того, мы попробуем уяснить его суть.

Сколько времени понадобится, чтобы удвоить ваши деньги при 100% ставке, нарастающей ежегодно?

Оп-па. Мы использовали натуральный логарифм для случая с непрерывным ростом, а теперь ты ведёшь речь о ежегодном начислении? Не станет ли это формула непригодной для такого случая? Да, станет, однако для реальных процентных ставок вроде 5%, 6% или даже 15%, разница между ежегодным начислением процентов и непрерывным ростом будет невелика. Так что грубая оценка работает, мм, грубо, так что мы сделаем вид, что у нас полностью непрерывное начисление.

Теперь вопрос прост: Как быстро можно удвоиться при 100%-ном росте? ln(2) = 0.693. Нужно 0.693 единиц времени (лет — в нашем случае), чтобы удвоить нашу сумму с непрерывным ростом 100%.

Так, а что если процентная ставка — не 100%, а скажем, 5% или 10%?

Легко! Поскольку ставка * время = 0.693, мы удвоим сумму:

ставка * время = 0.693
время = 0.693 / ставка

Получается, если рост 10%-ный, это займёт 0.693 / 0.10 = 6.93 лет на удвоение.

Чтобы упростить вычисления, давайте домножим обе части на 100, тогда можно будет говорить «10», а не «0.10»:

время на удвоение = 69.3 / ставка, где ставка выражена в процентах.

Теперь черёд удваиваться при ставке 5%, 69.3 / 5 = 13.86 лет. Однако 69.3 — не самое удобное делимое. Давайте выберем близкое число, 72, которое удобно делить на 2, 3, 4, 6, 8 и другие числа.

время на удвоение = 72 / ставка

что и является правилом семидесяти двух. Всё шито-крыто.

Если вам нужно найти время для утроения, можете использовать ln(3) ~ 109.8 и получить

время на утроение = 110 / ставка

Что является ещё одним полезным правилом. «Правило 72» применимо росту по процентным ставкам, росту населения, культур бактерий, и всего, что растёт экспоненциально.

Производная и разложение в ряд Тейлора

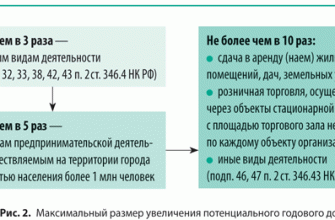
Многочлены Тейлора дают точную аппроксимацию для ln⁡(1+x){\displaystyle \ln(1+x)} только в области сходимости −1 < x ≤ 1.

Используя то, что производная натурального логарифма равна

(ln⁡x)′=1x,{\displaystyle (\ln x)’={\frac {1}{x}},}

можно выполнить разложение ln⁡(1+x){\displaystyle \ln(1+x)} в ряд Тейлора около x = 0, называемое иногда рядом Меркатора:

ln⁡(1+x)=∑n=1∞(−1)n+1nxn=x−x22+x33−…for|x|≤1{\displaystyle \ln(1+x)=\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}x^{n}=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-\dots \quad {\rm {for}}\quad \left|x\right|\leq 1\quad }

unlessx=−1{\displaystyle {\rm {unless}}\quad x=-1}

Ограничение этого бесконечного ряда i-м членом порождает многочлены Тейлора i-го порядка, содержащие степени не выше i-й. На рисунке справа приведены графики функции ln⁡(1+x){\displaystyle \ln(1+x)} и некоторых многочленов Тейлора около x = 0. Аппроксимации сходятся к функции только в области сходимости −1 < x ≤ 1, а за её пределами быстро отклоняются от точной функции, причем многочлены высших степеней дают бо́льшую ошибку.

Подставляя x−1 вместо x, получаем альтернативную форму для ln(x), а именно:

ln⁡(x)=∑n=1∞(−1)n+1n(x−1)n{\displaystyle \ln(x)=\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}(x-1)^{n}}

ln⁡(x)=(x−1)−(x−1)22+(x−1)33−(x−1)44+…{\displaystyle \ln(x)=(x-1)-{\frac {(x-1)^{2}}{2}}+{\frac {(x-1)^{3}}{3}}-{\frac {(x-1)^{4}}{4}}+\dots }

for|x−1|≤1unlessx={\displaystyle {\rm {for}}\quad \left|x-1\right|\leq 1\quad {\rm {unless}}\quad x=0.}

С помощью преобразования Эйлера из ряда Тейлора можно получить следующее выражение, справедливое для любого |x| > 1:

ln⁡xx−1=∑n=1∞1nxn=1x+12×2+13×3+…{\displaystyle \ln {x \over {x-1}}=\sum _{n=1}^{\infty }{1 \over {nx^{n}}}={1 \over x}+{1 \over {2x^{2}}}+{1 \over {3x^{3}}}+\dots }

Также заметим, что xx−1{\displaystyle x \over {x-1}} — это её собственная инверсная функция, поэтому для получения натурального логарифма определенного числа y нужно просто для x присвоить значение yy−1{\displaystyle y \over {y-1}}.

Некоторые применения

Теория чисел

Распределение простых чисел асимптотически подчиняется простым законам:

Число простых чисел в интервале от 1 до n{\displaystyle n} приблизительно равно nln⁡n{\displaystyle {\frac {n}{\ln n}}}.
k-е простое число приблизительно равно kln⁡k{\displaystyle k\ln k}.

Математический анализ

См. также: Список интегралов от логарифмических функций

Логарифмы нередко возникают при нахождении интегралов и при решении дифференциальных уравнений. Примеры:

∫tg⁡xdx=−ln⁡|cos⁡x|+C;∫dxx2+a=−ln⁡ | x+x2+a |+C{\displaystyle \int {\operatorname {tg} x}\,dx=-\ln |\cos x|+C;\quad \int {\frac {dx}{\sqrt {x^{2}+a}}}=-\ln \ \left|\ x+{\sqrt {x^{2}+a}}\ \right|+C}

Теория вероятностей и статистика

В статистике и теории вероятностей логарифм входит в ряд практически важных вероятностных распределений. Например, логарифмическое распределение используется в генетике и физике. Логнормальное распределение часто встречается в ситуациях, когда исследуемая величина есть произведение нескольких независимых положительных случайных переменных.

Для оценки неизвестного параметра широко применяются метод максимального правдоподобия и связанная с ним логарифмическая функция правдоподобия.

Флуктуации при случайном блуждании описывает закон Хинчина-Колмогорова.

Фракталы и размерность

Треугольник Серпинского (справа)

Логарифмы помогают выразить размерность Хаусдорфа для фрактала. Например, рассмотрим треугольник Серпинского, который получается из равностороннего треугольника последовательным удалением аналогичных треугольников, линейный размер каждого из которых на каждом этапе уменьшается вдвое (см. рисунок). Размерность результата определяется по формуле:

ln⁡3ln⁡2≈1,58{\displaystyle {\frac {\ln 3}{\ln 2}}\approx 1{,}58}

Механика и физика

в статистической термодинамике — одна из важнейших функций состояния термодинамической системы, характеризующая степень её хаотичности.

Формула Циолковского применяется для расчёта скорости ракеты.

Химия и физическая химия

Уравнение Нернста связывает окислительно-восстановительный потенциал системы с активностями веществ, входящих в электрохимическое уравнение, а также со стандартными электродными потенциалами окислительно-восстановительных пар.

Логарифм используется в определениях таких величин, как показатель константы автопротолиза (самоионизации молекулы) и водородный показатель (кислотности раствора).

Психология и физиология

Человеческое восприятие многих явлений хорошо описывается логарифмическим законом.

Закон Вебера — Фехнера — эмпирический психофизиологический закон, заключающийся в том, что интенсивность ощущения пропорциональна логарифму интенсивности стимула — громкости звука, яркости света.

Закон Фиттса: чем дальше или точнее выполняется движение организма, тем больше коррекции необходимо для его выполнения и тем дольше эта коррекция исполняется.

Время на принятие решения при наличии выбора можно оценить по .

Производная натурального логарифма и логарифма по основанию a