Линейная функция

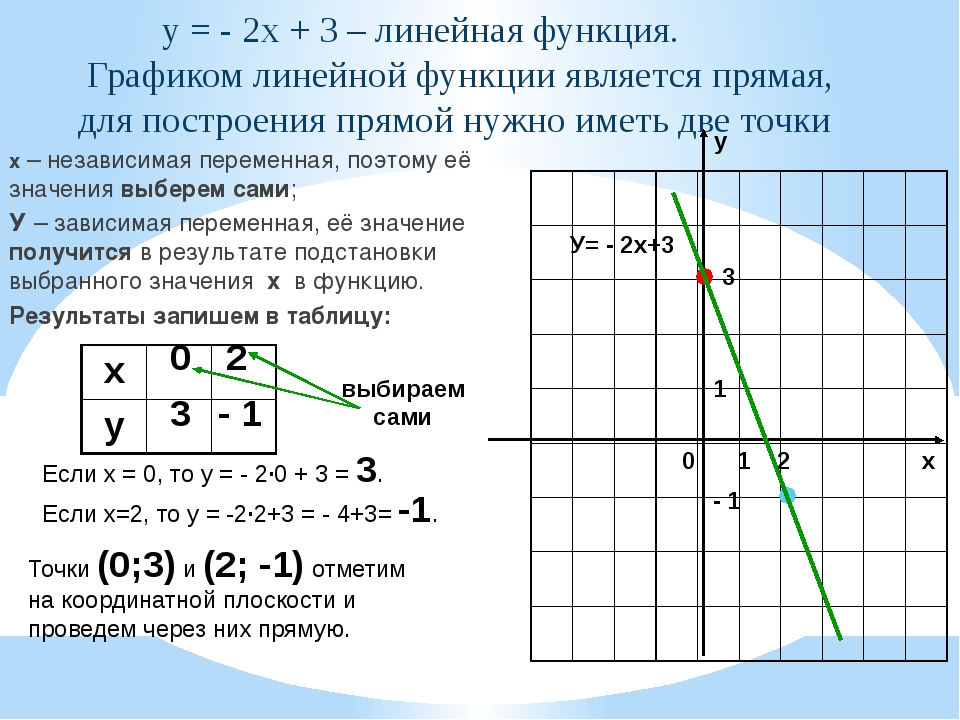
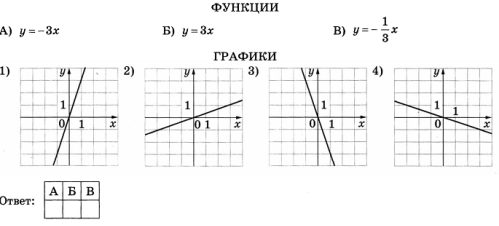
3. Рассмотрение примера на свойства параметров функции

Рас­смот­рим за­да­чи.

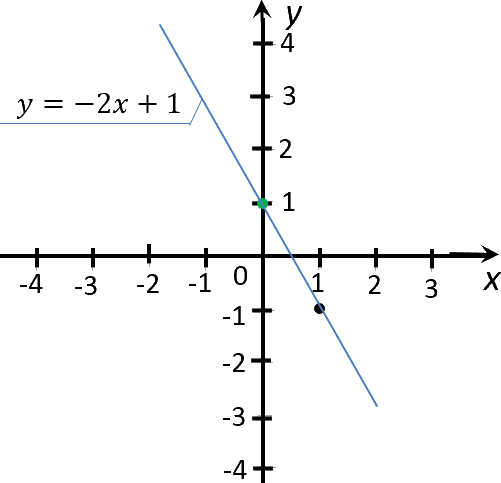
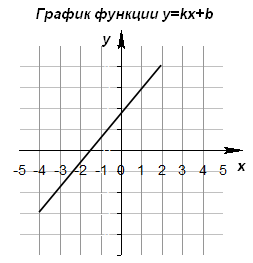
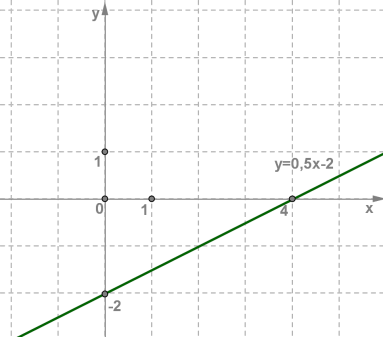
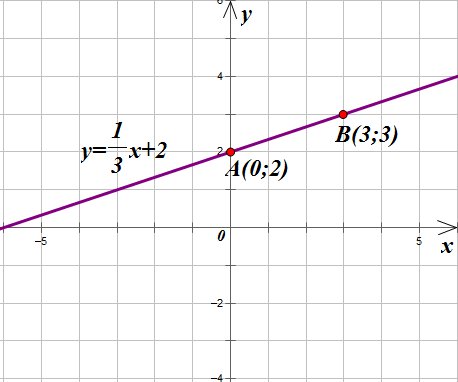
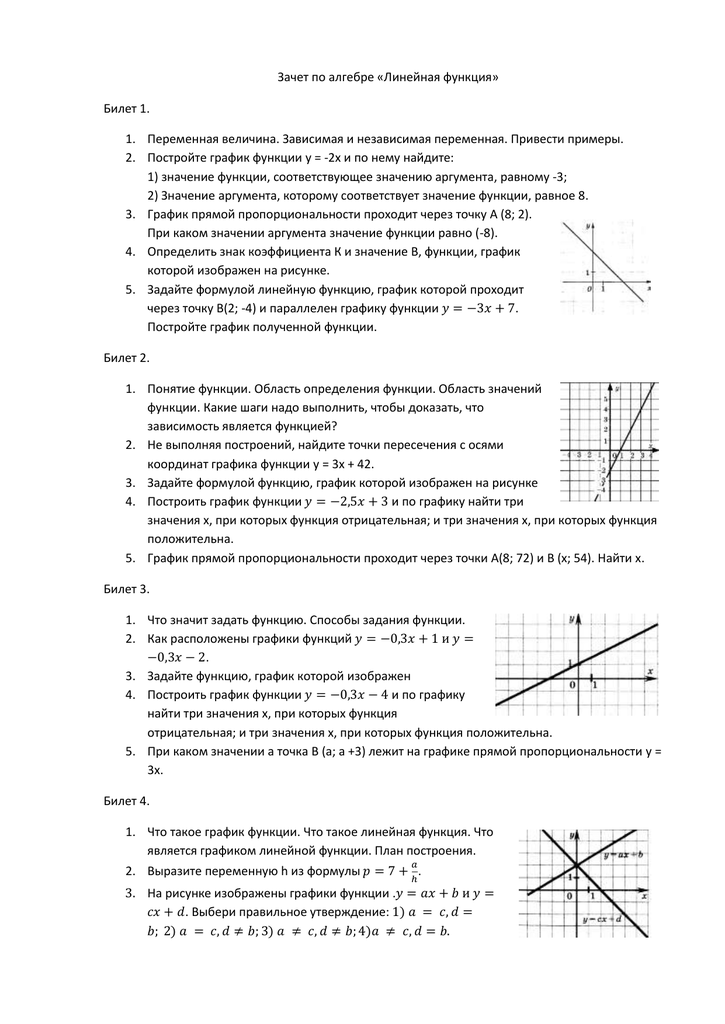
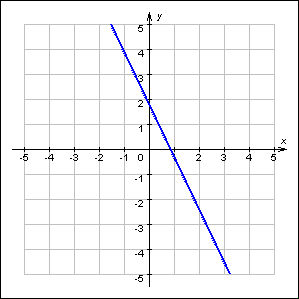
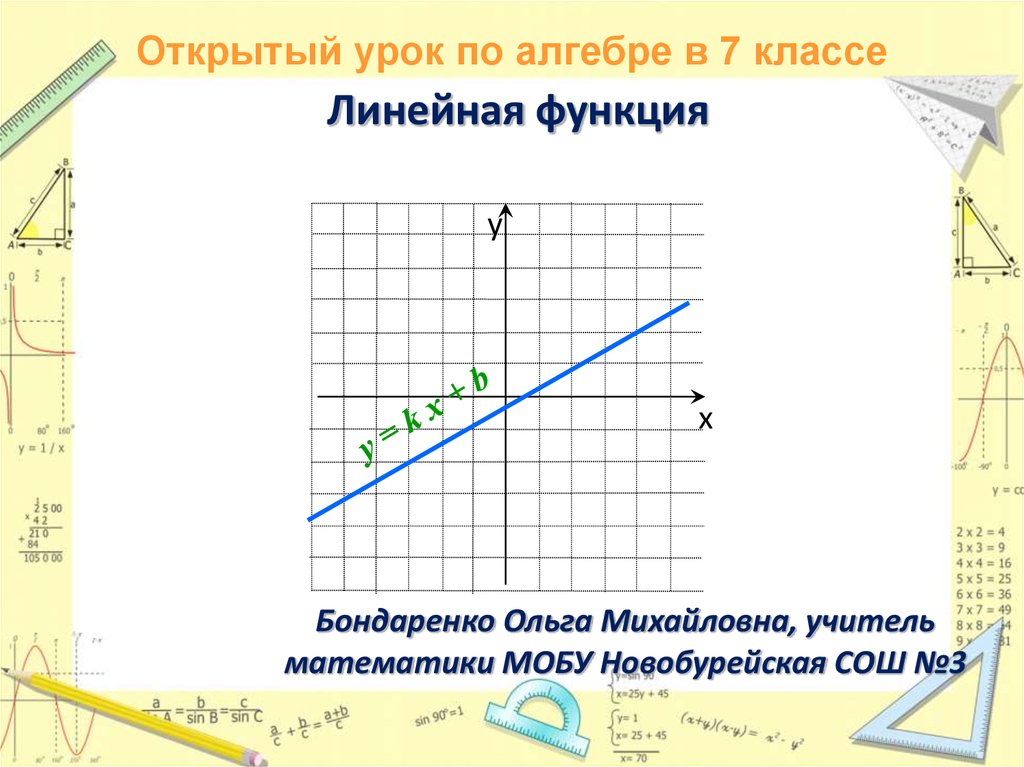
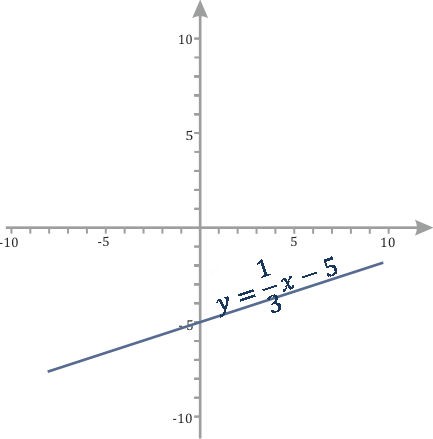
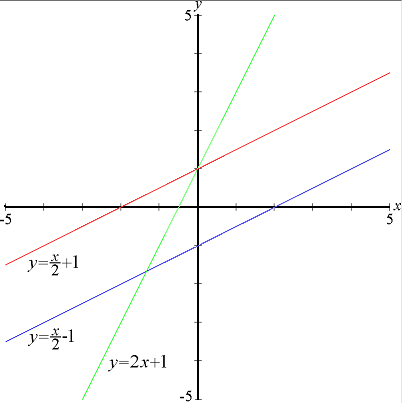
При­мер 2 – опре­де­лить знаки па­ра­мет­ров k и m по за­дан­но­му гра­фи­ку функ­ции:

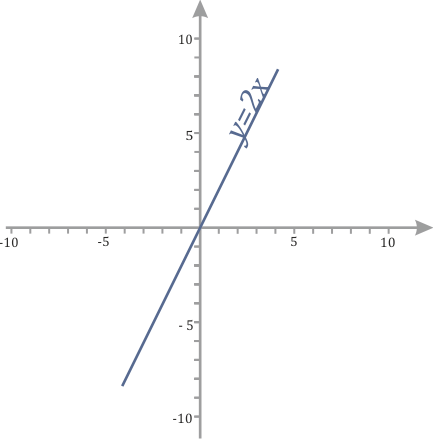
Пря­мая пе­ре­се­ка­ет ось у в по­ло­жи­тель­ном ее луче, зна­чит m имеет знак плюс, угол между пря­мой и по­ло­жи­тель­ным на­прав­ле­ни­ем оси х ост­рый, функ­ция воз­рас­та­ет, зна­чит знак k также плюс.

Рис. 2.

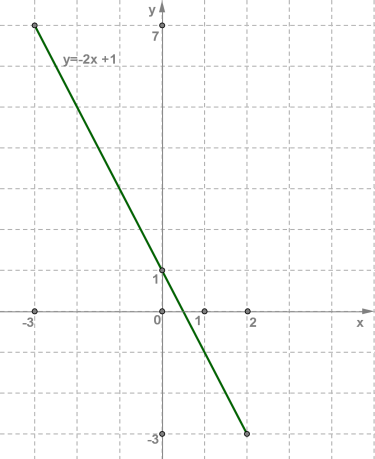
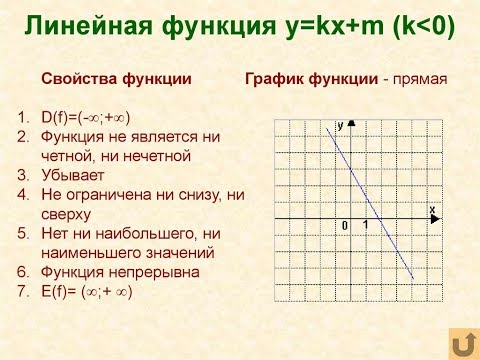
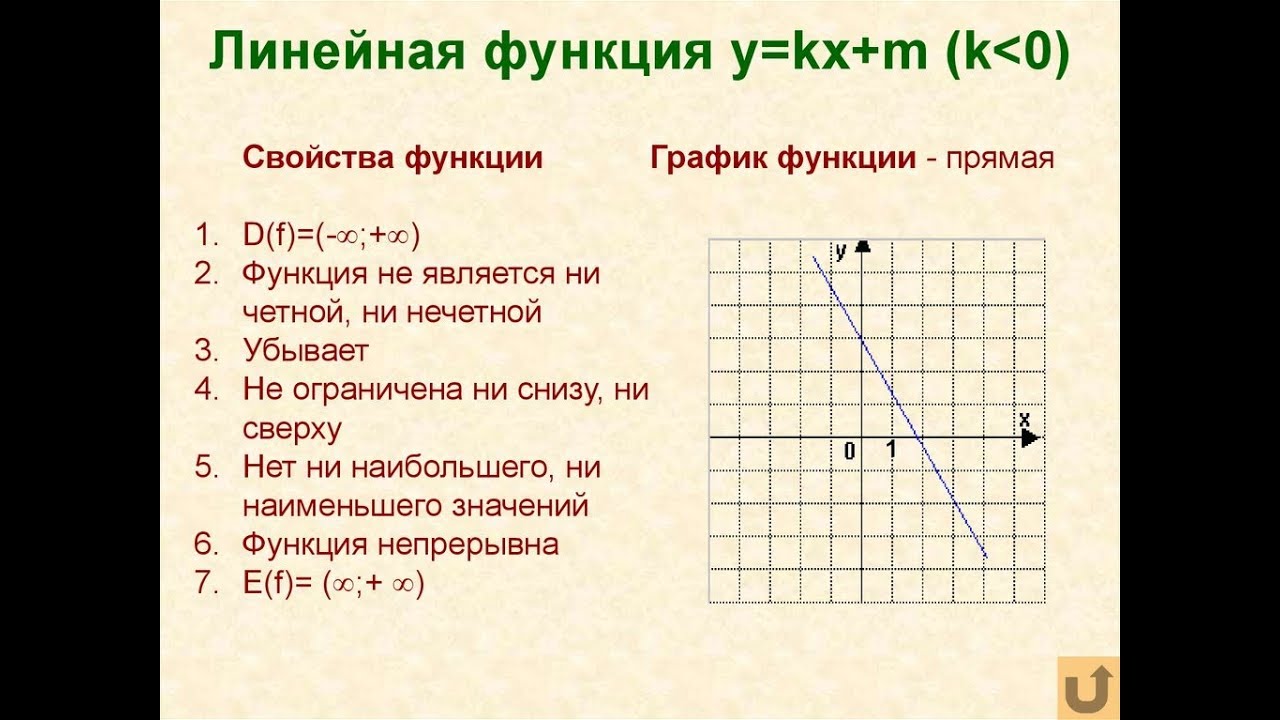
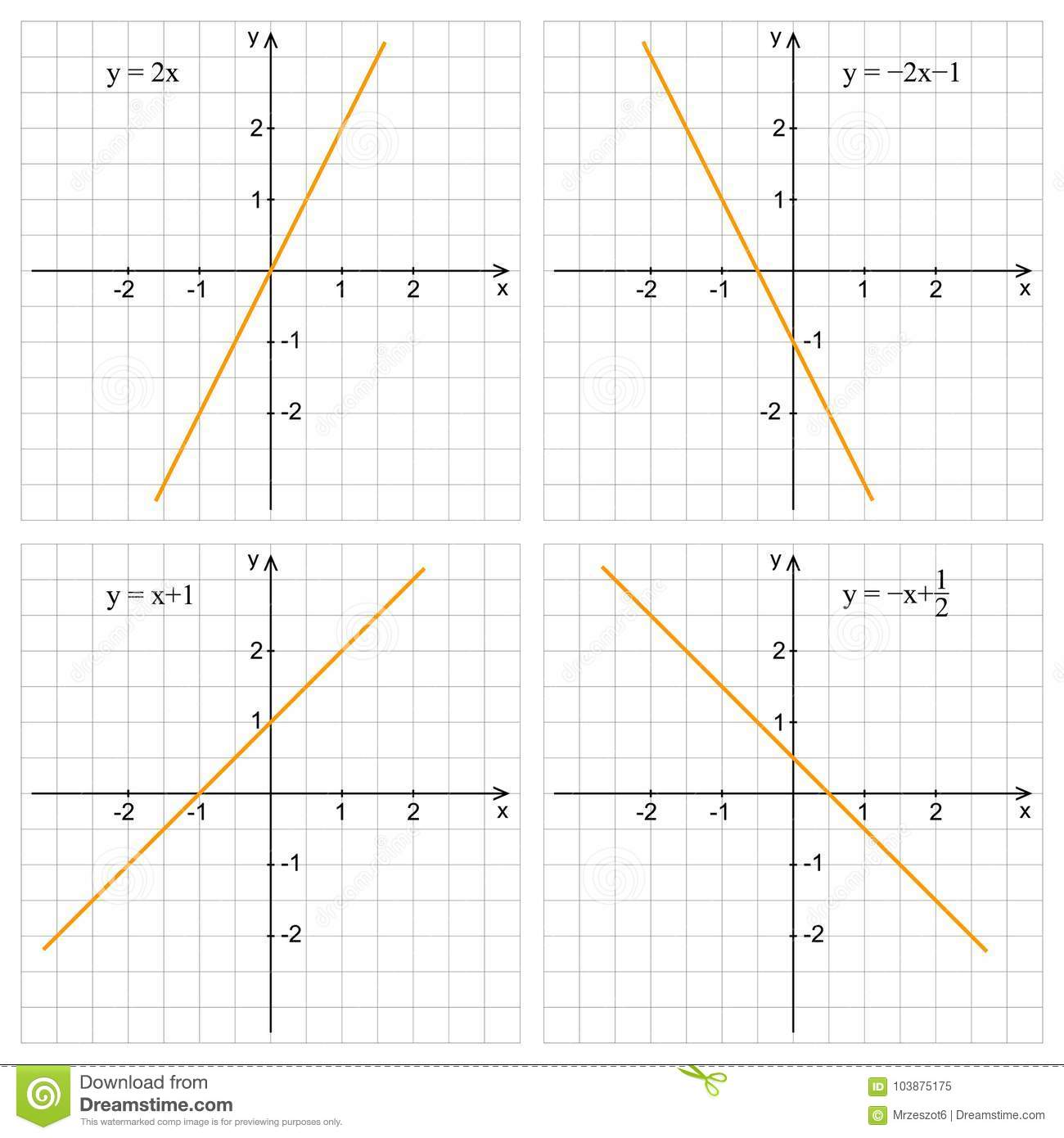
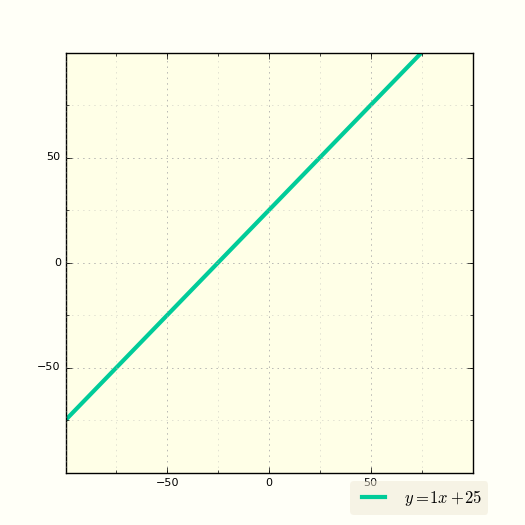
Пря­мая пе­ре­се­ка­ет ось у в по­ло­жи­тель­ном ее луче, зна­чит m имеет знак плюс, угол между пря­мой и по­ло­жи­тель­ным на­прав­ле­ни­ем оси х тупой, функ­ция убы­ва­ет, зна­чит знак k минус.

Рис. 3.

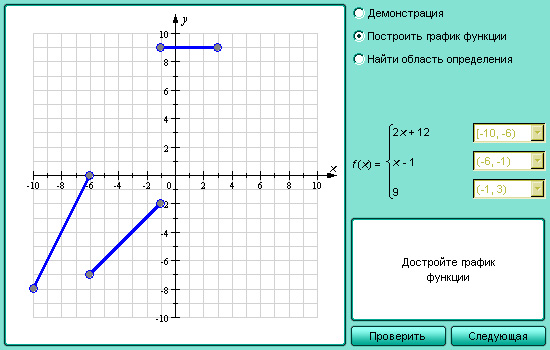
Пря­мая пе­ре­се­ка­ет ось у в от­ри­ца­тель­ном ее луче, зна­чит m имеет знак минус, угол между пря­мой и по­ло­жи­тель­ным на­прав­ле­ни­ем оси х ост­рый, функ­ция воз­рас­та­ет, зна­чит знак k плюс.

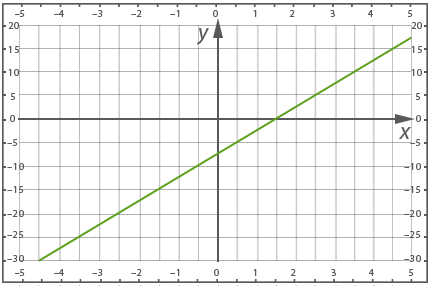
Рис. 4.

Пря­мая пе­ре­се­ка­ет ось у в от­ри­ца­тель­ном ее луче, зна­чит m имеет знак минус, угол между пря­мой и по­ло­жи­тель­ным на­прав­ле­ни­ем оси х тупой, функ­ция убы­ва­ет, зна­чит знак k также минус.

Рис. 5.

2. Рассмотрение случаев параллельных и совпадающих прямых

Рас­смот­рим при­мер:

При­мер 1:

, , 

По­стро­им гра­фи­ки дан­ных функ­ций. У каж­дой из них . У пер­вой , у вто­рой , у тре­тьей . На­пом­ним, что па­ра­мет­ры k и m опре­де­ля­ют­ся из стан­дарт­но­го вида ли­ней­но­го урав­не­ния , па­ра­метр  – это ор­ди­на­та точки пе­ре­се­че­ния пря­мой с осью у. Кроме того, от­ме­тим, что ко­эф­фи­ци­ент  от­ве­ча­ет за угол на­кло­на пря­мой к по­ло­жи­тель­но­му на­прав­ле­нию оси х, кроме того, если он по­ло­жи­тель­ный, то функ­ция будет воз­рас­тать, а если от­ри­ца­тель­ный – убы­вать. Ко­эф­фи­ци­ент  на­зы­ва­ет­ся уг­ло­вым ко­эф­фи­ци­ен­том.

Со­ста­вим таб­ли­цы для по­стро­е­ния гра­фи­ков:

х	-0,5
у	1

Таб­ли­ца для пер­вой функ­ции;

х	1
у	2

Таб­ли­ца для вто­рой функ­ции;

х	0,5
у	-1

Таб­ли­ца для тре­тьей функ­ции;

Оче­вид­но, что все по­стро­ен­ные пря­мые па­рал­лель­ны, по­то­му что их уг­ло­вые ко­эф­фи­ци­ен­ты оди­на­ко­вы. Функ­ции от­ли­ча­ют­ся толь­ко зна­че­ни­ем m.

Рис. 1.

Сде­ла­ем вывод. Пусть за­да­ны две про­из­воль­ные ли­ней­ные функ­ции:

 и  

Если  но  то за­дан­ные пря­мые па­рал­лель­ны.

Если  и  то за­дан­ные пря­мые сов­па­да­ют.

Изу­че­ние вза­им­но­го рас­по­ло­же­ния гра­фи­ков ли­ней­ных функ­ций и свойств их па­ра­мет­ров яв­ля­ет­ся ос­но­вой для изу­че­ния си­стем ли­ней­ных урав­не­ний. Мы долж­ны за­пом­нить, что если пря­мые па­рал­лель­ны, то си­сте­ма не будет иметь ре­ше­ний, а если пря­мые сов­па­да­ют – то си­сте­ма будет иметь бес­чис­лен­ное мно­же­ство ре­ше­ний.

Бывают ли зеленые розы — кто их вывел

Зеленая роза пришла из Голландии. Изначально она обитала в дикой природе, где и была замечена ученым-ботаником Майером. Тогда он решил самостоятельно воссоздать данный вид, для этого соединил белую розу и колючий терновник.

Зеленая роза

Полученный гибрид получил особое название — роза чайно-гибридная зеленая. Его описание было опубликовано во многих ботанических журналах и уже скоро цветок стал известен в каждом уголке планеты.

В настоящее время роза имеет широкое распространение по всему миру. Это обусловлено ее уникальными особенностями, к которым относят:

• Цвет. Бутоны имеют уникальный светло-зеленый оттенок.
• Форма куста преимущественно раскидистая.
• Высота взрослого растения может быть от 30 до 60 сантиметров в зависимости от сорта.
• Размер бутонов может быть от 5 до 10-15 сантиметров в зависимости от сорта, условий произрастания.
• Цветки бывают одиночные или в соцветиях.
• Лепестки могут быть обычные или махровые.

Единственное — данный вид не имеет запаха, присущего обычным розам. Но все компенсируется невероятно красивым внешним видом.

4. Решение типовых задач

При­мер 3 – найти k и m:

За­да­но ли­ней­ное урав­не­ние, так как х и у стоят в пер­вой сте­пе­ни, с двумя пе­ре­мен­ны­ми.

Чтобы найти k и m, вы­пол­ним пре­об­ра­зо­ва­ния:

За­пи­шем по­лу­чен­ное вы­ра­же­ние в стан­дарт­ном виде:

От­сю­да оче­вид­но, что , а 

При­мер 4 – найти k и m:

Пре­об­ра­зу­ем пра­вую часть:

За­пи­шем по­лу­чен­ное вы­ра­же­ние в стан­дарт­ном виде:

От­сю­да оче­вид­но, что , а 

Итак, одна из стан­дарт­ных задач – это на­хож­де­ние по за­дан­но­му ли­ней­но­му урав­не­нию па­ра­мет­ров ли­ней­ной функ­ции k и m.

Еще две стан­дарт­ные за­да­чи – по за­дан­но­му зна­че­нию х найти у и на­о­бо­рот, по за­дан­но­му зна­че­нию у найти х. Рас­смот­рим при­мер.

При­мер 5 – найти зна­че­ние у при :

Такую за­да­чу ино­гда на­зы­ва­ют пря­мой за­да­чей.

При­мер 6 – найти зна­че­ние ар­гу­мен­та, если :

Эта за­да­ча на­зы­ва­ет­ся об­рат­ной.

Свойства

• k{\displaystyle k} (угловой коэффициент прямой) является тангенсом угла α (α∈;π2)∪(π2;π)),{\displaystyle \alpha ~(\alpha \in [0;{\frac {\pi }{2}})\cup ({\frac {\pi }{2}};\pi )),} который прямая образует с положительным направлением оси абсцисс.
• При k>{\displaystyle k>0}, прямая образует острый угол с положительным направлением оси абсцисс.
• При k<{\displaystyle k<0}, прямая образует тупой угол с положительным направлением оси абсцисс.
• При k={\displaystyle k=0}, прямая параллельна оси абсцисс.

Угол между двумя прямыми, задаваемыми уравнениями
y=k1x+b1,{\displaystyle y=k_{1}x+b_{1},} и y=k2x+b2,{\displaystyle y=k_{2}x+b_{2},} определяется равенством:
tgα=|k1−k21+k1k2|,{\displaystyle \mathrm {tg} \,\alpha =\left|{\frac {k_{1}-k_{2}}{1+k_{1}k_{2}}}\right|,}
где k1k2≠−1,{\displaystyle k_{1}k_{2}\neq -1,} то есть прямые не являются взаимно перпендикулярными; при k1=k2, α={\displaystyle k_{1}=k_{2},~\alpha =0} и прямые параллельны.

• b{\displaystyle b} является показателем ординаты точки пересечения прямой с осью ординат.
• При b={\displaystyle b=0}, прямая проходит через начало координат.

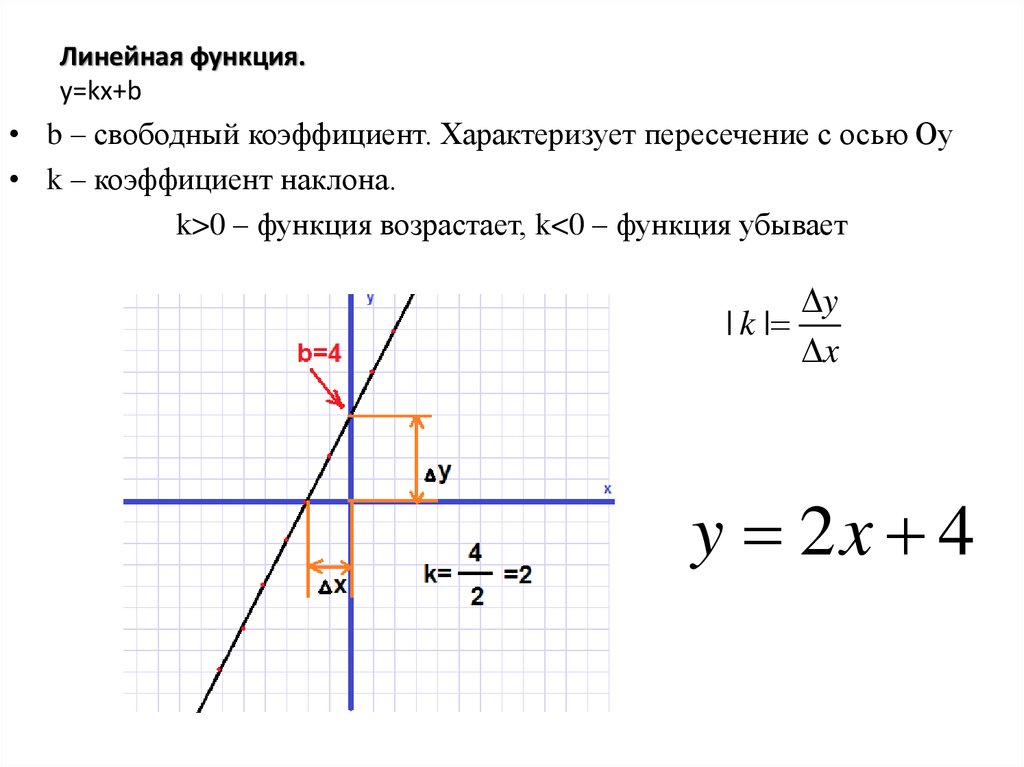
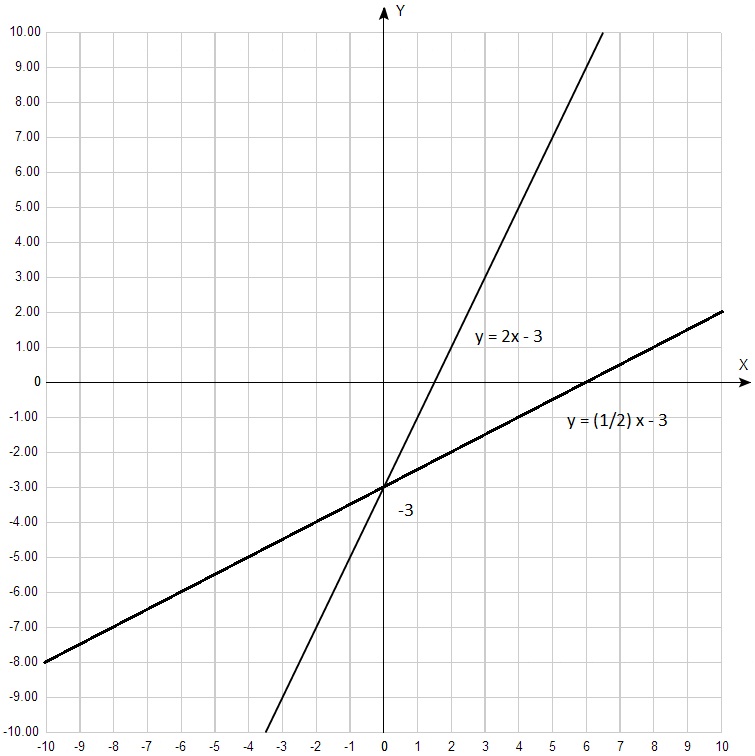
Как по графику определить коэффициент k?

1. Сначала определим, возрастает или убывает функция. Если возрастает – знак коэффициента \(k\) плюс, если убывает – минус.
2. Дальше надо построить на прямой прямоугольный треугольник, так чтобы гипотенуза лежала на графике функции, а вершины треугольника совпадали с вершинами клеточек. Примерно вот так:

Чтобы определить значение \(k\) по модулю (то есть, без учета знака), надо вертикальную сторону треугольника поделить на горизонтальную. Можно использовать правило для запоминания: «стоячий бьет лежачего». В данных случаях \(|k|=\frac{AC}{BC}\). То есть на первом графике \(k=2\),а на втором \(k=-\frac{1}{4}\).

Исследование линейной функции $f\left(x\right)=kx+b$ и её график

Вначале рассмотрим функцию $f\left(x\right)=kx+b$, где $k > 0$.

1. Область определения — все числа.
2. Область значения — все числа.
3. $f\left(-x\right)=-kx+b$. Функция не является ни четной, ни нечетной.
4. При $x=0,f\left(0\right)=b$. При $y=0,0=kx+b,\ x=-\frac{b}{k}$.

Точки пересечения с осями координат: $\left(-\frac{b}{k},0\right)$ и $\left(0,\ b\right)$

1. $f’\left(x\right)={\left(kx+b\right)}’=k>0$. Следовательно, данная функция возрастает на всей области определения. Точек экстремума нет.
2. $f^{»}\left(x\right)=k’=0$. Следовательно, функция не имеет точек перегиба.
3. ${\mathop{lim}_{x\to -\infty } kx\ }=-\infty $, ${\mathop{lim}_{x\to +\infty } kx\ }=+\infty $
4. График (рис. 2).

Рис. 2. Графики функции $y=kx+b$, при $k > 0$.

Теперь рассмотрим функцию $f\left(x\right)=kx$, где $k

1. Область определения — все числа.
2. Область значения — все числа.
3. $f\left(-x\right)=-kx+b$. Функция не является ни четной, ни нечетной.
4. При $x=0,f\left(0\right)=b$. При $y=0,0=kx+b,\ x=-\frac{b}{k}$.

Точки пересечения с осями координат: $\left(-\frac{b}{k},0\right)$ и $\left(0,\ b\right)$

1. $f’\left(x\right)={\left(kx\right)}’=k
2. $f^{»}\left(x\right)=k’=0$. Следовательно, функция не имеет точек перегиба.
3. ${\mathop{lim}_{x\to -\infty } kx\ }=+\infty $, ${\mathop{lim}_{x\to +\infty } kx\ }=-\infty $
4. График (рис. 3).

Рис. 3. Графики функции $y=kx+b$, при $k

Важно: для построения графика функции $y=kx$ достаточно найти две точки и провести прямую через эти точки

Абстрактная алгебра

Термин «линейная функция», или, точнее, «линейная однородная функция», часто применяется для линейного отображения векторного пространства X{\displaystyle X} над некоторым полем k{\displaystyle k} в это поле, то есть для такого отображения fX→k{\displaystyle f:X\to k}, что для любых элементов x,y∈X{\displaystyle x,y\in X} и любых α,β∈k{\displaystyle \alpha ,\beta \in k} справедливо равенство

f(αx+βy)=αf(x)+βf(y){\displaystyle f(\alpha x+\beta y)=\alpha f(x)+\beta f(y)}

причём в этом случае вместо термина «линейная функция» используются также термины линейный функционал и линейная форма — также означающие линейную однородную функцию определённого класса.

Определение линейной функции

Введем определение линейной функции

Определение

Функция вида $y=kx+b$, где $k$ отлично от нуля называется линейной функцией.

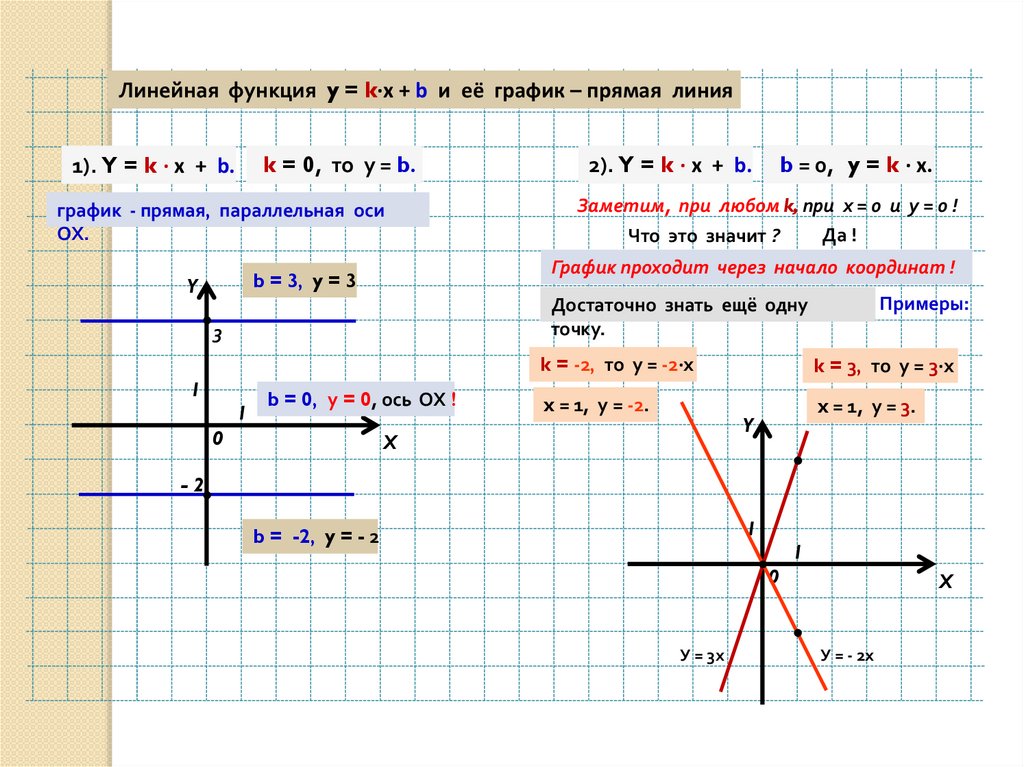
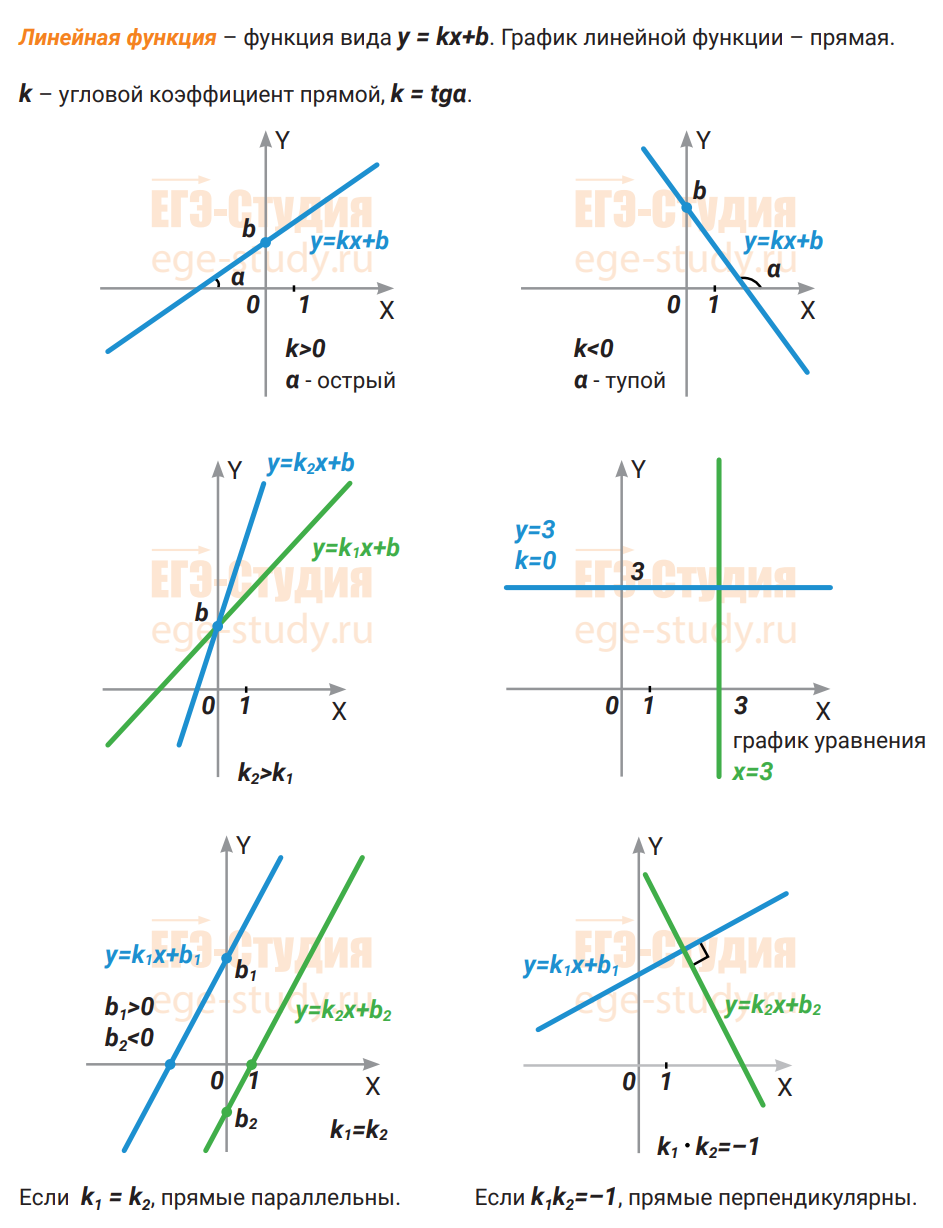
График линейной функции — прямая. Число $k$ называется угловым коэффициентом прямой.

При $b=0$ линейная функция называется функцией прямой пропорциональности $y=kx$.

Рассмотрим рисунок 1.

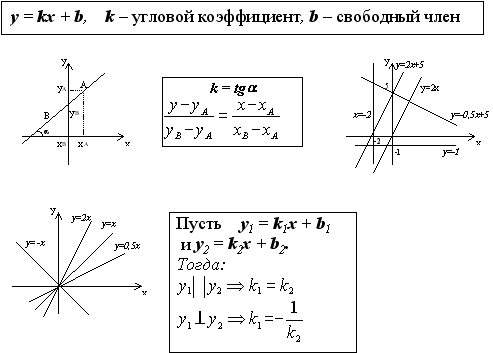
Рис. 1. Геометрический смысл углового коэффициента прямой

Рассмотрим треугольник АВС. Видим, что$ВС=kx_0+b$. Найдем точку пересечения прямой $y=kx+b$ с осью $Ox$:

\

\

Значит $AC=x_0+\frac{b}{k}$. Найдем отношение этих сторон:

\

С другой стороны $\frac{BC}{AC}=tg\angle A$.

Таким образом, можно сделать следующий вывод:

Вывод

Геометрический смысл коэффициента $k$. Угловой коэффициент прямой $k$ равен тангенсу угла наклона этой прямой к оси $Ox$.

Исследование линейной функции $f\left(x\right)=kx+b$ и её график

Вначале рассмотрим функцию $f\left(x\right)=kx+b$, где $k > 0$.

1. Область определения — все числа.
2. Область значения — все числа.
3. $f\left(-x\right)=-kx+b$. Функция не является ни четной, ни нечетной.
4. При $x=0,f\left(0\right)=b$. При $y=0,0=kx+b,\ x=-\frac{b}{k}$.

Точки пересечения с осями координат: $\left(-\frac{b}{k},0\right)$ и $\left(0,\ b\right)$

1. $f’\left(x\right)={\left(kx+b\right)}’=k>0$. Следовательно, данная функция возрастает на всей области определения. Точек экстремума нет.
2. $f^{»}\left(x\right)=k’=0$. Следовательно, функция не имеет точек перегиба.
3. ${\mathop{lim}_{x\to -\infty } kx\ }=-\infty $, ${\mathop{lim}_{x\to +\infty } kx\ }=+\infty $
4. График (рис. 2).

Рис. 2. Графики функции $y=kx+b$, при $k > 0$.

Теперь рассмотрим функцию $f\left(x\right)=kx$, где $k

1. Область определения — все числа.
2. Область значения — все числа.
3. $f\left(-x\right)=-kx+b$. Функция не является ни четной, ни нечетной.
4. При $x=0,f\left(0\right)=b$. При $y=0,0=kx+b,\ x=-\frac{b}{k}$.

Точки пересечения с осями координат: $\left(-\frac{b}{k},0\right)$ и $\left(0,\ b\right)$

1. $f’\left(x\right)={\left(kx\right)}’=k
2. $f^{»}\left(x\right)=k’=0$. Следовательно, функция не имеет точек перегиба.
3. ${\mathop{lim}_{x\to -\infty } kx\ }=+\infty $, ${\mathop{lim}_{x\to +\infty } kx\ }=-\infty $
4. График (рис. 3).

Рис. 3. Графики функции $y=kx+b$, при $k

Важно: для построения графика функции $y=kx$ достаточно найти две точки и провести прямую через эти точки

Задача на построение графиков функции прямой пропорциональности

Задача

Построить график функции $y=2x+3$

Найдем две точки, принадлежащие данной функции. Пусть $x=1$, тогда $y=5$. Пусть $x=-1$, тогда $y=1$. Проведем прямую через точки $\left(-1,1\right)\ и\ (1,\ 5)$. Получим

Алгебра логики

Основные статьи: Линейная булева функция, Полином Жегалкина, Критерий Поста

Булева функция f(x1,x2,…,xn){\displaystyle f(x_{1},x_{2},\dots ,x_{n})} называется линейной, если существуют такие a,a1,a2,…,an{\displaystyle a_{0},a_{1},a_{2},\dots ,a_{n}}, где ai∈{,1},∀i=1,n¯{\displaystyle a_{i}\in \{0,1\},\forall i={\overline {1,n}}}, что для любых x1,x2,…,xn{\displaystyle x_{1},x_{2},\dots ,x_{n}} имеет место равенство:

f(x1,x2,…,xn)=a⊕a1⋅x1⊕a2⋅x2⊕⋯⊕an⋅xn{\displaystyle f(x_{1},x_{2},\dots ,x_{n})=a_{0}\oplus a_{1}\cdot x_{1}\oplus a_{2}\cdot x_{2}\oplus \dots \oplus a_{n}\cdot x_{n}}.

Абстрактная алгебра

Термин «линейная функция», или, точнее, «линейная однородная функция», часто применяется для линейного отображения векторного пространства X{\displaystyle X} над некоторым полем k{\displaystyle k} в это поле, то есть для такого отображения fX→k{\displaystyle f:X\to k}, что для любых элементов x,y∈X{\displaystyle x,y\in X} и любых α,β∈k{\displaystyle \alpha ,\beta \in k} справедливо равенство

f(αx+βy)=αf(x)+βf(y){\displaystyle f(\alpha x+\beta y)=\alpha f(x)+\beta f(y)}

причём в этом случае вместо термина «линейная функция» используются также термины линейный функционал и линейная форма — также означающие линейную однородную функцию определённого класса.

Свойства

• k{\displaystyle k} (угловой коэффициент прямой) является тангенсом угла α (α∈;π2)∪(π2;π)),{\displaystyle \alpha ~(\alpha \in [0;{\frac {\pi }{2}})\cup ({\frac {\pi }{2}};\pi )),} который прямая образует с положительным направлением оси абсцисс.
• При k>{\displaystyle k>0}, прямая образует острый угол с положительным направлением оси абсцисс.
• При k<{\displaystyle k<0}, прямая образует тупой угол с положительным направлением оси абсцисс.
• При k={\displaystyle k=0}, прямая параллельна оси абсцисс.

Угол между двумя прямыми, задаваемыми уравнениями
y=k1x+b1,{\displaystyle y=k_{1}x+b_{1},} и y=k2x+b2,{\displaystyle y=k_{2}x+b_{2},} определяется равенством:
tgα=|k1−k21+k1k2|,{\displaystyle \mathrm {tg} \,\alpha =\left|{\frac {k_{1}-k_{2}}{1+k_{1}k_{2}}}\right|,}
где k1k2≠−1,{\displaystyle k_{1}k_{2}\neq -1,} то есть прямые не являются взаимно перпендикулярными; при k1=k2, α={\displaystyle k_{1}=k_{2},~\alpha =0} и прямые параллельны.

• b{\displaystyle b} является показателем ординаты точки пересечения прямой с осью ординат.
• При b={\displaystyle b=0}, прямая проходит через начало координат.

Свойства

• k{\displaystyle k} (угловой коэффициент прямой) является тангенсом угла α (α∈;π2)∪(π2;π)),{\displaystyle \alpha ~(\alpha \in [0;{\frac {\pi }{2}})\cup ({\frac {\pi }{2}};\pi )),} который прямая образует с положительным направлением оси абсцисс.
• При k>{\displaystyle k>0}, прямая образует острый угол с положительным направлением оси абсцисс.
• При k<{\displaystyle k<0}, прямая образует тупой угол с положительным направлением оси абсцисс.
• При k={\displaystyle k=0}, прямая параллельна оси абсцисс.

Угол между двумя прямыми, задаваемыми уравнениями
y=k1x+b1,{\displaystyle y=k_{1}x+b_{1},} и y=k2x+b2,{\displaystyle y=k_{2}x+b_{2},} определяется равенством:
tgα=|k1−k21+k1k2|,{\displaystyle \mathrm {tg} \,\alpha =\left|{\frac {k_{1}-k_{2}}{1+k_{1}k_{2}}}\right|,}
где k1k2≠−1,{\displaystyle k_{1}k_{2}\neq -1,} то есть прямые не являются взаимно перпендикулярными; при k1=k2, α={\displaystyle k_{1}=k_{2},~\alpha =0} и прямые параллельны.

• b{\displaystyle b} является показателем ординаты точки пересечения прямой с осью ординат.
• При b={\displaystyle b=0}, прямая проходит через начало координат.

Свойства

• k{\displaystyle k} (угловой коэффициент прямой) является тангенсом угла α (α∈;π2)∪(π2;π)),{\displaystyle \alpha ~(\alpha \in [0;{\frac {\pi }{2}})\cup ({\frac {\pi }{2}};\pi )),} который прямая образует с положительным направлением оси абсцисс.
• При k>{\displaystyle k>0}, прямая образует острый угол с положительным направлением оси абсцисс.
• При k<{\displaystyle k<0}, прямая образует тупой угол с положительным направлением оси абсцисс.
• При k={\displaystyle k=0}, прямая параллельна оси абсцисс.

Угол между двумя прямыми, задаваемыми уравнениями
y=k1x+b1,{\displaystyle y=k_{1}x+b_{1},} и y=k2x+b2,{\displaystyle y=k_{2}x+b_{2},} определяется равенством:
tgα=|k1−k21+k1k2|,{\displaystyle \mathrm {tg} \,\alpha =\left|{\frac {k_{1}-k_{2}}{1+k_{1}k_{2}}}\right|,}
где k1k2≠−1,{\displaystyle k_{1}k_{2}\neq -1,} то есть прямые не являются взаимно перпендикулярными; при k1=k2, α={\displaystyle k_{1}=k_{2},~\alpha =0} и прямые параллельны.

• b{\displaystyle b} является показателем ординаты точки пересечения прямой с осью ординат.
• При b={\displaystyle b=0}, прямая проходит через начало координат.

Абстрактная алгебра

Термин «линейная функция», или, точнее, «линейная однородная функция», часто применяется для линейного отображения векторного пространства X{\displaystyle X} над некоторым полем k{\displaystyle k} в это поле, то есть для такого отображения fX→k{\displaystyle f:X\to k}, что для любых элементов x,y∈X{\displaystyle x,y\in X} и любых α,β∈k{\displaystyle \alpha ,\beta \in k} справедливо равенство

f(αx+βy)=αf(x)+βf(y){\displaystyle f(\alpha x+\beta y)=\alpha f(x)+\beta f(y)}

причём в этом случае вместо термина «линейная функция» используются также термины линейный функционал и линейная форма — также означающие линейную однородную функцию определённого класса.

Нелинейные функции

Для функций, не являющихся линейными, употребляют термин нелинейные функции.
То же относится и к употреблению слова нелинейные в отношении других объектов, не обладающих свойством линейности, например — нелинейные дифференциальные уравнения.
Обычно термин используется, когда функциональную зависимость вначале приближают линейной, а потом переходят к изучению более общего случая, часто начиная с младших степеней, например рассматривая квадратичные поправки.

Нелинейные уравнения достаточно произвольны. К примеру, нелинейной является функция y=x2{\displaystyle y=x^{2}}.

В ряде случаев этот термин может применяться и к зависимостям f=kx+b{\displaystyle f=kx+b}, где b≠{\displaystyle b\neq 0}, то есть к неоднородным линейным функциям, поскольку они не обладают свойством линейности, а именно в этом случае f(x1+x2)≠f(x1)+f(x2){\displaystyle f(x_{1}+x_{2})\neq f(x_{1})+f(x_{2})} и f(cx)≠cf(x){\displaystyle f(cx)\neq cf(x)}.
Например, нелинейной зависимостью считают σ(τ){\displaystyle \sigma (\tau )} для материала с упрочнением (см. теория пластичности).

Свойства

• k{\displaystyle k} (угловой коэффициент прямой) является тангенсом угла α (α∈;π2)∪(π2;π)),{\displaystyle \alpha ~(\alpha \in [0;{\frac {\pi }{2}})\cup ({\frac {\pi }{2}};\pi )),} который прямая образует с положительным направлением оси абсцисс.
• При k>{\displaystyle k>0}, прямая образует острый угол с положительным направлением оси абсцисс.
• При k<{\displaystyle k<0}, прямая образует тупой угол с положительным направлением оси абсцисс.
• При k={\displaystyle k=0}, прямая параллельна оси абсцисс.

Угол между двумя прямыми, задаваемыми уравнениями
y=k1x+b1,{\displaystyle y=k_{1}x+b_{1},} и y=k2x+b2,{\displaystyle y=k_{2}x+b_{2},} определяется равенством:
tgα=|k1−k21+k1k2|,{\displaystyle \mathrm {tg} \,\alpha =\left|{\frac {k_{1}-k_{2}}{1+k_{1}k_{2}}}\right|,}
где k1k2≠−1,{\displaystyle k_{1}k_{2}\neq -1,} то есть прямые не являются взаимно перпендикулярными; при k1=k2, α={\displaystyle k_{1}=k_{2},~\alpha =0} и прямые параллельны.

• b{\displaystyle b} является показателем ординаты точки пересечения прямой с осью ординат.
• При b={\displaystyle b=0}, прямая проходит через начало координат.

Как решать задачи на линейную функцию «y = kx + b»

Рассмотрим задачу.

Построить график функции «». Найти по графику:

1. значение «» соответствующее значению «» равному ;
2. значение «», если значение «» равно
   .

Вначале построим график функции «».

Используем правила, по которым мы выше.
Для построения графика функции «» достаточно найти всего две точки.

Выберем два произвольных числовых значения для «». Для удобства расчетов выберем числа
«» и «».

Выполним расчеты и запишем их результаты в таблицу.

Точка	Координата по оси «»	Координата по оси «»

Отметим полученные точки на прямоугольной системе координат.

Соединим полученные точки прямой. Проведенная прямая будет являться графиком функции
«».

Теперь работаем с построенным графиком функции «».

Требуется найти значение «»,
соответствующее значению «», которое равно .

Тему
«» с графика функции
мы уже подробно рассматривали в уроке
«Как решать задачи на функцию».

В этому уроке для решения задачи выше вспомним только основные моменты.

Запомните!

Чтобы найти значение «» по известному значению «» на графике
функции необходимо:

1. провести перпендикуляр от оси «»
   ()
   из заданного числового значения «»
   до пересечения
   с графиком функции;
2. из полученной точки пересечения перпендикуляра и графика функции провести еще один перпендикуляр к оси
   «»
   ();
3. полученное числовое значение на оси «» и будет искомым значением.

По правилам выше найдем на построенном ранее графике функции «»
необходимые значения функции «» для
«» равным .

Запишем полученные результаты в таблицу.

Заданное значение «»	Полученное с графика значение «»

Переходим ко второму заданию задачи. Требуется найти значение «»,
если значение «» равно .

Выполним те же действия, что и при решении предыдущего задания.
Разница будет лишь в том, что изначально мы будем проводить перпендикуляры от оси
«».

Запишем полученные результаты в таблицу.

Заданное значение «»	Полученное с графика значение «»

Как проверить, проходит ли график через точку

Рассмотрим другое задание.

Запомните!

Чтобы проверить принадлежность точки графику функции нет необходимости строить график функции.

Достаточно подставить координаты точки в формулу функции (координату по оси
«» вместо
«», а координату по оси
«» вместо «») и выполнить арифметические расчеты.

• Если получится верное равенство, значит, точка принадлежит графику функции.
• Если получится неверное равенство, значит, точка
  не принадлежит графику функции.

(верно)

проходит
(неверно)

не проходит

Как найти точки пересечения графика с осями

Рассмотрим задачу.

Найти координаты точек пересечения графика функции «» с осями координат.

Для начала построим график функции «» и на графике отметим точки пересечения
с осями.

найдем координаты двух точек функции
«».

Выберем два произвольных числовых значения для «» и рассчитаем значение
«» по формуле
функции. Например, для и
.

Точка	Координата по оси «»	Координата по оси «»

Отметим полученные точки на системе координат и проведем через них прямую.
Тем самым мы построим график функции «».

Теперь найдем координаты точек пересечения графика функции с осями по формуле функции.

Запомните!

Чтобы найти координаты точки пересечения графика функции с осью
«»
()
нужно:

• приравнять координату точки по оси
  «» к нулю
  ;
• подставить вместо «» в формулу функции ноль и найти значение
  «»;
• записать полученные координаты точки пересечения с осью
  «».

Подставим вместо «» в формулу функции «» число ноль.

Запомните!

Чтобы найти координаты точки пересечения графика функции с осью
«»
()
нужно:

• приравнять координату точки по оси
  «» к нулю
  ;
• подставить вместо «» в формулу функции ноль и найти значение
  «»;
• записать полученные координаты точки пересечения с осью
  «».

Подставим вместо «» в формулу функции «» число ноль.

Чтобы было проще запомнить, какую координату точки нужно приравнивать к нулю, запомните
«правило противоположности».

Важно!

Если нужно найти координаты точки пересечения графика с осью
«», то приравниваем
«» к нулю.

И наооборот. Если нужно найти координаты точки пересечениа графика с осью
«»,
то приравниваем «» к нулю.

Линейная функция нескольких переменных

Линейная функция n{\displaystyle n} переменных x=(x1,x2,…,xn){\displaystyle x=(x_{1},x_{2},\dots ,x_{n})} — функция вида

f(x)=a+a1x1+a2x2+⋯+anxn{\displaystyle f(x)=a_{0}+a_{1}x_{1}+a_{2}x_{2}+\dots +a_{n}x_{n}}

где a,a1,a2,…,an{\displaystyle a_{0},a_{1},a_{2},\dots ,a_{n}} — некоторые фиксированные числа.
Областью определения линейной функции является всё n{\displaystyle n}-мерное пространство переменных x1,x2,…,xn{\displaystyle x_{1},x_{2},\dots ,x_{n}} вещественных или комплексных.
При a={\displaystyle a_{0}=0} линейная функция называется однородной, или линейной формой.

Если все переменные x1,x2,…,xn{\displaystyle x_{1},x_{2},\dots ,x_{n}} и коэффициенты a,a1,a2,…,an{\displaystyle a_{0},a_{1},a_{2},\dots ,a_{n}} — вещественные числа, то графиком линейной функции в (n+1){\displaystyle (n+1)}-мерном пространстве переменных x1,x2,…,xn,y{\displaystyle x_{1},x_{2},\dots ,x_{n},y} является n{\displaystyle n}-мерная гиперплоскость

y=a+a1x1+a2x2+⋯+anxn{\displaystyle y=a_{0}+a_{1}x_{1}+a_{2}x_{2}+\dots +a_{n}x_{n}}

в частности при n=1{\displaystyle n=1} — прямая линия на плоскости.