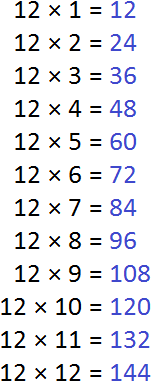Кратное число - что это такое, таблицы чисел кратных 2, 3, 4 и так далее

Кратное число — это …

Операция деления в математике может обозначаться разными значками. Это двоеточие (:), косая черта (/), горизонтальная черта (-) или специальным значком под названием «обелюс» (÷).

А у чисел, которые участвуют в делении, есть определенные названия:

Делимое – то число, которое собираются делить;
Делитель – число, на которое будут делить делимое. Соответственно, делитель чаще всего меньше делимого. Хотя не исключен и другой вариант. Единственное число, которое не может быть делителем, это ноль.
Частное – результат деления, то есть число, которое получается в результате выполнения математического действия.

Частное, которое получается полным или не полным. Первый вариант, это когда число-делимое, было полностью поделено на делитель. Например, 12 / 3 = 4. Но бывают варианты и с неполным частным, когда появляется некий остаток. Например, 14 / 3 = 4 (2), где 4 – это неполное частное, а 2 – остаток.

Почему мы так подробно рассказали о делении? Это имеет непосредственное отношение к теме статьи.

Но речь идет только о натуральных числах. То есть тех, которые мы используем для счета в обычной жизни. Например, 1, 2, 5, 10, 35, 100 и так далее. При этом дробные числа (например, 2/5 или 0,5) к натуральным не относятся, а значит, в отношении них понятие «кратности» не применяется.

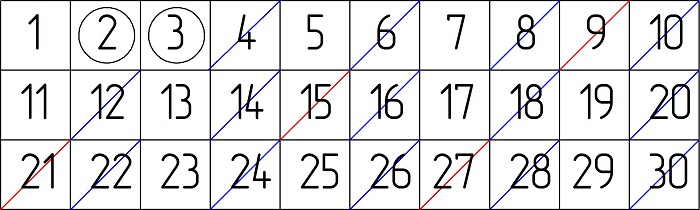
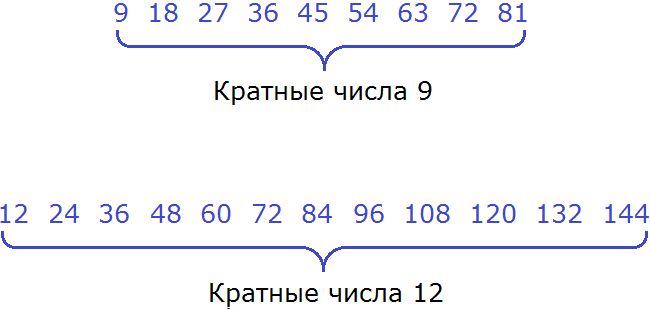
Например, возьмем число 12. Оно может быть кратно сразу нескольким числам.

Таким образом, можно сказать, что 12 – кратное число 2, 3, 4 и 6. И точно так же можно разложить по кратности любое число.

Внимательный читатель мог бы возразить, что есть еще два числа, на которые можно поделить 12 без остатка. Во-первых, это само 12. А во-вторых, это единица. Что ж, это абсолютная правда, и ее можно даже записать в одном математическом правиле:

Нахождение делителей числа

В начале данного урока было сказано, что делителем называется число, на которое другое число делится без остатка.

Например, число 2 является делителем числа 6, поскольку число 6 можно без остатка разделить на 2

6 : 2 = 3

Ещё делителем числа 6 является число 3

6 : 3 = 2

Ещё делителем числа 6 является число 1

6 : 1 = 6

Наконец, делителем числа 6 является само это число

6 : 6 = 1

Перечислим все делители числа 6

1, 2, 3, 6

Иногда возникает необходимость найти все делители какого-нибудь числа. Чтобы понять, как это делается, рассмотрим несколько примеров.

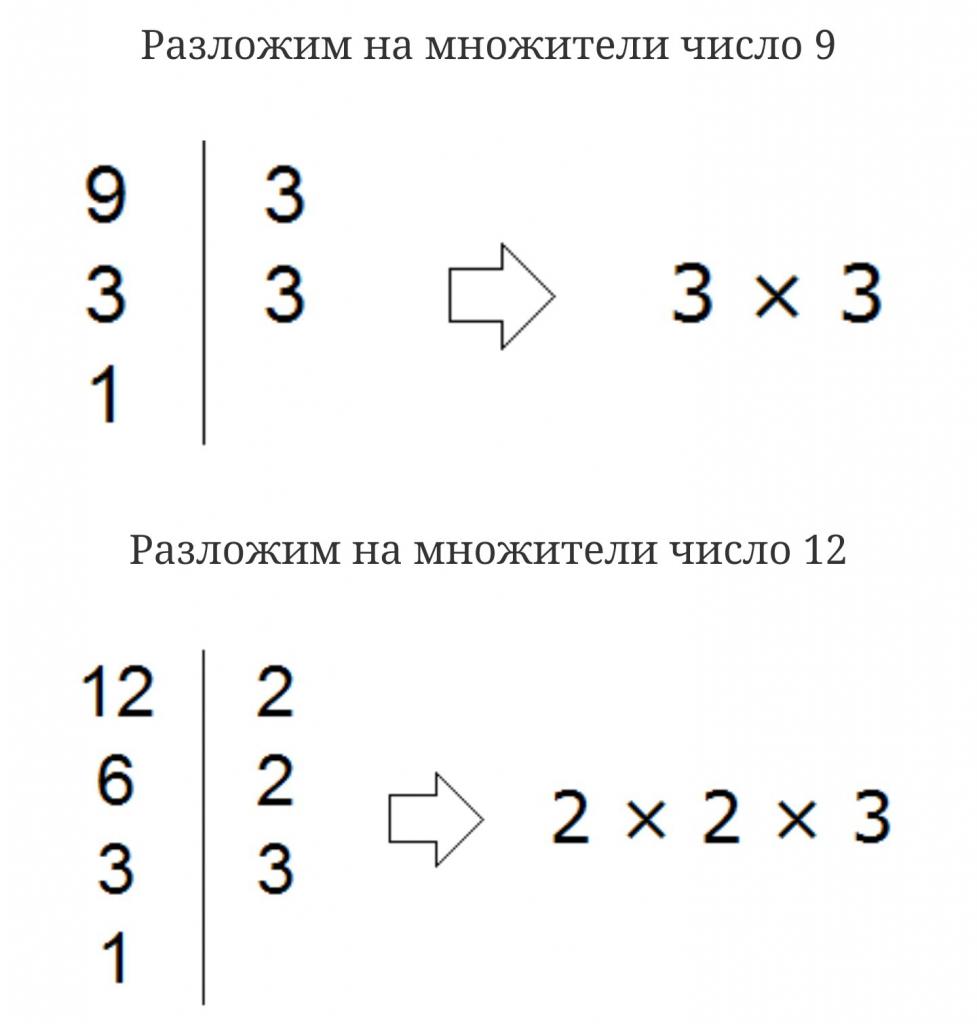
Пример 1. Найти делители числа 12

Во-первых, единица является делителем любого числа. Пусть и у нас первым делителем числа 12 будет 1

Теперь раскладываем число 12 на простые множители:

Получили разложение 2 × 2 × 3.

В процессе разложения числа 12 на простые множители, мы делили его на числа 2 и 3. На них число 12 разделилось без остатка, значит они тоже являются делителями числа 12. Внесём эти два числа в нашу таблицу делителей:

Чтобы получить остальные делители числа 12, нужно найти все возможные произведения его простых множителей между собой. Получаемые в результате ответы и будут остальными делителями числа 12.

Число 12 мы разложили на простые множители 2 × 2 × 3. Найдём все возможные произведения этих простых множителей между собой. Первое произведение это 2 × 2. Это произведение равно 4

2 × 2 = 4

Занесём число 4 в нашу таблицу делителей

Следующее возможное произведение из простых множителей числа 12 это произведение 2 × 3. Данное произведение равно 6. Занесём число 6 в нашу таблицу делителей:

Последнее возможное произведение из простых множителей числа 12 это произведение из всех его множителей, а именно 2 × 2 × 3. Это произведение равно 12. Занесём число 12 в нашу таблицу делителей:

Таким образом, делителями числа 12 являются числа 1, 2, 3, 4, 6, 12.

На основании приведённого примера можно сформировать правило для нахождения делителей числа:

Чтобы найти делители числа, нужно:

записать в качестве первого делителя единицу;
разложить исходное число на простые множители и выписать из полученных простых множителей те множители, которые являются делителями исходного числа (если множитель повторяется, то выписать его нужно только один раз);
найти все возможные произведения полученных простых множителей между собой. Получаемые в результате ответы будут остальными делителями исходного числа.

Пример 2. Найти делители числа 6

Первым делителем числа 6 запишем единицу:

Теперь разложим число 6 на простые множители:

Выпишем из полученного разложения те множители, которые являются делителями числа 6. Видим, что это множители 2 и 3. Они будут следующими делителями числа 6. Допишем их к нашим делителям:

1, 2, 3

Теперь найдём все возможные произведения простых множителей числа 6. В данном случае имеется только одно произведение, а именно 2 × 3. Это произведение равно 6. Допишем число 6 к нашим делителям:

1, 2, 3, 6

Таким образом, делителями числа 6 являются числа 1, 2, 3, 6.

Задания для самостоятельного решения

Задание 1. Разложите число 256 на простые множители

Решение:

Задание 2. Разложите число 52 на простые множители

Решение:

Задание 3. Разложите число 98 на простые множители

Решение:

Задание 4. Разложите число 116 на простые множители

Решение:

Задание 5. Разложите число 228 на простые множители

Решение:

Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Определение

Пусть fRn→R{\displaystyle f:\mathbb {R} ^{n}\to \mathbb {R} } — C∞{\displaystyle C^{\infty }}-гладкая функция от n{\displaystyle n} переменных x1,…,xn{\displaystyle x_{1},\ldots ,x_{n}}, имеющая O∈Rn{\displaystyle O\in \mathbb {R} ^{n}} своей критической точкой. Соответствующее градиентное отображение ∇fRn→Rn{\displaystyle \nabla f:\mathbb {R} ^{n}\to \mathbb {R} ^{n}} задается формулой (x1,…,xn)↦(∂f∂x1,…,∂f∂xn).{\displaystyle (x_{1},\ldots ,x_{n})\mapsto (\partial f/\partial x_{1},\ldots ,\partial f/\partial x_{n}).} Введем следующие обозначения:

Rx1,…,xn{\displaystyle \mathbb {R} ]} — алгебра формальных степенных рядов от переменных x1,…,xn{\displaystyle x_{1},\ldots ,x_{n}} с центром в O.{\displaystyle O.}
I∇f=(∂f∂x1,…,∂f∂xn){\displaystyle I_{\nabla f}=(\partial f/\partial x_{1},\ldots ,\partial f/\partial x_{n})} — идеал в алгебре гладких функций, порожденный образующими ∂f∂x1,…,∂f∂xn.{\displaystyle \partial f/\partial x_{1},\ldots ,\partial f/\partial x_{n}.}

Сопоставляя каждой гладкой функции её формальный ряд Тейлора, мы получаем вложение I∇f{\displaystyle I_{\nabla f}} в алгебру Rx1,…,xn{\displaystyle \mathbb {R} ]}. Локальной алгеброй градиентного отображения в точке O{\displaystyle O} называется факторалгебра Rx1,…,xnI∇f,{\displaystyle \mathbb {R} ]/I_{\nabla f},} а её размерность μ=dimRx1,…,xnI∇f{\displaystyle \mu =\dim \,\mathbb {R} ]/I_{\nabla f}} называется кратностью функции f{\displaystyle f} в точке O.{\displaystyle O.}

В случае, когда функции ∂f∂x1,…,∂f∂xn{\displaystyle \partial f/\partial x_{1},\ldots ,\partial f/\partial x_{n}} имеют в точке O{\displaystyle O} линейно независимые градиенты (это условие равносильно тому, что гессиан функции f{\displaystyle f} отличен от нуля), кратность μ=1{\displaystyle \mu =1}, и критическая точка O{\displaystyle O} называется невырожденной.
Удобно также положить μ={\displaystyle \mu =0} в случае некритической точки.

Кратность корня многочлена

Пусть F является полем и р ( х ) есть многочлен от одной переменной и коэффициентами в F . Элемент ∈ F является корнем кратности к из р ( х ) , если существует многочлен с ( х ) таким образом, что с ( ) ≠ 0 и р ( х ) = ( х — ) K сек ( х ). Если k = 1, то a называется простым корнем . Если k ≥ 2, то a называется кратным корнем .

Например, многочлен р ( х ) = х 3 + 2 х 2 — 7 х + 4 имеет 1 и -4 , как корни , и может быть записана в виде р ( х ) = ( х + 4) ( х — 1) 2 . Это означает, что 1 — корень кратности 2, а −4 — «простой» корень (кратности 1). Кратность корня — это количество вхождений этого корня в полную факторизацию многочлена с помощью основной теоремы алгебры .

Если a является корнем кратности k многочлена, то это корень кратности k — 1 своей производной . Дискриминант многочлена равен нулю тогда и только тогда , когда многочлен имеет кратный корень.

Поведение полиномиальной функции вблизи кратного корня

График многочлена p ( x ) = x 3 + 2 x 2 — 7 x + 4 с его корнями (нулями) −4 и 1. Корень −4 является «простым» корнем (кратности 1), поэтому График пересекает ось x в этом корне. Корень 1 имеет четную кратность, поэтому граф отскакивает от оси x в этом корне.

График из полиномиальной функции у = ф ( х ) пересекает й ось й на действительных корнях многочлена. График касается этой оси при кратных корнях функции f и не касается простых корней. График пересекает ось x в корнях с нечетной кратностью и отскакивает (не проходит) от оси x в корнях четной кратности.

Ненулевая полиномиальная функция всегда неотрицательна тогда и только тогда, когда все ее корни имеют четную кратность и существует x такое, что f ( x )> 0 .

Кратность пересечения

В алгебраической геометрии пересечение двух подмногообразий алгебраического многообразия является конечным объединением неприводимых многообразий . К каждому компоненту такого пересечения прикрепляется кратность пересечения . Это понятие является локальным в том смысле, что его можно определить, посмотрев на то, что происходит в окрестности любой общей точки этого компонента. Отсюда следует, что без ограничения общности, мы можем рассматривать, чтобы определить кратность пересечения, пересечение двух аффинных многообразий ( подмногообразий аффинного пространства).

Таким образом, для двух аффинных многообразий V ₁ и V ₂ рассмотрим неприводимую компоненту W пересечения V ₁ и V ₂ . Пусть d будет размерность из W и P быть любой общей точкой W . Пересечение W с д гиперплоскостями в общем положении , проходящем через P имеет неприводимый компонент , который сводится к единственной точке P . Следовательно, локальное кольцо в этой компоненте координатного кольца пересечения имеет только один первичный идеал и, следовательно, является артиновым кольцом . Таким образом, это кольцо представляет собой конечномерное векторное пространство над основным полем. Его размерность является кратность пересечения из V ₁ и V ₂ в Вт .

Это определение позволяет нам точно сформулировать теорему Безу и ее обобщения.

Это определение обобщает кратность корня многочлена следующим образом. Корни многочлена f — это точки на аффинной прямой , которые являются компонентами алгебраического множества, определяемого многочленом. Координатное кольцо этого аффинного множества , где К является алгебраически замкнутое поле , содержащее коэффициенты F . Если это факторизация F , то локальное кольцо R на простом идеале это Это векторное пространство над K , который имеет кратность корня как измерение.
рзнак равноKИкс⟨ж⟩,{\ Displaystyle R = К / \ langle f \ rangle,}ж(Икс)знак равно∏язнак равно1k(Икс-αя)мя{\ Displaystyle f (X) = \ prod _ {я = 1} ^ {k} (X- \ alpha _ {i}) ^ {m_ {i}}}⟨Икс-αя⟩{\ Displaystyle \ langle X- \ alpha _ {я} \ rangle}KИкс⟨(Икс-α)мя⟩.{\ displaystyle K / \ langle (X- \ alpha) ^ {m_ {i}} \ rangle.}мя{\ displaystyle m_ {i}}

Это определение кратности пересечения, которое по существу принадлежит Жан-Пьеру Серру в его книге « Локальная алгебра» , работает только для теоретико-множественных компонентов (также называемых изолированными компонентами ) пересечения, а не для вложенных компонентов . Были разработаны теории для обработки встроенного случая (подробности см. В разделе Теория пересечений ).

Основные признаки делимости

Приведем основные признаки делимости чисел:

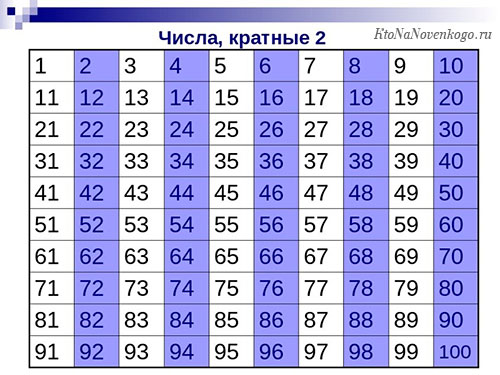
Признак делимости числа на «2»
Число делится нацело на 2, если число является четным (последняя цифра равна 0, 2, 4, 6 или 8)Пример: Число 1256 кратно 2, поскольку оно заканчивается на 6. А число 49603 не делится нацело на 2, поскольку оно заканчивается на 3.
Признак делимости числа на «3»
Число делится нацело на 3, если сумма его цифр делится на 3Пример: Число 4761 делится на 3 нацело, поскольку сумма его цифр равна 18 и она делится на 3. А число 143 не кратно 3, поскольку сумма его цифр равна 8 и она не делится на 3.
Признак делимости числа на «4»
Число делится нацело на 4, если последние две цифры числа равны нулю или число, составленное из двух последних цифр, делится на 4Пример: Число 2344 кратно 4, поскольку 44 / 4 = 11. А число 3951 не делится нацело на 4, поскольку 51 на 4 не делится.
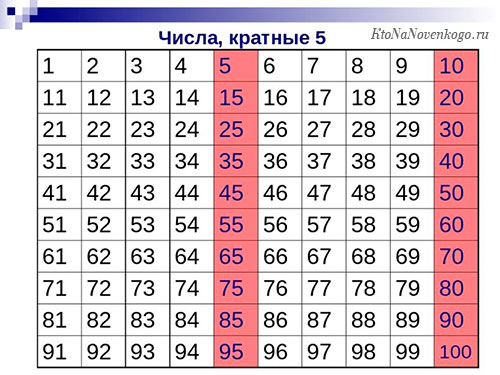
Признак делимости числа на «5»
Число делится нацело на 5, если последняя цифра числа равна 0 или 5Пример: Число 5830 делится нацело на 5, поскольку оно заканчивается на 0. А число 4921 не делится на 5 нацело, поскольку оно заканчивается на 1.
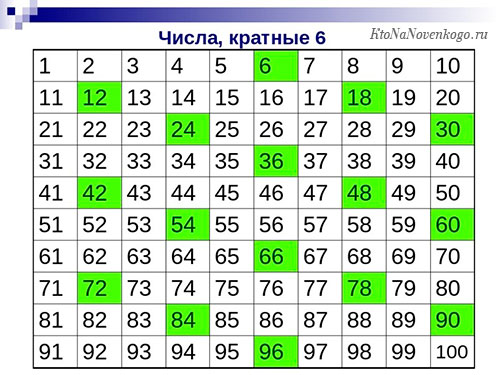
Признак делимости числа на «6»
Число делится нацело на 6, если оно делится нацело на 2 и на 3Пример: Число 3504 кратно 6, поскольку оно заканчивается на 4 (признак делимости на 2) и сумма цифр числа равна 12 и она делится на 3 (признак делимости на 3). А число 5432 на 6 нацело не делится, хотя число заканчивается на 2 (соблюдается признак делимости на 2), однако сумма цифр равна 14 и она не делится на 3 нацело.
Признак делимости числа на «8»
Число делится нацело на 8, если три последние цифры числа равны нулю или число, составленное из трех последних цифр числа, делится на 8Пример: Число 93112 делится нацело на 8, поскольку число 112 / 8 = 14. А число 9212 не кратно 8, поскольку 212 не делится на 8.
Признак делимости числа на «9»
Число делится нацело на 9, если сумма его цифр делится на 9Пример: Число 2916 кратно 9, поскольку сумма цифр равна 18 и она делится на 9. А число 831 не делится на 9 нацело, поскольку сумма цифр числа равна 12 и она не делится на 9.
Признак делимости числа на «10»
Число делится нацело на 10, если оно заканчивается на 0Пример: Число 39590 делится на 10 нацело, поскольку оно заканчивается на 0. А число 5964 не делится на 10 нацело, поскольку оно заканчивается не на 0.
Признак делимости числа на «11»
Число делится нацело на 11, если сумма цифр, стоящих на нечетных местах, равна сумме цифр, стоящих на четных местах или суммы должны отличаться на 11Пример: Число 3762 делится нацело на 11, поскольку 3 + 6 = 7 + 2 = 9. А число 2374 на 11 не делится, поскольку 2 + 7 = 9, а 3 + 4 = 7.
Признак делимости числа на «25»
Число делится нацело на 25, если оно заканчивается на 00, 25, 50 или 75Пример: Число 4950 кратно 25, поскольку оно заканчивается на 50. А 4935 не делится на 25, поскольку заканчивается на 35.

Литература

Арнольд В. И., Варченко А. Н., Гусейн-Заде С. М. Особенности дифференцируемых отображений, — Любое издание.
Брёкер Т., Ландер Л. Дифференцируемые ростки и катастрофы, — Любое издание.
Голубицкий М., Гийемин В. Устойчивые отображения и их особенности, — М.: Мир, 1977.
Хёрмандер Л. Введение в теорию функций нескольких комплексных переменных, — М.: Мир, 1968.
Сборник статей: Особенности дифференцируемых отображений, — М.: Мир, 1968.
Паламодов В.П. О кратности голоморфного отображения, — Функц. анализ и его прил., 1:3 (1967), стр. 54–65.
Арнольд В. И. Замечание о подготовительной теореме Вейерштрасса, — Функц. анализ и его прил., 1:3 (1967), стр. 1–8.

Деление

Операция деления является обратной для операции умножения. Деление показывает, сколько раз одно число умножили на другое, чтобы получить изначальный результат. Для нахождения результата простейших операций деления пользуются таблицей умножения.

Для более сложных примеров пользуются деление в столбик. Так же различают деление с остатком, нацело и деление с дробным остатком:

Деление с остатком. Деление с остатком подразумевает, что получился целый результат и такой же целый остаток, который записывается рядом с результатом.
Деление нацело означает, что в результате деления получилось целое число без всяких остатков. В математике деление нацело встречается крайне редко, куда чаще встречается дробный остаток.
Дробный остаток записывается через запятую. Если в результате деления не получается поделить число нацело, то можно продолжить делить для того, чтобы получить десятичную дробь.

Так же вместо деления всегда можно записать обычную или неправильную дробь, но в качестве ответа такая запись не подойдет.

Отрицательные числа так же можно поделить нацело. Так же, как и в делении отрицательных чисел на положительные и положительные на отрицательные. Нельзя так же забывать, что на деление действует правило знаков. То есть деление отрицательного числа на положительное дает отрицательный результат. Деление отрицательного числа на отрицательное – положительный результат.

В комплексном анализе

Пусть z — корень голоморфной функции f , и пусть n — наименьшее положительное целое число, такое, что n- я производная f, вычисленная в z _0, отлична от нуля. Тогда степенной ряд f относительно z начинается с n- го члена, и говорят , что f имеет корень кратности (или «порядка») n . Если n = 1, корень называется простым корнем.

Мы также можем определить кратность нулей и полюсов в виде мероморфной функции следующим образом: Если мы имеем мероморфную функцию ф = г / ч , принимают разложения Тейлора по г и ч о точке г , и найти первую ненулевой член в каждом (обозначим порядок членов m и n соответственно). если m = n , то точка имеет ненулевое значение. Если m > n , то точка является нулем кратности m — n . Если m < n , то точка имеет полюс кратности n — m .