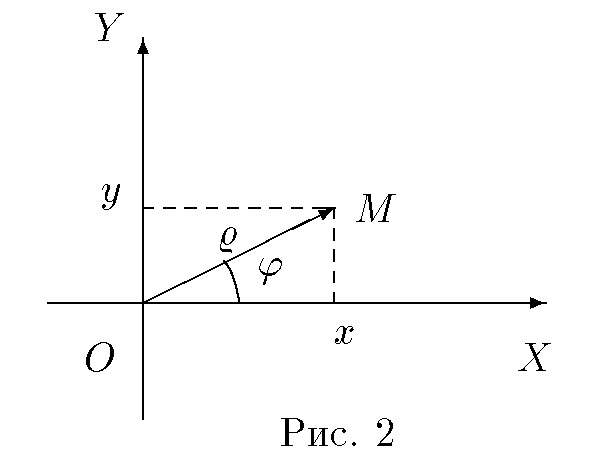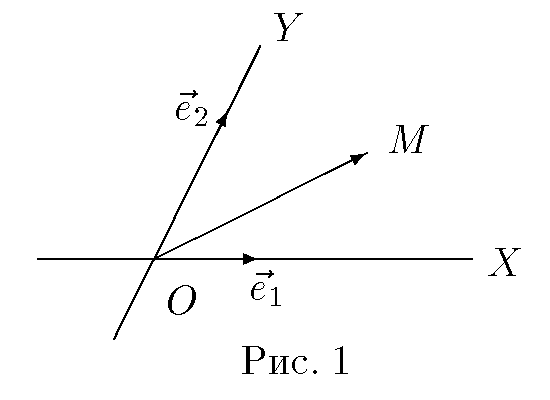Координаты на плоскости

Построение точки по заданным координатам

Пример 1

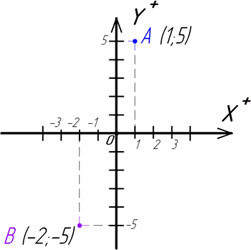
На координатной плоскости построить точки $A(2;5)$ и $B(3; –1).$

Решение.

Построение точки $A$:

отложим число $2$ на оси $x$ и проведем перпендикулярную прямую;
на оси у отложим число $5$ и проведем перпендикулярную оси $y$ прямую. На пересечении перпендикулярных прямых получим точку $A$ с координатами $(2; 5)$.

Построение точки $B$:

отложим на оси $x$ число $3$ и проведем перпендикулярную оси х прямую;
на оси $y$ отложим число $(–1)$ и проведем перпендикулярную оси $y$ прямую. На пересечении перпендикулярных прямых получим точку $B$ с координатами $(3; –1)$.

Пример 2

Построить на координатной плоскости точки с заданными координатами $C (3; 0)$ и $D(0; 2)$.

Решение.

Построение точки $C$:

отложим число $3$ на оси $x$;
координата $y$ равна нулю, значит точка $C$ будет лежать на оси $x$.

Построение точки $D$:

отложим число $2$ на оси $y$;
координата $x$ равна нулю, значит, точка $D$ будет лежать на оси $y$.

Замечание 1

Следовательно, при координате $x=0$ точка будет лежать на оси $y$, а при координате $y=0$ точка будет лежать на оси $x$.

Пример 3

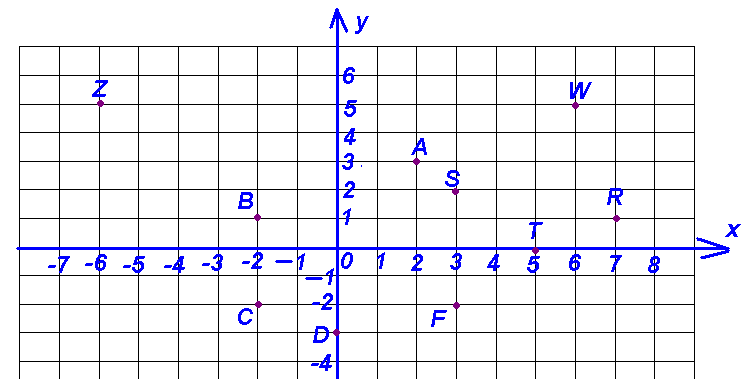
Определить координаты точек A, B, C, D.$

Решение.

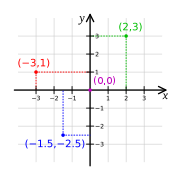
Определим координаты точки $A$. Для этого проведем через эту точку $2$ прямые, которые будут параллельными к координатным осям. Пересечение прямой с осью абсцисс дает координату $x$, пересечение прямой с осью ординат дает координату $y$. Таким образом, получаем, что точка $A (1; 3).$

Определим координаты точки $B$. Для этого проведем через эту точку $2$ прямые, которые будут параллельными к координатным осям. Пересечение прямой с осью абсцисс дает координату $x$, пересечение прямой с осью ординат дает координату $y$. Получаем, что точка $B (–2; 4).$

Определим координаты точки $C$. Т.к. она расположена на оси $y$, то координата $x$ этой точки равна нулю. Координата у равна $–2$. Таким образом, точка $C (0; –2)$.

Определим координаты точки $D$. Т.к. она находится на оси $x$, то координата $y$ равна нулю. Координата $x$ этой точки равна $–5$. Таким образом, точка $D (5; 0).$

Пример 4

Построить точки $E(–3; –2), F(5; 0), G(3; 4), H(0; –4), O(0; 0).$

Решение.

Построение точки $E$:

отложим число $(–3)$ на оси $x$ и проведем перпендикулярную прямую;
на оси $y$ отложим число $(–2)$ и проведем перпендикулярную прямую к оси $y$;
на пересечении перпендикулярных прямых получаем точку $E (–3; –2).$

Построение точки $F$:

координата $y=0$, значит, точка лежит на оси $x$;
отложим на оси $x$ число $5$ и получим точку $F(5; 0).$

Построение точки $G$:

отложим число $3$ на оси $x$ и проведем перпендикулярную прямую к оси $x$;
на оси $y$ отложим число $4$ и проведем перпендикулярную прямую к оси $y$;
на пересечении перпендикулярных прямых получаем точку $G(3; 4).$

Построение точки $H$:

координата $x=0$, значит, точка лежит на оси $y$;
отложим на оси $y$ число $(–4)$ и получим точку $H(0; –4).$

Построение точки $O$:

обе координаты точки равны нулю, значит, точка лежит одновременно и на оси $y$, и на оси $x$, следовательно является точкой пересечения обеих осей (началом координат).

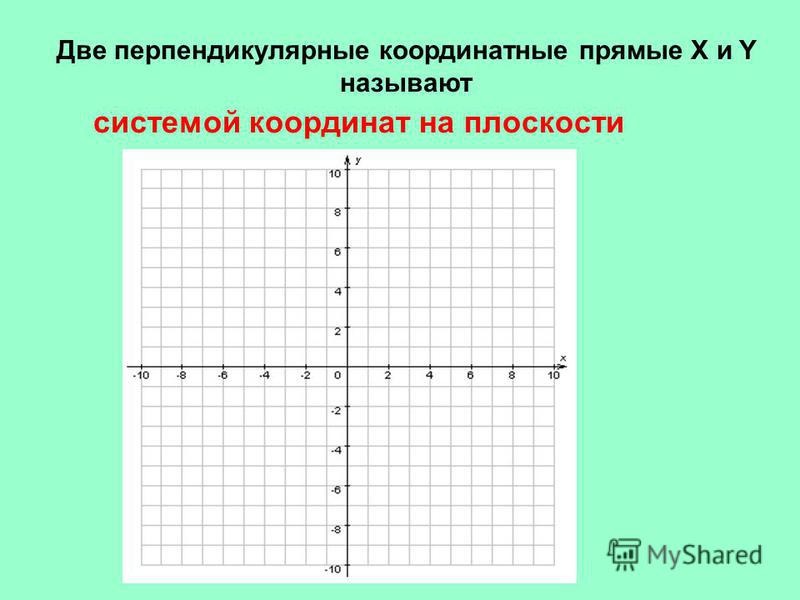
Прямоугольная система координат в пространстве

Прямоугольная система координат в пространстве (в этом параграфе имеется в виду трёхмерное пространство, о более многомерных пространствах — см. ниже) образуется тремя взаимно перпендикулярными осями координат OX{\displaystyle OX}, OY{\displaystyle OY} и OZ{\displaystyle OZ}. Оси координат пересекаются в точке O{\displaystyle O}, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно (не обязательно) одинаковы для всех осей. OX{\displaystyle OX} — ось абсцисс, OY{\displaystyle OY} — ось ординат, OZ{\displaystyle OZ} — ось аппликат.

Рис. 2

Положение точки A{\displaystyle A} в пространстве определяется тремя координатами x{\displaystyle x}, y{\displaystyle y} и z{\displaystyle z}. Координата x{\displaystyle x} равна длине отрезка OB{\displaystyle OB}, координата y{\displaystyle y} — длине отрезка OC{\displaystyle OC}, координата z{\displaystyle z} — длине отрезка OD{\displaystyle OD} в выбранных единицах измерения. Отрезки OB{\displaystyle OB}, OC{\displaystyle OC} и OD{\displaystyle OD} определяются плоскостями, проведёнными из точки A{\displaystyle A} параллельно плоскостям YOZ{\displaystyle YOZ}, XOZ{\displaystyle XOZ} и XOY{\displaystyle XOY} соответственно.

Координата x{\displaystyle x} называется абсциссой точки A{\displaystyle A},

координата y{\displaystyle y} — ординатой точки A{\displaystyle A},

координата z{\displaystyle z} — аппликатой точки A{\displaystyle A}.

Символически это записывают так:

A(x,y,z){\displaystyle A(x,\;y,\;z)}

или

A=(x,y,z){\displaystyle A=(x,\;y,\;z)}

или привязывают запись координат к конкретной точке с помощью индекса:

xA,yA,zA{\displaystyle x_{A},\;y_{A},\;z_{A}}

и т. п.

Каждая ось рассматривается как числовая прямая, т. е. имеет положительное направление, а точкам, лежащим на отрицательном луче приписываются отрицательные значения координаты (расстояние берется со знаком минус). То есть, если бы, например, точка B{\displaystyle B} лежала не как на рисунке — на луче OX{\displaystyle OX}, а на его продолжении в обратную сторону от точки O{\displaystyle O} (на отрицательной части оси OX{\displaystyle OX}), то абсцисса x{\displaystyle x} точки A{\displaystyle A} была бы отрицательной (минус расстоянию OB{\displaystyle OB}). Аналогично и для двух других осей.

Все прямоугольные системы координат в трехмерном пространстве делятся на два класса — правые (также используются термины положительные, стандартные) и левые. Обычно по умолчанию стараются использовать правые координатные системы, а при их графическом изображении еще и располагают их, если можно, в одном из нескольких обычных (традиционных) положений. (На рис. 2 изображена правая координатная система). Правую и левую системы координат невозможно поворотами совместить так, чтобы совпали соответствующие оси (и их направления). Определить, к какому классу относится какая-либо конкретно взятая система координат, можно, используя правило правой руки, правило винта и т. п. (положительное направление осей выбирают так, чтобы при повороте оси OX{\displaystyle OX} против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси OY{\displaystyle OY}, если этот поворот наблюдать со стороны положительного направления оси OZ{\displaystyle OZ}).

Любая из восьми областей, на которые пространство делится тремя взаимно перпендикулярными координатными плоскостями называться октант.

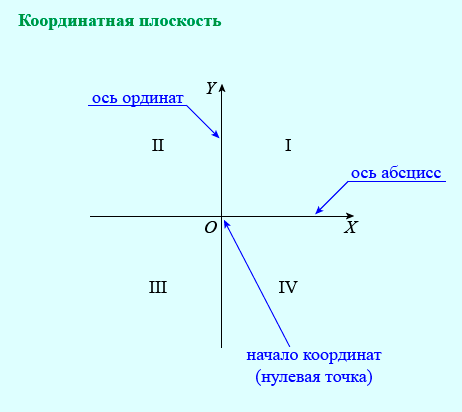
Четверти

Теперь скажем пару слов о таком понятии, как четверти координатной плоскости. Плоскость разбивается двумя осями на четыре четверти. Каждая из них имеет свой номер, при этом нумерация плоскостей ведется против часовой стрелки.

Каждая из четвертей имеет свои особенности. Так, в первой четверти абсцисса и ордината положительная, во второй четверти абсцисса отрицательная, ордината — положительная, в третьей и абсцисса, и ордината отрицательные, в четвертой же положительной является абсцисса, а отрицательной — ордината.

Запомнив эти особенности, можно с легкостью определить, к какой четверти относится та или иная точка. Кроме того, эта информация может пригодиться вам и в том случае, если придется делать вычисления, используя декартову систему.

Прямоугольные координаты вектора

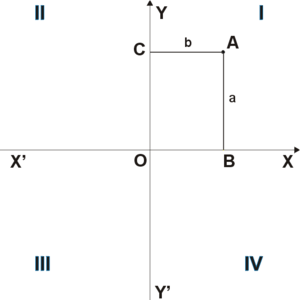
Рис. 1

Для определения прямоугольных координат вектора (применимых для представления векторов любой размерности) можно исходить из того, что координаты вектора (направленного отрезка), начало которого находится в начале координат, совпадают с координатами его конца.

Таким образом, например, координаты (x,y){\displaystyle (x,y)} на рис.1 являются координатами вектора OA→{\displaystyle {\vec {OA}}}.

Для векторов (направленных отрезков), начало которых не совпадает с началом координат, прямоугольные координаты можно определить одним из двух способов:

Вектор можно перенести так, чтобы его начало совпало с началом координат). Тогда его координаты определяются способом, описанным в начале параграфа: координаты вектора, перенесенного так, что его начало совпадает с началом координат, — это координаты его конца.
Вместо этого можно просто вычесть из координат конца вектора (направленного отрезка) координаты его начала.

Для прямоугольных координат понятие координаты вектора совпадает с понятием ортогональной проекции вектора на направление соответствующей координатной оси.

В прямоугольных координатах очень просто записываются все операции над векторами:

Сложение и умножение на скаляр:

a+b=(a1+b1,a2+b2,a3+b3,…,an+bn){\displaystyle \mathbf {a} +\mathbf {b} =(a_{1}+b_{1},a_{2}+b_{2},a_{3}+b_{3},\dots ,a_{n}+b_{n})}

или

(a+b)i=ai+bi,{\displaystyle (\mathbf {a} +\mathbf {b} )_{i}=a_{i}+b_{i},}

c a=(c a1,c a2,c a3,…,c an){\displaystyle c\ \mathbf {a} =(c\ a_{1},c\ a_{2},c\ a_{3},\dots ,c\ a_{n})}

или

(c a)i=c ai.{\displaystyle (c\ \mathbf {a} )_{i}=c\ a_{i}.}

а отсюда и вычитание и деление:

a−b=(a1−b1,a2−b2,a3−b3,…,an−bn){\displaystyle \mathbf {a} -\mathbf {b} =(a_{1}-b_{1},a_{2}-b_{2},a_{3}-b_{3},\dots ,a_{n}-b_{n})}

или

(a−b)i=ai−bi,{\displaystyle (\mathbf {a} -\mathbf {b} )_{i}=a_{i}-b_{i},}

aλ=(a1λ,a2λ,a3λ,…,anλ){\displaystyle {\frac {\mathbf {a} }{\lambda }}={\Big (}{\frac {a_{1}}{\lambda }},{\frac {a_{2}}{\lambda }},{\frac {a_{3}}{\lambda }},\dots ,{\frac {a_{n}}{\lambda }}{\Big )}}

или

(aλ)i=aiλ.{\displaystyle {\Big (}{\frac {\mathbf {a} }{\lambda }}{\Big )}_{i}={\frac {a_{i}}{\lambda }}.}

(Это верно для любой размерности n и даже, наравне с прямоугольными, для косоугольных координат).

Скалярное произведение:

a⋅b=a1b1+a2b2+a3b3+⋯+anbn{\displaystyle \mathbf {a} \cdot \mathbf {b} =a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}+\dots +a_{n}b_{n}}

или

a⋅b=∑i=1naibi,{\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum \limits _{i=1}^{n}a_{i}b_{i},}

(Только в прямоугольных координатах с единичным масштабом по всем осям).

Через скалярное произведение можно вычислить длину вектора

|a|=a⋅a{\displaystyle |\mathbf {a} |={\sqrt {\mathbf {a} \cdot \mathbf {a} }}}

и угол между векторами

∠(a,b)=arccosa⋅b|a|⋅|b|{\displaystyle \angle {(\mathbf {a} ,\mathbf {b} )}=\mathrm {arccos} {\frac {\mathbf {a} \cdot \mathbf {b} }{|\mathbf {a} |\cdot |\mathbf {b} |}}}

Внешнее произведение:

(a∧b)ij=aibj−ajbi{\displaystyle (\mathbf {a} \land \mathbf {b} )_{ij}=a_{i}b_{j}-a_{j}b_{i}}

для любой размерности пространства,

Векторное произведение (только для трехмерного же пространства, на котором оно и определено):

(a×b)x=aybz−azby{\displaystyle (\mathbf {a} \times \mathbf {b} )_{x}=a_{y}b_{z}-a_{z}b_{y}}

(a×b)y=azbx−axbz{\displaystyle (\mathbf {a} \times \mathbf {b} )_{y}=a_{z}b_{x}-a_{x}b_{z}}

(a×b)z=axby−aybx{\displaystyle (\mathbf {a} \times \mathbf {b} )_{z}=a_{x}b_{y}-a_{y}b_{x}}

Очевидно, всё это позволяет, если надо, свести все операции над векторами к достаточно простым операциям над числами.

Оси координат

Как уже говорилось, в системе координат выделяют две оси. Поговорим немного о них, так как они имеют немалое значение.

Первая ось — абсцисс — горизонтальная. Она обозначается как (Ox). Вторая ось — ординат, которая проходит вертикально через точку отсчета и обозначается как (Oy). Именно эти две оси образуют систему координат, разбивая плоскость на четыре четверти. Начало отсчета находится в точке пересечения этих двух осей и принимает значение . Только в случае если плоскость образована двумя пересекающимися перпендикулярно осями, имеющими точку отсчета, это координатная плоскость.

Также отметим, что каждая из осей имеет свое направление. Обычно при построении системы координат принято указывать направление оси в виде стрелочки. Кроме того, при построении координатной плоскости каждая из осей подписывается.

Четверти

Числовая ось

Определение 1. Числовой осью (числовой прямой, координатной прямой) Ox называют прямую линию, на которой точка O выбрана началом отсчёта (началом координат) (рис.1), направление

O → x

указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины.

Рис.1

Определение 2. Отрезок, длина которого принята за единицу длины, называют масштабом.

Каждая точка числовой оси имеет координату, являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA .

Уравнение плоскости

В задачах №14 (С2) ЕГЭ по профильной математике часто требуется найти угол между прямой и плоскостью и расстояние между скрещивающимися прямыми. Но для этого вы должны уметь выводить уравнение плоскости. В общем виде уравнение плоскости задается формулой:
$$ A*x+B*y+C*z+D=0,$$
где $A,B,C,D$ – какие-то числа.

Если найти $A,B,C,D$, то мы мы найдем уравнений плоскости. Плоскость однозначно задается тремя точками в пространстве, значит нужно найти координаты трех точек, лежащий в данной плоскости, а потом подставить их в общее уравнение плоскости.

Например, пусть даны три точки:

Подставим координаты точек в общее уравнение плоскости:

Получилась система из трех уравнений, но неизвестных 4: $A,B,C,D$. Если наша плоскость не проходит через начало координат, то мы можем $D$ приравнять $1$, если же проходит, то $D=0$. Объяснение этому простое: вы можете поделить каждое ваше уравнения на $D$, от этого уравнение не изменится, но вместо $D$ будет стоять $1$, а остальные коэффициенты будут в $D$ раз меньше.

Теперь у нас есть три уравнения и три неизвестные – можем решить систему:

Пример 3

Найти уравнение плоскости, проходящей через точки
$$ K(1;2;3);\,P(0;1;0);\,L(1;1;1). $$
Подставим координаты точек в уравнение плоскости $D=1$:
$$\begin{cases} A*1+B*2+C*3+1=0,\\ A*0+B*1+C*0+1=0, \\ A*1+B*1+C*1+1=0.\end{cases}$$
$$\begin{cases} A+2*B+3*C+1=0,\\ B+1=0, \\ A+B+C+1=0.\end{cases}$$
$$\begin{cases} A-2+3*C+1=0,\\ B=-1, \\ A=-C.\end{cases}$$
$$\begin{cases} A=-0.5,\\ B=-1, \\ C=0.5.\end{cases}$$
Получаем искомое уравнение плоскости:
$$ -0.5x-y+0.5z+1=0.$$

Использование координатной прямой

Интересен тот факт, что практически никогда координатную прямую не используют для нанесения координат. Она используется для наглядного изображения задач или сравнения чисел, упрощая решение и в том и в другом случае.

Решим небольшую задачу.

Необходимо сравнить пять чисел: $${4\over6}; {8\over15}; {17\over4}; {26\over7}$$

Нанесем значения на числовой луч. Каждой дроби будет соответствовать свое значение.

$${4\over6}$$ обозначим отрезком ОА. Он будет меньше единичного отрезка

$${6\over15}$$ обозначим отрезком ОВ. Он так же меньше единичного отрезка

$${17\over4}$$ обозначим отрезком ОС. Он будет больше значения 4, нанесенного на числовом луче.

$${26\over7}$$ обозначим отрезком ОD, который будет расположен между 3 и 4.

Значит, вместо сравнения 4 дробей, нам необходимо сравнить только две: $${5\over6} и {7\over15}$$.

Разложим 6 и 15 на простые числа и найдем НОК.

$$6=2*3$$

$$15=5*3$$

$$НОК=2*3*5=30$$

$${5\over6}={{5*5}\over{6*5}}={25\over30}$$

$${7\over15}={{7*2}\over{15*2}}={14\over30}$$

$${25\over30}>{14\over30}$$

Значит:

$${4\over6}>{6\over15}$$ – теперь можно обозначить точное положение этих чисел. Сравнение выполнено, задача решена.

Рис. 3. Рисунок к задаче.

Что мы узнали?

Мы дали понятие координатной прямой. Привели примеры и подробные объяснения. А также привели в пример задачу с координатной прямой, которую часто решают в рамках математики 6 класса.

Тест по теме

Вопрос 1 из 5

Координаты – это …
- Значения положения точки на плоскости или пространстве
- Числа, определяющие положение точки в пространстве
- Задают положение точки в пространстве
- Все верно

Начать тест(новая вкладка)

Историческая справка

Идеи о создании системы координат были еще во времена Птоломея. Уже тогда астрономы и математики думали о том, как научиться задавать положение точки на плоскости. К сожалению, в то время еще не было известной нам системы координат, и ученым приходилось пользоваться другими системами.

Изначально они задавали точки с помощью указания широты и долготы. Долгое время это был один из наиболее используемых способов нанесения на карту той или иной информации. Но в 1637 году Рене Декарт создал собственную систему координат, названную впоследствии в честь великого математика «декартовой».

После опубликования труда «Геометрия» система координат Рене Декарта завоевала признание в научных кругах.

Уже в конце XVII в. понятие «координатная плоскость» стало широко использоваться в мире математики. Несмотря на то что с момента создания данной системы прошло уже несколько веков, она до сих пор широко используется в математике и даже в жизни.

Работа с координатной плоскостью

Когда мы разобрались с понятием плоскости и поговорили о ее четвертях, можно перейти к такой проблеме, как работа с данной системой, а также поговорить о том, как наносить на нее точки, координаты фигур. На координатной плоскости сделать это не так тяжело, как может показаться на первый взгляд.

В первую очередь строится сама система, на нее наносятся все важные обозначения. Затем уже идет работа непосредственно с точками или фигурами. При этом даже при построении фигур сначала на плоскость наносятся точки, а затем уже прорисовываются фигуры.

Далее мы поговорим подробнее о построении системы и непосредственно нанесении точек и фигур.

Выводы

Итак, мы рассмотрели с вами одно из наиболее интересных и базовых для математики понятий, с которым приходится сталкиваться каждому школьнику.

Мы с вами выяснили, что координатная плоскость – это плоскость, образованная пересечением двух осей. С ее помощью можно задавать координаты точек, наносить на нее фигуры. Плоскость разделена на четверти, каждая из которых имеет свои особенности.

Основной навык, который следует выработать при работе с координатной плоскостью, – умение правильно наносить на нее заданные точки. Для этого следует знать правильное расположение осей, особенности четвертей, а также правила, по которым задаются координаты точек.

Надеемся, что изложенная нами информация была доступна и понятна, а также была полезна для вас и помогла лучше разобраться в данной теме.

Координаты на плоскости

Построение точки по заданным координатам

Прямоугольная система координат в пространстве

Четверти

Прямоугольные координаты вектора

Оси координат

Четверти

Числовая ось

Уравнение плоскости

Использование координатной прямой

Что мы узнали?

Тест по теме

Координаты – это …

Историческая справка

Работа с координатной плоскостью

Выводы

Выводы