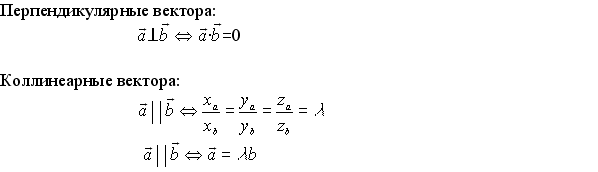Коллинеарность

Признак коллинеарности через пропорциональность или как определить коллинеарность векторов по координатам

Теорема 1

Главное условие коллинеарности векторов: чтобы ненулевые векторы были коллинеарны между собой, необходимо, чтобы их соответствующие координаты были пропорциональны друг другу.

Доказательство.

Необходимость: Пусть нам даны векторы $\overline{α}$ и $\overline{β}$, которые имеют координаты $(α_1,α_2,α_3)$ и $(β_1,β_2,β_3)$, соответственно, причем они коллинеарны друг другу. Тогда нам нужно доказать следующие равенства

$α_1=rβ_1$, $α_2=rβ_2$, $α_3=rβ_3$

$α_1=rβ_1$, $α_2=rβ_2$, $α_3=rβ_3$

Достаточность: Пусть верны равенства $α_1=rβ_1$, $α_2=rβ_2$, $α_3=rβ_3$. Докажем, что векторы $\overline{α}$ и $\overline{β}$ будут коллинеарными.

Из данных равенств следует, что $r\overline{α}=\overline{β}$.

Имеются два случая:

1. $r \lt 0$

2. $r >0$

   Тогда, в обоих случаях получаем доказательство коллинеарности векторов $\overline{α}$ и $\overline{β}$.

Ответ: теорема доказана.

Пример 1

Как проверить коллинеарность векторов $(3,-1)$ и $(9,-3)$.

Доказательство.

Разложим второй вектор:

$(9,-3)=(3\cdot 3,3\cdot (-1) )=3(3,-1)$

Получаем, что координаты этих векторов пропорциональны друг другу, что, по теореме 1, и доказывает наше утверждение.

Необходимое и достаточное условие коллинеарности двух векторов.

Напомним определение коллинеарных векторов, которое было дано в статье векторы – основные определения.

Определение.

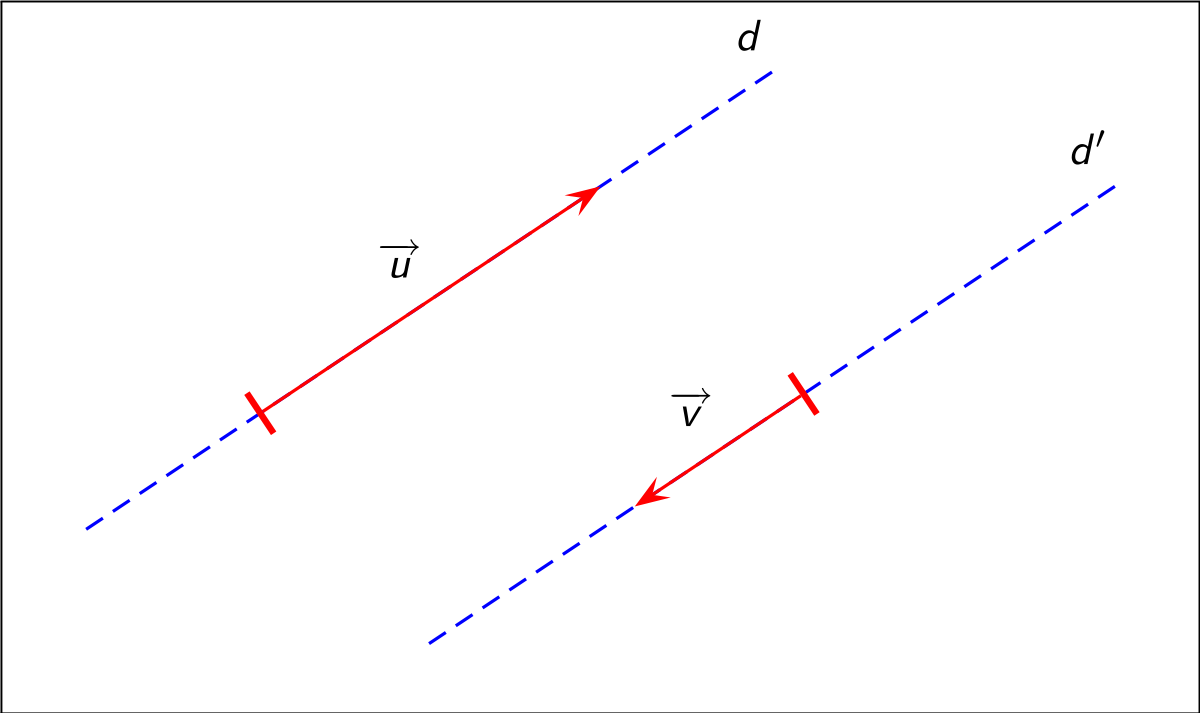
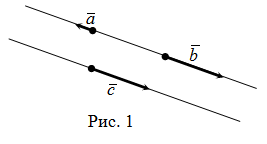
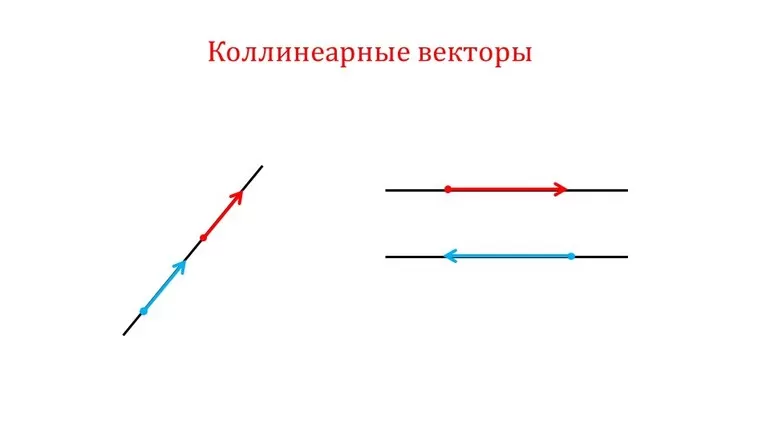
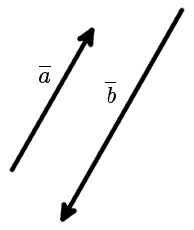
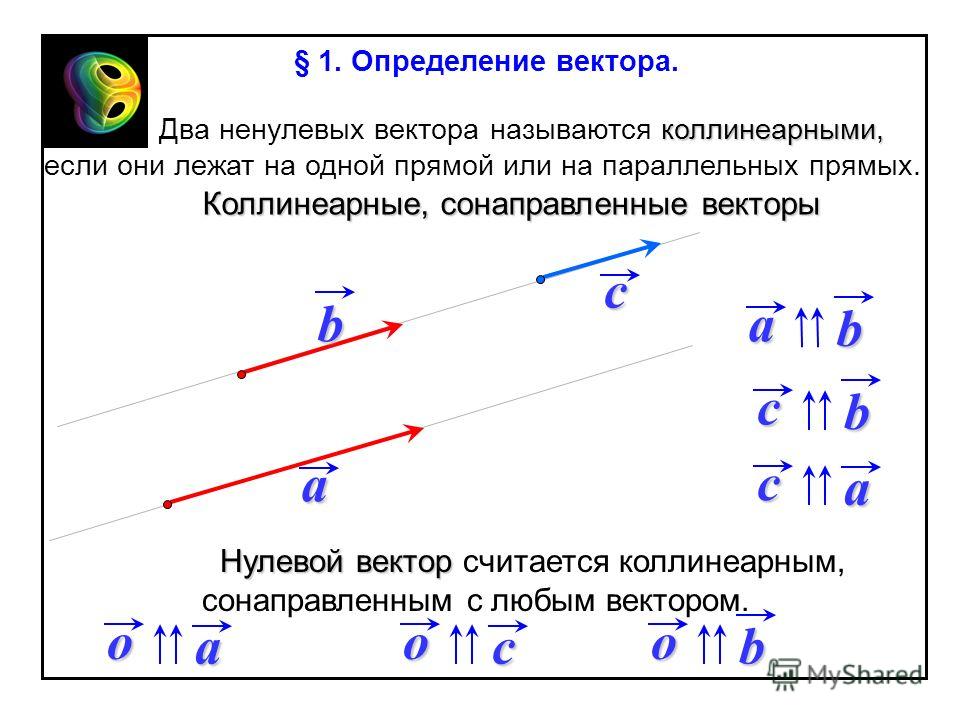
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому другому вектору.

Это определение позволяет установить коллинеарность векторов по их изображению на плоскости с некоторой степенью точности, которая зависит от качества чертежа. Поэтому, мы нуждаемся в алгебраическом (а не в геометрическом) условии, выполнение которого будет указывать на коллинеарность двух векторов. Получим его.

Так как соответствует сжатию или растяжению вектора при неизменном или противоположном направлении, то вектор , где — произвольное действительное число, коллинеарен вектору . Справедливо и обратное утверждение: если вектор коллинеарен ненулевому вектору , то он может быть представлен в виде .

Таким образом, мы пришли к необходимому и достаточному условию коллинеарности двух ненулевых векторов: для коллинеарности двух векторов и необходимо и достаточно, чтобы они были связаны равенствами или .

Перейдем к координатной форме полученного условия коллинеарности двух векторов.

Пусть вектор задан в прямоугольной декартовой системе координат на плоскости и имеет координаты , тогда вектор имеет координаты (при необходимости смотрите статью операции над векторами в координатах). Аналогично, если вектор задан в прямоугольной системе координат трехмерного пространства как , то вектор имеет координаты .

Следовательно, для коллинеарности двух ненулевых векторов и на плоскости необходимо и достаточно, чтобы их координаты были связаны соотношениями: или .

Для коллинеарности двух ненулевых векторов и в пространстве необходимо и достаточно, чтобы или .

Получим еще одно условие коллинеарности двух векторов, основанное на понятии векторного произведения векторов и .

Если ненулевые векторы и коллинеарны, то по определению векторного произведения , что равносильно равенству . А последнее равенство возможно лишь тогда, когда векторы и связаны соотношениями или , где — произвольное действительное число (это следует из теоремы о ранге матрицы), что указывает на коллинеарность векторов и . Таким образом, два ненулевых вектора и коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.

Перейдем к применению условий коллинеарности векторов при решении примеров.

Пример.

Коллинеарны ли векторы и .

Решение.

Проверим выполнение необходимого и достаточного условия коллинеарности двух векторов на плоскости в координатах :

Таким образом, , следовательно, векторы коллинеарны.

Ответ:

векторы и коллинеарные.

Пример.

Убедитесь, что векторы и коллинеарны.

Решение.

Справедливо равенство , так как . Таким образом, необходимое и достаточное условие коллинеарности векторов выполнено, следовательно, исходные векторы коллинеарны.

Можно также найти векторное произведение векторов и убедиться, что оно равно нулевому вектору:

Ответ:

векторы и действительно коллинеарны.

Пример.

При каком значении параметра p векторы и коллинеарны?

Решение.

Заданные векторы коллинеарны, если они связаны соотношением . Из второго уравнения системы имеем , тогда из первого уравнения системы находим .

Ответ:

векторы коллинеарны при .

Размерность и базис векторного пространства

Определение.Вектор
называется линейной комбинацией вектороввекторного пространства R, если он равен
сумме произведений этих векторов на
произвольные действительные числа:

(8.1)

где
–
какие угодно действительные числа.

Определение.Векторы
векторного пространстваназываются линейно зависимыми, если
существуют, такие числа,
не равные одновременно нулю, что:

(8.2)

В
противном случае векторы
называются
линейно независимыми.

Из
приведенных выше определений следует,
что векторы
линейно независимы, если равенствосправедливо лишь при,
и линейно зависимы, если это равенство
выполняется, когда хотя бы одно из чиселотлично от нуля.

Можно
показать, что если векторы
линейно зависимы, то, по крайней мере,
один из них линейно выражается через
остальные. Верно и обратное утверждение
о том, что если один из векторов выражается
линейно через остальные, то все эти
векторы в совокупности линейно зависимы.
В противном случае векторы
называются линейно независимыми.

Из
приведенных выше определений следует,
что векторы
линейно независимы, если равенство
(8.2) справедливо лишь при,
и линейно зависимы, если это равенство
выполняется, когда хотя бы одно из чиселотлично от нуля.

Примером
линейно независимых векторов являются
два неколлинеарных, т.е. не параллельных
одной прямой, вектора
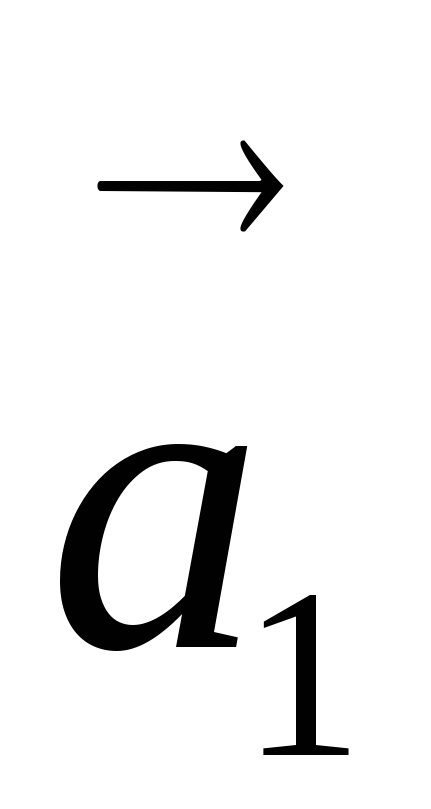ина плоскости. Действительно, условие
(8.2)
будет выполняться лишь в случае,
когда,
ибо если, например,,
то
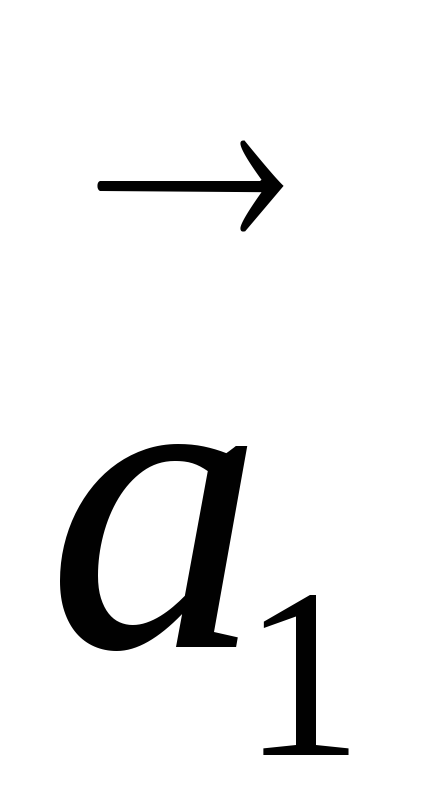и векторыи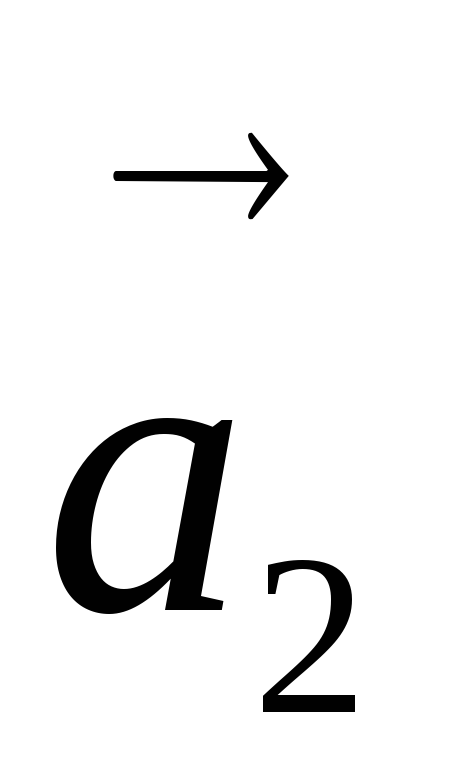коллинеарны. Однако любые три вектора
плоскости линейно зависимы.

Отметим
некоторые свойства векторов линейного
пространства.

1. Если среди векторов имеется нулевой вектор, то эти векторы
   линейно зависимы.

2. Если часть векторов являются линейно зависимыми, то и
   все эти векторы — линейно зависимые.

Определение.Линейное пространство
называется-мерным,
если в нем существует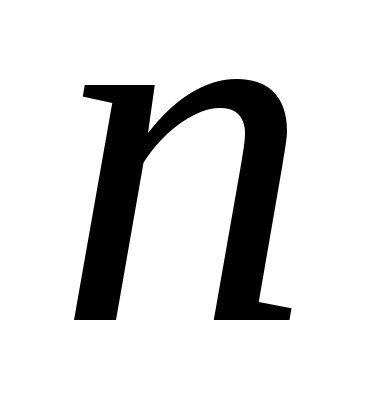линейно независимых векторов, а любые
извекторов уже являются зависимыми.
Другими словами, размерность
пространства — это максимальное число
содержащихся в нем линейно независимых
векторов. Числоназывается размерностью пространстваи обозначается.

Определение.Совокупность
линейно независимых векторов
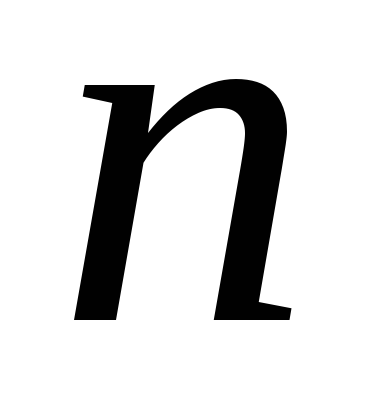-мерного
пространства
называется
базисом.

Справедлива
следующая теорема.

Теорема.Каждый вектор
линейного
пространстваможно представить и притом единственным
способом в виде линейной комбинации
векторов базиса

Это
равенство называется разложением
вектора
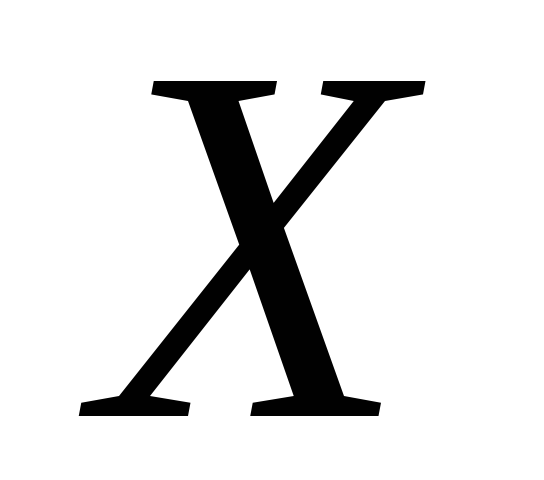по базису,
а числа—
координатами вектораотносительно этого базиса.
В силу единственности разложения
каждый вектор однозначно может быть
определен координатами в некотором
базисе.

Очевидно, что нулевой вектор имеет все
нулевые координаты, а вектор, противоположный
данному, – противоположные по знаку
координаты.

Теорема.Если
–
система линейно независимых векторов
пространстваи любой векторлинейно выражается через,
то пространствоявляется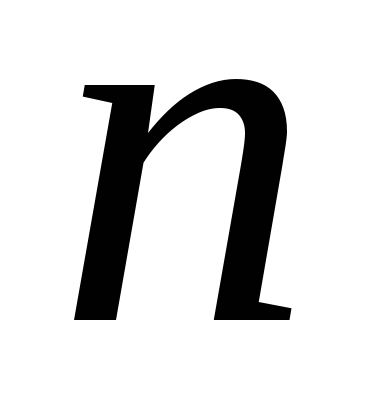-мерным
пространством,
а векторы– его базисом.

Базисом
векторного пространства
называется любая независимая система
линейно независимых–векторов
этого пространства, количество которых
равно,
т.е. выбор системы базисных векторов
векторного пространстванеоднозначен, и может быть осуществлен
большим числом способов.

Нередко
приходится встречаться с заменой
переменных, при которой старые переменные
линейно выражаются через новые, например,
при переходе от одного базиса пространства
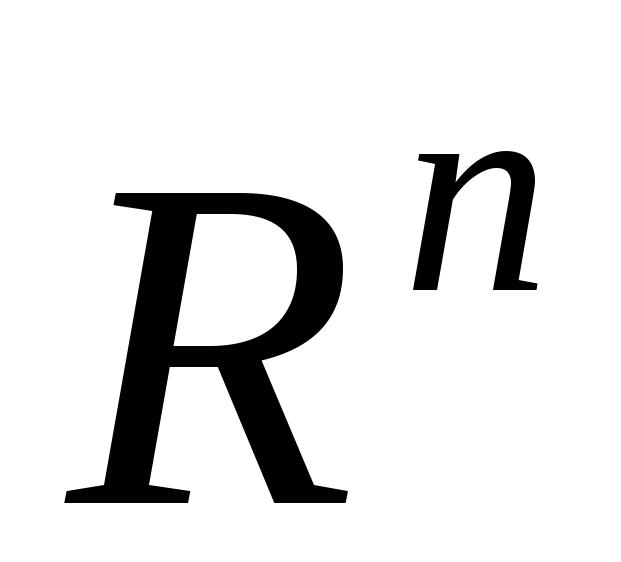к другому. Такую замену переменных
называют обычно их линейным преобразованием.

Линейным
преобразованием переменныхназывается
выражение системы переменныхчерез новую систему переменныхс помощью линейных однородных функций:

Линейное
преобразование вполне определяется
таблицей размером
,
составленной из коэффициентов при.
Такая таблица, составленная из элементовназываетсяматрицей,
а само преобразование представляет
собой пример матричной операции. Понятие
матрицы требует более детального
рассмотрения, что и будет сделано в
следующем разделе.

Геометрия 9 класс

«Центральная симметрия относительно точки» — Центр симметрии в начале луча. Правильный треугольник. Центр во внутренней области фигуры. Что такое симметрия. Центр во внешней области фигуры. Центр симметрии в вершине угла. Фигура называется симметричной относительно точки О. Центр симметрии расположен во внутренней области угла. Центр симметрии принадлежит стороне угла. Центр в вершине фигуры. Точка О – центр симметрии. Построить отрезок А1В1.

«Понятие вектора в геометрии» — Понятие вектора. Ненулевые векторы. Откладывание вектора от данной точки. Сегодня на уроке. Векторы называются равными, если они сонаправлены и их длины равны. Определение. Коллинеарные векторы. Шарада. Любая точка плоскости является нулевым вектором. Назвать все изображенные векторы. Проверь себя. Назовите коллинеарные векторы. Физминутка. Длина вектора. Что называется вектором. Вектор. Прямоугольный параллелепипед.

«Симметрия в живой природе» — Переносная симметрия. Функциональные нарушения. Микроорганизмы. Почему, если симметрично — это красиво. Поворотная симметрия. Симметрия в архитектуре. Наследственность. Золотое сечение. Натурные исследования. Пропорциональность. Билатеральная симметрия. Исследовательский блок. Красивые здания Сабинского района. Расположение. Зеркальная симметрия. Источник сохранения жизни. Закон красоты. Мир растений.

«Радиус вписанной и описанной окружности» — Окружность и правильные многоугольники. Выпуклый многоугольник. Окружность и треугольники. Трапеция. Вписанная окружность в четырёхугольник. Описанная окружность около четырёхугольника. Окружность. Параллелограмм. Окружность и прямоугольный треугольник. Вписанная окружность. Описанная окружность. Основные формулы для правильных многоугольников. Вписанные и описанные окружности.

«Геометрия вокруг нас» — Алмаз. Геометрия вокруг нас. Бордюры. Теоретичекая часть программы. Различные способы построения бордюров. Математик. Способы построения бордюров. Реализация задачи внутрипредметных и межпредметных связей. Зеркальное отражение и параллельный перенос. Практическая часть. Предполагаемый результат изучения элективного курса. Построить бордюр типа «параллельный перенос».

«Длина окружности и круг» — Закончите утверждение. Круговой сектор. Вычислить. Вычисли длину экватора. Длина окружности. Cамостоятельная работа. Площадь круга. Окружность. Найти площадь заштрихованной фигуры. Найди радиус окружности. Круг. Игра. Начерти окружность с центром К и радиусом 2 см. Найти длину окружности.

«Геометрия 9 класс»

Линейные операции над векторами

3.1. Суммой векторов
иназывается вектор, который находится
либо по правилу параллелограмма (рис.
2), либо по правилу треугольника (рис.
3). В первом случае для нахождения суммы
оба вектора откладываются от одной
точки, на этих векторах строится
параллелограмм. Тогда сумма данных
векторов есть вектор, начало которого
совпадает с началами обоих векторов-слагаемых
и направленный по диагонали параллелограмма
(рис. 2). Чтобы найти сумму двух векторов
и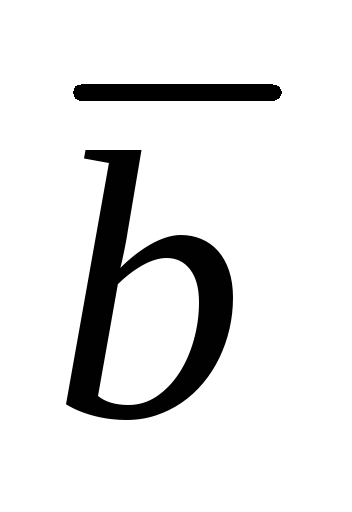по правилу треугольника, нужно расположить
векторы последовательно (от концавектора
отложить вектор
).
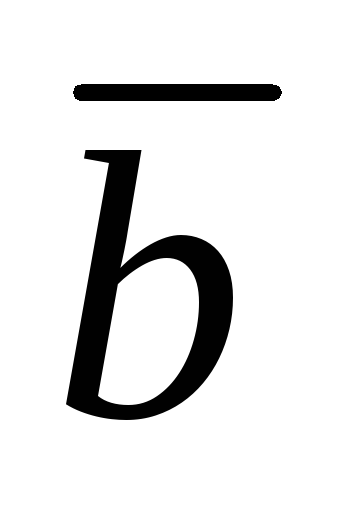Тогда их сумма – это вектор, начало
которого совпадает с началом первого
вектора (вектора
),
а конец совпадает с концом второго
вектора (вектора
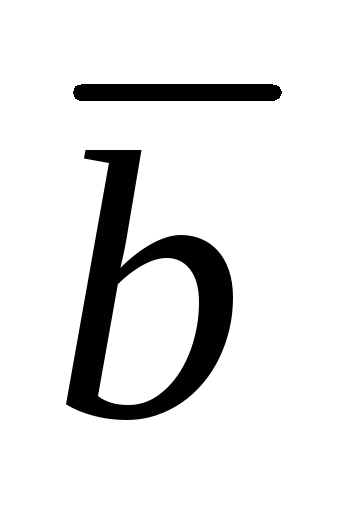)(рис.
3).

Рис. 2
Рис. 3

3.2. Сумму любого числа векторовнаходят по правилу многоугольника (рис.
4).

Рис. 4

По правилу многоугольника путем
параллельного переноса начало каждого
последующего вектора помещают в конец
предыдущего. Вектор
получен путем соединения начала первого
вектора и конца последнего вектора.

3.3. Произведением вектора
на числоназывается вектор,
удовлетворяющий условиям:

1.
,
если>
0;

,
если<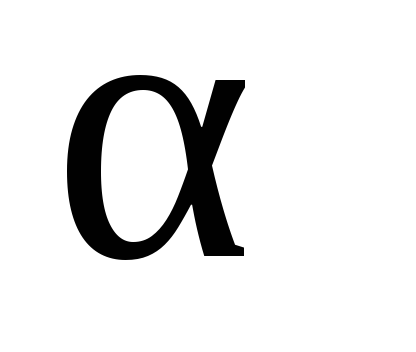
0.

2.
.

3.
.

При этом
принята запись
.

На рис.5 изображены векторы
.

Рис. 5

Примеры задач на коллинеарность векторов

Примеры задач на коллинеарность векторов на плоскости

Пример 1. Какие из векторов a = {1; 2}, b = {4; 8}, c = {5; 9} коллинеарны?

Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае плоской задачи для векторов a и b примет вид:

	=		.

Значит:

Вектора a и b коллинеарны т.к.	1	=	2	.
4	8

Вектора a и с не коллинеарны т.к.	1	≠	2	.
5	9

Вектора с и b не коллинеарны т.к.	5	≠	9	.
4	8

Пример 2. Доказать что вектора a = {0; 3} и b = {0; 6} коллинеарны.

Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число при котором:

b = a.

Для этого найдем ненулевой компонент вектора a в данном случае это . Если вектора колинеарны то

=		=	6	= 2
	3

Найдем значение a:

a = {2 · 0; 2 · 3} = {0; 6}

Так как b = a, то вектора a и b коллинеарны.

Пример 3. найти значение параметра при котором вектора a = {3; 2} и b = {9; } коллинеарны.

Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности

	=		.

Значит:

3	=	2	.
9

Решим это уравнение:

=	2 · 9	= 6
3

Ответ: вектора a и b коллинеарны при = 6.

Примеры задач на коллинеарность векторов в пространстве

Пример 4. Какие из векторов a = {1; 2; 3}, b = {4; 8; 12}, c = {5; 10; 12} коллинеарны?

Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае пространственной задачи для векторов a и b примет вид:

	=		=		.

Значит:

Вектора a и b коллинеарны т.к.	1	=	2	=	3	.
4	8	12

Вектора a и с не коллинеарны т.к.	1	=	2	≠	3	.
5	10	12

Вектора с и b не коллинеарны т.к.	5	=	10	≠	12	.
4	8	12

Пример 5. Доказать что вектора a = {0; 3; 1} и b = {0; 6; 2} коллинеарны.

Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число при котором:

b = a.

Для этого найдем ненулевой компонент вектора a в данном случае это . Если вектора колинеарны то

=		=	6	= 2
	3

Найдем значение a:

a = {2 · 0; 2 · 3; 2 · 1} = {0; 6; 2}

Так как b = a, то вектора a и b коллинеарны.

Пример 6. найти значение параметров и при которых вектора a = {3; 2; } и b = {9; ; 12} коллинеарны.

Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности

	=		=		.

Значит:

3	=	2	=
9		12

Из этого соотношения получим два уравнения:

3	=	2
9

3	=
9	12

Решим эти уравнения:

=	2 · 9	= 6
3

=	3 · 12	= 4
9

Ответ: вектора a и b коллинеарны при = 6 и = 4.