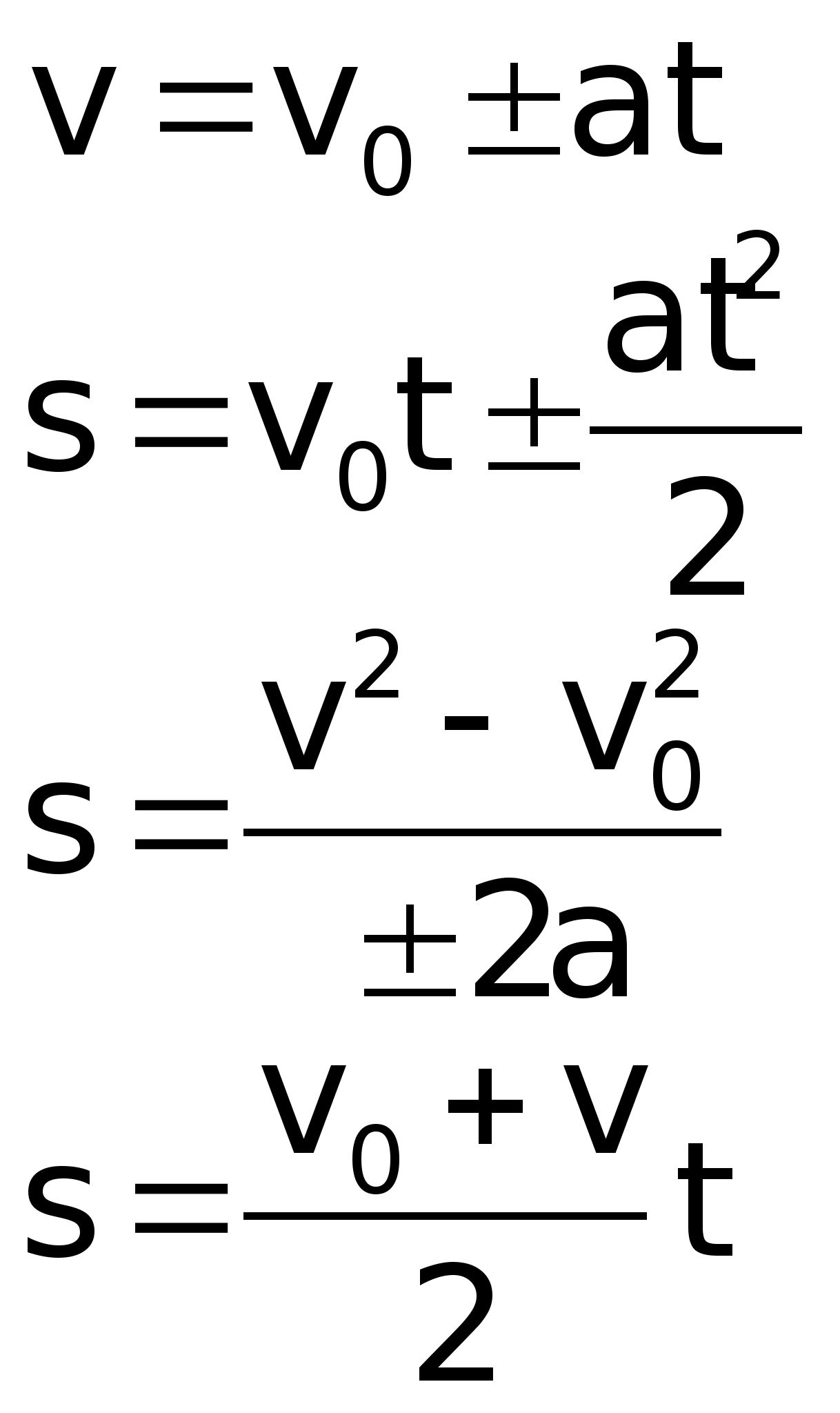Кинематика

История создания кинематики

Нам удалось разобраться с понятием и дать ответ на вопрос о том, что такое кинематика. Но какова же была история ее возникновения как подраздела механики? Вот об этом сейчас и следует поговорить. Достаточно продолжительное время все понятия этого подраздела базировались на работах, которые были написаны еще самим Аристотелем. В них существовали соответствующие утверждения о том, что скорость тела при падении прямо пропорционально численному показателю веса того или иного тела. Также упоминалось, что причиной движения является непосредственно сила, а при ее отсутствии ни о каком движении и речи быть не может.

Тело

В обычной жизни слово «тело» относится к организму человека или животного. Физическое понятие «тело» обозначает любой предмет, как правило, обладающий некоторой массой и некоторым объемом. Камень, Земля, человек, вещь – все это тела с точки зрения физики. Если положение тела с течением времени не меняется, говорят, что тело находится в покое.

Рис. 1. Тело в физике.

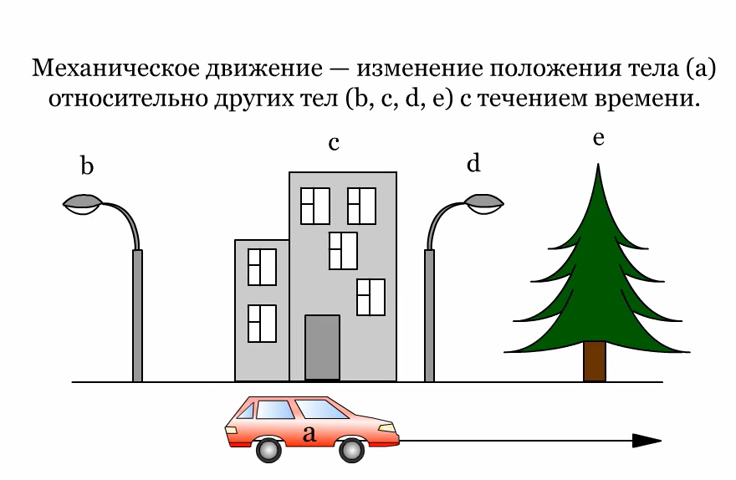
Механическим движением называется изменение положения тела с течением времени относительно других тел.

Из данного правила, следует важное следствие – о механическом движении можно говорить, если рассматривается, по крайней мере, два тела – одно, которое движется, и одно, относительно которого это движение совершается. Движение может совершаться и относительно многих тел

Однако, как правило, движение рассматривается относительно одного тела, которое называется телом отсчета.

Какие объекты рассматриваются?

Если кинематика — это раздел физики, который изучает способы описания движения тел в разноразмерных пространствах, значит, нужно оперировать и самими телами, верно? Чтобы быстрее понять, о чем идет речь, вы можете найти предназначенный для школьников мультимедийный урок. Кинематика для понимания вообще проста, если разобраться в ее основах. При ознакомлении с ними вы заметите, что в теории присутствует информация о том, что данный раздел физики изучает закономерности движения материальных точек. Заметьте, как обобщенно дано определение объектов. С другой стороны, материальные точки не являются единственными рассматриваемыми кинематикой объектами. Этот раздел физики изучает принципы движения также и абсолютно твердых тел, и идеальных жидкостей. Очень часто все эти три понятия объединяют в одно, говоря просто «идеализированные объекты». Идеализация в данном случае нужна для условностей расчетов и отхода от возможных систематических погрешностей. Если вы посмотрите определение материальной точки, то заметите, что о ней написано следующее: это тело, размерами которого в соответствующей ситуации можно пренебречь. Это можно понимать так: по сравнению с пройденным расстоянием линейные размеры объекта ничтожно малы.

Кинематика систем связанных точек и тел

Ма­ши­ны, ме­ха­низ­мы и др. объ­ек­ты тех­ни­ки час­то мо­де­ли­ру­ют сис­те­мой свя­зан­ных ма­те­ри­аль­ных то­чек и тел (см. Свя­зи ме­ха­ни­че­ские). В сис­те­ме со свя­зя­ми по­ло­же­ния и ско­ро­сти разл. то­чек сис­те­мы не мо­гут быть за­да­ны про­из­воль­но. Пер­вой за­да­чей К. та­ких сис­тем яв­ля­ет­ся фор­ма­ли­за­ция свя­зей, ко­то­рые за­пи­сы­ва­ют в ви­де урав­не­ний свя­зей – пол­но­го на­бо­ра не­за­ви­си­мых со­от­но­ше­ний ме­ж­ду ко­ор­ди­на­та­ми то­чек сис­те­мы. Вто­рая за­да­ча К. сис­тем свя­зан­ных то­чек и тел сво­дит­ся к со­кра­ще­нию чис­ла ве­ли­чин, не­об­хо­ди­мых для пол­но­го опи­са­ния дви­же­ния объ­ек­та. Для это­го из об­ще­го чис­ла ве­ли­чин ис­клю­ча­ют те, ко­то­рые вы­ра­жа­ют­ся че­рез дру­гие ве­ли­чи­ны при по­мо­щи урав­не­ний свя­зей. По­след­няя за­да­ча не­ред­ко ре­ша­ет­ся с по­мо­щью под­хо­дя­ще­го вы­бо­ра обоб­щён­ных ко­ор­ди­нат.

Обе за­да­чи К. до­пус­ка­ют не­од­но­знач­ные ре­ше­ния. Из всех ре­ше­ний вы­би­ра­ют­ся та­кие, ко­то­рые по­зво­ля­ют при­дать сис­те­ме диф­фе­рен­ци­аль­ных урав­не­ний дви­же­ния объ­ек­та наи­бо­лее удоб­ную фор­му. В тео­рии ма­шин и ме­ха­низ­мов, кро­ме то­го, не­об­хо­ди­мо свя­зать вход­ные и вы­ход­ные ха­рак­те­ри­сти­ки дви­же­ния (cм. Ки­не­ма­ти­ка ме­ха­низ­мов).

Примеры задач

В простейшей кинематике существуют целые категории самых разных задач. Все они так или иначе связаны с движением материальной точки. Например, в некоторых требуется определить расстояние, пройденное телом за определенное время. При этом могут быть известны такие параметры, как начальная скорость и ускорение. А может быть, перед учеником поставят задачу, которая как раз-таки будет заключаться в необходимости выразить и посчитать ускорение тела. Разберем пример. Автомобиль стартует из статичного положения. Какой путь он успеет пройти за 5 секунд, если его ускорение равно трем метрам, деленным на секунду в квадрате?

Для решения этой задачи нам потребуется формула S = VoT + at^2/2. В нее мы просто подставляем имеющиеся данные. Это ускорение и время

Следует обратить внимание на то, что слагаемое Vot уйдет на нуль, поскольку начальная скорость равна нулю. Таким образом, мы получаем численный ответ 75 метров

Вот и все, задача решена.

Литература

• Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. — М.: Изд-во Физического факультета МГУ, 1997.
• Матвеев А. Н. Механика и теория относительности. — М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.)
• Павленко Ю. Г. Лекции по теоретической механике. — М.: ФИЗМАТЛИТ, 2002. — 392 с.
• Сивухин Д. В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. — М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560с.

• Стрелков С. П. Механика. — М.: Наука, 1975.
• Яворский Б. М., Детлаф А. А. Справочник по физике для инженеров и студентов вузов (4-е изд.). — М.: Наука, 1968.

2.1.6. Связь между кинематическими характеристиками при различных видах движений

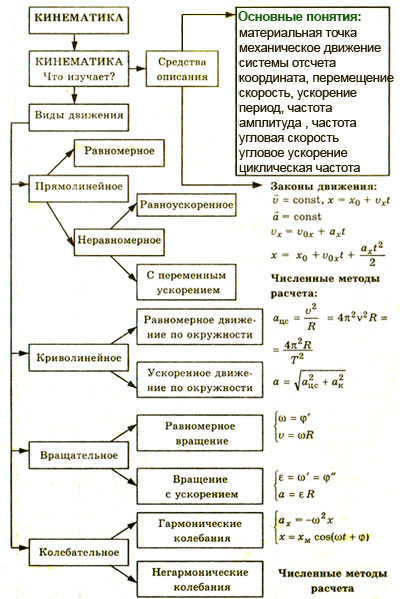
По зависимости скорости и ускорения от времени все механические движения делятся на равномерное, равнопеременное (равноускоренное и равнозамедленное) и неравномерное.

Рассмотрим кинематические характеристики и кинематические уравнения, введенные в предыдущих параграфах, для разных видов движений.

1. Прямолинейное движение

Прямолинейное равномерное движение.

Направление движения задается осью ОХ.

Ускорение а = 0 (а_n = 0, а_τ = 0), скорость v = const, путь s = v∙t, координата x = x v∙t, где x — начальная координата тела на оси ОХ.

Путь — величина всегда положительная. Координата может быть и положительной и отрицательной, поэтому в уравнении, задающем зависимость координаты от времени, перед величиной v∙t в уравнении стоит знак плюс, если направление оси ОХ и направление скорости совпадают, и знак минус, если они противоположно направлены.

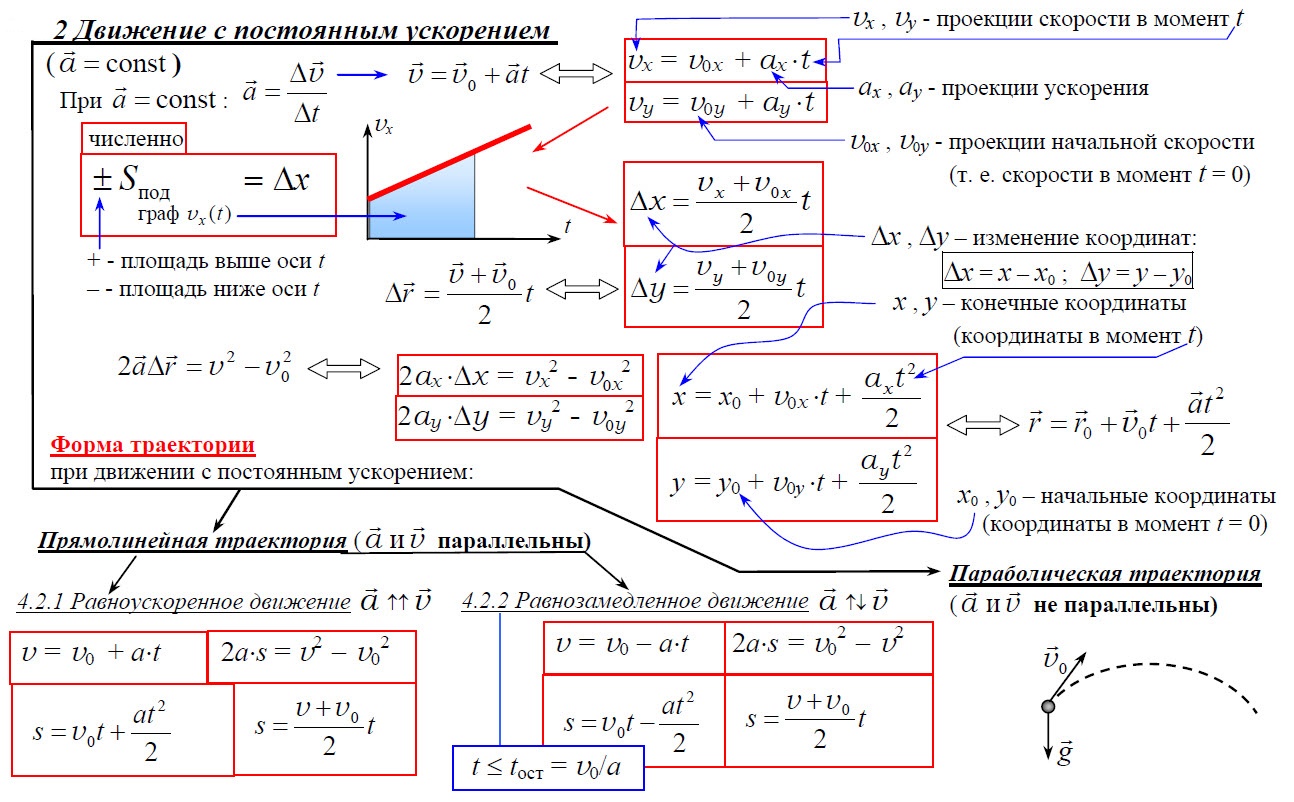
Прямолинейное равнопеременное движение.

Ускорение а = а_τ = const, а_n = 0, скорость , путь , координата .

Перед величиной (at) в кинематическом уравнении для скорости знак плюс соответствует равноускоренному движению, а знак минус — равнозамедленному движению. Это замечание верно и для кинематического уравнения пути, разные знаки перед величинами (at2/2) соответствуют разным видам равнопеременного движения.

В уравнении для координаты знак перед (vt) может быть и плюс, если направления vи оси ОХ совпадают, и минус, если они направлены в разные стороны.

Разные знаки перед величинами соответствуют равноускоренному или равнозамедленному движениям.

Прямолинейное неравномерное движение.

Ускорение а = а_τ>≠ const, а_n = 0,

скорость , путь .

2. Поступательное движение

Для описания поступательного движения можно использовать законы, приведенные в §2.1.6. (пункт 2) или §2.1.4. (пункт3). Использование тех или иных законов для описания поступательного движения зависит от его траектории. Для прямолинейной траектории используются формулы из §2.1.6. (пункт 2), для криволинейной — §2.1.4. (пункт3).

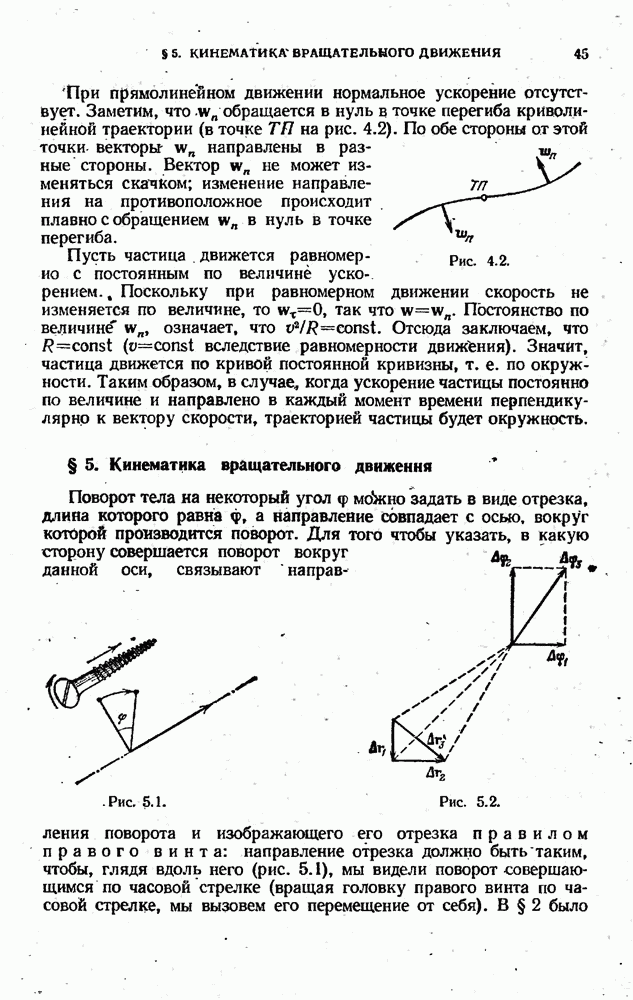
3. Вращательное движение

Отметим, что решение всех задач на вращательное движение твердого тела вокруг неподвижной оси аналогично по форме задачам на прямолинейное движение точки. Достаточно заменить линейные величины s, v_х, a_х на соответствующие угловые величины φ, ω, β, и мы получим все закономерности и соотношения для вращающегося тела.

Равномерное вращение по окружности

(R — радиус окружности).

Ускорение: полное а = а_n, нормальное , тангенциальное а_τ = 0, угловое β = 0.

Скорость: угловая ω = const, линейная v = ωR = const.

Угол поворота ∆φ = ∆ φ+ ωt, ∆φ — начальное значение угла. Угол поворота величина положительная (аналог пути).

Периодом вращения называется промежуток времени T, в течении которого тело, равномерно вращаясь с угловой скоростью ω, совершает один оборот вокруг оси вращения. При этом тело поворачивается на угол 2π.

.

Частота вращения показывает число оборотов, совершаемых телом за единицу времени при равномерном вращении с угловой скоростью ω:

.

Равнопеременное вращение по окружности

Ускорение: угловое β = const, тангенциальное а_τ = βR=const, нормальное а_n = ω 2R ≠ const, полное

Скорость: угловая ω = ω ( βt), линейная

Угловое перемещение .

Все сказанное ранее относительно знаков в кинематических уравнениях для прямолинейного равнопеременного движения остается верным и для кинематических уравнений вращательного движения: плюс в формулах относится к равноускоренному вращению, минус — к равнозамедленному.

2.1.4. Кинематические характеристики. Ускорение

1. Быстрота изменения вектора скорости характеризуется величиной, называемой ускорением. Ускорение может возникнуть как за счет изменения величины скорости, так и за счет изменения направления скорости.

Пусть в момент времени t скорость тела равна v₁, а через промежуток времени ∆t в момент времени t + ∆t равна v₂, приращение вектора скорости за ∆t равно ∆v.

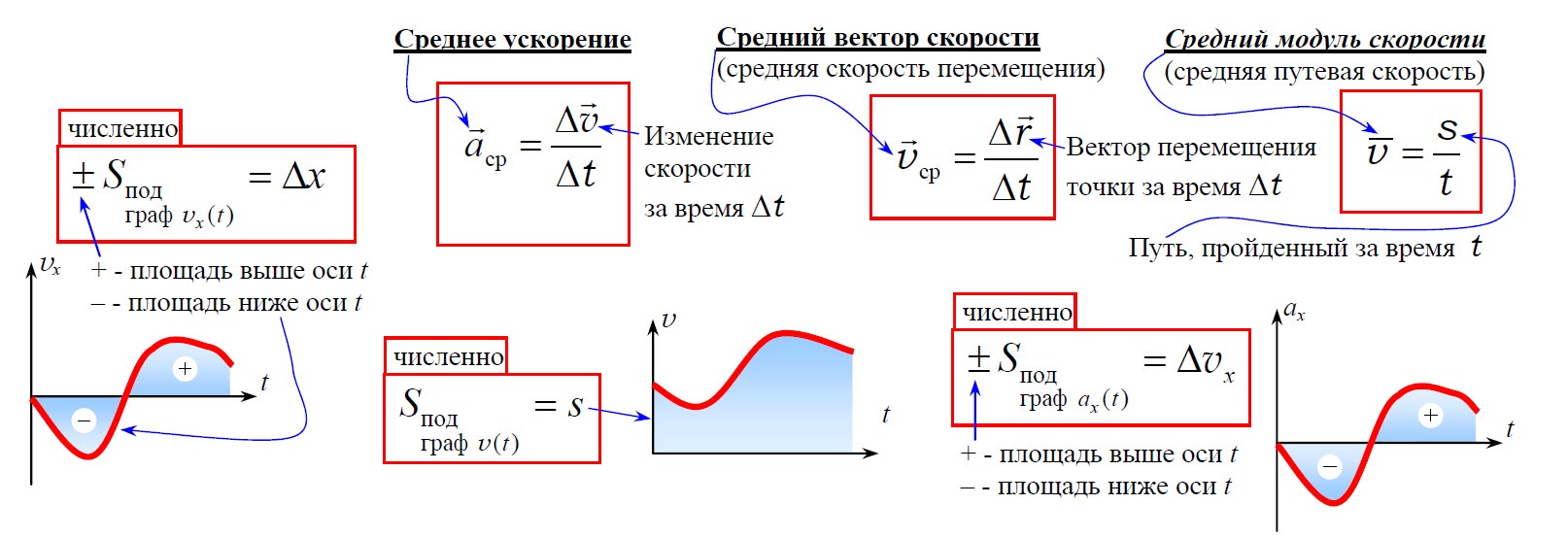
Средним ускорением тела в интервале времени от t до t + ∆t называется вектор а_ср, равный отношению приращения вектора скорости ∆v к промежутку времени ∆t:

Cреднее ускорение есть физическая величина, численно равная изменению скорости за единицу времени.

2. Для определения ускорения в данный момент времени, т.е. мгновенного ускорения, нужно рассмотреть малый интервал времени ∆t→0. Тогда вектор мгновенного ускорения равен пределу вектора среднего ускорения при стремлении промежутка времени ∆t к нулю:

Используя понятие производной, можно дать для ускорения следующее определение: Ускорением (или мгновенным ускорением) тела называется векторная величина а, равная первой производной по времени от скорости тела v или второй производной по времени от пути.

3. При вращении точки по окружности ее скорость может изменяться по величине и по направлению (рисунок 2)

Рисунок 2 — Изменение скорости точки при вращении по окружности

На рисунке 2 в положении 1 скорость точки v_1, в положении 2 скорость точки v₂. Модуль скорости v₂ больше модуля скорости v₁ , ∆v— вектор изменения скорости ∆v = v₂ —v₁

Вращающаяся точка имеет тангенциальное ускорение, равное а_τ=dv/dt, оно изменяет скорость по величине и направлено по касательной к траектории; и нормальное ускорение, равное а_n= v2/R, оно меняет направление скорости и направлено по радиусу окружности (R) (см. Pисунок 3)

Рисунок 3 — Полное, тангенциальное и нормальное ускорения вращающейся точки

Вектор полного ускорения равен , т.е. он может быть представлен как сумма векторов тангенциального a_τ и нормального a_n ускорений. Модуль полного ускорения равен:

2.1.1. Механическое движение. Физические модели реальных тел, используемые в механике. Система отсчета. Траектория. Виды движений

1. Механическое движение — изменение положения тела или отдельных его частей в пространстве с течением времени.

Внутреннее строение движущихся тел, их химический состав не влияет на механическое движение. Для описания движения реальных тел в зависимости от условий задачи пользуются различными моделями: материальная точка, абсолютно твердое тело, абсолютно упругое тело, абсолютно неупругое тело и т.д.

Материальной точкой называется тело, размерами и формой которого можно пренебречь в условиях данной задачи. В дальнейшем вместо термина «материальная точка» будем употреблять термин «точка». Одно и то же тело можно свести к материальной точке в одной задаче, и необходимо учитывать его размеры в условиях другой задачи. Например, расчет движения самолета, летящего над Землей, можно производить, считая его материальной точкой. А при расчете обтекания воздухом крыла того же самолета надо учитывать форму и размеры крыла.

Любое протяженное тело можно рассматривать как систему материальных точек.

Абсолютно твердое тело (а.т.т.) — тело, деформацией которого можно пренебречь в условиях данной задачи. А.т.т. можно рассматривать как систему жестко связанных между собой материальных точек, т.к. расстояние между ними не изменяются при любых взаимодействиях.

Абсолютно упругое тело — тело, деформация которого подчиняется закону Гука (см. § 2.2.2.), и после прекращения силового воздействия оно полностью восстанавливает первоначальные размеры и форму.

Абсолютно неупругое тело — тело, которое после прекращения силового воздействия на него не восстанавливается, а полностью сохраняет деформированное состояние.

2. Для определения положения тела в пространстве и во времени надо ввести понятие системы отсчета. Выбор системы отсчета произволен.

Системой отсчета называется тело или группа тел, считающиеся условно неподвижными и снабженные устройством отсчета времени (часами, секундомером и т.д.), относительно которых рассматривается движение данного тела.

Неподвижное тело (или группу тел) называют телом отсчета и для удобства описания движения с ним связывают систему координат (декартову, полярную, цилиндрическую и т.д.).

Выберем в качестве системы координат декартову прямоугольную систему XYZ (подробно см.). Положение точки С в пространстве можно определить координатами х, y, z (Рисунок 1).

Рисунок 1 — Определение положения точки в декартовой системе координат

Однако положение той же точки в пространстве можно задать с помощью одной векторной величины r = r(x, y, z), называемой радиус-вектором точки С (Рисунок 1).

3. Линия, которую тело описывает при своем движении, называется траекторией. По виду траектории движения можно разделить на прямолинейные и криволинейные. Траектория зависит от выбора системы отсчета. Так, траектория движения точек винта самолета относительно летчика — окружность, а относительно Земли — винтовая линия. Другой пример: какова траектория движения кончика иглы проигрывателя относительно пластинки? корпуса проигрывателя? корпуса звукоснимателя? Ответы таковы: спираль, дуга окружности, состояние покоя (игла неподвижна).

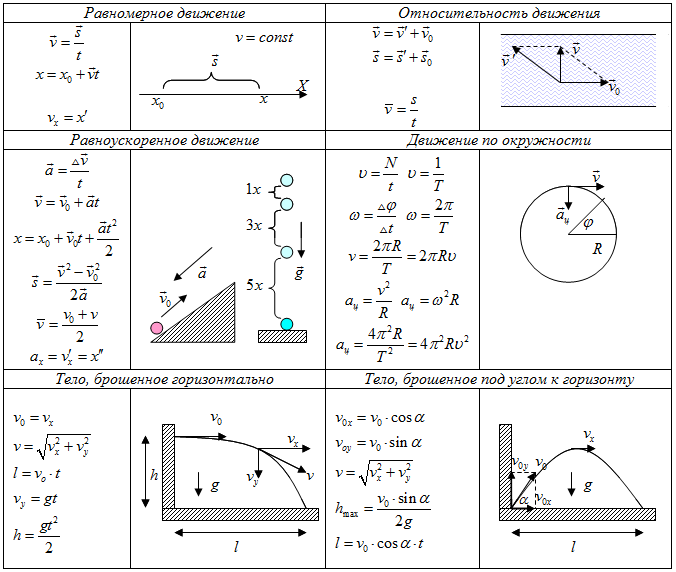
Движение по окружности с постоянной по модулю скоростью

Движение по окружности с постоянной по модулю скоростью – простейший вид криволинейного движения.

Траектория движения – окружность. Вектор скорости направлен по касательной к окружности.
Модуль скорости тела с течением времени не изменяется, а ее направление при движении по окружности в каждой точке изменяется, поэтому движение по окружности – это движение с ускорением.
Ускорение, которое изменяет направление скорости, называется центростремительным.
Центростремительное ускорение направлено по радиусу окружности к ее центру.

Центростремительное ускорение – это ускорение, характеризующее быстроту изменения направления вектора линейной скорости.
Обозначение – ​\( a_{цс} \)​, единицы измерения – ​м/с2​.

Движение тела по окружности с постоянной по модулю скоростью является периодическим движением, т. е. его координата повторяется через равные промежутки времени.Период – это время, за которое тело совершает один полный оборот.
Обозначение – ​\( T \)​, единицы измерения – с.

где ​\( N \)​ – количество оборотов, ​\( t \)​ – время, за которое эти обороты совершены.Частота вращения – это число оборотов за единицу времени.
Обозначение – ​\( \nu \)​, единицы измерения – с–1 (Гц).

Период и частота – взаимно обратные величины:

Линейная скорость – это скорость, с которой тело движется по окружности.
Обозначение – ​\( v \)​, единицы измерения – м/с.
Линейная скорость направлена по касательной к окружности:

Угловая скорость – это физическая величина, равная отношению угла поворота к времени, за которое поворот произошел.
Обозначение – ​\( \omega \)​, единицы измерения – рад/с .

Направление угловой скорости можно определить по правилу правого винта (буравчика).
Если вращательное движение винта совпадает с направлением движения тела по окружности, то поступательное движение винта совпадает с направлением угловой скорости.
Связь различных величин, характеризующих движение по окружности с постоянной по модулю скоростью:

Важно!
При равномерном движении тела по окружности точки, лежащие на радиусе, движутся с одинаковой угловой скоростью, т. к

радиус за одинаковое время поворачивается на одинаковый угол. А вот линейная скорость разных точек радиуса различна в зависимости от того, насколько близко или далеко от центра они располагаются:

Если рассматривать равномерное движение двух сцепленных тел, то в этом случае одинаковыми будут линейные скорости, а угловые скорости тел будут различны в зависимости от радиуса тела:

Когда колесо катится равномерно по дороге, двигаясь относительно нее с линейной скоростью ​\( v_1 \)​, и все точки обода колеса движутся относительно его центра с такой же линейной скоростью \( v_1 \), то относительно дороги мгновенная скорость разных точек колеса различна.

Мгновенная скорость нижней точки ​\( (m) \)​ равна нулю, мгновенная скорость в верхней точке ​\( (n) \)​ равна удвоенной скорости ​\( v_1 \)​, мгновенная скорость точки ​\( (p) \)​, лежащей на горизонтальном радиусе, рассчитывается по теореме Пифагора, а мгновенная скорость в любой другой точке ​\( (c) \)​ – по теореме косинусов.

Справочная информация

ДокументыЗаконыИзвещенияУтверждения документовДоговораЗапросы предложенийТехнические заданияПланы развитияДокументоведениеАналитикаМероприятияКонкурсыИтогиАдминистрации городовПриказыКонтрактыВыполнение работПротоколы рассмотрения заявокАукционыПроектыПротоколыБюджетные организацииМуниципалитетыРайоныОбразованияПрограммыОтчетыпо упоминаниямДокументная базаЦенные бумагиПоложенияФинансовые документыПостановленияРубрикатор по темамФинансыгорода Российской Федерациирегионыпо точным датамРегламентыТерминыНаучная терминологияФинансоваяЭкономическаяВремяДаты2015 год2016 годДокументы в финансовой сферев инвестиционной

Основные понятия кинематики

• Система отсчёта — сопоставленная с континуумом реальных или воображаемых тел отсчёта система координат и прибор(ы) для измерения времени (часы). Используется для описания движения.
• Координаты — способ определять положение точки или тела с помощью чисел или других символов.
• Радиус-вектор используется для задания положения точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.
• Траектория — непрерывная линия, которую описывает точка при своём движении.
• Скорость — векторная величина, характеризующая быстроту перемещения и направление движения материальной точки в пространстве относительно выбранной системы отсчёта.
• Ускорение — векторная величина, показывающая, насколько изменяется вектор скорости точки (тела) при её движении за единицу времени.
• Угловая скорость — векторная величина, характеризующая скорость вращения тела.
• Угловое ускорение — величина, характеризующая быстроту изменения угловой скорости.

Кинематика движения материальной точки

Кроме идеализированных тел, эта наука ввела понятие о материальной точке как об объекте, который имеет исчезающе малые размеры и бесконечно малый вес. Кинематика материальной точки исследует объекты, размерами которых можно легко пренебречь.

Так как в первую очередь изучаются составные движения, то есть ход в двух системах отсчета, взаимно перемещающихся относительно друг друга, кинематика точки полагает равными координаты всех точек, ускорение и саму скорость. А сама система координат, которая связана с точкой отсчета, и часы, которые отсчитывают время, являются системой отсчета, которая определяет положение движущегося объекта в момент времени.

Кинематика точки учитывает пройденный путь, скорость, ускорение и перемещение. Путь — длина траектории, описываемой точкой в заданный промежуток времени. Перемещение — это вектор, который соединяет начальное положение точки с конечным. Направление скорости будет оставаться неизменным, а ее величина, при неравномерном движении, может изменяться. Прямолинейное движение именуется равнопеременным в том случае, когда скорость объекта в любые временные промежутки изменяется одинаково.

В случае с бесконечно малой массой точка есть результат разделения объекта на бесконечное число бесконечно малых частиц. В случае с конечной массой точка есть результат беспредельного сжатия объекта. Представьте шарик заполненный материей, радиус которого уменьшается до бесконечно малого размера, а масса при этом сохраняется.

Кинематика

Раздел механики, изучающий законы движения, его геометрические свойства, законы скоростей и ускорений, называется кинематикой. Название дисциплины образовано от греческого слова «κινειν», означающего движение. Кинематика изучает чистое движение с точки зрения пространства и времени, не учитывая массы физических тел и действующие на них силы. Движение в кинематике описывается исключительно математическими средствами, для чего используются алгебраические и геометрические методы, матанализ и т.д. При этом в классической кинематике не рассматриваются причины, по которым происходит механическое движение тел, а характеристики, присущие движению, считаются абсолютными, т.е. на них не влияет выбор системы отсчёта. Помимо классической, существует релятивистская механика, которая рассматривает общее понятие пространства-времени с инвариантными интервалами.

Относительность движения

Телом отсчета может быть любое тело, из чего вытекает важное следствие относительности движения. Относительность движения означает, что, во-первых, бессмысленно говорить о движении, пока нет системы отсчета

А во-вторых, в разных системах отсчета движение тела может быть совершенно разным, и даже нулевым. Пассажир поезда не движется относительно других пассажиров этого поезда, однако движется и движется по-разному относительно людей, стоящих около железнодорожного полотна, и относительно пассажиров встречного поезда.

Рис. 3. Относительность движения.

Что мы узнали?

Кинематика изучает движение безотносительно его причин. Основные понятия кинематики включают систему отсчета, изучаемое тело и относительность его движения.

Тест по теме

1. Вопрос 1 из 5

Начать тест(новая вкладка)

Понятия и величины, используемые в разделе

Основы кинематики включают в себя несколько величин, которые применяются не только в теоретическом плане, но и имеют место в практических формулах, применяемых при моделировании и решении определенного спектра задач. Познакомимся с этими величинами и понятиями подробнее. Начнем, пожалуй, с последних.

1) Механическое движение. Определяется как изменения пространственного положения определенного идеализированного тела относительно других (материальных точек) в ходе изменения временного интервала. При это на тела, которые упоминаются, имеют между собой соответствующие силы взаимодействия.

2) Система отсчета. Кинематика, определение которой мы дали ранее, базируется на использовании системы координат. Наличие ее вариаций является одним из необходимых условий (вторым условием является применение приборов или средств для измерения времени). Вообще система отсчета необходима для успешного описания того или иного вида движения.

3) Координаты. Являясь условным мнимым показателем, неразрывно связанным с предыдущим понятием (системой отсчета), координаты представляют собой не что иное, как способ, при помощи которого определяется положение идеализированного тела в пространстве. При этом для описания могут быть применены цифры и специальные символы. Координатами нередко пользуются разведчики и артиллеристы.

4) Радиус-вектор. Это физическая величина, которую на практике применяют для задания положения идеализированного тела с оглядкой на первоначальное положение (и не только). Проще говоря, берется определенная точка и она фиксируется для условности. Чаще всего это начало координат. Так вот, после этого, допустим, идеализированное тело из это точки начинает движение по свободной произвольной траектории. В любой момент времени мы можем соединить положение тела с началом координат, и полученная прямая будет представлять собой не что иное как радиус-вектор.

5) Раздел кинематики использует понятие траектории. Она представляет собой обыкновенную непрерывную линию, которая создается в ходе движения идеализированного тела при произвольном свободном движении в разноразмерном пространстве. Траектория, соответственно, может быть прямолинейной, круговой и ломанной.

6) Кинематика тела неразрывно связана с такой физической величиной как скорость

На деле это векторная величина (очень важно помнить о том, что понятие скалярной величины к ней применимо только в исключительных ситуациях), которая будет давать характеристику быстроты изменения положения идеализированного тела. Векторной ее принято считать в силу того, что скорость задает направление происходящего движения

Для использования понятия необходимо применять систему отсчета, как и говорилось ранее.

7) Кинематика, определение которой рассказывает о том, что она не рассматривает причины, вызывающие движение, в определенных ситуациях рассматривает и ускорение. Оно также является векторной величиной, которая показывает, насколько интенсивно будет изменяться вектор скорости идеализированного тела при альтернативном (параллельном) изменении единицы времени. Зная одновременно, в какую сторону направлены оба вектора – скорости и ускорения – можно сказать о том, какой характер имеет движение тела. Оно может быть либо равноускоренным (вектора совпадают), либо равнозамедленным (вектора разнонаправлены).

8) Угловая скорость. Еще одна векторная величина. В принципе, ее определение совпадает с аналогичным, которое мы дали ранее. На самом деле, разница заключается только в том, что ранее рассмотренный случай происходил при движении по прямолинейной траектории. Тут же мы имеем круговое движение. Это может быть аккуратная окружность, а также эллипс. Аналогичное понятие дается и для углового ускорения.

2.1.3. Кинематические характеристики. Скорость

1. Для характеристики быстроты движения тел в физике вводится понятие скорости. Скорость — вектор, а значит, характеризуется величиной, направлением, точкой приложения.

Рассмотрим движение вдоль оси Х. Положение точки будет определяться изменением со временем координаты Х.

Если за время ∆ произошло перемещение точки на ∆r, то величина является средней скоростью движения: .

Средней скоростью движущегося тела называется вектор, равный отношению вектора перемещения к величине промежутка времени, за которое это перемещение произошло.

Модуль средней скорости есть физическая величина, численно равная изменению пути за единицу времени.

2. Для определения скорости в данный момент времени, мгновенной скорости, нужно рассмотреть интервал времени ∆t→0, тогда

Используя понятие производной, можно записать для скорости

Скорость тела в данный момент времени называется мгновенной скоростью (или просто скоростью).

Вектор V мгновенной скорости направлен по касательной к траектории в сторону движения тела.