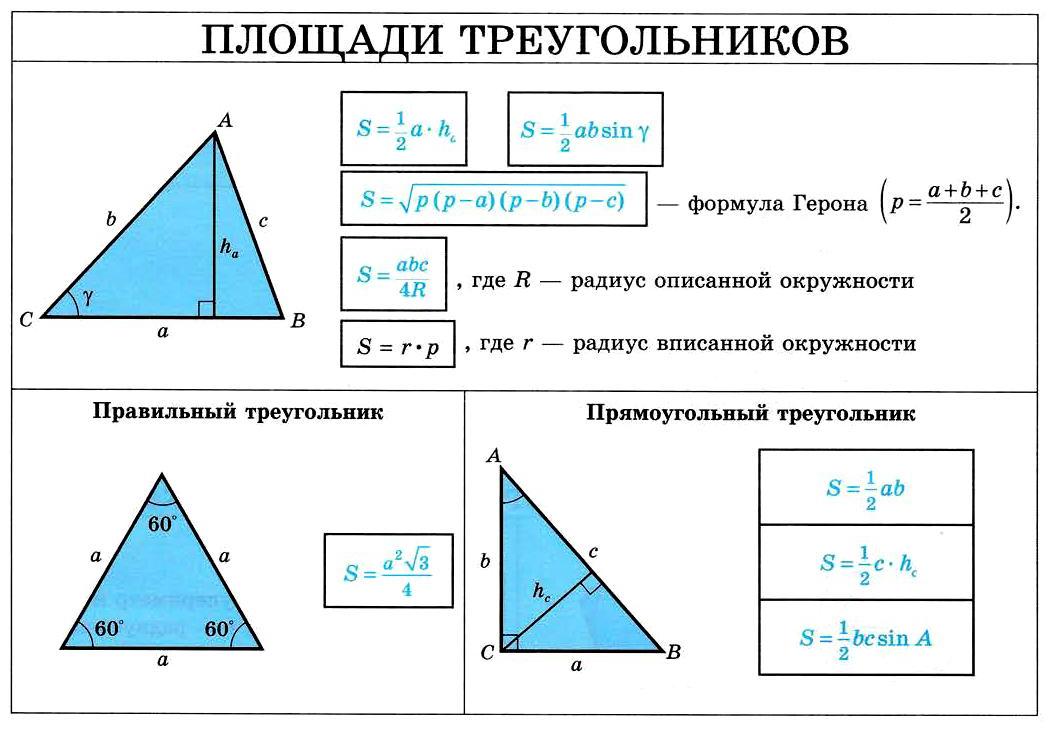
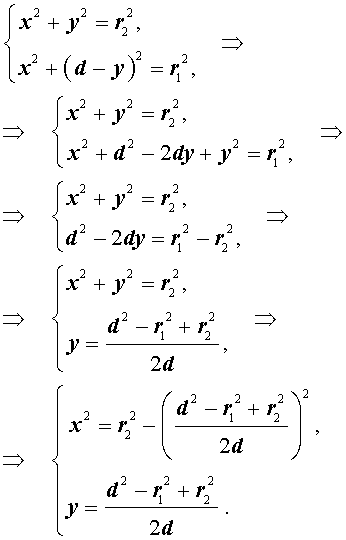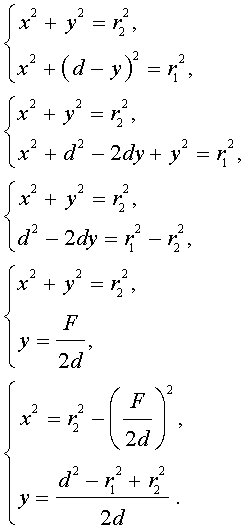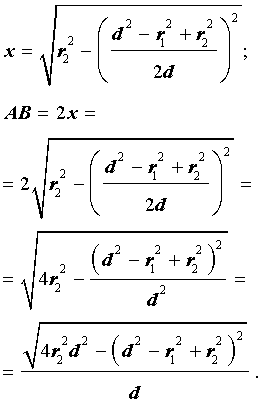Подготовка школьников к егэ и огэ (справочник по математике - планиметрия

Понятие касательной к окружности

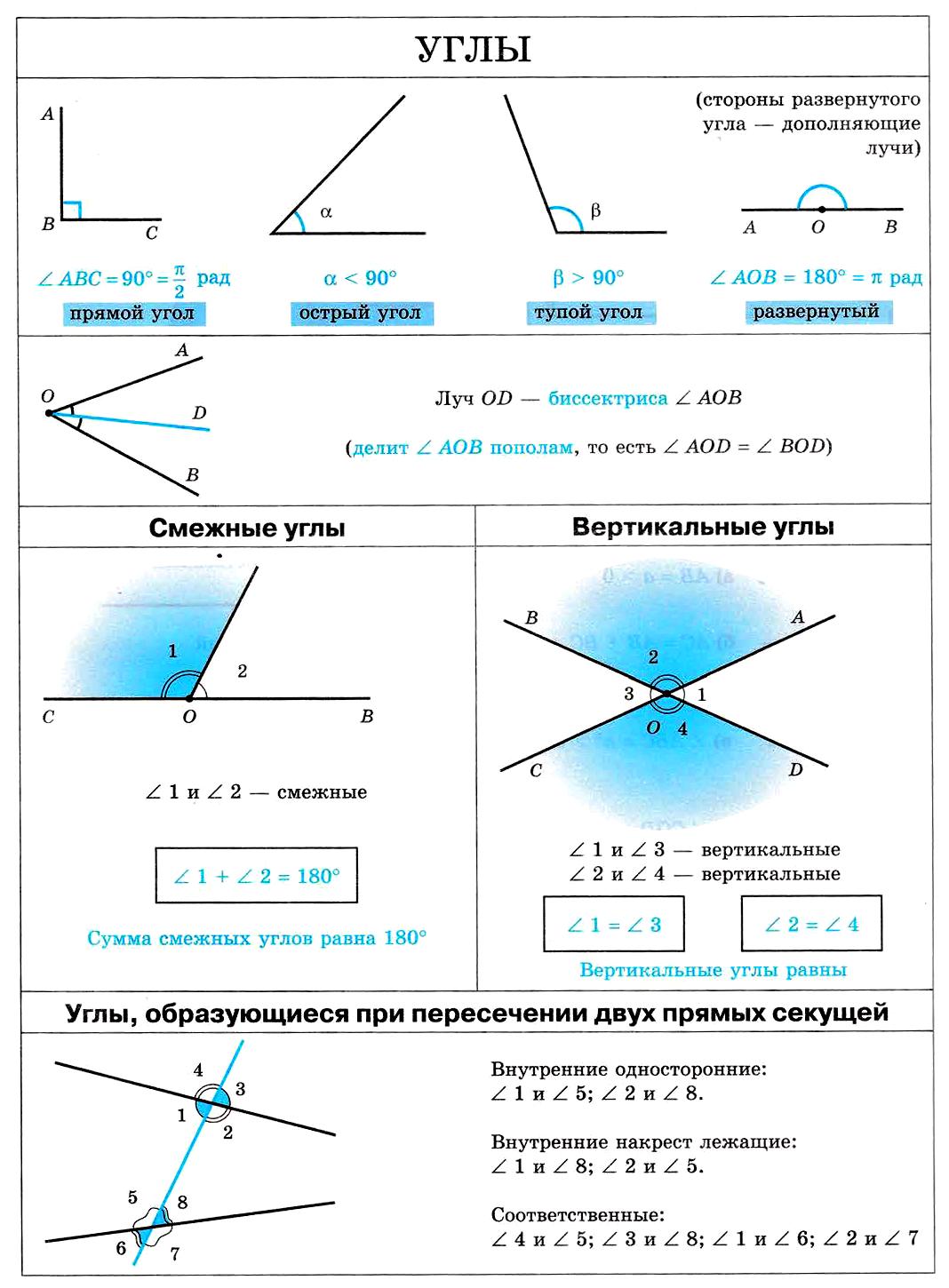
Окружность имеет три возможных взаимных расположений относительно прямой:

Если расстояние от центра окружности до прямой меньше радиуса, то прямая имеет две точки пересечения с окружностью.
Если расстояние от центра окружности до прямой равно радиусу, то прямая имеет две точки пересечения с окружностью.
Если расстояние от центра окружности до прямой больше радиуса, то прямая имеет две точки пересечения с окружностью.

Введем теперь понятие касательной прямой к окружности.

Определение 1

Касательной к окружности называется прямая, которая имеет с ней одну точку пересечения.

Общая точка окружности и касательной называется точкой касания (рис 1).

Рисунок 1. Касательная к окружности

Общие определения

Окружность — это множество точек, которое располагается на одинаковом расстоянии от ее центра, представленного точкой.

Радиус Для любой точки $ OL=R $. (Длина отрезка $ OL $ равняется радиусу окружности).

Хорда Отрезок, который соединяет две точки окружности, является ее хордой.

Диаметр Хорда, проходящая прямо через центр окружности, является диаметром этой окружности $ D=2R $

Длина окружности Длина окружности вычисляется по формуле: $ C=2\pi R $

Дуга окружностиДугой окружности называется та ее часть, которая располагается между двух ее точек. Эти две точки и определяют две дуги окружности. Хорда $ CD $ стягивает две дуги: $ CMD $ и $ CLD $. Одинаковые хорды стягивают одинаковые дуги.

Центральный угол Центральным углом называется такой угол, который находится между двух радиусов.

Длину дуги можно найти по формуле:

Используя градусную меру: $ CD = \dfrac{\pi R \alpha ^{\circ}}{180^{\circ}} $
Используя радианную меру: $ CD = \alpha R $

Диаметр, что перпендикулярен хорде, делит хорду и стянутые ею дуги пополам.

В случае, если хорды $ AB $ и $ CD $ окружности имеют пересечение в точке $ N $, то произведения отрезков хорд, разделенные точкой $ N $, равны между собой.

$ AN\cdot NB = CN \cdot ND $

Касательные прямые к одной окружности

Касательная прямая t к окружности C пересекает окружность в единственной точке T. Для сравнения, секущие прямые пересекают окружность в двух точках, в то время как некоторые прямые могут не пересекать окружность совсем. Это свойство касательной прямой сохраняется при многих геометрических , таких как подобие, вращение, параллельный перенос, инверсия и картографическая проекция. Говоря техническим языком, эти преобразования не меняют структуру инцидентности касательных прямых и окружностей, даже если сами прямые и окружности деформируются.

Радиус окружности, проведённый через точку касания, перпендикулярен касательной прямой. И обратно, перпендикуляр к радиусу в конечной точке (на окружности) является касательной прямой. Окружность вместе с касательной прямой имеют осевую симметрию относительно радиуса (к точке касания).

По теореме о степени точки произведение длин PM•PN для любого луча PMN равно квадрату PT, длине отрезка от точки P до точки касания (отрезок показан красным цветом).

Никакая касательная прямая не может проходить через точку внутри окружности, поскольку любая такая прямая должна быть секущей. В то же время для любой точки, лежащей вне круга, можно построить две проходящие через неё касательные прямые. Геометрическая фигура, состоящая из окружности и двух касательных прямых, также обладает осевой симметрией относительно прямой, соединяющей точку P с центром окружности O (см. рисунок справа). В этом случае отрезки от точки P до двух точек касания имеют одинаковую длину. По теореме о степени точки квадрат длины отрезка до точки касания равен степени точки P относительно окружности C. Эта степень равна произведению расстояний от точки P до двух точек пересечения окружности любой секущей линией, проходящей через P.

Угол θ между хордой и касательной равен половине дуги, заключённой между концами хорды.

Касательная прямая t и точка касания T обладают свойством сопряжённости друг другу; это соответствие можно обобщить в идею о полюсе и поляре. Такая же взаимосвязь существует между точкой P вне окружности и секущей линией, соединяющей две точки касания.

Если точка P лежит вне окружности с центром O, и если касательные прямые из P касаются окружности в точках T и S, то углы ∠TPS и ∠TOS дают в сумме 180°.

Если хорда TM проведена из точки касания T прямой P T и ∠PTM ≤ 90°, то ∠PTM = (1/2)∠MOT.

Геометрическое построение

Построение касательной прямой к окружности (выделена красным) перпендикулярно радиусу.

Относительно легко построить прямую t, касательную к окружности в точке T на окружности. Для этого следует провести прямую a через центр окружности O и точку T. Тогда прямая t является перпендикуляром к прямой a. Один из способов построения перпендикуляра следующий (см. рисунок). Проводим тем же радиусом (r) окружность с центром в точке T, получаем вторую точку G на прямой a, а точка T становится серединой отрезка OG. Проводим две окружности радиуса R>r с центрами в точках O и G. Прямая, проходящая через точки пересечения этих окружностей, будет касательной.

Построение касательной прямой к окружности

Для построения касательной прямой через точку P к окружности C можно использовать свойство угла, опирающегося на диаметр окружности. Проводится окружность с центром в точке H, середине отрезка OP, где O — центр окружности C. Пересечения T и T‘ являются точками касания прямых, проходящих через точку P, поскольку углы ∠OTP и ∠OT‘P опираются на диаметр OP окружности с центром в H.

Теорема об описанном четырёхугольнике и вписанные окружности

Описанный четырёхугольник ABCD — это замкнутая фигура с четырьмя сторонами, которые касаются окружности C. Соответственно, C — вписанная в четырёхугольник ABCD окружность. По теореме Пито суммы противоположных сторон любого такого четырёхугольника равны, то есть

AB¯+CD¯=BC¯+DA¯.{\displaystyle {\overline {AB}}+{\overline {CD}}={\overline {BC}}+{\overline {DA}}.}

Описанный четырёхугольник

Это заключение следует из равенства отрезков касательных от вершин четырёхугольника. Обозначим точки касания как P (на отрезке AB), Q (на отрезке BC), R (на отрезке CD) и S (на отрезке DA). Симметричные отрезки до точек касания от каждой вершины четырёхугольника ABCD равны, то есть BP=BQ=b, CQ=CR=c, DR=DS=d и AS=AP=a.
Но каждая сторона четырёхугольника состоит из двух таких отрезков

AB¯+CD¯=(a+b)+(c+d)=BC¯+DA¯=(b+c)+(d+a){\displaystyle {\overline {AB}}+{\overline {CD}}=(a+b)+(c+d)={\overline {BC}}+{\overline {DA}}=(b+c)+(d+a)},

что и доказывает утверждение.

Обратное утверждение также верно — окружность можно вписать в любой выпуклый четырёхугольник, у которого суммы длин противоположных сторон равны.

Касательные прямые и бильярд

Прицеливание удара в бильярде. Направление удара от битка (шар B) выбирается так, чтобы точка касания совпадала с точкой пересечения прямой, проходящей через центр лузы и центр прицельного шара. В этом случае прицельный шар поёдёт в сторону лузы, а биток пойдёт параллельно зелёной линии, касательной к прицельному шару (C) и воображаемому шару (M)

Система касательных прямых прицеливания битка использует прямую, проходящую через середину кия, для создания двух касательных прямых от битка в направлении прицельного шара. Две касательные прямые и прямая через середину битка пересекают прямую, проходящую через середину прицельного шара и центр лузы. Необходимо направить удар так, чтобы конечное положение битка (воображаемый шар на рисунке) касалось прицельного шара в точке касания прямой, перпендикулярной направлению на лузу (на рисунке эта касательная выделена зелёным цветом).

Решение задач

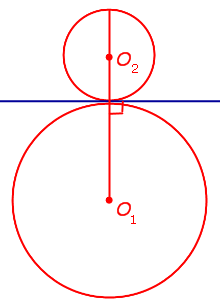
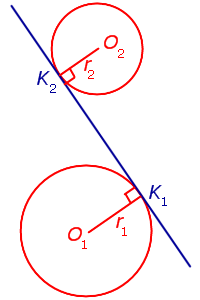
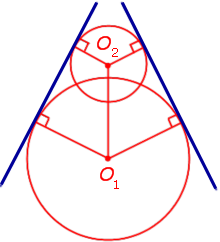
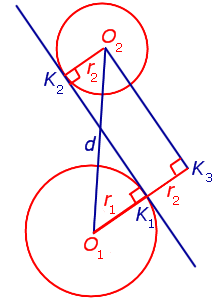
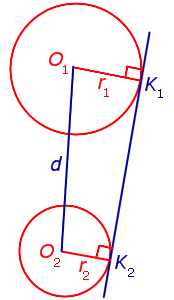
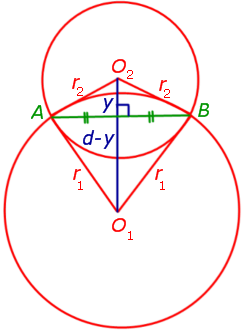
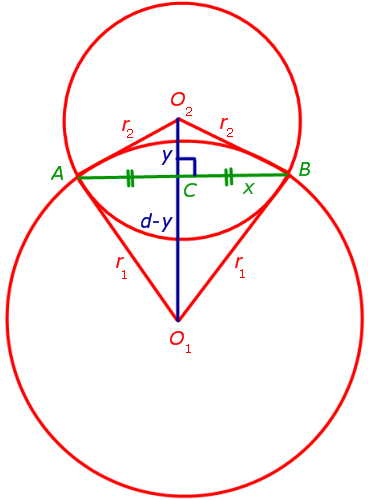
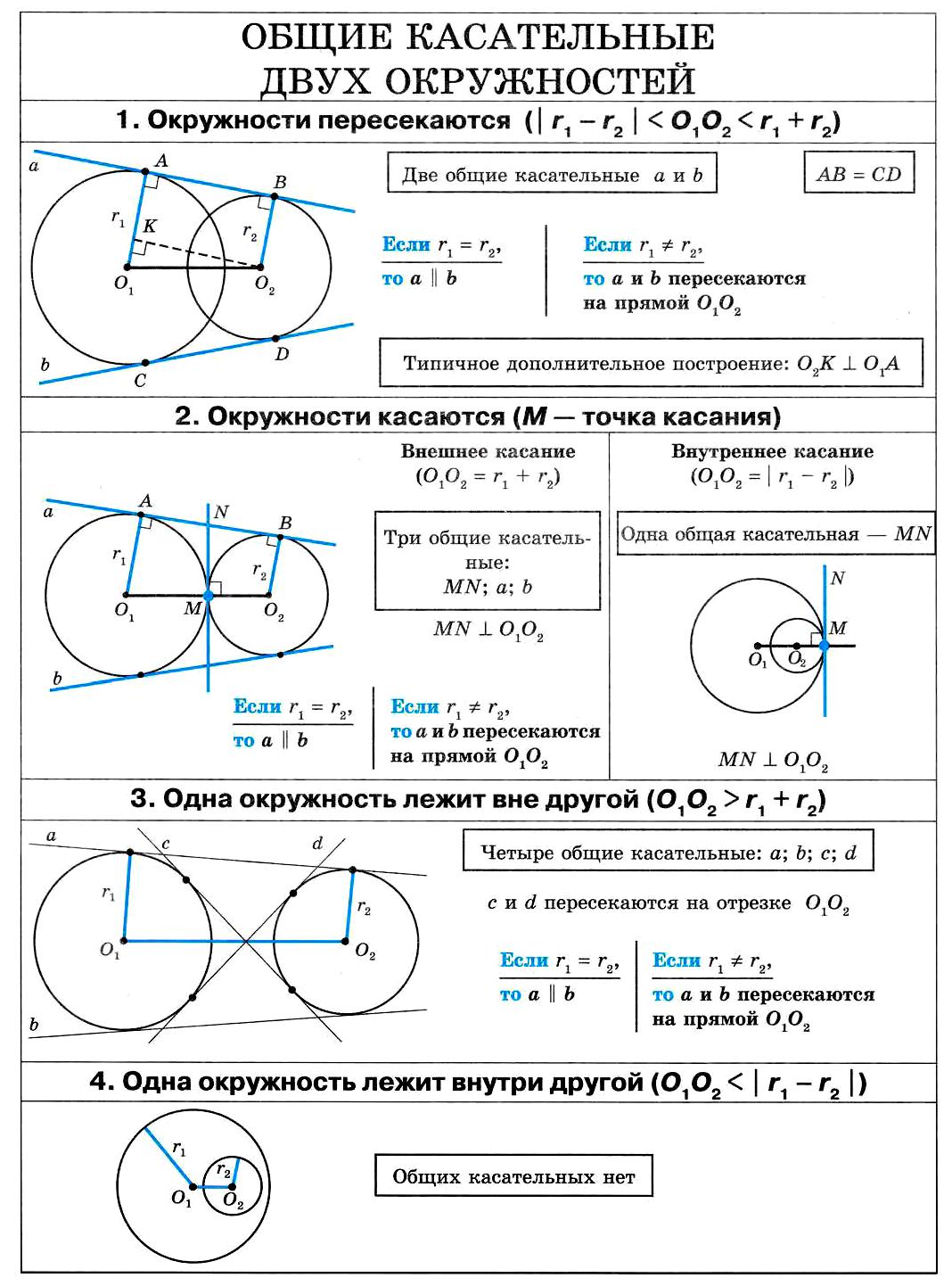
Как внутренняя, так и внешняя касательная к двум окружностям, в построении не так уж просты, хоть эта проблема и решаема. Дело в том, что для этого используется вспомогательная фигура, так что додуматься до такого способа самостоятельно 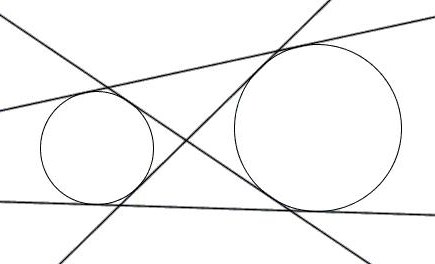довольно проблематично. Итак, даны две окружности с разным радиусом и центрами О1 и О2. Для них нужно построить две пары касательных.

Прежде всего, около центра большей окружности нужно построить вспомогательную. При этом на циркуле должна быть установлена разница между радиусами двух изначальных фигур. Из центра меньшей окружности строятся касательные к вспомогательной. После этого из О1 и О2 проводятся перепендикуляры к этим прямым до пересечения с изначальными фигурами. Как следует из основного свойства касательной, искомые точки на обеих окружностях найдены. Задача решена, по крайнем мере, ее первая часть.

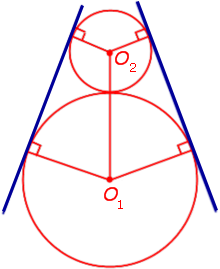
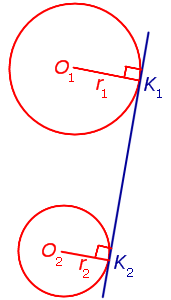
Для того чтобы построить внутренние касательные, придется решить практически 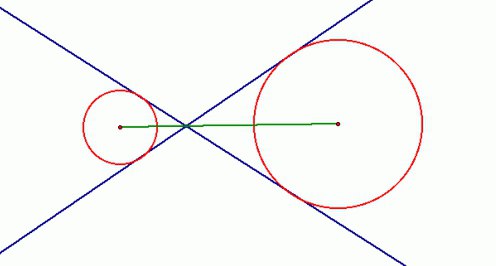аналогичную задачу. Снова понадобится вспомогательная фигура, однако на этот раз ее радиус будет равен сумме изначальных. К ней строятся касательные из центра одной из данных окружностей. Дальнейший ход решения можно понять из предыдущего примера.

Касательная к окружности или даже двум и больше — не такая уж сложная задача. Конечно, математики давно перестали решать подобные проблемы вручную и доверяют вычисления специальным программам. Но не стоит думать, что теперь необязательно уметь делать это самостоятельно, ведь для правильного формулирования задания для компьютера нужно многое сделать и понять. К сожалению, есть опасения, что после окончательного перехода на тестовую форму контроля знаний задачи на построение будут вызывать у учеников все больше трудностей.

Что же касается нахождения общих касательных для большего количества окружностей, это не всегда возможно, даже если они лежат в одной плоскости. Но в некоторых случаях можно найти такую прямую.

Интересный факт

Построение касательной.

Построение касательных – одна из тех задач, которые привели к рождению дифференциального исчисления. Первый опубликованный труд, относящийся к дифференциальному исчислению и принадлежащий перу Лейбница, имел название «Новый метод максимумов и минимумов, а также касательных, для которого не служат препятствием ни дробные, ни иррациональные величины, и особый для этого род исчисления».

Геометрические познания древних египтян.

Если не учитывать весьма скромный вклад древних обитателей долины между Тигром и Евфратом и Малой Азии, то геометрия зародилась в Древнем Египте до 1700 до н.э. Во время сезона тропических дождей Нил пополнял свои запасы воды и разливался. Вода покрывала участки обработанной земли, и в целях налогообложения нужно было установить, сколько земли потеряно. Землемеры использовали в качестве измерительного инструмента туго натянутую веревку. Еще одним стимулом накопления геометрических знаний египтянами стали такие виды их деятельности, как возведение пирамид и изобразительное искусство.

Об уровне геометрических познаний можно судить из древних рукописей, которые специально посвящены математике и являются чем-то вроде учебников, или, вернее, задачников, где даны решения разных практических задач.

Древнейшая математическая рукопись египтян переписана неким учеником между 1800 – 1600 г.г. до н.э. с более древнего текста. Папирус разыскал русский египтолог Владимир Семенович Голенищев. Он хранится в Москве — в Музее изобразительных искусств имени А.С. Пушкина, и называется Московским папирусом.

Другой математический папирус, написанный лет на двести-триста позднее Московского, хранится в Лондоне. Он называется: „Наставление, как достигнуть знания всех тёмных вещей, всех тайн, которые скрывают в себе вещи… По старым памятникам писец Ахмес написал это». Рукопись так и называют „папирусом Ахмеса», или папирусом Райнда — по имени англичанина, который разыскал и купил этот папирус в Египте. В папирусе Ахмеса даётся решение 84 задач на различные вычисления, которые могут понадобиться на практике.

История открытия и изучения

Понятие касательной появилось еще в древности. Построение этих прямых сначала к окружности, а потом к эллипсам, параболам и гиперболам с помощью линейки и циркуля проводилось еще на начальных этапах развития геометрии. Разумеется, история не сохранила имя первооткрывателя, но очевидно, что еще в то время людям были вполне известны свойства касательной к окружности.

В Новое время интерес к этому явлению разгорелся вновь — начался новый виток изучения этого понятия в сочетании с открытием новых кривых. Так, Галилей ввел понятие циклоиды, а Ферма и Декарт построили к ней касательную. Что же касается окружностей, кажется, еще для древних не осталось секретов в этой области.

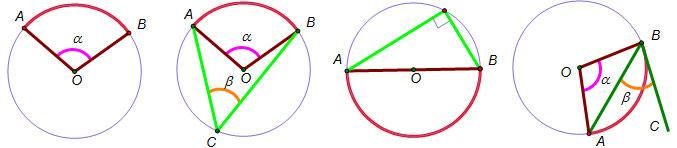
Определения и понятия.

Определение.

Углом наклона прямой y=kx+b называют угол , отсчитываемый от положительного направления оси абсцисс до прямой y=kx+b в положительном направлении (то есть, против часовой стрелки).

На рисунке положительное направление оси абсцисс показано горизонтальной зеленой стрелочкой, положительное направление отсчета угла изображено зеленой дугой, прямая показана синей линией, а угол наклона прямой — красной дугой.

Определение.

Угловым коэффициентом прямой y=kx+b называют числовой коэффициент k.

Угловой коэффициент прямой равен тангенсу угла наклона прямой, то есть, .

Угол наклона прямой равен нулю, когда прямая параллельна оси абсцисс. В этом случае нулю равен и угловой коэффициент, так как тангенс нуля есть ноль. Следовательно, уравнение прямой будет иметь вид y=b.
Когда угол наклона прямой y=kx+b является острым ( или ), то угловой коэффициент k является положительным числом (так как тангенс острого угла принимает положительные значения ) и указывает на возрастание графика прямой.
В случае, когда прямая располагается перпендикулярно оси абсцисс (параллельно оси ординат) и задается равенством x=c, где c — некоторое действительное число.
Когда угол наклона прямой y=kx+b является тупым ( или ), то угловой коэффициент k является отрицательным числом и указывает на убывание графика прямой.

Определение.

Прямую AB, проведенную через две точки графика функции y=f(x), называют секущей. Другими словами, секущая – это прямая, проходящая через две точки графика функции.

Две окружности на плоскости.общие касательные к двум окружностям

На рисунке секущая прямая AB изображена синей линией, график функции y=f(x) — черной кривой, угол наклона секущей — красной дугой.

Если принимать во внимание, что угловой коэффициент прямой равен тангенсу угла наклона (об этом говорили выше), и тангенс угла в прямоугольном треугольнике ABC есть отношение противолежащего катета к прилежащему (это определение тангенса угла), то для нашей секущей будет справедлива серия равенств , где — абсциссы точек А и В, — соответствующие значения функции.

То есть, угловой коэффициент секущей определяется равенством или , а уравнение секущей записывается в виде или (при необходимости обращайтесь к разделу ).

Секущая прямая разбивает график функции на три части: слева от точки А, от А до В и справа от точки В, хотя может иметь более чем две общих точки с графиком функции.

На рисунке ниже приведены три фактически разных секущих (точки А и В различны), но они совпадают и задаются одним уравнением.

Нам ни разу не встречались разговоры о секущей прямой для прямой. Но все же, если отталкиваться от определения, то прямая и ее секущая прямая совпадают.

В некоторых случаях секущая может иметь с графиком функции бесконечное число точек пересечения. Например, секущая, определяемая уравнением y=0, имеет бесконечное число общих точек с синусоидой.

Определение.

Касательной к графику функции y=f(x) в точке называют прямую, проходящую через точку , с отрезком которой практически сливается график функции при значениях х сколь угодно близких к .

Поясним это определение на примере. Покажем, что прямая y = x+1 является касательной к графику функции в точке (1; 2). Для этого покажем графики этих функций при приближении к точке касания (1; 2). Черным цветом показан график функции , касательная прямая показана синей линией, точка касания изображена красной точкой.

Каждый последующий рисунок является увеличенной областью предыдущего (эти области выделены красными квадратами).

Хорошо видно, что вблизи точки касания график функции практически сливается с касательной прямой y=x+1.

А сейчас перейдем к более значимому определению касательной.

Для этого покажем, что будет происходить с секущей АВ, если точку В бесконечно приближать к точке А.

Рисунок ниже иллюстрирует этот процесс.

Секущая АВ (показана синей пунктирной прямой) будет стремиться занять положение касательной прямой (показана синей сплошной линией), угол наклона секущей (показан красной прерывистой дугой) будет стремиться к углу наклона касательной (изображен красной сплошной дугой).

Определение.

Таким образом, касательная к графику функции y=f(x) в точке А – это предельное положение секущей AB при .

Вот теперь можно переходить к оописанию геометрического смысла производной функции в точке.

Построение касательных к окружности

А теперь давайте попробуем разобраться и узнать, что нужно сделать, чтобы построить касательную к окружности.

В этом случае, как правило, в задаче дается окружность и точка. А нам с вами необходимо построить касательную к окружности так, чтобы эта касательная проходила через заданную точку.

В том случае, если нам неизвестно месторасположение точки, то давайте рассмотрим случаи возможного расположения точек.

• Во-первых, точка может находиться внутри круга, который ограничен данной окружностью. В этом случае касательную через эту окружность построить нет возможности.

• Во втором случае, точка находится на окружности, и мы можем строить касательную, проведя перпендикулярную прямую к радиусу, которой проведен к известной нам точке.

• В-третьих, припустим, точка находится за приделами круга, который ограничен окружностью. В этом случае перед тем, как построить касательную, необходимо найти точку на окружности, через которую должна пройти касательная.

С первым случаем, я надеюсь вам все понятно, а вот для решения второго варианта нам необходимо на прямой, на которой лежит радиус, построить отрезок. Этот отрезок должен быть равен радиусу и отрезку, который лежит на окружности, на противоположной стороне.

Здесь мы с вами видим, что точка на окружности является серединой отрезка, который равен удвоенному радиусу. Следующим этапом будет построение двух окружностей. Радиусы этих окружностей будут равняться удвоенному радиусу первоначальной окружности, с центрами в концах отрезка, который равен удвоенному радиусу. Теперь мы можем через любую точку пересечения этих окружностей и заданную точку провести прямую. Такая прямая является срединным перпендикуляром к радиусу окружности, которая была начерчена вначале. Таким образом, мы с вами видим, что эта прямая перпендикулярна окружности и из этого следует, что она является касательной к окружности.

В третьем варианте у нас есть точка, лежащая за приделами круга, который ограничен окружностью. В этом случае мы вначале строим отрезок, который соединит центр предоставленной окружности и заданную точку. А дальше мы находим его середину. Но для этого необходимо построить серединный перпендикуляр. А как его построить вам уже известно. Потом нам нужно начертить окружность или хотя бы ее часть. Теперь мы видим, что точка пересечения заданной окружности и вновь построенной и есть та точка, через которую проходит касательная. Также она проходит и через точку, которая была задана по условию задачи. И наконец, уже через известные вам две точки вы можете провести касательную прямую.

Ну и наконец, чтобы доказать, то, что построенная нами прямая является касательной, нужно обратить внимание на угол, который был образован радиусом окружности и отрезком, известным по условию и соединяющим точку пересечения окружностей с точкой, данной по условию задачи. Теперь мы видим, что образовавшийся угол опирается на полуокружность

А из этого следует, что этот угол прямой. Следовательно, радиус будет перпендикулярен вновь построенной прямой, а эта прямая и есть касательная.

Проблема Аполлония

Анимация, показывающая обратное преобразование задачи Аполлония. Синие и красные круги расширяются до касания и перевернуты в сером круге, образуя две прямые линии. Желтые решения можно найти, перемещая круг между ними, пока он не коснется преобразованного зеленого круга изнутри или снаружи.

Многие частные случаи проблемы Аполлония связаны с поиском окружности, касающейся одной или нескольких прямых. Самый простой из них — построить окружности, которые касаются трех заданных прямых ( проблема LLL ). Чтобы решить эту проблему, центр любого такого круга должен лежать на биссектрисе любой пары прямых; на каждом пересечении двух прямых есть две линии, разделенные биссектрисой. Пересечения этих биссектрис углов дают центры окружностей решений. Всего таких кругов четыре: вписанный круг треугольника, образованный пересечением трех линий, и три выписанных круга.

Общая проблема Аполлония может быть преобразована в более простую задачу об окружности, касающейся одной окружности и двух параллельных прямых (которая сама по себе является частным случаем частного случая LLC ). Для этого достаточно масштабировать две из трех окружностей до тех пор, пока они не коснутся, т.е. не станут касательными. в их касательной точке относительно окружности соответствующих радиусов трансформируют два соприкасающихся данные окружностей на две параллельные линии, а третий круг дан в другой круг. Таким образом, решения могут быть найдены путем скольжения круга постоянного радиуса между двумя параллельными линиями до тех пор, пока он не коснется преобразованного третьего круга. Повторное обращение дает соответствующие решения исходной проблемы.

Касательные прямые к одной окружности

Угол θ между хордой и касательной равен половине дуги, заключённой между концами хорды.

Если хорда TM проведена из точки касания T прямой P T и ∠PTM ≤ 90°, то ∠PTM = (1/2)∠MOT.

Геометрическое построение

Построение касательной прямой к окружности (выделена красным) перпендикулярно радиусу.

Построение касательной прямой к окружности

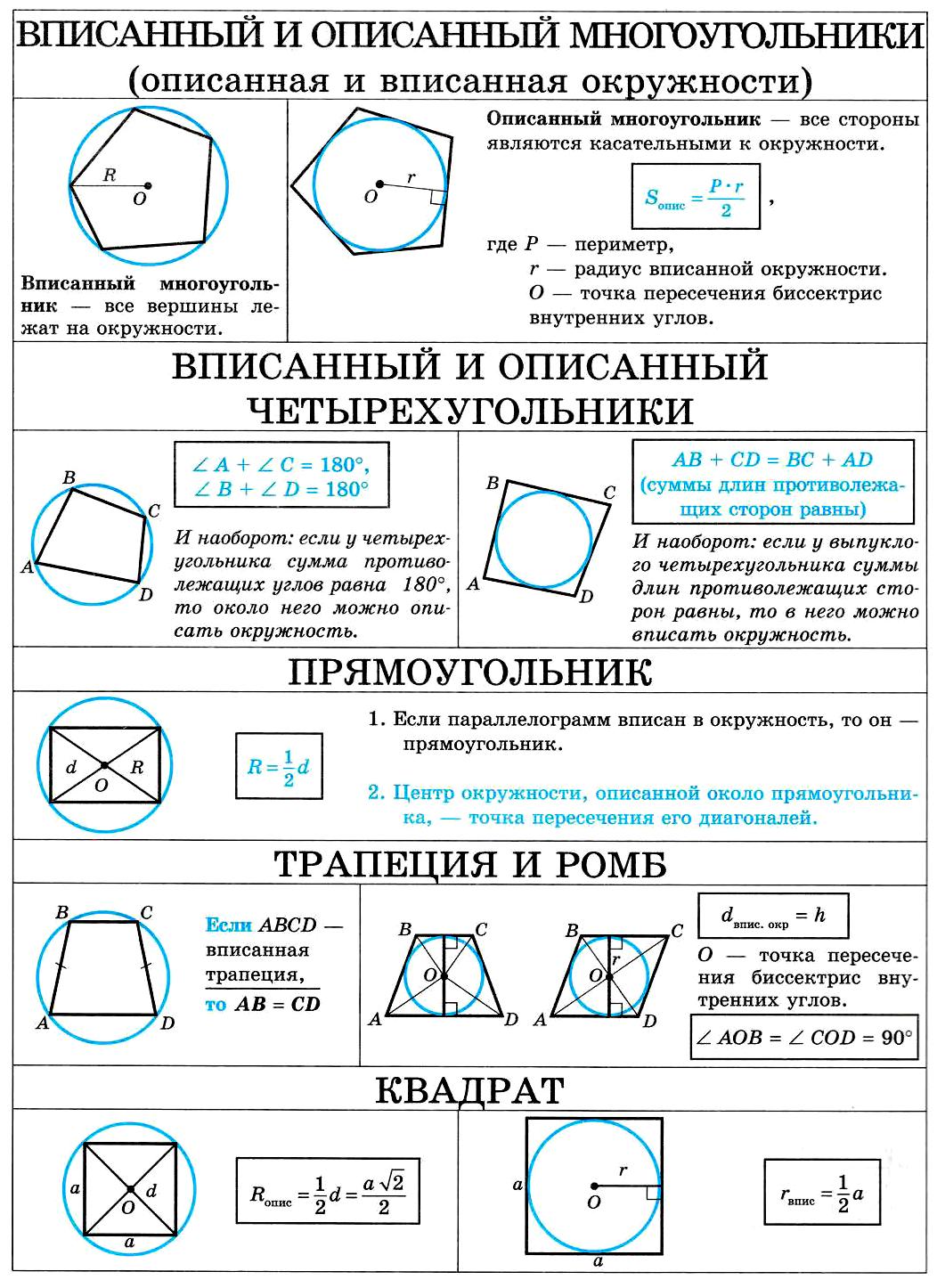
Теорема об описанном четырёхугольнике и вписанные окружности

AB¯+CD¯=BC¯+DA¯.{\displaystyle {\overline {AB}}+{\overline {CD}}={\overline {BC}}+{\overline {DA}}.}

Описанный четырёхугольник

AB¯+CD¯=(a+b)+(c+d)=BC¯+DA¯=(b+c)+(d+a){\displaystyle {\overline {AB}}+{\overline {CD}}=(a+b)+(c+d)={\overline {BC}}+{\overline {DA}}=(b+c)+(d+a)},

что и доказывает утверждение.

Касательные, секущие, хорды.

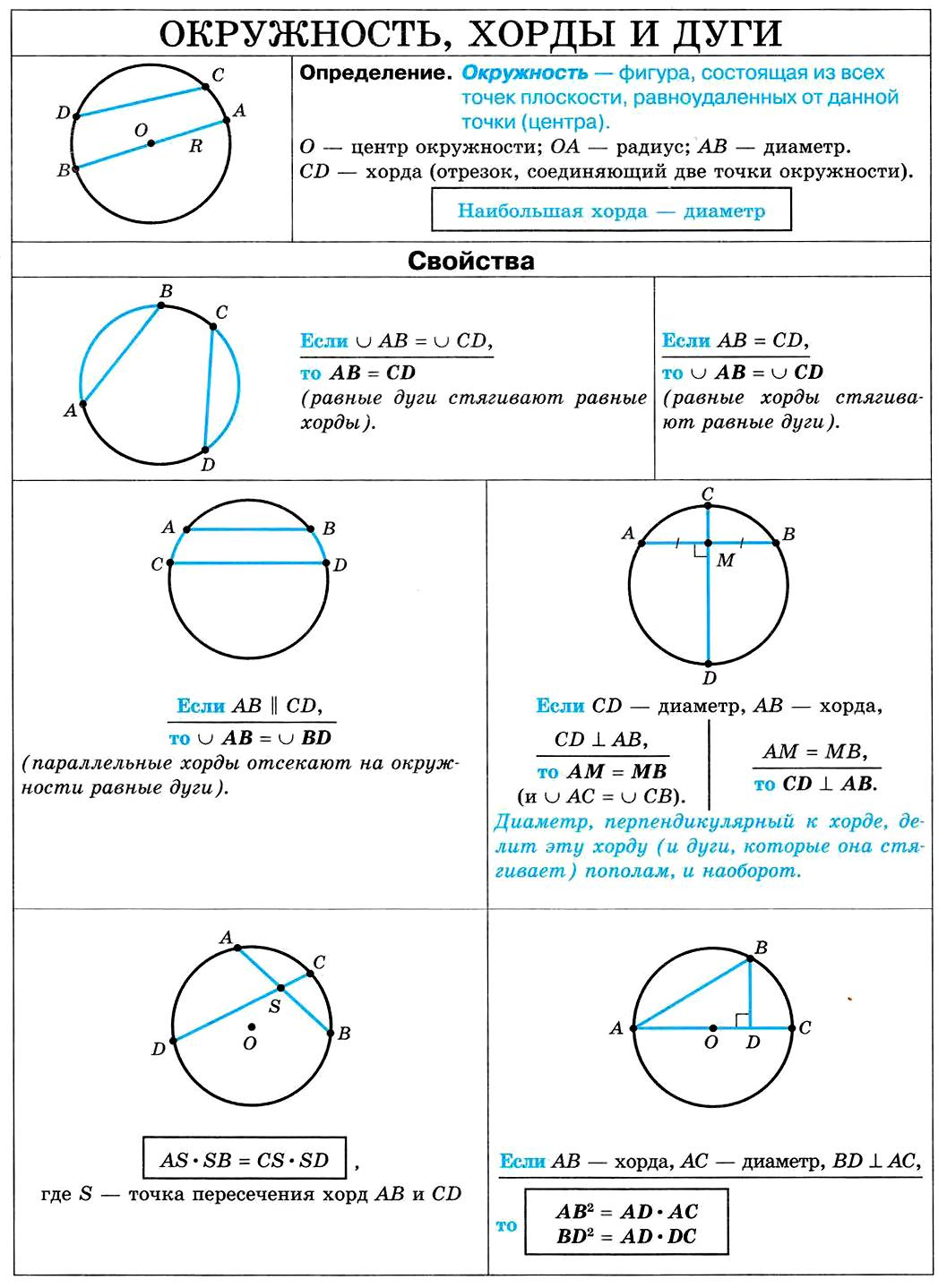
Окружность — это фигура, которая состоит из множества точек плоскости, равноудаленных от данной точки (центра).

Отрезок, соединяющий любую точку на окружности с центром окружности, называется радиусом ($R$).

$ОС=OD=OE=R.$

Отрезок, соединяющий любые две точки на окружности, называется хордой, а хорда, проходящая через центр, — диаметром ($d$).

$ВС$ – хорда

$СЕ$ — диаметр

Свойства хорды и диаметра:

1. Диаметр равен двум радиусам $d=2R; СЕ=2СО$

2. Равные хорды стягивают равные дуги

Если $AB=CD$, то $∪AB=∪CD$.

3.Вся окружность составляет $360°$. Диаметр делит окружность на две полуокружности по $180°$.

4. Хорды окружности, удаленные от центра на равные расстояния, равны.

5. Из двух хорд больше та, которая менее отдалена от центра.

Касательные и секущие:

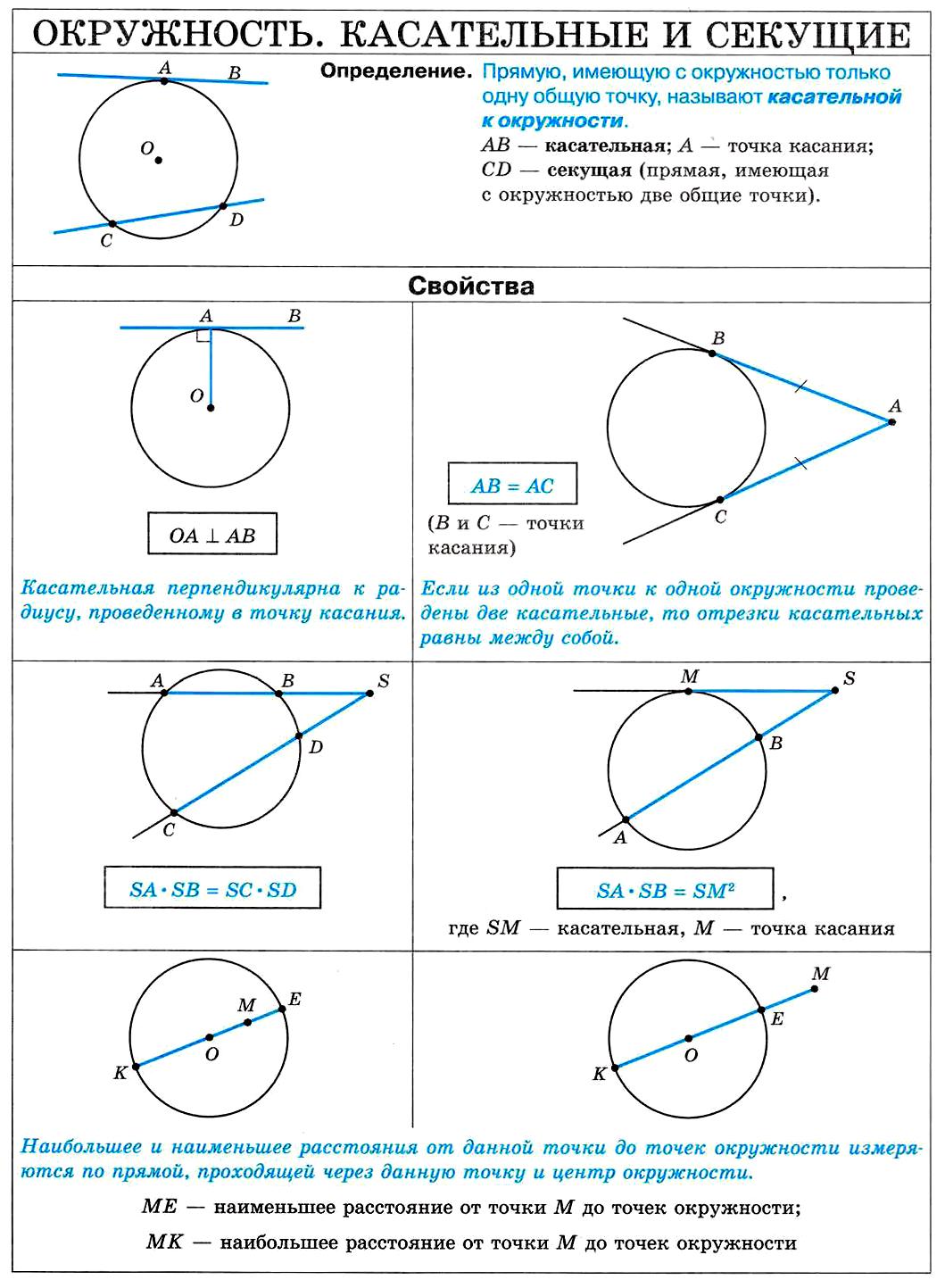
Прямая, имеющая с окружностью только одну общую точку, называется касательной. $АВ$ — касательная

Прямая, имеющая с окружностью две общие точки, называется секущей. $CD$ — секущая

Свойства:

1. Касательная перпендикулярна радиусу, проведенному в точку касания.

$ОА⊥АС; OB⊥BC$

2. Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

$АС=ВС; ОС$ — биссектриса

3. Если хорды $АС$ и $BD$ пересекаются в некоторой точке $N$, то произведение отрезков одной хорды равно произведению отрезков другой хорды.

$AN·NC=BN·ND$

Пример:

Хорды $АВ$ и $CD$ пересекаются в точке $Е$. Найдите $ЕD$, если $АЕ=16, ВЕ=9, СЕ=ED$.

Решение:

Если хорды $АВ$ и $СD$ пересекаются в некоторой точке $Е$, то произведение отрезков одной хорды равно произведению отрезков другой хорды.

$AЕ·ЕВ=СЕ·ЕD$

Так как $СЕ=ED$, данное выражение можно записать в виде:

$ЕD^2=AЕ·ЕВ$

Подставим числовые значения

$ЕD^2=16·9$

$ЕD=√{16·9}=4·3=12$

Ответ: $12$

4. Если из одной точки к одной окружности проведены две секущие, то произведение первой секущей на ее внешнюю часть равно произведению второй секущей на свою внешнюю часть.

$АС·ВС=EC·DC$

5. Если из одной точки к окружности проведены секущая и касательная, то произведение секущей на ее внешнюю часть равно квадрату длины касательной.

$BD·СB=AB^2$

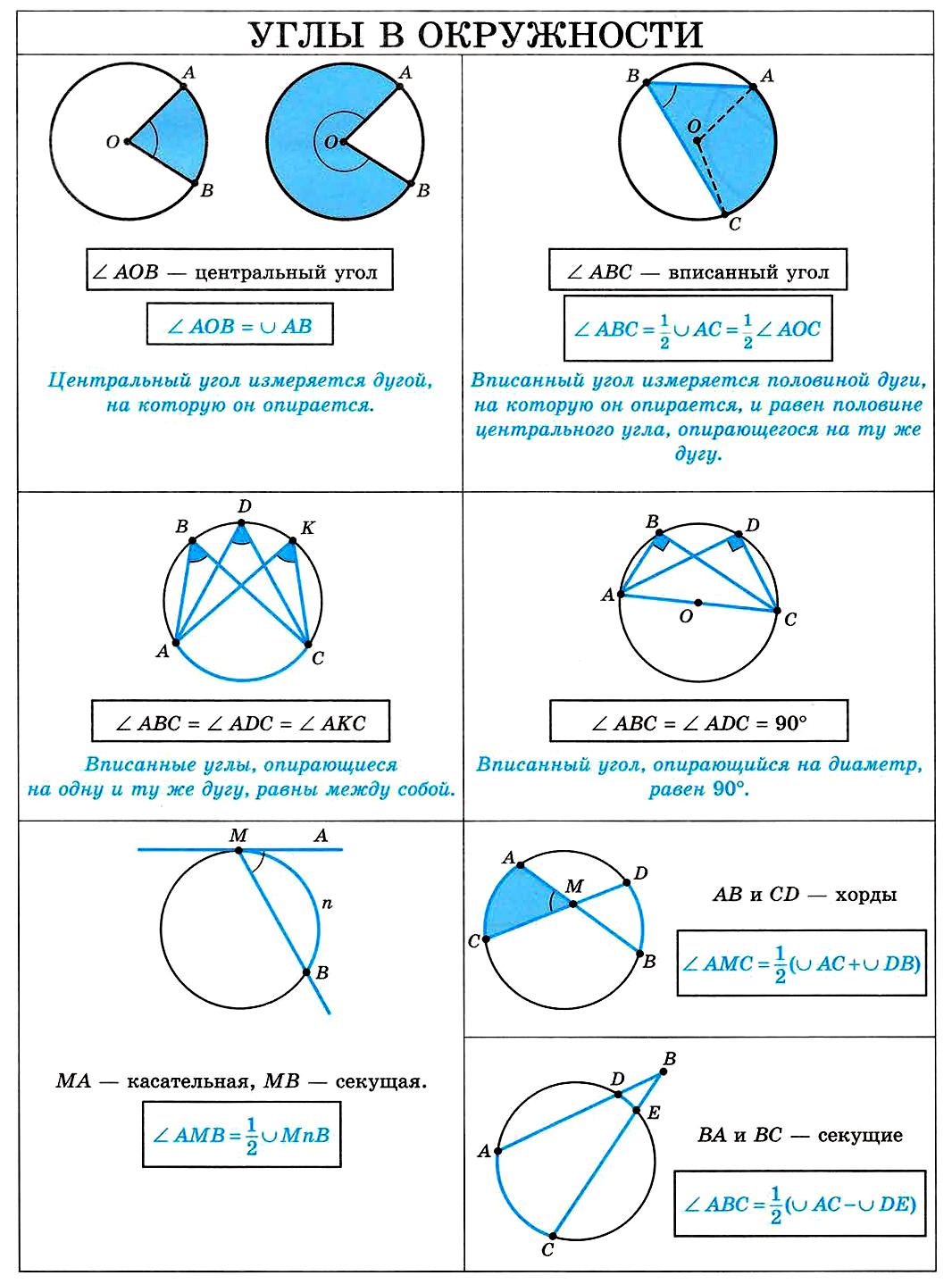
Углы в окружности:

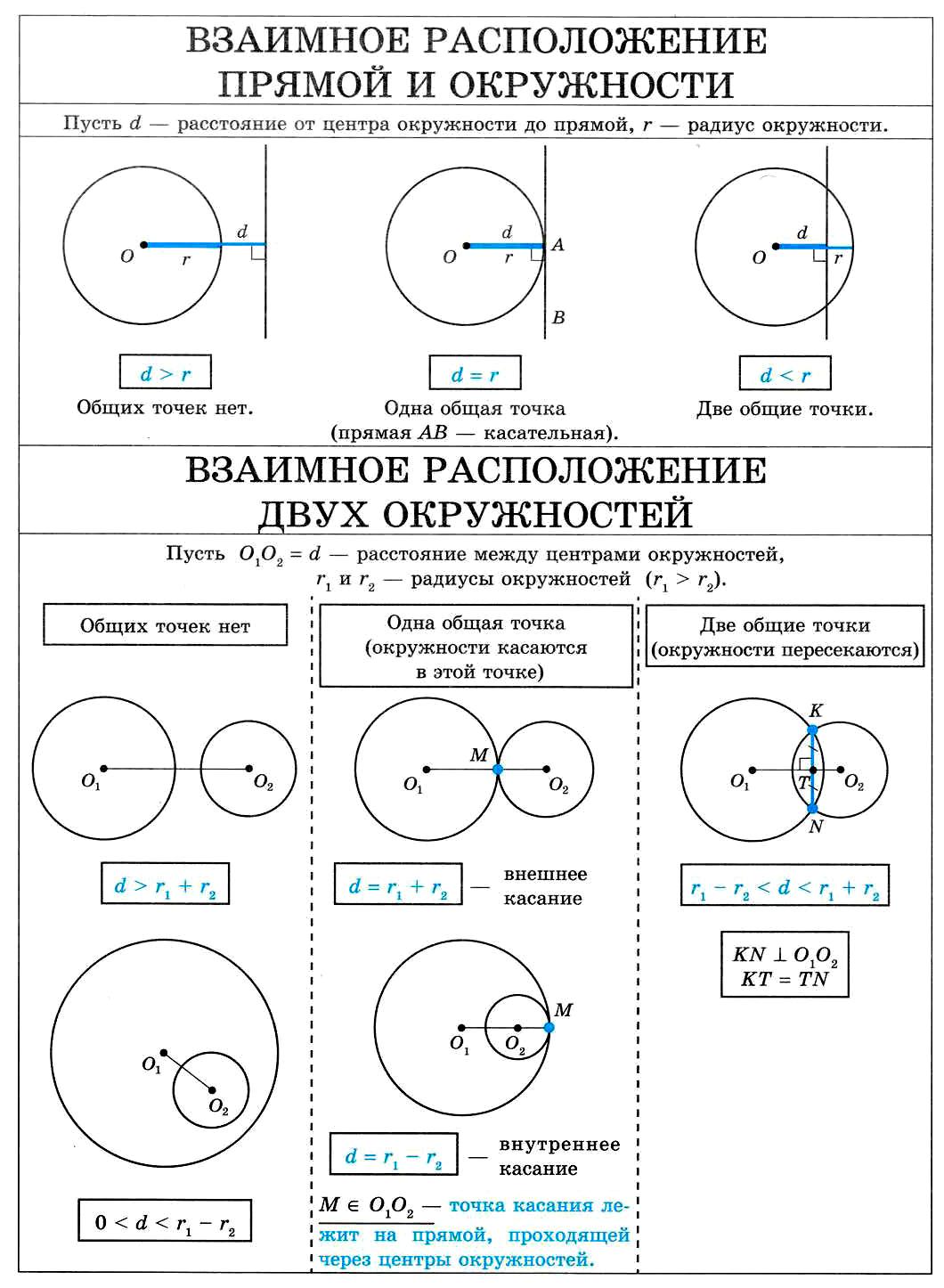
1. Угол, образованный двумя радиусами, называется центральным. Центральный угол равен градусной мере дуги, на которую он опирается

$∠О=∪BmA$

2. Угол, вершина которого лежит на окружности, а стороны являются хордами, называется вписанным. Вписанный угол равен половине градусной меры дуги, на которую он опирается

$∠B={∪AmC}/{2}$

Пример:

Точки $A, B, C$, расположенные на окружности, делят её на три дуги, градусные меры которых относятся как $2:3:7$. Найдите больший угол треугольника $ABC$. Ответ дайте в градусах.