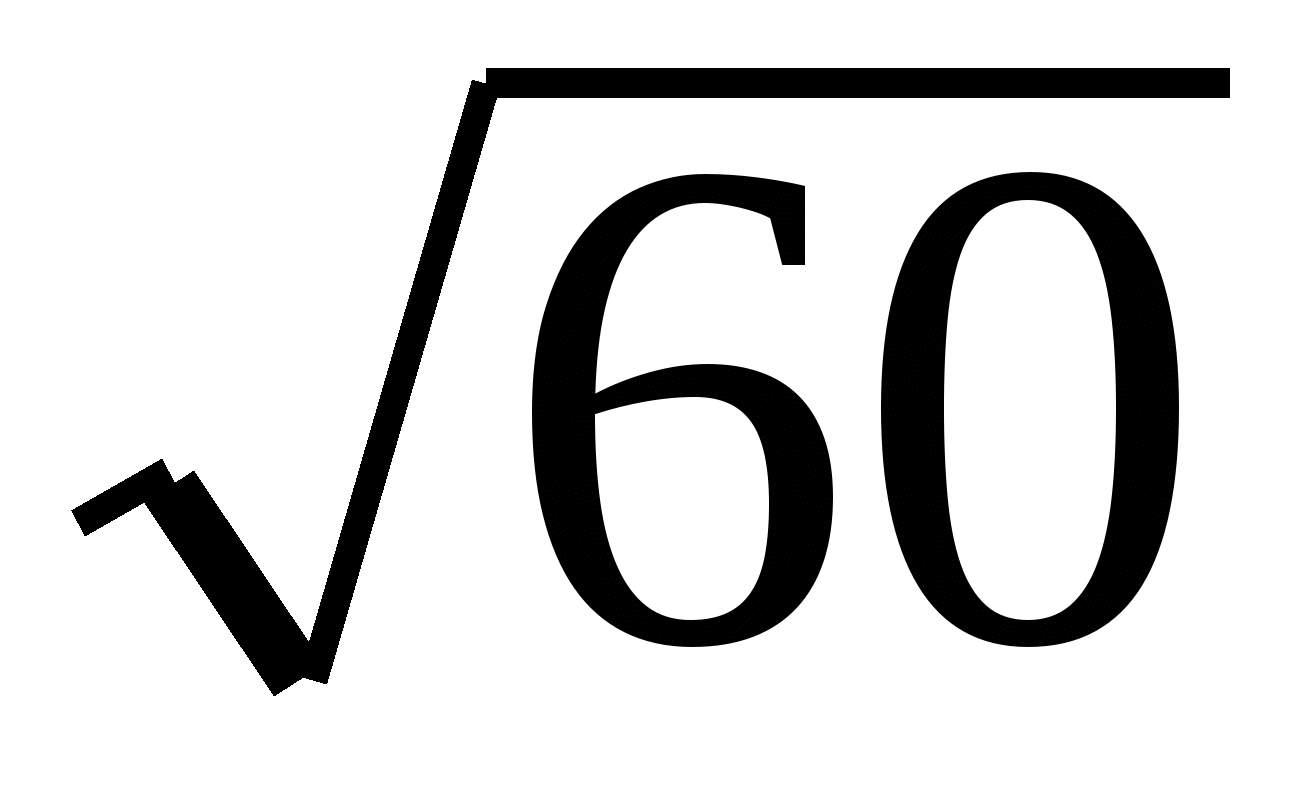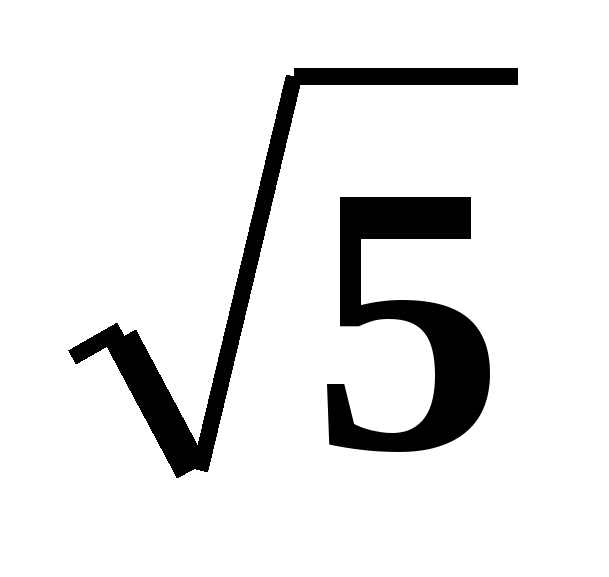Иррациональное число

Примечания

, Том 1, с. 73.
, с. 64.
.
James R. Choike. The Pentagram and the Discovery of an Irrational Number (англ.) // The Two-Year College Mathematics Journal (англ.)русск. : magazine. — 1980.
, p. 242—264.
, Т 1. С древнейших времен до начала Нового времени, с. 74.
Kline 1990, p.48.
Kline 1990, p.49.
↑ , p. 253–277 .
Jacques Sesiano, «Islamic mathematics», p. 148, in Selin, Helaine; D’Ambrosio, Ubiratan. Mathematics Across Cultures: The History of Non-western Mathematics (англ.). — Springer, 2000. — ISBN 1-4020-0260-2..
, p. 253–277 .
, p. 253–277 .
Cajori, Florian (1928), A History of Mathematical Notations (Vol.1), La Salle, Illinois: The Open Court Publishing Company pg. 269.
, pg.89

Некоторые признаки иррациональных выражений/чисел

Вот некоторые общеупотребительные признаки иррациональности исследуемого выражения/числа:

корень k-ой степени из целого числа будет рациональным только тогда, когда подкоренное выражение является k-ой степенью иного целого числа;

в случае использования обычных логарифмов иррациональность выражения непременно требует доказательства (здесь удобнее всего пользоваться методом “от противного”);

поскольку основанием натуральных логарифмов является иррациональное число e, то натуральный логарифм любого положительного числа также будет иррациональным;

иррациональное число e в любой рациональной (но отличной от нуля!) степени даёт иррациональный результат;

число Пи в любой целой и отличной от нуля степени даёт иррациональный результат;

все основные тригонометрические функции (такие как cos(a), sin(a), tg(a) и ctg(a)) при использовании отличного от нуля рационального аргумента в качестве результата дают иррациональное число.

[править] Существование

То, что не все (действительные) числа, являются рациональными, было выяснено математиками Древней Греции, которые доказали, что корень из 2 (длина диагонали квадрата со стороной 1) не является рациональным числом.

Действительно, пусть \sqrt 2 = m/n с целыми m и n, причем их можно выбрать натуральными и взаимно простыми (если они не взаимно просты, то можно сократить эту дробь на наибольший общий делитель). Возведём уравнение в квадрат: 2 = m2/n2. Следовательно, 2n2 = m2. Отсюда n2 = m2/2 и m2 делится на 2, значит m — чётное (делится на 2), оно может быть представлено как m = 2k, где k — любое целое, и 2n2 = 4k2, n2 = 2k2, при этом k2 = n2/2, то есть n2 тоже делится на 2, значит n — чётное, но это противоречит тому, что m и n — взаимно простые числа.

Полученное противоречие доказывает, что корень из 2 — иррациональное число. Аналогично доказывается иррациональность любого числа вида корень из k, если натуральное число k не является квадратом некоторого натурального числа. Таким образом, иррациональных чисел бесконечно много.

Примеры иррационального числа

Рассмотрим для наглядности небольшой пример иррационально числа. Как мы уже поняли, бесконечные десятичные непериодические дроби называются иррациональными, к примеру:

Число «-5,020020002… (прекрасно видно, что двойки разделены последовательностью из одного, двух, трех и т.д. нулей)
Число «7,040044000444… (здесь ясно, что число четверок и количество нулей каждый раз цепочкой увеличивается на единицу).
Всем известное число Пи (3,1415…). Да, да — оно тоже является иррациональным.

Вообще все действительные числа являются как рациональными так и иррациональными. Говоря простыми словами, иррациональное число нельзя представить ввиде обыкновенной дроби х/у.

[править] Литература

Бухштаб А. А. Теория чисел — М.: «Просвещение», 1966.
К. Айерленд, М. Роузен, Классическое введение в современную теорию чисел — М., 1987.

Числовые системы
Счётные множества	Натуральные числа (\scriptstyle\mathbb{N}) • Целые (\scriptstyle\mathbb{Z}) • Рациональные (\scriptstyle\mathbb{Q}) • Алгебраические (\scriptstyle\overline{\mathbb{Q}}) • Периоды • Вычислимые
Действительные числа и их расширения	Действительные (вещественные) (\scriptstyle\mathbb{R}) • Комплексные (\scriptstyle\mathbb{C}) • Кватернионы (\scriptstyle\mathbb{H}) • Числа Кэли (октавы, октонионы) (\scriptstyle\mathbb{O}) • Седенионы (\scriptstyle\mathbb{S}) • Альтернионы • Дуальные • Гиперкомплексные • Супердействительные • Гипервещественные • Сюрреальные
Другие числовые системы	Кардинальные числа • Порядковые числа (трансфинитные, ординал) • p-адические • Супернатуральные числа
См. также	Двойные числа • Иррациональные числа • Трансцендентные числа • Числовой луч • Бикватернионы • Координатизация • Расширение понятия числа

Общее понятие рационального числа

Рациональным числом считается то число, которое можно записать в виде:

Обыкновенной положительной дроби.
Отрицательной обыкновенной дроби.
В виде числа нуль (0).

Иными словами, к рациональному число подойдет следующие определения:

Любое натуральное число является по своей сути рациональным, так как любое натуральное число можно представить в виде обыкновенной дроби.
Любое целое число, включительно число нуль, так как любое целое число можно записать как ввиде положительной обыкновенной дроби, в виде отрицательной обыкновенной дроби, так и ввиде числа нуль.
Любая обыкновенная дробь, и здесь не имеет значение положительная она или отрицательная, тоже напрямую подходит к определению рационального числа.
Так же в определение можно отнести и смешанное число, конечную десятичную дробь либо бесконечную периодическую дробь.

Примеры доказательства иррациональности

Корень из 2

Допустим противное: 2{\displaystyle {\sqrt {2}}} рационален, то есть представляется в виде дроби mn{\displaystyle {\frac {m}{n}}}, где m{\displaystyle m} — целое число, а n{\displaystyle n} — натуральное число.

Возведём предполагаемое равенство в квадрат:

2=mn⇒2=m2n2⇒m2=2n2{\displaystyle {\sqrt {2}}={\frac {m}{n}}\Rightarrow 2={\frac {m^{2}}{n^{2}}}\Rightarrow m^{2}=2n^{2}}.

В каноническое разложение левой части равенства число 2{\displaystyle 2} входит в чётной степени, а в разложение 2n2{\displaystyle 2n^{2}} — в нечётной. Поэтому равенство m2=2n2{\displaystyle m^{2}=2n^{2}} невозможно. Значит, исходное предположение было неверным, и 2{\displaystyle {\sqrt {2}}} — иррациональное число.

Двоичный логарифм числа 3

Допустим противное: log2⁡3{\displaystyle \log _{2}3} рационален, то есть представляется в виде дроби mn{\displaystyle {\frac {m}{n}}}, где m{\displaystyle m} и n{\displaystyle n} — целые числа. Поскольку log2⁡3>{\displaystyle \log _{2}3>0}, m{\displaystyle m} и n{\displaystyle n} могут быть выбраны положительными. Тогда

log2⁡3=mn⇒m=nlog2⁡3⇒2m=2nlog2⁡3⇒2m=3n{\displaystyle \log _{2}3={\frac {m}{n}}\Rightarrow m=n\log _{2}3\Rightarrow 2^{m}=2^{n\log _{2}3}\Rightarrow 2^{m}=3^{n}}

Но 2m{\displaystyle 2^{m}} чётно, а правая часть получившегося равенства нечётна. Получаем противоречие.

Примеры доказательства иррациональности

Корень из 2

Возведём предполагаемое равенство в квадрат:

2=mn⇒2=m2n2⇒m2=2n2{\displaystyle {\sqrt {2}}={\frac {m}{n}}\Rightarrow 2={\frac {m^{2}}{n^{2}}}\Rightarrow m^{2}=2n^{2}}.

Двоичный логарифм числа 3

log2⁡3=mn⇒m=nlog2⁡3⇒2m=2nlog2⁡3⇒2m=3n{\displaystyle \log _{2}3={\frac {m}{n}}\Rightarrow m=n\log _{2}3\Rightarrow 2^{m}=2^{n\log _{2}3}\Rightarrow 2^{m}=3^{n}}

Но 2m{\displaystyle 2^{m}} чётно, а правая часть получившегося равенства нечётна. Получаем противоречие.

Знак радикала

Что такое знак радикала? Это знак корня. Корень может быть любой степени, важен сам факт наличия радикала. Отдельно отметим, что корень, который можно вычислить нельзя считать иррациональным числом. Отличительным признаком иррационального числа является невозможность точного подсчета его значения.

Это значит, что если вбить значение корня в калькулятор, то получившееся значение будет бесконечно. Ярким примером иррационального числа будет $\sqrt{2}$

В точных математических расчетах иррациональное число считается вычисленным, если можно точно узнать любое количество знаков после запятой. Количество вычисленных иррациональных чисел на сегодняшний момент минимально. Число пи так же является иррациональным и не вычисленным до конца.

В школьных примерах можно оставлять действия с корнем на самый конец вычислений, а потом считать на калькуляторе приближенное значение. Округление до 0,01 считается приемлемы для учебных вычислений. Можно и вовсе просто оставить пример с не вычисленными корнями, особенно это касается задач на упрощение примеров.

Общее понятие и определение иррационального числа

Помимо «рациональных чисел» нам известны и так называемые «иррациональные числа». Вкратце попробуем дать определение данным числам.

Еще древние математики, желая вычислить диагональ квадрата по его сторонам, узнали о существовании иррационального числа.
Исходя из определения о рациональных числах, можно выстроить логическую цепь и дать определение иррациональному числу.
Итак, по сути, те действительные числа, которые не являются рациональными, элементарно и есть иррациональными числами.
Десятичные дроби же, выражающие иррациональные числа, не периодичны и бесконечны.

Примеры доказательства иррациональности

Корень из 2

Возведём предполагаемое равенство в квадрат:

2=mn⇒2=m2n2⇒m2=2n2{\displaystyle {\sqrt {2}}={\frac {m}{n}}\Rightarrow 2={\frac {m^{2}}{n^{2}}}\Rightarrow m^{2}=2n^{2}}.

Двоичный логарифм числа 3

log2⁡3=mn⇒m=nlog2⁡3⇒2m=2nlog2⁡3⇒2m=3n{\displaystyle \log _{2}3={\frac {m}{n}}\Rightarrow m=n\log _{2}3\Rightarrow 2^{m}=2^{n\log _{2}3}\Rightarrow 2^{m}=3^{n}}

Но 2m{\displaystyle 2^{m}} чётно, а правая часть получившегося равенства нечётна. Получаем противоречие.

Примечания

, Том 1, с. 73.
, с. 64.
.
James R. Choike. The Pentagram and the Discovery of an Irrational Number (англ.) // The Two-Year College Mathematics Journal (англ.)русск. : magazine. — 1980.
, p. 242—264.
, Т 1. С древнейших времен до начала Нового времени, с. 74.
Kline 1990, p.48.
Kline 1990, p.49.
↑ , p. 253–277 .
Jacques Sesiano, «Islamic mathematics», p. 148, in Selin, Helaine; D’Ambrosio, Ubiratan. Mathematics Across Cultures: The History of Non-western Mathematics (англ.). — Springer, 2000. — ISBN 1-4020-0260-2..
, p. 253–277 .
, p. 253–277 .
Cajori, Florian (1928), A History of Mathematical Notations (Vol.1), La Salle, Illinois: The Open Court Publishing Company pg. 269.
, pg.89

Общие признаки рациональных выражений/чисел

Вопрос “как определить иррациональные числа” не имеет однозначного ответа: если имеется некое математическое выражение для числа, то для выяснения его рациональности/иррациональности потребуется произвести детальное исследование. Резко сократить время на поиск требуемого доказательства возможно, если пойти от противного: убрать из рассмотрения числа, не являющиеся иррациональными. По определению, к ним не могут принадлежать:

все целые, натуральные и рациональные числа;

обыкновенные дроби и смешанные числа;

бесконечные и конечные периодические десятичные дроби.

Результат математических операций (сложение, умножение, вычитание и деление) над рациональными числами также не является иррациональным числом. Если в исследуемое выражение входит единственное иррациональное число, то результат также будет иррациональным – однако для случая двух и более вхождений это, вообще говоря, неверно.

Примеры доказательства иррациональности

Корень из 2

Возведём предполагаемое равенство в квадрат:

2=mn⇒2=m2n2⇒m2=2n2{\displaystyle {\sqrt {2}}={\frac {m}{n}}\Rightarrow 2={\frac {m^{2}}{n^{2}}}\Rightarrow m^{2}=2n^{2}}.

Двоичный логарифм числа 3

log2⁡3=mn⇒m=nlog2⁡3⇒2m=2nlog2⁡3⇒2m=3n{\displaystyle \log _{2}3={\frac {m}{n}}\Rightarrow m=n\log _{2}3\Rightarrow 2^{m}=2^{n\log _{2}3}\Rightarrow 2^{m}=3^{n}}

Но 2m{\displaystyle 2^{m}} чётно, а правая часть получившегося равенства нечётна. Получаем противоречие.

Правила работы с корнем

Существуют определенные правила работы с корнями:

Корни можно возводить в степень

$${\sqrt{2}}^3={\sqrt{2^3}}={\sqrt{8}}$$

Из под корня можно выносит множители, выполняя действие корня

$${\sqrt{8}}={2*\sqrt{2}}$$

Можно перемножать корни между собой

$${\sqrt{2}}*{\sqrt{2}}={\sqrt{2*2}}={\sqrt{4}}=2$$

При решении уравнений можно возводить обе части выражения в степень. Но в четные степени можно возводить только при условии разделения решения. С одной стороны нужно решить пример с условием, что подстепенное выражение будет отрицательным, с другой – не отрицательным.

Для иррациональных уравнений это не критично, поскольку значение корня всегда неотрицательно

Но это важно учитывать при решении квадратных, степенных и прочих неравенств и уравнений

Что мы узнали?

Мы поговорили об иррациональных числах. Выяснили, чем они отличаются от рациональных. Поговорили о том, какое иррациональное число может считаться полностью посчитанным. Обговорили отдельно, как записываются иррациональные ответы в выражениях школьного курса. Привели основные возможные действия с корнями.

Аксиомы, позволяющие определить множество натуральных чисел

Аксиомы Пеано для натуральных чисел

Основная статья: Аксиомы Пеано

Множество N{\displaystyle \mathbb {N} } будем называть множеством натуральных чисел, если зафиксированы некоторый элемент 1 (единица), функция S{\displaystyle S} c областью определения N{\displaystyle \mathbb {N} }, называемая функцией следования (SN{\displaystyle S\colon \mathbb {N} }), и выполнены следующие условия:

элемент единица принадлежит этому множеству (1∈N{\displaystyle 1\in \mathbb {N} }), то есть является натуральным числом;
число, следующее за натуральным, также является натуральным (если x∈N{\displaystyle x\in \mathbb {N} }, то S(x)∈N{\displaystyle S(x)\in \mathbb {N} } или, в более короткой записи, SN→N{\displaystyle S\colon \mathbb {N} \to \mathbb {N} });
единица не следует ни за каким натуральным числом (∄x∈N (S(x)=1){\displaystyle \nexists x\in \mathbb {N} \ (S(x)=1)});
если натуральное число a{\displaystyle a} непосредственно следует как за натуральным числом b{\displaystyle b}, так и за натуральным числом c{\displaystyle c}, то b{\displaystyle b} и c{\displaystyle c} — это одно и то же число (если S(b)=a{\displaystyle S(b)=a} и S(c)=a{\displaystyle S(c)=a}, то b=c{\displaystyle b=c});
(аксиома индукции) если какое-либо предложение (высказывание) P{\displaystyle P} доказано для натурального числа n=1{\displaystyle n=1} (база индукции) и если из допущения, что оно верно для другого натурального числа n{\displaystyle n}, вытекает, что оно верно для следующего за n{\displaystyle n} натурального числа (индукционное предположение), то это предложение верно для всех натуральных чисел (пусть P(n){\displaystyle P(n)} — некоторый одноместный (унарный) предикат, параметром которого является натуральное число n{\displaystyle n}. Тогда, если P(1){\displaystyle P(1)} и ∀n(P(n)⇒P(S(n))){\displaystyle \forall n\;(P(n)\Rightarrow P(S(n)))}, то ∀nP(n){\displaystyle \forall n\;P(n)}).

Перечисленные аксиомы отражают наше интуитивное представление о натуральном ряде и числовой линии.

Принципиальным фактом является то, что эти аксиомы по сути однозначно определяют натуральные числа (категоричность системы аксиом Пеано). А именно, можно доказать (см., а также краткое доказательство), что если (N,1,S){\displaystyle (\mathbb {N} ,1,S)} и (N~,1~,S~){\displaystyle ({\tilde {\mathbb {N} }},{\tilde {1}},{\tilde {S}})} — две модели для системы аксиом Пеано, то они необходимо изоморфны, то есть существует обратимое отображение (биекция) fN→N~{\displaystyle f\colon \mathbb {N} \to {\tilde {\mathbb {N} }}} такая, что f(1)=1~{\displaystyle f(1)={\tilde {1}}} и f(S(x))=S~(f(x)){\displaystyle f(S(x))={\tilde {S}}(f(x))} для всех x∈N{\displaystyle x\in \mathbb {N} }.

Поэтому, достаточно зафиксировать в качестве N{\displaystyle \mathbb {N} } какую-либо одну конкретную модель множества натуральных чисел.

Иногда, особенно в иностранной и переводной литературе, в первой и третьей аксиомах Пеано заменяют единицу на ноль. В этом случае ноль считается натуральным числом. При определении через классы равномощных множеств ноль является натуральным числом по определению. Специально отбрасывать его было бы неестественно. Кроме того, это значительно усложнило бы дальнейшее построение и применение теории, так как в большинстве конструкций нуль, как и пустое множество, не является чем-то обособленным. Другим преимуществом считать ноль натуральным числом является то, что при этом N{\displaystyle \mathbb {N} } образует моноид. Как уже упоминалось , в русской литературе традиционно ноль исключён из числа натуральных чисел.

Теоретико-множественное определение натуральных чисел (определение Фреге — Рассела)

Положение натуральных чисел в иерархии числовых множеств

Согласно теории множеств, единственным объектом конструирования любых математических систем является множество.

Таким образом, и натуральные числа вводятся, исходя из понятия множества, по двум правилам:

=∅{\displaystyle 0=\varnothing };
S(n)=n∪{n}{\displaystyle S(n)=n\cup \left\{n\right\}}.

Числа, заданные таким образом, называются ординальными.

Опишем несколько первых ординальных чисел и соответствующих им натуральных чисел:

=∅{\displaystyle 0=\varnothing };
1=∅∪{}={∅}{\displaystyle 1=\varnothing \cup \left\{0\right\}=\left\{\varnothing \right\}};
2=1∪{1}={∅,{∅}}{\displaystyle 2=1\cup \left\{1\right\}={\big \{}\varnothing ,\;\left\{\varnothing \right\}{\big \}}};
3=2∪{2}={∅,{∅},{∅,{∅}}}{\displaystyle 3=2\cup \left\{2\right\}={\Big \{}\varnothing ,\;\left\{\varnothing \right\},\;{\big \{}\varnothing ,\;\left\{\varnothing \right\}{\big \}}{\Big \}}}.

Алгебраические и трансцендентные

Как уже было упомянуто, иррациональные числа условно разделяются на алгебраические и трансцендентные. Условно, поскольку, строго говоря, эта классификация используется для деления множества C.

Под этим обозначением скрываются комплексные числа, которые включают в себя действительные или вещественные.

Итак, алгебраическим называют такое значение, которое является корнем многочлена, не равного тождественно нулю. Например, квадратный корень из 2 будет относиться к этой категории, поскольку он является решением уравнения x2 — 2 = 0.

Все же остальные вещественные числа, не удовлетворяющие этому условию, называются трансцендентными. К этой разновидности относятся и наиболее известные и уже упомянутые примеры — число пи и основание натурального логарифма e.

Что интересно, ни одно, ни второе не были изначально выведены математиками в этом качестве, их иррациональность и трансцендентность были доказаны через много лет после их открытия. Для пи доказательство было приведено в 1882 году и упрощено в 1894, что положило конец спорам о проблеме квадратуры круга, которые длились на протяжении 2,5 тысяч лет. Оно до сих пор до конца не изучено, так что современным математикам есть над чем работать. Кстати, первое достаточно точное вычисление этого значения провел Архимед. До него все расчеты были слишком приблизительными.

Для е (числа Эйлера или Непера), доказательство его трансцендентности было найдено в 1873 году. Оно используется в решении логарифмических уравнений.

Среди других примеров — значения синуса, косинуса и тангенса для любых алгебраических ненулевых значений.

Определение и примеры иррациональных чисел

При изучении десятичных дробей мы отдельно рассмотрели бесконечные непериодические десятичные дроби. Такие дроби возникают при длин отрезков, несоизмеримых с единичным отрезком. Также мы отметили, что бесконечные непериодические десятичные дроби не могут быть переведены в обыкновенные дроби (смотрите перевод обыкновенных дробей в десятичные и обратно), следовательно, эти числа не являются рациональными числами, они представляют так называемые иррациональные числа.

Так мы подошли к определению иррациональных чисел.

Определение.

Числа, которые в десятичной записи представляют собой бесконечные непериодические десятичные дроби, называются иррациональными числами.

Озвученное определение позволяет привести примеры иррациональных чисел. Например, бесконечная непериодическая десятичная дробь 4,10110011100011110000… (количество единиц и нулей каждый раз увеличивается на одну) является иррациональным числом. Приведем еще пример иррационального числа: −22,353335333335… (число троек, разделяющих восьмерки, каждый раз увеличивается на две).

Следует отметить, что иррациональные числа достаточно редко встречаются именно в виде бесконечных непериодических десятичных дробей. Обычно они встречаются в виде корней, степеней, логарифмов и т.п., а также в виде специально введенных букв. Самыми известными примерами иррациональных чисел в такой записи являются арифметический квадратный корень из двух , число «пи» π=3,141592…, число e=2,718281… и золотое число .

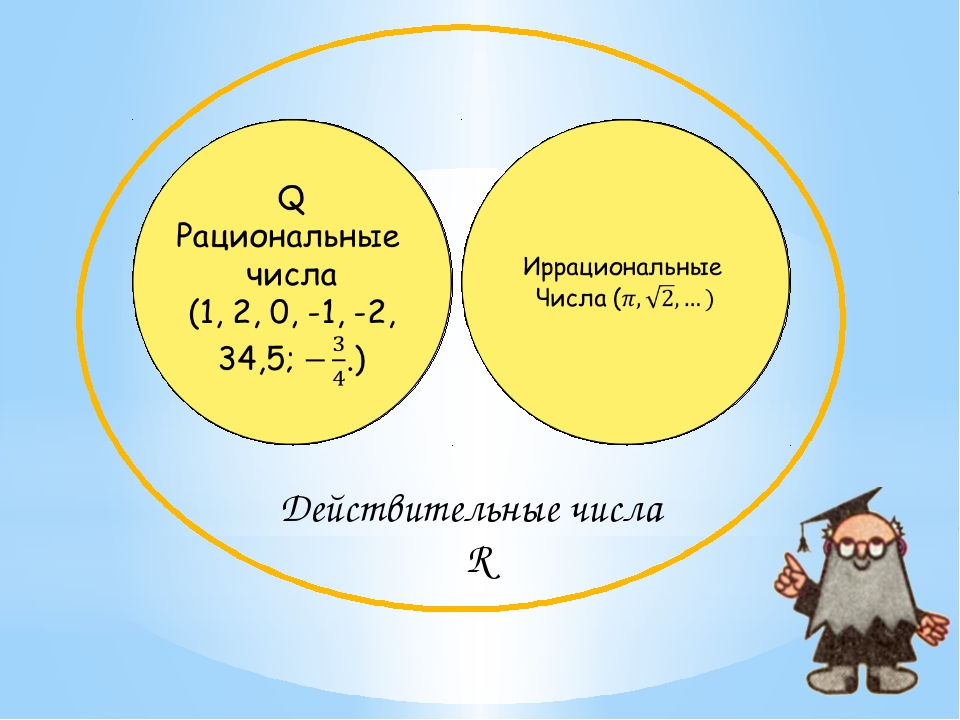
Иррациональные числа также можно определить через действительные числа, которые объединяют рациональные и иррациональные числа.

Определение.

Иррациональные числа – это действительные числа, не являющиеся рациональными.

Базовые понятия

Натуральными (от латинского “naturalis” – “естественный”) называют числа, возникшие из естественной нумерации предметов при счёте – например такие как 1, 2, 3 и так далее. Их последовательность, расположенная в порядке возрастания, образует так называемый натуральный ряд. Существует два конкурентных подхода к определению ряда натуральных чисел: в отечественной математической литературе он традиционно начинается с единицы, в зарубежной – с нуля.

Целыми называют числа, образованные расширением множества натуральных чисел посредством добавления отрицательных чисел и нуля: за счёт такого объединения в общем случае из меньшего числа можно вычесть большее, что уравнивает операции вычитания и сложения, образуя “кольцо целых чисел“.

Рациональными (от латинского “ratio” – “дробь”, “отношение”, часто в данном контексте неправильно толкуемое в популярных статьях как определение “разумный” либо аналогичное) числами называют числа вида m/n, где числитель m представлен целым числом, а знаменатель n – натуральным. Иначе говоря, рациональными являются те числа, которые возможно точно представить в виде обыкновенной дроби.

Примеры доказательства иррациональности

Корень из 2

Возведём предполагаемое равенство в квадрат:

2=mn⇒2=m2n2⇒m2=2n2{\displaystyle {\sqrt {2}}={\frac {m}{n}}\Rightarrow 2={\frac {m^{2}}{n^{2}}}\Rightarrow m^{2}=2n^{2}}.

Двоичный логарифм числа 3

log2⁡3=mn⇒m=nlog2⁡3⇒2m=2nlog2⁡3⇒2m=3n{\displaystyle \log _{2}3={\frac {m}{n}}\Rightarrow m=n\log _{2}3\Rightarrow 2^{m}=2^{n\log _{2}3}\Rightarrow 2^{m}=3^{n}}

Но 2m{\displaystyle 2^{m}} чётно, а правая часть получившегося равенства нечётна. Получаем противоречие.

Примеры доказательства иррациональности

Корень из 2

Возведём предполагаемое равенство в квадрат:

2=mn⇒2=m2n2⇒m2=2n2{\displaystyle {\sqrt {2}}={\frac {m}{n}}\Rightarrow 2={\frac {m^{2}}{n^{2}}}\Rightarrow m^{2}=2n^{2}}.

Двоичный логарифм числа 3

log2⁡3=mn⇒m=nlog2⁡3⇒2m=2nlog2⁡3⇒2m=3n{\displaystyle \log _{2}3={\frac {m}{n}}\Rightarrow m=n\log _{2}3\Rightarrow 2^{m}=2^{n\log _{2}3}\Rightarrow 2^{m}=3^{n}}

Но 2m{\displaystyle 2^{m}} чётно, а правая часть получившегося равенства нечётна. Получаем противоречие.

Общее заключение и краткое сравнение между числами

Мы рассмотрели каждое число по отдельности, осталось отличие между рациональным числом и иррациональным:

Иррациональное число встречается при извлечении квадратного корня, при делении окружности на диаметр и т.д.
Рациональное число представляет обыкновенную дробь.

Заключим нашу статью несколькими определениями:

Арифметическая операция, произведенная над рациональным числом, кроме деления на 0 (нуль), в конечном результате приведет тоже к рациональному числу.
Конечный результат же, при совершении арифметической операции над иррациональным числом, может привести как к рациональному так и к иррациональному значению.
Если же в арифметической операции принимают участие и те и другие числа (кроме деления или умножения на нуль), то результат нам выдаст иррациональное число.

https://youtube.com/watch?v=O8gtCqQXt9I