Связь с реальными системами отсчёта
Абсолютно инерциальные системы представляют собой математическую абстракцию и в природе не существуют. Однако существуют системы отсчёта, в которых относительное ускорение достаточно удалённых друг от друга тел (измеренное по эффекту Доплера) не превышает 10−10 м/с², например, Международная небесная система координат в сочетании с Барицентрическим динамическим временем дают систему, относительные ускорения в которой не превышают 1,5·10−10 м/с² (на уровне 1σ). Точность экспериментов по анализу времени прихода импульсов от пульсаров, а вскоре — и астрометрических измерений, такова, что в ближайшее время должно быть измерено ускорение Солнечной системы при её движении в гравитационном поле Галактики, которое оценивается в 2⋅10−10{\displaystyle 2\cdot 10^{-10}} м/с².
С разной степенью точности и в зависимости от области использования инерциальными системами можно считать системы отсчёта, связанные с: Землёй, Солнцем, неподвижные относительно звёзд.
Свойства инерциальных систем отсчёта
Всякая система отсчёта, движущаяся относительно ИСО равномерно, прямолинейно и без вращения, также является ИСО. Согласно принципу относительности, все ИСО равноправны, и все законы физики инвариантны относительно перехода из одной ИСО в другую. Это значит, что проявления законов физики в них выглядят одинаково, и записи этих законов имеют одинаковую форму в разных ИСО.
Предположение о существовании хотя бы одной ИСО в изотропном пространстве приводит к выводу о существовании бесконечного множества таких систем, движущихся друг относительно друга равномерно, прямолинейно и поступательно со всевозможными скоростями. Если ИСО существуют, то пространство будет однородным и изотропным, а время — однородным; согласно теореме Нётер, однородность пространства относительно сдвигов даст закон сохранения импульса, изотропность приведёт к сохранению момента импульса, а однородность времени — к сохранению энергии движущегося тела.
Если скорости относительного движения ИСО, реализуемых действительными телами, могут принимать любые значения, связь между координатами и моментами времени любого «события» в разных ИСО осуществляется преобразованиями Галилея.
В специальной теории относительности скорости относительного движения
ИСО, реализуемых действительными телами, не могут превышать некоторой конечной скорости «c» (скорость распространения света в вакууме) и связь между координатами и моментами времени любого «события» в разных ИСО осуществляется преобразованиями Лоренца.
Эффект Лензе — Тирринга
Ускорение Кориолиса в ньютоновской механике зависит только от ω→{\displaystyle {\vec {\omega }}} — угловой скорости неинерциальной системы отсчёта относительно инерциальной и линейной скорости пробной массы в неинерциальной системе отсчёта v→{\displaystyle {\vec {v}}} и равно
- a→=2ω→×v→.{\displaystyle {\vec {a}}=2{\vec {\omega }}\times {\vec {v}}.}
Лензе и Тирринг в 1918 году показали, что кориолисово ускорение с учётом эффектов ОТО для расстояния r{\displaystyle r} от вращающегося тела радиусом R{\displaystyle R} массы M{\displaystyle M} при rR≫1{\displaystyle r/R\gg 1} имеет дополнительный компонент:
- b→=2v→×H→,{\displaystyle {\vec {b}}=2{\vec {v}}\times {\vec {H}},}
где H→=2MGR25c2r3ω→−3(ω→r→)r→r2.{\displaystyle {\vec {H}}={{2MGR^{2}} \over {5c^{2}r^{3}}}\left.}
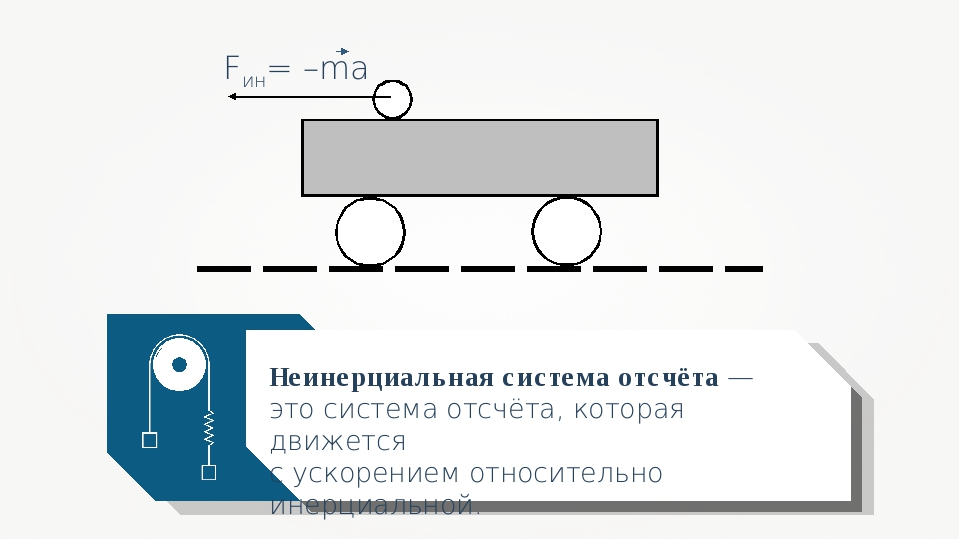
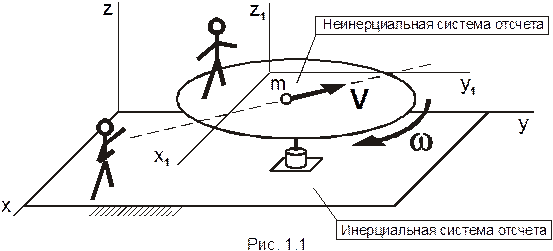
Неинерциальная система отсчета
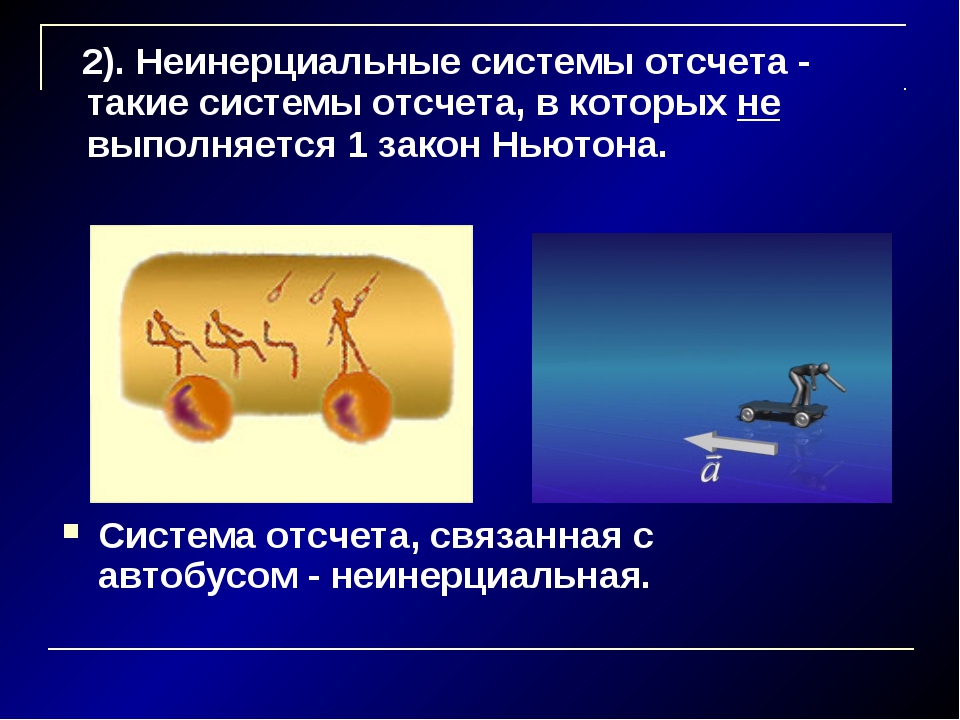
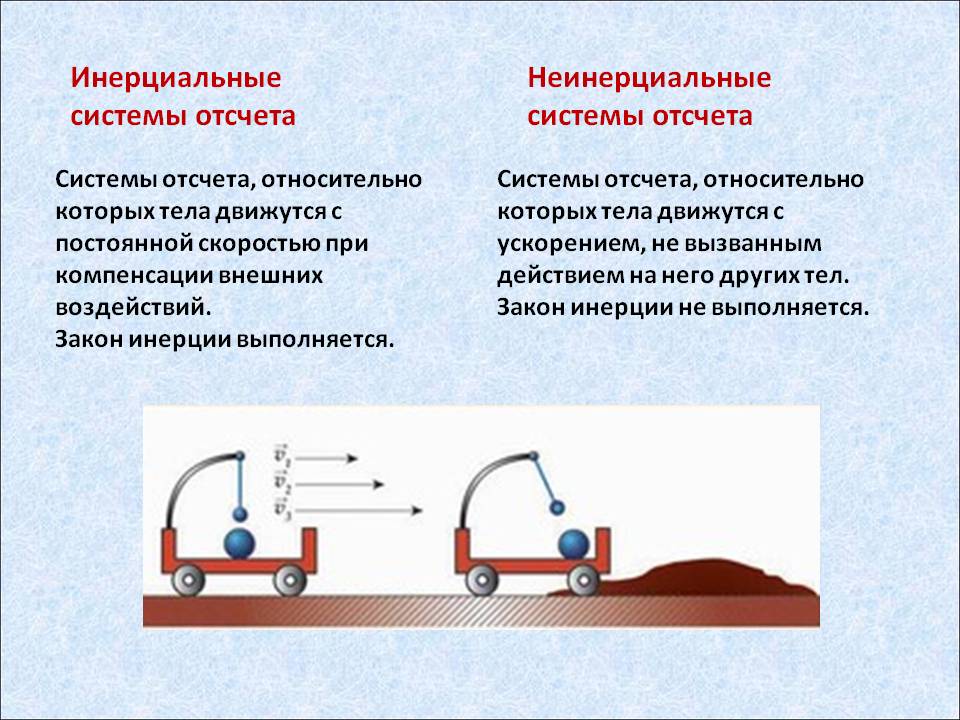
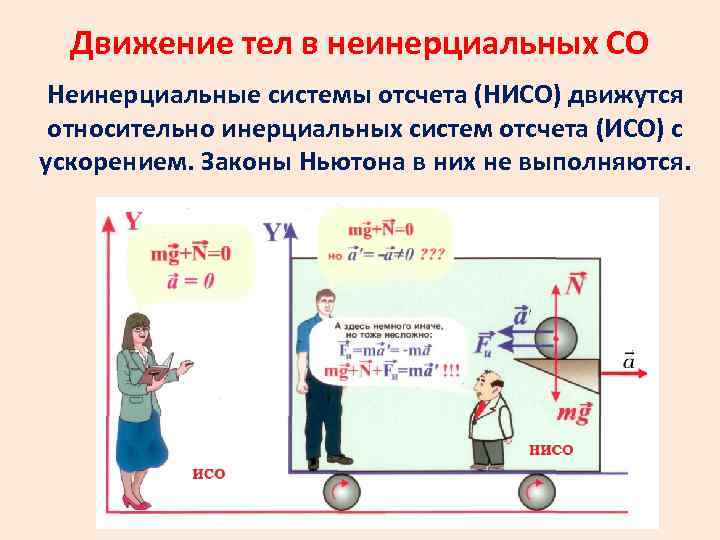
К неинерциальным системам отсчета относятся те системы, которые не являются инерциальными. Если система отсчета движется с ускорением относительно инерциальной системы, то эта система является неинерциальной. В таких системах могут возникать сила инерции, центробежная сила и сила Кориолиса.
Инерция – это сила, при которой тело пытается сохранить свое первоначальное состояние.
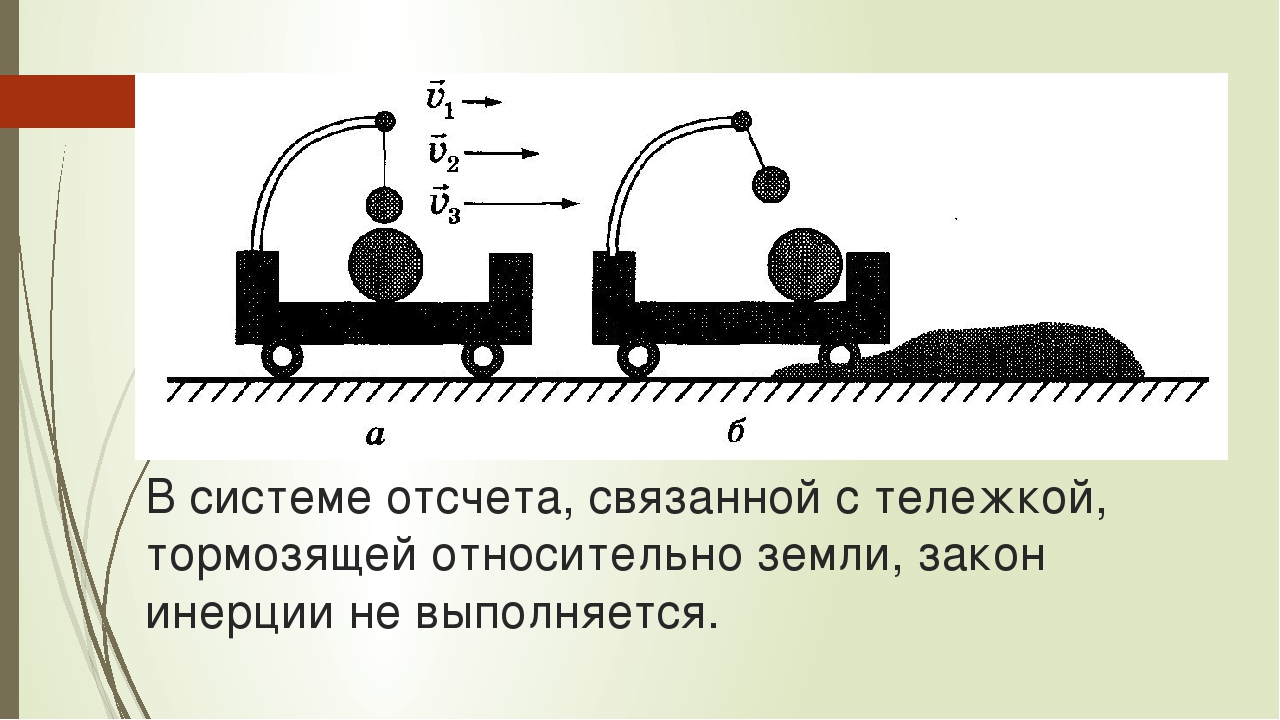
В неинерциальных системах отсчета законы Ньютона очень часто не работают. Примером силы, обусловленным таким движением, может служить, например, перемещение в лифте, катание на карусели.
Что мы узнали?
Существует два вида систем отсчета: инерциальные и неинерциальные системы отсчета. В системах отсчета первого типа тела движутся прямолинейно и равномерно. Для этой системы действуют законы Ньютона. К системам отсчета второго типа относятся те системы, которые движутся с ускорением относительно инерциальных систем.
Экспериментальная проверка и наблюдения эффекта в астрофизике
Эффект Лензе-Тирринга наблюдается как прецессия плоскости орбиты пробной массы, обращающейся вокруг массивного вращающегося тела, либо как прецессия оси вращения гироскопа в окрестностях такого тела.
Впервые в мире был измерен Иньяцио Чьюфолини (итал. Ignazio Ciufolini) из итальянского университета Лечче и Эррикосом Павлисом (Erricos Pavlis) из Мерилендского университета, Балтимор, США. Их результаты были опубликованы в октябре 2004 года. Чьюфолини и Павлис провели компьютерный анализ нескольких миллионов измерений дальности, полученных методом лазерной дальнометрии по уголковым отражателям на спутниках LAGEOS и LAGEOS II (LAser GEOdynamics Satellite), запущенных для изучения геодинамики и уточнения параметров гравитационного поля Земли. Обнаруженный средний поворот орбит спутников, вызванный эффектом Лензе — Тирринга, составляет 47,9 угловой микросекунды в год (mas/год), или 99 % от значения, предсказанного теорией Эйнштейна (48,2 mas/год), с оцененной погрешностью ±10 %. По мнению некоторых исследователей, реальная точность может быть порядка 20-30 %. G. Renzetti опубликовал в 2013 году обзорной статье, посвященной попытки измерить Лензе-Тирринга использованием искусственных спутников Земли.
Для экспериментального подтверждения эффекта, вместе с другим, более существенным эффектом геодезической прецессии, американское космическое агентство NASA осуществило спутниковую программу Gravity Probe B. Космический аппарат GP-B успешно завершил свою программу в космосе. Первые результаты обнародованы в апреле 2007 года, но в связи с выявившимся лишь на орбите эффектом влияния вмороженного распределения электрических зарядов на гироскопах на их вращение точность обработки данных была недостаточна, чтобы выделить эффект (поворот оси на 0,039 угловой секунды в год в плоскости земного экватора). Учёт мешающих эффектов позволил выделить ожидаемый сигнал, окончательные результаты ожидались в декабре 2007 года, но анализ данных продлился до мая 2011 года. Окончательные итоги миссии были объявлены на пресс-конференции по NASA-TV 4 мая 2011 года и опубликованы в Physical Review Letters.
Результат Gravity Probe B оказался менее точным (хотя проектная погрешность должна была составлять порядка 1 %, влияние электрического заряда привело к ухудшению относительной погрешности измерения эффекта Лензе — Тирринга до ~20 %), однако тоже подтвердил предсказания ОТО. Измеренная величина геодезической прецессии составила −6601,8±18,3 mas/год, а эффекта увлечения — −37,2±7,2 mas/год (ср. с предсказываемыми теоретическими значениями 6606,1 mas/год и 39,2 mas/год).
13 февраля 2012 года в 14:00 МСК ЕКА успешно осуществило запуск ракеты Vega c 9 различными спутниками на борту, одним из них был аппарат LARES, основной миссией которого является проверка эффекта Лензе-Тирринга. Существуют различные мнения о реальной точности, достижимой в такой миссии.