Введение
Простое фрактальное дерево, созданное с помощью JavaScript
Слово «фрактал» часто имеет разные коннотации для широкой публики, в отличие от математиков, которые, скорее всего, знакомы с фрактальным искусством, а не с математической концепцией. Математическую концепцию сложно определить формально даже математикам, но ключевые особенности можно понять, имея небольшой математический опыт.
Например, свойство «самоподобия» легко понять по аналогии с увеличением с помощью объектива или другого устройства, которое увеличивает цифровые изображения, чтобы выявить более тонкую, ранее невидимую новую структуру. Однако если это делается на фракталах, никаких новых деталей не появляется; ничего не меняется, и один и тот же узор повторяется снова и снова, или для некоторых фракталов почти один и тот же узор повторяется снова и снова. Самоподобие само по себе не обязательно противоречит интуиции (например, люди неформально размышляли о самоподобии, например, в бесконечном регрессе в параллельных зеркалах или гомункуле , маленьком человечке внутри головы маленького человека внутри головы …) . Отличие фракталов в том, что воспроизводимый узор должен быть детализированным.
Идея детализации связана с другой особенностью, которую можно понять без особой математической подготовки: например, наличие фрактальной размерности, превышающей ее топологическое измерение, относится к тому, как фрактал масштабируется по сравнению с тем, как обычно воспринимаются геометрические формы . Например, прямая линия обычно считается одномерной; если такую фигуру повторно разбить на части, каждая 1/3 длины оригинала, то всегда есть три равных части. Под сплошным квадратом понимается двумерное изображение; если такая фигура представляет собой повторяющиеся части, каждая из которых уменьшена в масштабе 1/3 в обоих измерениях, то всего получается 3 2 = 9 частей. Мы видим, что для обычных самоподобных объектов n-мерность означает, что при повторном разбиении на части, каждая из которых уменьшена с масштабным коэффициентом 1 / r , всего получается r n частей. Теперь рассмотрим кривую Коха . Его можно повторно разбить на четыре части, каждая из которых уменьшена в масштабе 1/3. Итак, строго по аналогии, мы можем рассматривать «размерность» кривой Коха как единственное действительное число D , удовлетворяющее 3 D = 4. Это число математики называют фрактальной размерностью кривой Коха; это определенно не то, что принято считать измерением кривой (это число даже не целое!). Тот факт, что кривая Коха имеет фрактальную размерность, отличную от ее традиционно понимаемой размерности (то есть ее топологической размерности), делает ее фрактальной.
3D компьютерный фрактал
Это также приводит к пониманию третьей особенности: фракталы как математические уравнения «нигде не дифференцируемы ». В конкретном смысле это означает, что фракталы нельзя измерить традиционными способами. Чтобы уточнить, при попытке найти длину волнистой нефрактальной кривой можно найти прямые сегменты некоего измерительного инструмента, достаточно маленькие, чтобы положить конец за концом на волны, где части могут стать достаточно маленькими, чтобы их можно было рассматривать как соответствующие. кривую обычным способом измерения с помощью рулетки. Но при измерении бесконечно «волнистой» фрактальной кривой, такой как снежинка Коха, невозможно найти достаточно маленький прямой сегмент, который соответствовал бы кривой, потому что зубчатый узор всегда появлялся снова в сколь угодно малых масштабах, по сути, немного оттягивая. больше рулетки в общую длину, измеренную каждый раз, когда кто-то пытался подогнать ее все туже и туже к кривой. В результате требуется бесконечная лента, чтобы полностью покрыть всю кривую, т.е. снежинка имеет бесконечный периметр.
Порядок в хаосе
Для того чтобы понять, что такое фрактал, следовало бы начать разбор полетов с позиции математики, однако прежде чем углубляться в точные науки, мы немного пофилософствуем. Каждому человеку присуща природная любознательность, благодаря которой он и познает окружающий мир. Зачастую в своем стремлении познания он старается оперировать логикой в суждениях. Так, анализируя процессы, которые происходят вокруг, он пытается вычислить взаимосвязи и вывести определенные закономерности. Самые большие умы планеты заняты решением этих задач. Грубо говоря, наши ученые ищут закономерности там, где их нет, да и быть не должно. И тем не менее даже в хаосе есть связь между теми или иными событиями. Вот этой связью и выступает фрактал. В качестве примера рассмотрим сломанную ветку, валяющуюся на дороге. Если внимательно к ней присмотреться, то мы увидим, что она со всеми своими ответвлениями и сучками сама похожа на дерево. Вот эта схожесть отдельной части с единым целым свидетельствует о так называемом принципе рекурсивного самоподобия. Фракталы в природе можно найти сплошь и рядом, ведь многие неорганические и органические формы формируются аналогично. Это и облака, и морские раковины, и раковины улиток, и кроны деревьев, и даже кровеносная система. Данный список можно продолжать до бесконечности. Все эти случайные формы с легкостью описывает фрактальный алгоритм. Вот мы подошли к тому, чтобы рассмотреть, что такое фрактал с позиции точных наук.

Литература
- Мандельброт Б. Фрактальная геометрия природы. — М.: «Институт компьютерных исследований», 2002.
- Пайтген Х.-О., Рихтер П. Х. Красота фракталов. Образы комплексных динамических систем. — М.: «Мир», 1993.
- Федер Е. Фракталы. — М: «Мир», 1991.
- Абачиев С. К. О треугольнике Паскаля, простых делителях и фрактальных структурах // В мире науки, 1989, № 9.
- Фоменко А. Т. Наглядная геометрия и топология. — М.: изд-во МГУ, 1993.
- Фракталы в физике. Труды 6-го международного симпозиума по фракталам в физике, 1985. — М.: «Мир», 1988.
- Шредер М. Фракталы, хаос, степенные законы. Миниатюры из бесконечного рая. — Ижевск: «РХД», 2001.
- Кроновер Р. М. Фракталы и хаос в динамических системах. Основы теории.
- Мандельброт Бенуа, Ричард Л. Хадсон. (Не)послушные рынки: фрактальная революция в финансах = The Misbehavior of Markets. — М.: «Вильямс», 2006. — 400 с. — ISBN 5-8459-0922-8.
- Красивая жизнь комплексных чисел // Hard’n’Soft, № 9, 2002. Стр. 90.
- М. Г. Иванов, «Размер и размерность» // «Потенциал», август 2006.
- Липов А.Н. Фракталы. Памяти Бенуа Мандельброта // Философия и культура № 9 (33) 2010. № 8. С. 39-54.
Как создать элемент фрактальной графики?
Создание фрактальной графики будет различаться в зависимости от ее классификации: геометрическая, алгебраическая или стохастическая. Несмотря на разницу, итог всегда будет одинаковым. Поскольку фрактальная графика начинается с геометрии, то следует рассмотреть ее создание на соответствующем примере:
- Задают условие. Это фигура, на основе которой будет строиться все изображение.
- Задают процедуру. Она преобразует условие.
- Получают геометрический фрактал.
Обычно нулевое условие представляется в виде треугольника.
 Чтобы построить изображение, нужно применить две процедуры. Во-первых, DrawTriangle. Она строит треугольник по точкам, заданным пользователем. Во-вторых, DrawGenerator. Она указывает количество точек. Каждая процедура может повторяться несколько раз или бесконечно долго. Для определения этого показателя применяется численный аргумент n.
Чтобы построить изображение, нужно применить две процедуры. Во-первых, DrawTriangle. Она строит треугольник по точкам, заданным пользователем. Во-вторых, DrawGenerator. Она указывает количество точек. Каждая процедура может повторяться несколько раз или бесконечно долго. Для определения этого показателя применяется численный аргумент n.
⇡#Бенуа Мандельброт: отец фрактальной геометрии
Само слово «фрактал» появилось благодаря гениальному ученому Бенуа Мандельброту (Benoît B. Mandelbrot).

Он сам придумал этот термин в семидесятых годах прошлого века, позаимствовав слово fractus из латыни, где оно буквально означает «ломанный» или «дробленный». Что же это такое? Сегодня под словом «фрактал» чаще всего принято подразумевать графическое изображение структуры, которая в более крупном масштабе подобна сама себе.
Математическая база для появления теории фракталов была заложена за много лет до рождения Бенуа Мандельброта, однако развиться она смогла лишь с появлением вычислительных устройств. В начале своей научной деятельности Бенуа работал в исследовательском центре компании IBM. В то время сотрудники центра трудились над передачей данных на расстояние. В ходе исследований ученые столкнулись с проблемой больших потерь, возникающих из-за шумовых помех. Перед Бенуа стояла сложная и очень важная задача — понять, как предсказать возникновение шумовых помех в электронных схемах, когда статистический метод оказывается неэффективным.
Просматривая результаты измерений шума, Мандельброт обратил внимание на одну странную закономерность — графики шумов в разном масштабе выглядели одинаково. Идентичная картина наблюдалась независимо от того, был ли это график шумов за один день, неделю или час
Стоило изменить масштаб графика, и картина каждый раз повторялась.

При жизни Бенуа Мандельброт неоднократно говорил, что он не занимается формулами, а просто играет с картинками. Этот человек мыслил очень образно, а любую алгебраическую задачу переводил в область геометрии, где, по его словам, правильный ответ всегда очевиден.
Неудивительно, что именно человек с таким богатым пространственным воображением стал отцом фрактальной геометрии. Ведь осознание сути фракталов приходит именно тогда, когда начинаешь изучать рисунки и вдумываться в смысл странных узоров-завихрений.
Фрактальный рисунок не имеет идентичных элементов, но обладает подобностью в любом масштабе. Построить такое изображение с высокой степенью детализации вручную ранее было просто невозможно, на это требовалось огромное количество вычислений. Например, французский математик Пьер Жозе Луи Фату (Pierre Joseph Louis Fatou) описал это множество более чем за семьдесят лет до открытия Бенуа Мандельбротом. Если же говорить про принципы самоподобия, то о них упоминалось еще в трудах Лейбница и Георга Кантора.
Один из первых рисунков фрактала был графической интерпретацией множества Мандельброта, которое родилось благодаря исследованиям Гастона Мориса Жюлиа (Gaston Maurice Julia).
Гастон Жюлиа (всегда в маске — травма с Первой мировой войны)
Этот французский математик задался вопросом, как будет выглядеть множество, если построить его на основе простой формулы, проитерированной циклом обратной связи. Если объяснить «на пальцах», это означает, что для конкретного числа мы находим по формуле новое значение, после чего подставляем его снова в формулу и получаем еще одно значение. Результат — большая последовательность чисел.
Чтобы получить полное представление о таком множестве, нужно проделать огромное количество вычислений — сотни, тысячи, миллионы. Вручную это сделать было просто нереально. Но когда в распоряжении математиков появились мощные вычислительные устройства, они смогли по-новому взглянуть на формулы и выражения, которые давно вызывали интерес. Мандельброт был первым, кто использовал компьютер для просчета классического фрактала. Обработав последовательность, состоящую из большого количества значений, Бенуа перенес результаты на график. Вот что он получил.
Впоследствии это изображение было раскрашено (например, один из способов окрашивания цветом — по числу итераций) и стало одним из самых популярных изображений, какие только были созданы человеком.
Как гласит древнее изречение, приписываемое Гераклиту Эфесскому, «В одну и ту же реку нельзя войти дважды». Оно как нельзя лучше подходит для трактования геометрии фракталов. Как бы детально мы ни рассматривали фрактальное изображение, мы все время будем видеть схожий рисунок.

⇡#Фрактальные антенны: лучше меньше, да лучше
За последние полвека жизнь стремительно стала меняться. Большинство из нас принимает достижения современных технологий как должное. Ко всему, что делает жизнь более комфортной, привыкаешь очень быстро. Редко кто задается вопросами «Откуда это взялось?» и «Как оно работает?». Микроволновая печь разогревает завтрак — ну и прекрасно, смартфон дает возможность поговорить с другим человеком — отлично. Это кажется нам очевидной возможностью.
Но жизнь могла бы быть совершенно иной, если бы человек не искал объяснения происходящим событиям. Взять, например, сотовые телефоны. Помните выдвижные антенны на первых моделях? Они мешали, увеличивали размеры устройства, в конце концов, часто ломались. Полагаем, они навсегда канули в Лету, и отчасти виной тому… фракталы.
Фрактальные рисунки завораживают своими узорами. Они определенно напоминают изображения космических объектов — туманностей, скопления галактик и так далее. Поэтому вполне закономерно, что, когда Мандельброт озвучил свою теорию фракталов, его исследования вызвали повышенный интерес у тех, кто занимался изучением астрономии. Один из таких любителей по имени Натан Коэн (Nathan Cohen) после посещения лекции Бенуа Мандельброта в Будапеште загорелся идеей практического применения полученных знаний. Правда, сделал он это интуитивно, и не последнюю роль в его открытии сыграл случай. Будучи радиолюбителем, Натан стремился создать антенну, обладающую как можно более высокой чувствительностью.
Единственный способ улучшить параметры антенны, который был известен на то время, заключался в увеличении ее геометрических размеров. Однако владелец жилья в центре Бостона, которое арендовал Натан, был категорически против установки больших устройств на крыше. Тогда Натан стал экспериментировать с различными формами антенн, стараясь получить максимальный результат при минимальных размерах. Загоревшись идеей фрактальных форм, Коэн, что называется, наобум сделал из проволоки один из самых известных фракталов — «снежинку Коха». Шведский математик Хельге фон Кох (Helge von Koch) придумал эту кривую еще в 1904 году. Она получается путем деления отрезка на три части и замещения среднего сегмента равносторонним треугольником без стороны, совпадающей с этим сегментом. Определение немного сложное для восприятия, но на рисунке все ясно и просто.
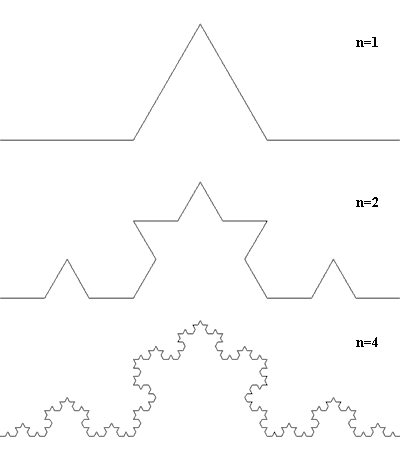
Существуют также другие разновидности «кривой Коха», но примерная форма кривой остается похожей
Когда Натан подключил антенну к радиоприемному устройству, он был очень удивлен — чувствительность резко увеличилась. После серии экспериментов будущий профессор Бостонского университета понял, что антенна, сделанная по фрактальному рисунку, имеет высокий КПД и покрывает гораздо более широкий частотный диапазон по сравнению с классическими решениями. Кроме того, форма антенны в виде кривой фрактала позволяет существенно уменьшить геометрические размеры. Натан Коэн даже вывел теорему, доказывающую, что для создания широкополосной антенны достаточно придать ей форму самоподобной фрактальной кривой.

В принципе, так и произошло. Правда, и по сей день Натан ведет судебную тяжбу с крупными корпорациями, которые незаконно используют его открытие для производства компактных устройств связи. Некоторые известные производители мобильных устройств, как, например, Motorola, уже пришли к мирному соглашению с изобретателем фрактальной антенны.
⇡#Mandelbulb3D: редактор трехмерных фракталов
Когда употребляется термин «фрактал», чаще всего подразумевается плоское двухмерное изображение. Однако фрактальная геометрия выходит за рамки 2D-измерения. В природе можно найти как примеры плоских фрактальных форм, скажем, геометрию молнии, так и трехмерные объемные фигуры. Фрактальные поверхности могут быть трехмерными, и одна из очень наглядных иллюстраций 3D-фракталов в повседневной жизни — кочан капусты. Наверное, лучше всего фракталы можно разглядеть в сорте романеско — гибриде цветной капусты и брокколи.

А еще этот фрактал можно съесть

Он может походить на растение, может напоминать странное животное, планету или что-нибудь другое. Этот эффект усиливается благодаря продвинутому алгоритму визуализации, который дает возможность получать реалистичные отражения, просчитывать прозрачность и тени, имитировать эффект глубины резкости и так далее. В Mandelbulb3D имеется огромное количество настроек и параметров визуализации. Можно управлять оттенками источников света, выбирать фон и уровень детализации моделируемого объекта.
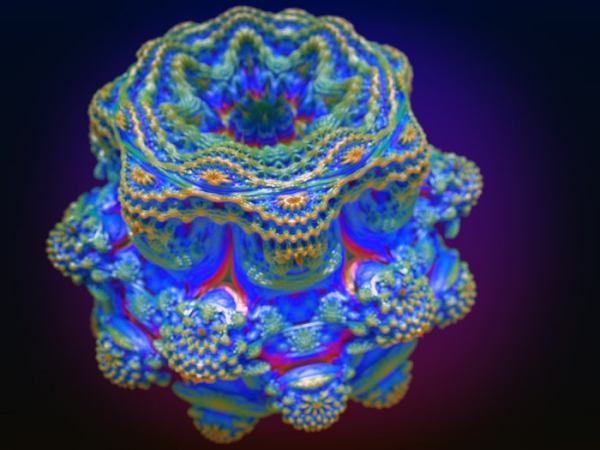
Фрактальный редактор позволяет создавать анимацию. Вы не только конфигурируете трехмерное множество Мандельброта, но и можете его вращать, масштабировать и менять параметры с течением времени.
Немного о фракталах. Интересные факты
Фрактал — геометрическая фигура обладающая свойством самоподобия. Слово «фрактал» является производным от латинского слова fractus, что означает дробный. Этим свойством обладают практически все объекты природы — начиная с гигантских скоплений Галактик и заканчивая элементарными частицами такими как кварки.
Галактики, рельефы планет, океанские волны, облака и молнии, реки, формы растений и животных, и даже человеческое тело можно рассматривать как фракталы…

Бенуа Мандельброт (на фото) — отец основатель фрактальной геометрии, бунтарь среди математиков, впервые подробно описал этот термин в книге «Фрактальная геометрия природы», изданной в 1977 году. Эта книга в значительной степени повлияла на развитие компьютерной графики, так представила простой способ для генерации сложных геометрических объектов, таких как горы, облака и растения, необходимых для создания фотореалистичных сцен.
Если бы эта книга не попала в нужный момент в руки Лорена Карпетнера — сооснователя анимационной компании Pixar, может мы бы и не увидели всей красоты декораций таких фильмов как «Властелин колец», «Аватар», «2012», «Матрица» и прочих. При создании этих фильмов использовался алгоритм Reyes rendering — алгоритм, который по утверждению самого автора «может отрисовать всё что ты когда-либо видел».
⇡#Лорен Карпентер: искусство, созданное природой
Теория фракталов скоро нашла практическое применение. Поскольку она тесно связана с визуализацией самоподобных образов, неудивительно, что первыми, кто взял на вооружение алгоритмы и принципы построения необычных форм, были художники.
Будущий сооснователь легендарной студии Pixar Лорен Карпентер (Loren C. Carpenter) в 1967 году начал работать в компании Boeing Computer Services, которая была одним из подразделений известной корпорации, занимающейся разработкой новых самолетов.
В 1977 году он создавал презентации с прототипами летающих моделей. В обязанности Лорена входила разработка изображений проектируемых самолетов. Он должен был создавать картинки новых моделей, показывая будущие самолеты с разных сторон. В какой-то момент в голову будущему основателю Pixar Animation Studios пришла в голову креативная идея использовать в качестве фона изображение гор. Сегодня такую задачу может решить любой школьник, но в конце семидесятых годов прошлого века компьютеры не могли справиться со столь сложными вычислениями — графических редакторов не было, не говоря уже о приложениях для трехмерной графики. В 1978 году Лорен случайно увидел в магазине книгу Бенуа Мандельброта «Фракталы: форма, случайность и размерность»
В этой книге его внимание привлекло то, что Бенуа приводил массу примеров фрактальных форм в реальной жизни и доказывал, что их можно описать математическим выражением
Такая аналогия была выбрана математиком не случайно. Дело в том, что как только он обнародовал свои исследования, ему пришлось столкнуться с целым шквалом критики. Главное, в чем упрекали его коллеги, — бесполезность разрабатываемой теории. «Да, — говорили они, — это красивые картинки, но не более. Практической ценности теория фракталов не имеет». Были также те, кто вообще считал, что фрактальные узоры — просто побочный результат работы «дьявольских машин», которые в конце семидесятых многим казались чем-то слишком сложным и неизученным, чтобы всецело им доверять. Мандельброт пытался найти очевидное применение теории фракталов, но, по большому счету, ему и не нужно было это делать. Последователи Бенуа Мандельброта в следующие 25 лет доказали огромную пользу от подобного «математического курьеза», и Лорен Карпентер был одним из первых, кто опробовал метод фракталов на практике.
Проштудировав книжку, будущий аниматор серьезно изучил принципы фрактальной геометрии и стал искать способ реализовать ее в компьютерной графике. Всего за три дня работы Лорен смог визуализировать реалистичное изображение горной системы на своем компьютере. Иными словами, он с помощью формул нарисовал вполне узнаваемый горный пейзаж.

Принцип, который использовал Лорен для достижения цели, был очень прост. Он состоял в том, чтобы разделять более крупную геометрическую фигуру на мелкие элементы, а те, в свою очередь, делить на аналогичные фигуры меньшего размера.

Используя более крупные треугольники, Карпентер дробил их на четыре мелких и затем повторял эту процедуру снова и снова, пока у него не получался реалистичный горный ландшафт. Таким образом, ему удалось стать первым художником, применившим в компьютерной графике фрактальный алгоритм для построения изображений. Как только стало известно о проделанной работе, энтузиасты по всему миру подхватили эту идею и стали использовать фрактальный алгоритм для имитации реалистичных природных форм.
Одна из первых визуализаций 3D по фрактальному алгоритму
Всего через несколько лет свои наработки Лорен Карпентер смог применить в куда более масштабном проекте. Аниматор создал на их основе двухминутный демонстрационный ролик Vol Libre, который был показан на Siggraph в 1980 году. Это видео потрясло всех, кто его видел, и Лоурен получил приглашение от Lucasfilm.
Анимация рендерилась на компьютере VAX-11/780 от Digital Equipment Corporation с тактовой частотой пять мегагерц, причем прорисовка каждого кадра занимала около получаса.

Работая для Lucasfilm Limited, аниматор создавал по той же схеме трехмерные ландшафты для второго полнометражного фильма саги Star Trek. В фильме «Гнев Хана» (The Wrath of Khan) Карпентер смог создать целую планету, используя тот же самый принцип фрактального моделирования поверхности.
В настоящее время все популярные приложения для создания трехмерных ландшафтов используют аналогичный принцип генерирования природных объектов. Terragen, Bryce, Vue и прочие трехмерные редакторы полагаются на фрактальный алгоритм моделирования поверхностей и текстур.
См. также
Общие методы создания фракталов
Самоподобный паттерн ветвления, смоделированный in silico с использованием принципов L-систем
Изображения фракталов могут быть созданы программами генерации фракталов . Из-за эффекта бабочки небольшое изменение одной переменной может иметь непредсказуемый результат.
- Системы повторяющихся функций (IFS) — используйте фиксированные геометрические правила замены; может быть стохастическим или детерминированным; например, Кривая Коха , канторово множество , Haferman ковер, ковер Серпинского , Серпинская прокладка , кривой Пеано , Хартер-Heighway кривой дракона , Т-квадрат , Менгер губка
- Странные аттракторы — используйте итерации карты или решения системы дифференциальных или разностных уравнений с начальным значением, которые демонстрируют хаос (например, см. изображение или логистическую карту )
- L-системы — использовать перезапись строк; может напоминать паттерны ветвления, например, в растениях, биологических клетках (например, нейронах и клетках иммунной системы), кровеносных сосудах, легочной структуре и т. д. или графические паттерны черепах, такие как кривые заполнения пространства и тилинги
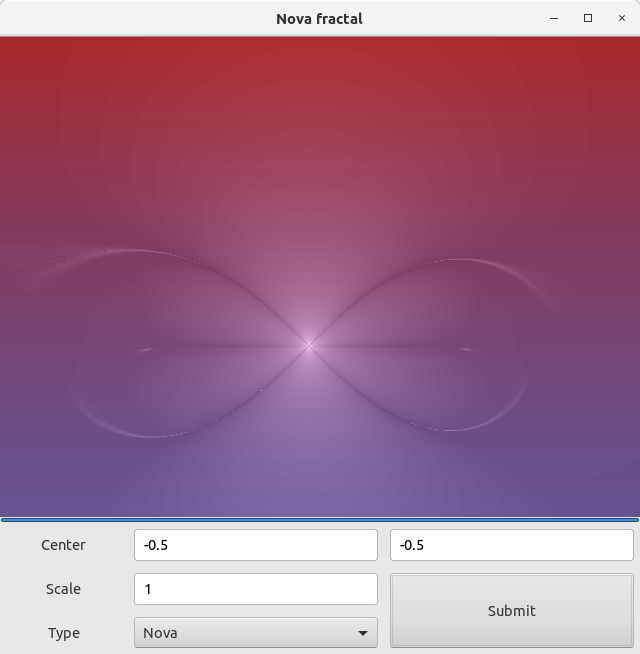
- Фракталы времени побега — используйте формулу или рекуррентное соотношение в каждой точке пространства (например, на комплексной плоскости ); обычно квази-самоподобный; также известные как фракталы «орбиты»; например, набор Мандельброта , Жюлиа , Горящий корабль фрактал , Нова фрактал и Ляпунову фрактал . Двухмерные векторные поля, которые генерируются одной или двумя итерациями формул времени ухода, также приводят к фрактальной форме, когда точки (или данные пикселей) повторно проходят через это поле.
- Случайные фракталы — используйте стохастические правила; например, полет Леви , перколяционные кластеры , самоизбегающие прогулки , фрактальные ландшафты , траектории броуновского движения и броуновское дерево (то есть дендритные фракталы, генерируемые путем моделирования агрегации, ограниченной диффузией, или кластеров агрегации, ограниченной реакцией).
Фрактал, созданный правилом конечного подразделения для чередующегося звена
Правила конечного подразделения — используйте рекурсивный топологический алгоритм для уточнения мозаик, и они похожи на процесс деления клеток . Итерационные процессы, используемые при создании множества Кантора и ковра Серпинского, являются примерами правил конечного подразделения, как и барицентрическое подразделение .
Фракталы и жизнь
В наши дни теория фракталов находит широкое применение в различных областях человеческой деятельности. Помимо чисто научного объекта для исследований и уже упоминавшейся фрактальной живописи, фракталы используются в теории информации для сжатия графических данных (здесь в основном применяется свойство самоподобия фракталов — ведь чтобы запомнить небольшой фрагмент рисунка и преобразования, с помощью которых можно получить остальные части, требуется гораздо меньше памяти, чем для хранения всего файла). Добавляя в формулы, задающие фрактал, случайные возмущения, можно получить стохастические фракталы, которые весьма правдоподобно передают некоторые реальные объекты — элементы рельефа, поверхность водоемов, некоторые растения, что с успехом применяется в физике, географии и компьютерной графике для достижения большего сходства моделируемых предметов с настоящими. В радиоэлектронике выпускают антенны, имеющие фрактальную форму. Занимая мало места, они обеспечивают вполне качественный прием сигнала. Экономисты используют фракталы для описания кривых колебания курсов валют (это свойство было открыто Мандельбротом). На этом мы завершим эту небольшую экскурсию в удивительный по красоте и разнообразию мир фракталов.
Фрактальная компьютерная графика
Введение
Слово фрактал образовано от латинского «fractus» и в переводе
означает состоящий из фрагментов. Оно было предложено Бенуа Мандельбротом в
1975 году. Определение фрактала, данное Мандельбротом, звучит так:
«Фракталом называется структура, состоящая из частей, которые в каком-то
смысле подобны целому». Одним из основных свойств фракталов является
самоподобие. В самом простом случае небольшая часть фрактала содержит
информацию о всем фрактале. Понятия фрактал и фрактальная геометрия, появившиеся
в конце 70-х, с середины 80-х прочно вошли в обиход математиков и
программистов.
Фракталы широко применяются в компьютерной графике для построения
изображений природных объектов, таких, как деревья, кусты, горные ландшафты,
поверхности морей и т. д. Роль фракталов в машинной графике сегодня достаточно
велика. Они приходят на помощь, например, когда требуется, получить линии и
поверхности очень сложной формы. Фракталы используются для описания кривизны
поверхностей. С точки зрения машинной графики, фрактальная геометрия незаменима
при генерации искусственных облаков, объемных рельефных гор, поверхности моря.
Фактически найден способ легкого представления сложных неевклидовых объектов,
образы которых весьма похожи на природные. Фрактальная компьютерная графика широко
используется при создании мультфильмов и фантастических художественных фильмов.
Используются антенны, имеющие фрактальные формы, что сильно уменьшает их
размеры и вес.
В творчестве
С 1999 года более 10 научных групп выполнили фрактальный анализ более чем 50 картин Джексона Поллока (1912–1956), которые были созданы путем заливки краски непосредственно на его горизонтальные холсты. В последнее время фрактальный анализ был использован для достижения 93% успеха. Оцените отличия настоящего минтая от имитации. Когнитивные нейробиологи показали, что фракталы Поллока вызывают такое же снижение стресса у наблюдателей, что и фракталы, созданные компьютером, и фракталы Природы.
Декалькомания , техника, используемая такими художниками, как Макс Эрнст , позволяет создавать фрактальные узоры. Он заключается в том, чтобы зажать краску между двумя поверхностями и раздвинуть их.
Кибернетик Рон Эглаш предположил, что фрактальная геометрия и математика преобладают в африканском искусстве , играх, гадании , торговле и архитектуре. Круглые дома появляются в кругах кругов, прямоугольные дома — в прямоугольниках прямоугольников и так далее. Такие узоры масштабирования также можно найти в африканском текстиле, скульптуре и даже прическах косички. Хокки Ситунгкир также предложил похожие свойства в индонезийском традиционном искусстве, батике и украшениях, которые можно найти в традиционных домах.
Этноматематик Рон Эглаш обсудил запланированную планировку города Бенина, взяв за основу фракталы не только в самом городе и деревнях, но даже в комнатах домов. Он заметил, что «когда европейцы впервые приехали в Африку, они считали архитектуру очень неорганизованной и, следовательно, примитивной. Им никогда не приходило в голову, что африканцы могли использовать форму математики, которую они еще даже не открыли».
В интервью с Майклом Сильверблаттом в 1996 году Дэвид Фостер Уоллес признал, что структура первого варианта « Бесконечной шутки», который он дал своему редактору Майклу Пичу, была вдохновлена фракталами, в частности треугольником Серпинского (он же прокладка Серпинского), но что отредактированный роман таков. «больше похоже на однобокую серпинскую прокладку».
Некоторые работы голландского художника MC Эшера , такие как Circle Limit III , содержат формы, повторяющиеся до бесконечности, которые становятся все меньше и меньше по мере приближения к краям, в шаблоне, который всегда будет выглядеть одинаково при увеличении.
Основы фрактальной графики
Что такое фрактальная графика? Это одна или несколько геометрических фигур, каждая из которых подобна другой. То есть, изображение составляется из одинаковых частей.
Само слово «фрактал» может употребляться, если фигура обладает одним или несколькими из этих свойств:
- Нетривиальная структура. Когда рассматривается небольшая деталь всего изображения, то фрагмент схож со всем рисунком. Увеличение масштаба не приводит к ухудшению. Изображение всегда остается одинаково сложным.
- Каждая часть рисунка является самоподобной.
- Имеется математическая размерность.
- Строится при помощи повторения.
Множество объектов природного или искусственного происхождения наделяются свойствами фракталов. К ним относятся кровеносные системы человека и животного, кроны и корни деревьев и так далее.
Фрактальная компьютерная графика становится популярной потому, что добиться красоты и реалистичности можно посредством простого построения при помощи соответствующего оборудования. Нужно только задать правильную математическую формулу и указать количество повторений.
⇡#Фрактал в браузере

В вашем распоряжении имеется всего две простейших формы — четырехугольник и круг. Вы можете добавлять их на холст, масштабировать (чтобы масштабировать вдоль одной из осей, удерживайте клавишу Shift) и вращать. Перекрываясь по принципу булевых операций сложения, эти простейшие элементы образуют новые, менее тривиальные формы. Далее эти новые формы можно добавлять в проект, а программа будет повторять генерирование этих изображений до бесконечности. На любом этапе работы над фракталом можно возвращаться к любой составляющей сложной формы и редактировать ее положение и геометрию. Увлекательное занятие, особенно если учесть, что единственный инструмент, который вам нужен для творчества, — браузер. Если вам будет непонятен принцип работы с этим рекурсивным векторным редактором, советуем вам посмотреть видео на официальном сайте проекта, на котором подробно показывается весь процесс создания фрактала.
Наука и искусство
В 1982 году вышла книга Мандельброта «Фрактальная геометрия природы», в которой автор собрал и систематизировал практически всю имевшуюся на тот момент информацию о фракталах и в легкой и доступной манере изложил ее. Основной упор в своем изложении Мандельброт сделал не на тяжеловесные формулы и математические конструкции, а на геометрическую интуицию читателей. Благодаря иллюстрациям, полученным при помощи компьютера, и историческим байкам, которыми автор умело разбавил научную составляющую монографии, книга стала бестселлером, а фракталы стали известны широкой публике. Их успех среди нематематиков во многом обусловлен тем, что с помощью весьма простых конструкций и формул, которые способен понять и старшеклассник, получаются удивительные по сложности и красоте изображения. Когда персональные компьютеры стали достаточно мощными, появилось даже целое направление в искусстве — фрактальная живопись, причем заниматься ею мог практически любой владелец компьютера. Сейчас в интернете можно легко найти множество сайтов, посвященных этой теме.
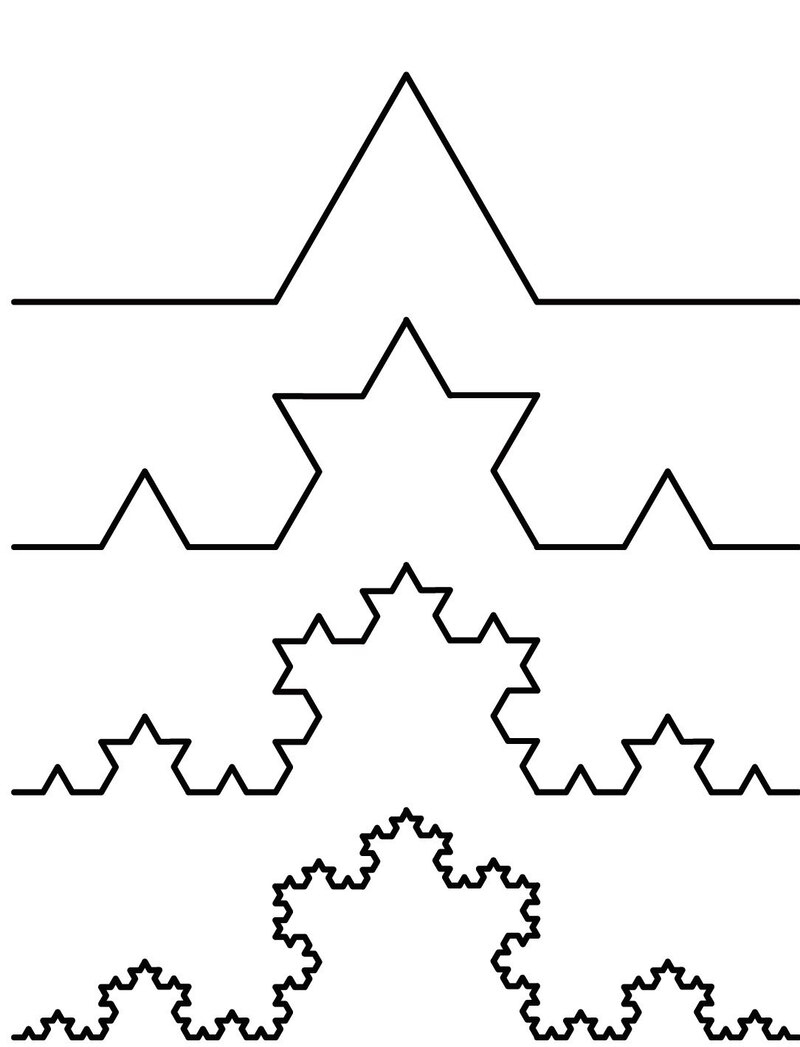
Схема получения кривой Коха
Заключение
Наука о фракталах очень молода, потому что они стали появляться с
развитием компьютерных технологий. Поэтому многое еще не изучено и многое еще
предстоит открыть. Основная причина применения фракталов в различных науках
заключается в том, что они описывают реальный мир иногда даже лучше, чем
традиционная физика или математика. Мы выяснили, что фракталы можно применять
не только в точных науках, но и практически во всем, что нас окружает. В этом
мы можем убедиться на конкретном примере, представленном в практической части
работы, а именно на примере создания фрактала треугольника Серпинского. Кроме
большой функциональности, возможности применения фракталов в самых различных
сферах жизни, это очень яркие, изумительные по своей красоте изображения,
которые доставляют огромное эстетическое удовольствие, позволяют насладиться
ими. Создавать свои собственные фракталы может каждый, используя доступные
программы. От самого процесса создания совершенно для нас нового и одновременно
невероятно красивого, порой фантастического, получаешь массу удовольствия.
Фракталы очень разнообразны, как и их применение. Изучая фрактальные модели для
практического применения, каждый сможет выбрать подходящее для себя
направление.