Физическая величина

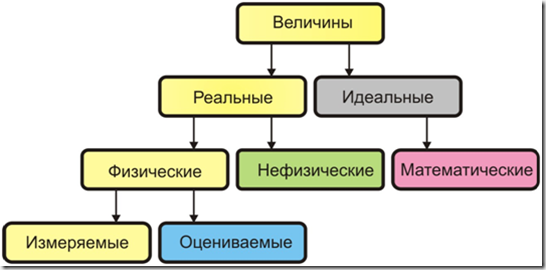
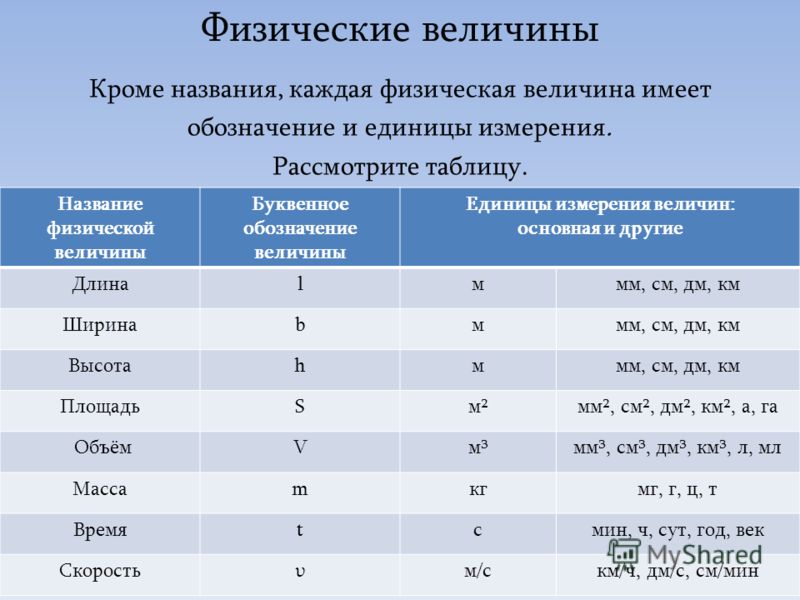
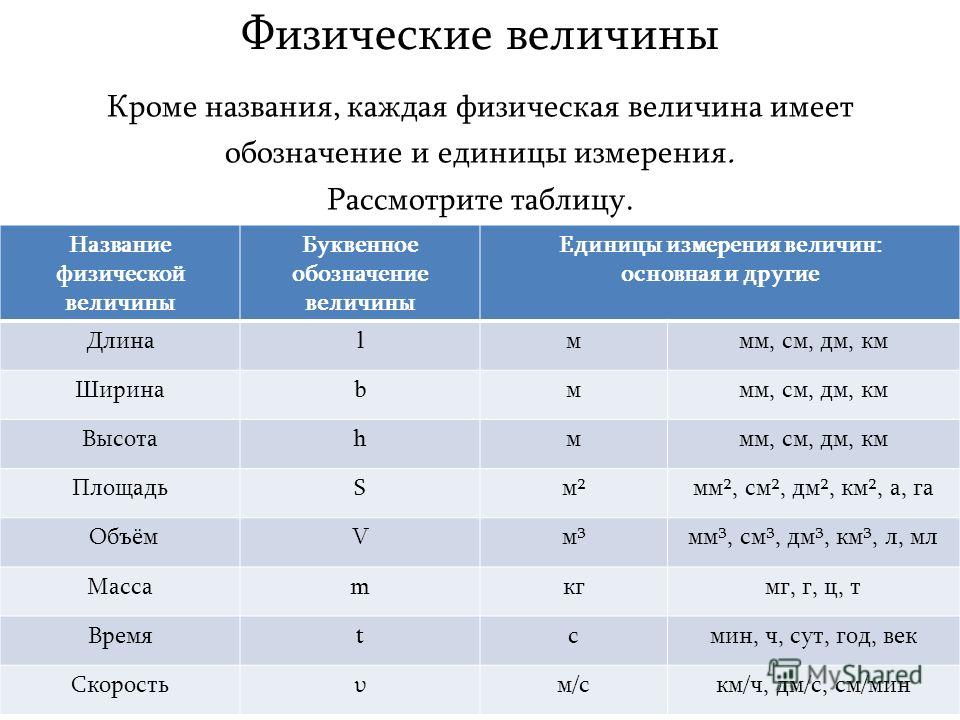
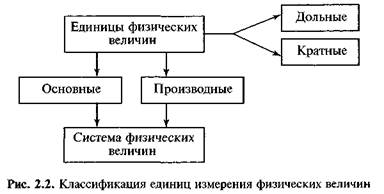
Классификация[править | править код]

Размерные и безразмерные физические величиныправить | править код

Размерная физическая величина — физическая величина, для определения значения которой нужно применить какую-то единицу измерения этой физической величины. Подавляющее большинство физических величин являются размерными.

Аддитивные и неаддитивные физические величиныправить | править код

Аддитивная физическая величина — физическая величина, разные значения которой могут быть суммированы, умножены на числовой коэффициент, разделены друг на друга. Например, физическая величина масса — аддитивная физическая величина (в классической механике).
Неаддитивная физическая величина — физическая величина, для которой суммирование, умножение на числовой коэффициент или деление друг на друга её значений не имеет физического смысла. Например, физическая величина температура — неаддитивная физическая величина.

Экстенсивные и интенсивные физические величиныправить | править код

Физическая величина называется[источник не указан 4154 дня]

Некоторые физические величины, такие как момент импульса, площадь, сила, длина, время, не относятся ни к экстенсивным, ни к интенсивным.

От некоторых экстенсивных величин образуются производные величины:

Общие свойства величин

Качественная определённость величины называется родом. Например, однородными величинами являются длина и ширина. Количественная определённость величины, присущая конкретному объекту или явлению, называется размером. Индивидуальность размеров совпадающих(однородных) величин объектов или явлений позволяет сравнивать и различать их.

Одна из реализаций единицы длины — метра

При измерении размер определяемой величины сравнивается с размером условной единицы. Результатом такого сравнения является измеренное значение величины, показывающее во сколько раз размер величины больше или меньше размера единицы. Следовательно, значение является целью и результатом измерения.

X=ax{\displaystyle X=a}, где X — измеряемая величина объекта или явления, a — значение, — единица величины.

Значение самой единицы всегда тождественно равно 1. Размер величины не зависит от выбранной единицы, а значение изменяется при выборе другой единицы. Например, гиря массой в 1 килограмм, также имеет массу 2,2 фунта или 0,001 тонны. Значения однородных величин применяются для сравнения объектов измерения.

Различают три вида значений величин, объединённые общим термином «опорное значение».

Истинное значение — идеальное, единственное значение величины. Термин используется тогда, когда можно пренебречь неопределённостью значения на микроуровне.
Действительное значение — получается экспериментальным путем, достаточно близко к истинному значению.
Принятое значение — значение, приписанное величине.

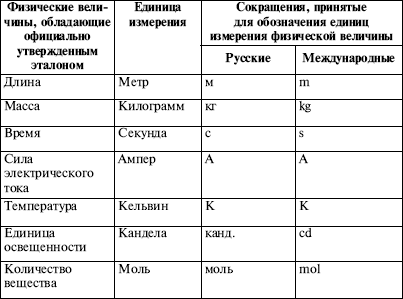
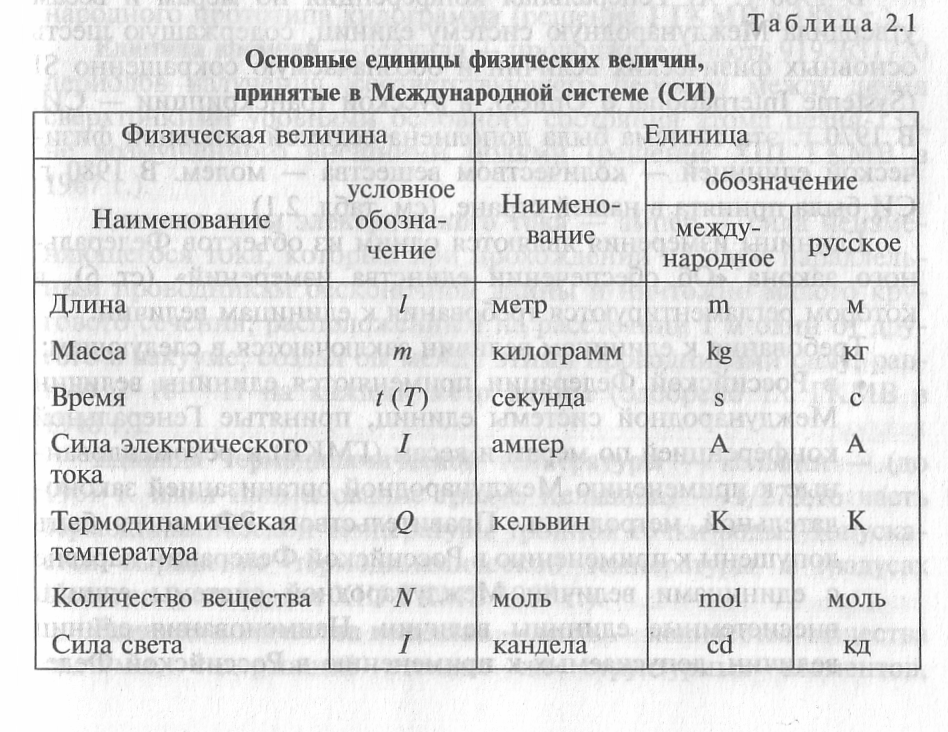
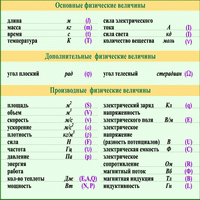
Разнообразие физических величин упорядочивается при помощи систем физических величин. В системе ограниченный перечень величин принимается за основные, а другие, производные, величины выводятся из них при помощи уравнений связи. В (англ. International System of Quantities, ISQ) в качестве основных выбрано семь величин:

L — длина;
M — масса;
T — время;
I — сила тока;
Θ — температура;
N — количество вещества;
J — сила света.

При анализе связей между величинами применяется понятие размерности физической величины. Так называют степенной одночлен, состоящий из произведений символов основных величин в различных степенях. При определении размерности, применяются стандартные математические операции — умножение, деление и сокращение степеней.Если после всех операций сокращений в размерности величины не осталось сомножителей с ненулевыми степенями, то величина называется безразмерной.

Определение размерности давления
Величина	Уравнение связи	Размерность в СИ	Название единицы
Ускорение	a=Vt=lt2{\displaystyle a={\frac {V}{t}}={\frac {l}{t^{2}}}}	L+1T−2{\displaystyle L^{+1}T^{-2}}	Нет
Сила	F=ma{\displaystyle F={m}{a}}	M+1L+1T−2{\displaystyle M^{+1}L^{+1}T^{-2}}	Ньютон
Площадь	S=l2{\displaystyle S=l^{2}}	L+2{\displaystyle L^{+2}}	Квадратный метр
Давление	P=FS{\displaystyle P={\frac {F}{S}}}	M+1L+1T−2L+2=M+1L−1T−2{\displaystyle M^{+1}L^{+1}T^{-2}L^{+2}=M^{+1}L^{-1}T^{-2}}	Паскаль

Физические величины, которые характеризуют объекты и явления в твёрдой Земле, а также в её жидких и газовых оболочках называются геофизическими величинами. Измерение геофизических величин в лаборатории или в полевых условиях позволяет лучше понять внутреннюю структуру планеты, а также искать и разведывать месторождения полезных ископаемых. Наука, основанная на измерениях физических величин горных пород в лабораторных условиях, называется петрофизикой.

Примечания[править | править код]

Чертов А. Г. Единицы физических величин. — М.: Высшая школа, 1977. — С. 9. — 287 с. (см. ISBN )
/ Пер. с англ. и фр.. — 2-е изд., испр. — СПб.: НПО «Профессионал», 2010. — С. 17. — 82 с. — ISBN 978-5-91259-057-3. (см. ISBN )
«скалярная физическая величина» — Яндекс. Словари
Векторная физическая величина. — Естественные науки — Яндекс. Словари

Википедия Физическая величина адрес
Викисловарь — адрес
Викицитатник — адрес
Викиучебник — адрес
Викитека — адрес
Викиновости — адрес
Викиверситет — адрес
Викигид — адрес

Выделить Физическая величина и найти в:

Вокруг света величина адрес
Академик величина/ru/ru/ адрес
Астронет адрес
Элементы величина+&search адрес
Научная Россия величина&mode=2&sort=2 адрес
Кругосвет величина&results_per_page=10 адрес
Научная Сеть
Традиция — адрес
Циклопедия — адрес
Викизнание — величина адрес

Bing
Yahoo
Яндекс
Mail.ru
Рамблер
Нигма.РФ
Спутник
Google Scholar
Апорт
Архив Интернета
Научно-популярные фильмы на Яндексе
Документальные фильмы

Список ru-вики
Вики-сайты на русском языке
Список крупных русскоязычных википроектов
Каталог wiki-сайтов
Русскоязычные wiki-проекты
Викизнание:Каталог wiki-сайтов
Научно-популярные сайты в Интернете
Лучшие научные сайты на нашем портале
Лучшие научно-популярные сайты
Каталог научно-познавательных сайтов
НАУКА В РУНЕТЕ: каталог научных и научно-популярных сайтов

Страница — краткая статья
Страница — энциклопедическая статья
Разное — на страницах: , , ,

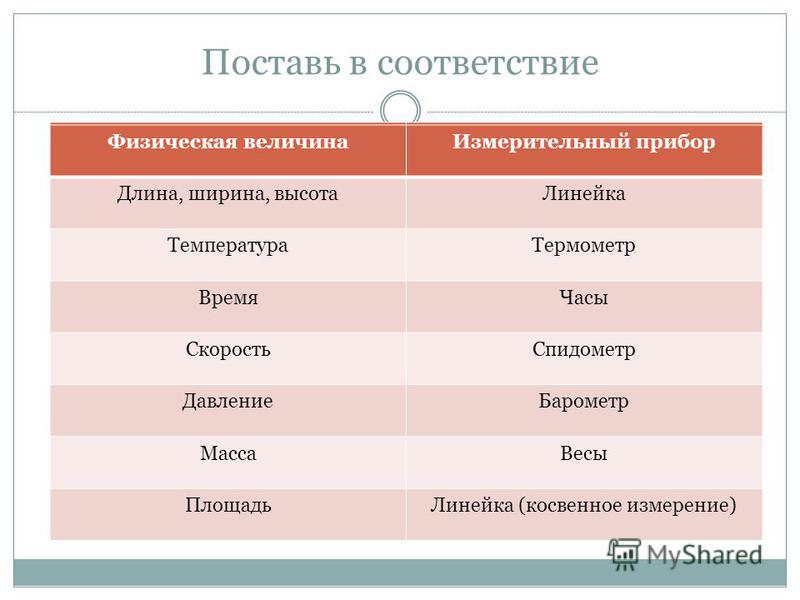
Как измерить длину. Погрешности измерений

На практике измерить длину отрезка достаточно просто:

Приложить линейку к отрезку.
Совместить ноль с началом отрезка.
Определить число, соответствующее концу отрезка.
Записать результат измерения.

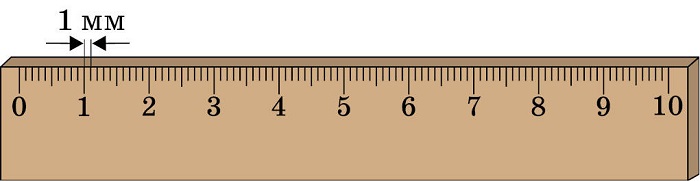
В приведенном примере длина отрезка 9,9 см. Как точен этот результат? Он точен до 1 мм, так как на линейке нет меньших делений. Не надо путать значения слов «штрих» и «деление».

()

Численное значение самого маленького деления шкалы прибора называется ценой деления.

Чтобы определить цену деления прибора (например, линейки), нужно взять любые два рядом стоящие числа и их разность поделить на число делений между ними (т.е. промежутков между штрихами).

Цена деления линейки = (7 см – 6 см)/10 = 0,1 см = 1 мм.

()

И чтобы начать измерение, прежде всего надо найти цену деления прибора, который используется в данном случае. Любое измерение дает некоторую погрешность, зависящую от качества прибора. Поэтому ее называют погрешностью прибора.

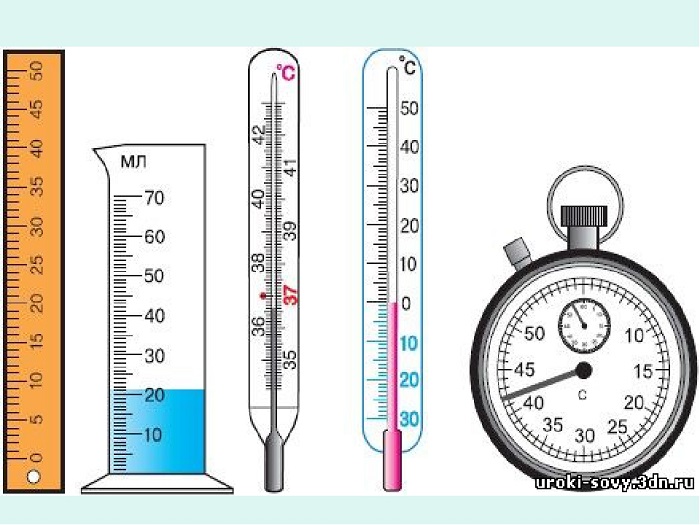Шкалы различных приборов. ()

Известно, что измерить какую-то величину – это значит сравнить ее с эталоном. На практике пользуются не эталонами, а специальными приборами (линейка, часы и др.), которые являются копиями с эталонов, изготовленными с определенной точностью. Абсолютно точных измерений не бывает. При использовании линейки допускается погрешность отсчета, которая равна половине цены деления прибора (0,5 мм). Сумма погрешностей прибора и отсчета называется абсолютной погрешностью. Она равна цене деления прибора.

Абсолютная погрешность обозначается значком Δ (дельта). Для школьной линейки Δ = 1 мм. Δ показывает, на сколько совершается ошибка при использовании того или иного прибора. Для более точных измерений используется штангенциркуль. В устройстве штангенциркуля заложено две шкалы, неподвижная (Δ = 1 мм) и подвижная (Δ = 0,1 мм).

Штангенциркуль. () Микрометр. ()

А вот при помощи микрометра, где используется не перемещение шкалы, а ее вращение измерить длину можно с точностью до 0,01 мм. Но это еще не предел. В очень точных технологиях определяются размеры с точностью до 10-7м, в научных разработках точность возрастает во много раз. Но для этого нужны сверхточные приборы.

На практике, используя приборы, необходимо учитывать качество измерения. Величина, которая помогает это учесть, называется относительной погрешностью σ (сигма) и выражается в процентах.

σ = Δ / L ( L – измеренная величина)

Пример: Требуется замерить длину L отрезка различными приборами: 1) линейкой, 2) штангенциркулем и 3) микрометром. Длина отрезка получилась 55 мм. Какова относительная погрешность этих трех измерений?

1) Δ₁ = 1 мм, L = 55 ± 1 мм, σ₁ = 1 мм / 55 мм ≈ 0,018 (1,8%);

2) Δ₂ = 0,1 мм, L = 55 ± 0,1 мм, σ₂ = 0,1 мм / 55мм ≈ 0,0018 (0,18);

3) Δ₃ = 0,01 мм, L = 55 ± 0,01 мм, σ₃ = 0,01 мм / 55мм ≈ 0,00018 (0,018%).

Как видно, более точный прибор (микрометр) дает меньший процент ошибки.

Для каждого конкретного измерения в технике, практической деятельности человека и в науке существует своя точность измерения, в соответствии с которой применяются измерительные приборы.

Классификация физических величин

Аддитивные и неаддитивные
- аддитивные величины — величины, значения которых могут быть суммированы, умножены на константу или разделены друг на друга. Например масса, длина, площадь.
- неаддитивные величины — величины, для которых суммирование значений бессмысленно, хотя и возможно математически. К таким величинами относится температура, плотность, удельное сопротивление.

Скалярные, векторные, тензорные величины
- скалярные величины имеют значение, выражаемое только одним числом, для них не определено направление. Ярким примером скалярной величины является потенциальная энергия.
- векторные величины описываются последовательностью из трёх (или двух) независимых значений, которые называются компонентами. Векторные величины имеют скалярный модуль и направление. Векторными величинами является сила, давление, скорость и ускорение.
- тензорные величины объединяют все остальные классы. Они возникают в материальных уравнениях для сред, например в теории упругости для описания деформаций, электромагнитной теории для уравнений материальной среды, в общей теории относительности для описания метрики.

Классификация физических величин

Аддитивные и неаддитивные
- аддитивные величины — величины, значения которых могут быть суммированы, умножены на константу или разделены друг на друга. Например масса, длина, площадь.
- неаддитивные величины — величины, для которых суммирование значений бессмысленно, хотя и возможно математически. К таким величинами относится температура, плотность, удельное сопротивление.

Скалярные, векторные, тензорные величины
- скалярные величины имеют значение, выражаемое только одним числом, для них не определено направление. Ярким примером скалярной величины является потенциальная энергия.
- векторные величины описываются последовательностью из трёх (или двух) независимых значений, которые называются компонентами. Векторные величины имеют скалярный модуль и направление. Векторными величинами является сила, давление, скорость и ускорение.
- тензорные величины объединяют все остальные классы. Они возникают в материальных уравнениях для сред, например в теории упругости для описания деформаций, электромагнитной теории для уравнений материальной среды, в общей теории относительности для описания метрики.

Что это такое

Измерение касается тех величин, которые подтверждают справедливость гипотезы о закономерностях. Физическая величина – это научная характеристика физического тела, качественное отношение которой является общим для множества аналогичных тел. Для каждого тела такая количественная характеристика сугубо индивидуальна.

Если обратиться к специальной литературе, то в справочнике М. Юдина и др. (1989 года издания) читаем, что физическая величина это: “характеристика одного из свойств физического объекта (физической системы, явления или процесса), общая в качественном отношении для многих физических объектов, но в количественном отношении индивидуальная для каждого объекта”.

Словарь Ожегова (1990 года издания) утверждает, что физическая величина это — «размер, объем, протяженность предмета».

К примеру, длина – физическая величина. Механика длину трактует как пройденное расстояние, электродинамика использует длину провода, в термодинамике аналогичная величина определяет толщину стенок сосудов. Суть понятия не меняется: единицы величин могут быть одинаковыми, а значение – различным.

Отличительной чертой физической величины, скажем, от математической, является наличие единицы измерения. Метр, фут, аршин – примеры единиц измерения длины.

Площадь и ее измерение

С измерением длин очень тесно связано измерение площадей. Из математики известны формулы площадей квадрата и прямоугольника. У квадрата все стороны равны, поэтому достаточно измерить одну сторону, а у прямоугольника противоположные стороны равны, поэтому надо знать длину и ширину. Площадь обозначается буквой S, и формулы для расчета площадей следующие:

S_кв = a2, S_пр = а ∙ в. Единицей измерения площади является квадратный метр (м2).

Для измерения малых площадей применяются см2 и мм2, а большие площади – в км2. В сельском хозяйстве для измерения земельных участков используют внесистемные единицы: гектар (га) – для больших, ар (а) или «сотка» — для небольших (приусадебных или дачных) участков земли. 1га = 10 000 м2, 1 а = 100 м2.

Очень часто на практике имеют дело с различными кругами. Это может быть цирковая арена, крышка стола, разрез ствола дерева. Формула нахождения площади круга: S = πR2. (π (пи) – это бесконечная дробь ≈ 3,14 подробно изучается в курсе алгебры).

Арена цирка. () Круглый стол. () Спил дерева. ()

А как определить площадь, ограниченную произвольной кривой линией? Такая площадь может быть у озера, полянки в лесу, листочка с дерева.

()

Существует правило нахождения площади тел произвольной формы:

Разбить всю поверхность на равные квадраты с известной площадью.
Подсчитать количество целых квадратов.
Подсчитать число нецелых квадратов и поделить это число на два. (Это будет примерное количество целых квадратов).
Сложить результаты пунктов 2 и 3.
Умножить площадь одного квадрата на общее число целых квадратов.

Площадь больших территорий изображают в условном масштабе или фотографируют, применяют прием разбиения на квадраты и находят площадь фотографии. Используя масштаб вычисляют реальную площадь поверхности.

()

Довольно часто площадь приходится находить в географии. Каждое государство, область, город имеют свои площади. В строительстве – любое здание имеет площадь, которую необходимо знать строителям. В сельском хозяйстве ведется постоянный учет площадей для посевных культур.

Измерить – значит, сравнить

На помощь человеку приходят числа, используя которые можно было сравнить предметы по величине. Так в одном известном мультфильме длину удава измеряли в «попугаях», сравнивая величину удава с длиной попугая.

Из мультфильма «38 попугаев». ()

Длина удава 38 «попугаев». Понятно, что удав в 38 раз длиннее попугая. Но попугаи бывают разными. Если взять другого попугая, тот же удав будет, например, 45 «попугаев». Что делать?

Нужно найти тело, принимаемое за единицу измерения, с которой сравниваются другие тела.

В практической деятельности человеку приходится часто измерять длину, массу и время. В разных странах вводились разные единицы измерения этих величин. Существовали такие единицы, как «лошадиная сила», локоть, бочка. Но ведь и локоть, и бочка могут быть разными, поэтому о точности выполнения работы говорилось приблизительно.

()

Сравнивать нужно только однородные физические величины. Длину тела нужно сравнивать с длиной другого тела, а массу тела – только с массой другого тела, принятого за единицу измерения. Так массу удава из мультфильма можно было сравнить с массой обезьянки. Удав имеет массу 195 «обезьянок». Что бы это значило?

Выход был найден, когда ввели систему единиц СИ. Чтобы измерить любую величину, нужно сравнить ее с однородной величиной, принятой за единицу. Как же выбирают эти единицы?

Наиболее распространено измерение длины, размеров пройденного пути, расстояния. Все эти величины измеряются в метрах. Один метр получили следующим образом. Взяли одну сорока миллионную часть меридиана, который проходит через столицу Франции – Париж. Длину этой части и приняли за 1 метр. На стержне, изготовленном из иридия и платины, нанесли два деления, расстояние между которыми равно одному метру. Такой сплав меньше всего подвержен температурному влиянию, которое может изменить длину тела. Это стержень и есть эталон длины, с которым сравнивают единицу длины во многих странах мира. Метровые линейки – это многочисленные копии эталона, которыми как раз и можно пользоваться.

Эталон длины

()

Первый эталон метра был изготовлен из латуни в 1795 г. С 1960 г. используется изготовленный с помощью электронных технологий эталон из сплава иридия и платины.

Существует и эталон массы, равный одному килограмму. Он также изготовлен из сплава иридия и платины.

()

Эталоны длины и массы хранятся в г. Севр, вблизи Парижа, где располагается Международная палата мер и весов. В 1960 году метр начали сравнивать с величинами, относящимися к разделу «Световые явления». Подробности о свете изучаются в старших классах.

Со светом связана и единица времени – 1 секунда. А до 1960 года (год введения СИ) за основу подсчета времени брали время оборота Земли вокруг Солнца – 1 год, который по календарю состоит из 12 месяцев. Месяцы делятся на сутки – время полного оборота Земли вокруг своей оси, сутки — 24 часа, в каждом из которых 60 минут. А одна шестидесятая часть минуты и есть одна секунда.

()

Время «хранят» при помощи очень точных часов – устройств, предназначенных для измерения времени. Действие любых часов основано на повторяющихся процессах – колебаниях. Чем меньше период (время одного полного колебания), тем часы более точные.

При изучении быстро протекающих процессов требуется измерять миллиардные и еще более мелкие доли секунды. Для этого служат атомные часы.

()

Ученик седьмого класса, конечно же, умеет измерять длину и время, массу продуктов определяют продавцы с помощью весов.

По мере изучения физики будет идти знакомство с различными физическими величинами, способами и приборами их измерения. А сейчас надо знать:

чтобы измерить физическую величину, ее надо сравнить с однородной величиной, принятой за единицу;
за основу физических величин берутся эталонные значения, то есть образец сравнения.
для всех величин существуют свои способы, устройства и единицы измерения.

Числа «карлики» и числа «великаны»

Солнечная система. () Лапка мухи под микроскопом. ()

Чтобы достать до Альфа Центавры, звезды, ближайшей к Солнечной системе, надо со скоростью света (300 000 км/с) лететь четыре года. Расстояния до небесных тел огромны.

К звездам. ()

Если определить расстояние от Земли до Солнца, то оно выразится числом 150 000 000 000 м. А бывают числа с еще большим количеством нулей. Масса Земли в килограммах выражается числом с 24 нулями. Такие числа называют «гигантами». Их записывать и использовать очень неудобно.

Существует способ краткой записи больших чисел в виде степени. Например, 1 000 000 = 106. 10 – основание, а 6 – показатель степени.

Используя этот способ, расстояние от нашей планеты до Солнца запишется так:

150 000 000 000 = 15 ∙ 1010 м – это промежуток называется астрономической единицей (1 а.е.) и служит единицей сравнения в Солнечной системе.

До Альфа-Центавры расстояние в 270 000 а.е., или 4 световых года. Световой год – это тоже астрономическая единица измерения расстояния. Астрономия – наука о космосе и космических телах. (1 св. год = 9,46 ∙ 1015 м = 68 000а.е.).

Фото двойной звезды Альфа созвездия Центавра. ()

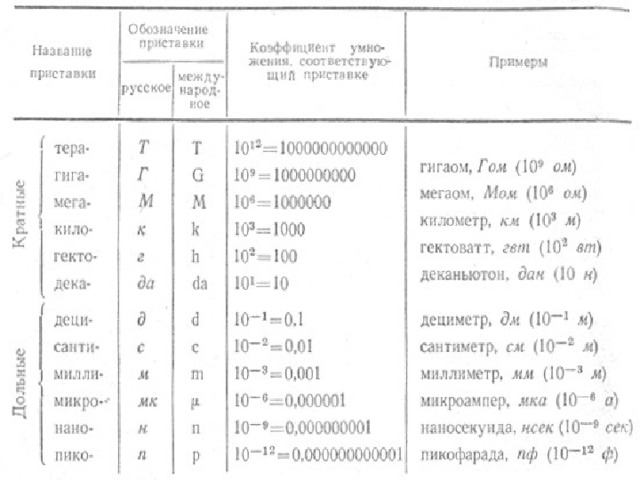
Большие числа записываются при помощи кратных приставок. Например, километр – это тысяча метров, килограмм – тысяча граммов. Приставка «кило» обозначает «тысяча». Есть и другие приставки, которые обозначают умножение величины на число, кратное десяти. Примеры и форма записи даны в таблице кратных приставок.

Используя эти приставки можно записывать очень большие числа.

1 а.е. = 150 000 000 000 м = 150 ∙ 109 м = 150Гм;

1 св. год = 9 460 000 000 000 м = 9,46 ∙ 1012 м = 9,46 Тм;

А теперь о числах – «карликах». Если сделать попытку измерить толщину одного листа книги, то сразу это не получится. Надо действовать по простому плану:

отобрать в книге некоторое число страниц N (N = 100, например);
измерить толщину L этих страниц (пусть L = 11 мм);
найти толщину одной страницы d по формуле d = L/N.

Получится d = 0,11 мм = 0, 00011 м. Это число очень маленькое.

Такой способ измерения малых величин называется методом рядов. Он достаточно прост.

Размеры пшена. () Толщина проволоки. ()

Но существуют и гораздо меньшие величины. Маленькие числа, так называемые «карлики», также записывают при помощи степеней или дольных приставок. (С приставками деци, санти, милли знакомятся еще в начальной школе).

Число меньше единицы, поэтому показатель степени – отрицательное число. Оно показывает количество цифр после запятой. Например, 0, 00011 м = 11 ∙ 10-5 м.

Число 0,00000625 можно записать по-разному, применяя степень:

625 ∙ 10-8, 62,5 ∙ 10-7, 6,25 ∙ 10-6 и т. д.

Очень маленькие числа по-другому можно записывать, используя таблицу дольных приставок.

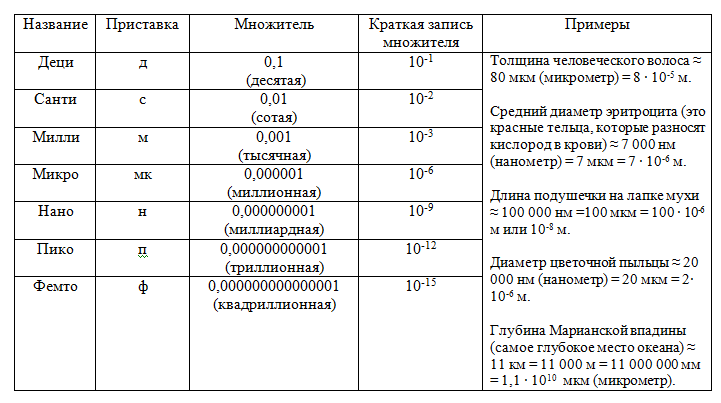
Например, при изготовлении сверхточных приборов (телескопов, микроскопов и др.), детали ошлифовываются до очень гладкой поверхности. Неровности должны быть меньше 2,5 ∙ 10-6 м или 2,5 мкм.

Большие и маленькие числа помогают человеку в различных отраслях деятельности: в науке, промышленности, медицине и т.д.

Производные единицы

Единицы измерения, которые формируются из семи основных, получили название производных. Кроме основных и производных единиц, возникла необходимость введения дополнительных (радиан и стерадиан). Их размерность принято считать нулевой. Отсутствие измерительных приборов для их определения делает невозможным их измерение. Их введение обусловлено применением в теоретических исследованиях. Например, физическая величина «сила» в этой системе измеряется в ньютонах. Поскольку сила – мера взаимного действия тел друг на друга, являющаяся причиной варьирования скорости тела определенной массы, то определить ее можно как произведение единицы массы на единицу скорости, деленную на единицу времени:

F = k٠M٠v/T, где k – коэффициент пропорциональности, M – единица массы, v – единица скорости, T – единица времени.

СИ дает следующую формулу размерностей: Н = кг٠м/с2, где использованы три единицы. И килограмм, и метр, и секунда отнесены к основным. Коэффициент пропорциональности равен 1.

Возможно введение безразмерных величин, которые определяются в виде соотношения однородных величин. К таковым можно отнести коэффициент трения, как известно, равный отношению силы трения к силе нормального давления.

Общие свойства величин

Одна из реализаций единицы длины — метра

X=ax{\displaystyle X=a}, где X — измеряемая величина объекта или явления, a — значение, — единица величины.

Различают три вида значений величин, объединённые общим термином «опорное значение».

Истинное значение — идеальное, единственное значение величины. Термин используется тогда, когда можно пренебречь неопределённостью значения на микроуровне.
Действительное значение — получается экспериментальным путем, достаточно близко к истинному значению.
Принятое значение — значение, приписанное величине.

L — длина;
M — масса;
T — время;
I — сила тока;
Θ — температура;
N — количество вещества;
J — сила света.

Определение размерности давления
Величина	Уравнение связи	Размерность в СИ	Название единицы
Ускорение	a=Vt=lt2{\displaystyle a={\frac {V}{t}}={\frac {l}{t^{2}}}}	L+1T−2{\displaystyle L^{+1}T^{-2}}	Нет
Сила	F=ma{\displaystyle F={m}{a}}	M+1L+1T−2{\displaystyle M^{+1}L^{+1}T^{-2}}	Ньютон
Площадь	S=l2{\displaystyle S=l^{2}}	L+2{\displaystyle L^{+2}}	Квадратный метр
Давление	P=FS{\displaystyle P={\frac {F}{S}}}	M+1L+1T−2L+2=M+1L−1T−2{\displaystyle M^{+1}L^{+1}T^{-2}L^{+2}=M^{+1}L^{-1}T^{-2}}	Паскаль

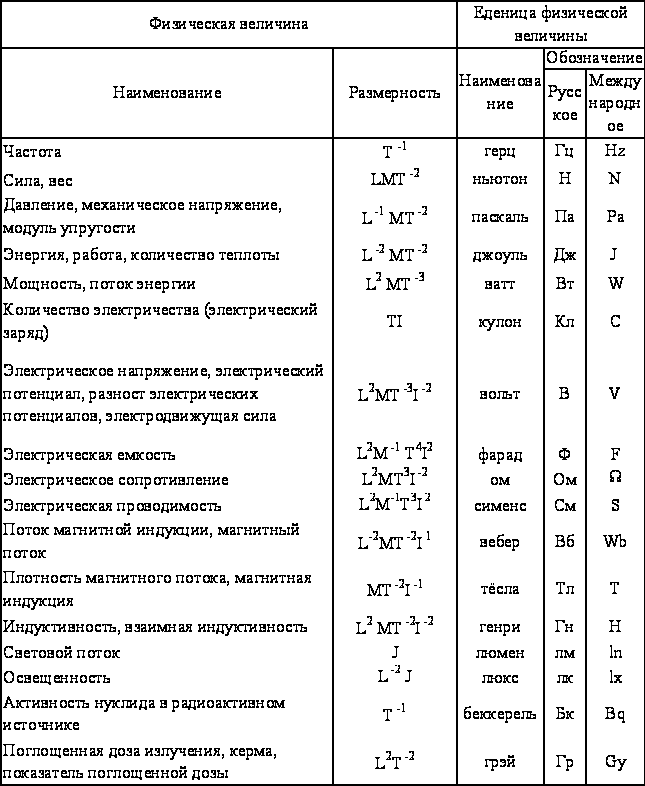
Таблица физических величин, производных от основных

Наименование единицы	Измеряемая величина	Формула размерностей
Джоуль	энергия	кг٠м2٠с-2
Паскаль	давление	кг٠ м-1 ٠с-2
Тесла	магнитная индукция	кг ٠А-1 ٠с-2
Вольт	электрическое напряжение	кг ٠м2 ٠с-3٠А-1
Ом	Электрическое сопротивление	кг ٠м2 ٠с-3٠А-2
кулон	Электрический заряд	А٠ с
Ватт	мощность	кг ٠м2 ٠с-3
Фарад	Электрическая емкость	м-2٠кг-1 ٠c4٠A2
Джоуль на Кельвин	Теплоемкость	кг ٠м2٠с-2 ٠К-1
Беккерель	Активность радиоактивного вещества	С-1
Вебер	Магнитный поток	м2 ٠кг ٠с-2٠А-1
Генри	Индуктивность	м2 ٠кг ٠с-2 ٠А-2
Герц	Частота	с-1
Грей	Поглощенная доза	м2 ٠с-1
Зиверт	Эквивалентная доза излучения	м2 ٠с-2
Люкс	Освещенность	м-2 ٠кд ٠ср-2
Люмен	Световой поток	кд ٠ср
Ньютон	Сила, вес	м ٠кг ٠с-2
Сименс	Электрическая проводимость	м-2 ٠кг-1 ٠с3 ٠А2
Фарад	Электрическая емкость	м-2 ٠кг-1 ٠c4 ٠A2

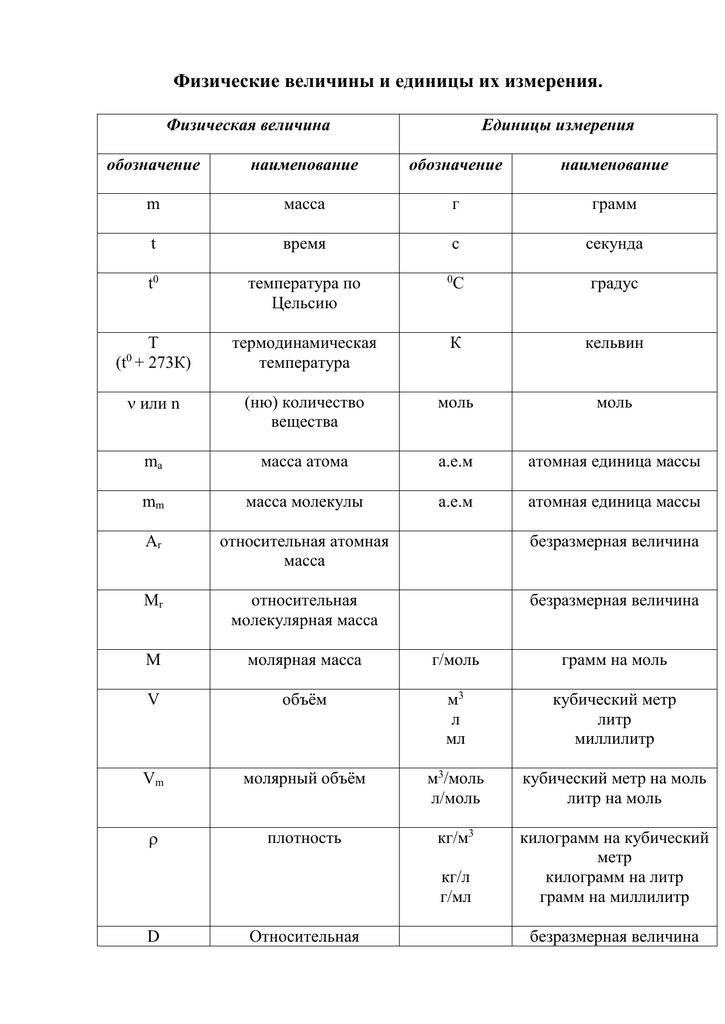
Соответствие физической величины в системе СИ

Основные величины

Величина	Символ	Единица СИ	Описание
Длина	l	метр (м)	Протяжённость объекта в одном измерении.
Вес	m	килограмм (кг)	Величина, определяющая инерционные и гравитационные свойства тел.
Время	t	секунда (с)	Продолжительность события.
Сила электрического тока	I	ампер (А)	Протекающий в единицу времени заряд.
Термодинамическая температура	T	кельвин (К)	Средняя кинетическая энергия частиц объекта.
Сила света	I_v	кандела (кд)	Количество световой энергии, излучаемой в заданном направлении в единицу времени.
Количество вещества	ν	моль (моль)	Количество частиц, отнесенное к количеству атомов в 0,012 кг12C

Производные величины

Величина	Символ	Единица СИ	Описание
Площадь	S	м2	Протяженность объекта в двух измерениях.
Объём	V	м3	Протяжённость объекта в трёх измерениях.
Скорость	v	м/с	Быстрота изменения координат тела.
Ускорение	a	м/с²	Быстрота изменения скорости объекта.
Импульс	p	кг·м/с	Произведение массы и скорости тела.
Сила	F	кг·м/с2 (ньютон, Н)	Действующая на объект внешняя причина ускорения.
Механическая работа	A	кг·м2/с2 (джоуль, Дж)	Скалярное произведение силы и перемещения.
Энергия	E	кг·м2/с2 (джоуль, Дж)	Способность тела или системы совершать работу.
Мощность	P	кг·м2/с3 (ватт, Вт)	Скорость изменения энергии.
Давление	p	кг/(м·с2) (паскаль, Па)	Сила, приходящаяся на единицу площади.
Плотность	ρ	кг/м3	Масса на единицу объёма.
Поверхностная плотность	ρ_A	кг/м2	Масса на единицу площади.
Линейная плотность	ρ_l	кг/м	Масса на единицу длины.
Количество теплоты	Q	кг·м2/с2 (джоуль, Дж)	Энергия, передаваемая от одного тела к другому немеханическим путём
Электрический заряд	q	А·с (кулон, Кл)
Напряжение	U	м2·кг/(с3·А) (вольт, В)	Изменение потенциальной энергии, приходящееся на единицу заряда.
Электрическое сопротивление	R	м2·кг/(с3·А2) (ом, Ом)	сопротивление объекта прохождению электрического тока
Магнитный поток	Φ	кг/(с2·А) (вебер, Вб)	Величина, учитывающая интенсивность магнитного поля и занимаемую им область.
Частота	ν	с−1 (герц, Гц)	Число повторений события за единицу времени.
Угол	α	радиан (рад)	Величина изменения направления.
Угловая скорость	ω	с−1 (радиан в секунду)	Скорость изменения угла.
Угловое ускорение	ε	с−2 (радиан на секунду в квадрате)	Быстрота изменения угловой скорости
Момент инерции	I	кг·м2	Мера инертности объекта при вращении.
Момент импульса	L	кг·м2/c	Мера вращения объекта.
Момент силы	M	кг·м2/с2	Произведение силы на длину перпендикуляра, опущенного из точки на линию действия силы.
Телесный угол	Ω	стерадиан (ср)

Смотри также:

Справочные материалы по физике
Закон Ома
Первый закон Ньютона
Второй закон Ньютона
Третий закон Ньютона
Формулы кинематики
Формулы МКТ

Классификация физических величин

Аддитивные и неаддитивные
- аддитивные величины — величины, значения которых могут быть суммированы, умножены на константу или разделены друг на друга. Например масса, длина, площадь.
- неаддитивные величины — величины, для которых суммирование значений бессмысленно, хотя и возможно математически. К таким величинами относится температура, плотность, удельное сопротивление.

Скалярные, векторные, тензорные величины
- скалярные величины имеют значение, выражаемое только одним числом, для них не определено направление. Ярким примером скалярной величины является потенциальная энергия.
- векторные величины описываются последовательностью из трёх (или двух) независимых значений, которые называются компонентами. Векторные величины имеют скалярный модуль и направление. Векторными величинами является сила, давление, скорость и ускорение.
- тензорные величины объединяют все остальные классы. Они возникают в материальных уравнениях для сред, например в теории упругости для описания деформаций, электромагнитной теории для уравнений материальной среды, в общей теории относительности для описания метрики.

Типология величин

Попытаемся указать несколько основных признаков, которые позволяют установить тип величины.

1. Направление. Если действие физической величины напрямую связано с направлением, ее называют векторной, иные – скалярные.

2. Наличие размерности. Существование формулы физических величин дает возможность называть их размерными. Если в формуле все единицы имеют нулевую степень, то их называют безразмерными. Правильнее было бы назвать их величинами с размерностью, равной 1. Ведь понятие безразмерной величины нелогично. Основное свойство – размерность – никто не отменял!

3. По возможности сложения. Аддитивная величина, значение которой можно складывать, вычитать, умножать на коэффициент и т. д. (например, масса) — физическая величина, являющаяся суммируемой.

4. По соотношению с физической системой. Экстенсивная — если ее значение можно составить из значений подсистемы. Примером может служить площадь, измеряемая в метрах квадратных. Интенсивная — величина, значение которой не зависит от системы. К таковым можно отнести температуру.