Эвольвента окружности

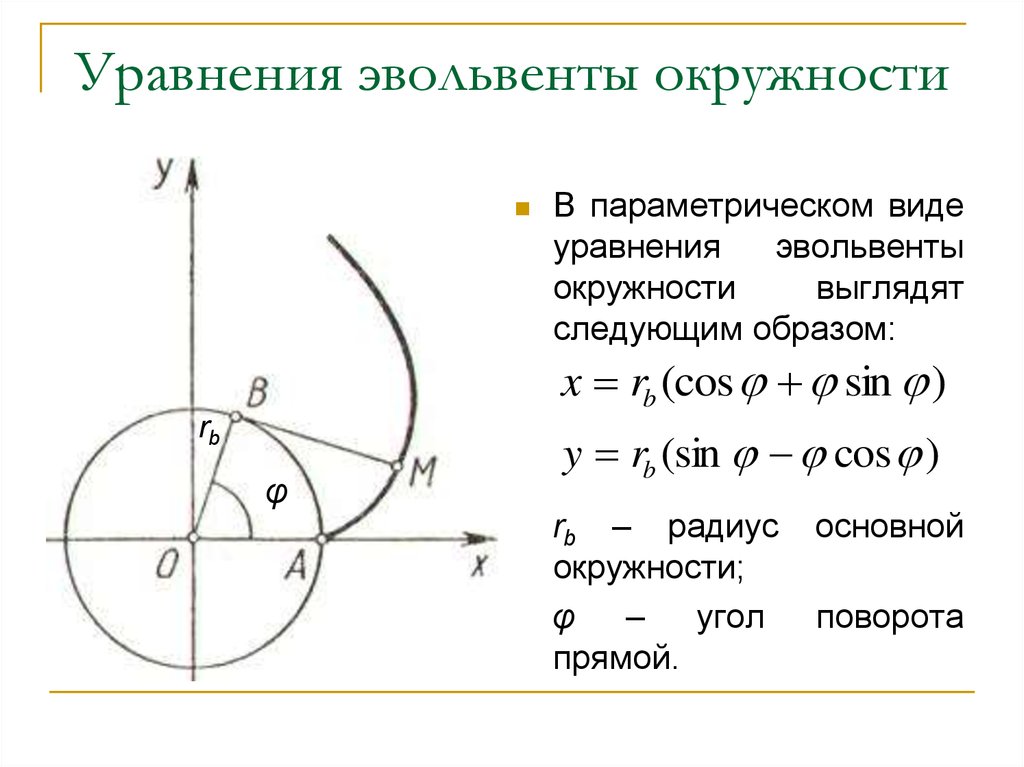
Стандартизация

В соответствии с принципом взаимозаменяемости ряд геометрических параметров эвольвентного зацепления стандартизован.
В России зубчатые колёса выбирают по числу зубьев z{\displaystyle z} и модулю m{\displaystyle m}, принимая следующие параметры за постоянные (по ГОСТ 13755-81):

высота головок зуба ha=ha∗⋅m{\displaystyle h_{a}={h_{a}^{*}}\cdot m};
высота ножки зуба hf=(ha∗+c∗)⋅m{\displaystyle h_{f}=({{h_{a}}^{*}}+c^{*})\cdot m};
подрезания нет, то есть x1=x2={\displaystyle x_{1}=x_{2}=0} или угол зацепления α{\displaystyle \alpha } равен основному углу зацепления αw{\displaystyle {\alpha }_{w}};
угол зацепления α=20{\displaystyle {\alpha }=20} °;
коэффициент высоты головки зуба ha∗=1.0{\displaystyle {h_{a}^{*}}=1.0};
коэффициент радиального зазора c∗=0.25{\displaystyle c^{*}=0.25}.

В США и Великобритании вместо модуля используется питч p=25.4m{\displaystyle p=25.4/m}, Питч — величина обратная модулю.

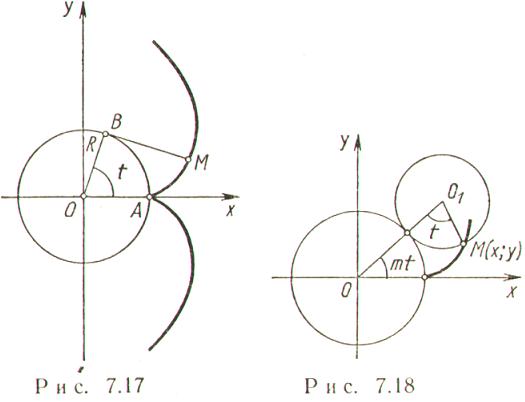
Построение эвольвентного зацепления

Существует несколько способов построения эвольвентного зацепления, используемого для изготовления зубчатых колес, которые можно выполнять вручную или с помощью систем автоматического построения.

При проектировании зацепления зубчатых колес учитывают не только геометрические параметры, но и технологические процесс изготовления, а также желаемые динамические и прочностные показатели готового механизма.

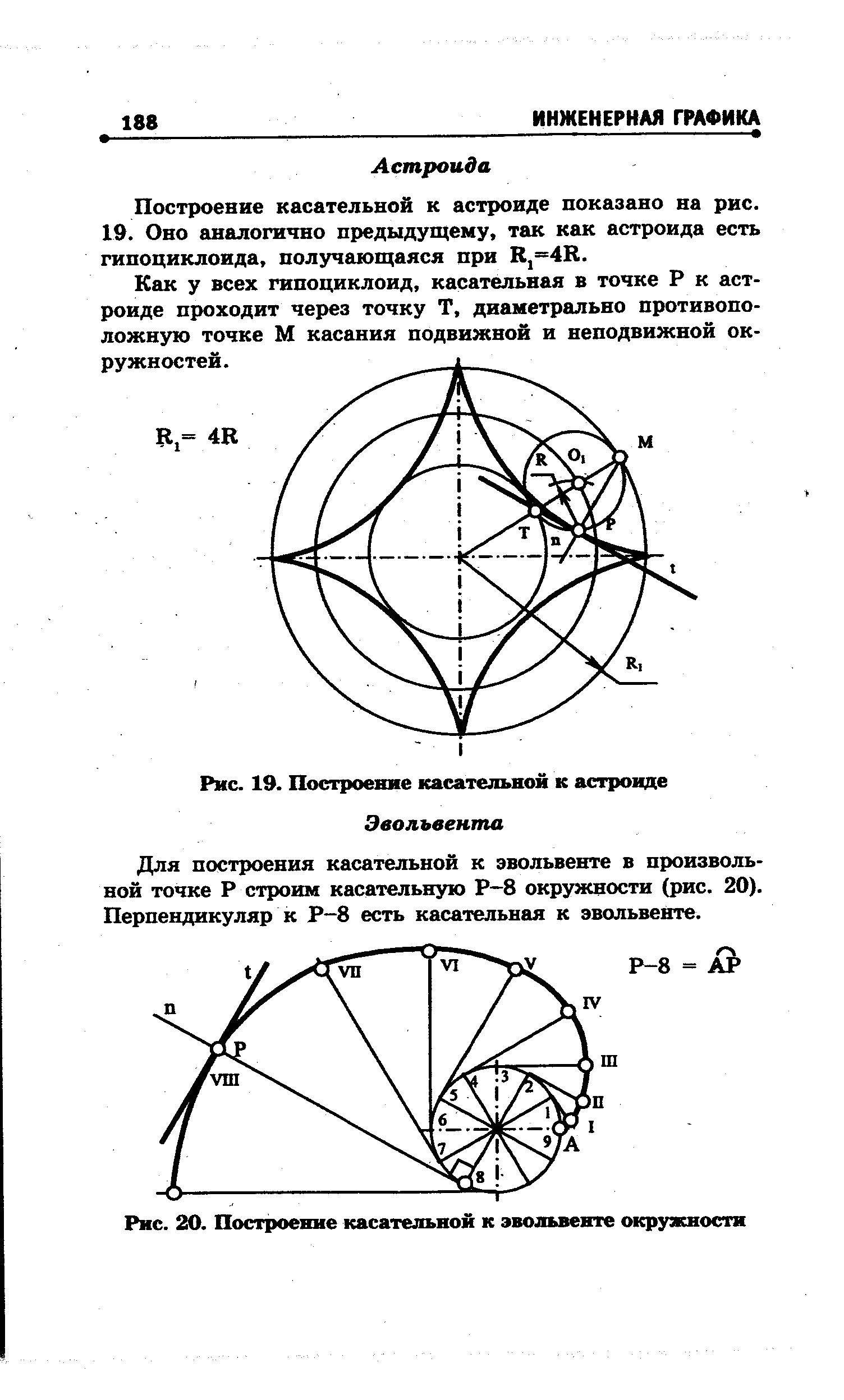
Построение эвольвенты зубчатого колеса состоит из нескольких этапов:

Графическое построение окружности радиусов (определяется исходя из необходимого количества зубьев и прочностных характеристик готового механизма).
Через полюс зацепления проводится прямая в токе касания изначальных окружностей (строится под необходимым углом зацепления).
Окружности колес должны соприкасается по полученной прямой. Обкатывание ее по окружности первого колеса, точка, совпадающая с полюсом, образует первую эвольвенту. Такая же манипуляция с колесом 2, позволяет получить вторую эвольвенту.

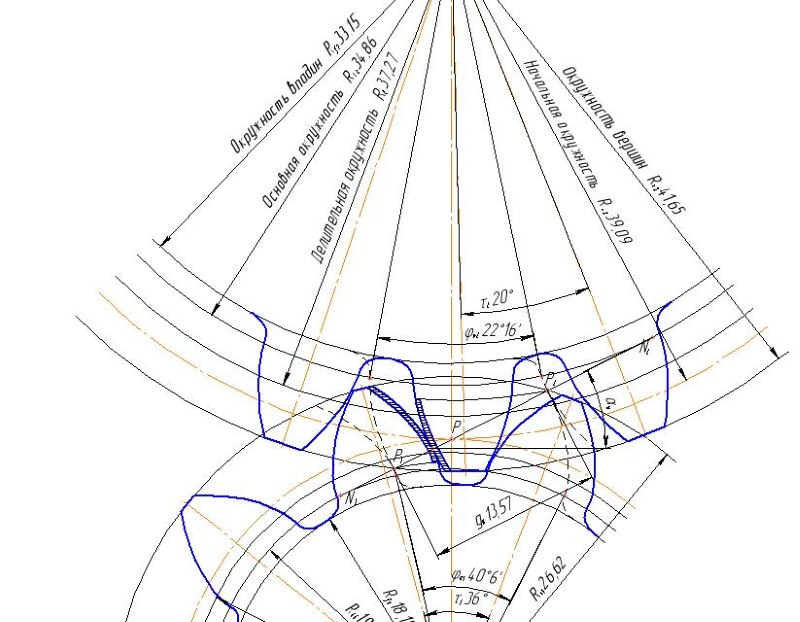
При производстве шестерен зубья несколькими методами: копирования и обкатки. Если необходимо изготовить мелкую деталь, прибегают к методу формообразования, другими словами – горячей накатки. Такой способ менее точен, но форма фрезы при копировании не позволяет выполнить миниатюрные вырезы.

Метод копирования предусматривает вращение фрезы вдоль поверхности, образующее зубья. Она прорезает одну впадину за один проход между соседними зубьями. Затем фреза возвращается в базовое положение с одновременным поворотом заготовки на необходимый угол шага. Такой способ изготовления довольно точный, но производительность его низкая.

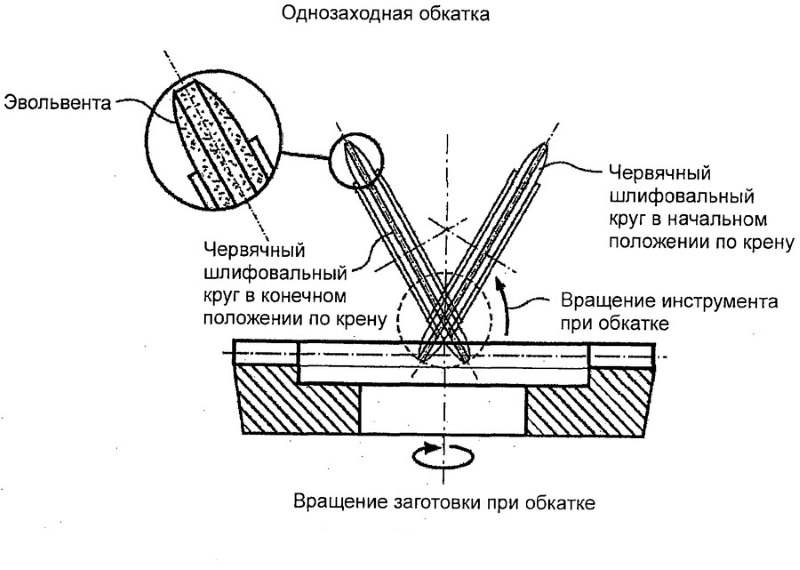
Более совершенным способом является метод обкатки. В его основе лежит огибающее движение, соответствующее желаемому движению зубчатого колеса при зацеплении. Процесс производства похож на движение шестерен в работе. Такое зацепление называется станочным. Рабочий инструмент в таком случае изготавливается в виде круглой, зубчатой фрезы или инструментной рейки.

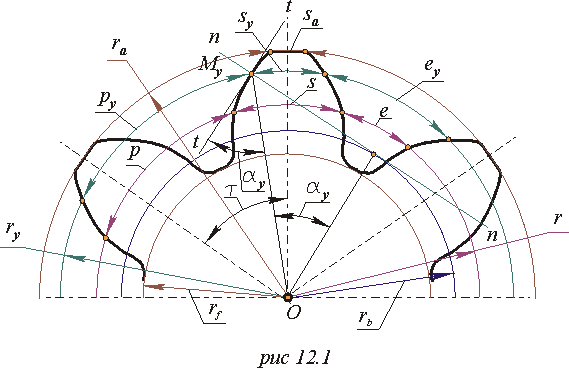
Геометрические параметры эвольвентного зубчатого колеса

Эвольвентным
зубчатым колесом
называют звено зубчатого механизма,
снабженное замкнутой системой зубьев.

При проектировании
зубчатого колеса вначале нужно определить
его число зубьев z,
а затем определить параметры зубьев.
Для этого нужно произвольную окружность
колеса r_y
разделить на z
частей,
каждая из которых называется окружным
шагом p_y,
где m_y=
p_y
= d_y/ z
— модуль
зацепления по окружности произвольного
радиуса.

Модулем
зацепления
называется линейная величина в 
раз меньшая окружного шага или отношение
шага по любой концентрической окружности
зубчатого колеса к .

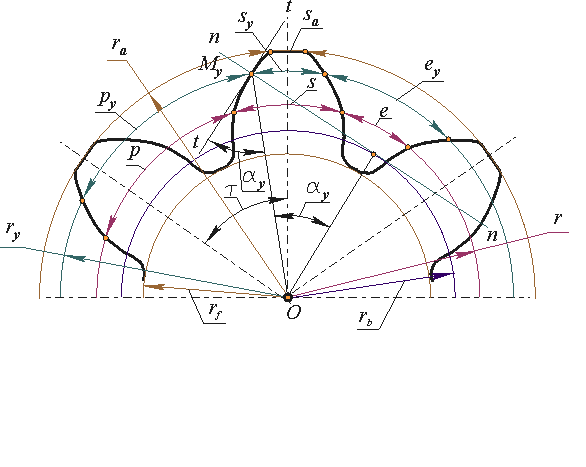
Рис. 7.3

В зависимости от
окружности, по которой определен модуль,
различают делительный, основной,
начальный. Для косозубых колес еще и
нормальный, торцевой и осевой модули.

В ряде стран
используется величина обратная модулю,
которая называется питчем.
Питч (диаметральный) — число зубьев
колеса, приходящееся на дюйм диаметра.
Исходя из
этого, модуль можно определить как число
миллиметров диаметра, приходящееся на
один зуб. На
колесе можно провести бесчисленное
число окружностей, на каждой из которых
будет свой модуль.

ГОСТом введен
стандартный ряд модулей.

Стандартной
модуль
определяется по окружности называемой
делительной.

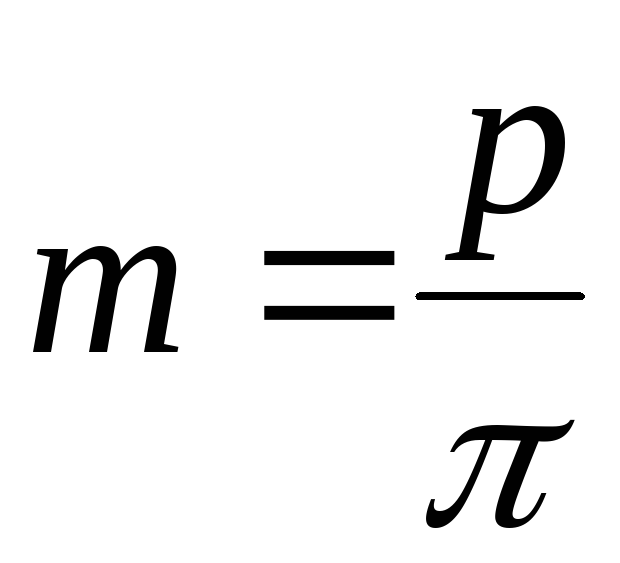
Делительной
называется такая окружность зубчатого
колеса, на которой модуль и шаг принимают
стандартное значение.
Делительная окружность делит зуб на
головку и ножку. Радиус делительной
окружности согласно ГОСТ обозначается
r.

Примечание:
Согласно ГОСТ основные элементы зубчатого
колеса обозначаются по следующим
правилам: линейные величины — строчными
буквами латинского алфавита, угловые
— греческими буками; установлены индексы
для величин:

по окружностям:
делительной — без индекса, вершин — a
, впадин — f
, основная
— b
, начальная — w
, нижних
точек активных профилей колес — p
, граничных
точек — l ;
по сечениям:
нормальное сечение — n
, торцевое сечение — t, осевое
сечение — x
;
относящихся к
зуборезному инструменту —
.

Окружность
вершин (r_a)
— очерчиваетвершины
зубьев.

где
—
коэффициент высоты головки зуба.

Окружность
впадин (r_f)
— очерчивает
ножки зубьев.

где
— коэффициент высоты ножки зуба.

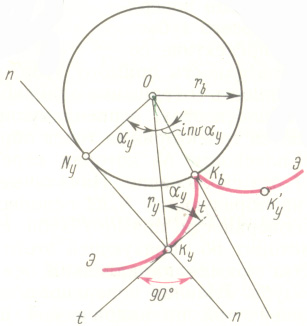
Основная
окружноcть
(r_b)– это
окружность, по которой перекатывается
нормаль
.

Окружным шагомилишагомназывается
расстояние по дуге окружности между
одноименными точками профилей соседних
зубьев (под одноименными понимаются
правые или левые профили зуба).

Угловой шаг 
— центральный
угол, соответствующий дуге p
— окружному
шагу.

Углом профиля
называется
острый угол между касательной к профилю
в данной точке и радиусом — вектором,
проведенным в данную точку из центра
колеса.

Шаг колеса делится
на толщину зуба s_yи ширину
впадины e_y.

Толщина зуба
s_y—
расстояние
по дуге окружности r_yмежду
разноименными точками профилей зуба.

Ширина впадины
e_y—
расстояние по дуге окружности r_yмежду
разноименными точками профилей соседних
зубьев.

В зависимости от
соотношения между толщиной зуба и
шириной впадины на делительной окружности
зубчатые колеса делятся на:

нулевые
s = e
; положительные
s > e;отрицательные
s < e.

§4.5 Эвольвентная зубчатая передача и ее свойства (рис. 11-86).

Эвольвентную зубчатую
передачу составляют, как минимум, из
2-х зубчатых колес, при этом в рассмотрение
вводится две начальные окружности
радиусами r_w1иr_w2.

Меньшее зубчатое
колесо в обычной понижающей зубчатой
передаче называется шестерня.

Вместо производящей
прямой здесь вводится в рассмотрение
линия зацепления
N₁N₂,
которая одновременно касается 2-х
основных окружностейr_b1иr_b2.

Линия
зацепленияявляется геометрическим
местом точек контакта сопряженных
эвольвентных профилей. В точкеВ₁пара эвольвент, которые в данный момент
времени контактируют в точкеК,
входят в зацепление. В точкеВ₂этаже пара эвольвент из зацепления
выходят.

На линии зацепления
N₁N₂все взаимодействующие эвольвенты
при зацеплении касаются друг друга. Вне
участкаN₁N₂эвольвенты пересекаются, и если такое
случится, то произойдет заклинивание
зубчатого колеса.

Угол
N₁O₁P
= N₂J₂P
= _w– угол зацепления.

Для передачи, составленной
из нулевых зубчатых колес _w=20o

Для передачи, составленной
из положительных з. к. _w>20o

Для передачи, составленной
из отрицательных з. к. _w<20o

c=c*.m—радиальный зазор,
величина стандартная, необходим для
нормального обеспечения смазки.

c*—коэффициент радиального
зазора, по ГОСТc*=0.25
(c*=0.35).

Между делительными
окружностями у.m– этовоспринимаемое
смещение.

у–коэффициент воспринимаемого
смещения, он имеет знак, и в
зависимости от знака различают:

1. у=0
у.m=0
–нулеваязубчатая передача;

2. у>0
у.m>0–положительнаязубчатая передача;

3. у<0
у.m<0–отрицательнаязубчатая передача;

Свойства
эвольвентного зацепления.

Эвольвентное
зацепление молочувствительно к
погрешностям изготовления, т.е. при
отклонении межосевого расстояния от
номинала передаточное отношение
зубчатой передачи не изменится.
Линия зацепления
N₁N₂является общей нормалью к сопряженным
эвольвентным профилям.
Контакт эвольвент
осуществляется только на линии
зацепления.

d3 = cos ? * D

От автора. Я нашел в интернете полезную программку в Excel 2007. Это автоматизированная табличка для расчета всех параметров прямозубого зубчатого колеса.

Скачать Скачать с зеркала

Итак, приступим к графическому построению профиля зубчатого колеса.

Изобразите делительный диаметр с диаметром D, и центром шестерни O. Окружность показана красным цветом.
Изобразите диаметр вершин зубьев (d₁) с центром в точке O с радиусом большим на высоту головки зуба(зелёного цвета).
Изобразите диаметр впадин зубьев (d2) с центром в точке O с радиусом меньшим на высоту ножки зуба (голубого цвета цвета).

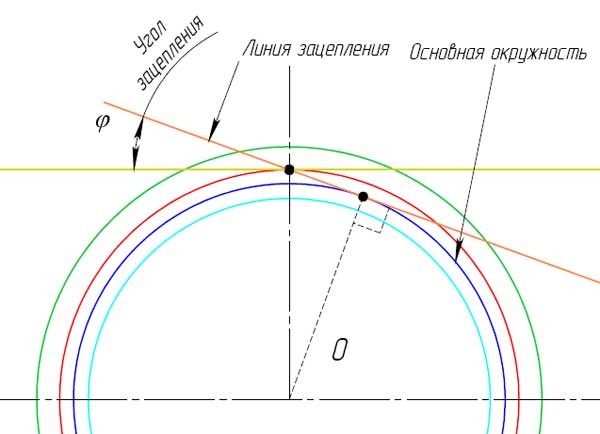
Проведите касательную к делительному диаметру (желтая).
В точке касания под углом ? проведите линию зацепления, оранжевого цвета.
Изобразите окружность касательную к линии зацепления, и центром в точке O. Эта окружность является основной и показана тёмно синего цвета.

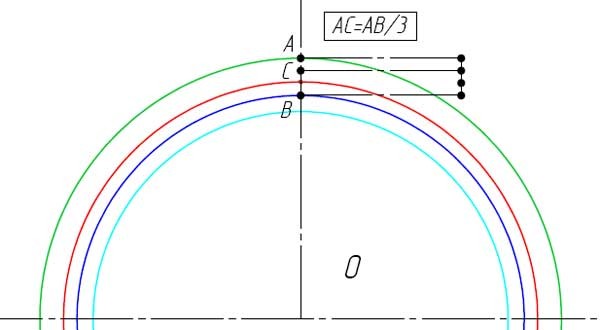
Отметьте точку A на диаметре вершин зубьев.
На прямой соединяющие точки A и O отметьте точку B находящуюся на основной окружности.
Разделите расстояние AB на 3 части и отметьте, точкой C, полученное значение от точки A в сторону точки B на отрезке AB.

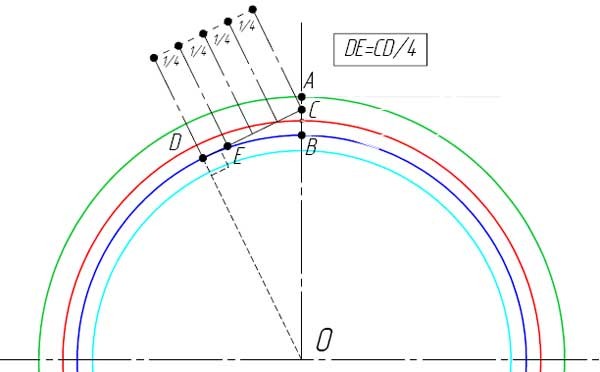
От точки C проведите касательную к основной окружности.
В точке касания отметьте точку D.
Разделите расстояние DC на четыре части и отметьте, точкой E, полученное значение от точки D в сторону точки C на отрезке DC.

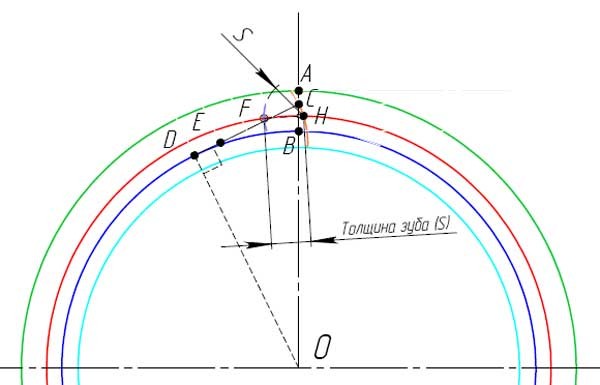
Изобразите дугу окружности с центром в точке E, что проходит через точку C. Это будет часть одной стороны зуба, показана оранжевым.
Изобразите дугу окружности с центром в точке H, радиусом, равным толщине зуба (s). Место пересечения с делительным диаметром отметьте точкой F. Эта точка находится на другой стороне зуба.

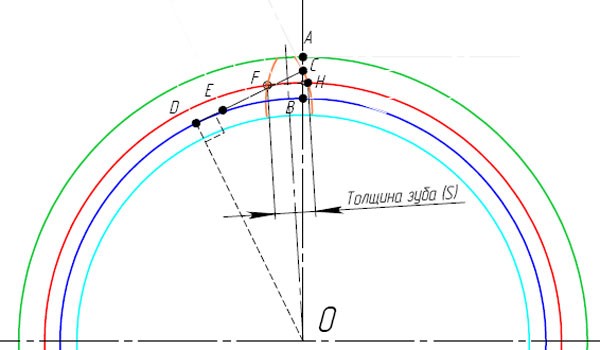
Изобразите ось симметрии проходящую через центр О и середину расстояния FH.
Линия профиля зуба отображенная зеркально относительно этой оси и будет второй стороной зуба.

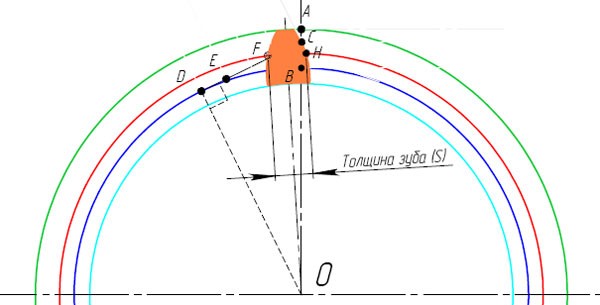
Вот и готов профиль зуба прямозубого зубчатого колеса. В этом примере использовались следующие параметры:

Модуль m=5 мм
Число зубьев z=20
Угол профиля исходного контура ?=20

Расчетные данные:

Делительный диаметр D=100 мм
Диаметр вершин зубьев d₁=110 мм
Диаметр впадин зубьев d₂=87.5 мм
Толщина зубьев по делительной окружности S=7.853975 мм

На этом первая часть урока является завершенной. Во второй части (видео) мы рассмотрим как применить полученный профиль зуба для построения модели зубчатого колеса. Для полного ознакомления с данной темой («зубчатые колеса и зубчатые зацепления», а также «динамические сопряжения в SolidWorks») необходимо вместе с изучением этого урока изучать урок №24.

Еще скажу пару слов о специальной программе, производящей расчет зубчатых колес и генерацию модели зубчатого колеса для SolidWorks. Это программа Camnetics GearTrax.