Эллипс

Как правильно заниматься на эллиптическом тренажёре

Чтобы добиться как можно большей эффективности от занятий на орбитреке, сходной с получаемой от бега, и в то же время не подвергать организм чрезмерным нагрузкам, нужно:

• начинать с небольшой скорости и малых нагрузок, не форсируя их в течение первого месяца кардиотренировки;
• повести небольшую разминку перед занятиями;
• не заниматься на тренажёре свыше 1 часа без перерыва;
• ноги держать полусогнутыми в коленных суставах;
• руки располагать на уровне груди или чуть выше;
• смотреть вперёд при прямо расположенной голове;
• плотно упирать стопу всей площадью в педаль устройства;
• тело располагать прямо, не делая прогибов вперёд или назад;
• держаться за устройство обеими руками.

Вам также будет интересно узнать что более эффективно для похудения: беговая дорожка или велотренажер.

Техника движений для похудения

При выполнении упражнений, предназначенных для сжигания жира, ставится задача сбросить вес. Для её выполнения следует знать, сколько следует заниматься на эллипс-тренажёре и как быстро худеть при этом получится. То есть главный вопрос во время занятий на орбитреке заключается не в том, можно ли похудеть вообще, а в том, как это сделать эффективнее и при этом без вреда для здоровья.

Видео: как похудеть с помощью эллиптического тренажера

Для ответа на этот вопрос, к примеру, была создана программа тренировок для начинающих. С ней можно ознакомиться посредством следующей таблицы:

5 Разогреться в оптимальном темпе, удерживая сопротивление на невысоком уровне. 1

3 Резко увеличить уровень сопротивления до ощущения нагрузки в мышцах, определить его в качестве базового уровня. 4–5

2 Превысить базовый уровень на единицу. 6

3 Вернуться к базовому уровню. 5

2 Снова на единицу превысить базовый уровень. 6

5 Снизить сопротивление и довести уровень до комфортного. 2

class=”table-bordered”>

Кроме того, для эффективного избавления от чрезмерного веса созданы специальные техники движений.

Классическая ходьба

Этот способ схож со скандинавской ходьбой. При выполнении упражнения, поочерёдно вдавливая педали в пол, необходимо одной рукой притягивать к себе рычаг, а второй его отталкивать.

Обратная ходьба

Данный вариант отличается от классической ходьбы тем, что здесь центр воздействия нагрузки концентрируется в районе ягодиц и нижней части спины. Следует учитывать, что этом виде ходьбы коленный сустав сгибается сильнее и более интенсивно нагружается.

Узнайте как правильно заниматься на орбитреке, чтобы похудеть.

Наклонная ходьба

При ходьбе с наклоном вперёд на 45° от первоначального вертикального положения тела усиливается нагрузка на мышцы голени и квадрицепсы. А при отклонении назад максимальное воздействие оказывается на бедренные и ягодичные мышцы. Во время данного упражнения рекомендуется держаться за неподвижный поручень.

Сидячая ходьба

Здесь прямую спину необходимо отклонить назад, держась при этом прямыми руками за неподвижные поручни. Ноги следует поднять так, чтобы бёдра были параллельны полу, а голени — перпендикулярны. Данным способ особо ценен для женщин, желающих улучшить ягодичную область своего тела.

Проработка мышц на тренажёре

Эллиптический тренажёр может тренировать практически все группы мышц человеческого тела, но не одновременно. Например, если возникнет вопрос насчёт того, как накачать ягодицы, то нужно знать алгоритм нужных для этого действий.

Важно! Чтобы оптимально управлять темпом движения педалей и уровнем напряжения в мышцах, необходимо избегать движений рывками. Нагрузка на различные мышцы зависит от наклона тела и способа движения конечностей:

Нагрузка на различные мышцы зависит от наклона тела и способа движения конечностей:

1. Чтобы нагрузить грудные мышцы и бицепсы, нужно стать вертикально и плавно двигать руками.
2. Подав туловище несколько вперёд, можно хорошо натренировать мышцы голеней и квадрицепсы.
3. При более активном притягивании рычагов тренируются спинальные мышцы.
4. Вдавливание педалей способствует проработке бедренных и ягодичных мышц.
5. Обратная ходьба при согнутых ногах загружает бедренные мышцы, подколенные сухожилия и большие ягодичные мышцы. Наилучший эффект при этом достигается при практически сидячей позе.
6. Во время активного толкания рычагов вперёд развиваются спинальные и дельтовидные мышцы.

Что дает эллиптический тренажер

 Похудение

Для эффективного похудения нужны интервальные тренировки.  После прогрева, в течение 30 секунд, начинать качать руки и ноги так быстро, как только можно. Затем снизить скорость до умеренной в течение 1 минуты, чтобы восстановиться.

Повторить процесс в течение 20-40 минут для достижения наилучшего результата. Этот вид эллиптической тренировки сжигает больше калорий, чем типичная медленная и устойчивая тренировка, Считают, что короткое 30-минутное пребывание на эллиптической машине может сжечь до 345 калорий.

Рекомендуем почитать статью про интервальные тренировки и о протоколе «Табата».

Укрепление сердечно-сосудистой системы

По данным Американской ассоциации сердца, физическая активность важна для предотвращения сердечно-сосудистых заболеваний и инсульта, главных убийц нации. Организация рекомендует, по крайней мере, 150 минут в неделю умеренных или 75 минут в неделю энергичных упражнений для поддержания здоровья сердца и сосудов. Посмотрите какие кардиотренажеры существуют.

Рост мышечной массы

В отличие от беговой дорожки, большинство эллипсоидов оснащены ручками. С помощью полюсов для  рук и обратного хода снаряда тренируется как верхняя часть тела (бицепсы, плечи, грудь и трицепсы),  так и нижняя ее часть (подколенные сухожилия, икры, квадроциклы и ягодицы) одновременно.

Длина дуги эллипса

Длина дуги плоской линии определяется по формуле:

l=∫t1t2(dxdt)2+(dydt)2dt.{\displaystyle l=\int \limits _{t_{1}}^{t_{2}}{\sqrt {\left({\frac {dx}{dt}}\right)^{2}+\left({\frac {dy}{dt}}\right)^{2}}}\,dt.}

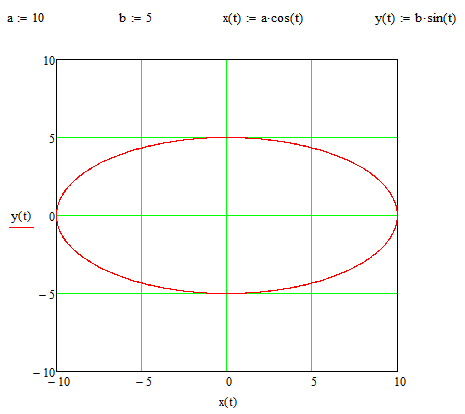
Воспользовавшись параметрическим представлением эллипса получаем следующее выражение:

l=∫t1t2a2sin2⁡t+b2cos2⁡tdt.{\displaystyle l=\int \limits _{t_{1}}^{t_{2}}{\sqrt {a^{2}\sin ^{2}t+b^{2}\cos ^{2}t}}\,dt.}

После замены b2=a2(1−e2){\displaystyle b^{2}=a^{2}\left(1-e^{2}\right)} выражение для длины дуги принимает окончательный вид:

l=a∫t1t21−e2cos2⁡tdt,e<1.{\displaystyle l=a\int \limits _{t_{1}}^{t_{2}}{\sqrt {1-e^{2}\cos ^{2}t}}\,dt,\;\;\;e<1.}

Получившийся интеграл принадлежит семейству эллиптических интегралов, которые в элементарных функциях не выражаются, и сводится к E(t,e){\displaystyle E\left(t,e\right)}. В частности, периметр эллипса равен:

l=4a∫π21−e2cos2⁡tdt=4aE(e){\displaystyle l=4a\int \limits _{0}^{\pi /2}{\sqrt {1-e^{2}\cos ^{2}t}}\,dt=4aE(e)},

где E(e){\displaystyle E\left(e\right)} — .

Приближённые формулы для периметра

L≈4πab+(a−b)2a+b.{\displaystyle L\approx 4{\frac {\pi ab+(a-b)^{2}}{a+b}}.}

Максимальная погрешность этой формулы ~0,63 % при эксцентриситете эллипса ~0,988 (соотношение осей ~1/6,5). Погрешность всегда положительная.

Приблизительно в два раза меньшие погрешности в широком диапазоне эксцентриситетов дает формула:

L≈4⋅(ax+bx)(1x){\displaystyle L\approx 4\cdot \left(a^{x}+b^{x}\right)^{\left(1/x\right)}}, где x=ln⁡2ln⁡π2.{\displaystyle x={\frac {\ln 2}{\ln {\frac {\pi }{2}}}}.}

Максимальная погрешность этой формулы ~0,36 % при эксцентриситете эллипса ~0,980 (соотношение осей ~1/5). Погрешность также всегда положительная.

Существенно лучшую точность при ,05<ab<20{\displaystyle 0,05<a/b<20} обеспечивает формула Рамануджана:

L≈π3(a+b)−(3a+b)(a+3b).{\displaystyle L\approx \pi \left.}

При эксцентриситете эллипса ~0,980 (соотношение осей ~1/5) погрешность составляет ~0,02 %. Погрешность всегда отрицательная.

Ещё точней оказалась вторая формула Рамануджана:

L≈π(a+b)1+3(a−ba+b)210+4−3(a−ba+b)2{\displaystyle L\approx \pi (a+b)\left}

Точные формулы для периметра

Джеймс Айвори и Фридрих Бессель независимо друг от друга получили формулу для периметра эллипса:

L=π(a+b)1+∑n=1∞(2n−1)!!(2n−1)⋅2n⋅n!(a−ba+b)n2{\displaystyle L=\pi (a+b)\left^{2}\right]}

Альтернативная формула

L=2πaN(1−e2)M(1−e2),{\displaystyle L={\frac {2\pi aN(1-e^{2})}{M({\sqrt {1-e^{2}}})}},}

где M(x){\displaystyle M(x)} — Арифметико-геометрическое среднее 1 и x{\displaystyle x},
а N(x){\displaystyle N(x)} — 1 и x{\displaystyle x}, которое было введено С. Ф. Адлаем в статье 2012 года.

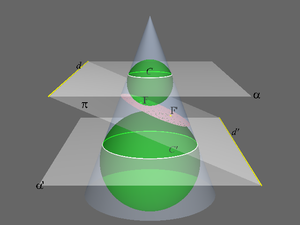
Другие свойства

• Оптические
  • Свет от источника, находящегося в одном из фокусов, отражается эллипсом так, что отраженные лучи пересекутся во втором фокусе.
  • Свет от источника, находящегося вне любого из фокусов, отражается эллипсом так, что отраженные лучи ни в каком фокусе не пересекутся.
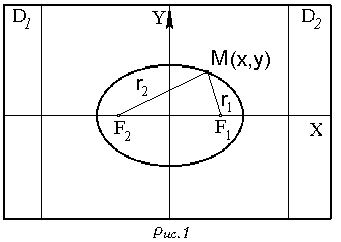
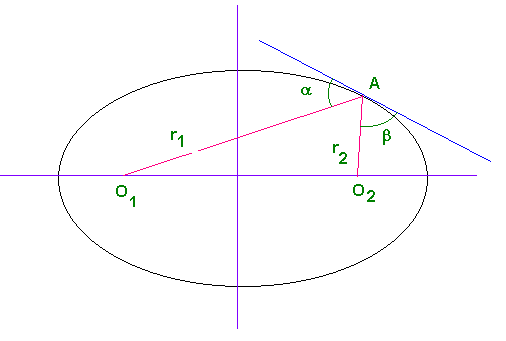
• Если F1{\displaystyle F_{1}} и F2{\displaystyle F_{2}} — фокусы эллипса, то для любой точки X, принадлежащей эллипсу, угол между касательной в этой точке и прямой (F1X){\displaystyle (F_{1}X)} равен углу между этой касательной и прямой (F2X){\displaystyle (F_{2}X)}.
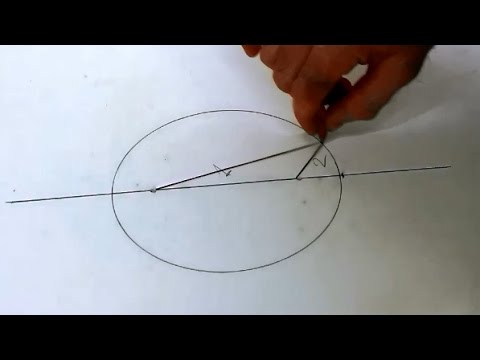
• Прямая, проведённая через середины отрезков, отсечённых двумя параллельными прямыми, пересекающими эллипс, всегда будет проходить через центр эллипса. Это позволяет построением с помощью циркуля и линейки легко получить центр эллипса, а в дальнейшем оси, вершины и фокусы.
• Эволютой эллипса является астроида, вытянутая вдоль вертикальной оси.
• Точки пересечения эллипса с осями являются его вершинами.
• Эксцентриситет эллипса, то есть отношение e=ca=1−b2a2(⩽e<1),{\displaystyle e={\frac {c}{a}}={\sqrt {1-{\frac {b^{2}}{a^{2}}}}}\;\;\;(0\leqslant e<1),}

  Если эксцентриситет эллипса равен нулю (что то же самое, что фокальное расстояние равно нулю: F1F2=0{\displaystyle F_{1}F_{2}=0}), то эллипс вырождается в окружность.

  характеризует вытянутость эллипса. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.

• Экстремальные свойства

  Если F{\displaystyle F} — выпуклая фигура и Tn{\displaystyle T_{n}} — вписанный в F{\displaystyle F} n{\displaystyle n}-угольник максимальной площади, то
  S(Tn)≥S(F)⋅nsin⁡(2⋅π/n)2⋅π,{\displaystyle S(T_{n})\geq S(F)\cdot {\frac {n}{\sin(2\cdot \pi /n)}}{2\cdot \pi },}

где S(F){\displaystyle S(F)} обозначает площадь фигуры F{\displaystyle F}

Более того в равенство достигается в том и только в том случае, если F{\displaystyle F} ограничено эллипсом.

.

Среди всех выпуклых замкнутых кривых, ограничивающих данную площадь, эллипс имеет максимальную аффинную длину.

Если произвольный эллипс вписан в треугольник ABC и имеет фокусы P и Q, тогда для него справедливо соотношение

PA¯⋅QA¯CA¯⋅AB¯+PB¯⋅QB¯AB¯⋅BC¯+PC¯⋅QC¯BC¯⋅CA¯=1.{\displaystyle {\frac {{\overline {PA}}\cdot {\overline {QA}}}{{\overline {CA}}\cdot {\overline {AB}}}}+{\frac {{\overline {PB}}\cdot {\overline {QB}}}{{\overline {AB}}\cdot {\overline {BC}}}}+{\frac {{\overline {PC}}\cdot {\overline {QC}}}{{\overline {BC}}\cdot {\overline {CA}}}}=1.}

Если лестницу (бесконечно тонкий отрезок прямой) прислонить к вертикальной стенке с горизонтальным полом, и один конец лестницы будет скользить по стенке (всё время касаясь её) а второй конец лестницы будет скользить по полу (всё время касаясь его), тогда любая фиксированная точка лестницы (не на её концах), будет двигаться по дуге некоторого эллипса. Это свойство остаётся верным, если мы возьмём точку не внутри лестницы-отрезка, а на её мыслимом продолжении. Последнее свойство используется в описанном выше.mw-parser-output .ts-Переход img{margin-left:.285714em} эллипсографе.

Касательная, проходящая через точку (x0,y0){\displaystyle (x_{0},y_{0})}, принадлежащую эллипсу, имеет следующее уравнение:

xxa2+yyb2=1.{\displaystyle {\frac {xx_{0}}{a^{2}}}+{\frac {yy_{0}}{b^{2}}}=1.}

Связанные определения

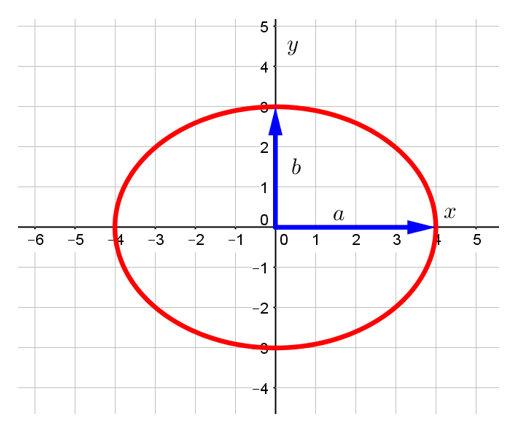
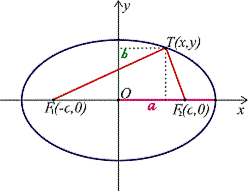
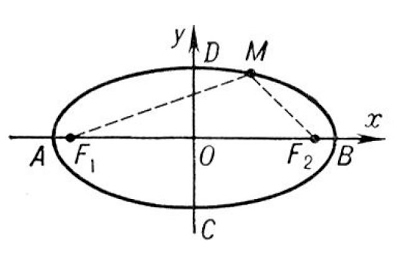
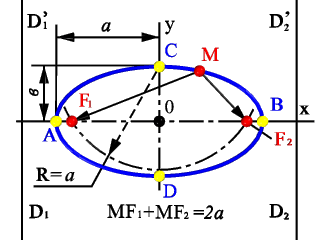
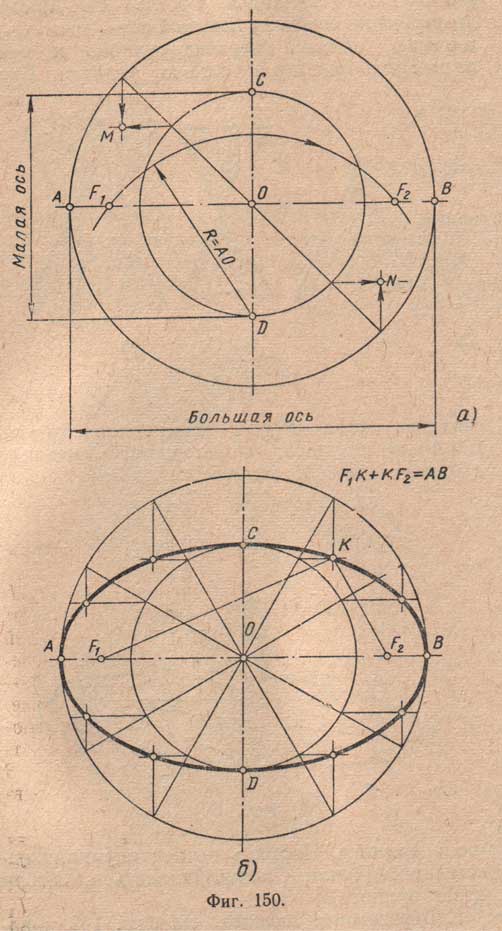
• Проходящий через фокусы эллипса отрезок AB, концы которого лежат на эллипсе, называется большой осью данного эллипса. Длина большой оси равна 2a в вышеприведённом уравнении.
• Отрезок CD, перпендикулярный большой оси эллипса, проходящий через центральную точку большой оси, концы которого лежат на эллипсе, называется малой осью эллипса.
• Точка пересечения большой и малой осей эллипса называется его центром.
• Отрезки, проведённые из центра эллипса к вершинам на большой и малой осях называются, соответственно, большой полуосью и малой полуосью эллипса, и обозначаются a и b.
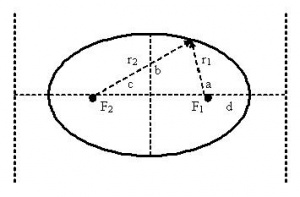
• Расстояния r1{\displaystyle r_{1}} и r2{\displaystyle r_{2}} от каждого из фокусов до данной точки на эллипсе называются фокальными радиусами в этой точке.
• Расстояние c=|F1F2|2{\displaystyle c={\frac {|F_{1}F_{2}|}{2}}} называется фокальным расстоянием.
• Величина e=ca=1−b2a2{\displaystyle e={\frac {c}{a}}={\sqrt {1-{\frac {b^{2}}{a^{2}}}}}} называется эксцентриситетом.
• Диаметром эллипса называют произвольную хорду, проходящую через его центр. Сопряжёнными диаметрами эллипса называют пару его диаметров, обладающих следующим свойством: середины хорд, параллельных первому диаметру, лежат на втором диаметре. В этом случае и середины хорд, параллельных второму диаметру, лежат на первом диаметре.
• Радиус эллипса в данной точке это отрезок, соединяющий центр эллипса с точкой, а также его длина, которая вычисляется по формуле r=abb2cos2⁡φ+a2sin2⁡φ=b1−e2cos2⁡φ{\displaystyle r={\frac {ab}{\sqrt {b^{2}\cos ^{2}\varphi +a^{2}\sin ^{2}\varphi }}}={\frac {b}{\sqrt {1-e^{2}\cos ^{2}\varphi }}}}, где φ{\displaystyle \varphi } — угол между радиусом и большой полуосью.
• Фокальным параметром p=b2a{\displaystyle p={\frac {b^{2}}{a}}} называется половина длины хорды, проходящей через фокус и перпендикулярной большой оси эллипса.
• Отношение длин малой и большой полуосей называется коэффициентом сжатия эллипса или эллиптичностью: k=ba.{\displaystyle k={\frac {b}{a}}.} Величина, равная (1−k)=a−ba,{\displaystyle (1-k)={\frac {a-b}{a}},} называется сжатием эллипса. Для окружности коэффициент сжатия равен единице, сжатие — нулю. Коэффициент сжатия и эксцентриситет эллипса связаны соотношением k2=1−e2.{\displaystyle k^{2}=1-e^{2}.}
• Для каждого из фокусов существует прямая, называемая директрисой, такая, что отношение расстояния от произвольной точки эллипса до его фокуса к расстоянию от этой точки до данной прямой равно эксцентриситету эллипса. Весь эллипс лежит по ту же сторону от такой прямой, что и фокус. Уравнения директрис эллипса в каноническом виде записываются как x=±pe(1+e){\displaystyle x=\pm {\frac {p}{e\left(1+e\right)}}} для фокусов (∓p1+e,){\displaystyle \left(\mp {\frac {p}{1+e}},\,0\right)} соответственно. Расстояние между фокусом и директрисой равно pe.{\displaystyle {\frac {p}{e}}.}

Программы для разных уровней подготовки

В зависимости от того, как давно вы занимаетесь фитнесом, тренировки могут отличаться по уровню сложности. Тренировка на эллиптическом тренажере усложняется через увеличение сопротивления тренажера и скорости выполнения задания. Возможно усложнение тренировки за счет увеличения длительности выполнения программы. Любое упражнение, которое вы выполняете на эллипсоиде, может быть упрощено или усложнено в зависимости от подготовки или от состояния здоровья в отдельно взятый момент времени. Начиная занятие, ориентируетесь на собственные ощущения. Никто лучше вас не чувствует ваше тело и уровень подготовки. Выбирайте тот уровень, который кажется вам правильным, но используйте возможность посоветоваться со специалистом. Чаще всего программы разделяют на три уровня сложности: новичок, средний уровень и опытный.

Новичок

Занятия на начальном уровне осуществляются 3-4 раза в неделю с продолжительностью выполнения упражнений по 25-35 минут. Перед выполнением упражнения необходимо разогреть мышцы, размявшись. Разминка должна длиться 5-10 минут. Выполняйте разминку самостоятельно или на тренажере. Разминку можно включить и в упражнения, просто начав выполнять ее в спокойном темпе. Общее время тренировки составит 30-40 минут.

При начальном уровне выполнять упражнения следует медленно, постепенно увеличивая скорость от тренировки к тренировке. Как только почувствуете себя достаточно уверенно, можете увеличить скорость выполнения и сопротивление эллипсоида. При таком ритме выполнения упражнений начинает равномерно снижаться вес, повышается уровень выносливости. Как только вы сможете непрерывно тренироваться заданные 25-35 минут, увеличьте время выполнения упражнений. Придерживайтесь этой программы первые месяцы, но, если почувствуете себя достаточно уверенно, переходите к следующему уровню сложности. Постепенно вы сможете перейти к продвинутому уровню для опытных любителей фитнеса.

Продолжающий

Этот уровень подходит для тех, кто уже занимается на эллиптическом тренажере некоторое время и готов повысить интенсивность выполнения упражнений. Показателем интенсивности выполнения упражнений является частота пульса. Максимальный возрастной пульс высчитывается путем вычитания возраста спортсмена из двухсот двадцати. Если у вас хорошая физическая подготовка, то частота пульса при выполнении упражнений может составлять до 80 процентов от максимального возрастного пульса. Помните, что перенапрягаться, чтобы достигнуть этого значения, не стоит. Лучше заниматься в комфортном темпе, ведь результаты достигаются в том числе за счет длительности выполнения упражнений, а не только за счет интенсивности выполнения.

Для спортсменов этого уровня рекомендуются тренировки от 3 до 5 раз в неделю. Продолжительность должна составлять от 35 до 45 минут в зависимости от состояния и целей. Помните, что на любом уровне подготовки необходима разминка, чтобы мышцы были разогреты и готовы к более интенсивному воркауту. В данном случае можно повысить частоту шагов. Рекомендуется использование основных вариантов работы на эллипсе. Выбирайте один из четырех основных способов выполнения упражнения в зависимости от того, какие именно группы мышц хотите нагрузить.

Опытный

Опытным спортсменам подойдет программа, которая отличается частотой тренировок, длительностью выполнения упражнений и повышенной интенсивностью. Программа рассчитана на тех, кто занимается на кросс-тренажере уже длительное время и готов к серьезным физическим нагрузкам. Время занятий составляет 45-60 минут, частота занятий – от 4 до 6 раз в неделю. Этого достаточно для поддержания физической формы. При занятиях на этом уровне, частота пульса может достигать до 90 процентов от максимально допустимого количества частоты сердечных сокращений.

Сопротивление на этом уровне занятий выставите на максимальное значение. Рекомендуется упражняться либо в едином темпе полное занятие, либо интервально – несколько минут в спокойном темпе, 30-40 секунд в интенсивном. Этот уровень работает почти со всеми другими видами упражнений – чередуйте тренировки на эллипсоиде с фитнесом или силовыми тренировками.

Тренировки на эллиптическом тренажере подойдут как для новичков, так и для опытных спортсменов. Главное – соблюдать правила безопасности, не рисковать собственным здоровьем и ориентироваться, в первую очередь, на собственные физические ощущения.

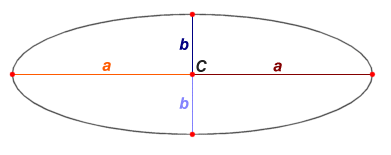
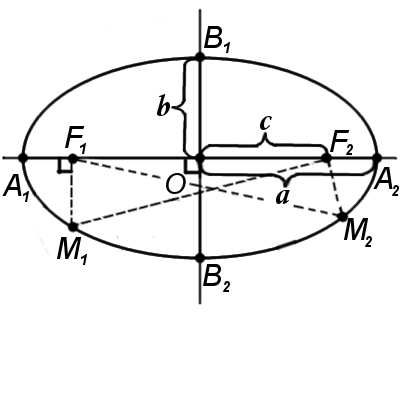
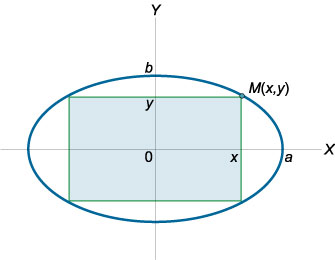
Соотношения между элементами эллипса

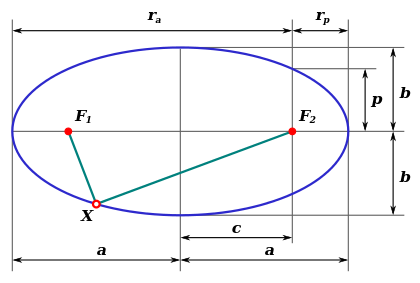
Части эллипса (описание см. в разделе «Связанные определения»)

• a{\displaystyle {\boldsymbol {a}}} — большая полуось;
• b{\displaystyle {\boldsymbol {b}}} — малая полуось;
• c{\displaystyle {\boldsymbol {c}}} — фокальное расстояние (полурасстояние между фокусами);
• p{\displaystyle {\boldsymbol {p}}} — фокальный параметр;
• rp{\displaystyle {\boldsymbol {r}}_{p}} — перифокусное расстояние (минимальное расстояние от фокуса до точки на эллипсе);
• ra{\displaystyle {\boldsymbol {r}}_{a}} — апофокусное расстояние (максимальное расстояние от фокуса до точки на эллипсе);

a2=b2+c2{\displaystyle a^{2}=b^{2}+c^{2}}

e=ca=1−b2a2(⩽e<1).{\displaystyle e={\frac {c}{a}}={\sqrt {1-{\frac {b^{2}}{a^{2}}}}}\;\;\;(0\leqslant e<1).}.

p=b2a{\displaystyle p={\frac {b^{2}}{a}}}

	a{\displaystyle {\boldsymbol {a}}}	b{\displaystyle {\boldsymbol {b}}}	c{\displaystyle {\boldsymbol {c}}}	p{\displaystyle {\boldsymbol {p}}}	rp{\displaystyle {\boldsymbol {r_{p}}}}	ra{\displaystyle {\boldsymbol {r_{a}}}}
a{\displaystyle {\boldsymbol {a}}} — большая полуось	a{\displaystyle {\boldsymbol {a}}}	a=b1−e2{\displaystyle a={\frac {b}{\sqrt {1-e^{2}}}}}	a=ce{\displaystyle a={\frac {c}{e}}}	a=p1−e2{\displaystyle a={\frac {p}{1-e^{2}}}}	a=rp1−e{\displaystyle a={\frac {r_{p}}{1-e}}}	a=ra1+e{\displaystyle a={\frac {r_{a}}{1+e}}}
b{\displaystyle {\boldsymbol {b}}} — малая полуось	b=a1−e2{\displaystyle b=a{\sqrt {1-e^{2}}}}	b{\displaystyle {\boldsymbol {b}}}	b=c 1−e2e{\displaystyle b={\frac {c~{\sqrt {1-e^{2}}}}{e}}}	b=p1−e2{\displaystyle b={\frac {p}{\sqrt {1-e^{2}}}}}	b=rp1+e1−e{\displaystyle b=r_{p}{\sqrt {\frac {1+e}{1-e}}}}	b=ra1−e1+e{\displaystyle b=r_{a}{\sqrt {\frac {1-e}{1+e}}}}
c{\displaystyle {\boldsymbol {c}}} — фокальное расстояние	c=ae{\displaystyle c=ae}	c=be1−e2{\displaystyle c={\frac {be}{\sqrt {1-e^{2}}}}}	c{\displaystyle {\boldsymbol {c}}}	c=pe1−e2{\displaystyle c={\frac {pe}{1-e^{2}}}}	c=rpe1−e{\displaystyle c={\frac {r_{p}e}{1-e}}}	c=rae1+e{\displaystyle c={\frac {r_{a}e}{1+e}}}
p{\displaystyle {\boldsymbol {p}}} — фокальный параметр	p=a(1−e2){\displaystyle p=a(1-e^{2})}	p=b 1−e2{\displaystyle p=b~{\sqrt {1-e^{2}}}}	p=c 1−e2e{\displaystyle p=c~{\frac {1-e^{2}}{e}}}	p{\displaystyle {\boldsymbol {p}}}	p=rp(1+e){\displaystyle p=r_{p}(1+e)}	p=ra(1−e){\displaystyle p=r_{a}(1-e)}
rp{\displaystyle {\boldsymbol {r}}_{p}} — перифокусное расстояние	rp=a(1−e){\displaystyle r_{p}=a(1-e)}	rp=b 1−e1+e{\displaystyle r_{p}=b~{\sqrt {\frac {1-e}{1+e}}}}	rp=c 1−ee{\displaystyle r_{p}=c~{\frac {1-e}{e}}}	rp=p1+e{\displaystyle r_{p}={\frac {p}{1+e}}}	rp{\displaystyle {\boldsymbol {r}}_{p}}	rp=ra1−e1+e{\displaystyle r_{p}=r_{a}{\frac {1-e}{1+e}}}
ra{\displaystyle {\boldsymbol {r}}_{a}} — апофокусное расстояние	ra=a(1+e){\displaystyle r_{a}=a(1+e)}	ra=b 1+e1−e{\displaystyle r_{a}=b~{\sqrt {\frac {1+e}{1-e}}}}	ra=c 1+ee{\displaystyle r_{a}=c~{\frac {1+e}{e}}}	ra=p1−e{\displaystyle r_{a}={\frac {p}{1-e}}}	ra=rp 1+e1−e{\displaystyle r_{a}=r_{p}~{\frac {1+e}{1-e}}}	ra{\displaystyle {\boldsymbol {r}}_{a}}

Другие свойства эллипса

• Оптические
  • Свет от источника, находящегося в одном из фокусов, отражается эллипсом так, что отраженные лучи пересекутся во втором фокусе.
  • Свет от источника, находящегося вне любого из фокусов, отражается эллипсом так, что отраженные лучи ни в каком фокусе не пересекутся.
• Если и  — фокусы эллипса, то для любой точки X, принадлежащей эллипсу, угол между касательной в этой точке и прямой равен углу между этой касательной и прямой .
• Точки пересечения эллипса с осями являются его .
• эллипса, то есть отношение характеризует вытянутость эллипса. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.
• Экстремальные свойства

  Если  — выпуклая фигура и  — вписанный в -угольник максимальной площади, то

где обозначает площадь фигуры .

Среди всех выпуклых замкнутых кривых, ограничивающих данную площадь, эллипс имеет максимальную аффинную длину.

Если произвольный эллипс вписан в треугольник ABC и имеет фокусы P и Q, тогда для него справедливо соотношение

Если лестницу (бесконечно тонкий отрезок прямой) прислонить к вертикальной стенке с горизонтальным полом, и один конец лестницы будет скользить по стенке (всё время касаясь её) а второй конец лестницы будет скользить по полу (всё время касаясь его), тогда любая фиксированная точка лестницы (не на её концах), будет двигаться по дуге некоторого эллипса. Это свойство остаётся верным, если мы возьмём точку не внутри лестницы-отрезка, а на её мыслимом продолжении. Последнее свойство используется в описанном вышеШаблон:Переход эллипсографе.

Касательная, проходящая через точку , принадлежащую эллипсу, имеет следующее уравнение:

1. Если же в правой части стоит единица со знаком минус, то получившееся уравнение:: описывает мнимый эллипс, он не имеет точек на вещественной плоскости.
2. Allaire, Patricia R.; Zhou, Junmin; and Yao, Haishen, «Proving a nineteenth century ellipse identity», Mathematical Gazette 96, March 2012, 161—165.