Электромагнитные колебания

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. На рисунке приведена схема электрической цепи, состоящей из источника тока, ключа и двух параллельно соединённых резисторов. Для измерения напряжения на резисторе ​\( R_2 \)​ вольтметр можно включить между точками

1) только Б и В
2) только А и В
3) Б и Г или Б и В
4) А и Г или А и В

2. На рисунке представлена электрическая цепь, состоящая из источника тока, резистора и двух амперметров. Сила тока, показываемая амперметром А₁, равна 0,5 А. Амперметр А₂ покажет силу тока

1) меньше 0,5 А
2) больше 0,5 А
3) 0,5 А
4) 0 А

3. Ученик исследовал зависимость силы тока в электроплитке от приложенного напряжения и получил следующие данные.

Проанализировав полученные значения, он высказал предположения:

А. Закон Ома справедлив для первых трёх измерений.
Б. Закон Ома справедлив для последних трёх измерений.

Какая(-ие) из высказанных учеником гипотез верна(-ы)?

1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б

4. На рисунке изображён график зависимости силы тока в проводнике от напряжения на его концах. Чему равно сопротивление проводника?

1) 0,25 Ом
2) 2 Ом
3) 4 Ом
4) 8 Ом

5. На диаграммах изображены значения силы тока и напряжения на концах двух проводников. Сравните сопротивления этих проводников.

1) ​\( R_1=R_2 \)​
2) \( R_1=2R_2 \)​
3) \( R_1=4R_2 \)​
4) \( 4R_1=R_2 \)​

6. На рисунке приведена столбчатая диаграмма. На ней представлены значения мощности тока для двух проводников (1) и (2) одинакового сопротивления. Сравните значения напряжения ​\( U_1 \)​ и ​\( U_2 \)​ на концах этих проводников.

1) ​\( U_2=\sqrt{3}U_1 \)​
2) \( U_1=3U_2 \)
3) \( U_2=9U_1 \)
4) \( U_2=3U_1 \)

7. Необходимо экспериментально обнаружить зависимость электрического сопротивления круглого угольного стержня от его длины. Какую из указанных пар стержней можно использовать для этой цели?

1) А и Г
2) Б и В
3) Б и Г
4) В и Г

8. Два алюминиевых проводника одинаковой длины имеют разную площадь поперечного сечения: площадь поперечного сечения первого проводника 0,5 мм2, а второго проводника 4 мм2. Сопротивление какого из проводников больше и во сколько раз?

1) Сопротивление первого проводника в 64 раза больше, чем второго.
2) Сопротивление первого проводника в 8 раз больше, чем второго.
3) Сопротивление второго проводника в 64 раза больше, чем первого.
4) Сопротивление второго проводника в 8 раз больше, чем первого.

9. В течение 600 с через потребитель электрического тока проходит заряд 12 Кл. Чему равна сила тока в потребителе?

1) 0,02 А
2) 0,2 А
3) 5 А
4) 50 А

10. В таблице приведены результаты экспериментальных измерений площади поперечного сечения ​\( S \)​, длины ​\( L \)​ и электрического сопротивления ​\( R \)​ для трёх проводников, изготовленных из железа или никелина.

На основании проведённых измерений можно утверждать, что электрическое сопротивление проводника

1) зависит от материала проводника
2) не зависит от материала проводника
3) увеличивается при увеличении его длины
4) уменьшается при увеличении его площади поперечного сечения

11. Для изготовления резисторов использовался рулон нихромовой проволоки. Поочередно в цепь (см. рисунок) включали отрезки проволоки длиной 4 м, 8 м и 12 м. Для каждого случая измерялись напряжение и сила тока (см. таблицу).

Какой вывод можно сделать на основании проведённых исследований?

1) сопротивление проводника обратно пропорционально площади его поперечного сечения
2) сопротивление проводника прямо пропорционально его длине
3) сопротивление проводника зависит от силы тока в проводнике
4) сопротивление проводника зависит от напряжения на концах проводника
5) сила тока в проводнике обратно пропорциональна его сопротивлению

12. В справочнике физических свойств различных материалов представлена следующая таблица.

Используя данные таблицы, выберите из предложенного перечня два верных утверждения. Укажите их номера.

1) При равных размерах проводник из алюминия будет иметь меньшую массу и большее электрическое сопротивление по сравнению с проводником из меди.
2) Проводники из нихрома и латуни при одинаковых размерах будут иметь одинаковые электрические сопротивления.
3) Проводники из константана и никелина при одинаковых размерах будут иметь разные массы.
4) При замене никелиновой спирали электроплитки на нихромовую такого же размера электрическое сопротивление спирали уменьшится.
5) При равной площади поперечного сечения проводник из константана длиной 4 м будет иметь такое же электрическое сопротивление, что и проводник из никелина длиной 5 м.

Часть 2

13. Меняя электрическое напряжение на участке цепи, состоящем из никелинового проводника длиной 5 м, ученик полученные данные измерений силы тока и напряжения записал в таблицу. Чему равна площадь поперечного сечения проводника?

Справочная информация

ДокументыЗаконыИзвещенияУтверждения документовДоговораЗапросы предложенийТехнические заданияПланы развитияДокументоведениеАналитикаМероприятияКонкурсыИтогиАдминистрации городовПриказыКонтрактыВыполнение работПротоколы рассмотрения заявокАукционыПроектыПротоколыБюджетные организацииМуниципалитетыРайоныОбразованияПрограммыОтчетыпо упоминаниямДокументная базаЦенные бумагиПоложенияФинансовые документыПостановленияРубрикатор по темамФинансыгорода Российской Федерациирегионыпо точным датамРегламентыТерминыНаучная терминологияФинансоваяЭкономическаяВремяДаты2015 год2016 годДокументы в финансовой сферев инвестиционной

Электромагнитная индукция. Магнитный поток

Подробности

Просмотров: 449

«Физика — 11 класс»

Электромагнитная индукция

Английский физик Майкл Фарадей был уверен в единой природе электрических и магнитных явлений.
Изменяющееся во времени магнитное поле порождает электрическое поле, а изменяющееся электрическое поле — магнитное.
В 1831 году Фарадей открыл явление электромагнитной индукции, легшее в основу устройства генераторов, превращающих механическую энергию в энергию электрического тока.

Явление электромагнитной индукции

Явление электромагнитной индукции — это возникновении электрического тока в проводящем контуре, который либо покоится в переменном во времени магнитном поле, либо движется в постоянном магнитном поле таким образом, что число линий магнитной индукции, пронизывающих контур, меняется.

Для своих многочисленных опытов Фарадей использовал две катушки, магнит, выключатель, источник постоянного тока и гальванометр.

Электрический ток способен намагнитить кусок железа. Не может ли магнит вызвать появление электрического тока?

В результате опытов Фарадей установил главные особенности явления электромагнитной индукции:
1). индукционный ток возникает в одной из катушек в момент замыкания или размыкания электрической цепи другой катушки, неподвижной относительно первой.

.

Вывод:

В замкнутом проводящем контуре возникает ток при изменении числа линий магнитной индукции, пронизывающих поверхность, ограниченную этим контуром.
И чем быстрее меняется число линий магнитной индукции, тем больше возникающий индукционный ток.

При этом не важно. что является причиной изменения числа линий магнитной индукции

Это может быть и изменение числа линий магнитной индукции, пронизывающих поверхность, ограниченную неподвижным проводящим контуром, вследствие изменения силы тока в соседней катушке,

и изменение числа линий индукции вследствие движения контура в неоднородном магнитном поле, густота линий которого меняется в пространстве, и т.д.

Магнитный поток

Магнитный поток — это характеристика магнитного поля, которая зависит от вектора магнитной индукции во всех точках поверхности, ограниченной плоским замкнутым контуром.

Есть плоский замкнутый проводник (контур), ограничивающий поверхность площадью S и помещенный в однородное магнитное поле.
Нормаль (вектор, модуль которого равен единице) к плоскости проводника составляет угол α с направлением вектора магнитной индукции .

Магнитным потоком Ф (потоком вектора магнитной индукции) через поверхность площадью S называют величину, равную произведению модуля вектора магнитной индукции на площадь S и косинус угла α между векторами и :

Ф = BScos α

гдеВcos α = В_n — проекция вектора магнитной индукции на нормаль к плоскости контура.
Поэтому

Ф = B_nS

Магнитный поток тем больше, чем больше В_n и S.

Магнитный поток зависит от ориентации поверхности, которую пронизывает магнитное поле.

Магнитный поток графически можно истолковать как величину, пропорциональную числу линий магнитной индукции, пронизывающих поверхность площадью S.

Единицей магнитного потока является вебер.
Магнитный поток в 1 вебер (1 Вб) создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м2, расположенную перпендикулярно вектору магнитной индукции.

Следующая страница «Направление индукционного тока. Правило Ленца»

Назад в раздел «Физика — 11 класс, учебник Мякишев, Буховцев, Чаругин»

Электромагнитная индукция. Физика, учебник для 11 класса — Класс!ная физика

Электромагнитная индукция. Магнитный поток —
Направление индукционного тока. Правило Ленца —
Закон электромагнитной индукции —
ЭДС индукции в движущихся проводниках. Электродинамический микрофон —
Вихревое электрическое поле —
Самоиндукция. Индуктивность. Энергия магнитного поля тока —
Электромагнитное поле —
Примеры решения задач —
Краткие итоги главы

Бизнес и финансы

БанкиБогатство и благосостояниеКоррупция(Преступность)МаркетингМенеджментИнвестицииЦенные бумагиУправлениеОткрытые акционерные обществаПроектыДокументыЦенные бумаги — контрольЦенные бумаги — оценкиОблигацииДолгиВалютаНедвижимость(Аренда)ПрофессииРаботаТорговляУслугиФинансыСтрахованиеБюджетФинансовые услугиКредитыКомпанииГосударственные предприятияЭкономикаМакроэкономикаМикроэкономикаНалогиАудитМеталлургияНефтьСельское хозяйствоЭнергетикаАрхитектураИнтерьерПолы и перекрытияПроцесс строительстваСтроительные материалыТеплоизоляцияЭкстерьерОрганизация и управление производством

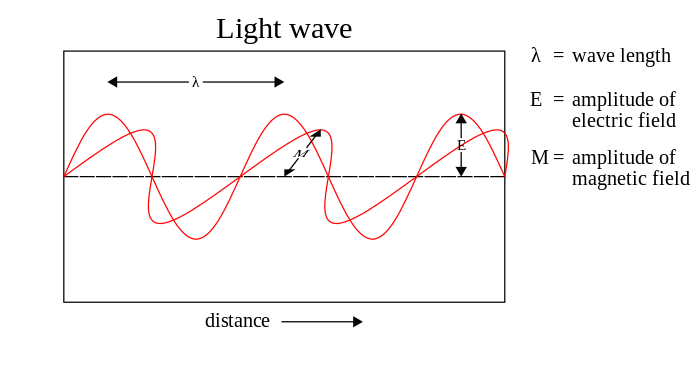
Понятие электромагнитной волны

Любое изменение состояния электромагнитного поля (возмущение поля) имеет волновой характер. При ускоренном движении заряда в поле осуществляется излучение электромагнитных волн, распространяющихся в пространстве с некоторой конечной скоростью. Так, например, в вакууме электромагнитные волны излучаются со скоростью света, т.е. примерно 300 км/сек.

Волны расходятся от источника возмущения. В случае с электромагнитными волнами источниками возмущения следует принимать передвигающиеся магнитные и электрические поля.

Главный источник электромагнитных волн на Земле – Солнце. Часть испускаемых Солнцем электромагнитных волн улавливается человеческим глазом (как следствие – ощущение цвета). Особенно стоит отметить радиоволны – волны, длина которых превышает 500 мкм, а частота составляет менее $6 • 10^{12}$ Гц.

В целом, длина радиоволны определяется по формуле:

$\lambda = \frac{300}{f}$, где:

• $\lambda$ — длина волны, м
• $f$ — частота волны.

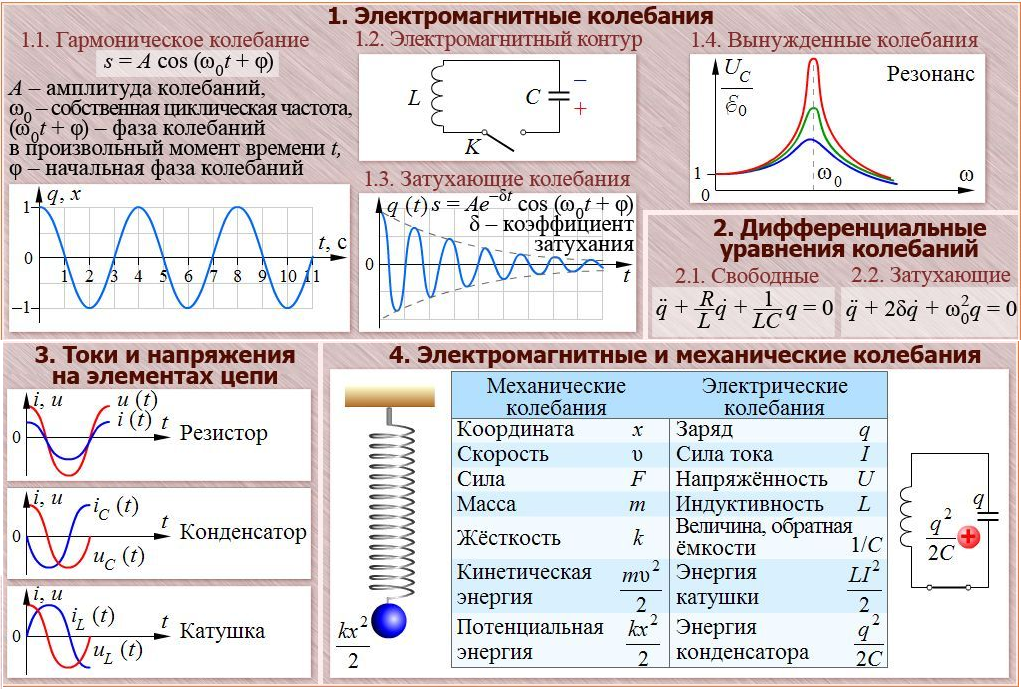
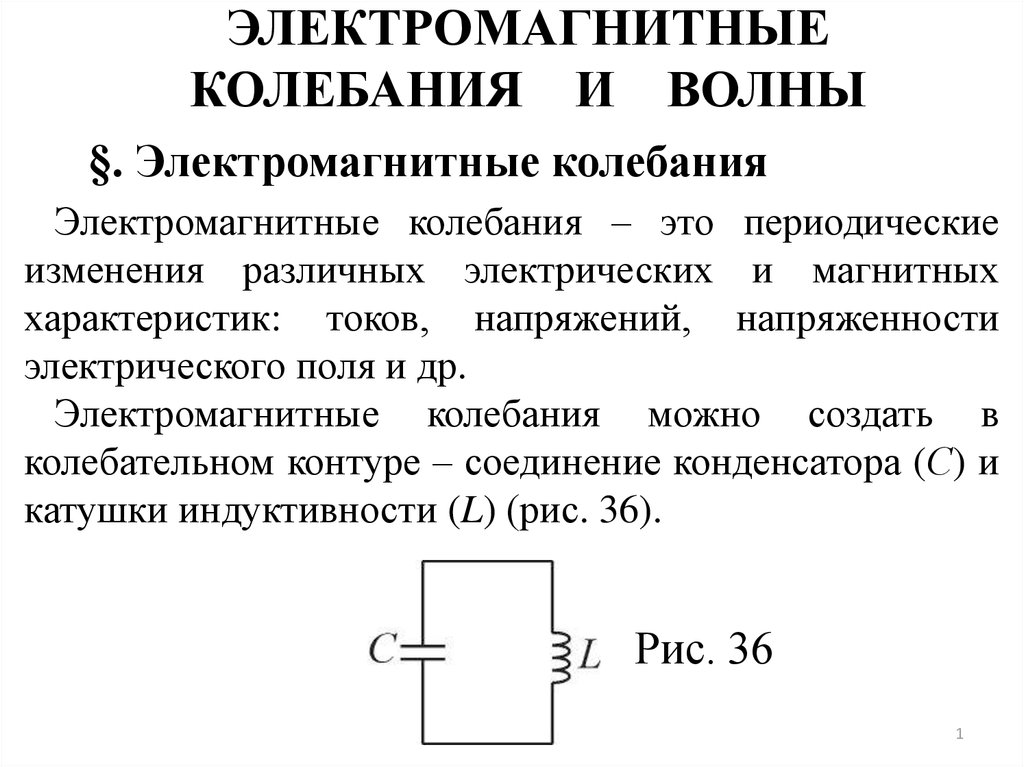
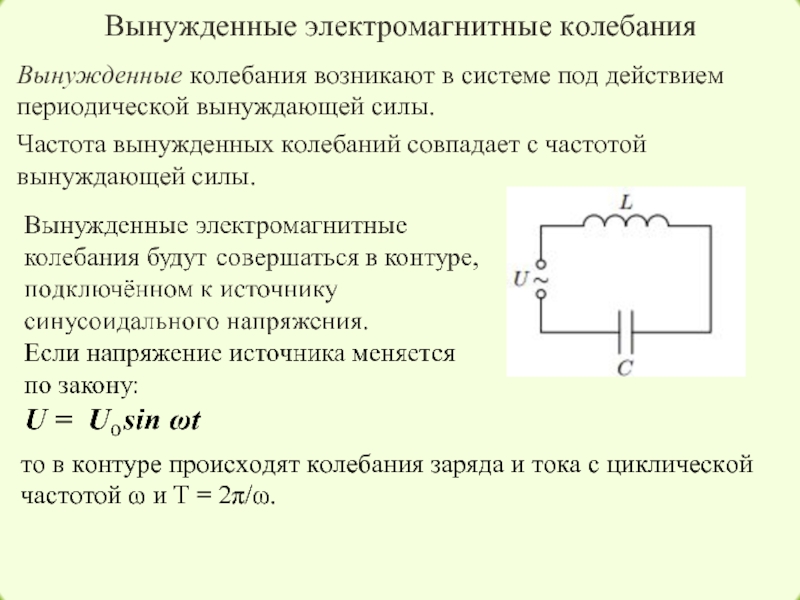
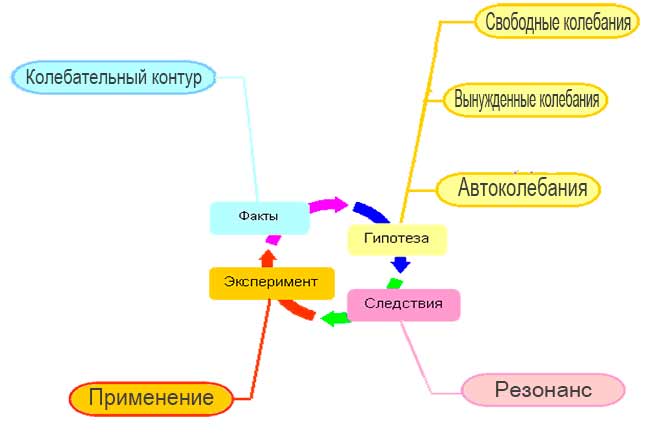
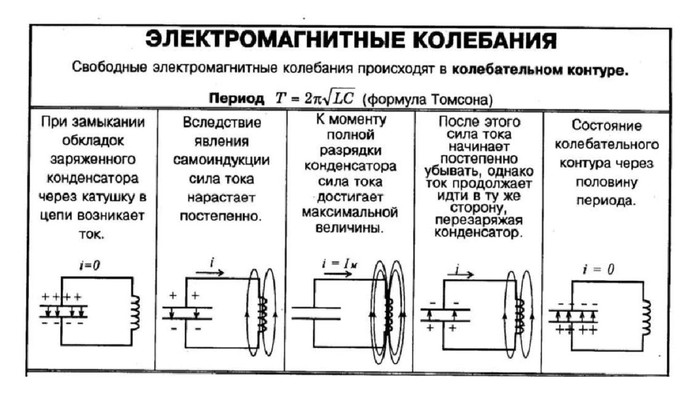
Колебательный контур и его основные характеристики

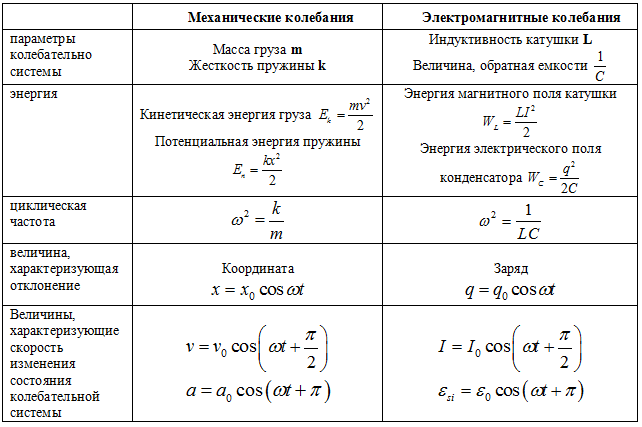
В механике простейшей колебательной системой является груз, который подвешен на пружине. Этот груз движется без трения. Массой подвеса пренебрегаю в сравнении с массой груза. Упругость считают сосредоточенной в пружине. Такая система совершает гармонические колебания, если ее вывели из состояния равновесия. При колебаниях кинетическая энергия переходит в потенциальную и обратно.

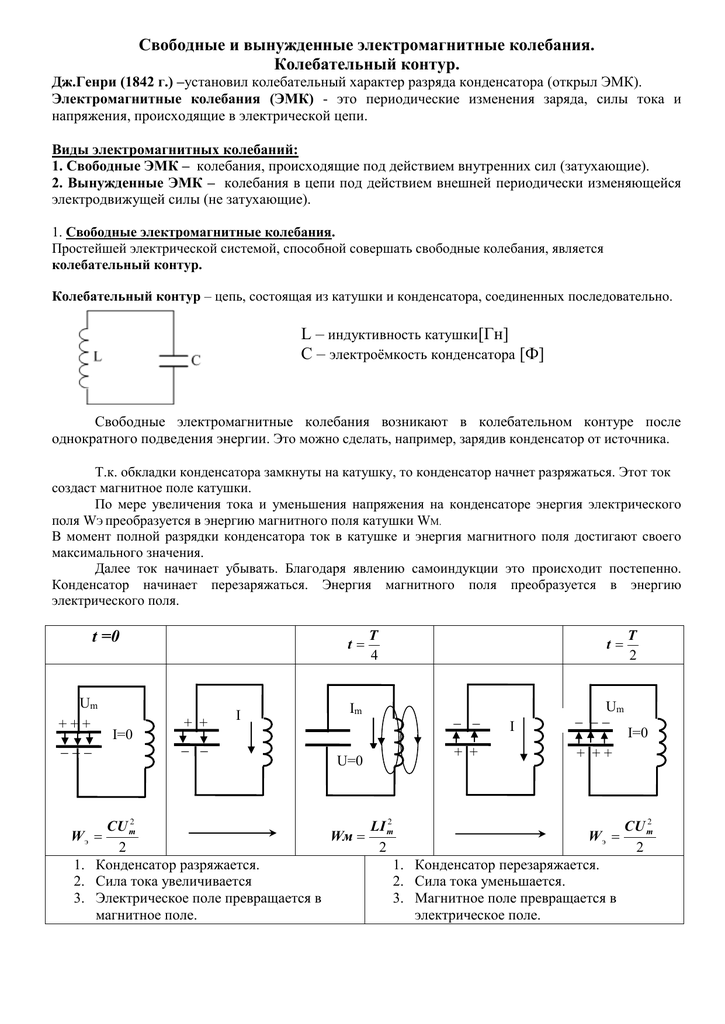
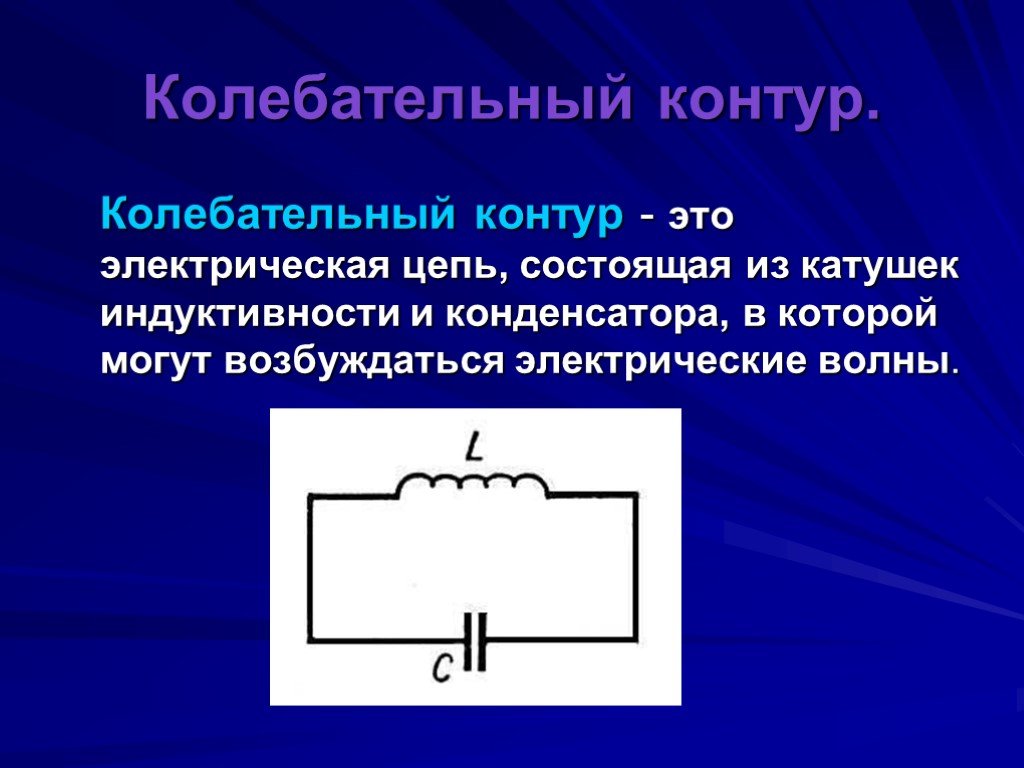
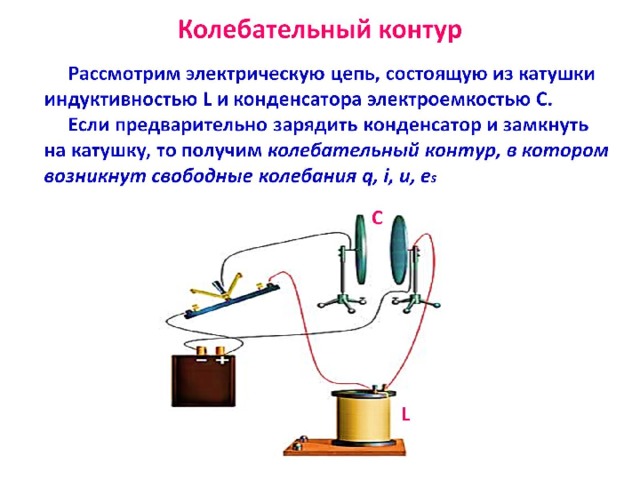
Аналогичные процессы можно наблюдать при электрических колебаниях. Простейшей колебательный контур, который рассматривают в электричестве состоит из конденсатора и катушки индуктивности, соединенных между собой. Считается, что емкость витков катушки мала в сравнении с емкостью конденсатора, а индуктивностью конденсатора и соединительных проводов можно пренебречь в сравнении с индуктивностью катушки. Такой контур называют закрытым или контуром с сосредоточенными емкостью и индуктивностью. Если считают, что в таком контуре сопротивление равно нулю, то его называют идеализированным. Колебания в этом контуре не затухают.

В общем случае в контур включают сопротивление ($R$), конденсатор емкостью $C$, катушку индуктивности $L$, тогда такой контур имеет вид указанный на рис.1. Колебания в таком контуре являются затухающими.

Рисунок 1.

Изменение заряда ($q$) на обкладках конденсатора в таком контуре описывается дифференциальным уравнением вида:

Если сопротивление, которое входит в состав контура $R
\

где $\omega =\sqrt{\frac{1}{LC}-\frac{R^2}{4L^2}}$ — циклическая частота колебаний. $\beta =\frac{R}{2L}-$коэффициент затухания. Амплитуда затухающих колебаний выражается как:

В том случае, если при $t=0$ заряд на конденсаторе равен $q=q_0$, тока в цепи нет, то для $A_0$ можно записать:

Начальная фаза колебаний (${\alpha }_0$) равна:

При $R>2\sqrt{\frac{L}{C}}$ изменение заряда не является колебаниями, разряд конденсатора называют апериодическим.

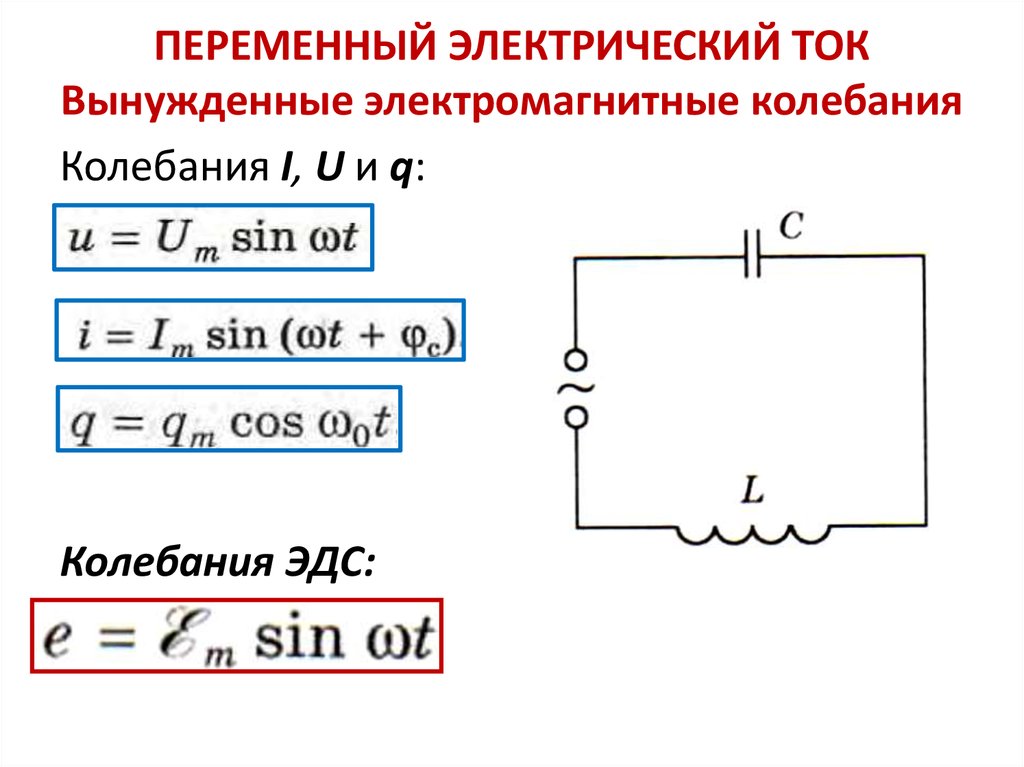
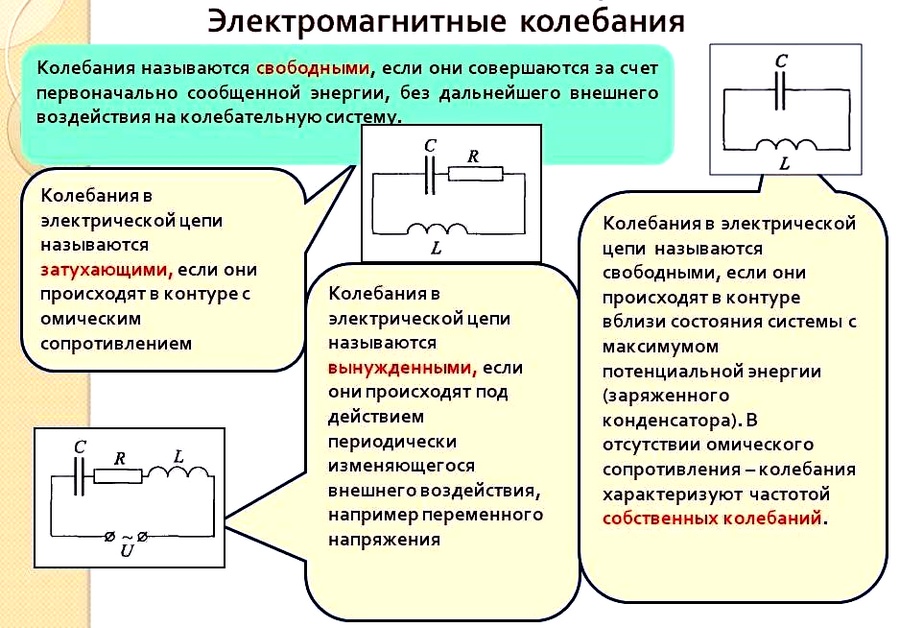
Свободные колебания. Вынужденные колебания

Свободные колебания заряда, силы тока и разности потенциалов называют свободными электромагнитными колебаниями.

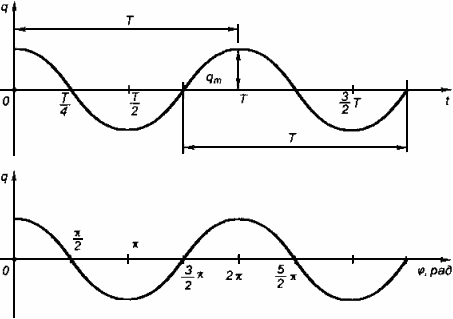
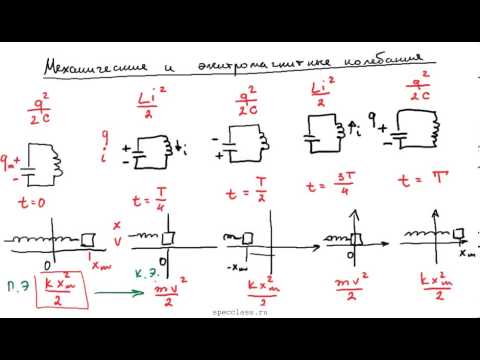
Если электромагнитные колебания являются свободными и незатухающими, то в контуре происходит периодический переход электрической энергии конденсатора в магнитную энергию электрического тока и наоборот. В моменты времени, равные $t=0,\ \frac{T}{2},\ T\ \dots $ энергия электрического поля является максимальной ($W_q$), а энергия магнитного поля ($W_m$) равна нулю:

В моменты времени равные $t=\ \frac{T}{4},\ \frac{3T}{4}\ \dots энергия\ магнитного\ поля\ \left(W_m\right)$ максимальна, энергия электрического поля $W_q=0:$

Из закона сохранения энергии:

получаем, что:

где величина $\sqrt{L/C}$ — волновое сопротивление контура.

Если колебательный контур имеет сопротивление, то для того, чтобы колебания не были затухающими к контуру подводят энергию, которая компенсирует затраты на джоулево тепло. Такие колебания называют вынужденными.

Пример 1

Задание: Исходя из уравнений, которые описывают изменения заряда в колебательном контуре, напишите законы колебаний: заряда, силы тока и разности потенциалов для незатухающих колебаний.

Решение:

Основой для решения задачи по условию сделаем уравнение:

\

Для незатухающих колебаний коэффициент $\beta =0$, тогда уравнение (1.1) примет вид:

\

где ${\omega }_0=\sqrt{\frac{1}{LC}}$ — циклическая частота свободных незатухающих колебаний.

Для того чтобы получить закон изменения силы тока в колебательном контуре используем формулу, связывающую ток и заряд:

\

где знак минус означает, что положительное направление тока соответствует уменьшению положительного заряда на конденсаторе.

Применим операцию дифференцирования к уравнению (1.2), получим:

\

Разность потенциалов найдем, используя формулу:

\

Ответ: $q=А_0{sin \left({\omega }_0t+{\alpha }_0\right),\ }I=-А_0{\omega }_0{cos \left({\omega }_0t+{\alpha }_0\right)\ },\ \triangle \varphi =\frac{А_0}{C}{sin \left({\omega }_0t+{\alpha }_0\right).\ }$

Пример 2

Задание: Напишите выражение для периода свободных незатухающих колебаний.

Решение:

За основание для решения задачи возьмем определение периода ($T$) как:

\

где ${частота\ \omega }_0$- равна:

\

Тогда подставив частоту (${\omega }_0)$ из (2.2) в правую часть выражения (2.1), получим известное выражение Томсона:

\

Ответ: $T=2\pi \sqrt{LC}.$

Причины и условия возникновения

Как и любое другое явление, колебания возникают только в том случае, если выполнены определенные условия. Механические вынужденные колебания, как и свободные, возникают при выполнении таких условий, как:

1. Наличие силы, выводящей тело из состояния устойчивого равновесия. К примеру, толчка математического маятника, при котором начинается движение.

2. Наличие минимальной силы трения в системе. Как известно, трение замедляет те или иные физические процессы. Чем больше сила трения, тем меньше вероятность возникновения колебаний.

3. Одна из сил должна зависеть от координат. То есть тело изменяет свое положение в определенной системе координат относительно определенной точки.

14.1. Свободные электромагнитные колебания

Свободными
(собственными) электромагнитными
ко­лебаниями
называют такие, которые совершаются
без внешнего воздействия за счет
первона­чально
накопленной энергии.

Рассмотрим
колебательный контур, состоящий
из резистора R,
катушки
индуктивности Lи конденсатора С
(рис. 14.1); сопротивлением
проводов и возможным излучением
электромагнитных волн пренебрегаем.
Конденсатор
ключом К
заряжается
от источника
*
, а затем разряжается на резистор и
катушку индуктивности. При этом в контуре
возникает ЭДС

самоиндукции
,
которая,
согласно закону Ома, будет Рис.
14.1
равна сумме напряжений на элементах
цепи: на резисторе U_R=
IRи
конденсаторе
.
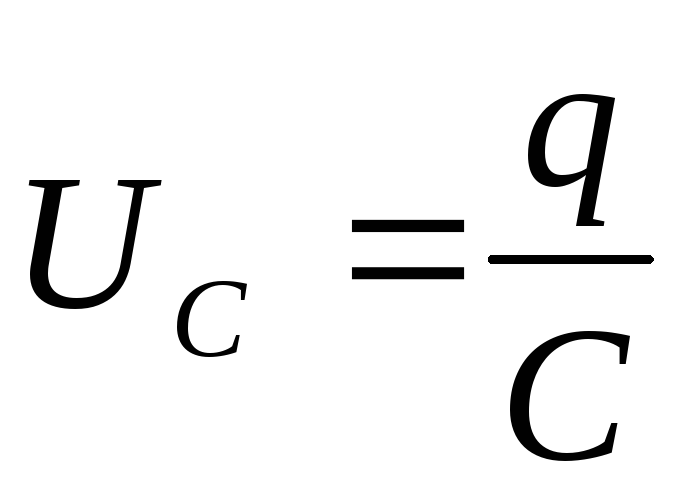Поэтомузапишем

(14.1)

Преобразуем
это уравнение, поделив все члены на Lи
учитывая,
что
и:

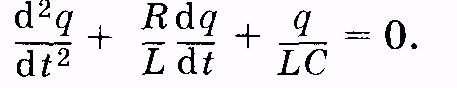(14.2)

Это есть
дифференциальное
уравнение свободных электроманитных
колебаний. Произведя
замены:

(14.3)

получим уравнение

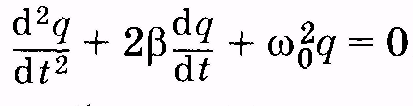(14.4)

Незатухающие
колебания.
Если контур не содержит резистора
(рис. 14.2), то из (14.4) имеем:

(14.5)

Известно,
что (14.5) является дифференциальным
уравнением гармонического
колебания, его решение имеет
вид

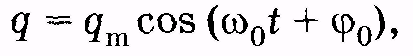(14.6)

где q_m—
наибольший (начальный) заряд на обкладках
конденсатора,

— круговая частота собственных колебаний
(собственная
круговая частота) контура,

— начальная фаза.

По
гармоническому закону изменяется не
только заряд на обкладках
конденсатора, но и напряжение, и сила
тока в контуре, соответственно:

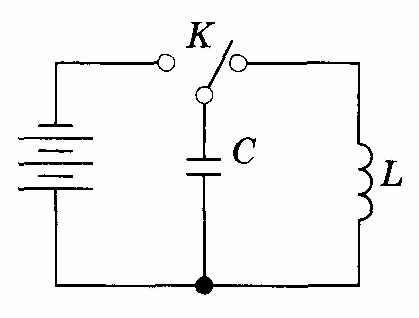Рис.
14.2(14.7)

(14.8)

где U_m
и I_т
— амплитуды напряжения и силы
тока.

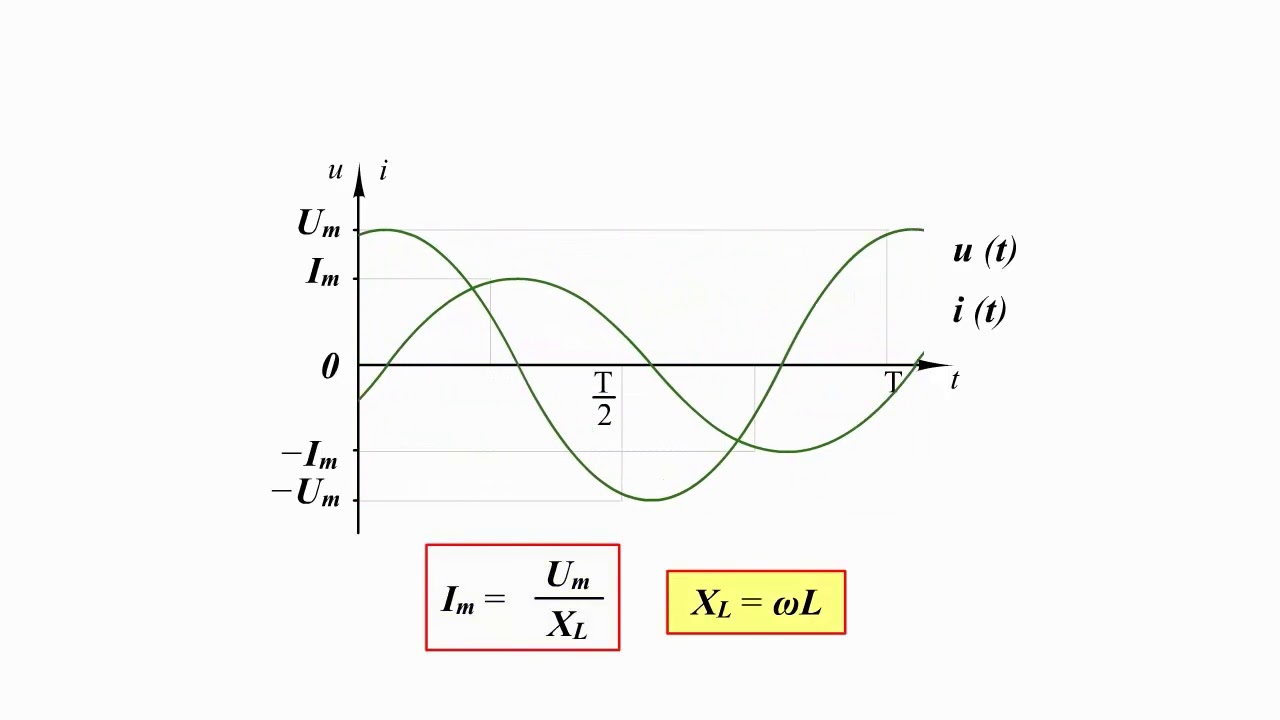
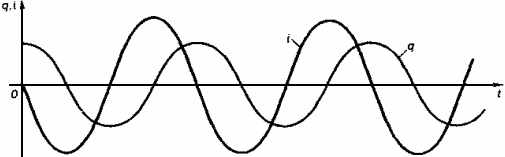
Графики
зависимости заряда (напряжения) от
времени аналогичны
графику зависимости смещения x(t),
а график
зависимости силы
тока от времени — графику скорости 
(t)
(см.
рис. 5.4).

Из
(14.3) найдем выражение для периода
собственных колебаний
(формула
Томсона):

(14.9)

Затухающие колебания. При
наличии резистора (рис. 14.1) процесс
в контуре описывается уравнением (14.4),
которое аналогично
уравнению (5.19) для механических колебаний.
При условии, что затухание не слишком
велико, то есть
находим
следующее решение :

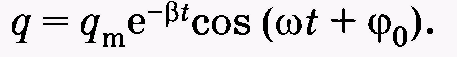
(14.10)

График
этой функции аналогичен графику на рис.
5.6. Если затухание
мало (),
то 

.
В этом случае логарифмический декремент
затухания

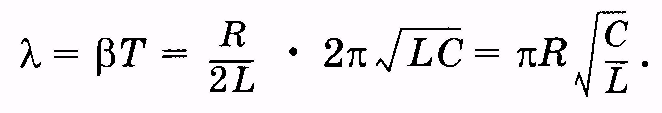(14.11)

Апериодический
разряд конденсатора на резистор (силь­ное
затухание). При сильном затухани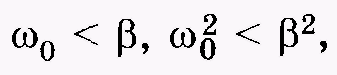иили,
используя (14.3),

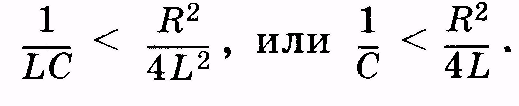(14.12)

Неравенство
(14.12) выполняется, в частности, в контуре
при отсутствии
индуктивности (L
0). Для этого случая (разряд кон­денсатора
на резистор) из (14.1) имеем

(14.13)

Интегрируя последнее уравнение, находим

(14.14)

Потенцируя второе из выражений (14.14),
имеем

(14.15)

Рис. 14.3

Уравнение
(14.15) описывает процесс разрядки
конденсатора С на
резистор R.
При отсутствии
индуктивности колебания не воз­никают
(рис. 14.3, а).
По такому закону изменяется и напряжение
на обкладках конденсатора. Теоретически
такой процесс, как это
следует из (14.15), протекает бесконечно
долго, однако принято
длительность подобных процессов
оценивать временем, в течение
которого параметр, характеризующий
процесс (в данном случае
заряд и напряжение), уменьшится в е
раз
(постоянная
времени,).

Выражение
для постоянной времени можно получить
из (14.15), если
вместо qподставить
,a
tзаменить
на :

откуда
для контура с конденсатором и резистором
постоянная времени равна



=

RС.(14.16)

Можно
показать, что зарядка конденсатора от
источника постоянной
ЭДС * также
происходит по экспоненциальному закону

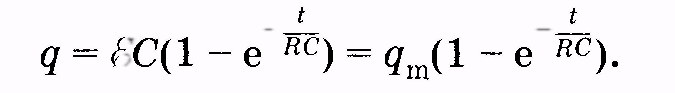(14.17)

График этой зависимости представлен
на рис. 14.3,6.

Электромагнитное поле

Электромагнитное поле – это особый вид материи, с помощью которого осуществляется электромагнитное взаимодействие заряженных тел или частиц.

Это понятие было введено Д. Максвеллом, развившим идеи Фарадея о том, что переменное магнитное поле порождает вихревое электрическое поле.

Всякое изменение магнитного поля порождает в окружающем пространстве вихревое электрическое поле, силовые линии которого замкнуты. Вихревое электрическое поле порождает появление вихревого магнитного поля и так далее. Эти переменные электрическое и магнитное поля, существующие одновременно, и образуют единое электромагнитное поле.

Характеристиками этого поля являются вектор напряженности и вектор магнитной индукции.

Если электрический заряд покоится, то вокруг него существует только электрическое поле.

Если напряженность электрического поля равна нулю, а магнитная индукция отлична от нуля, то обнаруживается только магнитное поле.

Если электрический заряд двигается с постоянной скоростью, то вокруг него существует электромагнитное поле.

Максвелл предположил, что при ускоренном движении зарядов в пространстве будет возникать возмущение, которое будет распространяться в вакууме с конечной скоростью. Когда это возмущение достигнет второго заряда, то изменится сила, с которой электромагнитное поле действует на этот заряд.

При ускоренном движении заряда происходит излучение электромагнитной волны. Электромагнитное поле материально. Оно распространяется в пространстве в виде электромагнитной волны.

Свободные колебания

Данный вид колебаний возникает под воздействием внутренних сил тогда, когда система выводится из состояния устойчивого равновесия или покоя. Свободные колебания всегда являются затухающими, а значит, их амплитуда и частота со временем уменьшаются. Ярким примером подобного вида раскачиваний служит движение груза, подвешенного на нить и колеблющегося из одной стороны в другую; груза, прикрепленного к пружине, то опускающегося вниз под действием тяжести, то поднимающегося вверх под действием пружины

Кстати, именно такого рода колебаниям уделяют внимание при изучении физики. Да и большинство задач посвящено как раз-таки свободным колебаниям, а не вынужденным

Понятие колебания и его характеристики

В общем смысле, колебание – это процесс или движение, характеризующийся определенной повторяемостью во времени. В зависимости от природы колебаний, их объединяют в две основные группы – механические и электромагнитные. К изучению и тех и других применяют единый подход, поскольку их характеристики сходны по многим параметрам.

Итак, значительную группу процессов относят к свободным или собственным колебаниям. Собственные колебания совершаются под действием единожды сообщенной энергии без последующего воздействия внешних сил на колебательную систему в целом.

Отдельно стоит выделить гармонические колебания. При гармоническом колебательном процессе рассматриваемая величина изменяется во времени согласно закону синуса (косинуса). Многие явления, встречаемые в природе и технике, близки по своим характеристикам гармоническим колебаниям. Многие периодические процессы можно представить как наложение гармонических колебаний.

Приведем уравнение, описывающее гармоническое колебание величины $s$:

$s = A\cos{\omega_0 t + \varpi}$, где:

• $\omega_0$ — циклическая частота;
• $A$ — амплитуда колебания (максимальное значение величины $s$).

Здесь периодически меняющийся аргумент косинуса $(\omega_0 t + \varpi)$ будет называться фазой колебания. Фаза колебания характеризует отклонение величины $s$ от точки равновесия в момент времени $t$.

Определение 2

Значение $\varpi$ в уравнении называется начальной фазой. Начальная фаза характеризует отклонение колеблющейся величины от точки равновесия в начальный момент времени. Таким образом, значение $\varpi$ зависит от выбора начала отсчета времени.

Косинус меняется в пределах от -1 до 1, следовательно, величина $s$ может принимать значение от $-A$ до $A$.

Колебательная система возвращается в начальное состояние через промежуток времени $T$, названный периодом колебания. За один $T$ система получает приращение в $2\pi$:

$\omega_0 (t+T) = (\omega_0 t + \varpi) +2\pi$

Путем преобразования получаем: $T = \frac{2\pi}{\omega_0}$.

Введем понятие частоты колебаний. Так, частота колебаний есть величина, обратная периоду колебаний:

$\nu = \frac{1}{T}$

Численно она равна количеству полных колебаний, совершенных за единицу времени. Стандартная единица частоты – герц (Гц). Один Гц – частота колебания, при котором за 1 секунду совершается 1 колебательный цикл.

Запишем дифференциальное уравнение для гармонических колебаний:

$\frac{d^2 s}{dt^2} + (\omega_0)^2 s = 0$

Решением этого уравнения является уже приведенное выражение:

$s = A\cos{\omega_0 t + \varpi}$