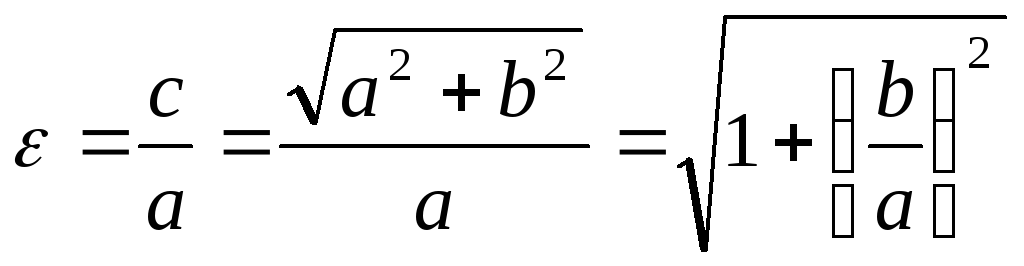Эксцентриситет

Свойства

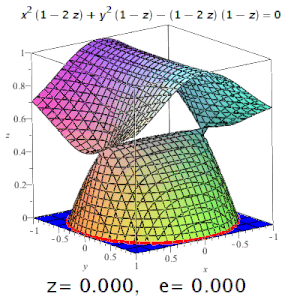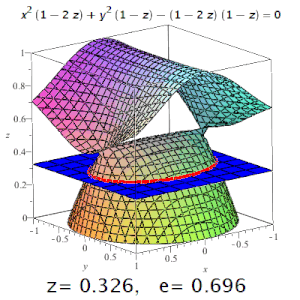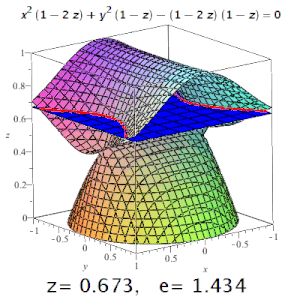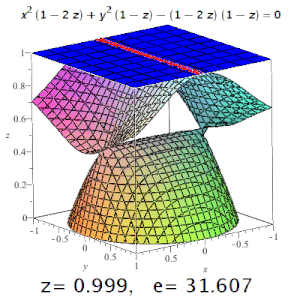
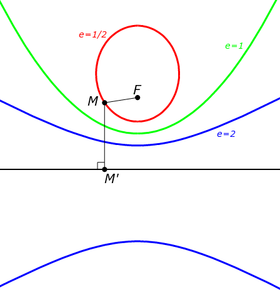
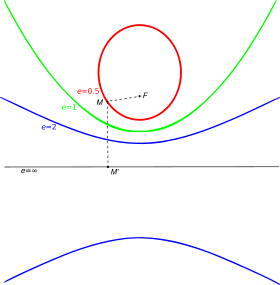
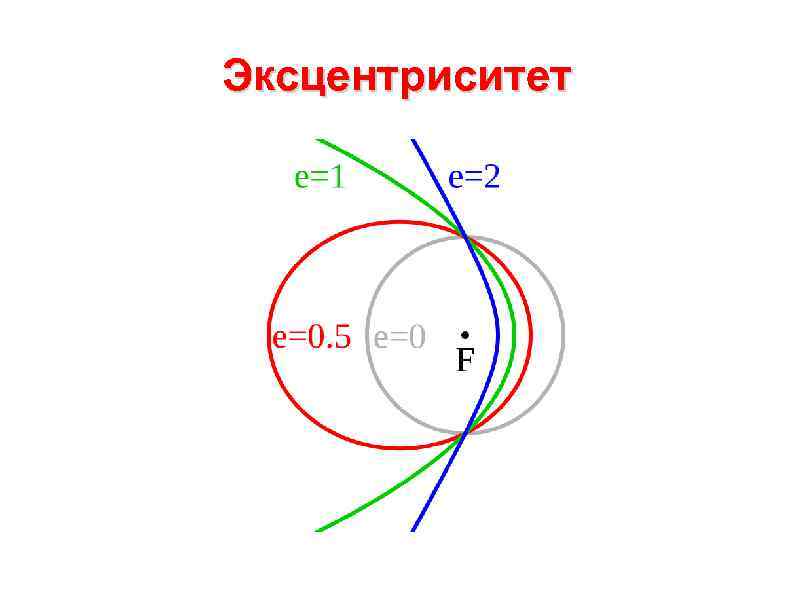
Эллипсы и гиперболы всех возможных эксцентриситетов (e) от нуля до бесконечности, а также парабола (при y=0), составляющие одну поверхность третьего порядка (являясь ее горизонтальными сечениями: у = соnst)

В зависимости от эксцентриситета, получится:
- при e>1{\displaystyle e>1} — гипербола. Чем больше эксцентриситет гиперболы, тем больше две её ветви похожи на параллельные прямые линии;
- при e=1{\displaystyle e=1} — парабола;
- при e<1{\displaystyle e<1} — эллипс;
- для окружности полагают e={\displaystyle e=0}.

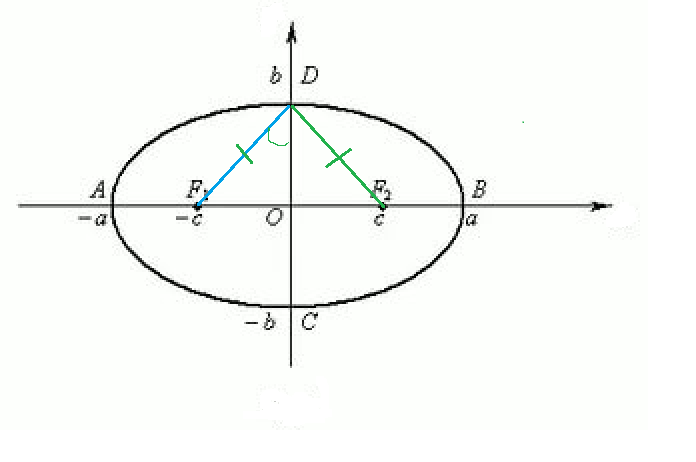
Эксцентриситет эллипса и гиперболы равен отношению расстояния от фокуса до центра к большой полуоси. Это свойство иногда принимают за определение эксцентриситета. В прежние времена (например, в 1787 году) на большую полуось не делили — эксцентриситетом эллипса называли расстояние от фокуса до центра.
Эксцентриситет эллипса может быть также выражен через отношение малой (b{\displaystyle b}) и большой (a{\displaystyle a}) полуосей:

e=1−b2a2{\displaystyle e={\sqrt {1-{\frac {b^{2}}{a^{2}}}}}}.

Эксцентриситет гиперболы может быть выражен через отношение мнимой (b{\displaystyle b}) и действительной (a{\displaystyle a}) полуосей:

e=1+b2a2{\displaystyle e={\sqrt {1+{\frac {b^{2}}{a^{2}}}}}}

Эксцентриситет равносторонней гиперболы, являющейся графиком обратной пропорциональности и задаваемой уравнением f(x)=kx,x≠0,k≠0{\displaystyle f(x)={k \over x},x\neq 0,k\neq 0}, равен 2{\displaystyle {\sqrt {2}}}.

Для эллипса также может быть выражен через отношение радиусов пери- (rper{\displaystyle r_{\mathrm {per} }}) и апоцентров (rap{\displaystyle r_{\mathrm {ap} }}):

e=rap−rperrap+rper=1−2raprper+1{\displaystyle e={\frac {r_{\mathrm {ap} }-r_{\mathrm {per} }}{r_{\mathrm {ap} }+r_{\mathrm {per} }}}=1-{\frac {2}{{\frac {r_{\mathrm {ap} }}{r_{\mathrm {per} }}}+1}}}.

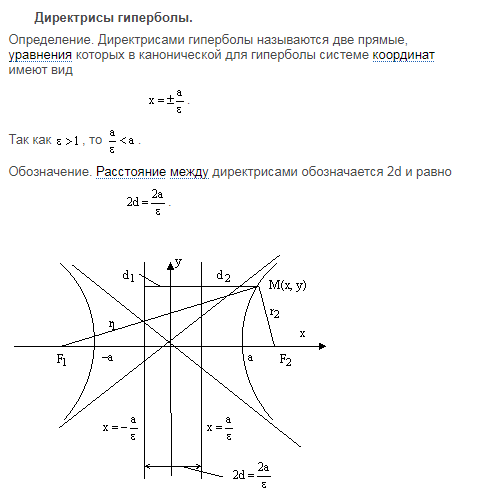
Определение

е = 0

е = 0,5

Орбиты в системе двух тел для двух значений эксцентриситета e. (NB: + — барицентр )

В задаче двух тел с силой закона обратных квадратов каждая орбита является орбитой Кеплера. Эксцентриситет этой Kepler орбиты является неотрицательным числом , которое определяет его форму.

Эксцентриситет может принимать следующие значения:

круговая орбита : e = 0
эллиптическая орбита : 0 < e <1 (см. эллипс )
параболическая траектория : e = 1 (см. параболу )
гиперболическая траектория : e > 1 (см. гиперболу )

Эксцентриситет e определяется выражением

езнак равно1+2EL2мкрасныйα2{\ displaystyle e = {\ sqrt {1 + {\ frac {2EL ^ {2}} {m _ {\ text {red}} \ alpha ^ {2}}}}}}

где E — полная орбитальная энергия , L — угловой момент , m _red — приведенная масса , а α — коэффициент центральной силы закона обратных квадратов, такой как гравитация или электростатика в классической физике :

Fзнак равноαр2{\ displaystyle F = {\ frac {\ alpha} {r ^ {2}}}}

( α отрицательно для силы притяжения, положительно для силы отталкивания; см. также задачу Кеплера )

или в случае силы тяжести:

езнак равно1+2εчас2μ2{\ displaystyle e = {\ sqrt {1 + {\ frac {2 \ varepsilon h ^ {2}} {\ mu ^ {2}}}}}}

где ε — удельная орбитальная энергия (общая энергия, деленная на приведенную массу), μ — стандартный гравитационный параметр, основанный на общей массе, а h — удельный относительный угловой момент ( угловой момент, деленный на приведенную массу).

Для значений e от 0 до 1 форма орбиты представляет собой все более вытянутый (или более плоский) эллипс; для значений е от 1 до бесконечности орбиты является гипербола ветвь делает общий поворот 2 arccsc е , уменьшающийся от 180 до 0 градусов. Предельный случай между эллипсом и гиперболой, когда е равно 1, — это парабола.

Радиальные траектории классифицируются как эллиптические, параболические или гиперболические в зависимости от энергии орбиты, а не эксцентриситета. Радиальные орбиты имеют нулевой угловой момент и, следовательно, эксцентриситет равен единице. Сохранение постоянной энергии и уменьшение углового момента, эллиптическая, параболическая и гиперболическая орбиты стремятся к соответствующему типу радиальной траектории, в то время как e стремится к 1 (или, в параболическом случае, остается 1).

Для силы отталкивания применима только гиперболическая траектория, включая радиальный вариант.

Для эллиптических орбит простое доказательство показывает, что arcsin ( ⁠) дает угол проекции идеального круга на эллипс с эксцентриситетом e . Например, чтобы увидеть эксцентриситет планеты Меркурий ( e = 0,2056), нужно просто вычислить обратный синус, чтобы найти угол проекции 11,86 градусов. Затем наклоните любой круглый объект (например, кофейную кружку, если смотреть сверху) на этот угол, и видимый эллипс, проецируемый вашему глазу, будет иметь ту же эксцентриситет.
е{\ displaystyle e}

Эксцентриситеты в других системах

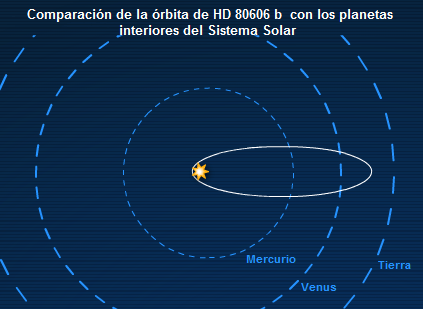
Сравнение орбиты HD 80606 b с внутренними планетами Солнечной системы

Открытие других солнечных систем неизбежно влечёт открытие планет с очень причудливыми параметрами орбит. Примером тому служат эксцентричные юпитеры, газовые гиганты с довольно высокими эксцентриситетами. В системах, имеющие такие планеты невозможно существование планет, подобных Земле. Они неизбежно упадут на гиганты или же статут их спутниками. Среди обнаруженных на данный момент эксцентричных юпитеров самым большим эксцентриситетом обладает HD 80606b. Он движется вокруг звезды чуть меньшей, чем наше Солнце. Эта планета в перигелии приближается к звезде в 10 раз ближе, чем Меркурий к Солнцу, тогда как в афелии она удаляется от неё почти на астрономическую единицу. Таким образом, она имеет эксцентриситет 0,933.

Стоит отметить, что хоть данная планета и пересекает зону жизни, ни о каких видах привычной биосферы не может идти и речи. Её орбита создаёт на планете экстремальный климат.За короткий период сближения со звездой температура её атмосферы за считанные часы меняется на сотни градусов, в результате чего скорость ветров достигают многих километров в секунду. Подобными условиями обладают прочие планеты с высокими коэффициентами. Тот же Плутон, к примеру, при приближение к Солнцу приобретает обширную атмосферу, которая оседает в виде снега при удалении. В тоже время все Землеподобные планеты обладают орбитами, близкими к круговым. Поэтому эксцентриситет можно назвать одним из параметров, определяющим возможность наличия органической жизни на планете.

Эксцентриситеты объектов Солнечной Системы

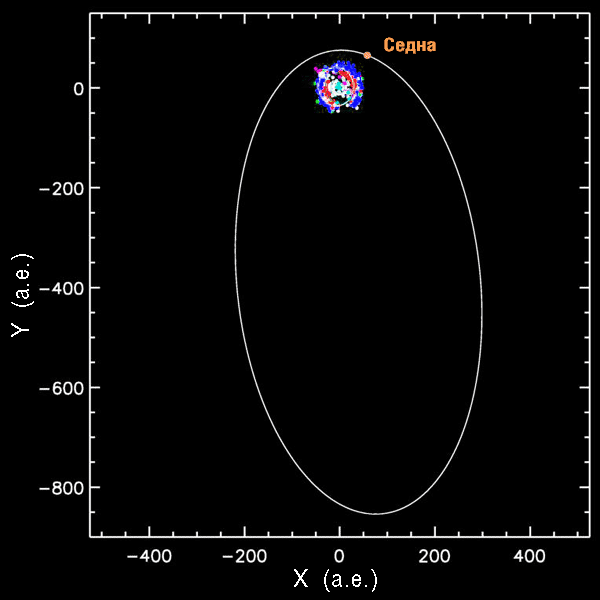
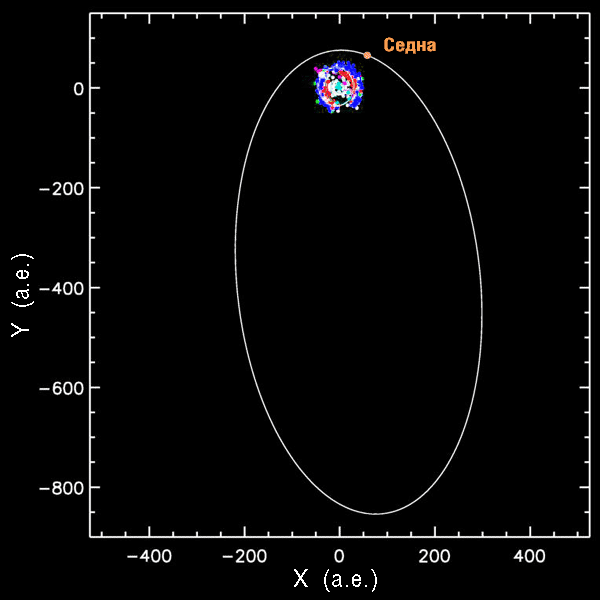
Орбита Седны. В центре координат — Солнечная система, окруженная роем планет и известных объектов пояса Койпера.

В нашей системе орбиты планет ничем не примечательны. Самой «круговой» орбитой обладает Венера. Её афелий всего-лишь на 1,4 млн. км.больше перигелия, а эксцентриситет равен 0,007 (у Земли – 0,016). По довольно вытянутой орбите движется Плутон. Обладая ε = 0,244, он временами приближается к Солнцу даже ближе чем Нептун. Однако, поскольку Плутон не так давно попал в разряд карликовых планет, самую вытянутую орбит среди планет теперь имеет Меркурий, обладающий ε = 0,204.

Среди карликовых планет наиболее примечательна Седна. Обладая ε = 0,86, она делает полный оборот вокруг Солнца почти за 12 тысяч лет, удаляясь от неё в афелии более чем на тысячу астрономический единиц. Однако даже это несравнимо с параметрами орбит долгопериодических комет. Периоды их обращения порой исчисляются миллионами лет, а многих из них и вовсе никогда не вернутся к Солнцу – т.е. обладают эксцентриситетом, большем 1. Облако Оорта может содержать триллионы комет, удалённых от Солнца на 50-100 тысяч астрономических единиц (0,5 – 1 световых лет). На таких расстояниях на нихмогут влиять другие звёзды и галактические приливные силы. Поэтому такие кометы могут обладать очень непредсказуемыми и непостоянными орбитами с самими различными эксцентриситетами.

Наконец, самым интересным является то, что даже Солнце обладает совсем ни круговой орбитой, как это может показаться на первый взгляд. Как известно, Солнце движется вокруг центра Галактики, проделывая свой путь за 223 млн. лет. Причём, из-за бесчисленного взаимодействия со звездами она получила довольно ощутимый эксцентриситет, равный 0,36.

Примеры

Эксцентриситет тел Солнечной системы
Объект	эксцентриситет
Тритон	0,000 02
Венера	0,006 8
Нептун	0,008 6
Земля	0,016 7
Титан	0,028 8
Уран	0,047 2
Юпитер	0,048 4
Сатурн	0,054 1
Луна	0,054 9
1 Церера	0,075 8
4 Веста	0,088 7
Марс	0,093 4
10 Гигея	0,114 6
Makemake	0,155 9
Хаумеа	0,188 7
Меркурий	0,205 6
2 Паллада	0,231 3
Плутон	0,248 8
3 Юнона	0,255 5
324 Бамберга	0,340
Эрис	0,440 7
Нереида	0,750 7
Седна	0,854 9
Комета Галлея	0,967 1
Комета Хейла-Боппа	0,995 1
Комета Икея-Секи	0,999 9
C / 1980 E1	1.057
ʻOumuamua	1,20
C / 2019 Q4 (Борисов)	3.5

В таблице перечислены значения для всех планет и карликовых планет, а также выбранных астероидов, комет и лун. У Меркурия самый большой эксцентриситет орбиты из всех планет Солнечной системы ( e = 0,2056). Такого эксцентриситета достаточно, чтобы Меркурий получил вдвое больше солнечного излучения в перигелии по сравнению с афелием. До того , как Плутон был понижен в должности в 2006 году , он считался планетой с наиболее эксцентричной орбитой ( e = 0,248). Другие транснептуновые объекты обладают значительным эксцентриситетом, особенно карликовая планета Эрида (0,44). Еще дальше, Седна , имеет чрезвычайно высокий эксцентриситет0,855 из-за предполагаемого афелия 937 а.е. и перигелия около 76 а.е.

Большинство астероидов Солнечной системы имеют эксцентриситет орбиты от 0 до 0,35 со средним значением 0,17. Их сравнительно высокие эксцентриситета, вероятно, связаны с влиянием Юпитера и прошлыми столкновениями.

Значение Луны составляет 0,0549, это самый эксцентричный из больших спутников Солнечной системы. У четырех галилеевых спутников эксцентриситет <0,01. Самый большой спутник Нептуна Тритон имеет эксцентриситет1,6 × 10 −5 (0,000 016 ), наименьший эксцентриситет любой известной луны в Солнечной системе; его орбита настолько близка к идеальному кругу, насколько это возможно в настоящее время. Однако спутники меньшего размера, особенно спутники неправильной формы , могут иметь значительный эксцентриситет, например, третья по величине луна Нептуна Нереида (0,75).

Кометы имеют очень разные значения эксцентриситета. Периодические кометы имеют эксцентриситет в основном от 0,2 до 0,7, но некоторые из них имеют сильно эксцентричные эллиптические орбиты с эксцентриситетом чуть меньше 1, например, комета Галлея имеет значение 0,967. Непериодические кометы движутся по почти параболическим орбитам и поэтому имеют эксцентриситет даже ближе к 1. Примеры включают комету Хейла – Боппа со значением 0,995 и комету C / 2006 P1 (МакНота) со значением1.000 019 . Поскольку значение Хейла-Боппа меньше 1, его орбита эллиптическая, и он вернется. Комета МакНота движется по гиперболической орбите, пока находится под влиянием планет, но все еще связана с Солнцем с периодом обращения около 10 5 лет. По состоянию на Эпоху 2010 года комета C / 1980 E1 имеет самый большой эксцентриситет из всех известных гиперболических комет с эксцентриситетом 1,057 и в конечном итоге покинет Солнечную систему .

`Оумуамуа — первый обнаруженный межзвездный объект, проходящий через Солнечную систему. Его орбитальный эксцентриситет 1,20 указывает на то, что Оумуамуа никогда не был гравитационно привязан к нашему Солнцу. Он был обнаружен в 0,2 а.е. (30 000 000 км; 19 000 000 миль) от Земли и имеет диаметр примерно 200 метров. Он имеет межзвездную скорость (скорость на бесконечности) 26,33 км / с (58 900 миль в час).

Ценности

Коническое сечение	Уравнение	Эксцентриситет ( e )	Линейный эксцентриситет ( c )
Круг	Икс2+y2знак равнор2{\ displaystyle x ^ {2} + y ^ {2} = r ^ {2}}	{\ displaystyle 0}	{\ displaystyle 0}
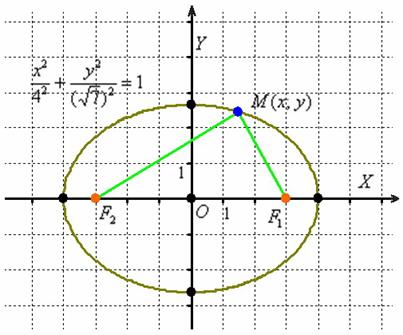
Эллипс	Икс2а2+y2б2знак равно1{\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} + {\ frac {y ^ {2}} {b ^ {2}}} = 1}или гдеy2а2+Икс2б2знак равно1{\ displaystyle {\ frac {y ^ {2}} {a ^ {2}}} + {\ frac {x ^ {2}} {b ^ {2}}} = 1}а>б{\ displaystyle a> b}	1-б2а2{\ displaystyle {\ sqrt {1 — {\ frac {b ^ {2}} {a ^ {2}}}}}}	а2-б2{\ displaystyle {\ sqrt {a ^ {2} -b ^ {2}}}}
Парабола	Икс2знак равно4аy{\ displaystyle x ^ {2} = 4ay}	1{\ displaystyle 1}	—
Гипербола	Икс2а2-y2б2знак равно1{\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} — {\ frac {y ^ {2}} {b ^ {2}}} = 1} или y2а2-Икс2б2знак равно1{\ displaystyle {\ frac {y ^ {2}} {a ^ {2}}} — {\ frac {x ^ {2}} {b ^ {2}}} = 1}	1+б2а2{\ displaystyle {\ sqrt {1 + {\ frac {b ^ {2}} {a ^ {2}}}}}}	а2+б2{\ displaystyle {\ sqrt {a ^ {2} + b ^ {2}}}}

Здесь для эллипса и гиперболы a — длина большой полуоси, а b — длина малой полуоси.

Когда коническое сечение задано в общей квадратичной форме

АИкс2+BИксy+Cy2+DИкс+Ey+Fзнак равно,{\ displaystyle Ax ^ {2} + Bxy + Cy ^ {2} + Dx + Ey + F = 0,}

следующая формула дает эксцентриситет e, если коническое сечение не является параболой (с эксцентриситетом, равным 1), не вырожденной гиперболой или вырожденным эллипсом , и не воображаемым эллипсом:

езнак равно2(А-C)2+B2η(А+C)+(А-C)2+B2{\ Displaystyle е = {\ sqrt {\ frac {2 {\ sqrt {(AC) ^ {2} + B ^ {2}}}} {\ eta (A + C) + {\ sqrt {(AC) ^ {2} + B ^ {2}}}}}}}

где если определитель матрицы 3 × 3
ηзнак равно1{\ displaystyle \ eta = 1}

АB2D2B2CE2D2E2F{\ displaystyle {\ begin {bmatrix} A & B / 2 & D / 2 \\ B / 2 & C & E / 2 \\ D / 2 & E / 2 & F \ end {bmatrix}}}

отрицательный или если этот определитель положительный.
ηзнак равно-1{\ displaystyle \ eta = -1}

Эллипс и гипербола с постоянным a и изменяющимся эксцентриситетом e .

Свойства

В зависимости от эксцентриситета, получится:
- при e>1{\displaystyle e>1} — гипербола. Чем больше эксцентриситет гиперболы, тем больше две её ветви похожи на параллельные прямые линии;
- при e=1{\displaystyle e=1} — парабола;
- при e<1{\displaystyle e<1} — эллипс;
- для окружности полагают e={\displaystyle e=0}.

Эксцентриситет эллипса и гиперболы равен отношению расстояния от фокуса до центра к большой полуоси. Это свойство иногда принимают за определение эксцентриситета. В прежние времена (например, в 1787 году) на большую полуось не делили — эксцентриситетом эллипса называли расстояние от фокуса до центра.
Эксцентриситет эллипса может быть также выражен через отношение малой (b{\displaystyle b}) и большой (a{\displaystyle a}) полуосей:

e=1−b2a2{\displaystyle e={\sqrt {1-{\frac {b^{2}}{a^{2}}}}}}.

e=1+b2a2{\displaystyle e={\sqrt {1+{\frac {b^{2}}{a^{2}}}}}}

Климатический эффект

Орбитальная механика требует, чтобы продолжительность сезонов была пропорциональна площади орбиты Земли, проходящей между солнцестоянием и равноденствием , поэтому, когда эксцентриситет орбиты является экстремальным, времена года, которые происходят на обратной стороне орбиты ( афелий ), могут быть существенно дольше по продолжительности. Сегодня осень и зима в северном полушарии происходят при ближайшем приближении ( перигелий ), когда Земля движется с максимальной скоростью, тогда как в южном полушарии происходит противоположное. В результате в северном полушарии осень и зима немного короче, чем весна и лето, но в глобальном плане это уравновешивается тем, что они длиннее ниже экватора. В 2006 году в северном полушарии лето было на 4,66 дня длиннее зимы, а весна была на 2,9 дня дольше осени из-за циклов Миланковича .

Апсидальная прецессия также медленно меняет место на орбите Земли, где происходят солнцестояния и равноденствия

Обратите внимание, что это медленное изменение орбиты Земли, а не оси вращения, которое называется осевой прецессией (см. )

В течение следующих 10 000 лет зимы в северном полушарии будут постепенно становиться длиннее, а лето — короче. Однако любой охлаждающий эффект в одном полушарии уравновешивается потеплением в другом, и любому общему изменению будет противодействовать тот факт, что эксцентриситет орбиты Земли уменьшится почти вдвое. Это уменьшит средний радиус орбиты и повысит температуру в обоих полушариях ближе к среднему межледниковому пику.

Эллипсы

Эксцентриситет эллипса строго меньше 1. Когда круги (с эксцентриситетом 0) считаются эллипсами, эксцентриситет эллипса больше или равен 0; если кругам присвоена специальная категория и они исключены из категории эллипсов, то эксцентриситет эллипса строго больше 0.

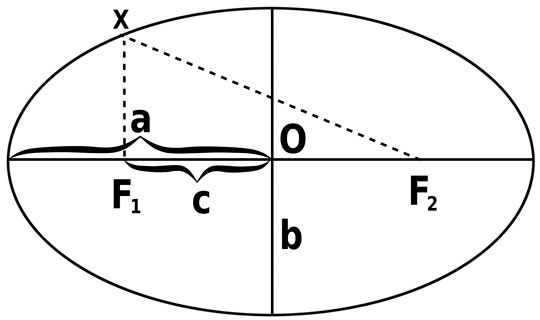
Для любого эллипса пусть a будет длиной его большой полуоси, а b будет длиной его малой полуоси .

Мы определяем ряд связанных дополнительных понятий (только для эллипсов):

название	Условное обозначение	с точки зрения a и b	с точки зрения е
Первая эксцентриситет	е{\ displaystyle e}	1-б2а2{\ displaystyle {\ sqrt {1 — {\ frac {b ^ {2}} {a ^ {2}}}}}}	е{\ displaystyle e}
Второй эксцентриситет	е′{\ displaystyle e ‘}	а2б2-1{\ displaystyle {\ sqrt {{\ frac {a ^ {2}} {b ^ {2}}} — 1}}}	е1-е2{\ displaystyle {\ frac {e} {\ sqrt {1-e ^ {2}}}}}
Третья эксцентриситет	е″знак равном{\ displaystyle e » = {\ sqrt {m}}}	а2-б2а2+б2{\ displaystyle {\ frac {\ sqrt {a ^ {2} -b ^ {2}}} {\ sqrt {a ^ {2} + b ^ {2}}}}}	е2-е2{\ displaystyle {\ frac {e} {\ sqrt {2-e ^ {2}}}}}
Угловой эксцентриситет	α{\ displaystyle \ alpha}	потому что-1⁡(ба){\ displaystyle \ cos ^ {- 1} \ left ({\ frac {b} {a}} \ right)}	грех-1⁡е{\ displaystyle \ sin ^ {- 1} e}

Другие формулы эксцентриситета эллипса

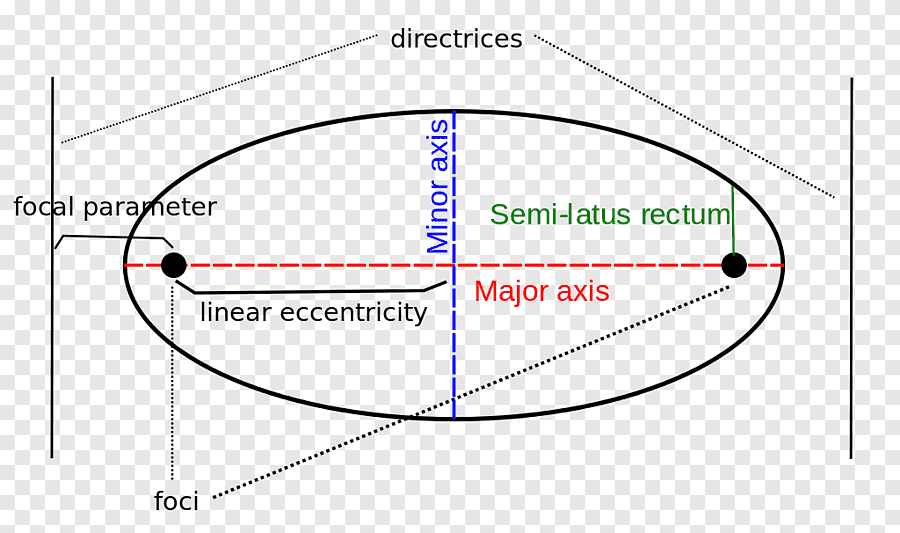
Эксцентриситет эллипса — это, проще всего, отношение расстояния c между центром эллипса и каждым фокусом к длине большой полуоси a .

езнак равноcа.{\ displaystyle e = {\ frac {c} {a}}.}

Эксцентриситет — это также отношение большой полуоси a к расстоянию d от центра до направляющей:

езнак равноаd.{\ displaystyle e = {\ frac {a} {d}}.}

Эксцентриситет можно выразить через уплощение f (определенное как для большой полуоси a и малой полуоси b ):
жзнак равно1-ба{\ displaystyle f = 1-b / a}

езнак равнож(2-ж).{\ displaystyle e = {\ sqrt {f (2-f)}}.}

(Сглаживание может обозначаться буквой g в некоторых предметных областях, если f — линейный эксцентриситет.)

Определить максимальный и минимальный радиусы и как максимальные и минимальные расстояния от любого фокуса к эллипсу (то есть расстояние от фокуса либо к двум концам главной оси). Тогда для большой полуоси a эксцентриситет определяется выражением
рМаксимум{\ displaystyle r _ {\ text {max}}}рмин{\ displaystyle r _ {\ text {min}}}

езнак равнорМаксимум-рминрМаксимум+рминзнак равнорМаксимум-рмин2а,{\ displaystyle e = {\ frac {r _ {\ text {max}} — r _ {\ text {min}}} {r _ {\ text {max}} + r _ {\ text {min}}}} = {\ frac {r _ {\ text {max}} — r _ {\ text {min}}} {2a}},}

это расстояние между фокусами, деленное на длину большой оси.

Расчет

Эксцентриситет из орбиты можно вычислить из орбитальных векторов состояния , как этого вектора эксцентриситета :

езнак равно|е|{\ Displaystyle е = \ влево | \ mathbf {е} \ вправо |}

где:

e — вектор эксцентриситета .

Для эллиптических орбит это также можно вычислить по перицентру и апоапсису, поскольку r _p = a (1 — e ) и r _a = a (1 + e ) , где a — большая полуось .

езнак равнора-рпра+рпзнак равно1-2рарп+1{\ displaystyle {\ begin {align} e & = {{r _ {\ text {a}} — r _ {\ text {p}}} \ over {r _ {\ text {a}} + r _ {\ text {p} }}} \\ & = 1 — {\ frac {2} {{\ frac {r _ {\ text {a}}} {r _ {\ text {p}}}} + 1}} \ end {выровнено}} }

где:

r _a — это радиус в апоапсисе (т. е. наибольшее расстояние от орбиты до центра масс системы, который является фокусом эллипса).
r _p — радиус в перицентре (ближайшее расстояние).

Эксцентриситет эллиптической орбиты также можно использовать для получения отношения перицентра к апоапсису :

рпразнак равно1-е1+е{\ displaystyle {{r _ {\ text {p}}} \ over {r _ {\ text {a}}}} = {{1-e} \ over {1 + e}}}

Для Земли эксцентриситет орбиты ≈ 0,0167 , апоапсис — это афелий, а периапсис — это перигелий относительно Солнца.

Для годовой орбитальной траектории Земли соотношение r _a / r _p = наибольший_радиус / наименьший_радиус ≈ 1,034 относительно центральной точки пути.