Примеры
Во всех следующих примерах рассматриваются многочлены с вещественными коэффициентами и отличным от нуля старшим коэффициентом.
Многочлен второй степени
Дискриминант квадратного трёхчлена ax2+bx+c{\displaystyle ax^{2}+bx+c} равен D=b2−4ac.{\displaystyle D=b^{2}-4ac.}
При D>0{\displaystyle D>0} вещественных корней — два, и они вычисляются по формуле
- x1,2=−b±b2−4ac2a{\displaystyle x_{1,2}={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}}.
При D=0{\displaystyle D=0} корень один (в некоторых контекстах говорят также о двух равных или совпадающих корнях), кратности 2:
- x=−b2a{\displaystyle x={\frac {-b}{2a}}}.
При D
- x1,2=−b±i4ac−b22a{\displaystyle x_{1,2}={\frac {-b\pm i{\sqrt {4ac-b^{2}}}}{2a}}}.
Многочлен третьей степени
Дискриминант кубического многочлена ax3+bx2+cx+d{\displaystyle ax^{3}+bx^{2}+cx+d} равен
- D=b2c2−4ac3−4b3d−27a2d2+18abcd.{\displaystyle D=b^{2}c^{2}-4ac^{3}-4b^{3}d-27a^{2}d^{2}+18abcd.}
В частности, дискриминант кубического многочлена x3+px+q{\displaystyle x^{3}+px+q} (корни которого вычисляются по формуле Кардано) равен −27q2−4p3{\displaystyle -27q^{2}-4p^{3}}.
- При D>{\displaystyle D>0} кубический многочлен имеет три различных вещественных корня.
- При D={\displaystyle D=0} он имеет кратный корень (либо один корень кратности 2 и один корень кратности 1, и тот, и другой вещественные; либо один-единственный вещественный корень кратности 3).
- При D<{\displaystyle D<0} кубический многочлен имеет один вещественный корень и два комплексных корня (являющихся комплексно-сопряжёнными).
Многочлен четвёртой степени
Дискриминант многочлена четвёртой степени ax4+bx3+cx2+dx+e{\displaystyle ax^{4}+bx^{3}+cx^{2}+dx+e} равен
- D=256a3e3−192a2bde2−128a2c2e2+144a2cd2e−27a2d4+144ab2ce2−6ab2d2e−80abc2de+18abcd3+16ac4e−4ac3d2−27b4e2+18b3cde−4b3d3−4b2c3e+b2c2d2.{\displaystyle {\begin{aligned}&D=256a^{3}e^{3}-192a^{2}bde^{2}-128a^{2}c^{2}e^{2}+144a^{2}cd^{2}e-27a^{2}d^{4}\\&+144ab^{2}ce^{2}-6ab^{2}d^{2}e-80abc^{2}de+18abcd^{3}+16ac^{4}e\\&-4ac^{3}d^{2}-27b^{4}e^{2}+18b^{3}cde-4b^{3}d^{3}-4b^{2}c^{3}e+b^{2}c^{2}d^{2}.\end{aligned}}}
Для многочлена x4+qx2+rx+s{\displaystyle x^{4}+qx^{2}+rx+s} дискриминант имеет вид
- D=256s3−128q2s2+144qr2s−27r4+16q4s−4q3r2{\displaystyle D=256s^{3}-128q^{2}s^{2}+144qr^{2}s-27r^{4}+16q^{4}s-4q^{3}r^{2}}
и равенство D={\displaystyle D=0} определяет в пространстве (q,r,s){\displaystyle (q,r,s)} поверхность, называемую ласточкиным хвостом.
- При D<{\displaystyle D<0} многочлен имеет два различных вещественных корня и два комплексных корня.
- При D>{\displaystyle D>0} многочлен имеет четыре различных корня: либо все вещественные, либо все комплексные.
- А именно, для многочлена x4+qx2+rx+s{\displaystyle x^{4}+qx^{2}+rx+s}:
- если q⩾{\displaystyle q\geqslant 0}, то все корни комплексные,
- если q<{\displaystyle q<0} и s>q24{\displaystyle s>{\frac {q^{2}}{4}}}, то все корни комплексные,
- если q<{\displaystyle q<0} и s<q24{\displaystyle s<{\frac {q^{2}}{4}}}, то все корни вещественные.
При D=0{\displaystyle D=0} многочлен имеет по меньшей мере один кратный корень (вещественный или комплексный). Во втором случае многочлен имеет два комплексно сопряжённых кратных корня и, следовательно, распадается в произведение двух многочленов второй степени, неприводимых над полем вещественных чисел.
- Точнее:
- если q<{\displaystyle q<0} и s>q24{\displaystyle s>{\frac {q^{2}}{4}}}, то один вещественный корень кратности 2 и два комплексных корня,
- если q<{\displaystyle q<0} и −q212<s<q24{\displaystyle -{\frac {q^{2}}{12}}<s<{\frac {q^{2}}{4}}}, то три различных вещественных корня, один из которых кратности 2,
- если q<{\displaystyle q<0} и s=q24{\displaystyle s={\frac {q^{2}}{4}}}, то два вещественных корня, каждый из которых кратности 2,
- если q<{\displaystyle q<0} и s=−q212{\displaystyle s=-{\frac {q^{2}}{12}}}, то два вещественных корня, один из которых кратности 3,
- если q>{\displaystyle q>0}, s>{\displaystyle s>0} и r≠{\displaystyle r\neq 0}, то один вещественный корень кратности 2 и два комплексных корня,
- если q>{\displaystyle q>0}, s=q24{\displaystyle s={\frac {q^{2}}{4}}} и r={\displaystyle r=0}, то одна пара комплексно сопряжённых корней кратности 2,
- если q>{\displaystyle q>0} и s={\displaystyle s=0}, то один вещественный корень кратности 2 и два комплексных корня,
- если q={\displaystyle q=0} и s>{\displaystyle s>0}, то один вещественный корень кратности 2 и два комплексных корня,
- если q={\displaystyle q=0} и s={\displaystyle s=0}, то один вещественный корень кратности 4.
Дискриминант
Эту формулу надо знать наизусть
Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение
А именно:
- Если < 0, корней нет;
- Если = 0, есть ровно один корень;
- Если > 0, корней будет два.
Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:. Выпишем коэффициенты для первого уравнения и найдем дискриминант: = 1, = −8, = 12; = (−8)2 − 4 · 1 · 12 = 64 − 48 = 16
Выпишем коэффициенты для первого уравнения и найдем дискриминант: = 1, = −8, = 12; = (−8)2 − 4 · 1 · 12 = 64 − 48 = 16
Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение: = 5; = 3; = 7; = 32 − 4 · 5 · 7 = 9 − 140 = −131.
Дискриминант отрицательный, корней нет. Осталось последнее уравнение: = 1; = −6; = 9; = (−6)2 − 4 · 1 · 9 = 36 − 36 = 0.
Дискриминант равен нулю — корень будет один.
Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок
Выбирайте сами: скорость или качество.
Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.
Дискриминант полиномиала по коммутативному кольцу
Определение дискриминанта полиномиала с точки зрения результанта может легко быть расширено на полиномиалы, коэффициенты которых принадлежат любому коммутативному кольцу. Однако, поскольку подразделение не всегда определяется в таком кольце, вместо того, чтобы делить детерминант на ведущий коэффициент, каждый заменяет ведущим коэффициентом 1 в первой колонке детерминанта. У этого обобщенного дискриминанта есть следующая собственность, которая фундаментальна в алгебраической геометрии.
Позвольте f быть полиномиалом с коэффициентами в коммутативном кольце A и D его дискриминант. Позвольте φ быть кольцевым гомоморфизмом в область К и φ (f) быть полиномиалом по K, полученному, заменив коэффициенты f их изображениями φ. Тогда у φ (D) = 0, если и только если или различие степеней f и φ (f) — по крайней мере 2 или φ (f), есть многократный корень в алгебраическом закрытии K. Первый случай может интерпретироваться, говоря, что у φ (f) есть многократный корень в бесконечности.
Типичная ситуация, где эта собственность применена, состоит в том, когда A (одномерный или многомерный), многочленное кольцо по области k и φ — замена indeterminates в элементами полевого расширения K k.
Например, позвольте f быть двумерным полиномиалом в X и Y с реальными коэффициентами, такими, что f = 0 является неявным уравнением самолета алгебраическая кривая. Рассматривая f как одномерный полиномиал в Y с коэффициентами в зависимости от X, тогда дискриминант — полиномиал в X, чьи корни — X-координаты особых точек вопросов с тангенсом, параллельным Оси Y и некоторых асимптот, параллельных Оси Y. Другими словами, вычисление корней Y-дискриминанта и X-дискриминанта позволяет вычислять все замечательные пункты кривой, кроме точек перегиба.
Дискриминант полиномиала
Чтобы найти формулу для дискриминанта полиномиала с точки зрения его коэффициентов, является самым легким ввести результант. Так же, как дискриминант единственного полиномиала — продукт квадрата различий между отличными корнями, результант двух полиномиалов — продукт различий между их корнями, и так же, как дискриминант исчезает, если и только если у полиномиала есть повторный корень, результант исчезает, если и только если эти два полиномиала разделяют корень.
Так как у полиномиала есть повторный корень, если и только если он делит корень со своей производной, у дискриминанта и результанта и есть собственность, что они исчезают, если и только если у p есть повторный корень, и у них есть почти та же самая степень (степень результанта — одно большее, чем степень дискриминанта), и таким образом равны до фактора степени один.
Выгода результанта — то, что он может быть вычислен как детерминант, а именно, как детерминант матрицы Сильвестра, (2n − 1) × (2n − 1) матрица, n − 1 которой первые ряды содержат коэффициенты p и n последние коэффициенты его производной.
Результант общего полиномиала
до фактора, равного детерминанту (2n − 1) × (2n − 1) матрица Сильвестра:
& a_n & a_ {n-1} & a_ {n-2} & \ldots & a_1 & a_0 & 0 \ldots & \ldots & 0 \\
& 0 & a_n & a_ {n-1} & a_ {n-2} & \ldots & a_1 & a_0 & 0 \ldots & 0 \\
& \vdots\&&&&&&&& \vdots \\
& 0 & \ldots\& 0 & a_n & a_ {n-1} & a_ {n-2} & \ldots & a_1 & a_0 \\
& na_n & (n-1) a_ {n-1} & (n-2) a_ {n-2} & \ldots\& a_1 & 0 & \ldots &\\ldots & 0 \\
& 0 & na_n & (n-1) a_ {n-1} & (n-2) a_ {n-2} & \ldots\& a_1 & 0 & \ldots & 0 \\
& \vdots\&&&&&&&& \vdots \\
& 0 & 0 & \ldots & 0 & na_n & (n-1) a_ {n-1} & (n-2) a_ {n-2} & \ldots\& a_1 \\
Дискриминант теперь дан формулой
Например, в случае n = 4, вышеупомянутый детерминант —
& a_4 & a_3 & a_2 & a_1 & a_0 & 0 & 0 \\
& 0 & a_4 & a_3 & a_2 & a_1 & a_0 & 0 \\
& 0 & 0 & a_4 & a_3 & a_2 & a_1 & a_0 \\
& 4a_4 & 3a_3 & 2a_2 & 1a_1 & 0 & 0 & 0 \\
& 0 & 4a_4 & 3a_3 & 2a_2 & 1a_1 & 0 & 0 \\
& 0 & 0 & 4a_4 & 3a_3 & 2a_2 & 1a_1& 0 \\
& 0 & 0 & 0 & 4a_4 & 3a_3 & 2a_2 & 1a_1 \\
Дискриминант степени 4 полиномиала тогда получен из этого детерминанта после деления на.
С точки зрения корней дискриминант равен
где r…, r являются сложными корнями (подсчитывающий разнообразие) полиномиала:
Это второе выражение проясняет, что у p есть многократный корень, если и только если дискриминант — ноль. (Этот многократный корень может быть сложным.)
Дискриминант может быть определен для полиномиалов по произвольным областям точно тем же самым способом как выше. Формула продукта, включающая корни r, остается действительной; корни должны быть пущены в некоторой разделяющейся области полиномиала. Дискриминант может даже быть определен для полиномиалов по любому коммутативному кольцу. Однако, если кольцо не составная область, выше подразделения результанта должен быть заменен, заняв место 1 в первой колонке матрицы.
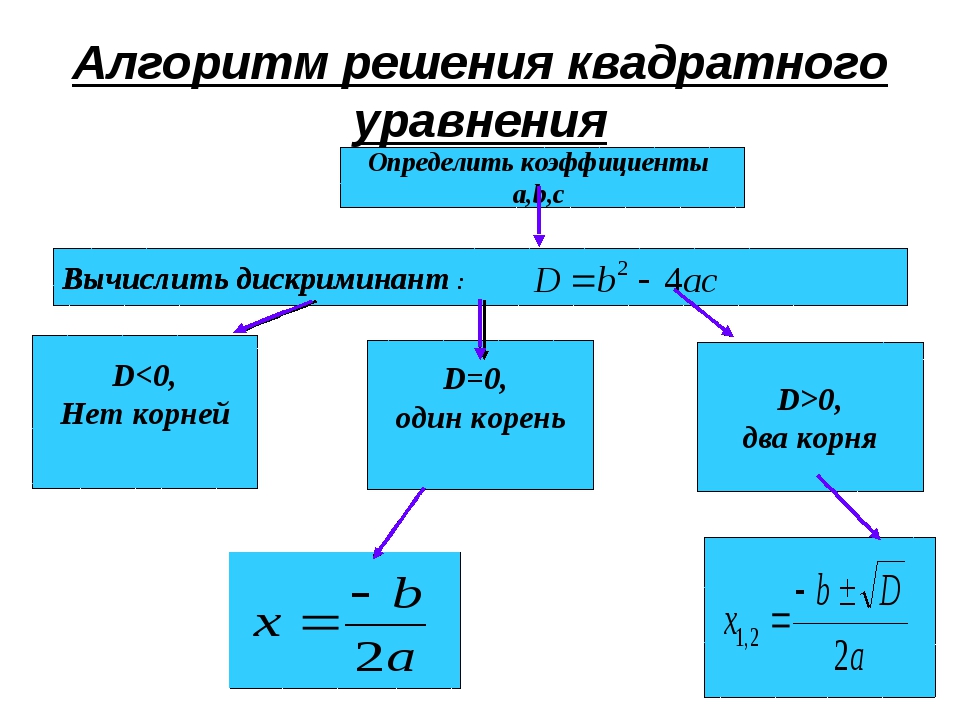
Корни квадратного уравнения
Теперь перейдем, собственно, к решению. Если дискриминант > 0, корни можно найти по формулам:
Основная формула корней квадратного уравнения
Когда = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если < 0, корней нет — ничего считать не надо.
Первое уравнение:2 − 2 − 3 = 0 ⇒ = 1; = −2; = −3; = (−2)2 − 4 · 1 · (−3) = 16.
> 0 ⇒ уравнение имеет два корня. Найдем их:
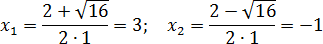
Второе уравнение:15 − 2 − 2 = 0 ⇒ = −1; = −2; = 15; = (−2)2 − 4 · (−1) · 15 = 64.
> 0 ⇒ уравнение снова имеет два корня. Найдем их
\
Наконец, третье уравнение:2 + 12 + 36 = 0 ⇒ a = 1; b = 12; c = 36;D = 122 − 4 · 1 · 36 = 0.
D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:
\
Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Решение квадратных уравнений.
Решение полных квадратных уравнений.
Квадратные уравнения решаются просто. По формулам и чётким несложным правилам. На первом этапе надо заданное уравнение привести к стандартному виду, т.е. к виду:
Если уравнение вам дано уже в таком виде — первый этап делать не нужно.) Главное — правильно определить все коэффициенты, а, b и c.
Формула для нахождения корней квадратного уравнения выглядит так:
Выражение под знаком корня называется дискриминант. Но о нём — ниже. Как видим, для нахождения икса, мы используем только a, b и с. Т.е. коэффициенты из квадратного уравнения. Просто аккуратно подставляем значения a, b и с в эту формулу и считаем. Подставляем со своими знаками! Например, в уравнении:
а =1; b = 3; c = -4. Вот и записываем:
Пример практически решён:
Это ответ.
Всё очень просто. И что, думаете, ошибиться нельзя? Ну да, как же…
Самые распространённые ошибки – путаница со знаками значений a, b и с. Вернее, не с их знаками (где там путаться?), а с подстановкой отрицательных значений в формулу для вычисления корней. Здесь спасает подробная запись формулы с конкретными числами. Если есть проблемы с вычислениями, так и делайте!
Предположим, надо вот такой примерчик решить:
Здесь a = -6; b = -5; c = -1
Допустим, вы знаете, что ответы у вас редко с первого раза получаются.
Ну и не ленитесь. Написать лишнюю строчку займёт секунд 30. А количество ошибок резко сократится. Вот и пишем подробно, со всеми скобочками и знаками:
Это кажется невероятно трудным, так тщательно расписывать. Но это только кажется. Попробуйте. Ну, или выбирайте. Что лучше, быстро, или правильно?
Кроме того, я вас обрадую. Через некоторое время отпадёт нужда так тщательно всё расписывать. Само будет правильно получаться. Особенно, если будете применять практические приёмы, что описаны чуть ниже. Этот злой пример с кучей минусов решится запросто и без ошибок!
Но, частенько, квадратные уравнения выглядят слегка иначе. Например, вот так:
Или так:
Узнали?) Да! Это неполные квадратные уравнения.
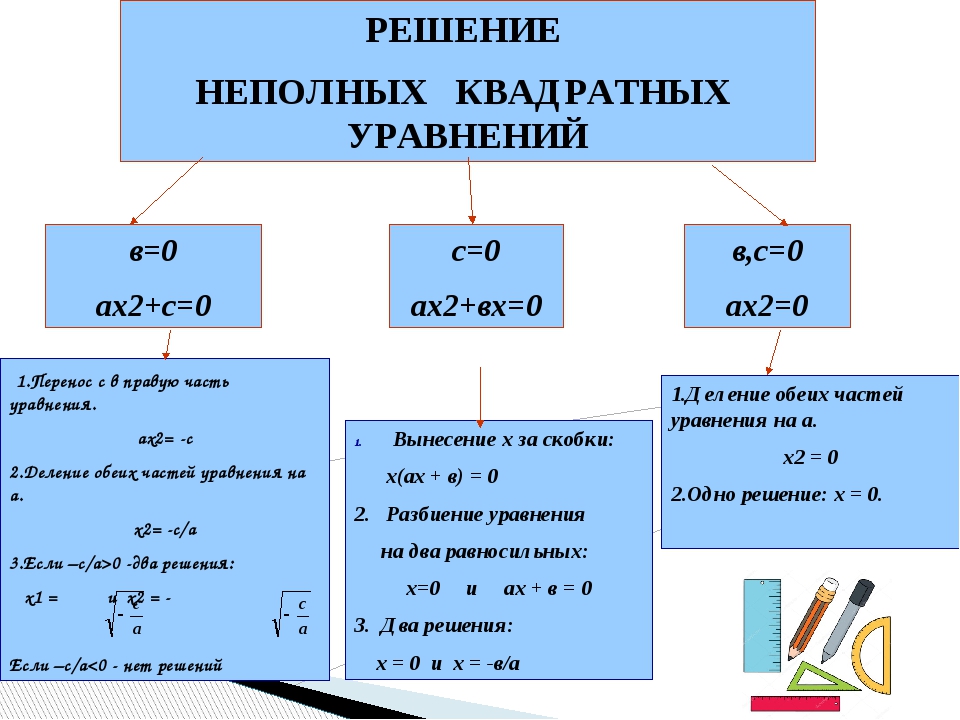
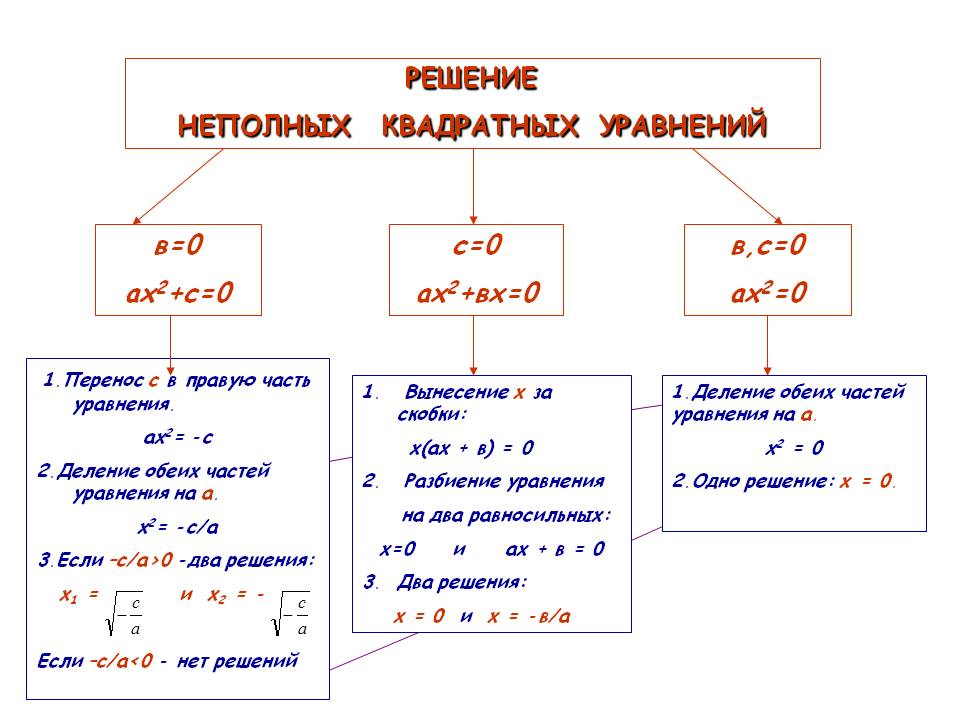
Решение неполных квадратных уравнений.
Их тоже можно решать по общей формуле. Надо только правильно сообразить, чему здесь равняются a, b и с.
Сообразили? В первом примере a = 1; b = -4; а c? Его вообще нет! Ну да, правильно. В математике это означает, что c = 0! Вот и всё. Подставляем в формулу ноль вместо c, и всё у нас получится. Аналогично и со вторым примером. Только ноль у нас здесь не с, а b !
Но неполные квадратные уравнения можно решать гораздо проще. Безо всяких формул. Рассмотрим первое неполное уравнение. Что там можно сделать в левой части? Можно икс вынести за скобки! Давайте вынесем.
И что из этого? А то, что произведение равняется нулю тогда, и только тогда, когда какой-нибудь из множителей равняется нулю! Не верите? Хорошо, придумайте тогда два ненулевых числа, которые при перемножении ноль дадут!
Не получается? То-то…
Следовательно, можно уверенно записать:
х1 = 0, х2 = 4.
Всё. Это и будут корни нашего уравнения. Оба подходят. При подстановке любого из них в исходное уравнение, мы получим верное тождество 0 = 0. Как видите, решение куда проще, чем по общей формуле. Замечу, кстати, какой икс будет первым, а какой вторым — абсолютно безразлично. Удобно записывать по порядочку, х1 — то, что меньше, а х2 — то, что больше.
Второе уравнение тоже можно решить просто. Переносим 9 в правую часть. Получим:
Остаётся корень извлечь из 9, и всё. Получится:
Тоже два корня. х1 = -3, х2 = 3.
Так решаются все неполные квадратные уравнения. Либо с помощью вынесения икса за скобки, либо простым переносом числа вправо с последующим извлечением корня.
Спутать эти приёмы крайне сложно. Просто потому, что в первом случае вам придется корень из икса извлекать, что как-то непонятно, а во втором случае выносить за скобки нечего…
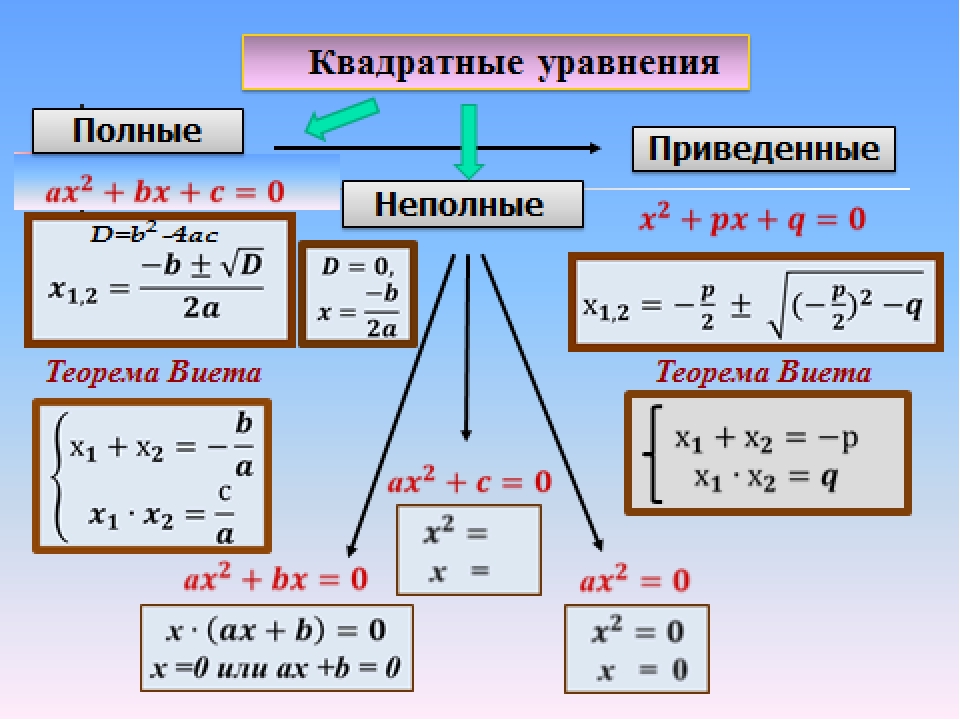
Виды квадратных уравнений
Что такое квадратное уравнение? Как оно выглядит? В термине квадратное уравнение ключевым словом является «квадратное». Оно означает, что в уравнении обязательно должен присутствовать икс в квадрате. Кроме него, в уравнении могут быть (а могут и не быть!) просто икс (в первой степени) и просто число (свободный член). И не должно быть иксов в степени, больше двойки.
Говоря математическим языком, квадратное уравнение — это уравнение вида:
Здесь a, b и с – какие-то числа. b и c – совсем любые, а а – любое, кроме нуля. Например:
Здесь а =1; b = 3; c = -4
Или:
Здесь а =2; b = -0,5; c = 2,2
Или:
Здесь а =-3; b = 6; c = -18
Ну, вы поняли…
В этих квадратных уравнениях слева присутствует полный набор членов. Икс в квадрате с коэффициентом а, икс в первой степени с коэффициентом b и свободный член с.
Такие квадратные уравнения называются полными.
А если b = 0, что у нас получится? У нас пропадёт икс в первой степени. От умножения на ноль такое случается.) Получается, например:
5х2-25 = 0,
Или:
х2+4 = 0
И так далее. Если же c = 0, получим уравнение без свободного члена:
2х2-6х=0,
Или:
-х2+4х=0
И т.п. А если уж оба коэффицента, b и c равны нулю, то всё ещё проще:
2х2=0,
Или:
-0,3х2=0
Такие уравнения, где чего-то не хватает, называются неполными квадратными уравнениями. Что вполне логично.) Прошу заметить, что икс в квадрате присутствует во всех уравнениях.
Кстати, почему а не может быть равно нулю? А вы подставьте вместо а нолик.) У нас исчезнет икс в квадрате! Уравнение станет линейным. И решается уже совсем иначе…
Вот и все главные виды квадратных уравнений. Полные и неполные.