Дифференциалы — это что такое? как найти дифференциал функции?

Дифференциал функции.

Определение 2.

Если функция \(y=f(x)\) определена в \(\delta\)-окрестности точки \(x_0\), а приращение \(\Delta y\) функции \(y=f(x)\) в точке \(x_0\) представимо в виде
$$
\Delta y=A\Delta x+\Delta x\varepsilon(\Delta x),\label{ref19}
$$
где \(A=A(x_0)\) не зависит от \(\Delta x\), a \(\varepsilon(\Delta x)\rightarrow 0\) при \(\Delta x\rightarrow 0\), то функция \(f\) называется дифференцируемой в точке \(x_0\), а произведение \(A\Delta x\) называется ее дифференциалом в точке \(x_0\) и обозначается \(df(x_0)\) или \(dy\).

Таким образом,
$$
\Delta y=dy+o(\Delta x)\ при\ \Delta x\rightarrow 0,\label{ref20}
$$
где
$$
dy=A\Delta x.\label{ref21}
$$
Отметим, что приращение \(\Delta y=f(x_0+\Delta x)-f(x_0)\) можно рассматривать только для таких \(\Delta x\), при которых точка \(x_0+\Delta x\) принадлежит области определения функции \(f\), в то время как дифференциал \(dy\) определен при любых \(\Delta x\).

Теорема 2.

Для того чтобы функция \(y=f(x)\) была дифференцируемой в точке \(x_0\), необходимо и достаточно, чтобы эта функция имела производную в точке \(x_0\). При этом дифференциал и производная связаны равенством
$$
dy=f'(x_{0})\Delta x.\label{ref22}
$$

\(\circ\) Если функция \(y=f(x)\) дифференцируема в точке \(x_0\), то выполняется условие \eqref{ref19}, и поэтому \(\displaystyle \frac{\Delta y}{\Delta x}=A+\varepsilon(\Delta x)\), где \(\varepsilon(\Delta x)\rightarrow 0\) при \(\Delta x\rightarrow 0(\Delta x\neq 0)\), откуда следует, что существует \(\displaystyle \lim_{\Delta x\rightarrow 0}\frac{\Delta y}{\Delta x}=A\), то есть существует \(f'(x_0)=A\).

Обратно: если существует \(f'(x_{0})\), то справедливо равенство \eqref{ref5}, и поэтому выполняется условие \eqref{ref19}. Это означает, что функция \(f\) дифференцируема в точке \(x=x_0\), причем коэффициент \(A\) в формулах \eqref{ref19} и \eqref{ref21} равен \(f'(x_{0})\), и поэтому дифференциал записывается в виде \eqref{ref22}. \(\bullet\)

Таким образом, существование производной функции в данной точке равносильно дифференцируемости функции в этой точке. Функцию, имеющую производную в каждой точке интервала \((a,b)\), называют дифференцируемой на интервале \((a,b)\).

Если функция \(f\) дифференцируема на интервале \((a,b)\) и, кроме того, существуют \(f_{+}'(a)\) и \(f_{-}'(b)\), то функцию \(f\) называют дифференцируемой на отрезке \(\).

Замечание 3.

Если \(f'(x_0)\neq 0\), то из равенств \eqref{ref20} и \eqref{ref22} следует, что \(dy\neq 0\) при \(\Delta x\neq 0\) и
$$
\Delta y\sim dy\ при\ \Delta x\rightarrow 0.\nonumber
$$
В этом случае говорят, что дифференциал есть главная линейная часть приращения функции, так как дифференциал есть линейная функция от \(\Delta x\) и отличается от \(\Delta y\) на бесконечно малую более высокого порядка, чем \(\Delta x\).

Замечание 4.

Приращение \(\Delta x\) часто обозначают символом \(dx\) и называют дифференциалом независимого переменного. Поэтому формулу \eqref{ref22} записывают в виде
$$
dy=f'(x_{0})dx.\label{ref23}
$$
По формуле \eqref{ref23} можно найти дифференциал функции, зная ее производную. Например, \(d\sin x=\cos x dx,\;de^{x}=e^{x}dx\). Из формулы \eqref{ref23} получаем
$$
f'(x_{0})=\frac{dy}{dx}.\label{ref24}
$$
Согласно формуле \eqref{ref24} производную можно рассматривать как отношение дифференциала функции к дифференциалу независимого переменного.

Замечание 5.

Отбрасывая в формуле \eqref{ref20} член \(o(\Delta x)\), то есть заменяя приращение функции ее дифференциалом, получаем приближенное равенство \(\Delta y\approx f'(x_0)\Delta x\), или
$$
f(x_{0}+\Delta x)\approx f(x_{0})+f'(x_{0})\Delta x.\label{ref25}
$$
Формулу \eqref{ref25} можно использовать для вычисления приближенного значения \(f(x_{0}+\Delta x)\) при малых \(\Delta x\), если известны значения \(f(x_{0})\) и \(f'(x_0)\).

Пример 6.

Найти с помощью формулы \eqref{ref25} приближенное значение функции \(y=\sqrt{x}\) при \(x=90\).

\(\triangle\) Полагая в формуле \eqref{ref25} \(f(x)=\sqrt{x}\), \(x_0=81,\ \Delta x=9\) и учитывая, что \(f(x_{0})=\sqrt{81}=3\), \(f'(x)=\displaystyle \frac{1}{4}x^{-3/4}\), \(f'(x_{0})=\displaystyle \frac{1}{3^3}\), получаем \(\sqrt{90}\approx 3+\displaystyle \frac{1}{12}\), то есть \(\sqrt{90}\approx 3,083.\ \blacktriangle\)

Обозначения

Обычно дифференциал функции f{\displaystyle f} обозначается df{\displaystyle df}.
Некоторые авторы предпочитают обозначать df{\displaystyle {\rm {d}}f} шрифтом прямого начертания, желая подчеркнуть, что дифференциал является оператором.

Дифференциал в точке x{\displaystyle x_{0}} обозначается dxf{\displaystyle d_{x_{0}}f}, а иногда dfx{\displaystyle df_{x_{0}}} или dfx{\displaystyle df},
а также df{\displaystyle df}, если значение x{\displaystyle x_{0}} ясно из контекста.

Соответственно, значение дифференциала в точке x{\displaystyle x_{0}} от h{\displaystyle h}
может обозначаться как dxf(h){\displaystyle d_{x_{0}}f(h)}, а иногда dfx(h){\displaystyle df_{x_{0}}(h)} или dfx(h){\displaystyle df(h)},
а также df(h){\displaystyle df(h)}, если значение x{\displaystyle x_{0}} ясно из контекста.

Обозначения

Обычно дифференциал функции f{\displaystyle f} обозначается df{\displaystyle df}.
Некоторые авторы предпочитают обозначать df{\displaystyle {\rm {d}}f} шрифтом прямого начертания, желая подчеркнуть, что дифференциал является оператором.

Дифференциал в точке x{\displaystyle x_{0}} обозначается dxf{\displaystyle d_{x_{0}}f}, а иногда dfx{\displaystyle df_{x_{0}}} или dfx{\displaystyle df},
а также df{\displaystyle df}, если значение x{\displaystyle x_{0}} ясно из контекста.

Соответственно, значение дифференциала в точке x{\displaystyle x_{0}} от h{\displaystyle h}
может обозначаться как dxf(h){\displaystyle d_{x_{0}}f(h)}, а иногда dfx(h){\displaystyle df_{x_{0}}(h)} или dfx(h){\displaystyle df(h)},
а также df(h){\displaystyle df(h)}, если значение x{\displaystyle x_{0}} ясно из контекста.

Использование знака дифференциала

• Знак дифференциала используется в выражении для интеграла ∫f(x)dx{\displaystyle \int f(x)\,dx}. При этом иногда (и не вполне корректно) дифференциал dx{\displaystyle dx} вводится как часть определения интеграла[источник не указан 229 дней].
• Также знак дифференциала используется в обозначении Лейбница для производной f′(x)=dfdx(x){\displaystyle f'(x_{0})={\frac {df}{dx}}(x_{0})}. Это обозначение мотивировано тем, что для дифференциалов функции f{\displaystyle f} и тождественной функции x{\displaystyle x} верно соотношение

  dxf=f′(x)⋅dxx.{\displaystyle d_{x_{0}}f=f'(x_{0}){\cdot }d_{x_{0}}x.}

Определения

Для функций

Дифференциал функции fR→R{\displaystyle f\colon \mathbb {R} \to \mathbb {R} } в точке x∈R{\displaystyle x_{0}\in \mathbb {R} } может быть определён как линейная функция

dxf(h)=f′(x)h,{\displaystyle d_{x_{0}}f(h)=f'(x_{0})h,}

где f′(x){\displaystyle f'(x_{0})} обозначает производную f{\displaystyle f} в точке x{\displaystyle x_{0}}, а h{\displaystyle h} — приращение аргумента при переходе от x{\displaystyle x_{0}} к x+h{\displaystyle x_{0}+h}.

Таким образом df{\displaystyle df} есть функция двух аргументов df(x,h)↦dxf(h){\displaystyle df\colon (x_{0},h)\mapsto d_{x_{0}}f(h)}.

Дифференциал может быть определён напрямую, то есть, без привлечения определения производной, как функция dxf(h){\displaystyle d_{x_{0}}f(h)}, линейно зависящая от h{\displaystyle h}, и для которой верно следующее соотношение

dxf(h)=f(x+h)−f(x)+o(h).{\displaystyle d_{x_{0}}f(h)=f(x_{0}+h)-f(x_{0})+o(h).}

Для отображений

Дифференциалом отображения fRn→Rm{\displaystyle f\colon \mathbb {R} ^{n}\to \mathbb {R} ^{m}} в точке x∈Rn{\displaystyle x_{0}\in \mathbb {R} ^{n}} называют линейный оператор dxfRn→Rm{\displaystyle d_{x_{0}}f\colon \mathbb {R} ^{n}\to \mathbb {R} ^{m}} такой, что выполняется условие

dxf(h)=f(x+h)−f(x)+o(h).{\displaystyle d_{x_{0}}f(h)=f(x_{0}+h)-f(x_{0})+o(h).}

Приближенные вычисления с применением дифференциала

Вычислить функцию f (x), а также ее производную f ‘(x) при x=a часто нетрудно, а вот сделать то же самое в окрестности точки x=a бывает нелегко. Тогда на помощь приходит приближенное выражение

f(a + Δх) ≈ f ‘(a)Δх + f(a).

Оно дает приближенное значение функции при малых приращениях Δх через ее дифференциал f ‘(a)Δх.

Следовательно, данная формула дает приближенное выражение для функции в конечной точке некоторого участка длиной Δх в виде суммы ее значения в начальной точке этого участка (x=a) и дифференциала в той же начальной точке. Погрешность такого способа определения значения функции иллюстрирует рисунок ниже.

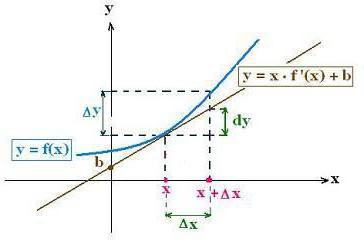
Однако известно и точное выражение значения функции для x=a+Δх, даваемое формулой конечных приращений (или, иначе, формулой Лагранжа)

f(a+ Δх) ≈ f ‘(ξ) Δх + f(a),

где точка x = a+ ξ находится на отрезке от x = a до x = a + Δх, хотя точное положение ее неизвестно. Точная формула позволяет оценивать погрешность приближенной формулы. Если же в формуле Лагранжа положить ξ = Δх /2, то хотя она и перестает быть точной, но дает, как правило, гораздо лучшее приближение, чем исходное выражение через дифференциал.

Использование знака дифференциала

• Знак дифференциала используется в выражении для интеграла ∫f(x)dx{\displaystyle \int f(x)\,dx}. При этом иногда (и не вполне корректно) дифференциал dx{\displaystyle dx} вводится как часть определения интеграла[источник не указан 894 дня].
• Также знак дифференциала используется в обозначении Лейбница для производной f′(x)=dfdx(x){\displaystyle f'(x_{0})={\frac {df}{dx}}(x_{0})}. Это обозначение мотивировано тем, что для дифференциалов функции f{\displaystyle f} и тождественной функции x{\displaystyle x} верно соотношение:

  dxf=f′(x)⋅dxx.{\displaystyle d_{x_{0}}f=f'(x_{0}){\cdot }d_{x_{0}}x.}

Использование знака дифференциала

• Знак дифференциала используется в выражении для интеграла ∫f(x)dx{\displaystyle \int f(x)\,dx}. При этом иногда (и не вполне корректно) дифференциал dx{\displaystyle dx} вводится как часть определения интеграла[источник не указан 229 дней].
• Также знак дифференциала используется в обозначении Лейбница для производной f′(x)=dfdx(x){\displaystyle f'(x_{0})={\frac {df}{dx}}(x_{0})}. Это обозначение мотивировано тем, что для дифференциалов функции f{\displaystyle f} и тождественной функции x{\displaystyle x} верно соотношение

  dxf=f′(x)⋅dxx.{\displaystyle d_{x_{0}}f=f'(x_{0}){\cdot }d_{x_{0}}x.}

Определения

Для функций

Дифференциал функции fR→R{\displaystyle f\colon \mathbb {R} \to \mathbb {R} } в точке x∈R{\displaystyle x_{0}\in \mathbb {R} } может быть определён как линейная функция

dxf(h)=f′(x)h,{\displaystyle d_{x_{0}}f(h)=f'(x_{0})h,}

где f′(x){\displaystyle f'(x_{0})} обозначает производную f{\displaystyle f} в точке x{\displaystyle x_{0}}, а h{\displaystyle h} — приращение аргумента при переходе от x{\displaystyle x_{0}} к x+h{\displaystyle x_{0}+h}.

Таким образом df{\displaystyle df} есть функция двух аргументов df(x,h)↦dxf(h){\displaystyle df\colon (x_{0},h)\mapsto d_{x_{0}}f(h)}.

Дифференциал может быть определён напрямую, то есть, без привлечения определения производной, как функция dxf(h){\displaystyle d_{x_{0}}f(h)}, линейно зависящая от h{\displaystyle h}, и для которой верно следующее соотношение

dxf(h)=f(x+h)−f(x)+o(h).{\displaystyle d_{x_{0}}f(h)=f(x_{0}+h)-f(x_{0})+o(h).}

Для отображений

Дифференциалом отображения fRn→Rm{\displaystyle f\colon \mathbb {R} ^{n}\to \mathbb {R} ^{m}} в точке x∈Rn{\displaystyle x_{0}\in \mathbb {R} ^{n}} называют линейный оператор dxfRn→Rm{\displaystyle d_{x_{0}}f\colon \mathbb {R} ^{n}\to \mathbb {R} ^{m}} такой, что выполняется условие

dxf(h)=f(x+h)−f(x)+o(h).{\displaystyle d_{x_{0}}f(h)=f(x_{0}+h)-f(x_{0})+o(h).}

Что более универсально: приращение аргумента или его дифференциал

Здесь необходимо сделать некоторые пояснения. Представление величиной f ‘(x)Δх дифференциала возможно при рассмотрении х в качестве аргумента. Но функция может быть сложной, в которой х может быть функцией некоторого аргумента t. Тогда представление дифференциала выражением f ‘(x)Δх, как правило, невозможно; кроме случая линейной зависимости х = at + b.

Что же касается формулы f ‘(x)dx= dy, то и в случае независимого аргумента х (тогда dx = Δх), и в случае параметрической зависимости х от t, она представляет дифференциал.

Например, выражение 2 x Δх представляет для y = x2 ее дифференциал, когда х есть аргумент. Положим теперь х= t2 и будем считать t аргументом. Тогда y = x2 = t4.

Далее следует (t +Δt)2 = t2 + 2tΔt + Δt2. Отсюда Δх = 2tΔt + Δt2. Значит: 2xΔх = 2t2 (2tΔt + Δt2 ).

Это выражение не пропорционально Δt и потому теперь 2xΔх не является дифференциалом. Его можно найти из уравнения y = x2 = t4. Он оказывается равен dy=4t3Δt.

Если же взять выражение 2xdx, то оно представляет дифференциал y = x2 при любом аргументе t. Действительно, при х= t2 получим dx = 2tΔt.

Значит 2xdx = 2t22tΔt = 4t3Δt, т. е. выражения дифференциалов, записанные через две разные переменные, совпали.

Обозначения

Обычно дифференциал функции f{\displaystyle f} обозначается df{\displaystyle df}.
Некоторые авторы предпочитают обозначать df{\displaystyle {\rm {d}}f} шрифтом прямого начертания, желая подчеркнуть, что дифференциал является оператором.

Дифференциал в точке x{\displaystyle x_{0}} обозначается dxf{\displaystyle d_{x_{0}}f}, а иногда dfx{\displaystyle df_{x_{0}}} или dfx{\displaystyle df},
а также df{\displaystyle df}, если значение x{\displaystyle x_{0}} ясно из контекста.

Соответственно, значение дифференциала в точке x{\displaystyle x_{0}} от h{\displaystyle h}
может обозначаться как dxf(h){\displaystyle d_{x_{0}}f(h)}, а иногда dfx(h){\displaystyle df_{x_{0}}(h)} или dfx(h){\displaystyle df(h)},
а также df(h){\displaystyle df(h)}, если значение x{\displaystyle x_{0}} ясно из контекста.

Возникновение понятия о дифференциале

Впервые разъяснил, что такое дифференциал, один из создателей (наряду с Исааком Ньютоном) дифференциального исчисления знаменитый немецкий математик Готфрид Вильгельм Лейбниц. До этого математиками 17 ст. использовалось весьма нечеткое и расплывчатое представление о некоторой бесконечно малой «неделимой» части любой известной функции, представлявшей очень малую постоянную величину, но не равную нулю, меньше которой значения функции быть просто не могут. Отсюда был всего один шаг до введения представления о бесконечно малых приращениях аргументов функций и соответствующих им приращениях самих функций, выражаемых через производные последних. И этот шаг был сделан практически одновременно двумя вышеупомянутыми великими учеными.

Исходя из необходимости решения насущных практических задач механики, которые ставила перед наукой бурно развивающаяся промышленность и техника, Ньютон и Лейбниц создали общие способы нахождения скорости изменения функций (прежде всего применительно к механической скорости движения тела по известной траектории), что привело к введению таких понятий, как производная и дифференциал функции, а также нашли алгоритм решения обратной задачи, как по известной (переменной) скорости найти пройденный путь, что привело к появлению понятия интеграла.

В трудах Лейбница и Ньютона впервые появилось представление о том, что дифференциалы — это пропорциональные приращениям аргументов Δх основные части приращений функций Δу, которые могут быть с успехом применены для вычисления значений последних. Иначе говоря, ими было открыто, что приращение функции может быть в любой точке (внутри области ее определения) выражено через ее производную как Δу = y'(x) Δх + αΔх, где α Δх – остаточный член, стремящийся к нулю при Δх→0, гораздо быстрее, чем само Δх.

Согласно основоположникам матанализа, дифференциалы – это как раз и есть первые члены в выражениях приращений любых функций. Еще не обладая четко сформулированным понятием предела последовательностей, они интуитивно поняли, что величина дифференциала стремится к производной функции при Δх→0 — Δу/Δх→ y'(x).

В отличие от Ньютона, который был прежде всего физиком, и рассматривал математический аппарат как вспомогательный инструмент исследования физических задач, Лейбниц уделял большее внимание самому этому инструментарию, включая и систему наглядных и понятных обозначений математических величин. Именно он предложил общепринятые обозначения дифференциалов функции dy = y'(x)dx, аргумента dx и производной функции в виде их отношения y'(x) = dy/dx

Определения

Для функций

Дифференциал функции fR→R{\displaystyle f\colon \mathbb {R} \to \mathbb {R} } в точке x∈R{\displaystyle x_{0}\in \mathbb {R} } может быть определён как линейная функция

dxf(h)=f′(x)h,{\displaystyle d_{x_{0}}f(h)=f'(x_{0})h,}

где f′(x){\displaystyle f'(x_{0})} обозначает производную f{\displaystyle f} в точке x{\displaystyle x_{0}}, а h{\displaystyle h} — приращение аргумента при переходе от x{\displaystyle x_{0}} к x+h{\displaystyle x_{0}+h}.

Таким образом df{\displaystyle df} есть функция двух аргументов df(x,h)↦dxf(h){\displaystyle df\colon (x_{0},h)\mapsto d_{x_{0}}f(h)}.

Дифференциал может быть определён напрямую, то есть, без привлечения определения производной, как функция dxf(h){\displaystyle d_{x_{0}}f(h)}, линейно зависящая от h{\displaystyle h}, и для которой верно следующее соотношение

dxf(h)=f(x+h)−f(x)+o(h).{\displaystyle d_{x_{0}}f(h)=f(x_{0}+h)-f(x_{0})+o(h).}

Для отображений

Дифференциалом отображения fRn→Rm{\displaystyle f\colon \mathbb {R} ^{n}\to \mathbb {R} ^{m}} в точке x∈Rn{\displaystyle x_{0}\in \mathbb {R} ^{n}} называют линейный оператор dxfRn→Rm{\displaystyle d_{x_{0}}f\colon \mathbb {R} ^{n}\to \mathbb {R} ^{m}} такой, что выполняется условие

dxf(h)=f(x+h)−f(x)+o(h).{\displaystyle d_{x_{0}}f(h)=f(x_{0}+h)-f(x_{0})+o(h).}

Использование знака дифференциала

• Знак дифференциала используется в выражении для интеграла ∫f(x)dx{\displaystyle \int f(x)\,dx}. При этом иногда (и не вполне корректно) дифференциал dx{\displaystyle dx} вводится как часть определения интеграла[источник не указан 229 дней].
• Также знак дифференциала используется в обозначении Лейбница для производной f′(x)=dfdx(x){\displaystyle f'(x_{0})={\frac {df}{dx}}(x_{0})}. Это обозначение мотивировано тем, что для дифференциалов функции f{\displaystyle f} и тождественной функции x{\displaystyle x} верно соотношение

  dxf=f′(x)⋅dxx.{\displaystyle d_{x_{0}}f=f'(x_{0}){\cdot }d_{x_{0}}x.}

Схема дифференциала, виды дифференциалов

Если говорить о конструкции дифференциала, то он построен на основе редуктора. В зависимости от того, какой вид зубчатой передачи использовался, конструктивно различают конический, цилиндрический и червячный дифференциалы.

Конический дифференциал, как правило, используется как межколесный дифференциал, цилиндрический — между осями в полноприводных автомобилях. Червячный дифференциал может быть установлен как между колесами, так и между осями.

В конструкцию любого дифференциала входит корпус, сателлиты и полуосевые шестерни. Корпусом воспринимается крутящий момент от главной передачи, после чего он передается на шестерни и сателлиты. Ведомая шестерня главной передачи закрепляется непосредственно на корпусе. Внутри корпуса располагаются оси, на которых происходит вращение сателлитов.

Именно по полуосевым шестерням через полуоси на ведущие колеса передается крутящий момент. Если левая и правая шестерни имеют одинаковое число зубьев, дифференциал называется симметричным. Для несимметричных дифференциалов, которые устанавливают между ведущими осями машины, так как они распределяют крутящий момент между колесами в некотором соотношении, характерно разное количество зубьев.

На силу тяги на колесе машины влияют радиус колеса, а также подводимый к нему крутящий момент. На динамический радиус колеса производится определенная сила тяги, что и обеспечивает крутящий момент, который должен передаться дифференциалом на колеса.

Если автомобиль имеет слабое сцепление с дорогой или же одно из колес разгружено, то сила тяги и крутящий момент на этом колесе практически отсутствуют. Это значит, что автомобиль не сможет продолжать движение. Подобную особенность имеет конический дифференциал, который часто встречается на отечественных легковых авто. Такой дифференциал, обычно используемый в качестве межколесного, называют симметричным, так как он равномерно разделяет между колесами крутящий момент.

Таким образом, когда одно из колес автомобиля имеет плохое сцепление с дорогой и крутящий момент на нем практически отсутствует, то же самое происходит и со вторым колесом, так как симметричный дифференциал передает к нему такое же усилие. Получается, если одно из колес забуксует, на втором колесе сила тяги приблизится к нулю, что негативно повлияет на проходимость автомобиля.