Целое число

Применение

В прикладных науках

Отметки целых значений температуры на шкале термометра

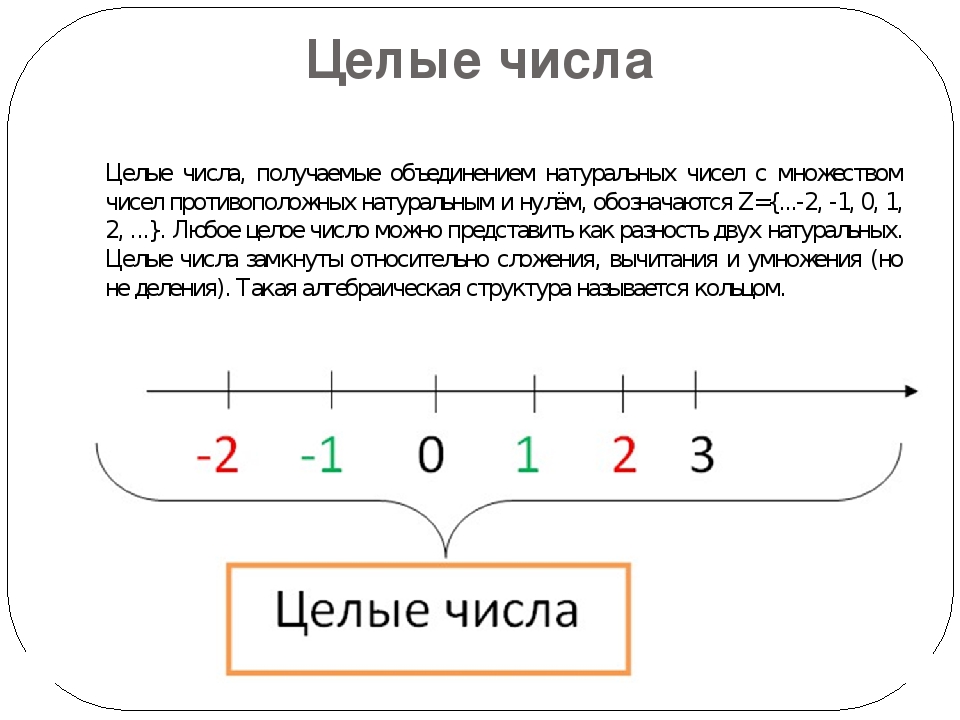
Целые числа широко применяются при исследовании объектов, которые по своей природе или по особенностям постановки задачи неделимы (например, люди, суда, строения, иногда дни и т. п.). Отрицательные числа также могут найти применение в таких моделях — скажем, при планировании торговых сделок можно продажи обозначать положительными числами, а покупки — отрицательными. Пример из физики — квантовые числа, играющие фундаментальную роль в микромире; все они — целые (или полуцелые) числа со знаком.

Для решения возникающих при этом задач разработаны специальные математические методы, учитывающие специфику проблем. В частности, решение в целых числах алгебраических уравнений (разных степеней) рассматривает теория «диофантовых уравнений». Вопросы целочисленной оптимизации исследует целочисленное программирование.

В информатике

Основная статья: Целое (тип данных)

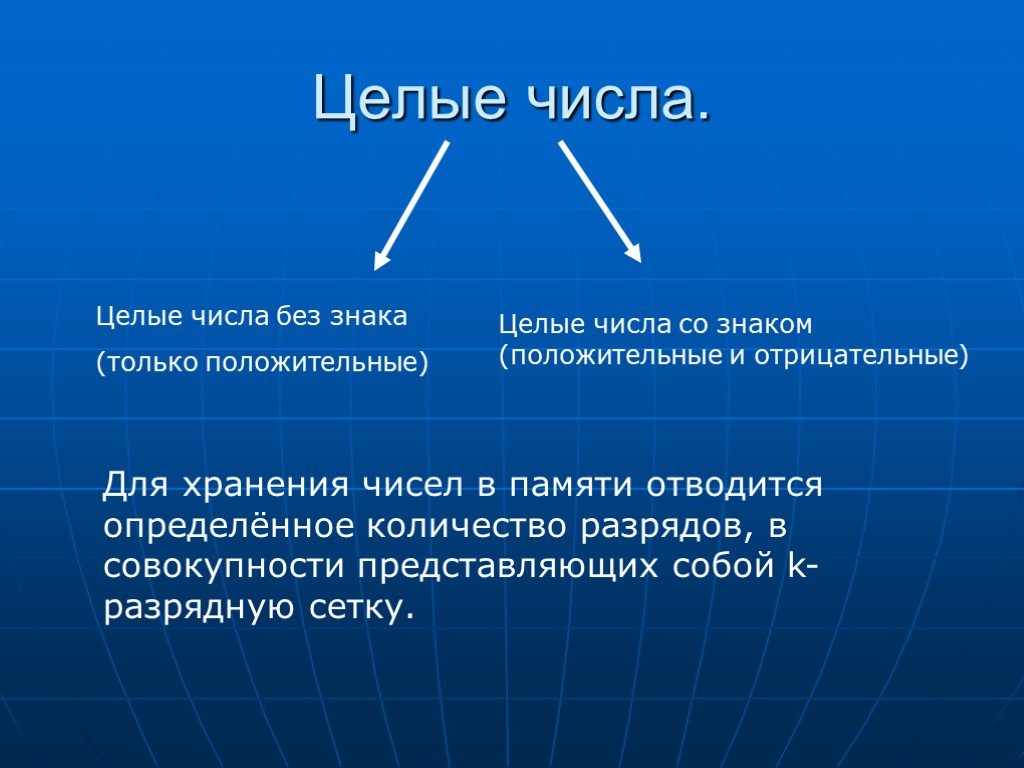
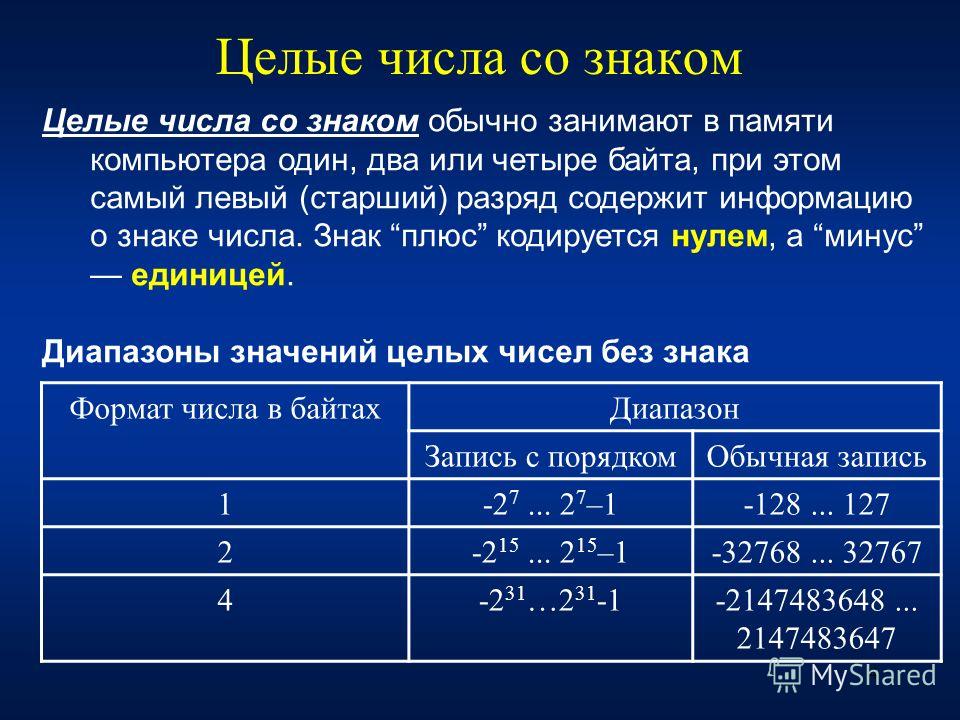
Тип целое число — зачастую один из основных типов данных в языках программирования. Целые типы данных обычно реализуются как фиксированный набор битов, один из которых кодирует знак числа, а прочие — двоичные цифры. Современные компьютеры имеют богатый набор команд для арифметических операций с целыми числами.

История

См. также: Возникновение математики и История арифметики

Развитие математики началось с навыков практического счёта (один, два, три, четыре…), поэтому натуральные числа возникли ещё в доисторический период как идеализация конечного множества однородных, устойчивых и неделимых предметов (людей, овец, дней и т. п.). Сложение появилось как математическая модель таких важных событий, как объединение нескольких множеств (стад, мешков и т. д.) в одно, а вычитание отражало, наоборот, отделение части множества. Умножение для натуральных чисел появилось в качестве, так сказать, пакетного сложения: 3 × 4 означало сумму «3 раза по 4», то есть 4 + 4 + 4. Свойства и взаимосвязь операций открывались постепенно.

Начальным шагом на пути расширения натуральных чисел стало появление нуля; первыми этот символ стали применять, по-видимому, индийские математики. Вначале ноль применялся не как число, а как цифра при позиционной записи чисел, затем постепенно стал признаваться и как полноценное число, обозначающее отсутствие чего-либо (например, полное разорение торговца).

Отрицательные числа впервые стали использовать в древнем Китае и в Индии, где их рассматривали как математический образ «долга». Древний Египет, Вавилон и Древняя Греция не использовали отрицательных чисел, а если получались отрицательные корни уравнений (при вычитании), они отвергались как невозможные. Исключение составлял Диофант, который в III веке уже знал «правило знаков» и умел умножать отрицательные числа. Однако он рассматривал их лишь как промежуточный этап, полезный для вычисления окончательного, положительного результата. Полезность и законность отрицательных чисел утверждались постепенно. Индийский математик Брахмагупта (VII век) уже рассматривал их наравне с положительными.

В Европе признание наступило на тысячу лет позже, да и то долгое время отрицательные числа называли «ложными», «мнимыми» или «абсурдными». Первое описание их в европейской литературе появилось в «Книге абака» Леонарда Пизанского (1202 год), который также трактовал отрицательные числа как долг. Бомбелли и Жирар в своих трудах считали отрицательные числа вполне допустимыми и полезными, в частности, для обозначения нехватки чего-либо. Свободно использовали отрицательные числа Никола Шюке (1484 год) и Михаэль Штифель (1544).

В XVII веке, с появлением аналитической геометрии, отрицательные числа получили наглядное геометрическое представление на числовой оси. С этого момента наступает их полное равноправие. Легализация отрицательных чисел привела к многочисленным удобствам — например, перенос слагаемых уравнения в другую его часть стал возможен независимо от знака этого слагаемого (ранее, скажем, уравнения x3+ax=b{\displaystyle x^{3}+ax=b} и x3=ax+b{\displaystyle x^{3}=ax+b} считались принципиально различными).

Тем не менее теория отрицательных чисел долго находилась в стадии становления. Паскаль, например, считал, что −4={\displaystyle 0-4=0}, так как «ничто не может быть меньше, чем ничто». Оживлённо обсуждалась странная пропорция 1(−1)=(−1)1{\displaystyle 1:\left(-1\right)=\left(-1\right):1} — в ней первый член слева больше второго, а справа — наоборот, и получается, что большее равно меньшему («парадокс Арно»). Валлис считал, что отрицательные числа меньше нуля, но в то же время больше, чем бесконечность. Непонятно было также, какой смысл имеет умножение отрицательных чисел, и почему произведение отрицательных положительно; на эту тему проходили жаркие дискуссии. Отголоском тех времён является то обстоятельство, что в современной арифметике операция вычитания и знак отрицательных чисел обозначаются одним и тем же символом (минус), хотя алгебраически это совершенно разные понятия. Гаусс в 1831 году считал нужным разъяснить, что отрицательные числа принципиально имеют те же права, что и положительные, а то, что они применимы не ко всем вещам, ничего не означает, потому что дроби тоже применимы не ко всем вещам (например, неприменимы при счёте людей).

Полная и вполне строгая теория отрицательных чисел была создана только в XIX веке (Уильям Гамильтон и Герман Гюнтер Грассман).

Примечания

1. Здесь имеется в виду самое древнее понимание натуральных чисел с первым элементом единица: 1,2,3,4,5…{\displaystyle 1,2,3,4,5\dots }
2. ↑ , с. 111—113.
3. , с. 37.
4. Paul Pollack.  (недоступная ссылка). Дата обращения 22 октября 2017.
5. , с. 18.
6. , с. 114.
7. ↑ , с. 24—28.
8. ↑ , с. 39.
9. , с. 114—115.
10. ↑ , с. 172—173.
11. ↑ Деление // Математическая энциклопедия (в 5 томах). — М.: Советская энциклопедия, 1979. — Т. 2.
12. Сушкевич А. К. Теория чисел. Элементарный курс. — Х.: Изд-во Харьковского университета, 1954. — С. 5.
13. , с. 20.
14. // Элементы теории делимости: Методические рекомендации для студентов факультета педагогики и психологии детства / сост. С. В. Поморцева, О. В. Иванова. — Омск: Омский гос. пед. университет, 2008. — 37 с.
15. Кнут Д. Искусство программирования для ЭВМ. Т. 1. Основные алгоритмы. — М.: Мир, 1976. — С. 68. — 735 с.
16. Мах Э. Познание и заблуждение // Альберт Эйнштейн и теория гравитации. — М.: Мир, 1979. — С. 74 (подстрочное примечание). — 592 с.: «прежде чем возникнет понятие о числе, должен существовать опыт, что в известном смысле равноценные объекты существуют множественно и неизменно».
17. Клайн М. Математика. Утрата определённости. — М.: Мир, 1984. — С. 109—112. — 446 с.
18. Ламберто Гарсия дель Сид. Особые числа других культур // Замечательные числа. Ноль, 666 и другие бестии. — DeAgostini, 2014. — Т. 21. — С. 115. — 159 с. — (Мир математики). — ISBN 978-5-9774-0716-8.
19. ↑ Глейзер Г. И. История математики в школе. — М.: Просвещение, 1964. — С. 132—135. — 376 с.
20. , с. 113—114.
21. Сухотин А. К. Превратности научных идей. М.: Мол. гвардия. 1991, стр. 34.
22. Панов В. Ф. Отрицательные числа // Математика древняя и юная. — Изд. 2-е, исправленное. — М.: МГТУ им. Баумана, 2006. — С. 399. — 648 с. — ISBN 5-7038-2890-2.
23. Александрова Н. В. Математические термины.(справочник). М.: Высшая школа, 1978, стр. 164.
24. Математика XVIII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1972. — Т. III. — С. 48—49.
25. Сивухин Д. В. § 38. Четыре квантовых числа электрона и тонкая структура спектральных термов // Общий курс физики. — М., 2005. — Т. V. Атомная и ядерная физика. — С. 226.
26. Карманов В. Г. Математическое программирование. — М.: Наука, 1986. — 288 с.
27. М. Бен-Ари. Глава 4. Элементарные типы данных // Языки программирования. Практический сравнительный анализ = Understanding Programming Language. — М.: Мир, 2000. — С. 53—74. — 366 с. — ISBN 5-03-003314-9.
28. ↑ Винберг Э. Б. Курс алгебры. 2-е изд. — М.: Изд-во МЦНМО, 2013. — С. 15—16, 113—114. — 590 с. — ISBN 978-5-4439-0209-8.
29. Атья М., Макдональд И. Введение в коммутативную алгебру. — М.: Мир, 1972. — С. 94. — 160 с.
30. Дональд Кнут. Искусство программирования, том I. Основные алгоритмы. — М.: Мир, 1976. — С. 571 (15b). — 736 с.
31. , с. 100.
32. , с. 95—96.
33. , с. 160—162.
34. , с. 96—98.
35. , с. 170—171.
36. , с. 98.
37. ↑ , с. 100—102.
38. ↑ , с. 162—168.
39. Окунев Л. Я. Целые комплексные числа. — М.: Гос. уч.-пед. изд-во Наркомпроса РСФСР, 1941. — 56 с.
40. Eric W. Weisstein. . Дата обращения 19 августа 2017.

Место в общей алгебре

Иерархия числовых множеств:N{\displaystyle \mathbb {N} } — натуральные числаZ{\displaystyle \mathbb {Z} } — целые числаQ{\displaystyle \mathbb {Q} } — рациональные числаR{\displaystyle \mathbb {R} } — вещественные числаR∖Q{\displaystyle \mathbb {R} \setminus \mathbb {Q} } — иррациональные числа

С точки зрения общей алгебры, Z{\displaystyle \mathbb {Z} } относительно сложения и умножения является бесконечным коммутативным кольцом с единицей, без делителей нуля (область целостности). Кольцо целых чисел является евклидовым (и, следовательно, факториальным) и нётеровым кольцом, но не является артиновым. Если расширить это кольцо, добавив к нему всевозможные дроби (см. поле частных), получится поле рациональных чисел (Q{\displaystyle \mathbb {Q} }); в нём уже выполнимо любое деление, кроме деления на ноль.

Относительно операции сложения Z{\displaystyle \mathbb {Z} } является абелевой группой, и, следовательно, также циклической группой, так как каждый ненулевой элемент Z{\displaystyle \mathbb {Z} } может быть записан в виде конечной суммы 1 + 1 + … + 1 или (−1) + (−1) + … + (−1). Фактически, Z{\displaystyle \mathbb {Z} } является единственной бесконечной циклической группой по сложению в силу того, что любая бесконечная циклическая группа изоморфна группе (Z,+){\displaystyle (\mathbb {Z} ,+)}. Относительно умножения Z{\displaystyle \mathbb {Z} } не образует группу, поскольку во множестве целых чисел деление, вообще говоря, невозможно.

Множество целых чисел с обычным порядком является упорядоченным кольцом, но не является вполне упорядоченным, так как, например, среди отрицательных чисел нет наименьшего. Однако его можно сделать вполне упорядоченным, если определить нестандартное отношение «меньше или равно», которое обозначим ≼{\displaystyle \preccurlyeq } и определим следующим образом:

a≼b,{\displaystyle a\preccurlyeq b,} если либо a=b,{\displaystyle a=b,} либо |a|<|b|,{\displaystyle |a|<|b|,} либо |a|=|b|{\displaystyle |a|=|b|} и a<<b.{\displaystyle a<0<b.}

Тогда порядок целых чисел будет таким: ≼−1≼1≼−2≼2…{\displaystyle 0\preccurlyeq -1\preccurlyeq 1\preccurlyeq -2\preccurlyeq 2\dots } В частности, −1{\displaystyle -1} будет наименьшим отрицательным числом. Z{\displaystyle \mathbb {Z} } с новым порядком будет вполне упорядоченным множеством, но уже не будет упорядоченным кольцом, так как этот порядок не согласован с операциями кольца: например, из 1≼−2{\displaystyle 1\preccurlyeq -2}, прибавив слева и справа 1, получаем неверное неравенство 2≼−1.{\displaystyle 2\preccurlyeq -1.}

Любое упорядоченное кольцо с единицей и без делителей нуля содержит одно и только одно подкольцо, изоморфное Z{\displaystyle \mathbb {Z} }.

Целые и вещественные числа

Существуют практические задачи, в которых необходимо округлить вещественное значение до целого, то есть заменить его на ближайшее (в ту или иную сторону) целое. Поскольку выполнять округление можно разными способами, для уточнения можно использовать «символы Айверсона»:

⌊x⌋{\displaystyle \lfloor x\rfloor } — ближайшее к x{\displaystyle x} целое в меньшую сторону (функция «пол», англ. floor, или «целая часть»). Традиционно используются также обозначение Гаусса x{\displaystyle } или обозначение Лежандра E(x){\displaystyle E\left(x\right)}.

⌈x⌉{\displaystyle \lceil x\rceil } — ближайшее к x{\displaystyle x} целое в бо́льшую сторону (функция «потолок», англ. ceiling).

В зависимости от особенностей постановки задачи, могут встретиться и другие методы: округлить до ближайшего целого или отсечь дробную часть (последний вариант для отрицательных x{\displaystyle x} отличается от функции «целая часть»).

Другой класс задач, связывающих целые и вещественные числа — приближение вещественного числа отношением целых, то есть рациональным числом. Доказано, что любое вещественное число можно с любой желаемой точностью приблизить рациональным, наилучшим инструментом для такого приближения служат непрерывные (цепные) дроби.