Что такое теорема
Совсем по-другому обстоят дела с теоремами. Слово теорема происходит
от древнегреческого слова «theorema» — смотреть, рассматривать какое-либо утверждение.
Запомните!
Теорема — утверждение,
которое требует доказательства.
Теоремы менее «любимы» учащимися, чем аксиомы. Если учитель попросит рассказать теорему, будет недостаточно,
как для аксиомы, сообщить только её формулировку. Потребуется также дать доказательство теоремы.
Примеры формулировок теорем:
- сумма углов треугольника равна 180 градусов;
- площадь прямоугольника равна произведению его смежных сторон;
- теорема Пифагора. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Важно!
Формулировки аксиом и теорем необходимо учить строго наизустьбез искажений.
Каждое слово или предлог в формулировке играет существенную роль в передаче смысла выражения.
Даже просто поменяв порядок слов можно сильно изменить смысл утверждения.
Помните, что все формулировки в геометрии были выверены несколькими тысячами лет развития математики лучшими умами планеты и не терпят
никаких словесных изменений.
Что такое лемма
Среди теорем выделяют такие теоремы, которые сами по себе не используются в решениях задач.
Но их используют для доказательства других теорем.
Лемма происходит от древнегреческого слова «lemma» – предположение.
Запомните!
Лемма — это вспомогательная теорема, с помощью которой доказываются другие теоремы.
Пример леммы:
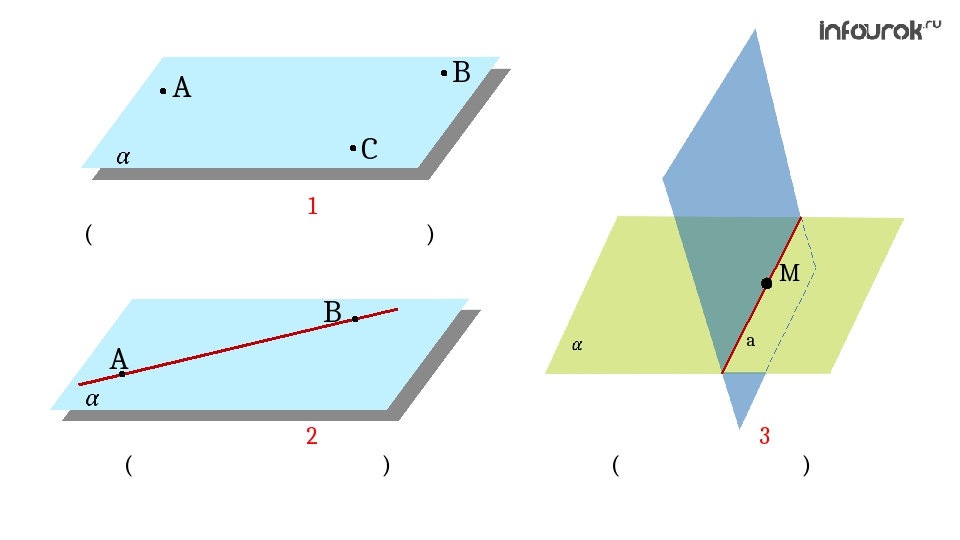
если одна из двух параллельных прямых пересекает плоскость, то и вторая прямая тоже пересекает эту плоскость.
Что такое следствие в геометрии
Запомните!
Следствие — утверждение, которое выводится непосредственно из аксиомы или теоремы.
Следствие, как и теорему, необходимо доказывать.
Приведем примеры следствий из аксиомы о параллельности прямых:
- если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую;
- если две прямые параллельны третьей прямой, то они параллельны.
Если подытожить все вышесказанное, то сравнивая геометрию с высотным домом, можно представить, что:
- аксиомы — фундамент дома;
- теоремы — основные кирпичи дома;
- леммы и следствия — вспомогательные кирпичи для упрочнения конструкции.
Каждая доказанная теорема служит основанием доказательства для следующей теоремы.
Именно поэтому так важно изучать геометрию последовательно, переходя с самых основ (аксиом) к теоремам. Невозможно понять геометрию 9 и 10 класса, не выучив аксиомы и теоремы 7 и 8 класса
Невозможно понять геометрию 9 и 10 класса, не выучив аксиомы и теоремы 7 и 8 класса.
Простыми словами о сложных вещах
Аксиома – основное понятие любой науки или теории, которое основано на общеизвестных или общепризнанных фактах. Данный научный и философский термин берет свое начало из древнейшей истории возникновения науки, когда люди пытались сформулировать основы изучения мира.
В те времена, когда человечество только начало изучать Землю, все окружавшие их явления и предметы были непонятными и неизведанными. К примеру, то, какой формы и строения Земля, из чего она состоит, что является причиной смены дня и ночи, времен года, и многое другое было неизвестным. Человечество во многом жило мифами и верованиями, которые, однако, были не научными, а вымышленными.
Однако, для изучения мира научными методами мифы и верования не подходили, поскольку они основывались на выдумке, а не на реальности. Легко сказать, что земля стоит на слонах или плавает в большом медном тазу – таких утверждений можно придумать тысячи, но они не являются научными аксиомами или теориями. Это пример выдумки, который нельзя использовать в науке.

Наука же для изучения мира создает гипотезы – те формулы, которые в дальнейшем можно или доказать, или опровергнуть. Так, два разных ученых несколько тысяч лет назад могли выдвинуть две различные гипотезы: «Земля вращается вокруг Солнца» и «Солнце и звезды вращаются вокруг Земли». Мы, как люди современные, конечно же прекрасно понимаем, что только первое утверждение верное – Земля вращается вокруг Солнца. Но наши предки не имели таких книг и научной литературы, а потом обе эти теории были для них по сути равнозначными.
Для того же, чтобы доказать одну из них и опровергнуть другую необходимо было собрать огромное количество доказательств, подтверждений, провести научные эксперименты. Именно таким образом любая теория может быть доказана или опровергнута.
Несколько фактов
Но для того, чтобы доказать теорию, ее нужно сначала придумать, а сделать это тоже не так уж просто. Ведь для формулировки теории, нужно отталкиваться от одного или нескольких уже доказанных фактов. Например, если мы хотим изучить теорию «Солнце обращается вокруг Земли», нам сначала нужно понимать, что такое Земля и что такое Солнце. Именно поэтому, любая теория опирается на определенные аксиомы, то есть те утверждения, которые понятны, очевидны и не требуют доказательств.
Говоря простыми словами, утверждение «Земля круглая (земля имеет форму шара)» – аксиома. Конечно, ученые и философы с таким утверждением не согласятся, и скажут, что аксиома – термин из математики, а в естественных науках это называется «постулат», но если говорить, что такое аксиома простыми словами, то разница не очень важна.
Утверждение о том, что Земля имеет форму шара очевидно для всех взрослых грамотных людей и не требует какого-либо подтверждения. По этой причине это – аксиома, которая в наше время не требует каких-либо проверок или доказательств. То же самое можно сказать и о математических аксиомах:
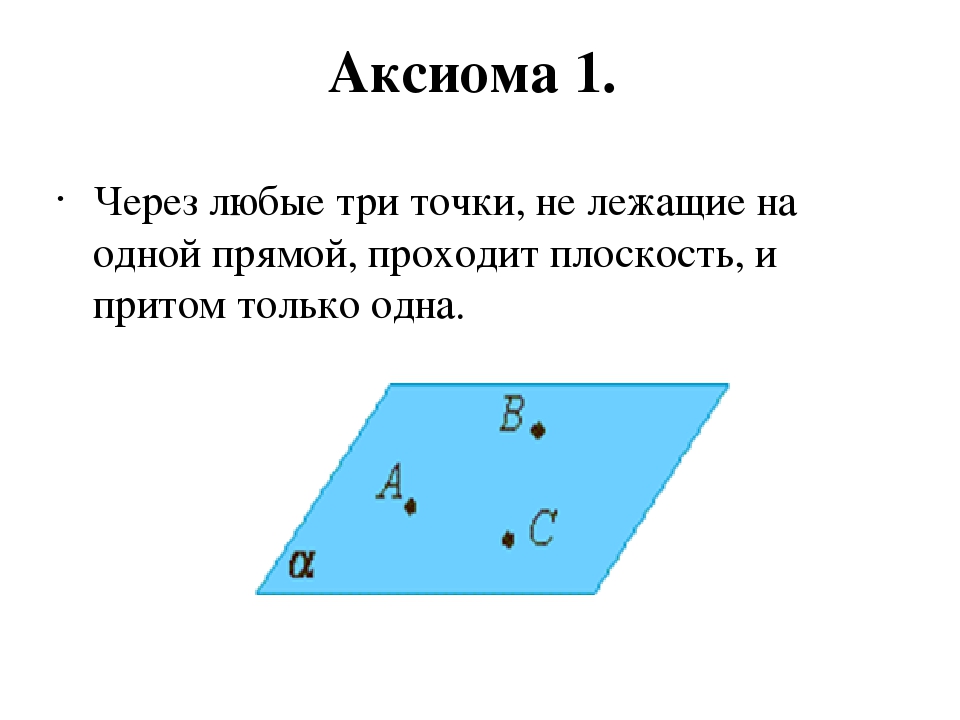
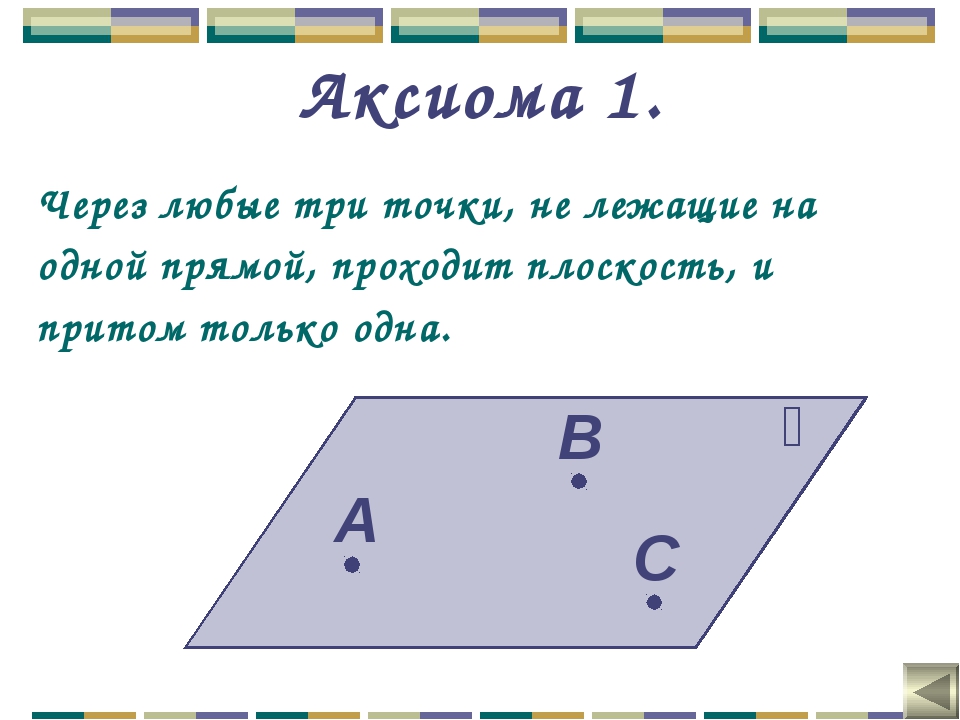
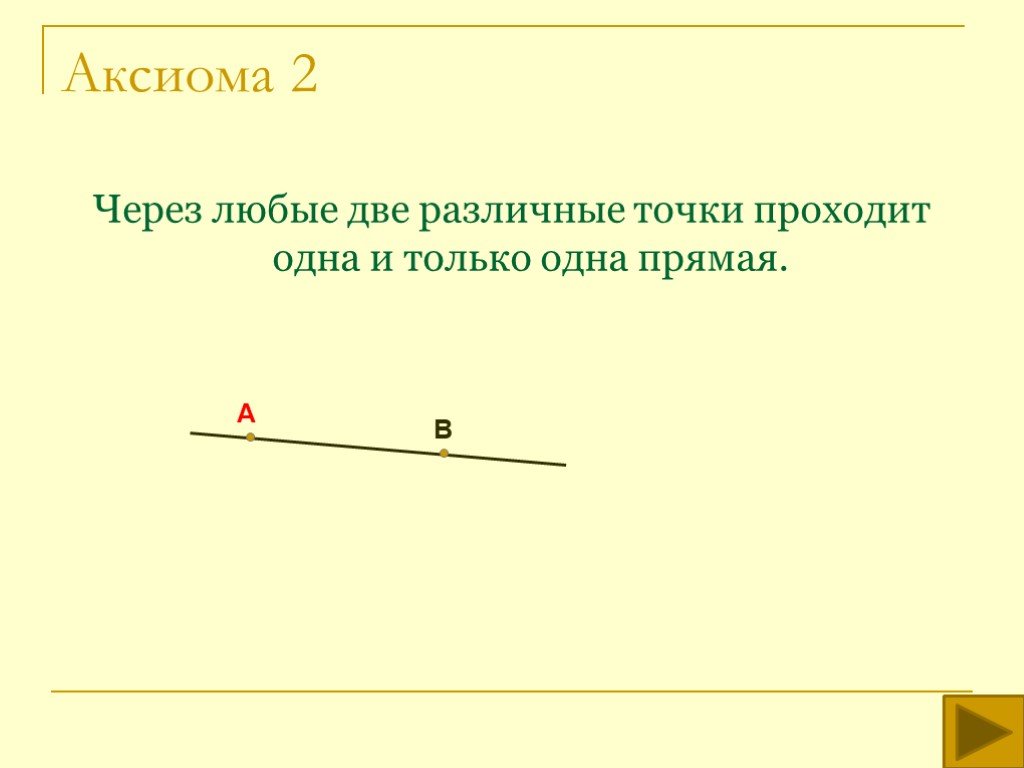
- через любые две точки на одной плоскости можно провести прямую, и только одну;
- если на одной прямой есть три точки, то одна, и только одна из этих точек всегда находится между двух других;
- через любую точку, которая находится вне прямой можно провести параллельную ей прямую, при чем только одну.
Самое главное, что нужно понимать, изучая понятие «аксиома» — это то, что без знания и понимания аксиом, невозможно решать математические задачи, связанные с применением тех или иных теорем, поскольку аксиома — это начальная и базовая часть для любой теоремы.
Выводы
Если же говорить не о математике, а любой другой сфере жизни, то аксиома – это то утверждение, которое не может подвергаться сомнению. Однако, в этом смысле нужно быть очень осторожным, не путая утверждения очевидные для одного человека с общепризнанными утверждениями. К примеру, сегодня то, что земля вращается вокруг Солнца понятно и очевидно всем, и это – аксиома. Однако несколько столетий назад это утверждение было не то что понятным, а даже вызывало огромные споры и было малопонятной для многих теорией.
По мере развития науки, отдельные утверждения становятся очевидными и из гипотез превращаются в теории, а в отдельных случаях и в аксиомы, но торопить этот процесс нельзя. К примеру, в повседневной жизни некоторые люди могут сказать какое-то утверждение (в любом споре), подкрепив его словами «это же аксиома»
Но такие слова нельзя считать безусловно истинными, потому что сегодня слово «аксиома» стало крылатым и очень часто используется только для того, чтобы убедить своего собеседника и подчеркнуть важность и точность сказанных человеком слов
Правовая аксиома
Это правило, которое рассматривается как истина, не допускает иного толкования. По мнению некоторых учёных-правоведов, они закреплены в официальных документах — нормативно-правовых актах. Например, в Конституции России:
- каждый имеет право на жизнь;
- осуществление прав и свобод человека и гражданина не должно нарушать права и свободы других лиц;
- каждому гарантируется свобода мысли и слова; и др.
По мнению других учёных, такие правила появились как результат общественных отношений. Например:
- что не запрещено, то разрешено;
- закон обратной силы не имеет;
- суд выслушивает обе стороны; и др.
Узнайте также, что такое Догма.
Назначение
Необходимость в принятии аксиом без доказательств следует из индуктивного соображения: любое доказательство вынуждено опираться на какие-либо утверждения, и если для каждого из них требовать своих доказательств, цепочка получится бесконечной. Чтобы не уходить в бесконечность, нужно где-то эту цепочку разорвать — то есть какие-то утверждения принять без доказательств, как исходные. Именно такие, принятые в качестве исходных, утверждения и называются аксиомами.
В современной науке вопрос об истинности аксиом, лежащих в основе какой-либо теории, решается либо в рамках других научных теорий, либо посредством интерпретации данной теории.
Аксиоматиза́ция теории — явное указание конечного или счётного, рекурсивно перечислимого (как, например, в аксиоматике Пеано) набора аксиом и правил вывода. После того как даны названия изучаемым объектам и их основным отношениям, а также аксиомы, которым эти отношения должны подчиняться, всё дальнейшее изложение должно основываться исключительно на этих аксиомах и не опираться на обычное конкретное значение этих объектов и их отношений.
Выбор аксиом, которые составляют основу конкретной теории, не является единственным. Примеры различных, но равносильных наборов аксиом можно встретить в математической логике и евклидовой геометрии.
Набор аксиом называется непротиворечивым, если исходя из аксиом набора, пользуясь правилами логики, нельзя прийти к противоречию, то есть доказать одновременно и некое утверждение, и его отрицание.
Австрийский математик Курт Гёдель доказал «теоремы о неполноте», согласно которым всякая система математических аксиом (формальная система), в которой можно определить натуральные числа, сложение и умножение, неполна. Это значит, что найдётся бесконечное количество математических утверждений (функций, выражений), ни истинность, ни ложность которых не сможет быть доказана на основании данной системы аксиом. Также, по теореме о неполноте, среди этих невыводимых утверждений будет утверждение о непротиворечивости этой системы.