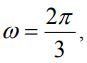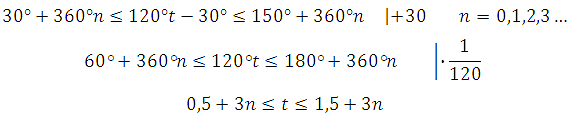Датчик сконструирован таким образом что его антенна ловит радиосигнал который затем преобразуется

Реальная математика (2 уровень)

Прототип задания 11 (№ 28000)

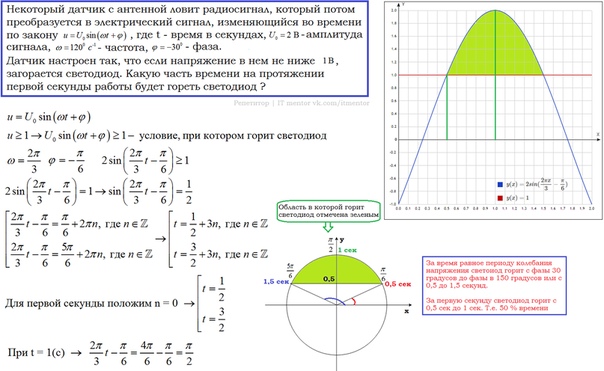
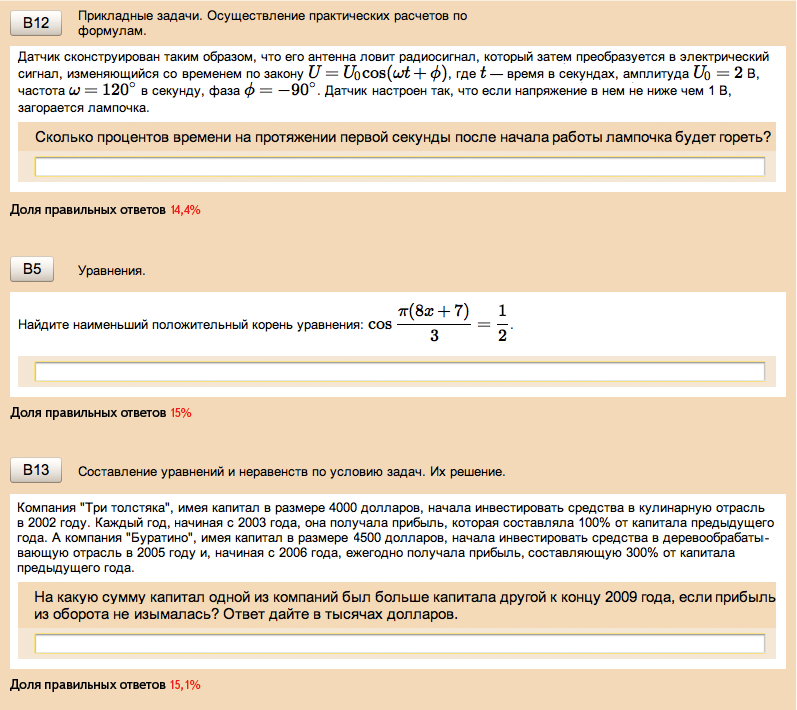
Датчик сконструирован таким образом, что его антенна ловит радиосигнал, который затем преобразуется в электрический сигнал, изменяющийся со временем по закону $U = U_0 \sin (\omega t + \varphi )$, где t — время в секундах, амплитуда $U_0 = 2$ В, частота $\omega = 120^\circ/с$, фаза $\varphi = -30^\circ$. Датчик настроен так, что если напряжение в нeм не ниже чем 1 В, загорается лампочка. Какую часть времени (в процентах) на протяжении первой секунды после начала работы лампочка будет гореть?

Решение

$$U_0 \sin (\omega t + \varphi ) = 1,$$

$$2 \sin (120 t -30 ) = 1,$$

$$\sin (120 t -30 ) = 0,5,$$

$$120 t -30 = 30,$$

$$120t = 60,$$

$$t = 0,5.$$

$$0,5:1\cdot 100\% = 50\%.$$

Лампочка будет гореть 50% времени.

Ответ: 50.

Прототип задания 11 (№ 28002)

Очень лeгкий заряженный металлический шарик зарядом $q = 2 \cdot 10^{-6}$ Кл скатывается по гладкой наклонной плоскости. В момент, когда его скорость составляет v = 5 м/с, на него начинает действовать постоянное магнитное поле, вектор индукции B которого лежит в той же плоскости и составляет угол \alpha с направлением движения шарика. Значение индукции поля $B = 4 \cdot 10^{-3}$ Тл. При этом на шарик действует сила Лоренца, равная $F_{\text{л}} = qvB\sin \alpha$ (Н) и направленная вверх перпендикулярно плоскости. При каком наименьшем значении угла $\alpha \in \left$ шарик оторвeтся от поверхности, если для этого нужно, чтобы сила $F_{\text{л}}$ была не менее чем $2 \cdot 10^{-8}$ Н? Ответ дайте в градусах.

Решение

$$qvB\sin \alpha \ge 2 \cdot 10^{-8},$$

$$ 2\cdot 10^{-6} \cdot 5 \cdot 4 \cdot 10^{-3} \sin \alpha \ge 2 \cdot 10^{-8},$$

$$4 \sin \alpha \ge 2,$$

$$\sin \alpha \ge 0,5.$$

Учитывая, что $\alpha \in \left$ и нам нужно наименьшее значение угла, то

$$\alpha = 30^\circ.$$

Ответ: 30.

Прототип задания 11 (№ 28003)

Небольшой мячик бросают под острым углом $\alpha$ к плоской горизонтальной поверхности земли. Максимальная высота полeта мячика, выраженная в метрах, определяется формулой $H=\frac{{v_0^2 }}{{4g}}(1 — \cos 2\alpha )$, где $v_0 = 20$ м/с — начальная скорость мячика, а g — ускорение свободного падения (считайте g=10 м/с${}^2$). При каком наименьшем значении угла $\alpha$ (в градусах) мячик пролетит над стеной высотой 4 м на расстоянии 1 м?

Решение

$$\frac{{v_0^2 }}{{4g}}(1 — \cos 2\alpha) = 5,$$

$$\frac{{20^2 }}{{40}}(1 — \cos 2\alpha) = 5,$$

$$10(1 — \cos 2\alpha) = 5,$$

$$1 — \cos 2\alpha = 0,5,$$

$$\cos 2\alpha = 0,5,$$

$$2\alpha = 60^\circ,$$

$$\alpha = 30^\circ.$$

Ответ: 30.

Прототип задания 11 (№ 28004)

Небольшой мячик бросают под острым углом $\alpha$ к плоской горизонтальной поверхности земли. Расстояние, которое пролетает мячик, вычисляется по формуле $L=\frac{{v_0^2 }}{g}\sin 2\alpha$ (м), где $v_0=20$ м/с — начальная скорость мячика, а g — ускорение свободного падения (считайте g=10 м/с${}^2$). При каком наименьшем значении угла (в градусах) мячик перелетит реку шириной 20 м?