Вертикальные углы

Плоские углы

Термин плоский угол употребляется как синоним термина угол, определённого в начале статьи, для отличия его от употребляемого в стереометрии понятия (в том числе двугранного, трёхгранного или многогранного угла).

Под свойствами плоских углов нередко понимают соотношения величин углов (смежных, дополнительных, прилегающих, вертикальных — см. ниже) в случае, когда углы лежат в одной плоскости (для планиметрии это подразумевается само собой, однако для стереометрии уточнение необходимо, иначе перечисленные ниже соотношения не имеют места, а сами углы, если не лежат в одной плоскости, не называются смежными или прилегающими (вертикальные всегда лежат в одной плоскости автоматически).

Вертикальные и прилежащие углы

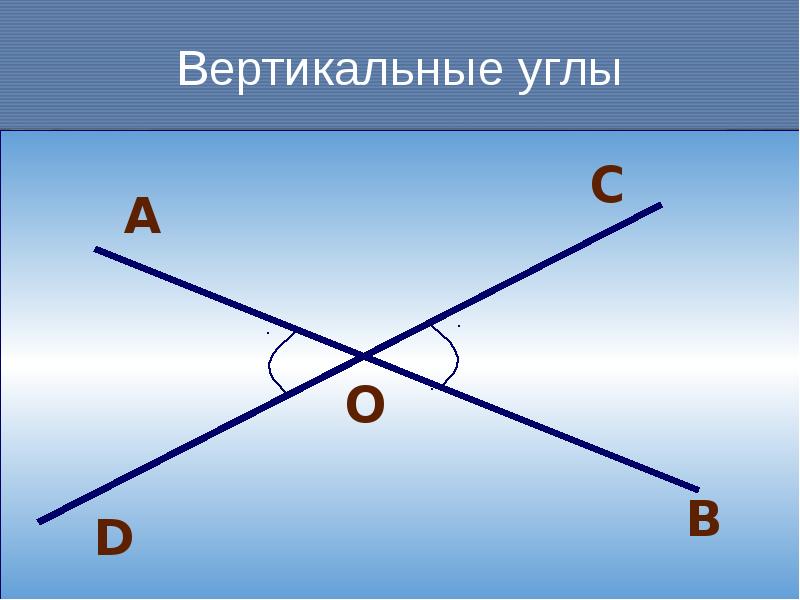
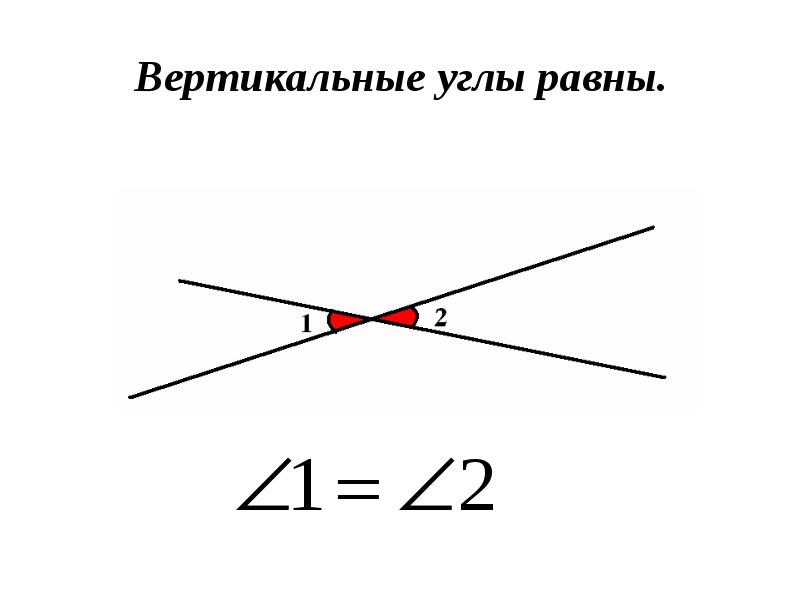
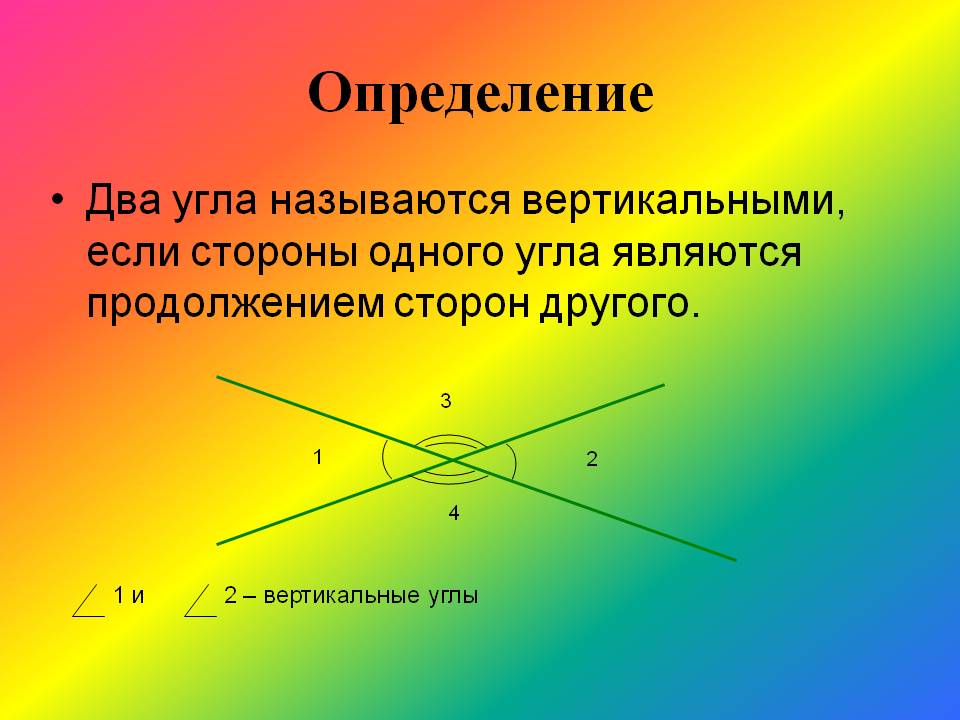
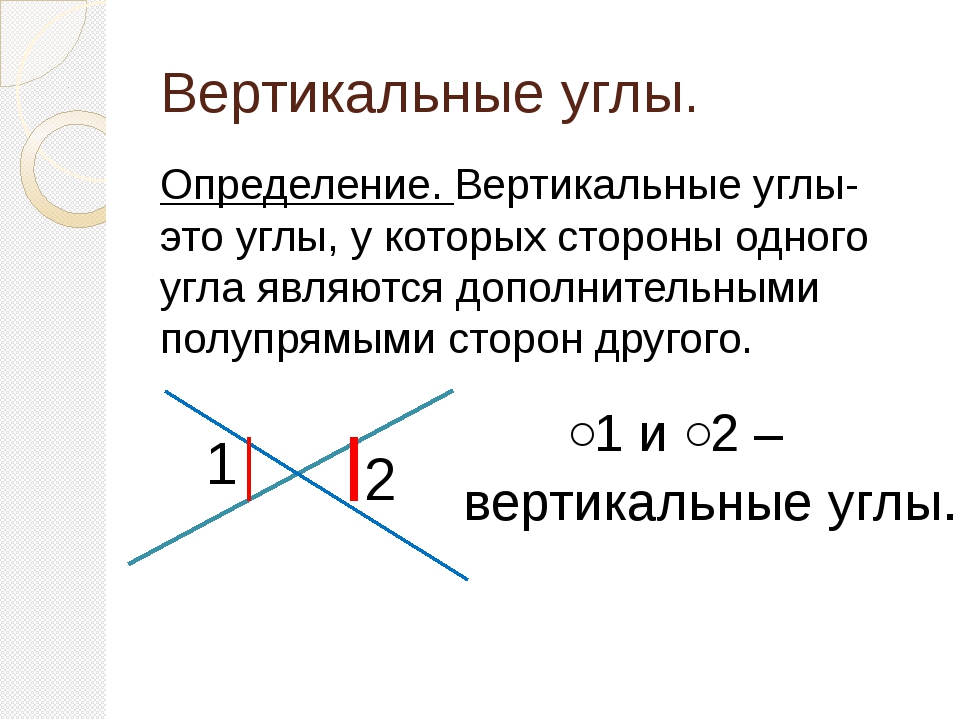
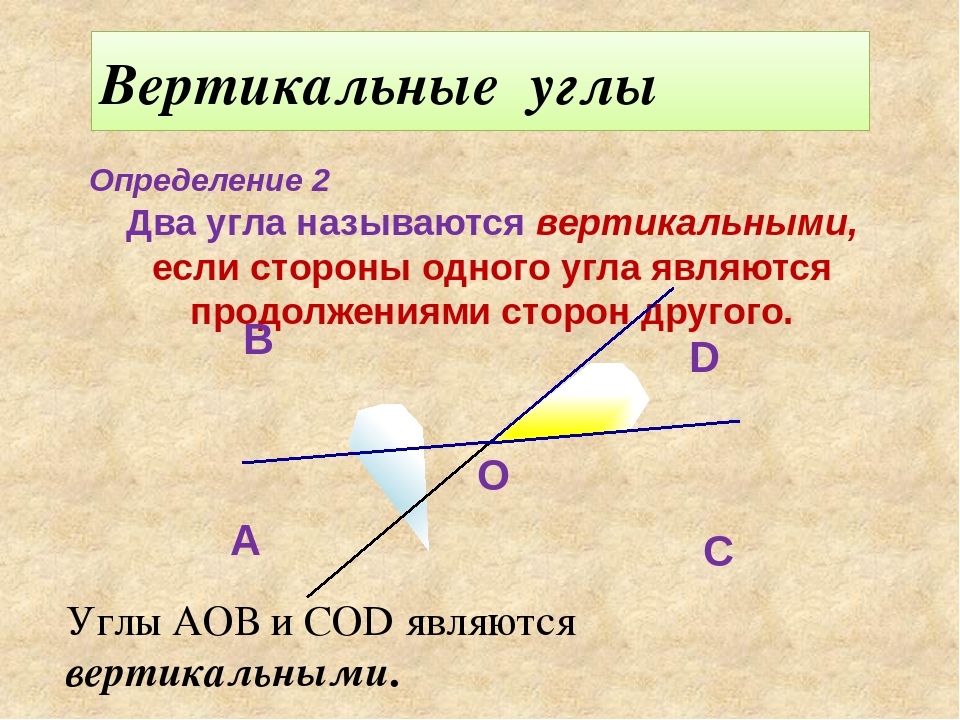
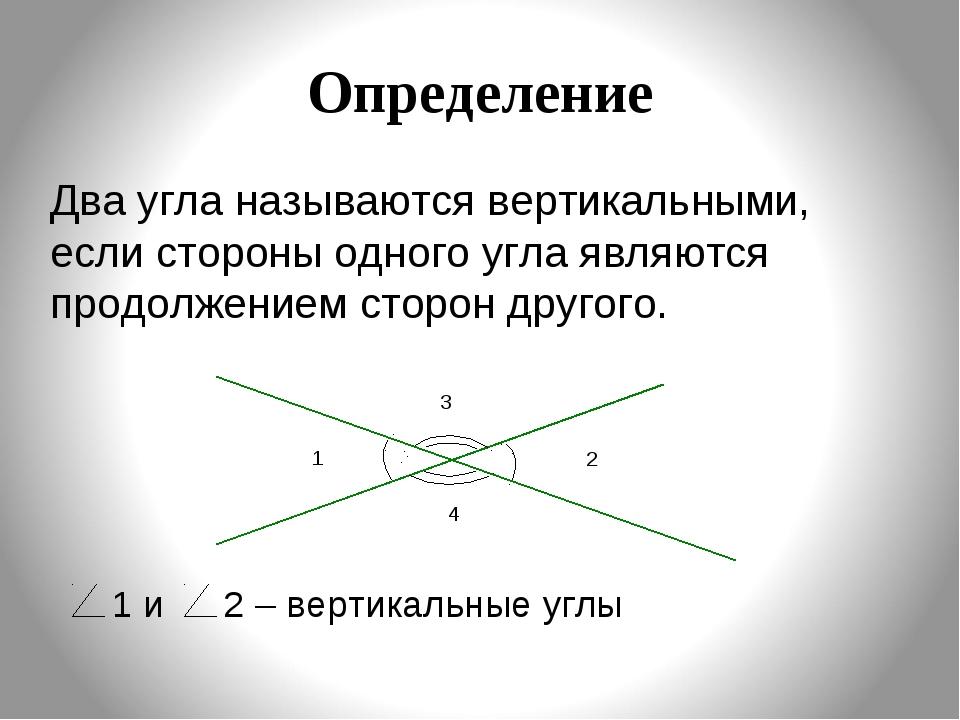
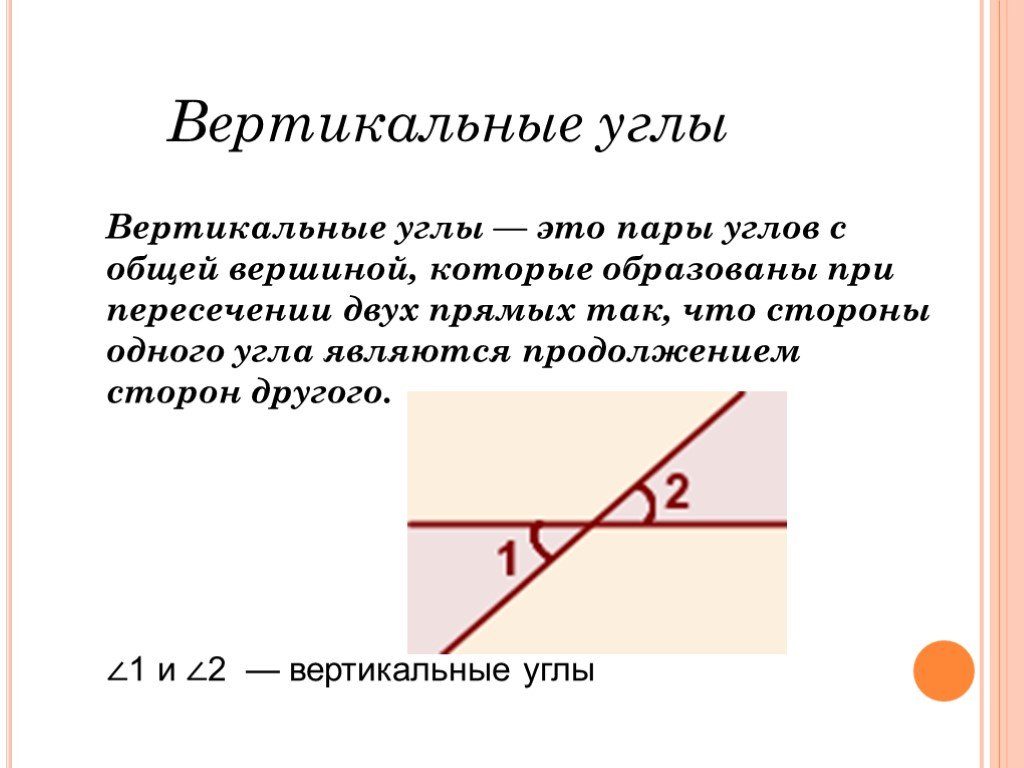
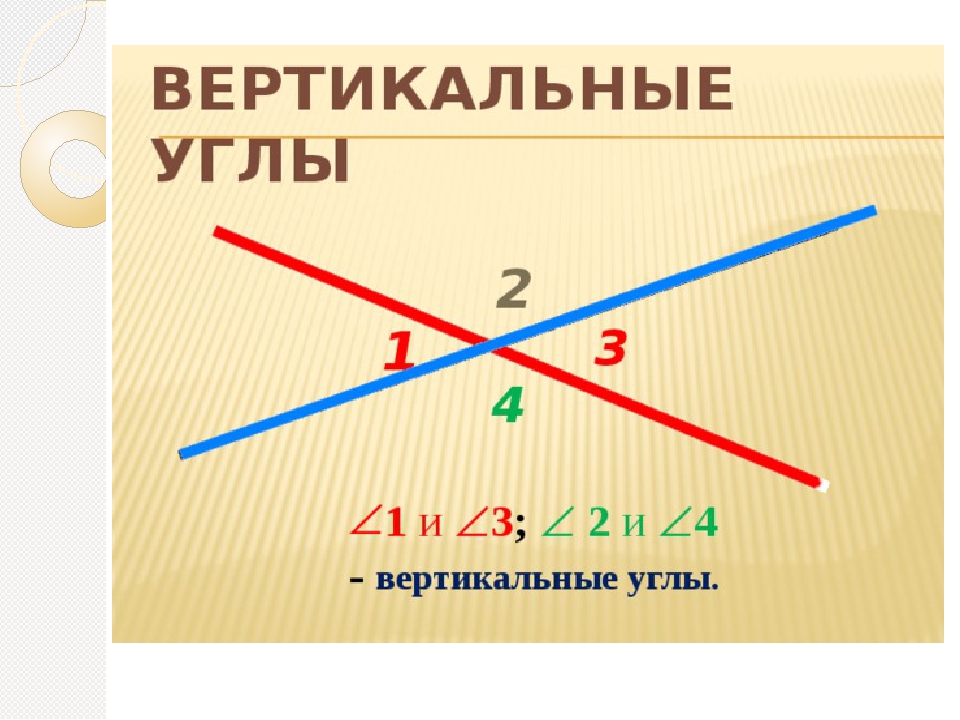
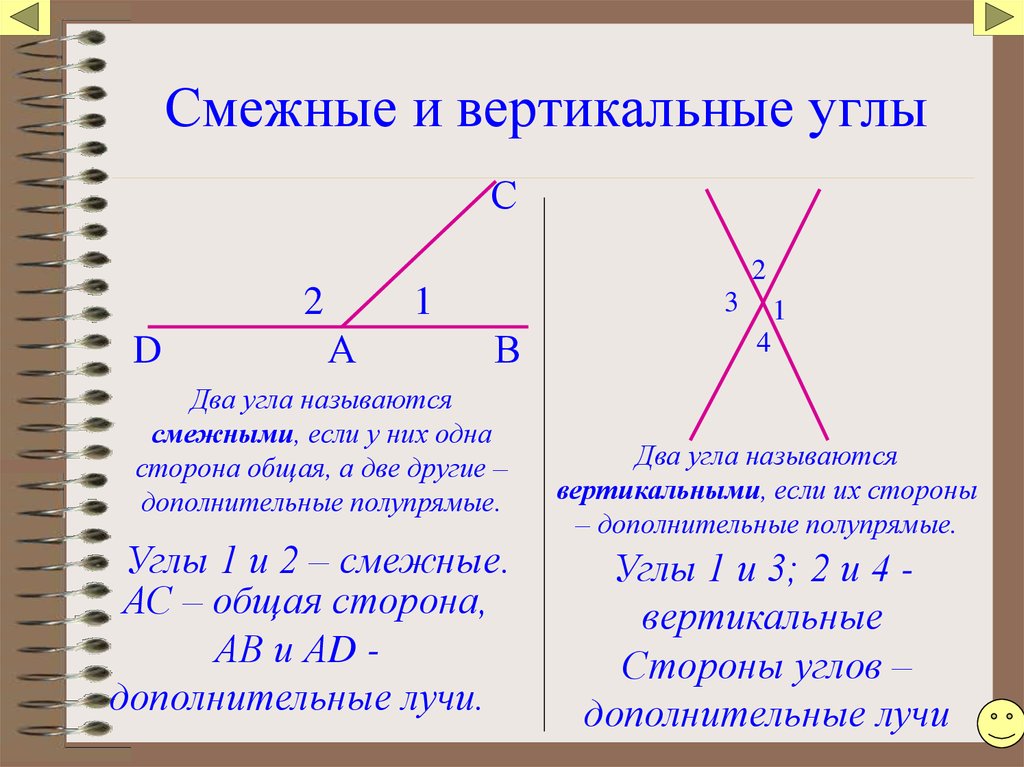
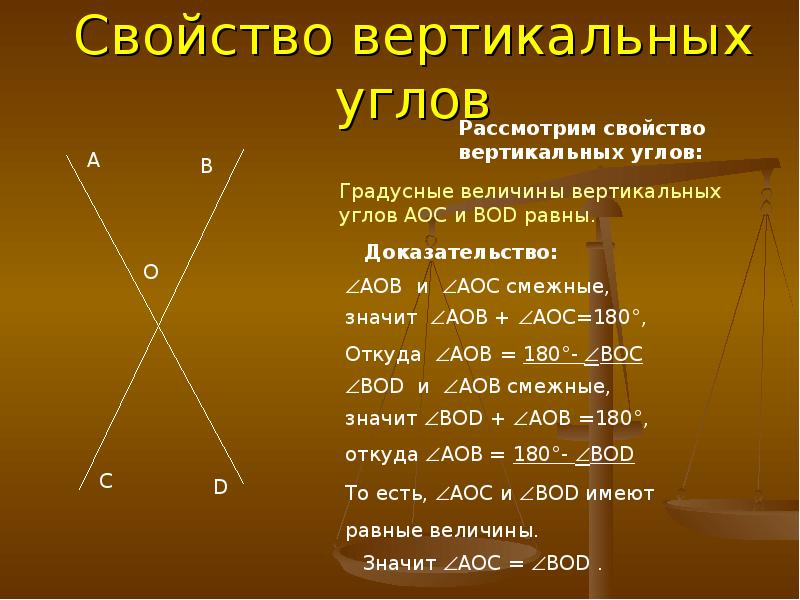
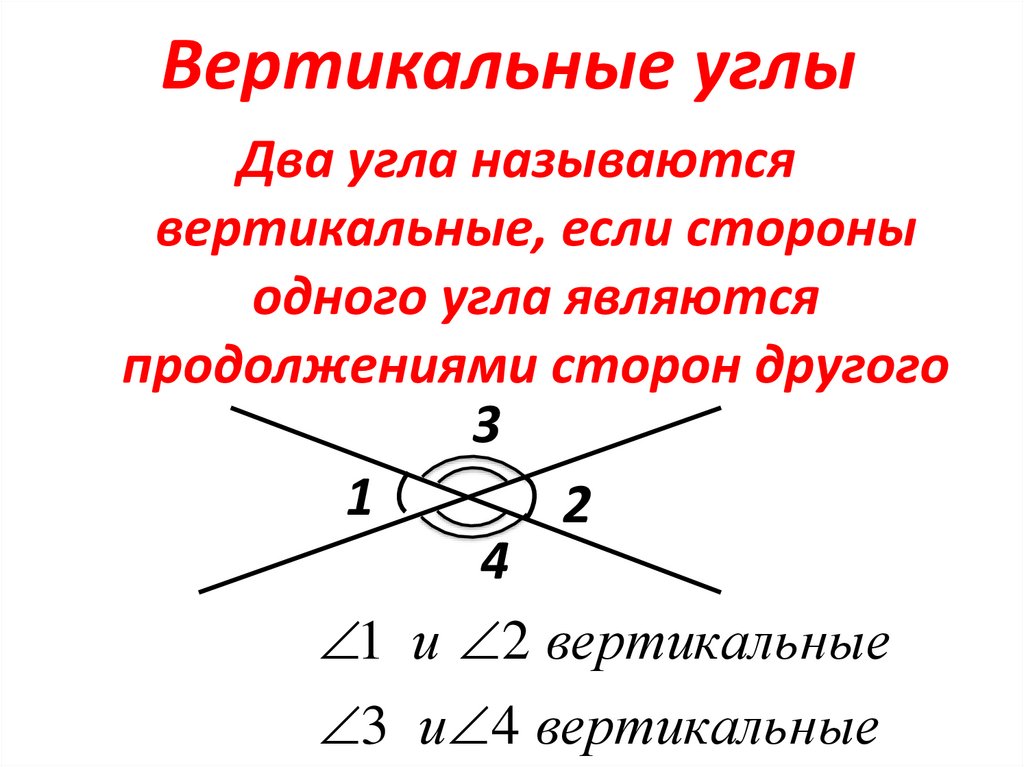
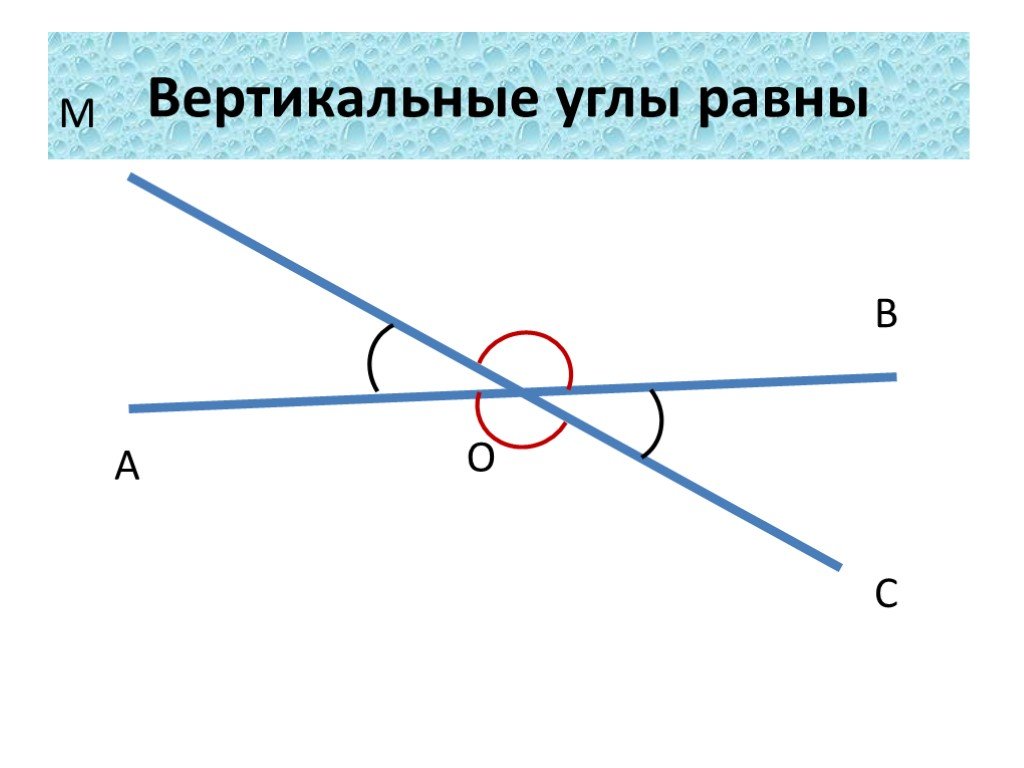
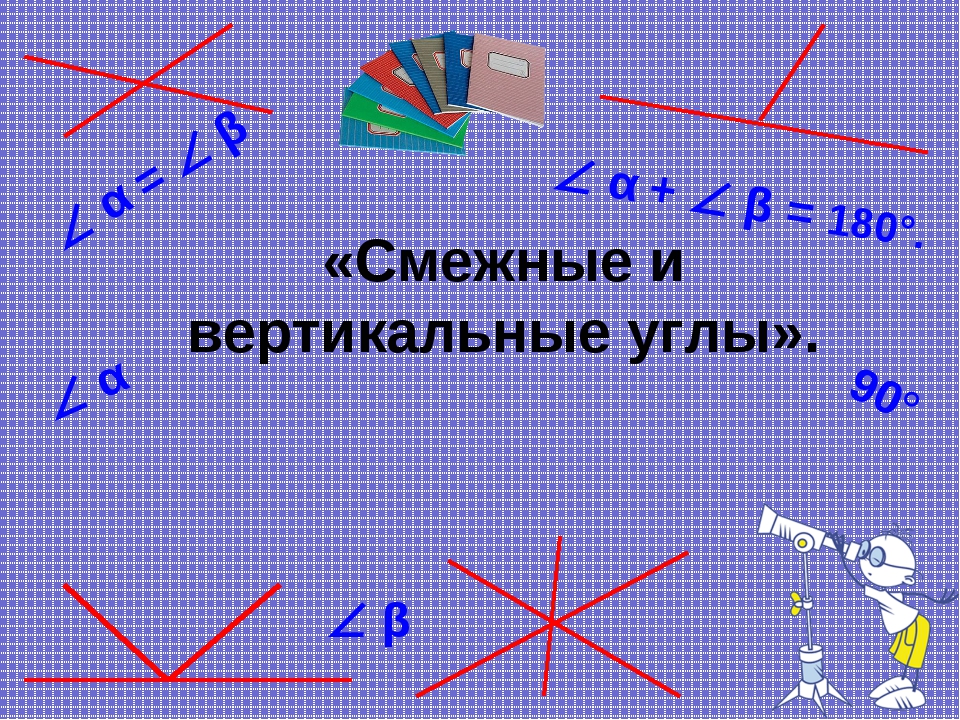
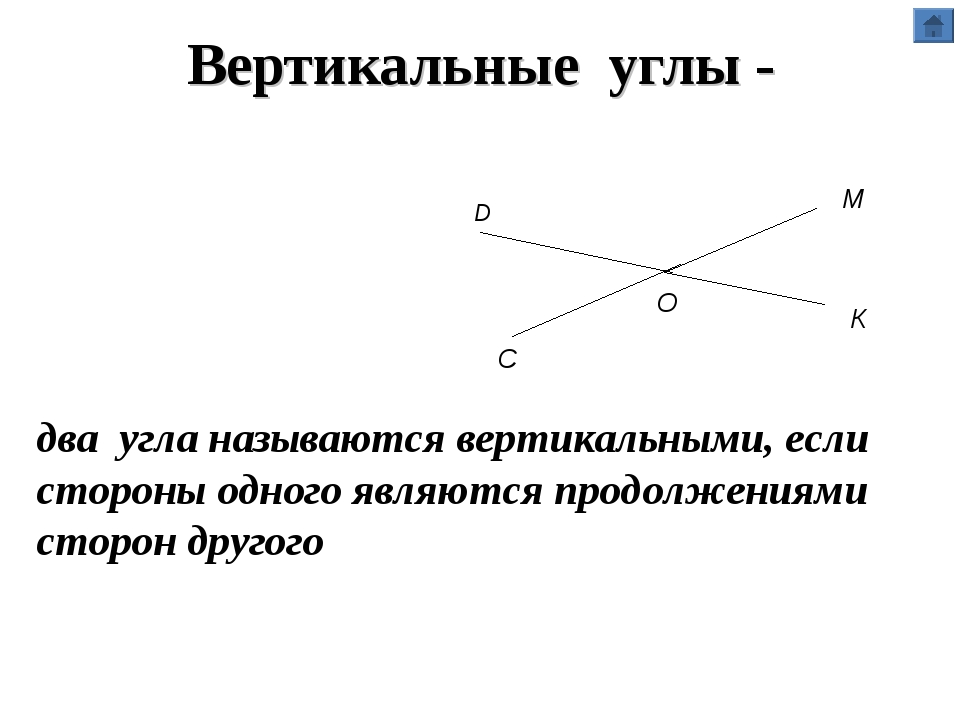
• Вертикальные углы — два угла, которые образуются при пересечении двух прямых, эти углы не имеют общих сторон. Другими словами — два угла называют вертикальными, если стороны одного угла являются продолжением сторон другого. Их основное свойство: вертикальные углы равны.
• Прилежащие углы — два угла, имеющие общую вершину и одну из сторон, но не пересекающиеся внутренними областями, лежащими в одной плоскости. Величина угла, образованного внешними (не общими) сторонами прилежащих углов равна сумме величин самих прилежащих углов (на рисунке α + β).

Частные случаи прилежащих углов.

Плоские углы с (анти)параллельными сторонами

Углы с параллельными сторонами.

Углы, стороны которых попарно параллельны и сонаправлены (или попарно параллельны и противоположно направлены), равны друг другу. Пара углов, у которых одна пара сторон параллельна и сонаправлена друг другу, а вторая пара сторон параллельна и противоположно направлена, составляют в сумме по величине развёрнутый угол, то 180° (см. рисунок) — поскольку их можно параллельным переносом превратить в смежные углы («склеив» сонаправленные стороны).

Внешний угол треугольника

Основная статья: Теорема о внешнем угле треугольника

Теорема о внешнем угле треугольника. Внешний угол треугольника равен сумме двух оставшихся углов треугольника, не смежных с внешним углом.

Углы многоугольника

Основная статья: Теорема о сумме углов многоугольника

Сумма внутренних углов α_i произвольного n-угольника без самопересечений равна ∑i=1nαi=(n−2)⋅180∘.{\displaystyle \sum _{i=1}^{n}\alpha _{i}=(n-2)\cdot 180^{\circ }.}

Так,

• сумма внутренних углов треугольника равна 180°,
• четырёхугольника — 360°,
• пятиугольника — 540° и так далее.

Следствие

Назовём внешним углом βi (внимание, это не обычное определение внешнего угла) угол, дополняющий внутренний угол αi до полного угла: βi = 360° − αi.

Сумма внешних углов произвольного n-угольника без самопересечений равна ∑i=1nβi=n⋅360∘−∑i=1nαi=(n+2)⋅180∘.{\displaystyle \sum _{i=1}^{n}\beta _{i}=n\cdot 360^{\circ }-\sum _{i=1}^{n}\alpha _{i}=(n+2)\cdot 180^{\circ }.}

Обозначение углов

«∠», обозначение угла в геометрии.

Для обозначения угла имеется общепринятый символ: ∠,{\displaystyle \angle ,} предложенный в 1634 году французским математиком Пьером Эригоном.

В математических выражениях углы часто обозначают строчными греческими буквами: α, β, γ, θ, φ и др. Как правило, данные обозначения также наносятся на чертёж для устранения неоднозначности в выборе внутренней области угла. Чтобы избежать путаницы с числом пи, символ π, как правило, для этой цели не используется. Для обозначения телесных углов (см. ниже) часто применяют буквы ω и Ω.

Также часто угол обозначают тремя символами точек, например ∠ABC.{\displaystyle \angle ABC.} В такой записи B{\displaystyle B} — вершина, а A{\displaystyle A} и C{\displaystyle C} — точки, лежащие на разных сторонах угла. В связи с выбором в математике направления отсчёта углов против часовой стрелки, точки, лежащие на сторонах в обозначении угла принято перечислять также против часовой стрелки. Это соглашение позволяет обеспечить однозначность при различении двух плоских углов с общими сторонами, но различными внутренними областями. В тех случаях, когда выбор внутренней области плоского угла ясен из контекста, либо указывается другим способом, данное соглашение может нарушаться.
См. .

Реже используются обозначения прямых, образующих стороны угла. Например, ∠(bc){\displaystyle \angle (bc)} — здесь предполагается, что имеется в виду внутренний угол треугольника ∠BAC{\displaystyle \angle BAC}, α, который надо было бы обозначить ∠(cb){\displaystyle \angle (cb)}.

Так, для рисунка справа записи γ, ∠ACB{\displaystyle \angle ACB} и ∠(ba){\displaystyle \angle (ba)} означают один и тот же угол.

Иногда для обозначения углов используются строчные латинские буквы (a, b, c, …) и цифры.

На чертежах углы отмечаются небольшими одинарными, двойными или тройными дужками, проходящими по внутренней области угла с центрами в вершине угла. Равенство углов может отмечаться одинаковой кратностью дужек или одинаковым количеством поперечных штрихов на дужке. Если необходимо указать направление отсчёта угла, оно отмечается стрелкой на дужке. Прямые углы отмечаются не дужками, а двумя соединёнными равными отрезками, расположенными таким образом, что вместе со сторонами они образуют небольшой квадрат, одна из вершин которого совпадает с вершиной угла.

Вариации и обобщения

Величиной ориентированного угла между прямыми AB{\displaystyle AB}и CD{\displaystyle CD} (обозначение: ∠(AB,CD){\displaystyle \angle (AB,CD)}) называют величину угла, на который нужно повернуть против часовой стрелки прямую AB{\displaystyle AB} так, чтобы она стала параллельна прямой CD.{\displaystyle CD.} При этом углы, отличающиеся на n·180° (n — целое число), считаются равными. Следует отметить, что ориентированный угол между прямыми CD{\displaystyle CD} и AB{\displaystyle AB} не равен ориентированному углу между прямыми AB{\displaystyle AB} и CD{\displaystyle CD} (они составляют в сумме 180° или, что по нашему соглашению то же самое, 0°). Ориентированные углы обладают следующими свойствами: а) ∠(AB,BC)=−∠(BC,AB);{\displaystyle \angle (AB,BC)=-\angle (BC,AB);} б) ∠(AB,CD)+∠(CD,EF)=∠(AB,EF);{\displaystyle \angle (AB,CD)+\angle (CD,EF)=\angle (AB,EF);} в) точки A,B,C,D,{\displaystyle A,B,C,D,} не лежащие на одной прямой, принадлежат одной окружности тогда и только тогда, когда ∠(AB,BC)=∠(AD,DC).{\displaystyle \angle (AB,BC)=\angle (AD,DC).}

Ряд практических задач приводит к целесообразности рассматривать угол как фигуру, получающуюся при вращении фиксированного луча вокруг точки О (из которой исходит луч) до заданного положения. В этом случае угол является мерой поворота луча. Такое определение позволяет обобщить понятие угла, расширив его область определения на всю числовую прямую (−∞;+∞){\displaystyle (-\infty ;+\infty )}: вводятся углы, большие 360°, в зависимости от направления вращения различают положительные и отрицательные углы. В тригонометрии такое рассмотрение позволяет изучать тригонометрические функции для любых значений аргумента.

Понятие угла обобщается на рассматриваемый в стереометрии телесный угол.

Телесный угол

Основная статья: Телесный угол

Обобщением плоского угла на стереометрию является телесный угол — часть пространства, которая является объединением всех лучей, выходящих из данной точки (вершины угла) и пересекающих некоторую поверхность (которая называется поверхностью, стягивающей данный телесный угол).

Телесные углы измеряются в стерадианах (одна из основных единиц СИ), а также во внесистемных единицах — в частях полной сферы (то есть полного телесного угла, составляющего 4π стерадиан), в квадратных градусах, квадратных минутах и квадратных секундах.

Телесными углами являются, в частности, следующие геометрические тела:

• двугранный угол — часть пространства, ограниченная двумя пересекающимися плоскостями;
• трёхгранный угол — часть пространства, ограниченная тремя пересекающимися плоскостями;
• многогранный угол — часть пространства, ограниченная несколькими плоскостями, пересекающимися в одной точке.

Двугранный угол может характеризоваться как линейным углом (углом между образующими его плоскостями), так и телесным углом (в качестве вершины может быть выбрана любая точка на его ребре — прямой пересечения его граней). Если линейный угол двугранного угла (в радианах) равен φ, то его телесный угол (в стерадианах) равен 2φ.

Угол между кривыми

Угол между двумя кривыми в точке Р определяется как угол между касательными А и В в P.

Как в планиметрии, так и в стереометрии, а также в ряде других геометрий можно определить угол между гладкими кривыми в точке пересечения: по определению, его величина равна величине угла между касательными к кривым в точке пересечения.

Центральный и вписанный угол

Любой конкретной дуге окружности можно сопоставить единственный центральный и бесконечное множество вписанных углов.

• Центральный угол — угол с вершиной в центре окружности. Величина центрального угла равна градусной мере дуги, заключённой между сторонами этого угла.
• Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают эту окружность. Величина вписанного угла равна половине градусной меры дуги, ограниченной его сторонами. Все вписанные углы, опирающиеся на одну и ту же дугу, равны.

Вписанный угол θ равен половине величины центрального угла 2θ, , опирающегося у основания на окружности на ту же самую дугу (розового цвета). То есть угол θ не меняет своей величины от вершины к вершине, взятой на окружности (зелёный и голубой углы). Внешний угол для вписанного с другой стороны угла окружности имеет ту же величину θ (коричневого цвета)

Величина вписанного угла равна половине величины центрального угла, опирающегося у основания на окружности на ту же самую дугу (см. рис.).

Типы углов

В зависимости от величины углы называются следующим образом.

• Нулевой угол (0°); стороны нулевого угла совпадают, его внутренняя область — пустое множество.
• Острый угол (от 0° до 90°, не включая граничные значения).
• Прямой угол (90°); стороны прямого угла перпендикулярны друг другу.
• Тупой угол (от 90° до 180°, не включая граничные значения).
• Косой угол (любой, не равный 0°, 90°, 180° или 270°).
• Развёрнутый угол (180°); сторонами развёрнутого угла являются две полупрямые одной прямой, то есть два луча, направленных в противоположные стороны.
• Выпуклый угол (от 0° до 180° включительно)[источник не указан 154 дня].
• Невыпуклый угол (от 180° до 360°, не включая граничные значения)[источник не указан 154 дня].
• Полный угол (360°) — см. оборот (единица измерения).

См. также: Центральный угол

Угол и скалярное произведение

Понятие угла можно определить для линейных пространств произвольной природы (и произвольной, в том числе бесконечной размерности), на которых аксиоматически введено положительно определённое скалярное произведение (x,y){\displaystyle (x,y)} между двумя элементами пространства x{\displaystyle x} и y.{\displaystyle y.} Скалярное произведение позволяет определить также и так называемую норму (длину) элемента как квадратный корень произведения элемента на себя ||x||=(x,x).{\displaystyle ||x||={\sqrt {(x,x)}}.} Из аксиом скалярного произведения следует неравенство Коши — Буняковского (Коши — Шварца) для скалярного произведения: |(x,y)|⩽||x||⋅||y||,{\displaystyle |(x,y)|\leqslant ||x||\cdot ||y||,} откуда следует, что величина (x,y)||x||⋅||y||{\displaystyle {\frac {(x,y)}{||x||\cdot ||y||}}} принимает значения от −1 до 1, причём крайние значения достигаются тогда и только тогда, когда элементы пропорциональны (коллинеарны) друг другу (говоря геометрически — их направления совпадают или противоположны). Это позволяет интерпретировать отношение (x,y)||x||⋅||y||{\displaystyle {\frac {(x,y)}{||x||\cdot ||y||}}} как косинус угла между элементами x{\displaystyle x} и y.{\displaystyle y.} В частности, элементы называют ортогональными, если скалярное произведение (или косинус угла) равно нулю.

В частности, можно ввести понятие угла между непрерывными на некотором интервале a,b{\displaystyle } функциями, если ввести стандартное скалярное произведение (f,g)=∫abf(x)g(x)dx,{\displaystyle (f,g)=\int _{a}^{b}f(x)g(x)dx,} тогда нормы функций определяются как ||f||2=∫abf2(x)dx.{\displaystyle ||f||^{2}=\int _{a}^{b}f^{2}(x)dx.} Тогда косинус угла определяется стандартным образом как отношение скалярного произведения функций к их нормам. Функции также можно назвать ортогональными, если их скалярное произведение (интеграл их произведения) равно нулю.

В римановой геометрии можно аналогично определить угол между касательными векторами с помощью метрического тензора gij.{\displaystyle g_{ij}.} Скалярное произведение касательных векторов u{\displaystyle u} и v{\displaystyle v} в тензорной записи будет иметь вид: (u,v)=gijuivj,{\displaystyle (u,v)=g_{ij}u^{i}v^{j},} соответственно нормы векторов — ||u||=|gijuiuj|{\displaystyle ||u||={\sqrt {|g_{ij}u^{i}u^{j}|}}} и ||v||=|gijvivj|.{\displaystyle ||v||={\sqrt {|g_{ij}v^{i}v^{j}|}}.} Поэтому косинус угла будет определяться по стандартной формуле отношения указанного скалярного произведения к нормам векторов: cos⁡θ=(u,v)||u||⋅||v||=gijuivj|gijuiuj|⋅|gijvivj|.{\displaystyle \cos \theta ={\frac {(u,v)}{||u||\cdot ||v||}}={\frac {g_{ij}u^{i}v^{j}}{\sqrt {|g_{ij}u^{i}u^{j}|\cdot |g_{ij}v^{i}v^{j}|}}}.}

Литература

• Барабанов О.О. Начала истории прямого угла // История науки и техники, 2015. №1. С. 16-27.*
• Сидоров Л. А. Угол // Математическая энциклопедия / И. М. Виноградов (гл. ред.). — М.: Советская энциклопедия, 1985. — Т. 5. — С. 459‒460. — 623 с. — 150 000 экз.
• Двугранный угол // Математическая энциклопедия / И. М. Виноградов (гл. ред.). — М.: Советская энциклопедия, 1979. — Т. 2. — С. 50. — 552 с. — 150 000 экз.
• Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 30‒31. — ISBN 5-94057-170-0.
• Угломерные приборы/Угол (плоский) // Большая Советская энциклопедия (в 30 т.) / Гл. ред. А. М. Прохоров. — 3-е изд. — М.: «Советская Энциклопедия», 1977. — Т. XXVI. — С. 459‒460. — 624 с.
• K. Menger. New Fondations of Euclidean Geometry (англ.) // THE AMERICAN JOURNAL OF MATHEMATICS 53 : журнал. — 1931. — P. 721‒745.