Что такое умножение

Определение слова «Умножение» по БСЭ:

Умножение — операция образования по двум данным объектам а и b, называемым сомножителями, третьего объекта с, называемого произведением. У. обозначается знаком Х (ввёл англ. математик У. Оутред в 1631) или · (ввёл нем. учёный Г. Лейбниц в 1698). в буквенном обозначении эти знаки опускаются и вместо аЧ b или а · b пишут ab. У. имеет различный конкретный смысл и соответственно различные конкретные определения в зависимости от конкретного вида сомножителей и произведения. У. целых положительных чисел есть, по определению, действие, относящее числам а и b третье число c, равное сумме b слагаемых, каждое из которых равно а, так что ab = а + а +… + а (b слагаемых). Число а называется множимым, b — множителем. У. дробных чисел m &frasl. _n и p &frasl. _q определяется равенством m &frasl. _n · p &frasl. _q = m·p &frasl. _n·q (см. Дробь). У. рациональных чисел даёт число, абсолютная величина которого равна произведению абсолютных величин сомножителей, имеющее знак плюс (+), если оба сомножителя одинакового знака, и знак минус (-), если они разного знака. У. иррациональных чисел определяется при помощи У. их рациональных приближений.У. комплексных чисел, заданных в форме &alpha. = а + bi и &beta. = с + di, определяется равенством &alpha.&beta. = ac — bd + (ad + bc) i. При У. комплексных чисел, записанных в тригонометрической форме:&alpha. = r₁ (cos&phi.₁ + isin &phi.₁),&beta. = r₂ (cos&phi.₂ + isin &phi.₂),их модули перемножаются, а аргументы складываются:&alpha.&beta. = r₁r₂{cos (&phi.₁ + &phi.₂) + i sin ((&phi.₁ + &phi.₂)}.У. чисел однозначно и обладает следующими свойствами:1) ab = ba (коммутативность, переместительный закон).2) a (bc) = (ab) c (ассоциативность, сочетательный закон).3) a (b + c) = ab + ac (дистрибутивность, распределительный закон). При этом всегда а ·0 = 0. a·1 = а. Указанные свойства лежат в основе обычной техники У. многозначных чисел.Дальнейшее обобщение понятия У. связано с возможностью рассматривать числа как операторы в совокупности векторов на плоскости. Например, комплексному числу r (cos&phi. + i sin &phi.) соответствует оператор растяжения всех векторов в r раз и поворота их на угол&phi. вокруг начала координат. При этом У. комплексных чисел отвечает У. соответствующих операторов, т. е. результатом У. будет оператор, получающийся последовательным применением двух данных операторов. Такое определение У. операторов переносится и на другие виды операторов, которые уже нельзя выразить при помощи чисел (например, линейные преобразования). Это приводит к операциям У. матриц, кватернионов, рассматриваемых как операторы поворота и растяжения в трёхмерном пространстве, ядер интегральных операторов и т.д. При таких обобщениях могут оказаться невыполненными некоторые из перечисленных выше свойств У., чаще всего — свойство коммутативности (некоммутативная алгебра). Изучение общих свойств операции У. входит в задачи общей алгебры, в частности теории групп и колец.

Умножение физических величин

Единица измерения физической величины имеет определенное наименование (размерность): для длины (L) — метр (м), для времени (T) — секунда (с), для массы (M) — грамм (г) и так далее. Поэтому, результат измерения той или иной величины представляет собой не просто число, а число с наименованием. Наименование представляет собой самостоятельный объект, который равноправно участвует в операции умножения. При производстве операции умножения над физическими величинами, умножаются как сами числовые составляющие, так и их наименования.

Помимо размерных физических величин существуют безразмерные (количественные) величины, которые формально являются элементами числовой оси, то есть числами, не имеющие привязки к определенным физическим явлениям (измеряются «штуками», «разами» и тому подобное). При умножении чисел представляющих собой физические величины на безразмерную величину, множимое число увеличивается по величине кратно множителю и сохраняет единицу измерения. Например если взять 5-метровые рейки в количестве 3 штуки, то в результате умножения получим общую длину реек 15 метров:

5 м · 3 = 15 м.

Умножение разнородных физических величин надо рассматривать как нахождение новой физической величины, принципиально отличающейся от величин, которые мы умножаем. Если физически возможно создание такого произведения, например, при нахождении работы, скорости или других величин, то эта величина образует множество, отличное от начальных. В этом случае композиции этих величин  присваивается новое обозначение (новый термин), например: плотность, ускорение, мощность и прочее.

Например, если умножить скорость V = 4 м/с на время T = 2 с, соответствующие одному физическому процессу, то получится именованное число (физическая величина) соответствующее этому же физическому процессу, которая называется «длина» и измеряется в метрах: L = 8 м.

L = V · T = 4 м/с · 2 с = 8 (м/с) · с = 8 м.

При описании математическими средствами физических процессов немаловажную роль играет понятие однородности, которое означает например, что «1 кг муки» и «1 кг меди» принадлежат разным множествам {мука} и {медь} соответственно[уточнить]. Также понятие однородности предполагает, что умножаемые величины принадлежат одному физическому процессу.

Выполнение умножения

При практическом решении задачи умножения двух чисел необходимо свести её к последовательности более простых операций: «простое умножение», сложение, сравнение и др. Для этого разработаны различные методы умножения, например для чисел, дробей, векторов и др. На множестве натуральных чисел в настоящее время используется алгоритм поразрядного умножения. При этом следует рассматривать умножение как процедуру (в отличие от операции).

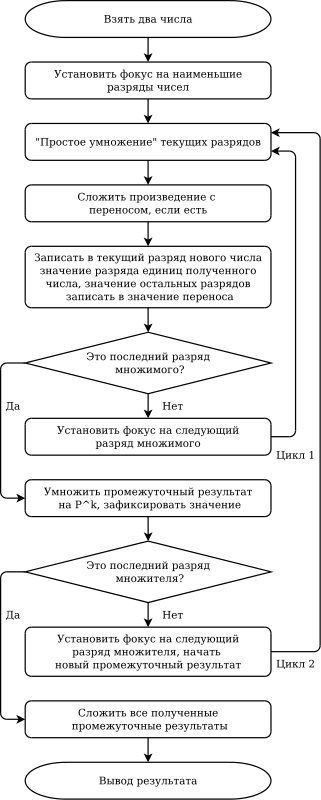
Примерный алгоритм процедуры поразрядного умножения двух чисел

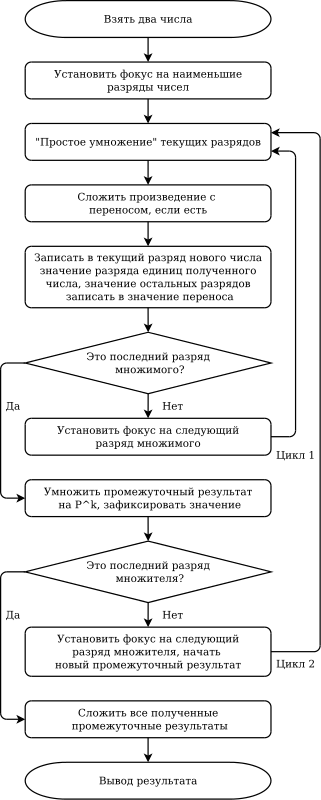
Процедура достаточно сложная, состоит из относительно большого числа шагов и при умножении больших чисел может занять продолжительное время.

Пример пошагового умножения 3 ∙ 3 = 9 на числовой прямой.

«Простое умножение» в данном контексте обозначает операцию умножения одноразрядных чисел, которая может быть легко сведена к сложению. Является гипероператором сложения:

a⋅b=hyper2⁡(a,b)=hyper⁡(a,2,b)=a(2)b.{\displaystyle a\cdot b=\operatorname {hyper2} (a,b)=\operatorname {hyper} (a,2,b)=a^{(2)}b.}

a(2)b=a⋅b=a+a+⋯+a⏟b.{\displaystyle a{^{(2)}}b=a\cdot b=\underbrace {a+a+\dots +a} _{b}.}

где a+a+⋯+a{\displaystyle a+a+\dots +a} — последовательное сложение b{\displaystyle b} элементов.

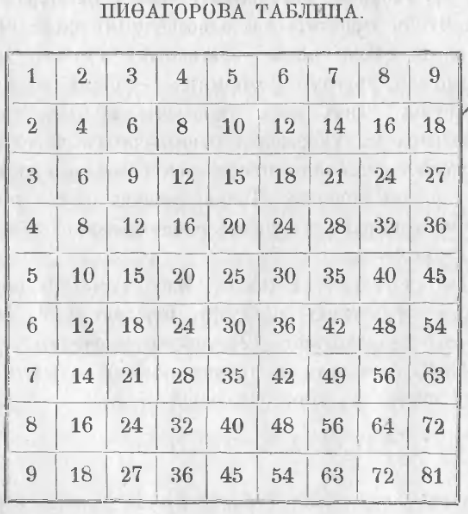
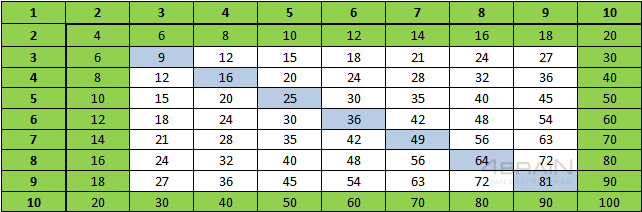
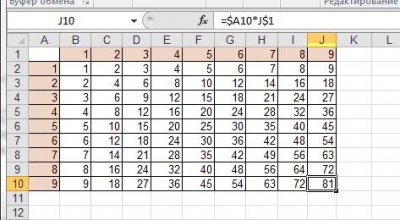
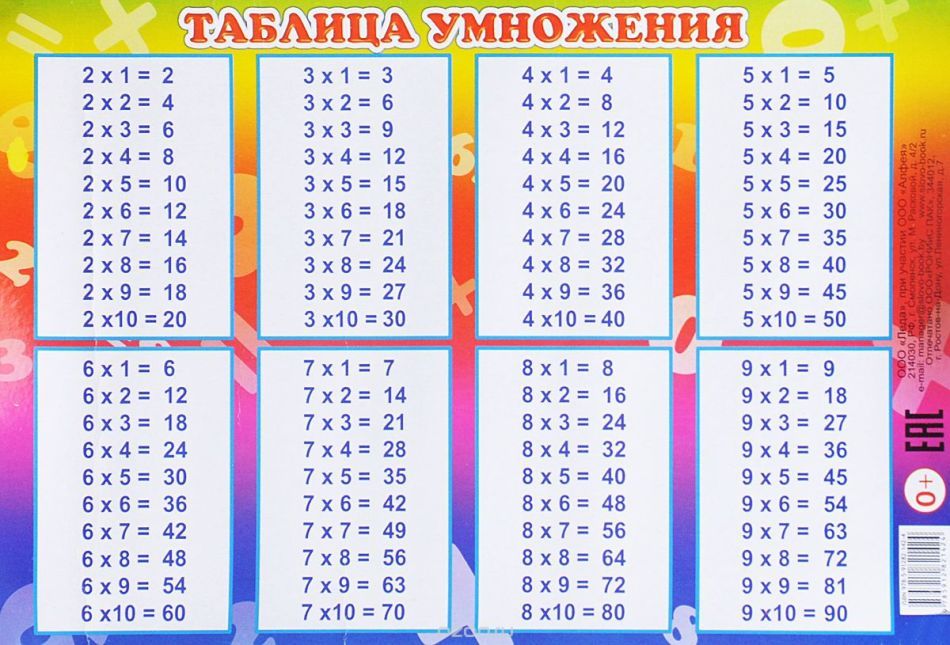
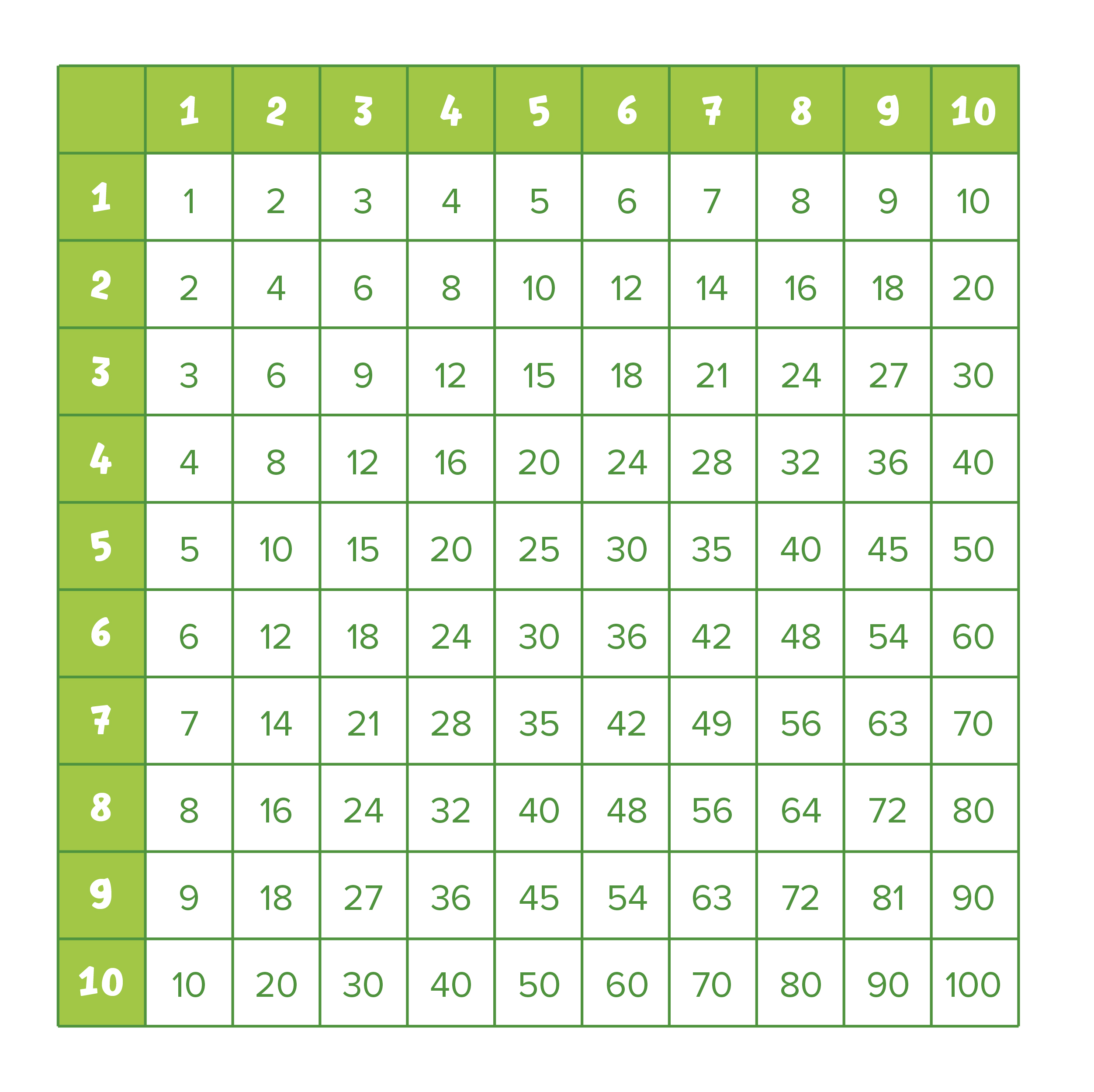
Чтобы упростить и ускорить процесс умножения используют табличный метод «простого умножения», для этого заранее вычисляют все комбинации произведений чисел от 0 до 9 и берут готовый результат из этой таблицы:

Таблица для умножения в десятичной системе счисления

*	1	2	3	4	5	6	7	8	9
1	1	2	3	4	5	6	7	8	9
2	2	4	6	8	10	12	14	16	18
3	3	6	9	12	15	18	21	24	27
4	4	8	12	16	20	24	28	32	36
5	5	10	15	20	25	30	35	40	45
6	6	12	18	24	30	36	42	48	54
7	7	14	21	28	35	42	49	56	63
8	8	16	24	32	40	48	56	64	72
9	9	18	27	36	45	54	63	72	81

Данная процедура применима к умножению натуральных и целых (с учётом знака) чисел. Для других чисел используются более сложные алгоритмы.

Определение умножения

Умножение целых чисел есть такое действие, в котором нужно взять одно число слагаемым столько раз, сколько в другом содержится единиц, и найти сумму этих слагаемых.

Умножить 7 на 3 значит взять число 7 слагаемым три раза и найти сумму. Искомая сумма есть 21.

Умножение есть сложение равных слагаемых.

Данные в умножении называются множимым и множителем, а искомое — произведением.

В предложенном примере данными будут множимое 7, множитель 3, а искомым произведением 21.

Множимое. Множимое есть то число, которое умножается или повторяется слагаемым. Множимое выражает величину равных слагаемых.

Множитель. Множитель показывает, сколько раз множимое повторяется слагаемым. Множитель показывает число равных слагаемых.

Произведение. Произведение есть число, которое получается от умножения. Оно есть сумма равных слагаемых.

Множимое и множитель вместе называются производителями.

При умножении целых чисел одно число увеличивается во столько раз, сколько в другом содержится единиц.

Знак умножения. Действие умножения обозначают знаком × (косвенным крестом) или . (точкой). Знак умножения ставится между множимым и множителем.

Повторить число 7 три раза слагаемым и найти сумму значит 7 умножить на 3. Вместо того, чтобы писать

7 + 7 + 7

пишут при помощи знака умножения короче:

7 × 3 или 7 · 3

Умножение есть сокращенное сложение равных слагаемых.

Знак (×) был введен Отредом (1631 г.), а знак . Христианом Вольфом (1752 г.).

Связь между данными и искомым числом выражается в умножении

письменно:

7 × 3 = 21 или 7 · 3 = 21

словесно:

семь, умноженное на три, составляет 21.

Чтобы составить произведение 21, нужно 7 повторить три раза

21 = 7 + 7 + 7

Чтобы составить множитель 3, нужно единицу повторить три раза

3 = 1 + 1 + 1

Отсюда имеем другое определение умножения: Умножение есть такое действие, в котором произведение точно так же составляется из множимого, как множитель составлен из единицы.

Умножение многозначного числа на многозначное

Чтобы умножить многозначное число 3029 на многозначное 429, или найти произведение 3029 * 429, нужно повторить 3029 слагаемым 429 раз и найти сумму. Повторить 3029 слагаемым 429 раз значит повторить его слагаемым сначала 9, потом 20 и, наконец, 400 раз. Следовательно, чтобы умножить 3029 на 429, нужно 3029 умножить сначала на 9, потом на 20 и, наконец, на 400 и найти сумму этих трех произведений.

Три произведения

называются частными произведениями.

Полное произведение 3029 × 429 равно сумме трех частных:

3029 × 429 = 3029 × 9 + 3029 × 20 + 3029 × 400.

Найдем величины этих трех частных произведений.

1. Умножая 3029 на 9, находим:

    3029
   ×   9 
   27261 первое частное произведение

2. Умножая 3029 на 20, находим:

    3029
   ×   20 
    60580 второе частное произведение

3. Умножая 3026 на 400, находим:

    3029
   ×   400 
   1211600 третье частно произведение

Сложив эти частные произведения, получим произведение 3029 × 429:

Не трудно заметить, что все эти частные произведения есть произведения числа 3029 на однозначные числа 9, 2, 4, причем ко второму произведению, происходящему от умножения на десятки, приписывается один нуль, к третьему два нуля.

Нули, приписываемые к частным произведениям, опускают при умножении и ход вычисления выражают письменно:

В таком случае, при умножении на 2 (цифру десятков множителя) подписывают 8 под десятками, или отступают влево на одну цифру; при умножении на цифру сотен 4, подписывают 6 в третьем столбце, или отступают влево на 2 цифры. Вообще каждое частное произведение начинают подписывать от правой руки к левой под тем порядком, к которому принадлежит цифра множителя.

Отыскивая произведение 3247 на 209, имеем:

Здесь второе частное произведение начинаем подписывать под третьим столбцом, ибо оно выражает произведение 3247 на 2, третью цифру множителя.

Мы здесь опустили только два нуля, которые должны были явиться во втором частном произведении, как как оно выражает произведение числа на 2 сотни или на 200.

Из всего сказанного выводим правило. Чтобы умножить многозначное число на многозначное,

1. нужно множителя подписать под множимым так, чтобы цифры одинаковых порядков находились в одном вертикальном столбце, поставить слева знак умножения и провести черту.

2. Умножение начинают с простых единиц, затем переходят от правой руки к левой, умножают последовательное множимое на цифру десятков, сотен и т. д. и составляют столько частных произведений, сколько значащих цифр во множителе.

   

   

   

   

   

   

   

   

   

   

3. Единицы каждого частного произведения подписывают под тем столбцом, к которому принадлежит цифра множителя.

4. Все частные произведения, найденные таким образом, складывают вместе и получают в сумме произведение.

Чтобы умножить многозначное число на множитель, оканчивающейся нулями, нужно отбросить нули во множителе, умножить на оставшееся число и потом приписать к произведению столько нулей, сколько их находится во множителе.

Пример. Найти произведение 342 на 2700.

Если множимое и множитель оба оканчиваются нулями, при умножении отбрасывают их и затем к произведению приписывают столько нулей, сколько их содержится в обоих производителях.

Пример. Вычисляя произведение 2700 на 35000, умножаем 27 на 35

Приписывая к 945 пять нулей, получаем искомое произведение:

2700 × 35000 = 94500000.

Число цифр произведения. Число цифр произведения 3728 × 496 можно определить следующим образом. Это произведение более 3728 × 100 и меньше 3728 × 1000. Число цифр первого произведения 6 равно числу цифр в множимом 3728 и во множителе 496 без единицы. Число цифр второго произведения 7 равно числу цифр во множимом и во множителе. Данное произведение 3728 × 496 не может иметь цифр менее 6 (числа цифр произведения 3728 × 100, и более 7 (числа цифр произведения 3728 × 1000).

Откуда заключаем: число цифр всякого произведения или равно числу цифр во множимом и во множителе, или равно этому числу без единицы.

В нашем произведении может содержаться или 7 или 6 цифр.

Выполнение умножения

При практическом решении задачи умножения двух чисел необходимо свести её к последовательности более простых операций: «простое умножение», сложение, сравнение и др. Для этого разработаны различные методы умножения, например для чисел, дробей, векторов и др. На множестве натуральных чисел в настоящее время используется алгоритм поразрядного умножения. При этом следует рассматривать умножение как процедуру (в отличие от операции).

Примерный алгоритм процедуры поразрядного умножения двух чисел

Процедура достаточно сложная, состоит из относительно большого числа шагов и при умножении больших чисел может занять продолжительное время.

Пример пошагового умножения 3 ∙ 3 = 9 на числовой прямой.

«Простое умножение» в данном контексте обозначает операцию умножения одноразрядных чисел, которая может быть легко сведена к сложению. Является гипероператором сложения:

a⋅b=hyper2⁡(a,b)=hyper⁡(a,2,b)=a(2)b.{\displaystyle a\cdot b=\operatorname {hyper2} (a,b)=\operatorname {hyper} (a,2,b)=a^{(2)}b.}

a(2)b=a⋅b=a+a+⋯+a⏟b.{\displaystyle a{^{(2)}}b=a\cdot b=\underbrace {a+a+\dots +a} _{b}.}

где a+a+⋯+a{\displaystyle a+a+\dots +a} — последовательное сложение b{\displaystyle b} элементов.

Чтобы упростить и ускорить процесс умножения используют табличный метод «простого умножения», для этого заранее вычисляют все комбинации произведений чисел от 0 до 9 и берут готовый результат из этой таблицы:

Таблица для умножения в десятичной системе счисления

*	1	2	3	4	5	6	7	8	9
1	1	2	3	4	5	6	7	8	9
2	2	4	6	8	10	12	14	16	18
3	3	6	9	12	15	18	21	24	27
4	4	8	12	16	20	24	28	32	36
5	5	10	15	20	25	30	35	40	45
6	6	12	18	24	30	36	42	48	54
7	7	14	21	28	35	42	49	56	63
8	8	16	24	32	40	48	56	64	72
9	9	18	27	36	45	54	63	72	81

Данная процедура применима к умножению натуральных и целых (с учётом знака) чисел. Для других чисел используются более сложные алгоритмы.

Умножение многозначного числа на однозначное

Чтобы умножить многозначное число на однозначное, надо умножить каждую цифру многозначного числа на это однозначное число. Например, найдем значение выражения 12 × 3. Записываем данное выражение в столбик, при этом единицы должны быть под единицами. Всё это соединяется знаком умножения ( × )

Далее каждая цифра многозначного числа умножается на 3. Умножать начинаем с разряда единиц, то есть с цифры 2. Два умножить на три будет шесть. Записываем цифру 6 в разряде единиц нашего ответа:

Теперь умножаем 1 на 3, получаем 3. Записываем цифру 3 в разряде десятков нашего ответа:

Получили ответ 36.

В данном примере множимым было число 12, а множителем число 3. Число 12 это две единицы и один десяток. Наша задача заключалась в том, чтобы увеличить эти две единицы и один десяток в 3 раза. Тогда решая этот пример, можно было бы рассуждать следующим образом:

Увеличим две единицы в 3 раза: 2 × 3 = 6. Получили шесть единиц. Записываем цифру 6 в разряде единиц нового числа

Увеличим один десяток в 3 раза: 1 × 3 = 3. Получили три десятка. Записываем цифру 3 в разряде десятков нового числа:

Иногда при умножении одной цифры многозначного числа на однозначное число получается многозначное число. В этом случае сначала записывается одна цифра из разряда единиц, а остальные цифры переносятся на следующий разряд, к которому они будут добавлены после вычисления.

Например, найдем значение выражения 23 × 6

Умножаем каждую цифру числа 23 на 6. Начинаем с тройки: 3 × 6 = 18. Восемнадцать не вмещается в разряд единиц нашего ответа, поэтому сначала записывается 8, а 1 переносится на следующий разряд. Эта единица будет прибавлена к результату умножения 2 на 6

Теперь умножаем 2 на 6, получаем 12, плюс единица, которая досталась от предыдущего умножения. На рисунке эта единица выделена синим цветом. Вычисляем (2 × 6) + 1 = 13

Получили ответ 138. В данном примере множимым было число 23, а множителем число 6. Число 23 это три единицы и два десятка. Наша задача заключалась в том, чтобы увеличить эти три единицы и два десятка в 6 раз. Тогда решая этот пример, можно было бы рассуждать следующим образом:

Увеличим три единицы в 6 раз: 3 × 6 = 18. Получили восемнадцать единиц. Произошло переполнение разряда в разряде единиц. Число 18 это 8 единиц и 1 десяток. 8 единиц записываем в разряде единиц нового числа, а 1 десяток отправляем к разряду десятков. Этот десяток мы прибавим, когда увеличим два десятка в шесть раз:

Увеличим два десятка в 6 раз: 2 × 6 = 12. Получили двенадцать десятков. Плюс прибавляем один десяток, который остался от числа 18.

12 десятков плюс 1 десяток будет 13 десятков. Записываем число 13 в разряде десятков нового числа, образуя окончательный ответ:

Пример 3. Найти значение выражения 326 × 5

Записываем в столбик данное выражение:

Умножаем каждую цифру числа 326 на 5. Начинаем с шестёрки: 6 × 5 = 30. Число 30 не вмещается в разряд единиц нашего ответа, поэтому сначала записываем 0, а тройку переносим на следующий разряд:

Теперь умножаем 2 на 5, получаем 10 плюс тройка, которая досталась от предыдущей операции: (2 × 5) + 3 = 13. Получили число 13, которое не вмещается в разряд десятков нашего ответа. Поэтому записываем сначала 3, а единицу переносим на следующий разряд:

Теперь умножаем последнюю тройку на 5, плюс прибавляем единицу, которая досталась от предыдущей операции: (3 × 5) + 1 = 16. Получили 16. Записываем это число целиком, образуя окончательный ответ:

Степени

Между различными произведениями заслуживают особого внимания такие, в которых производители равны. Так, например:

2 × 2 = 4,    3 × 3 = 9.

Квадраты. Произведение двух равных множителей называется квадратом числа.

В наших примерах 4 есть квадрат 2, 9 есть квадрат 3.

Кубы. Произведение трех равных множителей называется кубом числа.

Так, в примерах 2 × 2 × 2 = 8, 3 × 3 × 3 = 27, число 8 есть куб 2, 27 есть куб 3.

Вообще произведение нескольких равных множителей называется степенью числа. Степени получают свои названия от числа равных множителей.

Произведения двух равных множителей или квадраты называются вторыми степенями.

Произведения трех равных множителей или кубы называются третьими степенями, и т. д.

Умножение физических величин

Единица измерения физической величины имеет определенное наименование (размерность): для длины (L) — метр (м), для времени (T) — секунда (с), для массы (M) — грамм (г) и так далее. Поэтому, результат измерения той или иной величины представляет собой не просто число, а число с наименованием. Наименование представляет собой самостоятельный объект, который равноправно участвует в операции умножения. При производстве операции умножения над физическими величинами, умножаются как сами числовые составляющие, так и их наименования.

Помимо размерных физических величин существуют безразмерные (количественные) величины, которые формально являются элементами числовой оси, то есть числами, не имеющие привязки к определенным физическим явлениям (измеряются «штуками», «разами» и тому подобное). При умножении чисел представляющих собой физические величины на безразмерную величину, множимое число увеличивается по величине кратно множителю и сохраняет единицу измерения. Например если взять 5-метровые рейки в количестве 3 штуки, то в результате умножения получим общую длину реек 15 метров:

5 м · 3 = 15 м.

Умножение разнородных физических величин надо рассматривать как нахождение новой физической величины, принципиально отличающейся от величин, которые мы умножаем. Если физически возможно создание такого произведения, например, при нахождении работы, скорости или других величин, то эта величина образует множество, отличное от начальных. В этом случае композиции этих величин  присваивается новое обозначение (новый термин), например: плотность, ускорение, мощность и прочее.

Например, если умножить скорость V = 4 м/с на время T = 2 с, соответствующие одному физическому процессу, то получится именованное число (физическая величина) соответствующее этому же физическому процессу, которая называется «длина» и измеряется в метрах: L = 8 м.

L = V · T = 4 м/с · 2 с = 8 (м/с) · с = 8 м.

При описании математическими средствами физических процессов немаловажную роль играет понятие однородности, которое означает например, что «1 кг муки» и «1 кг меди» принадлежат разным множествам {мука} и {медь} соответственно[уточнить]. Также понятие однородности предполагает, что умножаемые величины принадлежат одному физическому процессу.

Однозначные и многозначные числа

Для начала введём два новых понятия: однознáчные и многознáчные числа.

Однознáчным называется число, которое состоит из одной цифры. Например, следующие числа являются однознáчными:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Слово «однознáчные» говорит само за себя. Однознáчное — значит состоит из одного знака (цифру иногда называют знáком).

Многознáчным называется число, которое состоит из двух и более цифр. Например, следующие цифры являются многознáчными:

10, 11, 15, 255, 350, 1000, 12500

Многознáчных чисел бесконечно много. Их не сосчитать. Кроме того, они подразделяются на следующие виды:

• двузнáчные, которые состоят из двух цифр (например, 25);
• трёхзнáчные, которые состоят из трёх цифр (например, 563);
• четырёхзнáчные, которые состоят из четырёх цифр (например, 1400)

и так далее, в зависимости от того сколько цифр в числе.

Как работают фонды?

Фонд ведет деятельность, основываясь на внутренние правила и положения. Они регламентируют требования и условия, согласно им частные инвесторы доверяют сбережения в распоряжение управляющей компании. УК обязана иметь лицензионное разрешение на деятельность, дающее ей право на распоряжение собственностью, принадлежащей ПИФам. Разрешение выдается в органе Федеральной комиссии по рынку ценных бумаг. Управляющая организация имеет возможность создать несколько ПИФов. Сразу после получения разрешающей лицензии, управляющая структура обязывается подписать договор о сотрудничестве и совместной работе с депозитарием, независимым оценщиком, регистрирующим органом и аудитором. Внутренние правила и положения, принятые в конкретном ПИФе обязательны к внесению в реестры ФКЦБ.

Зарегистрировать в ответственной государственной структуре необходимо и особенное разрешение – Проспект эмиссии паев. Только после прохождения управляющей организацией всех процедур по регистрации и постановке на учет деятельности структуры возможно начало работы. Одним из первых этапов деятельности распоряжающейся организации является первичное размещение паев. В процессе этой работы организация обязана собрать наименьший объем капиталовложений, в противном случае производится ликвидация паевого фонда с дальнейшим возвратом вкладчикам денежных средств. Государство строго контролирует деятельность ПИФов через соответствующий орган – ФКЦБ.

Астигматизм

Являет собой особенность строения роговицы, которая приводит к искажению зрения и / или появлению двоения. Может присутствовать как изолированно в глазу, так и сопутствовать миопии или близорукости. С целью коррекции выписываются очки с цилиндрическим компонентом в линзе или мягкие контактные линзы (МКЛ). Внешне такие очки ничем не отличаются от обычных. Выполнение LASIK может исправить строение роговицы, и пациент забудет про астигматизм.

Важно понимать, что правильно подобранные очки не ухудшают зрение! Это миф. Увеличение задач, при которых необходима зрительная нагрузка, причём длительная, а также появление новых профессий, когда основная деятельность выполняется за компьютером, приводит к учащению расстройств, связанных с повышенной зрительной нагрузкой

Увеличение задач, при которых необходима зрительная нагрузка, причём длительная, а также появление новых профессий, когда основная деятельность выполняется за компьютером, приводит к учащению расстройств, связанных с повышенной зрительной нагрузкой.

Эти состояния могут быть острыми, подострыми, переходить в стадию хроническую или приводить к изменениям в строении глаза:

• Пресбиопия.
• Спазм аккомодации.
• ПИНА (привычно-избыточное напряжение аккомодации).
• Парез и паралич аккомодации.
• Аккомодативная астенопия.

Умножение в Энциклопедическом словаре:

Умножение — арифметическое действие. Обозначается точкой «.» или знаком»?» (в буквенном исчислении знаки умножения опускаются). Умножение целыхположительных чисел (натуральных чисел) есть действие, позволяющее по двумчислам а (множимому) и b (множителю) найти третье число ab (произведение),равное сумме b слагаемых, каждое из которых равно а. а и b называютсятакже сомножителями. Умножение дробных чисел а/b и с/d определяетсяравенством Умножение двух рациональных чисел дает число, абс. величинакоторого равна произведению абсолютных величин сомножителей и котороеимеет знак плюс (+), если у обоих сомножителей одинаковые знаки, или минус(-), если у них различные знаки. Умножение иррациональных чиселопределяется при помощи их рациональных приближений. Умножение комплексныхчисел, данных в форме ? = а+bi и ? = с+di, определяется равенством ?? = ас — bd + (a + bc)i.

Формы записи и терминология

Умножение записывается с использованием знака умножения (∙, ×, *) между аргументами, такая форма записи называется инфиксной нотацией. В данном контексте знак умножения является бинарным оператором. Знак умножения не имеет специального названия, тогда как, например, знак сложения называется «плюс».

Самый старый из используемых символов — диагональный крестик (×). Впервые его использовал английский математик Уильям Отред в своём труде «Clavis Mathematicae» 1631 г.
Немецкий математик Лейбниц предпочитал знак в виде приподнятой точки (∙). Этот символ он использовал в письме 1698 года.
Йоханн Ран ввёл звёздочку (∗) в качестве знака умножения, она появилась в его книге «Teutsche Algebra» 1659 г.

В российских учебниках математики в основном используется знак в виде приподнятой точки (∙). Звёздочка (∗) используется, как правило, в текстах компьютерных программ.

Результат записывается с использованием знака равенства «={\displaystyle =}», например:

a⋅b=c{\displaystyle a\cdot b=c}

6⋅3=18{\displaystyle 6\cdot 3=18} («шесть умножить на три равно восемнадцать» или «шестью три равно восемнадцать»).

Часто в математических выражениях знак умножения опускается, если это не вызывает неоднозначного прочтения. Например вместо y=6⋅x+3⋅z{\displaystyle y=6\cdot x+3\cdot z} пишется y=6x+3z{\displaystyle y=6x+3z}. Как правило, знак умножения опускают, если одним из сомножителей является переменная, функция или вложенное выражение в скобках: b2−4ac{\displaystyle b^{2}-4ac}, nsin⁡x{\displaystyle n\sin x}, a(b+c){\displaystyle a(b+c)}.

Свойства

Далее описаны основные свойства операция умножения на числовых множествах N,Z,Q,R,C{\displaystyle \mathbb {N} ,\mathbb {Z} ,\mathbb {Q} ,\mathbb {R} ,\mathbb {C} }.

Умножение коммутативно, то есть от перемены мест сомножителей произведение не меняется. Свойство также известно как переместительный закон умножения:

Коммутативность: a⋅b=b⋅a;{\displaystyle a\cdot b=b\cdot a;}

Умножение ассоциативно, то есть при последовательном выполнении умножения трёх или более чисел последовательность выполнения операций не имеет значения. Свойство также известно как сочетательный закон умножения:

Ассоциативность: (a⋅b)⋅c=a⋅(b⋅c);{\displaystyle (a\cdot b)\cdot c=a\cdot (b\cdot c);}

Умножение дистрибутивно, это свойство согласованности двух бинарных операций, определённых на одном и том же множестве. Свойство также известно как распределительный закон:

Дистрибутивность: x⋅(a+b)=(x⋅a)+(x⋅b),∀a,b∈ A;{\displaystyle x\cdot (a+b)=(x\cdot a)+(x\cdot b),\quad \forall a,b\in \ A;}

Относительно умножения в множестве A{\displaystyle A} существует единственный нейтральный элемент — 1{\displaystyle 1} (число «один»). Умножение любого числа на 1{\displaystyle 1} (нейтральный элемент) даёт число, равное исходному:

Нейтральный элемент: x⋅1=1⋅x=x,∃!1∈A;{\displaystyle x\cdot 1=1\cdot x=x,\quad \exists !1\in A;}

Умножение на 1{\displaystyle 1} идемпотентно, то есть повторное применение операции к объекту даёт тот же результат, что и одинарное:

Идемпотентность: x=x⋅1=(x⋅1)⋅1=((x⋅1)⋅1)⋅…⋅1,∀x∈A,∃!1∈A;{\displaystyle x=x\cdot 1=(x\cdot 1)\cdot 1=((x\cdot 1)\cdot 1)\cdot …\cdot 1,\quad \forall x\in A,\quad \exists !1\in A;}

Умножение на 0{\displaystyle 0} (нулевой элемент) даёт 0{\displaystyle 0} (нуль):

Нулевой элемент: x⋅=⋅x=,∃!∈A.{\displaystyle x\cdot 0=0\cdot x=0,\quad \exists !0\in A.}

Операция умножения чисел, определённых на множествах N,Z,Q,R{\displaystyle \mathbb {N} ,\mathbb {Z} ,\mathbb {Q} ,\mathbb {R} }, даёт произведение, принадлежащее этому же множеству. Следовательно, операция умножения относится к замкнутым операциям, то есть множества чисел Z,Q,R{\displaystyle \mathbb {Z} ,\mathbb {Q} ,\mathbb {R} } образуют кольца относительно операции умножения.

На языке общей алгебры вышеперечисленные свойства сложения говорят о том, что Z−,Q−,R−{\displaystyle \mathbb {Z} _{-0},\mathbb {Q} _{-0},\mathbb {R} _{-0}} являются абелевыми группами относительно операции умножения.

В математических выражениях операция умножения имеет более высокий приоритет по отношению к операциям сложения и вычитания, то есть она выполняется перед ними.

На множестве вещественных чисел область значений функции умножения графически имеет вид поверхности проходящей через начало координат и изогнутой с двух сторон в виде параболы.

Умножение на 10, 100, 1000

Чтобы умножить любое число на 10,  100 или 1000, достаточно дописáть к множимому количество нулей из множителя.

Например, чтобы умножить 12 на 10, нужно к множимому 12 дописать в конце ноль из множителя 10. В результате получим ответ 120

Еще примеры:

12 × 100 = 1200 (к 12 дописали два нуля, поскольку в числе 100 два нуля)

12 × 1000 = 12000 (к 12 дописали три нуля, поскольку в числе 1000 три нуля)

15 × 100 = 1500 (к 15 дописали два нуля, поскольку в числе 100 два нуля)

320 × 100 = 32000 (к 320 дописали два нуля, поскольку в 100 два нуля)

Если нулём оканчивается не множитель, а множимое, то для получения ответа нужно дописать ноль после множителя.

Например, чтобы умножить 10 на 12, нужно в ответе записать множитель 12 и дописать в конце один ноль:

10 × 12 = 120