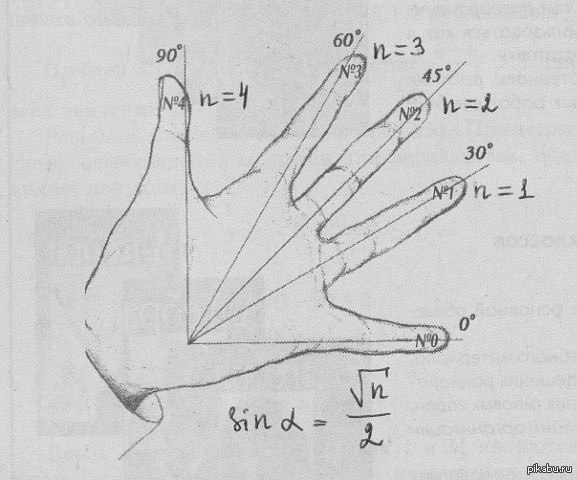
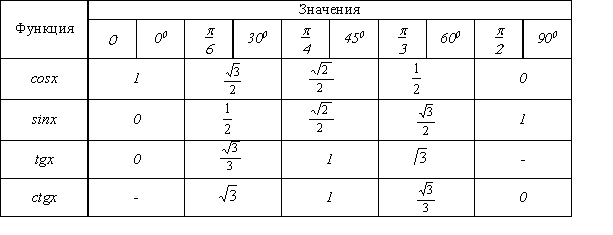
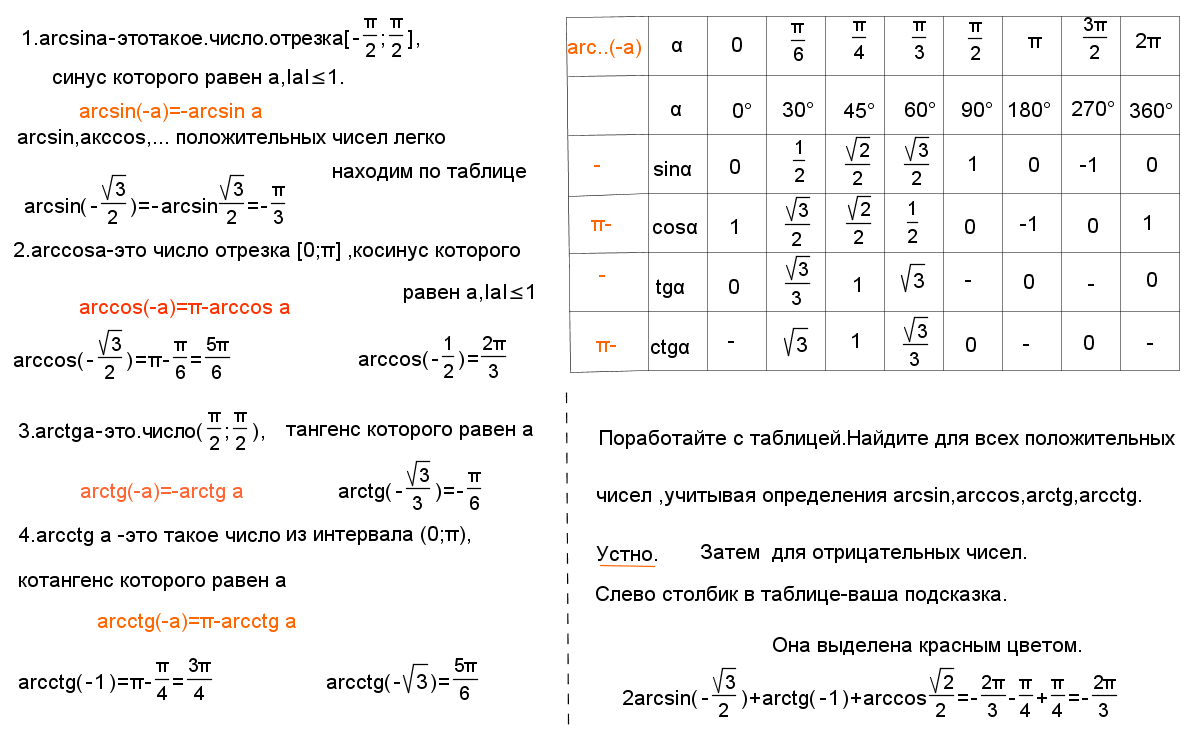
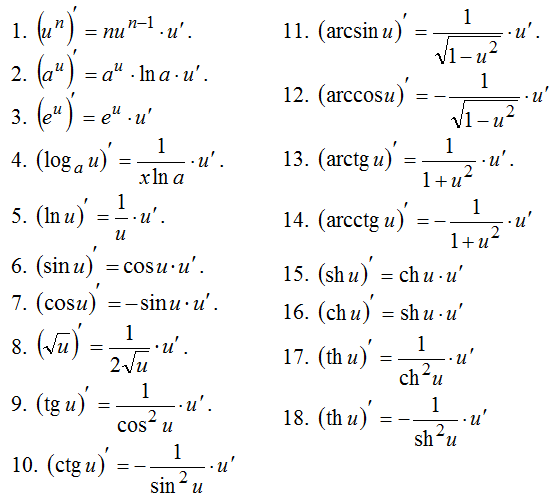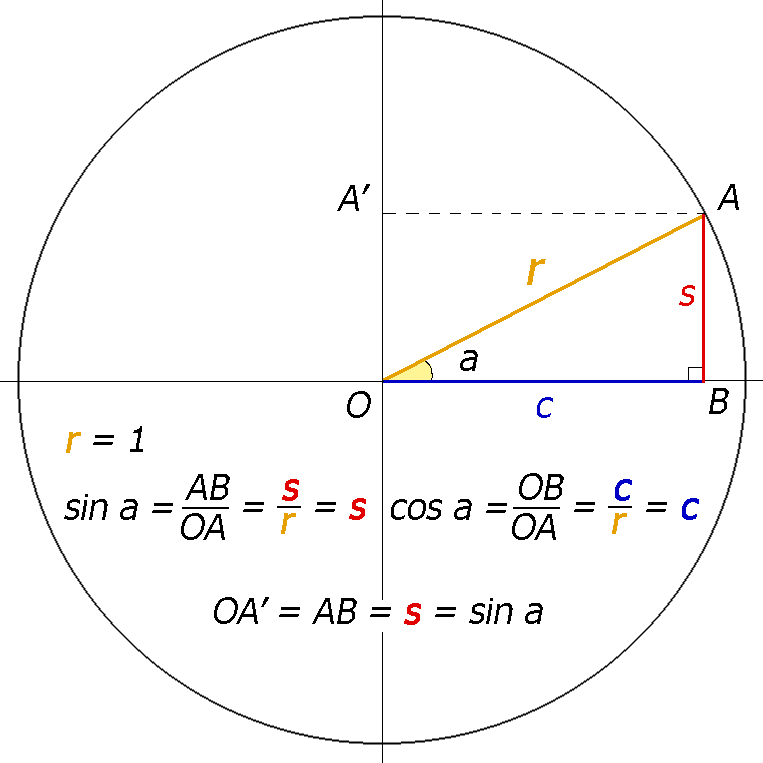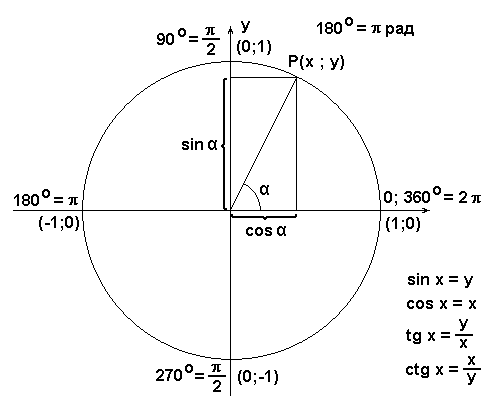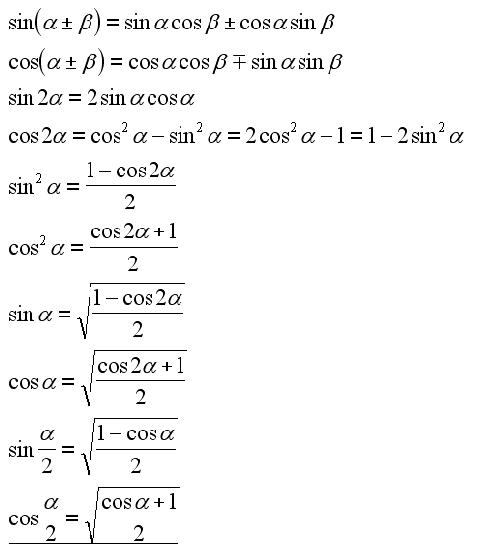Решение простых тригонометрических уравнений
-
- Если |a|>1{\displaystyle |a|>1} — вещественных решений нет.
- Если |a|⩽1{\displaystyle |a|\leqslant 1} — решением является число вида x=(−1)narcsina+πn; n∈Z.{\displaystyle x=(-1)^{n}\arcsin a+\pi n;\ n\in \mathbb {Z} .}
cosx=a.{\displaystyle \cos x=a.}
-
- Если |a|>1{\displaystyle |a|>1} — вещественных решений нет.
- Если |a|⩽1{\displaystyle |a|\leqslant 1} — решением является число вида x=±arccosa+2πn; n∈Z.{\displaystyle x=\pm \arccos a+2\pi n;\ n\in \mathbb {Z} .}
tgx=a.{\displaystyle \operatorname {tg} \,x=a.}
-
- Решением является число вида x=arctga+πn; n∈Z.{\displaystyle x=\operatorname {arctg} \,a+\pi n;\ n\in \mathbb {Z} .}
ctgx=a.{\displaystyle \operatorname {ctg} \,x=a.}
-
- Решением является число вида x=arcctga+πn; n∈Z.{\displaystyle x=\operatorname {arcctg} \,a+\pi n;\ n\in \mathbb {Z} .}
Формулы преобразования суммы углов
- sin(A±B)=sinA cosB±cosA sinB.{\displaystyle \sin(A\pm B)=\sin A\ \cos B\pm \cos A\ \sin B.}
- cos(A±B)=cosA cosB∓sinA sinB.{\displaystyle \cos(A\pm B)=\cos A\ \cos B\mp \sin A\ \sin B.}
- tg(A±B)=tgA±tgB1∓tgA tgB.{\displaystyle \mathop {\operatorname {tg} } (A\pm B)={\frac {\mathop {\operatorname {tg} } A\pm \mathop {\operatorname {tg} } B}{1\mp \mathop {\operatorname {tg} } A\ \mathop {\operatorname {tg} } B}}.}
- ctg(A±B)=ctgA ctgB∓1ctgB±ctgA.{\displaystyle \mathop {\operatorname {ctg} } (A\pm B)={\frac {\mathop {\operatorname {ctg} } A\ \mathop {\operatorname {ctg} } B\mp 1}{\mathop {\operatorname {ctg} } B\pm \mathop {\operatorname {ctg} } A}}.}
Идентичности
Треугольник со сторонами a , b , c и соответственно противоположными углами A , B , C
Тригонометрия известна своими многочисленными идентичностями, то есть уравнениями, которые верны для всех возможных входных данных.
Тождества, включающие только углы, известны как тригонометрические тождества . Другие уравнения, известные как тождества треугольников , связывают как стороны, так и углы данного треугольника.
Тождества треугольников
В следующих тождествах A , B и C — углы треугольника, а a , b и c — длины сторон треугольника, противоположные соответствующим углам (как показано на диаграмме).
Закон синусов
Закон синусов (также известный как «синус правила») для произвольных состояний треугольника:
- агрехАзнак равнобгрехBзнак равноcгрехCзнак равно2рзнак равноабc2Δ,{\ displaystyle {\ frac {a} {\ sin A}} = {\ frac {b} {\ sin B}} = {\ frac {c} {\ sin C}} = 2R = {\ frac {abc} {2 \ Delta}},}
где — площадь треугольника, а R — радиус описанной окружности треугольника:
Δ{\ displaystyle \ Delta}
- рзнак равноабc(а+б+c)(а-б+c)(а+б-c)(б+c-а).{\ displaystyle R = {\ frac {abc} {\ sqrt {(a + b + c) (a-b + c) (a + bc) (b + ca)}}}.}
Закон косинусов
Закон косинусов (известно как формула косинуса, или «совы правило») является продолжением теоремы Пифагора на произвольные треугольниках:
- c2знак равноа2+б2-2абпотому чтоC,{\ displaystyle c ^ {2} = a ^ {2} + b ^ {2} -2ab \ cos C,}
или эквивалентно:
- потому чтоCзнак равноа2+б2-c22аб.{\ displaystyle \ cos C = {\ frac {a ^ {2} + b ^ {2} -c ^ {2}} {2ab}}.}
Закон касательных
Закон касательных , разработанный Вьют , является альтернативой косинусов при решении по неизвестным краям треугольника, обеспечивая простые вычисления при использовании тригонометрических таблиц. Выдается:
- а-ба+бзнак равнозагар12(А-B)загар12(А+B){\ displaystyle {\ frac {ab} {a + b}} = {\ frac {\ tan \ left } {\ tan \ left }}}
Площадь
Учитывая две стороны a и b и угол между сторонами C , площадь треугольника равна половине произведения длин двух сторон и синуса угла между двумя сторонами:
Формула Герона — еще один метод, который можно использовать для вычисления площади треугольника. Эта формула утверждает, что если треугольник имеет стороны длиной a , b и c , и если полупериметр равен
- sзнак равно12(а+б+c),{\ displaystyle s = {\ frac {1} {2}} (a + b + c),}
тогда площадь треугольника равна:
- Площадьзнак равноΔзнак равноs(s-а)(s-б)(s-c)знак равноабc4р{\ displaystyle {\ mbox {Area}} = \ Delta = {\ sqrt {s (sa) (sb) (sc)}} = {\ frac {abc} {4R}}},
где R — радиус описанной окружности треугольника.
- Площадьзнак равноΔзнак равно12абгрехC.{\ displaystyle {\ mbox {Area}} = \ Delta = {\ frac {1} {2}} ab \ sin C.}
Тригонометрические тождества
Пифагорейские тождества
Следующие тригонометрические тождества связаны с теоремой Пифагора и верны для любого значения:
- грех2А+потому что2Азнак равно1 {\ Displaystyle \ грех ^ {2} А + \ соз ^ {2} А = 1 \}
- загар2А+1знак равносек2А {\ displaystyle \ tan ^ {2} A + 1 = \ sec ^ {2} A \}
- детская кроватка2А+1знак равноcsc2А {\ displaystyle \ cot ^ {2} A + 1 = \ csc ^ {2} A \}
Формула Эйлера
Формула Эйлера , в которой говорится, что дает следующие аналитические тождества для синуса, косинуса и тангенса в терминах e и мнимой единицы i :
еяИксзнак равнопотому чтоИкс+ягрехИкс{\ Displaystyle е ^ {ix} = \ соз х + я \ грех х}
- грехИксзнак равноеяИкс-е-яИкс2я,потому чтоИксзнак равноеяИкс+е-яИкс2,загарИксзнак равноя(е-яИкс-еяИкс)еяИкс+е-яИкс.{\ displaystyle \ sin x = {\ frac {e ^ {ix} -e ^ {- ix}} {2i}}, \ qquad \ cos x = {\ frac {e ^ {ix} + e ^ {- ix }} {2}}, \ qquad \ tan x = {\ frac {i (e ^ {- ix} -e ^ {ix})} {e ^ {ix} + e ^ {- ix}}}.}.
Другие тригонометрические тождества
Другие часто используемые тригонометрические тождества включают тождества половинного угла, тождества суммы углов и разностей, а также тождества произведения к сумме.
Формулы преобразования суммы углов
- sin(A±B)=sinA cosB±cosA sinB.{\displaystyle \sin(A\pm B)=\sin A\ \cos B\pm \cos A\ \sin B.}
- cos(A±B)=cosA cosB∓sinA sinB.{\displaystyle \cos(A\pm B)=\cos A\ \cos B\mp \sin A\ \sin B.}
- tg(A±B)=tgA±tgB1∓tgA tgB.{\displaystyle \mathop {\operatorname {tg} } (A\pm B)={\frac {\mathop {\operatorname {tg} } A\pm \mathop {\operatorname {tg} } B}{1\mp \mathop {\operatorname {tg} } A\ \mathop {\operatorname {tg} } B}}.}
- ctg(A±B)=ctgA ctgB∓1ctgB±ctgA.{\displaystyle \mathop {\operatorname {ctg} } (A\pm B)={\frac {\mathop {\operatorname {ctg} } A\ \mathop {\operatorname {ctg} } B\mp 1}{\mathop {\operatorname {ctg} } B\pm \mathop {\operatorname {ctg} } A}}.}
[править] Сферическая тригонометрия
Сферическая тригонометрия — раздел сферической геометрии, главными объектами которого являются многоугольники (особенно треугольники) на сфере и соотношение между сторонами и углами. Возникновение сферической геометрии связано с задачами сферической астрономии.
Основными элементами сферической геометрии являются точки и большие круги сферы. Большие круги являются геодезическими линиями сферы, поэтому они в сферической геометрии играют роль, аналогичную роли прямых в планиметрии. Расстояние между двумя точками в сферической геометрии измеряется углом между радиусами сферы, проведенными в эти точки. Угол между двумя «прямыми» равен двугранному углу между плоскостями больших кругов, которые определяют эти «прямые». Две любые «прямые» в сферической геометрии пересекаются в двух точках и разбивают поверхность сферы на 4 двуугольника. Три «прямые», пересекаясь попарно, образуют 8 сферических треугольников. Эти треугольники имеют много необычных свойств, которые отличают их от плоских треугольников. Например, сумма углов сферического треугольника всегда больше 180° и меньше 540°.
Стороны и углы сферического треугольника связаны зависимостями:
- \frac{\sin\frac{a}{R}}{\sin A}=\frac{\sin\frac{b}{R}}{\sin B}=\frac{\sin\frac{c}{R}}{\sin C};
- \cos\frac{c}{R}=\cos\frac{a}{R}\cos\frac{b}{R}+\sin\frac{a}{R}\sin\frac{b}{R}\cos C;
- \cos\frac{a}{R}=\frac{\cos A + \cos B\cos C}{\sin B\sin C}.
где a, b, c — стороны сферического треугольника; A, B, C — углы, противоположные этим сторонам; R — радиус сферы.
Сферическая тригонометрия очень важна в астрономических вычислениях (небесной механике), а также в орбитальной, космической навигации и навигации на поверхности Земли.
Применение
Одними из первых специалистов, использующих тригонометрию, были моряки, не имеющие никакого другого ориентира в открытом море, кроме неба над головой. Сегодня капитаны кораблей (самолётов и других видов транспорта) не ищут кратчайший путь по звёздам, зато активно прибегают к помощи GPS-навигации, которая без использования тригонометрии была бы невозможна.
Практически в каждом разделе физики вас ждут расчёты с использованием синусов и косинусов: будь то приложение силы в механике, расчёты пути объектов в кинематике, колебания, распространение волн, преломление света – без базовой тригонометрии в формулах просто не обойтись.
Ещё одна профессия, которая немыслима без тригонометрии – это геодезист. Используя теодолит и нивелир либо более сложный прибор – тахиометр, эти люди измеряют разницу в высоте между различными точками на земной поверхности.
Формулы преобразования суммы углов
- sin(A±B)=sinA cosB±cosA sinB.{\displaystyle \sin(A\pm B)=\sin A\ \cos B\pm \cos A\ \sin B.}
- cos(A±B)=cosA cosB∓sinA sinB.{\displaystyle \cos(A\pm B)=\cos A\ \cos B\mp \sin A\ \sin B.}
- tg(A±B)=tgA±tgB1∓tgA tgB.{\displaystyle \mathop {\operatorname {tg} } (A\pm B)={\frac {\mathop {\operatorname {tg} } A\pm \mathop {\operatorname {tg} } B}{1\mp \mathop {\operatorname {tg} } A\ \mathop {\operatorname {tg} } B}}.}
- ctg(A±B)=ctgA ctgB∓1ctgB±ctgA.{\displaystyle \mathop {\operatorname {ctg} } (A\pm B)={\frac {\mathop {\operatorname {ctg} } A\ \mathop {\operatorname {ctg} } B\mp 1}{\mathop {\operatorname {ctg} } B\pm \mathop {\operatorname {ctg} } A}}.}
Приложения
Астрономия
На протяжении веков сферическая тригонометрия использовалась для определения положения Солнца, Луны и звезд, предсказания затмений и описания орбит планет.
В наше время метод триангуляции используется в астрономии для измерения расстояния до ближайших звезд, а также в системах спутниковой навигации .
Навигация
Секстанты используются для измерения угла солнца или звезд по отношению к горизонту. Используя тригонометрию и морской хронометр , можно определить положение корабля по таким измерениям.
Исторически тригонометрия использовалась для определения широты и долготы парусных судов, построения курсов и расчета расстояний во время навигации.
Тригонометрия по-прежнему используется в навигации с помощью таких средств, как глобальная система позиционирования и искусственный интеллект для автономных транспортных средств .
Геодезия
В земельной съемке , тригонометрия используется при расчете длины, площади и относительных углов между объектами.
В более крупном масштабе тригонометрия используется в географии для измерения расстояний между ориентирами,
Периодические функции
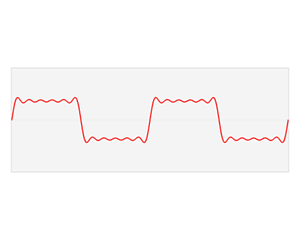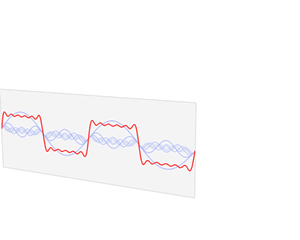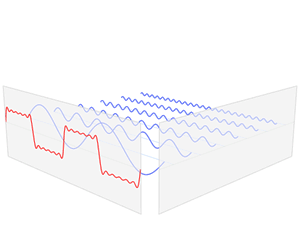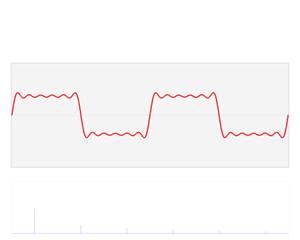 Функция ( выделена красным) — это сумма шести синусоидальных функций разных амплитуд и гармонически связанных частот. Их суммирование называется рядом Фурье. Преобразование Фурье (синим цветом), которое отображает зависимость амплитуды от частоты, показывает 6 частот ( в нечетных гармониках ) и их амплитуды ( 1 / нечетное число ).s(Икс){\ displaystyle s (x)}S(ж){\ Displaystyle S (е)}
Функция ( выделена красным) — это сумма шести синусоидальных функций разных амплитуд и гармонически связанных частот. Их суммирование называется рядом Фурье. Преобразование Фурье (синим цветом), которое отображает зависимость амплитуды от частоты, показывает 6 частот ( в нечетных гармониках ) и их амплитуды ( 1 / нечетное число ).s(Икс){\ displaystyle s (x)}S(ж){\ Displaystyle S (е)}
Функции синуса и косинуса являются фундаментальными для теории периодических функций , например, описывающих звуковые и световые волны. Фурье обнаружил , что каждая непрерывная , периодическая функция может быть описана как бесконечная сумма тригонометрических функций.
Даже непериодические функции могут быть представлены как интеграл синусов и косинусов с помощью преобразования Фурье . Это, помимо прочего, имеет приложения к квантовой механике и коммуникациям.
Оптика и акустика
Тригонометрия полезна во многих физических науках , включая акустику и оптику . В этих областях они используются для описания звуковых и световых волн , а также для решения проблем, связанных с границами и передачей.
Другие приложения
Другие области, в которых используются тригонометрия или тригонометрические функции, включают теорию музыки , геодезию , синтез звука , архитектуру , электронику , биологию , медицинскую визуализацию ( компьютерная томография и ультразвук ), химию , теорию чисел (и, следовательно, криптологию ), сейсмологию , метеорологию , океанографию , сжатие изображений. , фонетика , экономика , электротехника , машиностроение , гражданское строительство , компьютерная графика , картография , кристаллография и разработка игр .
Формулы преобразования суммы углов
- sin(A±B)=sinA cosB±cosA sinB.{\displaystyle \sin(A\pm B)=\sin A\ \cos B\pm \cos A\ \sin B.}
- cos(A±B)=cosA cosB∓sinA sinB.{\displaystyle \cos(A\pm B)=\cos A\ \cos B\mp \sin A\ \sin B.}
- tg(A±B)=tgA±tgB1∓tgA tgB.{\displaystyle \mathop {\operatorname {tg} } (A\pm B)={\frac {\mathop {\operatorname {tg} } A\pm \mathop {\operatorname {tg} } B}{1\mp \mathop {\operatorname {tg} } A\ \mathop {\operatorname {tg} } B}}.}
- ctg(A±B)=ctgA ctgB∓1ctgB±ctgA.{\displaystyle \mathop {\operatorname {ctg} } (A\pm B)={\frac {\mathop {\operatorname {ctg} } A\ \mathop {\operatorname {ctg} } B\mp 1}{\mathop {\operatorname {ctg} } B\pm \mathop {\operatorname {ctg} } A}}.}
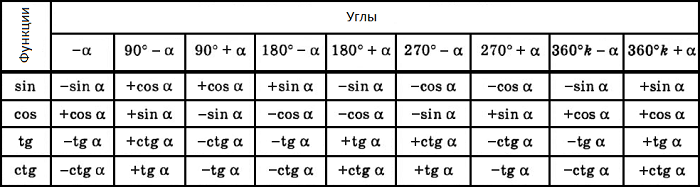
Формулы приведения.
По этим формулам значение тригонометрической функции аргумента a, где p/2 a p, можно привести к значению функции аргумента a, где 0 a p/2, как той же, так и дополнительной к ней.
| Аргумент b
Функция |
– a | + a | p – a | p + a | + a | + a | 2p – a |
| sin b | cos a | cos a | sin a | –sin a | –cos a | –cos a | –sin a |
| cos b | sin a | –sin a | –cos a | –cos a | –sin a | sin a | cos a |
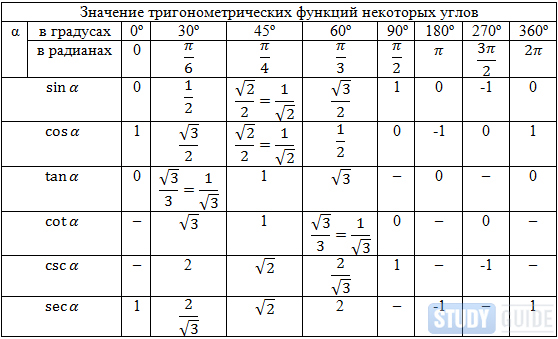
Поэтому в таблицах тригонометрических функций даются значения только для острых углов, причем достаточно ограничиться, например, синусом и тангенсом. В таблице даны только наиболее употребительные формулы для синуса и косинуса. Из них легко получить формулы для тангенса и котангенса. При приведении функции от аргумента вида kp/2 ± a, где k – целое число, к функции от аргумента a:
1) название функции сохраняется, если k четное, и меняется на «дополнительное», если k нечетное;
2) знак в правой части совпадает со знаком приводимой функции в точке kp/2 ± a, если угол a острый.
Например, при приведении ctg (a – p/2) убеждаемся, что a – p/2 при 0 a p/2 лежит в четвертом квадранте, где котангенс отрицателен, и, по правилу 1, меняем название функции: ctg (a – p/2) = –tg a.
История
Гиппарх , которому приписывают составление первой тригонометрической таблицы , был описан как «отец тригонометрии».
Шумерские астрономы изучали измерение углов, используя разделение окружностей на 360 градусов. Они, а затем и вавилоняне , изучили отношения сторон подобных треугольников и обнаружили некоторые свойства этих соотношений, но не превратили это в систематический метод нахождения сторон и углов треугольников. В древних нубийцев использовали подобный метод.
В III веке до нашей эры эллинистические математики, такие как Евклид и Архимед, изучали свойства хорд и вписанных углов в окружности, и они доказали теоремы, эквивалентные современным тригонометрическим формулам, хотя они представили их геометрически, а не алгебраически. В 140 г. до н.э. Гиппарх (из Никеи , Малая Азия) дал первые таблицы аккордов, аналогичные современным таблицам значений синусов , и использовал их для решения задач тригонометрии и сферической тригонометрии . Во II веке нашей эры греко-египетский астроном Птолемей (из Александрии, Египет) построил подробные тригонометрические таблицы ( таблицу аккордов Птолемея ) в книге 1, главе 11 своего Альмагеста . Птолемей использовал длину хорды для определения своих тригонометрических функций, что незначительно отличается от принятого сегодня соглашения о синусе . (Значение, которое мы называем sin (θ), можно найти, посмотрев длину хорды для удвоенного угла интереса (2θ) в таблице Птолемея, а затем разделив это значение на два.) Прошли столетия, прежде чем были составлены более подробные таблицы, и Трактат Птолемея использовался для выполнения тригонометрических вычислений в астрономии в течение следующих 1200 лет в средневековом византийском , исламском и, позднее, западноевропейском мирах.
Современное синусоидальное соглашение впервые засвидетельствовано в Сурья-сиддханте , а его свойства были дополнительно задокументированы индийским математиком и астрономом 5-го века (н.э.) Арьябхатой . Эти греческие и индийские труды были переведены и дополнены средневековыми исламскими математиками . К 10 веку исламские математики использовали все шесть тригонометрических функций, составили таблицы своих значений и применяли их к задачам сферической геометрии . Персидский эрудит Насир ад-Дин ат-Туси был описан как создатель тригонометрии как математической дисциплины в своем собственном праве. Насир ад-Дин ат-Туси первым начал рассматривать тригонометрию как математическую дисциплину, независимую от астрономии, и развил сферическую тригонометрию в ее нынешней форме. Он перечислил шесть различных случаев прямоугольного треугольника в сферической тригонометрии, а в своей работе « На секторном рисунке» сформулировал закон синусов для плоских и сферических треугольников, открыл закон касательных для сферических треугольников и представил доказательства для обоих. эти законы. Знания о тригонометрических функциях и методах достигли Западной Европы благодаря латинским переводам греческого Альмагеста Птолемея, а также работ персидских и арабских астрономов, таких как Аль Баттани и Насир ад-Дин ат-Туси . Одна из самых ранних работ по тригонометрии по северной европейской математике является De Triangulis от 15 — го века немецкого математика Regiomontanus , который поощрял к записи, и снабженный копией Альмагеста , по византийскому греческому ученому кардиналу Виссарион Никейского , с которым он жил на несколько лет. В то же время еще один перевод Альмагеста с греческого на латынь завершил критский Георгий Трапезундский . Тригонометрия была еще так мало известна в Северной Европе 16-го века, что Николай Коперник посвятил две главы De Revolutionibus orbium coelestium объяснению ее основных понятий.
Из-за требований навигации и растущей потребности в точных картах больших географических областей тригонометрия превратилась в важную отрасль математики. Варфоломей Питискус был первым, кто использовал это слово, опубликовав свою « Тригонометрию» в 1595 году. Джемма Фризиус впервые описала метод триангуляции, который до сих пор используется в геодезической съемке. Это был Leonhard Euler , которые полностью включены в комплексные числа в тригонометрии. Работы шотландских математиков Джеймса Грегори в 17 веке и Колина Маклорена в 18 веке оказали влияние на развитие тригонометрических рядов . Также в 18 веке Брук Тейлор определил общий ряд Тейлора .
Презентация на тему: » Тригонометрия – слово греческое Metrew — измеряю Trigwnon – треугольник Тригонометрия в буквальном переводе означает – измерение треугольников Возникновение.» — Транскрипт:

2
Тригонометрия – слово греческое Metrew — измеряю Trigwnon – треугольник Тригонометрия в буквальном переводе означает – измерение треугольников Возникновение связано с землемерением, астрономией и строительным делом

3
Тригонометрические сведения были известны древним вавилонянам и египтянам, но основы тригонометрии как науки — были заложены в древней Греции.

4
Впервые способы решения треугольников, основанные на зависимостях между сторонами и углами треугольника, были найдены древнегреческими астрономами 2 в. до н.э. 2 в. н.э. Гиппарх Клавдий Птолемей

5
Значительный вклад в развитие тригонометрии внесли арабские ученые Абу-ль-Вафа Мухамед-бен Мухамед (940 – 998) Аль-Батани (850 – 929) Составил таблицы синусов и тангенсов через каждые 10 с точностью до 1/604

6
и азербайджанскому астроному и математику Насиреддин Туси Мухамеду (1201 – 1274) Теорема синусов уже была известна индийскому ученому Бхаскара (р ?)

7
Длительную историю имеет понятие синус. Различные отношения отрезков треугольника и окружности (а по существу, и тригонометрические функции) встречаются уже в III веке до н.э. в работах великих математиков Древней Греции – Евклида, Архимеда, Апполония Пергского В римский период эти отношения достаточно систематично исследовались Менелаем (I век н.э.), хотя и не приобрели специального названия.

8
В IV – V веках появился специальный термин в трудах индийского ученого Ариабхаты. Отрезок CB — он назвал АРДХАДЖИВА АРДХА – половина ДЖИВА – тетива лука ДЖИВА пер. на арабский ДЖАЙБ — выпуклость лат. СИНУС – изгиб, кривизна

9
КОСИНУС – это сокращение латинского выражения completely sinus, т.е. «дополнительный синус» Тангенс и котангенс были введены в Х веке арабским математиком Абу-ль Вафой, который составил первые таблицы для их нахождения. Заново открыты лишь в XIV веке немецким математиком и астрономом Региомонтаном Доказал теорему тангенсов Составил подробные тригонометрические таблицы Благодаря его трудам плоская и сферическая тригонометрия стала самостоятельной дисциплиной в Европе ТАНГЕНС от латинского tanger – касаться (линия тангенсов – касательная к единичной окружности)

10
Вслед за Региомонтаном, тригонометрией много занимался Николай Коперник (1473 – 1543). Он добавил к таблице тангенсов — таблицу секансов. Знаменитый астроном Тихо-Браге (1546 – 1601) разработал много вычислительных приемов, облегчающих задачу решения треугольников. Франсуа Виет (1540 – 1603) уже полностью решил задачу об определениях всех элементов плоского и сферического треугольника по трем данным. Среди его результатов появились такие, которые устанавливали связи между тригонометрией и алгеброй. Иоган Кеплер ( )

11
Начиная с XVII в., тригонометрические функции начали применять : -К решению уравнений; -К решению задач механики, оптики, электричества, радиотехники; — Для описания колебательных процессов, распространения волн, движения различных механизмов; — Для изучения переменного электрического тока и т.д. Механические колебательные системы Графики координаты x(t), скорости υ(t) и ускорения a(t) тела, совершающего гармонические колебания «Моментальные фотографии» бегущей синусоидальной волны в момент времени t и t + Δt Образование стоячей волны в струне, закрепленной на обоих концах

12
ввел известные определения тригонометрических функций Аналитическая теория тригонометрических функций в основном была создана выдающимся математиком XVIII века Леонардом Эйлером, членом Петербургской Академии наук. рассматривал функции произвольного угла получил формулы приведения

13
Таким образом, тригонометрия, возникшая как наука о решении треугольников, со временем развилась и в науку о тригонометрических функциях.

14
СПАСИБО ЗА ВНИМАНИЕ СПАСИБО ЗА ВНИМАНИЕ Презентацию подготовила Башкирцева Г.А
Отзывы россиян, играющих в американские лотереи
Для начала – о цене билетов. Не удивляйтесь, что при покупке игрового талона через интернет вы заплатите несколько больше, чем рассчитывали.
Приобретение билетов иностранных лотерей без посредников невозможно, а посредник всегда возьмет себе процент вознаграждения – это его заработок, причем заслуженный.
Посреднику нужно нанять человека, который будет будет покупать и сканировать, купленные билеты, более того им нужно платить деньги за организацию остальных процессов. Обязательно учитывайте нюанс цены, когда покупаете билеты американских лотерей онлайн.
Ну, а об остальном – читайте в отзывах реальных игроков, которые мне удалось найти на форумах. Я буду обобщать, поскольку мнения многих игроков сходятся.
Опытные «лотерейщики» утверждают, что не стоит прельщаться низкой стоимостью минимальной ставки (до 2$), поскольку это, в большинстве случаев, деньги, выброшенные на ветер. Такие ставки практически никогда не приносят выигрыша. Лучше, по их мнению, делать развернутые ставки –это несколько дороже, но повышает шансы выиграть.
Название
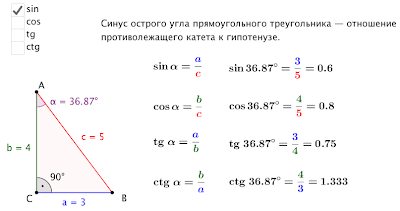
Дословно термин «тригонометрия» можно перевести как «измерение треугольников». Основным объектом изучения в рамках данного раздела науки на протяжении многих веков был прямоугольный треугольник, а точнее – взаимосвязь между величинами углов и длинами его сторон (сегодня с этого раздела начинается изучение тригонометрии с нуля). В жизни нередки ситуации, когда практически измерить все требуемые параметры объекта (или расстояние до объекта) невозможно, и тогда возникает необходимость недостающие данные получить посредством расчётов.
Например, в прошлом человек не мог измерить расстояние до космических объектов, а вот попытки эти расстояния рассчитать встречаются задолго до наступления нашей эры. Важнейшую роль играла тригонометрия и в навигации: обладая некоторыми знаниями, капитан всегда мог сориентироваться ночью по звездам и скорректировать курс.
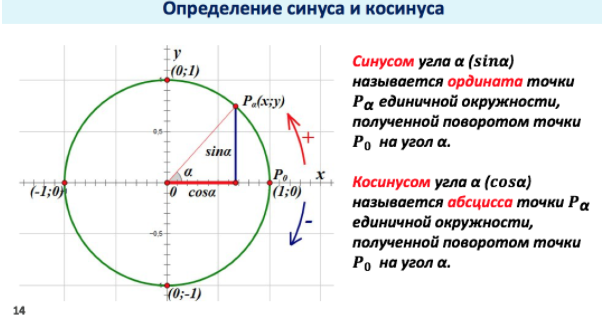
Функция y = sin х.
На единичной окружности углу x соответствует точка А (рис. 7),а ее проекцией на ось Оу будет точка N. Значение функции у= sin xопределяется как ордината точки А.Точка В (угол x, у)принадлежит графику функции y = sin x (рис. 8).Ясно, что функция y = sin x периодическая, ее период равен 2p:
sin (x + 2p) = sin (x).
Для двух значений аргумента, х и – ,проекции соответствующих им точек Аx и А-x на ось Оу расположены симметрично относительно точки О. Поэтому
sin (–x) = –sin (x),
т.е. синус – функция нечетная, f(–x) = –f(x)(рис. 9).

Если точку A повернуть относительно точки О на угол p/2 против часовой стрелки (другими словами, если угол х увеличить на p/2), то ее ордината в новом положении будет равна абсциссе в старом. А значит,
sin (x + p/2) = cos x.
Иначе, синус – это косинус, «запоздавший» на p/2, поскольку любое значение косинуса «повторится» в синусе, когда аргумент возрастет на p/2. И чтобы построить график синуса, достаточно сдвинуть график косинуса на p/2 вправо (рис. 10)
Чрезвычайно важное свойство синуса выражается равенством
.

Геометрический смысл равенства виден из рис. 11. Здесь х – это половина дуги АВ,а sin х – половина соответствующей хорды. Очевидно, что по мере сближения точек А и В длина хорды все точнее приближается к длине дуги. Из того же рисунка несложно извлечь неравенство
|sin x| x|, верное при любом х.

Формулу (*) математики называют замечательным пределом. Из нее, в частности, следует, что sin х х при малых х.
Функции у = tg х, у = ctg х.Две другие тригонометрические функции – тангенс и котангенс проще всего определить как отношения уже известных нам синуса и косинуса:
Как синус и косинус, тангенс и котангенс – функции периодические, но их периоды равны p, т.е. они вдвое меньше, чем у синуса и косинуса. Причина этого понятна: если синус и косинус оба поменяют знаки, то их отношение не изменится.
Поскольку в знаменателе тангенса находится косинус, то тангенс не определен в тех точках, где косинус равен 0, – когда х = p/2 + kp.Во всех остальных точках он монотонно возрастает. Прямые х = p/2 + kp для тангенса являются вертикальными асимптотами. В точках kp тангенс и угловой коэффициент составляют 0 и 1 соответственно (рис. 12).

Котангенс не определен там, где синус равен 0 (когда х = kp).В остальных точках он монотонно убывает, а прямые х = kp – его вертикальные асимптоты. В точках х = p/2 + kp котангенс обращается в 0, а угловой коэффициент в этих точках равен –1 (рис. 13).

Универсальная тригонометрическая подстановка

Обзор основных формул тригонометрии завершаем формулами, выражающими тригонометрические функции через тангенс половинного угла. Такая замена получила название универсальной тригонометрической подстановки. Ее удобство заключается в том, что все тригонометрические функции выражаются через тангенс половинного угла рационально без корней.
Для более полной информации смотрите статью универсальная тригонометрическая подстановка.
Список литературы.
- Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
- Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
- Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
- Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
Формулы преобразования суммы углов
- sin(A±B)=sinA cosB±cosA sinB.{\displaystyle \sin(A\pm B)=\sin A\ \cos B\pm \cos A\ \sin B.}
- cos(A±B)=cosA cosB∓sinA sinB.{\displaystyle \cos(A\pm B)=\cos A\ \cos B\mp \sin A\ \sin B.}
- tg(A±B)=tgA±tgB1∓tgA tgB.{\displaystyle \mathop {\operatorname {tg} } (A\pm B)={\frac {\mathop {\operatorname {tg} } A\pm \mathop {\operatorname {tg} } B}{1\mp \mathop {\operatorname {tg} } A\ \mathop {\operatorname {tg} } B}}.}
- ctg(A±B)=ctgA ctgB∓1ctgB±ctgA.{\displaystyle \mathop {\operatorname {ctg} } (A\pm B)={\frac {\mathop {\operatorname {ctg} } A\ \mathop {\operatorname {ctg} } B\mp 1}{\mathop {\operatorname {ctg} } B\pm \mathop {\operatorname {ctg} } A}}.}
Этимология слова «синус»
История слова «синус» поистине необычна. Дело в том, что буквальный перевод этого слова с латыни означает «впадина». Всё потому, что верное понимание слова затерялось при переводе с одного языка на другой.
Названия базовых тригонометрических функций произошли из Индии, где понятие синуса обозначалось словом «тетива» на санскрите — дело в том, что отрезок вместе с дугой окружности, на которую он опирался, походил на лук. Во времена расцвета арабской цивилизации индийские достижения в области тригонометрии были заимствованы, и термин перешел в арабский язык в виде транскрипции. Случилось так, что в этом языке уже было похожее слово, обозначающее впадину, и если арабы понимали фонетическую разницу между родным и заимствованным словом, то европейцы, переводящие научные трактаты на латынь, по ошибке буквально перевели арабское слово, никакого отношения к понятию синуса не имеющее. Им мы и пользуемся по сей день.
Применение тригонометрии
Секстант — навигационный измерительный инструмент, используемый для измерения высоты светила над горизонтом с целью определения географических координат той местности, в которой производится измерение.
Существует множество областей, в которых применяются тригонометрия и тригонометрические функции. Например, метод триангуляции используется в астрономии для измерения расстояния до ближайших звезд, в географии для измерения расстояний между объектами, а также в спутниковых навигационных системах. Синус и косинус имеют фундаментальное значение для теории периодических функций, например при описании звуковых и световых волн.
Тригонометрия или тригонометрические функции используются в астрономии (особенно для расчётов положения небесных объектов, когда требуется сферическая тригонометрия), в морской и воздушной навигации, в теории музыки, в акустике, в оптике, в анализе финансовых рынков, в электронике, в теории вероятностей, в статистике, в биологии, в медицинской визуализации (например, компьютерная томография и ультразвук), в аптеках, в химии, в теории чисел (следовательно, и в криптологии), в сейсмологии, в метеорологии, в океанографии, во многих физических науках, в межевании и геодезии, в архитектуре, в фонетике, в экономике, в электротехнике, в машиностроении, в гражданском строительстве, в компьютерной графике, в картографии, в кристаллографии, в разработке игр и многих других областях.
Формулы понижения степени.
Из формул кратного аргумента выводятся формулы:
| sin2a = (1 – cos 2a)/2; | cos2a = (1 + cos 2a)/2; |
| sin3a = (3 sin a – sin 3a)/4; | cos3a = (3 cosa + cos 3a)/4. |
С помощью этих формул тригонометрические уравнения можно приводить к уравнениям более низких степеней. Таким же образом можно вывести и формулы понижения для более высоких степеней синуса и косинуса.
| Производные и интегралы тригонометрических функций | |
| (sin x)` = cos x; | (cos x)` = –sin x; |
| (tg x)` = ; | (ctg x)` = – ; |
| т sin x dx = –cos x + C; | т cos x dx = sin x + C; |
| т tg x dx = –ln |cos x| + C; | т ctg x dx = ln |sin x| + C; |
Каждая тригонометрическая функция в каждой точке своей области определения непрерывна и бесконечно дифференцируема. Причем и производные тригонометрических функций являются тригонометрическими функциями, а при интегрировании получаются так же тригонометрические функции или их логарифмы. Интегралы от рациональных комбинаций тригонометрических функций всегда являются элементарными функциями.