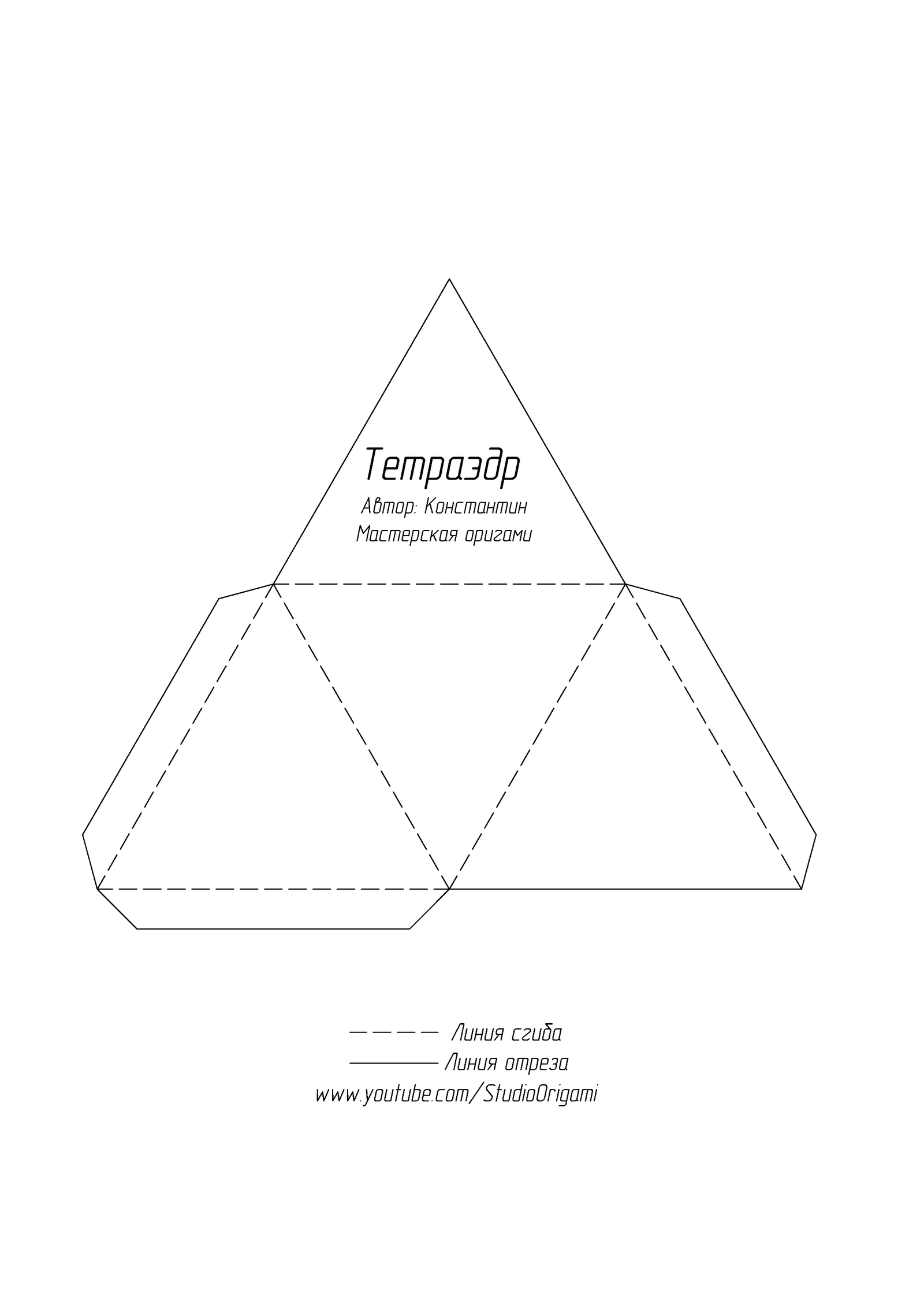
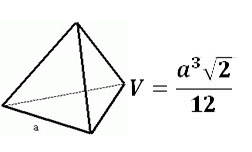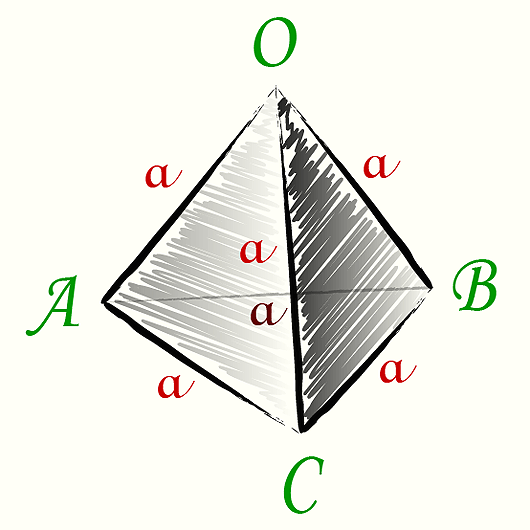Теория o тетраэдрах и параллелепипедах — урок. Геометрия, 10 класс.
Тетраэдр. Виды тетраэдров
Тетраэдр (четырёхгранник) — многогранник, гранями которого являются четыре треугольника (от греческого tetra — четыре и hedra — грань).
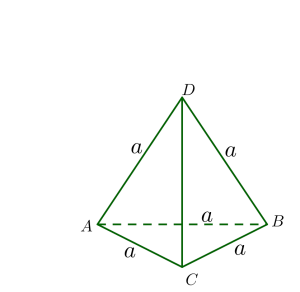
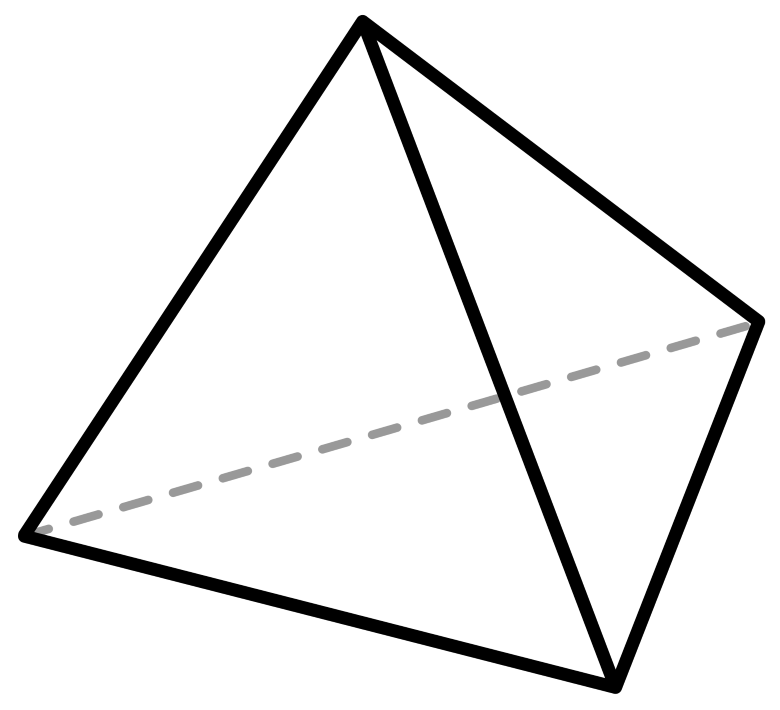
Рис. 1
У тетраэдра \(4\) грани, \(4\) вершины и \(6\) рёбер (Рис. 1).
Один из треугольников называется основанием тетраэдра, а три остальные — боковыми гранями тетраэдра.
В зависимости от видов треугольников и их расположения выделяют разные виды тетраэдров.
В школьном курсе чаще говорят о следующих видах тетраэдра:
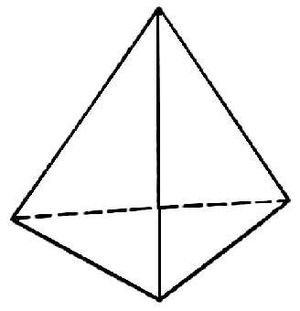
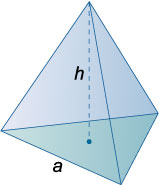
— правильная треугольная пирамида — основание — равносторонний треугольник, все боковые грани — одинаковые равнобедренные треугольники (Рис. 3);
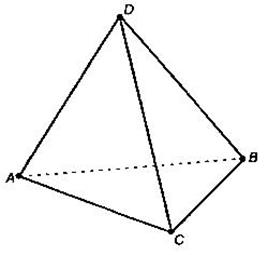
— правильный тетраэдр, у которого все четыре грани — равносторонние треугольники (Рис. 2).
Рис. 2 Рис. 3
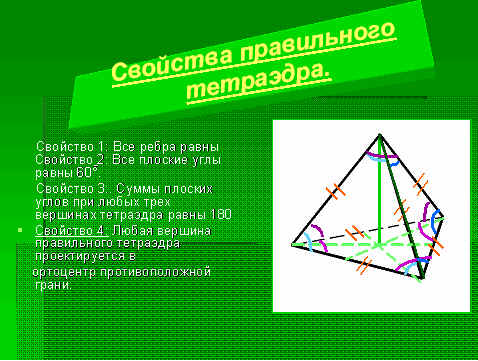
Свойство правильного тетраэдра:
из определения правильного многогранника следует, что все рёбра тетраэдра имеют равную длину, а грани — равную площадь.
Параллелепипед. Виды параллелепипедов
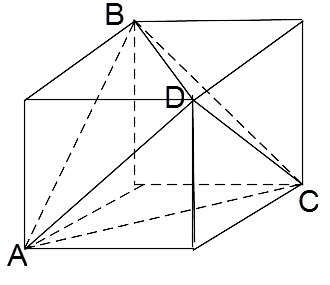
Параллелепипедом называется многогранник, у которого \(6\) граней — параллелограммы.
Рис. 4
У параллелепипеда, как отмечено, \(6\) граней, \(8\) вершин и \(12\) рёбер (Рис. 4).
Две грани параллелепипеда, имеющие общее ребро, называются смежными, а не имеющие общих рёбер — противоположными.
Обычно выделяют какие-нибудь две противоположные грани и называют их основаниями, а остальные грани — боковыми гранями параллелепипеда.
Рёбра параллелепипеда, не принадлежащие основаниям, называют боковыми рёбрами.
Рис. 5
В зависимости от видов параллелограммов и их расположения выделяют разные виды параллелепипедов:
параллелепипеды могут быть прямые и наклонные.
У прямых параллелепипедов боковые грани — прямоугольники (Рис. 5),
у наклонных — параллелограммы (Рис. 4).
Прямой параллелепипед, у которого основанием тоже является прямоугольник, называется прямоугольным параллелепипедом.
Рис. 6
Длины непараллельных рёбер прямоугольного параллелепипеда называются его линейными размерами (измерениями).
У прямоугольного параллелепипеда — три линейных размера: DA, DC, DD1 (Рис. 6).
Свойства параллелепипеда: — противоположные грани параллелепипеда равны и параллельны.
— Все четыре диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
— Боковые грани прямого параллелепипеда — прямоугольники.
Построение сечения тетраэдра и параллелепипеда
Плоскостью сечения многогранника можно назвать любую плоскость, по обе стороны которой находятся точки многогранника.
Секущая плоскость пересекает грани многогранников по отрезкам.
Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника.
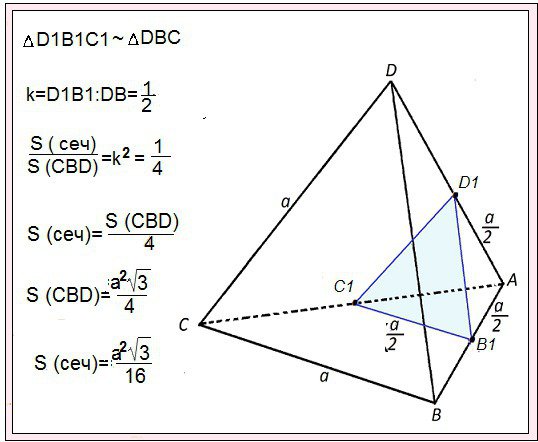
Так как у тетраэдра \(4\) грани, то сечением тетраэдра может быть треугольник (Рис. 7) или
четырёхугольник (Рис. 8).
Рис. 7 Рис. 8
У параллелепипеда \(6\) граней, поэтому сечением этого многогранника может быть треугольник (Рис. 9), четырёхугольник ( Рис. 10), пятиугольник (Рис. 11) или шестиугольник (Рис. 12).
| Рис. 9 | Рис. 10 | Рис. 11 | Рис. 12 |
При построении сечения надо вспомнить следующие знания из предыдущих тем:
1. если две точки прямой принадлежат плоскости, то прямая находится в этой плоскости.
2. Если две плоскости имеют общую точку, то эти плоскости пересекаются по прямой.
3. Если плоскость пересекает две параллельные плоскости, то линии пересечения параллельны.
Пример:
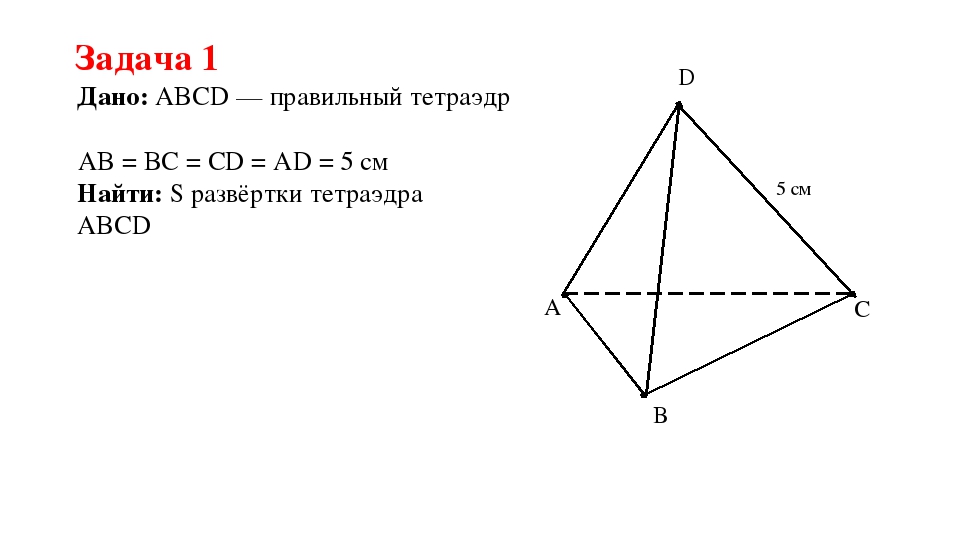
Задача
Построить сечение параллелепипеда плоскостью, которая проходит через точки \(K\), \(M\) и \(N\).
1. Проводим \(MK\), так как обе точки находятся в одной плоскости;
2. MK∩CC1=X — непараллельные прямые в одной плоскости пересекаются;
3. проводим \(XN\), так как обе точки находятся в одной плоскости;
4. XN∩D1C1=P;
5. проводим \(MP\), так как обе точки находятся в одной плоскости;
6. через точку \(N\) в плоскости основания NL∥MP, так как линии пересечения параллельных плоскостей с третьей плоскостью должны быть параллельны;
7. соединяем \(N\) и \(L\) и получаем сечение \(MPNLK\).
Тетраэдр — это… Что такое Тетраэдр?
Тетра́эдр (греч. τετραεδρον — четырёхгранник) — простейший многогранник, гранями которого являются четыре треугольника. У тетраэдра 4 грани, 4 вершины и 6 рёбер.
Связанные определения
- Отрезок, соединяющий вершину тетраэдра с точкой пересечения медиан противоположной грани, называется его медианой, опущенной из данной вершины.
- Отрезок, соединяющий середины скрещивающихся рёбер тетраэдра, называется его бимедианой, соединяющей данные рёбра.
- Отрезок, соединяющий вершину с точкой противоположной грани и перпендикулярный этой грани, называется его высотой, опущенной из данной вершины.
Свойства тетраэдра
- Параллельные плоскости, проходящие через пары скрещивающихся рёбер тетраэдра, определяют описанный около тетраэдра параллелепипед.
- Все медианы и бимедианы тетраэдра пересекаются в одной точке. Эта точка делит медианы в отношении 3:1, считая от вершины. Эта точка делит бимедианы пополам.
- Плоскость, проходящая через середины двух скрещивающихся рёбер тетраэдра, делит его на две равные по объёму части.:216-217
Выделяют следующие специальные виды тетраэдров.
- Равногранный тетраэдр, у которого все грани — равные между собой треугольники.
- Ортоцентрический тетраэдр, у которого все высоты, опущенные из вершин на противоположные грани, пересекаются в одной точке.
- Прямоугольный тетраэдр, у которого все ребра, прилежащие к одной из вершин, перпендикулярны между собой.
- Правильный тетраэдр, у которого все грани — равносторонние треугольники.
- Каркасный тетраэдр — тетраэдр, отвечающий любому из следующих условий:
- существует сфера, касающаяся всех ребер,
- суммы длин скрещивающихся ребер равны,
- суммы двугранных углов при противоположных ребрах равны,
- окружности, вписанные в грани, попарно касаются,
- все четырехугольники, получающиеся на развертке тетраэдра, — описанные,
- перпендикуляры, восставленные к граням из центров вписанных в них окружностей, пересекаются в одной точке.
- Соразмерный тетраэдр, бивысоты которого равны.
- Инцентрический тетраэдр, у которого отрезки, соединяющие вершины тетраэдра с центрами окружностей, вписанных в противоположные грани, пересекаются в одной точке.
Объём тетраэдра (с учетом знака), вершины которого находятся в точках ,
, , , равен
Тетраэдры в микромире
- Вода, Лёд, Н2О
- Молекула метана СН4
- Молекула аммиака Nh4
- Алмаз C — тетраэдр с ребром равным 2,5220 ангстрем
- Флюорит CaF2, тетраэдр с ребром равным 3, 8626 ангстрем
- Сфалерит, ZnS, тетраэдр с ребром равным 3,823 ангстрем
- Комплексные ионы -, 2-, 2-, 2+
- Силикаты, в основе структур которых лежит кремнекислородный тетраэдр 4-
Тетраэдры в живой природе
Некоторые плоды, находясь вчетвером на одной кисти, располагаются в вершинах тетраэдра, близкого к правильному. Такая конструкция обусловлена тем, что центры четырёх одинаковых шаров, касающихся друг друга, находятся в вершинах правильного тетраэдра. Поэтому похожие на шар плоды образуют подобное взаимное расположение. Например, таким образом могут располагаться грецкие орехи.
Тетраэдры в технике
- Тетраэдр образует жёсткую, статически определимую конструкцию. Тетраэдр, выполненный из стержней, часто используется в качестве основы для пространственных несущих конструкций пролётов зданий, перекрытий, балок, ферм мостов и т. д. Стержни испытывают только продольные нагрузки.
- Прямоугольный тетраэдр используется в оптике. Если грани, имеющие прямой угол, покрыть светоотражающим составом или весь тетраэдр выполнить из материала с сильным светопреломлением, чтобы возникал эффект полного внутреннего отражения, то свет, направленный в грань, противоположную вершине с прямыми углами, будет отражаться в том же направлении, откуда он пришёл. Это свойство используется для создания уголковых отражателей, катафотов.
- Граф четверичного триггера представляет собой тетраэдр.
Формулы тетраэдра в декартовых координатах в пространстве
Обозначения:
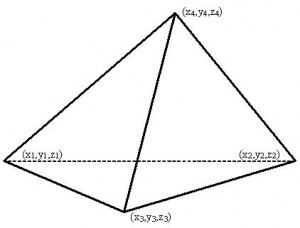
r1(x1,y1,z1),{\displaystyle \mathbf {r} _{1}(x_{1},y_{1},z_{1}),} r2(x2,y2,z2),{\displaystyle \mathbf {r} _{2}(x_{2},y_{2},z_{2}),}r3(x3,y3,z3),{\displaystyle \mathbf {r} _{3}(x_{3},y_{3},z_{3}),}r4(x4,y4,z4){\displaystyle \mathbf {r} _{4}(x_{4},y_{4},z_{4})}— координаты вершин тетраэдра.
Объём тетраэдра (с учётом знака):
V=16|1x1y1z11x2y2z21x3y3z31x4y4z4|{\displaystyle V={\frac {1}{6}}{\begin{vmatrix}1&x_{1}&y_{1}&z_{1}\\1&x_{2}&y_{2}&z_{2}\\1&x_{3}&y_{3}&z_{3}\\1&x_{4}&y_{4}&z_{4}\end{vmatrix}}}.
Координаты центра тяжести(пересечение медиан):rT(xT,yT,zT){\displaystyle \mathbf {r} _{T}(x_{T},y_{T},z_{T})}
xT=x1+x2+x3+x44;{\displaystyle x_{T}={\frac {x_{1}+x_{2}+x_{3}+x_{4}}{4}};}yT=y1+y2+y3+y44;{\displaystyle y_{T}={\frac {y_{1}+y_{2}+y_{3}+y_{4}}{4}};}zT=z1+z2+z3+z44.{\displaystyle z_{T}={\frac {z_{1}+z_{2}+z_{3}+z_{4}}{4}}.}
Координаты центра вписанной сферы:rr(xr,yr,zr){\displaystyle \mathbf {r} _{r}(x_{r},y_{r},z_{r})}
xr=S1x1+S2x2+S3x3+S4x4S1+S2+S3+S4;{\displaystyle x_{r}={\frac {S_{1}x_{1}+S_{2}x_{2}+S_{3}x_{3}+S_{4}x_{4}}{S_{1}+S_{2}+S_{3}+S_{4}}};}yr=S1y1+S2y2+S3y3+S4y4S1+S2+S3+S4;{\displaystyle y_{r}={\frac {S_{1}y_{1}+S_{2}y_{2}+S_{3}y_{3}+S_{4}y_{4}}{S_{1}+S_{2}+S_{3}+S_{4}}};}zr=S1z1+S2z2+S3z3+S4z4S1+S2+S3+S4,{\displaystyle z_{r}={\frac {S_{1}z_{1}+S_{2}z_{2}+S_{3}z_{3}+S_{4}z_{4}}{S_{1}+S_{2}+S_{3}+S_{4}}},}
где S1{\displaystyle S_{1}}-площадь грани противолежащей первой вершине, S2{\displaystyle S_{2}}-площадь грани противолежащей второй вершине и т. д.
Соответственно уравнение вписанной сферы:
(x−S1x1+S2x2+S3x3+S4x4S1+S2+S3+S4)2+(y−S1y1+S2y2+S3y3+S4y4S1+S2+S3+S4)2+(z−S1z1+S2z2+S3z3+S4z4S1+S2+S3+S4)2=(3VS1+S2+S3+S4)2,{\displaystyle (x-{\frac {S_{1}x_{1}+S_{2}x_{2}+S_{3}x_{3}+S_{4}x_{4}}{S_{1}+S_{2}+S_{3}+S_{4}}})^{2}+(y-{\frac {S_{1}y_{1}+S_{2}y_{2}+S_{3}y_{3}+S_{4}y_{4}}{S_{1}+S_{2}+S_{3}+S_{4}}})^{2}+(z-{\frac {S_{1}z_{1}+S_{2}z_{2}+S_{3}z_{3}+S_{4}z_{4}}{S_{1}+S_{2}+S_{3}+S_{4}}})^{2}=({\frac {3V}{S_{1}+S_{2}+S_{3}+S_{4}}})^{2},}
Уравнение вневписанной сферы противолежащей первой вершине:
(x−−S1x1+S2x2+S3x3+S4x4−S1+S2+S3+S4)2+(y−−S1y1+S2y2+S3y3+S4y4−S1+S2+S3+S4)2+(z−−S1z1+S2z2+S3z3+S4z4−S1+S2+S3+S4)2=(3V−S1+S2+S3+S4)2,{\displaystyle (x-{\frac {-S_{1}x_{1}+S_{2}x_{2}+S_{3}x_{3}+S_{4}x_{4}}{-S_{1}+S_{2}+S_{3}+S_{4}}})^{2}+(y-{\frac {-S_{1}y_{1}+S_{2}y_{2}+S_{3}y_{3}+S_{4}y_{4}}{-S_{1}+S_{2}+S_{3}+S_{4}}})^{2}+(z-{\frac {-S_{1}z_{1}+S_{2}z_{2}+S_{3}z_{3}+S_{4}z_{4}}{-S_{1}+S_{2}+S_{3}+S_{4}}})^{2}=({\frac {3V}{-S_{1}+S_{2}+S_{3}+S_{4}}})^{2},}
Уравнение вневписанной сферы противолежащей первой и второй вершин(количество таких сфер может варьироваться от 0 до 3-х):
(x−−S1x1−S2x2+S3x3+S4x4−S1−S2+S3+S4)2+(y−−S1y1−S2y2+S3y3+S4y4−S1−S2+S3+S4)2+(z−−S1z1−S2z2+S3z3+S4z4−S1−S2+S3+S4)2=(3V−S1−S2+S3+S4)2,{\displaystyle (x-{\frac {-S_{1}x_{1}-S_{2}x_{2}+S_{3}x_{3}+S_{4}x_{4}}{-S_{1}-S_{2}+S_{3}+S_{4}}})^{2}+(y-{\frac {-S_{1}y_{1}-S_{2}y_{2}+S_{3}y_{3}+S_{4}y_{4}}{-S_{1}-S_{2}+S_{3}+S_{4}}})^{2}+(z-{\frac {-S_{1}z_{1}-S_{2}z_{2}+S_{3}z_{3}+S_{4}z_{4}}{-S_{1}-S_{2}+S_{3}+S_{4}}})^{2}=({\frac {3V}{-S_{1}-S_{2}+S_{3}+S_{4}}})^{2},}
Уравнение описанной сферы:
|x2+y2+z2xyz1x12+y12+z12x1y1z11x22+y22+z22x2y2z21x32+y32+z32x3y3z31x42+y42+z42x4y4z41|={\displaystyle {\begin{vmatrix}x^{2}+y^{2}+z^{2}&x&y&z&1\\x_{1}^{2}+y_{1}^{2}+z_{1}^{2}&x_{1}&y_{1}&z_{1}&1\\x_{2}^{2}+y_{2}^{2}+z_{2}^{2}&x_{2}&y_{2}&z_{2}&1\\x_{3}^{2}+y_{3}^{2}+z_{3}^{2}&x_{3}&y_{3}&z_{3}&1\\x_{4}^{2}+y_{4}^{2}+z_{4}^{2}&x_{4}&y_{4}&z_{4}&1\end{vmatrix}}=0.}
Полное число решений
Последующие секции показывают все из полного набора решений тетраэдров Гурса для 3-сферы, евклидова 3-мерного пространства и гиперболического 3-мерного пространства. Расширенная симметрия каждого тетраэдра тоже указана.
Цветные тетраэдральные диаграммы ниже являются вершинными фигурами многогранников и сот из каждого семейства симметрий. Метки рёбер представляют порядки многоугольных граней, которые являются удвоенными порядками ветвей графа Коксетера. Двугранный угол ребра, помеченного 2n, равен πn{\displaystyle \pi /n}. Жёлтые рёбра, помеченные цифрой 4, получаются из прямого угла (несвязанных) зеркал (узлов) диаграммы Коксетера.
(Конечные) решения на 3-сфере
Изоморфизм конечных групп Коксетера
Решения для 3-сферы с плотностью 1: ()
| Группа Коксетераи диаграмма | |||||||
|---|---|---|---|---|---|---|---|
| Порядок группы симметрии | 16 | 8p | 4pq | 4p2 | 48 | 96 | 240 |
| Симметриитетраэдра | (порядок 24) | (порядок 4) | (порядок 4) | (порядок 8) | (порядок 2) | +(порядок 1) | +(порядок 1) |
| Расширенные симметрии | ]= | ]= | ]= | ]=] | ]= | ||
| Порядок расширенных групп симметрии | 384 | 32p | 16pq | 32p2 | 96 | 96 | 240 |
| Тип графа | Линейный | Трёхлистный | |||
|---|---|---|---|---|---|
| Группа Коксетераи диаграмма | Пяти-ячейный | Шестнадцати-ячейный | Двадцати-четырёхъ-ячейный]] | Шестисот-ячейный | Полутессеракт |
| Вершинная фигура всеусечённых однородных многогранников | |||||
| Тетраэдр | |||||
| Порядок группы симметрии | 120 | 384 | 1152 | 14400 | 192 |
| Тетраэдральнаясимметрия | +(порядок 2) | +(порядок 1) | +(порядок 2) | +(порядок 1) | (порядок 6) |
| Расширеннаясимметрия | ] | ] | ]= | ||
| Порядок группы расширенной симметрии | 240 | 384 | 2304 | 14400 | 1152 |
Решения в евклидовом 3-мерном пространстве
Изоморфизмы евклидовых групп Коксетера
Решения плотности 1: :
| Тип графа | Линейный | Трёхлистный | Кольцо | Призматический | Вырожденный | ||
|---|---|---|---|---|---|---|---|
| Группа КоксетераДиаграмма Коксетера | ,2] | ||||||
| Вершинная фигура всеусечённых сот | |||||||
| Тетраэдр | |||||||
| Тетраэдральнаясимметрия | +(порядок 2) | (порядок 2) | (порядок 8) | (порядок 2) | +(порядок 1) | (порядок 6) | (порядок 8) |
| Расширеннаясимметрия | ] | ]= | ]]=] | ]= | ,2]]= | ]=] |
Решения для гиперболических 3-пространств
Решения плотности 1: () ()
| Тип графа | Линейный | Трёхлистный | |||
|---|---|---|---|---|---|
| Группа КоксетераДиаграмма Коксетера | |||||
| Вершинный фигуры всеусечённых сот | |||||
| Тетраэдр | |||||
| Тетраэдральнаясимметрия | +(порядок 2) | +(порядок 1) | +(порядок 2) | (порядок 2) | |
| Расширеннаясимметрия | ] | ] | ]= | ||
| Тип графа | Кольцо | ||||
| Группа КоксетераДиаграмма Коксетера | |||||
| Вершинные фигуры всеусечённых сот | |||||
| Тетраэдр | |||||
| Тетраэдральнаясимметрия | +(порядок 2) | +(порядок 4) | +(порядок 2) | +(порядок 2) | +(порядок 4) |
| Расширеннаясимметрия | ] | ] | ] | ] | ] |
Решения в паракомпактных гиперболических 3-пространствах
Здесь показана связь подгрупп паракомпактного гиперболического тетраэдра Гурса. Подгруппы порядка 2 представляют разбиение тетраэдра Гурса плоскостью зеркальной симметрии
Решения плотности 1: (См. )
| Тип графа | Линейные графы | |||||||
|---|---|---|---|---|---|---|---|---|
| Группа КоксетераДиаграмма Коксетера | ||||||||
| Тетраэдральнаясимметрия | +(порядок 1) | +(порядок 2) | +(порядок 1) | +(порядок 1) | +(порядок 2) | +(порядок 1) | +(порядок 2) | |
| Расширеннаясимметрия | ] | ] | ] | |||||
| Тип графа | Кольцевые графы | |||||||
| Группа КоксетераДиаграмма Коксетера | ×] | ] | ] | |||||
| Тетраэдральнаясимметрия | (порядок 4) | (порядок 2) | +(порядок 2) | (порядок 8) | +(порядок 2) | +(порядок 2) | +(порядок 2) | +(порядок 4) |
| Расширеннаясимметрия | ×]]= | ]= | ] | ]]=] | ] | ] | ] | ]] |
| Тип графа | Трёхлистный | Кольцо с хвостом | Симлекс | |||||
| Группа КоксетераДиаграмма Коксетера | ] | ] | ] | ] | ] | |||
| Тетраэдральнаясимметрия | (порядок 2) | (порядок 2) | (порядок 6) | (порядок 2) | (порядок 2) | (порядок 2) | (порядок 2) | (порядок 24) |
| Расширеннаясимметрия | ]= | ]= | ]= | ]]= | ]]= | ]]= | ]]= | ]]= |
Доходы на фрилансе
Заглянем на популярную биржу фриланса fl.ru. Здесь есть предложения с разной ценой: от смешных 300 рублей за доработки сайта, до разработки серьезных проектов за 10-40 тыс. рублей:
Тетраэдры в микромире
- Правильный тетраэдр образуется при sp3-гибридизации атомных орбиталей (их оси направлены в вершины правильного тетраэдра, а ядро центрального атома расположено в центре описанной сферы правильного тетраэдра), поэтому немало молекул, в которых такая гибридизация центрального атома имеет место, имеют вид этого многогранника
- Молекула метана СН4
- Ион аммония NH4+
- Сульфат-ион SO42-, фосфат-ион PO43-, перхлорат-ион ClO4— и многие другие ионы
- Алмаз C — тетраэдр с ребром равным 2,5220 ангстрем
- Флюорит CaF2, тетраэдр с ребром равным 3, 8626 ангстрем
- Сфалерит, ZnS, тетраэдр с ребром равным 3,823 ангстрем
- Оксид цинка, ZnO
- Комплексные ионы [BF4] -, [ZnCl4]2-, [Hg(CN)4]2-, [Zn(NH3)4]2+
- Силикаты, в основе структур которых лежит кремнекислородный тетраэдр [SiO4]4-
Объём тетраэдра
- V=16|1x1y1z11x2y2z21x3y3z31x4y4z4|=16|x2−x1y2−y1z2−z1x3−x1y3−y1z3−z1x4−x1y4−y1z4−z1|,{\displaystyle V={\frac {1}{6}}{\begin{vmatrix}1&x_{1}&y_{1}&z_{1}\\1&x_{2}&y_{2}&z_{2}\\1&x_{3}&y_{3}&z_{3}\\1&x_{4}&y_{4}&z_{4}\end{vmatrix}}={\frac {1}{6}}{\begin{vmatrix}x_{2}-x_{1}&y_{2}-y_{1}&z_{2}-z_{1}\\x_{3}-x_{1}&y_{3}-y_{1}&z_{3}-z_{1}\\x_{4}-x_{1}&y_{4}-y_{1}&z_{4}-z_{1}\end{vmatrix}},}
или
- V=13 SH,{\displaystyle V={\frac {1}{3}}\ SH,}
где S{\displaystyle S} — площадь любой грани, а H{\displaystyle H} — высота, опущенная на эту грань.
Объём тетраэдра через длины рёбер выражается с помощью определителя Кэли-Менгера:
- 288⋅V2=|11111d122d132d1421d122d232d2421d132d232d3421d142d242d342|.{\displaystyle 288\cdot V^{2}={\begin{vmatrix}0&1&1&1&1\\1&0&d_{12}^{2}&d_{13}^{2}&d_{14}^{2}\\1&d_{12}^{2}&0&d_{23}^{2}&d_{24}^{2}\\1&d_{13}^{2}&d_{23}^{2}&0&d_{34}^{2}\\1&d_{14}^{2}&d_{24}^{2}&d_{34}^{2}&0\end{vmatrix}}.}
- Эта формула имеет плоский аналог для площади треугольника в виде варианта формулы Герона через аналогичный определитель.
- Объём тетраэдра через длины двух противоположных рёбер a и b , как скрещивающихся линий, которые удалены на расстояние h друг от друга и образуют друг с другом угол ϕ{\displaystyle \phi }, находится по формуле:
V=16abhsinϕ.{\displaystyle V={\frac {1}{6}}abh\sin \phi .}
Объём тетраэдра через длины трёх его рёбер a,b и c, выходящих из одной вершины и образующих между собой попарно соответственно плоские углы α,β,γ{\displaystyle \alpha ,\beta ,\gamma }, находится по формуле
- V=16 abcD,{\displaystyle V={\frac {1}{6}}\ abc{\sqrt {D}},}
где
D=|1cosγcosβcosγ1cosαcosβcosα1|.{\displaystyle D={\begin{vmatrix}1&\cos \gamma &\cos \beta \\\cos \gamma &1&\cos \alpha \\\cos \beta &\cos \alpha &1\end{vmatrix}}.}
Аналогом для плоскости последней формулы является формула площади треугольника через длины двух его сторон a и b, выходящих из одной вершины и образующих между собой угол γ{\displaystyle \gamma }:
- S=12 abD,{\displaystyle S={\frac {1}{2}}\ ab{\sqrt {D}},}
где
D=|1cosγcosγ1|.{\displaystyle D={\begin{vmatrix}1&\cos \gamma \\\cos \gamma &1\\\end{vmatrix}}.}
Ссылки[править | править код]
-
История математики в школе. IX — X классы. — М.: Просвещение, 1983. — 351 с. (см. ISBN )
— С. 312. - В. Э. МАТИЗЕН Равногранные и каркасные тетраэдры «Квант» № 7, 1983 г.
- Триггер
| Это заготовка статьи по стереометрии. |
|
Выделить Тетраэдр и найти в:
|
|
|
- Страница — краткая статья
- Страница — энциклопедическая статья
- Разное — на страницах: , , ,