Примеры
4-тензоры в ОТО
- метрический тензор (играет определённую техническую роль и в отсутствии гравитационных полей, то есть часто применяется и за рамками ОТО, однако в этом случае он — обычно — имеет очень частный вид лоренцевой метрики).
- тензор кривизны
- тензор Риччи
- тензор энергии-импульса (достаточно широко применим и вне ОТО).
4-тензор электромагнитного поля
Соответствующий 4-тензор существует также и для описания электромагнитного поля. Это 4-тензор второго ранга. При его использовании основные уравнения для электромагнитного поля: уравнение Максвелла и уравнение движения заряженной частицы в поле имеют особенно простую и элегантную форму.
Определение через 4-потенциал
4-тензор определяется через производные от 4-потенциала:
- Fik=∂Ak∂xi−∂Ai∂xk{\displaystyle F_{ik}={\frac {\partial A_{k}}{\partial x^{i}}}-{\frac {\partial A_{i}}{\partial x^{k}}}}.
Определение через трёхмерные векторы
4-тензор определяется через обычные трёхмерные составные векторов напряжённости следующим образом:
- Fik=(ExcEycEzc−Exc−BzBy−EycBz−Bx−Ezc−ByBx){\displaystyle F_{ik}=\left({\begin{matrix}0&E_{x}/c&E_{y}/c&E_{z}/c\\-E_{x}/c&0&-B_{z}&B_{y}\\-E_{y}/c&B_{z}&0&-B_{x}\\-E_{z}/c&-B_{y}&B_{x}&0\end{matrix}}\right)}
- Fik=(−Exc−Eyc−EzcExc−BzByEycBz−BxEzc−ByBx){\displaystyle F^{ik}=\left({\begin{matrix}0&-E_{x}/c&-E_{y}/c&-E_{z}/c\\E_{x}/c&0&-B_{z}&B_{y}\\E_{y}/c&B_{z}&0&-B_{x}\\E_{z}/c&-B_{y}&B_{x}&0\end{matrix}}\right)}
Первая форма — это ковариантный тензор, а вторая форма — это контравариантный тензор.
Сила Лоренца
Записанное в 4-векторной форме уравнение движения заряженной частицы в электромагнитном поле приобретает вид
- mcduids=qcFikuk{\displaystyle mc{\frac {du^{i}}{ds}}={\frac {q}{c}}F^{ik}u_{k}},
где uk{\displaystyle u^{k}} — 4-скорость, q — электрический заряд частицы, c — скорость света, m — масса. Правая часть этого уравнения — это сила Лоренца.
Тензорные операции
Тензоры допускают следующие алгебраические операции:
- Умножение на скаляр — умножение каждого компонента тензора на скаляр. Аналогично умножению вектора или скалярной величины (и то, и другое являются частными случаями тензора);
- Сложение тензоров одинаковой валентности и состава индексов (вычислять сумму можно покомпонентно, как и для векторов);
- Тензорное произведение — без ограничений. Произведением тензора ранга (m,n){\displaystyle (m,n)} на тензор ранга (m′,n′){\displaystyle (m’,n’)} является тензор суммарного ранга (m+m′,n+n′){\displaystyle (m+m’,n+n’)}, то есть если σ∈Tnm{\displaystyle \sigma \in T_{n}^{m}} и τ∈Tn′m′{\displaystyle \tau \in T_{n’}^{m’}} то их произведение
-
- σ⊗τ∈Tn+n′m+m′=Tnm⊗Tn′m′.{\displaystyle \sigma \otimes \tau \in T_{n+n’}^{m+m’}=T_{n}^{m}\otimes T_{n’}^{m’}.}
- Компоненты тензорного произведения суть произведения соответствующих компонент множителей, например:
- P klij =AijBkl{\displaystyle P_{\ \ kl}^{ij}\ =A^{ij}B_{kl}}
-
Свёртка тензора — специфическая тензорная операция, понижающая валентность тензора, вычисляется суммированием по паре индексов (верхнего и нижнего, если они различаются) и пробегающих, оставаясь равными друг другу, все свои значения, например:
- B kli =∑jA jklji=A jklji{\displaystyle B_{\ kl}^{i}\ =\sum _{j}A_{\ \ jkl}^{ji}=A_{\ \ jkl}^{ji}}
- (последнее в эйнштейновских обозначениях, где суммирование по повторяющемуся верхнему и нижнему индексу подразумевается автоматически). Часто, если не как правило, свёртка (то есть результат операции свёртки) обозначается той же буквой, что и тензор, к которому свёртка применена, только, конечно, с количеством индексов, на два меньшим.
- След матрицы — частный случай свёртки тензора с собой.
-
Свёртка двух или нескольких тензоров (в том числе тензоров и векторов), например:
- Cjki =∑mBmiAjkm=BmiAjkm{\displaystyle C_{jk}^{i}\ =\sum _{m}B_{m}^{i}A_{jk}^{m}=B_{m}^{i}A_{jk}^{m}} (последнее — в записи Эйнштейна).
- — операция, которую можно свести к последовательному тензорному умножению этих тензоров (см. чуть ниже) и затем свёртке получившегося тензора (возможно, несколько раз). Очевидно, эта операция линейна по всем входным каналам. Таким образом, свёртка с тензором реализует линейное или полилинейное отображение пространств тензоров на пространство тензоров (в общем случае — на другое), в частности, векторов на векторы и векторов на скаляры.
Свёртка вектора с тензором валентности два есть действие линейного оператора, определяемого этим тензором, на вектор:
- ui =∑jAjivj=Ajivj{\displaystyle u^{i}\ =\sum _{j}A_{j}^{i}v^{j}=A_{j}^{i}v^{j}} (последнее — в записи Эйнштейна).
Свёртка (однократная) двух тензоров валентности два реализует композицию линейных операторов, определяемых этими тензорами:
- Cji =∑kBkiAjk=BkiAjk{\displaystyle C_{j}^{i}\ =\sum _{k}B_{k}^{i}A_{j}^{k}=B_{k}^{i}A_{j}^{k}} (последнее — в записи Эйнштейна).
- Симметризация и антисимметризация — конструирование тензора того же типа с определённым видом симметрии. Для примера, симметризация тензора Tij{\displaystyle T_{ij}} — это симметричный тензор T(ij)=12(Tij+Tji){\displaystyle \scriptstyle T_{(ij)}={1 \over 2}\left(T_{ij}+T_{ji}\right)}, а антисимметризация — антисимметричный тензор Tij=12(Tij−Tji){\displaystyle \scriptstyle T_{}={1 \over 2}\left(T_{ij}-T_{ji}\right)}. В общем случае симметризация по n{\displaystyle n} индексам имеет вид
- T(i1…in)=1n!∑σTσ(i1)…σ(in),{\displaystyle T_{(i_{1}\ldots i_{n})}={1 \over n!}\sum _{\sigma }T_{\sigma (i_{1})\ldots \sigma (i_{n})},}
- а антисимметризация:
- Ti1…in=1n!∑σsign(σ)Tσ(i1)…σ(in){\displaystyle T_{}={1 \over n!}\sum _{\sigma }\mathrm {sign} \,(\sigma )T_{\sigma (i_{1})\ldots \sigma (i_{n})}}
- Здесь σ{\displaystyle \sigma } — всевозможные перестановки индексов i1,…,in,{\displaystyle i_{1},\ldots ,i_{n},} а sign(σ){\displaystyle \mathrm {sign} \,(\sigma )} — чётность перестановки σ.{\displaystyle \sigma .} Разумеется, не обязательно симметризовать тензор по всем индексам, здесь это используется лишь для упрощения записи.
- Если Ti1…in{\displaystyle T_{i_{1}\ldots i_{n}}} симметричен по i1…in,{\displaystyle i_{1}\ldots i_{n},} то симметризация по этим индексам совпадает с T,{\displaystyle T,} а антисимметризация даёт нулевой тензор. Аналогично в случае антисимметричности по некоторым индексам.
- Если Tij∈V⊗V,{\displaystyle T_{ij}\in V\otimes V,} то T(ij)∈V∨V,{\displaystyle T_{(ij)}\in V\vee V,} Tij∈V∧V.{\displaystyle T_{}\in V\wedge V.} Здесь ∨{\displaystyle \vee } — симметричное, а ∧{\displaystyle \wedge } — внешнее произведение векторных пространств.
Определения
О классическом определении
Тензор определяется как геометрический объект, который описывается многомерным массивом, то есть набором чисел, занумерованных несколькими индексами, или, иначе говоря, n{\displaystyle n}-мерной таблицей, где n{\displaystyle n} — валентность тензора (см. выше).
Так, вектор (тензор первого ранга) задаётся одномерным массивом, либо в виде строки x=x1x2…xm{\displaystyle \mathbf {x} ={\begin{bmatrix}x_{1}&x_{2}&\dots &x_{m}\end{bmatrix}}\,}, либо в виде столбца
x=x1x2⋮xm{\displaystyle \mathbf {x} ={\begin{bmatrix}x_{1}\\x_{2}\\\vdots \\x_{m}\end{bmatrix}}\,}
а такие объекты, как линейный оператор и квадратичная форма, — двумерной матрицей
T=σ11σ12σ13σ21σ22σ23σ31σ32σ33{\displaystyle \mathbf {T} ={\begin{bmatrix}\sigma _{11}&\sigma _{12}&\sigma _{13}\\\sigma _{21}&\sigma _{22}&\sigma _{23}\\\sigma _{31}&\sigma _{32}&\sigma _{33}\end{bmatrix}}}
Скаляр же (тензор нулевого ранга) задаётся одним числом x{\displaystyle \mathbf {x} }, которое можно рассматривать как сокращённую запись нульмерного массива с единственным элементом, то есть x=x1{\displaystyle \mathbf {x} ={\begin{bmatrix}x_{1}\end{bmatrix}}}. Такие нульмерные матрицы удобно рассматривать в качестве частных случаев тензоров, так как все тензорные определения и теоремы для них в силе, и векторы со скалярами можно при общем рассмотрении не упоминать отдельно.
Но следует понимать, что не всякая матрица есть тензор. Тензор лишь иногда записывают в матричной форме (для этого в пространстве задачи обязательно нужно выбрать базис), но иногда матричная форма неудобна и избыточна. Таким образом, матрица является лишь одним из способов записи тензора, а не самим математическим объектом — тензором.
Также следует понимать, что не всякий линейный оператор T{\displaystyle \mathbf {T} } является тензором. Тензор отличается от других математических объектов, которые также могут быть записаны в матричной форме, законом преобразования координат.
Таким образом тензор не просто массив чисел. Можно дать такое псевдоопределение тензора:
|
тензор = массив компонент + закон преобразования компонент при замене базиса |
Современное определение
Тензор ранга (n,m){\displaystyle (n,m)} над d{\displaystyle d}-мерным векторным пространством V{\displaystyle V} — это элемент тензорного произведения n{\displaystyle n} пространств V{\displaystyle V} и m{\displaystyle m} сопряжённых пространств V∗{\displaystyle V^{*}} (то есть пространств линейных функционалов (ковекторов) на V{\displaystyle V})
- τ∈Tmn(V)=V⊗…⊗V⏟⊗V∗⊗…⊗V∗⏟nm{\displaystyle {\begin{matrix}\tau \in T_{m}^{n}(V)&=&\underbrace {V\otimes \ldots \otimes V} &\otimes &\underbrace {V^{*}\otimes \ldots \otimes V^{*}} \\&&n&&m\end{matrix}}}
Сумма чисел n+m{\displaystyle n+m} называется валентностью тензора (её также часто называют рангом).
Тензор ранга (n,m){\displaystyle (n,m)} также называется n{\displaystyle n} раз контравариантным и m{\displaystyle m} раз ковариантным, иногда говорят тензор n-ранга, имея в виду ранг (0, n) или (n, 0), например, εijk{\displaystyle \varepsilon _{ijk}} — тензор 3-го ранга (3 индекса).
Тензор как полилинейная функция
Точно так же, как тензор ранга (,1){\displaystyle (0,1)} можно представлять как линейный функционал на пространстве V{\displaystyle V}, тензор τ{\displaystyle \tau } ранга (,n){\displaystyle (0,n)} удобно представлять себе как функцию τ(v1,v2,…,vn){\displaystyle \tau (v_{1},v_{2},\ldots ,v_{n})} от n{\displaystyle n} векторных аргументов vi∈V{\displaystyle v_{i}\in V}, которая линейна по каждому аргументу vi{\displaystyle v_{i}} (такие функции называются ), то есть для любой константы c{\displaystyle c} из поля F{\displaystyle F} (над которым определено векторное пространство).
- τ(v1,…,cvA,…,vn)=cτ(v1,…,vA,…,vn){\displaystyle \tau (v_{1},\ldots ,cv_{A},\ldots ,v_{n})=c\tau (v_{1},\ldots ,v_{A},\ldots ,v_{n})}
- τ(v1,…,vA+vA′,…,vn)=τ(v1,…,vA,…,vn)+τ(v1,…,vA′,…,vn).{\displaystyle \tau (v_{1},\ldots ,v_{A}+v_{A}’,\ldots ,v_{n})=\tau (v_{1},\ldots ,v_{A},\ldots ,v_{n})+\tau (v_{1},\ldots ,v_{A}’,\ldots ,v_{n}).}
В том же ключе, тензор τ{\displaystyle \tau } произвольного ранга (n,m){\displaystyle (n,m)} представляется полилинейным функционалом от m{\displaystyle m} векторов и n{\displaystyle n} ковекторов:
- τ(v1,v2,…,vm,ω1,ω2,…,ωn){\displaystyle \tau (v_{1},v_{2},\ldots ,v_{m},\omega ^{1},\omega ^{2},\ldots ,\omega ^{n})}
- τVm×(V∗)n→F{\displaystyle \tau \colon V^{m}\times (V^{*})^{n}\to F}
Телепортация тонн данных в PostgreSQL
Сегодня я поделюсь некоторыми полезными архитектурными решениями, которые возникли в процессе развития нашего инструмента массового анализа производительности серверов PostgeSQL, и которые помогают нам сейчас «умещать» полноценный мониторинг и анализ более тысячи хостов в то же «железо», которого сначала едва хватало для одной сотни.
Intro
Напомню некоторые вводные:
- мы строим сервис, который получает информацию из логов серверов PostgreSQL
- собирая логи, мы хотим что-то с ними делать (парсить, анализировать, запрашивать дополнительную информацию) в режиме онлайн
- все собранное и «наанализированное» надо куда-то сохранить
Именно про последний пункт — как все это можно доставить в PostgreSQL-хранилище, и поговорим. В нашем случае таких данных кратно больше, чем исходных — статистика нагрузки в разрезе конкретного приложения и шаблона плана, потребление ресурсов и вычисление производных проблем с точностью до отдельного узла плана, мониторинг блокировок и многое другое.
[править] Деятельность
Компания «Тензор» является аккредитованным ФНС, ПФ и Росстатом оператором электронного документооборота, сертифицированным EDI-провайдером и оператором фискальных данных.
Главным продуктом является облачная система автоматизации бизнеса СБИС. В него входят 22 сервиса:
Отчетность через интернет
Бухгалтерия и учет
Управление персоналом
Учет и контроль рабочего времени
ОФД
Маркировка товаров
Автоматизация магазинов и аптек
Автоматизация салонов и сферы услуг
Presto – автоматизация ресторанов, кафе и столовых
Все для удаленной работы
CRM
Облачная телефония
Корпоративная социальная сеть
Электронный документооборот
Управление бизнес-процессами
Заказы и поставки (EDI)
Торговля, закупки и складской учет
Все о компаниях и владельцах
Поиск и анализ закупок
Корпоративный удостоверяющий центр
Мобильные сотрудники
Видеокоммуникации
[править] Социальные проекты
Компания «Тензор» развивает обучающие программы для школьников, студентов и молодых IT-специалистов. Ежегодно проходят бесплатные митапы по frontend, backend разработке и тестированию.
С 2012 года компания «Тензор» проводила «IT-десант» — курс бесплатных открытых лекций по программированию в ЯрГУ им. П. Г. Демидова. В 2014 году начала работать Кафедра «Тензор» — углубленные курсы для студентов ЯрГУ им. П. Г. Демидова. В 2019 году на их базе была создана базовая кафедра разработки облачных сервисов.
Ежегодно проводится конкурс на стипендию «Тензор». Это трехдневный хакатон для студентов IT-специальностей, где необходимо создать проекты приложений, игр и др. Победители получают денежную стипендию и возможность трудоустройства в компанию. Хакатон проводится в Ярославле и Новосибирске.
В 2018 году совместно с музеем занимательных наук Эйнштейна «Тензор» открыл школу программирования для детей «CODDY School». Для школьников совместно с ЯрГУ им. П.Г. Демидова «Тензор» проводит «Час Кода» — мероприятие с лекциями и мастер-классами по программированию.
Способы задания
Координатное представление
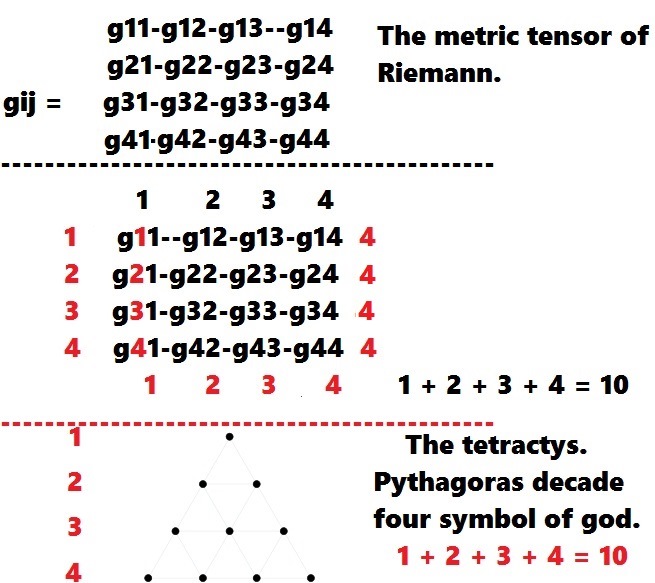
Метрический тензор в локальных координатах x1,x2,…,xn{\displaystyle x^{1},x^{2},\dots ,x^{n}}, обычно задаётся как ковариантное тензорное поле gij {\displaystyle g_{ij}\ }.
Через него определяются скалярные произведения координатных векторных полей ∂i=∂∂xi{\displaystyle \partial _{i}={\frac {\partial }{\partial x^{i}}}}:
- ⟨∂i,∂j⟩=gij.{\displaystyle \left\langle \partial _{i},\partial _{j}\right\rangle =g_{ij}.}
А для любых векторных полей скалярное произведение вычисляется по формуле
- ⟨v,w⟩=gijviwj{\displaystyle \left\langle v,w\right\rangle =g_{ij}v^{i}w^{j}},
где v=vi∂i ,w=wi∂i{\displaystyle v=v^{i}\partial _{i}\ ,w=w^{i}\partial _{i}} — представление векторных полей в локальных координатах.
Замечания
Иногда метрический тензор задаётся двойственным способом, с помощью контравариантного тензора gij{\displaystyle g^{ij}}.
В случае невырожденных метрик
- gijgjk=δki,{\displaystyle g^{ij}g_{jk}=\delta _{k}^{i},}
где δki{\displaystyle \delta _{k}^{i}} — символ Кронекера. В этом случае оба способа эквивалентны, и оба представления метрики бывают полезны.
Для вырожденных метрик иногда удобнее пользоваться именно контравариантной метрикой. Например, субриманова метрика может быть определена через тензор gij{\displaystyle g^{ij}}, но тензор gij{\displaystyle g_{ij}} для неё не определён.
Представление в поле реперов
Иногда удобно задавать метрический тензор через выбранное (не обязательно координатное, как это описано выше) поле реперов, то есть выбором реперного поля {ei(p)}{\displaystyle \{e_{i}(p)\}} и матрицы gik(p)=⟨ei(p),ek(p)⟩{\displaystyle g_{ik}(p)=\langle e_{i}(p),e_{k}(p)\rangle }.
Например, риманов метрический тензор может быть задан ортонормированным полем реперов.
Индуцированная метрика
Метрика, которая индуцируется гладким вложением r{\displaystyle r} многообразия M{\displaystyle M} в евклидово пространство E{\displaystyle E}, может быть посчитана по формуле:
- g=JrTJr,{\displaystyle g=J_{r}^{T}J_{r},}
где Jr{\displaystyle J_{r}} означает матрицу Якоби вложения r{\displaystyle r} и JrT{\displaystyle J_{r}^{T}} — транспонированная к ней. Иначе говоря, скалярные произведения базисных координатных векторов касательного пространства ∂∂xi{\displaystyle {\frac {\partial }{\partial x_{i}}}}, которые в этом случае можно отождествить с ∂r∂xi{\displaystyle {\frac {\partial r}{\partial x_{i}}}}, определяются как
- gij=g(∂∂xi,∂∂xj)=⟨∂r∂xi,∂r∂xj⟩,{\displaystyle g_{ij}=g\left({\frac {\partial }{\partial x_{i}}},{\frac {\partial }{\partial x_{j}}}\right)=\left\langle {\frac {\partial r}{\partial x_{i}}},{\frac {\partial r}{\partial x_{j}}}\right\rangle ,}
где ⟨∗,∗⟩{\displaystyle \langle *,*\rangle } обозначает скалярное произведение в E{\displaystyle E}.
Более обобщенно
Пусть (N,h){\displaystyle (N,h)} многообразие с метрикой и rM→N{\displaystyle r:M\to N} гладкое вложение.
Тогда метрика g{\displaystyle g} на M{\displaystyle M}, определённая равенством
- g(X,Y)=h(dr(X),dr(Y)){\displaystyle g(X,Y)=h(dr(X),dr(Y))}
называется индуцированной метрикой.
Здесь dr{\displaystyle dr} обозначает дифференциал отображения r{\displaystyle r}.
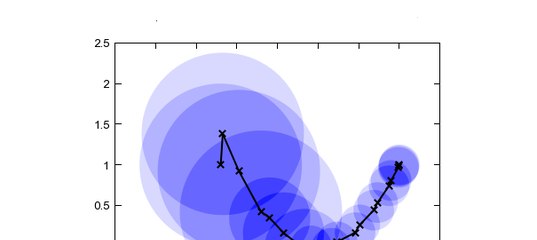
Вектор на плоскости. Контравариантные, ковариантные координаты и связь между ними
Рассмотрим вектор, и без потери общности наших рассуждений, рассмотрим вектор заданный на плоскости. Как известно из курса ещё школьной геометрии, любой вектор можно задать на плоскости с помощью двух неколлинеарных векторов
Здесь — коэффициенты разложения, (под верхним индексом следует понимать именно номер компоненты, а не возвдение в степень), называемые контрвариантные координаты вектора . Геометрически это можно изобразить так, как показано на рисунке ниже. Векторы называют базисными, угол между ними, при условии , может быть произвольным, произвольна так же ненулевая длина базисных векторов. Указанный базис задает косоугольную систему координат на плоскости, с осями .
Исходя из чертежа длины отрезков и равны
Однако, это не единственный способ определить вектор в данной системе координат. Его можно так же задать ортогональными проекциями на оси . Нетрудно видеть, что эти проекции равны
С другой стороны, выразим длины этих проекций через длины базисных векторов таким образом
где и — ковариантные координаты вектора .
Сравниваем (3), (5) и (4), (6)
Умножим (7) на , а (8)
на и преобразуем их
Введем матрицу
тогда (9) и (10) можно выразить следующим соотношением
Выражение (12) дает связь между ковариантными и контрaвариантными координатами вектора, определяемую лишь видом матрицы , зависящей от длин взаимного расположения базисных векторов. Пока никак не будем интерпретировать полученный результат, а просто запомним его.
Набор контравариантных и ковариантных компонент, по сути, задают в выбранном базисе один и тот же вектор. При использовании контравариантных координат этот вектор задается матрицей-столбцом
а в ковариантной форме — матрицей-строкой
Деятельность
Всероссийские направления
Основное направление деятельности холдинга «Тензор» — это разработка программного обеспечения. Продукты линейки СБИС предназначены для электронного документооборота с госорганами, обмена первичными бухгалтерскими документами между организациями, ведения бухгалтерской и учётной деятельности предприятия.
Удостоверяющий центр «Тензор» выпускает и обслуживает сертификаты ключей электронной подписи, которые используются физическими и юридическими лицами при сдаче налоговой и бухгалтерской отчётности через ТКС, при участии в электронных торгах, при обмене электронными документами.
Типы метрических тензоров
Совокупность метрических тензоров g{\displaystyle g} подразделяется на два класса:
- невырожденные или псевдоримановы метрики, когда det(gij)≠{\displaystyle \ \det(g_{ij})\neq 0} во всех точках многообразия. Среди невырожденных метрических тензоров, в свою очередь, различаются:
- Риманов метрический тензор (или риманова метрика), для которого квадратичная форма является положительно определенной. Многообразие с выделенным римановым метрическим тензором называется римановым, они имеют естественную структуру метрического пространства.
-
Собственно псевдориманов метрический тензор (или индефинитная метрика), когда форма не является знакоопределённой. Многообразие с выделенным псевдоримановым метрическим тензором называется (собственно) псевдоримановым
К этому классу относится метрика Лоренца.
.
- Вырожденные метрики, когда det(gij)={\displaystyle \ \det(g_{ij})=0} либо det(gij)={\displaystyle \ \det(g^{ij})=0} в некоторых точках.
- Многообразие Mn{\displaystyle M^{n}}, метрика которого является вырожденной в любой точке, называется изотропным (например, световой конус в пространстве Минковского).
- Субримановы метрики.
Обычно под метрическим тензором без специального на то указания в математике понимается риманов метрический тензор; но если, рассматривая невырожденный метрический тензор, хотят подчеркнуть, что речь идет именно о римановом, а не псевдоримановом метрическом тензоре, то о нём говорят как о собственно римановом метрическом тензоре. В физике под метрическим тензором обычно подразумевают лоренцеву метрику пространства-времени.
Иногда под псевдоримановым тензором и псевдоримановым многообразием понимают то, что выше определено как собственно псевдоримановы метрика и многообразие, а для первых сохраняется только термин «невырожденная метрика» и соответственно «многообразие с невырожденной метрикой».
Ранг тензора. Ковариантные и контравариантные компоненты
p, qpqpqp+q
- Тензор ранга (0,0) — это скаляр, величина, значение которой может быть выражено одним числом, со значением инвариантным относительно смены системы координат. У скаляра нет индексов, и он вообще не преобразуется при смене базиса. Но, повторимся, не всякое число есть скаляр. Так например, компонент вектора или тензора не есть скаляр, ибо он изменяется при смене базиса.
- Тензор ранга (1,0) — вектор. Для вектора естественно контравариантное представление, для вычисления скалярного произведения векторов требуется их свертка с метрическим тензором.
Преобразование компонент вектора производится путем применения к нему линейного оператора, по сути умножением матрицы преобразования на столбец, содержащий компоненты вектора, что в тензорной форме выглядит как -
Тензор ранга (0,1) — ковектор. Если в рассматриваемом пространстве определен невырожденный метрический тензор
то вектор и ковектор — это два разных представления одного и того же геометрического объекта — вектора. В ортогональном базисе (векторы которого взаимно перпендикулярны) контравариантные и ковариантные координаты cовпадают. Переход от одного представления к другому производится сверткой с метрическим тензором
где контрвариантный метрический тензор, компоненты которого — матрица,
обратная матрице компонент тензора .
Для скалярного умножения ковектора на вектор не нужно использовать метрический тензор, оно производится прямой сверткой с вектором.Преобразование компонент ковектора так же производится путем применения к нему линейного оператора, но в отличие от вектора, производится умножение строки, содержащей компоненты ковектора на матрицу преобразования координат
- Тензор ранга (0,2) — билинейная форма, примером которой может служить дважды ковариантный метрический тензор gij. Компоненты метрического тензора преобразуются путем двукратного применения к нему линейного оператора преобразования координат, что соответствует умножению транспонированной матрицы преобразования на матрицу метрического тензора и последующему умножению результата на матрицу преобразования
- Тензор ранга (2,0) — примером может служить диада (8). Вообще, все тензоры рангов (k,0) называются поливекторами или полиадами (триады, тетрады и т.д.), и образованы они как линейные комбинации тензорных произведений соответствующего количества векторов. Их компоненты преобразуются соответствующим рангу количеством применения линейных
операторов, преобразующих исходные векторы. -
Тензор ранга (1,1) — линейный оператор. Примером может служить матрица поворота или любого другого преобразования координат векторов и ковекторов. Вообще, применение линейного оператора сводится к операции матричного умножения
где — результат преобразования; — исходный вектор; — компоненты матрицы линейного оператора. Рассмотрим процесс преобразования линейного оператора. Пусть S матрица перехода от одно базиса к другому. Тогда, при смене базиса преобразуются оба вектора — и аргумент и результат
Подставляя (24) в (23) получаем
откуда, умножая слева на матрицу получаем
где — компоненты матрицы . С другой стороны, для векторов в новом базисе справедливо
сравнивая (25) и (26), получаем выражение преобразования линейного оператора
Все перечисленные объекты обладают общностью свойств: имеют набор компонент и правило преобразования при смене базиса.
Продукты
СБИС Электронная отчётность и документооборот — единая система для работы с отчётными данными и программный комплекс для автоматизации потока внутренних и внешних организационных документов. Юридическая значимость документов и отчётов обусловлена использованием электронной цифровой подписи (ЭЦП) и средств криптографической защиты информации. Программный комплекс СБИС сертифицирован ФГУП ГНИВЦ РФ, соответствует государственным стандартам, и рекомендован ФНС и ПФР РФ к использованию в качестве решения для специальных операторов связи и налогоплательщиков.
СБИС Бухгалтерия — программный комплекс для автоматизации бухгалтерской, налоговой и учетной деятельности на предприятиях различных отраслей.