Статистика

Введение

Рассмотрение
понятия статистических показателей я
бы хотела начать в первую очередь с
определения статистического показателя.

Статистический
показатель
представляет собой количественную
характеристику социально-экономических
явлений и процессов в условиях качественной
определённости. Качественная определённость
показателя заключается в том, что он
непосредственно связан с внутренним
содержанием изучаемого явления или
процесса, его сущностью.
С помощью показателей определяется,
что, где, когда и каким образом следует
численно измерить. Каждый статистический
показатель с возможной точностью должен
соответствовать сущности того явления,
которое должно быть измерено с его
помощью. Например, измерение объёма
промышленной продукции требует
предварительного установления тех
видов деятельности предприятия, которые
будут учтены в составе промышленной
продукции, и определения тех результатов
этой деятельности, которые могут быть
включены в её объём.

Процессы и явления,
изучаемые статистикой достаточно
сложны, и они не могут раскрыться при
использовании одного лишь показателя.
В таких случаях используется система
статистических показателей.

Система
статистических показателей—
совокупность взаимосвязанных показателей,
имеющая одноуровневую или многоуровневую
структуру и нацеленная на решение
конкретной статистической задачи.
Важнейшей особенностью системы
показателей является содержательное
единство, связанное с характеристиками
объекта исследования. Так, система
стоимостных показателей продукции
промышленного предприятия включает
следующие показатели: товарная продукция,
отгруженная продукция, реализованная
продукция, чистая продукция, стоимость
добавленная обработкой и др.

Вычислительная статистика

Развитие вычислительной техники во второй половине XX века оказало значительное влияние на статистику. Ранее статистические модели были представлены преимущественно линейными моделями. Увеличение быстродействия ЭВМ и разработка соответствующих численных алгоритмов послужило причиной повышенного интереса к нелинейным моделям таким, как искусственные нейронные сети, и привело к разработке сложных статистических моделей, например обобщённая линейная модель и иерархическая модель.

Получили широкое распространение вычислительные методы, основанные на повторной выборке как критерий перестановок и бутстреппинг, наряду методы как семплирование по Гиббсу позволили более доступно использовать байесовские алгоритмы. В настоящее время существует разнообразное статистическое программное обеспечение общего и специализированного назначения.

Мода и медиана

Модой называют элемент, который встречается в выборке чаще других.

Рассмотрим следующую выборку: шестеро спортсменов, а также время в секундах за которое они пробегают 100 метров

Элемент 14 встречается в выборке чаще других, поэтому элемент 14 назовем модой.

Рассмотрим еще одну выборку. Тех же спортсменов, а также смартфоны, которые им принадлежат

Элемент iphone встречается в выборке чаще других, значит элемент iphone является модой. Говоря простым языком, носить iphone модно.

Конечно элементы выборки в этот раз выражены не числами, а другими объектами (смартфонами), но для общего представления о моде этот пример вполне приемлем.

Рассмотрим следующую выборку: семеро спортсменов, а также их рост в сантиметрах:

Упорядочим данные в таблице так, чтобы рост спортсменов шел по возрастанию. Другими словами, построим спортсменов по росту:

Выпишем рост спортсменов отдельно:

180, 182, 183, 184, 185, 188, 190

В получившейся выборке 7 элементов. Посередине этой выборки располагается элемент 184. Слева и справа от него по три элемента. Такой элемент как 184 называют медианой упорядоченной выборки.

Медианой упорядоченной выборки называют элемент, располагающийся посередине.

Отметим, что данное определение справедливо в случае, если количество элементов упорядоченной выборки является нечётным.

В рассмотренном выше примере, количество элементов упорядоченной выборки было нечётным. Это позволило нам быстро указать медиану

Но возможны случаи, когда количество элементов выборки чётно.

К примеру, рассмотрим выборку в которой не семеро спортсменов, а шестеро:

Построим этих шестерых спортсменов по росту:

Выпишем рост спортсменов отдельно:

180, 182, 184, 186, 188, 190

В данной выборке не получается указать элемент, который находился бы посередине. Если указать элемент 184 как медиану, то слева от этого элемента будут располагаться два элемента, а справа — три. Если как медиану указать элемент 186, то слева от этого элемента будут располагаться три элемента, а справа — два.

В таких случаях для определения медианы выборки, нужно взять два элемента выборки, находящихся посередине и найти их среднее арифметическое. Полученный результат будет являться медианой.

Вернемся к нашим спортсменам. В упорядоченной выборке 180, 182, 184, 186, 188, 190 посередине располагаются элементы 184 и 186

Найдем среднее арифметическое элементов 184 и 186

Элемент 185 является медианой выборки, несмотря на то, что этот элемент не является членом исходной и упорядоченной выборки. Спортсмена с ростом 185 нет среди остальных спортсменов. Рост в 185 см используется в данном случае для статистики, чтобы можно было сказать о том, что срединный рост спортсменов составляет 185 см.

Поэтому более точное определение медианы зависит от количества элементов в выборке.

Если количество элементов упорядоченной выборки нечётно, то медианой выборки называют элемент, располагающийся посередине.

Если количество элементов упорядоченной выборки чётно, то медианой выборки называют среднее арифметическое двух чисел, располагающихся посередине этой выборки.

Медиана и среднее арифметическое по сути являются «близкими родственниками», поскольку и то и другое используют для определения среднего значения. Например, для предыдущей упорядоченной выборки 180, 182, 184, 186, 188, 190 мы определили медиану, равную 185. Этот же результат можно получить путем определения среднего арифметического элементов 180, 182, 184, 186, 188, 190

Но медиана в некоторых случаях отражает более реальную ситуацию. Например, рассмотрим следующий пример:

Было подсчитано количество имеющихся очков у каждого спортсмена. В результате получилась следующая выборка:

0, 1, 1, 1, 2, 1, 2, 3, 5, 4, 5, 0, 1, 6, 1

Определим среднее арифметическое для данной выборки — получим значение 2,2

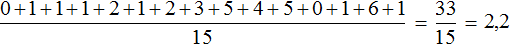
По данному значению можно сказать, что в среднем у спортсменов 2,2 очка

Теперь определим медиану для этой же выборки. Упорядочим элементы выборки и укажем элемент, находящийся посередине:

0, 0, 1, 1, 1, 1, 1, 1, 2, 2, 3, 4, 5, 5, 6

В данном примере медиана лучше отражает реальную ситуацию, поскольку половина спортсменов имеет не более одного очка.

Прикладная статистика

Этот раздел науки занимается обработкой данных произвольной природы. В качестве математической основы прикладной статистики и её методов анализа выступают математическая статистика и теория вероятностей. Всё начинается с описания вида полученных данных, а также механизма их происхождения. Для этого используются вероятностные и детерминированные методы. Последние можно применять только в тех случаях, когда в распоряжении исследователя достаточно данных (пример – отчеты государственных органов статистики, что основываются на информации, предоставленной предприятиями). А вот перенести полученный результат на больший масштаб и оценить перспективы можно исключительно с использованием вероятностно-статистического моделирования.

В простейшей ситуации имеющиеся данные выступают в качестве значения определённого признака, который свойственен изучаемому объекту. Параметры здесь бывают количественными или указательными (в зависимости от категории, к которой они относятся). Второй вариант обычно говорит о качественной характеристике. А что, если взять их несколько? Или добавить количественные? Тогда можно говорить, что получен вектор объекта. Он рассматривается в качестве нового вида данных. При масштабных исследованиях выборки составляются из нескольких наборов векторов. Важным является уточнение и перепроверка полученной информации. Для этого используется повторная выборка.

Примечания

1. Малая советская энциклопедия. — М.: Советская энциклопедия, 1960. — Т. 8. — С. 1090.
2. Райзберг Б. А., Лозовский Л. Ш., Стародубцева Е. Б. Современный экономический словарь. 5-е изд., перераб. и доп. — М.: ИНФРА-М, 2007. — 495 с. — (Библиотека словарей «ИНФРА-М»)
3. Никитина Е. П., Фрейдлина В. Д., Ярхо А. В. Коллекция определений термина «статистика». — Москва: МГУ, 1972.
4. Чупров А. А. Вопросы статистики. — М.: Госстатиздат ЦСУ СССР, 1960.
5. Никитина Е. П., Фрейдлина В. Д., Ярхо А. Коллекция определений термина «статистика»
6. Гнеденко Б. В. Очерк по истории теории вероятностей. — Москва: УРСС, 2001.
7. Клейн Ф. Лекции о развитии математики в XIX столетии. Часть I. — Москва, Ленинград: Объединенное научно-техническое издательство НКТП СССР, 1937.
8. Плошко Б. Г., Елисеева И. И. История статистики: Учеб. пособие. — Москва, Ленинград: Финансы и статистика, 1990.
9. Huff, Darrell, How to Lie With Statistics, WW Norton & Company, Inc. New York, NY, 1954. ISBN 0-393-31072-8
10. Warne, R. Lazo, M., Ramos, T. and Ritter, N. (2012). Statistical Methods Used in Gifted Education Journals, 2006—2010. Gifted Child Quarterly, 56(3) 134—149. doi: 10.1177/0016986212444122
11. ↑ Encyclopedia of Archaeology. — Credo Reference : Oxford: Elsevier Science, 2008.
12. ↑ Cohen, Jerome B. (December 1938). «Misuse of Statistics». Journal of the American Statistical Association 33 (204): 657-674. Проверено 19 September 2012.
13. Freund, J. F. (1988). «Modern Elementary Statistics». Credo Reference. Проверено 21 September 2012.

5.2 Абсолютные статистические показатели

Исходной,
первичной формой выражения статистических
показателей являются абсолютные
величины.

Абсолютные
статистические показатели
характеризуют абсолютные размеры
изучаемых процессов и явлений: их массу,
площадь, объем, протяженность; отражают
их временные характеристики, а также
могут представлять объем совокупности,
т. е. число составляющих ее единиц.

Абсолютные
статистические показатели всегда
являются именованными числами, т.е.
имеют единицы измерения.

1
Натуральные
единицы измерения–

тонны, килограммы, унции, квадратные,
кубические и простые метры, мили,
километры, галлоны, литры, штуки,
тонно-километры и т. д.

2
Условно-натуральные
единицы измерения–
используются в тех случаях, когда
какой-либо продукт имеет несколько
разновидностей, и общий объем можно
определить только исходя из общего для
всех разновидностей потребительского
свойства.

Перевод
в условные единицы измерения осуществляется
на основе специальных коэффициентов
(k_i),
рассчитываемых как отношение
потребительских свойств отдельных
разновидностей продукта к эталонному
значению.

где
q
_i
– объем продукции в натуральных единицах.

3
Стоимостные
единицы измерения
–дают
денежную оценку социально-экономическим
явлениям и процессам. Эти показатели
используются для определения общей
стоимости или общих затрат на производство
и реализацию разнородных товаров и
услуг.

При
анализе и сопоставлении стоимостных
показателей необходимо иметь в виду,
что в условиях высоких темпов инфляции
они становятся несопоставимыми. Для
того чтобы произвести подобные сравнения,
осуществляют пересчет в сопоставимые
цены.

4
Трудовые
единицы измерения (человеко-день,
человеко-час)
–
используются
дляучета
как общие затраты труда на предприятии,
так и для характеристики трудоемкости
отдельных операций технологического
процесса.

Что такое статистика?

Так называют отрасль знаний, где излагают общие вопросы по сбору, измерению и анализу массовых (количественных или качественных) данных. Также статистика занимается изучением количественной стороны общественных массовых явлений с точки зрения их числовой формы. Происходит данное слово от латинского status, что означает «состояние дел». Первоначально данная наука называлась «Государствоведением».

Впервые термин «статистика» использовали в 1746 году, и этот момент положил начало такой учебной дисциплине и науке. Правда, нельзя сказать, что с этим началось ее непосредственное использование, поскольку учёт, измерение и анализ данных проводились значительно раньше. Важным параметром является мода. Что-то похожее можно вспомнить из геометрии, но это не совсем то. Но что такое мода в статистике? Так называют значение из линейного ряда, которое встречается чаще всего.

Виды группировки

Под статистической группировкой понимают разделение совокупности на группы (интервалы изменения параметра) однородные в каком-либо отношении. Число таких интервалов (групп) рассчитывается по формуле Стёрджеса:

k=1+3,322lg⁡n{\displaystyle k=1+3,322\lg n},

где k — число интервалов, n — число наблюдений.

Существует три вида группировки: аналитическая, типологическая, структурная.

Аналитическая группировка — позволяет выявить связь между группировками.

Типологическая группировка — разделение исследуемой совокупности на однородные группы.

Структурная группировка — в которой происходит разделение однородной совокупности на группы, по определенному признаку.

Типические группы: максимально однородные внутри и разнородными снаружи.
Группировки бывают первичными и вторичными.
Первичные группировки получаются в ходе статистических наблюдений. А вторичные осуществляются на основании первичной.

Статистические методы

Статисти́ческие ме́тоды — методы анализа статистических данных. Выделяют методы прикладной статистики, которые могут применяться во всех областях научных исследований и любых отраслях народного хозяйства, и другие статистические методы, применимость которых ограничена той или иной сферой. Имеются в виду такие методы, как статистический приемочный контроль, статистическое регулирование технологических процессов, надёжность и испытания, планирование экспериментов.

Классификация статистических методов

Статистические методы анализа данных применяются практически во всех областях деятельности человека. Их используют всегда, когда необходимо получить и обосновать какие-либо суждения о группе (объектов или субъектов) с некоторой внутренней неоднородностью.

Целесообразно выделить три вида научной и прикладной деятельности в области статистических методов анализа данных (по степени специфичности методов, сопряженной с погруженностью в конкретные проблемы):

а) разработка и исследование методов общего назначения, без учёта специфики области применения;

б) разработка и исследование статистических моделей реальных явлений и процессов в соответствии с потребностями той или иной области деятельности;

в) использование статистических методов и моделей для статистического анализа конкретных данных в решении прикладных задач, например, с целью проведения выборочных обследований.

Средняя скорость движения

При изучении задач на движение мы определяли скорость движения следующим образом: делили пройденное расстояние на время. Но тогда подразумевалось, что тело движется с постоянной скоростью, которая не менялась на протяжении всего пути.

В реальности, это происходит довольно редко или не происходит совсем. Тело, как правило, движется с различной скоростью.

Когда мы ездим на автомобиле или велосипеде, наша скорость часто меняется. Когда впереди нас помехи, нам приходиться сбавлять скорость. Когда же трасса свободна, мы ускоряемся. При этом за время нашего ускорения скорость изменяется несколько раз.

Речь идет о средней скорости движения. Чтобы её определить нужно сложить скорости движения, которые были в каждом часе/минуте/секунде и результат разделить на время движения.

Задача 1. Автомобиль первые 3 часа двигался со скоростью 66,2 км/ч, а следующие 2 часа — со скоростью 78,4 км/ч. С какой средней скоростью он ехал?

Сложим скорости, которые были у автомобиля в каждом часе и разделим на время движения (5ч)

Значит автомобиль ехал со средней скоростью 71,08 км/ч.

Определять среднюю скорость можно и по другому — сначала найти расстояния, пройденные с одной скоростью, затем сложить эти расстояния и результат разделить на время. На рисунке видно, что первые три часа скорость у автомобиля не менялась. Тогда можно найти расстояние, пройденное за три часа:

66,2 × 3 = 198,6 км.

Аналогично можно определить расстояние, которое было пройдено со скоростью 78,4 км/ч. В задаче сказано, что с такой скоростью автомобиль двигался 2 часа:

78,4 × 2 = 156,8 км.

Сложим эти расстояния и результат разделим на 5

Задача 2. Велосипедист за первый час проехал 12,6 км, а в следующие 2 часа он ехал со скоростью 13,5 км/ч. Определить среднюю скорость велосипедиста.

Скорость велосипедиста в первый час составляла 12,6 км/ч. Во второй и третий час он ехал со скоростью 13,5. Определим среднюю скорость движения велосипедиста:

Краткая история статистических методов

Типовые примеры раннего этапа применения статистических методов описаны в Библии, в Ветхом Завете. Там, в частности, приводится число воинов в различных племенах. С математической точки зрения дело сводилось к подсчёту числа попаданий значений наблюдаемых признаков в определённые градации.

Сразу после возникновения теории вероятностей (Паскаль, Ферма, XVII век) вероятностные модели стали использоваться при обработке статистических данных. Например, изучалась частота рождения мальчиков и девочек, было установлено отличие вероятности рождения мальчика от 0,5, анализировались причины того, что в парижских приютах эта вероятность не та, что в самом Париже, и так далее.

В 1794 году (по другим данным — в 1795) немецкий математик Карл Гаусс формализовал один из методов современной математической статистики — метод наименьших квадратов. В XIX веке значительный вклад в развитие практической статистики внёс бельгиец Кетле, на основе анализа большого числа реальных данных показавший устойчивость относительных статистических показателей, таких, как доля самоубийств среди всех смертей.

Первая треть XX века прошла под знаком параметрической статистики. Изучались методы, основанные на анализе данных из параметрических семейств распределений, описываемых кривыми семейства Пирсона. Наиболее популярным было нормальное распределение. Для проверки гипотез использовались критерии Пирсона, Стьюдента, Фишера. Были предложены метод максимального правдоподобия, дисперсионный анализ, сформулированы основные идеи планирования эксперимента.

Разработанную в первой трети XX века теорию анализа данных называют параметрической статистикой, поскольку её основной объект изучения — это выборки из распределений, описываемых одним или небольшим числом параметров. Наиболее общим является семейство кривых Пирсона, задаваемых четырьмя параметрами. Как правило, нельзя указать каких-либо веских причин, по которым распределение результатов конкретных наблюдений должно входить в то или иное параметрическое семейство. Исключения хорошо известны: если вероятностная модель предусматривает суммирование независимых случайных величин, то сумму естественно описывать нормальным распределением; если же в модели рассматривается произведение таких величин, то итог, видимо, приближается логарифмически нормальным распределением и так далее.