Среднее арифметическое в excel

Введение

Обозначим множество чисел X = (x₁, x₂, …, x_n), тогда выборочное среднее обычно обозначается горизонтальной чертой над переменной (x¯{\displaystyle {\bar {x}}}, произносится «x с чертой»).

Для обозначения среднего арифметического всей совокупности чисел обычно используется греческая буква μ. Для случайной величины, для которой определено среднее значение, μ есть вероятностное среднее или математическое ожидание случайной величины. Если множество X является совокупностью случайных чисел с вероятностным средним μ, тогда для любой выборки x_i из этой совокупности μ = E{x_i} есть математическое ожидание этой выборки.

На практике разница между μ и x¯{\displaystyle {\bar {x}}} в том, что μ является типичной переменной, потому что видеть можно скорее выборку, а не всю генеральную совокупность. Поэтому, если выборку представлять случайным образом (в терминах теории вероятностей), тогда x¯{\displaystyle {\bar {x}}} (но не μ) можно трактовать как случайную переменную, имеющую распределение вероятностей на выборке (вероятностное распределение среднего).

Обе эти величины вычисляются одним и тем же способом:

x¯=1n∑i=1nxi=1n(x1+⋯+xn).{\displaystyle {\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}={\frac {1}{n}}(x_{1}+\cdots +x_{n}).}

Если X — случайная переменная, тогда математическое ожидание X можно рассматривать как среднее арифметическое значений в повторяющихся измерениях величины X. Это является проявлением закона больших чисел. Поэтому выборочное среднее используется для оценки неизвестного математического ожидания.

В элементарной алгебре доказано, что среднее n + 1 чисел больше среднего n чисел тогда и только тогда, когда новое число больше чем старое среднее, меньше тогда и только тогда, когда новое число меньше среднего, и не меняется тогда и только тогда, когда новое число равно среднему. Чем больше n, тем меньше различие между новым и старым средними значениями.

Заметим, что имеется несколько других «средних» значений, в том числе среднее степенное, среднее Колмогорова, гармоническое среднее, арифметико-геометрическое среднее и различные средне-взвешенные величины (например, среднее арифметическое взвешенное, среднее геометрическое взвешенное, среднее гармоническое взвешенное).

Примеры

Для получения среднего арифметического трёх чисел необходимо сложить их и разделить на 3:

x1+x2+x33.{\displaystyle {\frac {x_{1}+x_{2}+x_{3}}{3}}.}

Для получения среднего арифметического четырёх чисел необходимо сложить их и разделить на 4:

x1+x2+x3+x44.{\displaystyle {\frac {x_{1}+x_{2}+x_{3}+x_{4}}{4}}.}

Непрерывная случайная величина

Если существует интеграл от некоторой функции f(x){\displaystyle f(x)} одной переменной, то среднее арифметическое этой функции на отрезке a;b{\displaystyle } определяется через определённый интеграл:

f(x)¯a;b=1b−a∫abf(x)dx.{\displaystyle {\overline {f(x)}}_{}={\frac {1}{b-a}}\int _{a}^{b}f(x)dx.}

Здесь подразумевается, что b>a.{\displaystyle b>a.}

Введение

Обе эти величины вычисляются одним и тем же способом:

x¯=1n∑i=1nxi=1n(x1+⋯+xn).{\displaystyle {\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}={\frac {1}{n}}(x_{1}+\cdots +x_{n}).}

Примеры

Для получения среднего арифметического трёх чисел необходимо сложить их и разделить на 3:

x1+x2+x33.{\displaystyle {\frac {x_{1}+x_{2}+x_{3}}{3}}.}

Для получения среднего арифметического четырёх чисел необходимо сложить их и разделить на 4:

x1+x2+x3+x44.{\displaystyle {\frac {x_{1}+x_{2}+x_{3}+x_{4}}{4}}.}

Непрерывная случайная величина

f(x)¯a;b=1b−a∫abf(x)dx.{\displaystyle {\overline {f(x)}}_{}={\frac {1}{b-a}}\int _{a}^{b}f(x)dx.}

Здесь подразумевается, что b>a.{\displaystyle b>a.}

Какие способы вычисления среднего бывают?

Первым способом является вычисление уже упомянутого среднего арифметического, являющегося суммой всех значений, деленной на их количество.

Формула:

x– среднее арифметическое;
x_n– конкретное значение;
n – количество значений.

Плюсы:

Хорошо работает при нормальном распределении значений в выборке;
Легко вычислить;
Интуитивно понятно.

Минусы:

Не дает реального представления о распределении значений;
Неустойчивая величина легко поддающаяся выбросам (как в случае с генеральным директором).

Вторым способом является вычисление моды, то есть наиболее часто встречающегося значения.

Формула:

M– мода;
x– нижняя граница интервала, который содержит моду;
n – величина интервала;
f_m– частота (сколько раз в ряду встречается то или иное значение);
f_m-1 – частота интервала предшествующего модальному;
f_m+1 – частота интервала следующего за модальным.

Плюсы:

Прекрасно подходит для получения представления об общественном мнении;
Хорошо подходит для нечисловых данных (цвета сезона, хиты продаж, рейтинги);
Проста для понимания.

Минусы:

Моды может просто не быть (нет повторов);
Мод может быть несколько (многомодальное распределение).

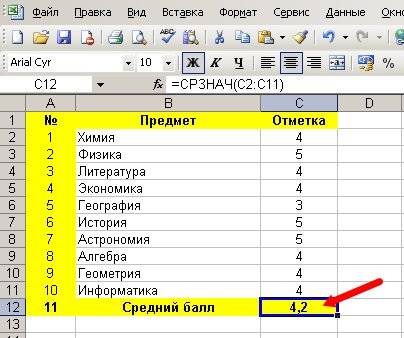
Третий способ — это вычисление медианы, то есть значения, которое делит упорядоченную выборку на две половины и находится между ними. А если такого значения нет, то за медиану принимается среднее арифметическое между границами половин выборки.

Формула:

M_e – медиана;
x– нижняя граница интервала, который содержит медиану;
h – величина интервала;
f _i– частота (сколько раз в ряду встречается то или иное значение);
S_m-1 – сумма частот интервалов предшествующих медианному;
f_m – число значений в медианном интервале (его частота).

Плюсы:

Дает самую реалистичную и репрезентативную оценку;
Устойчива к выбросам.

Минусы:

Сложнее вычислить, так как перед вычислением выборку нужно упорядочить.

Мы рассмотрели основные методы нахождения среднего значения, называющиеся мерами центральной тенденции (на самом деле их больше, но это наиболее популярные).

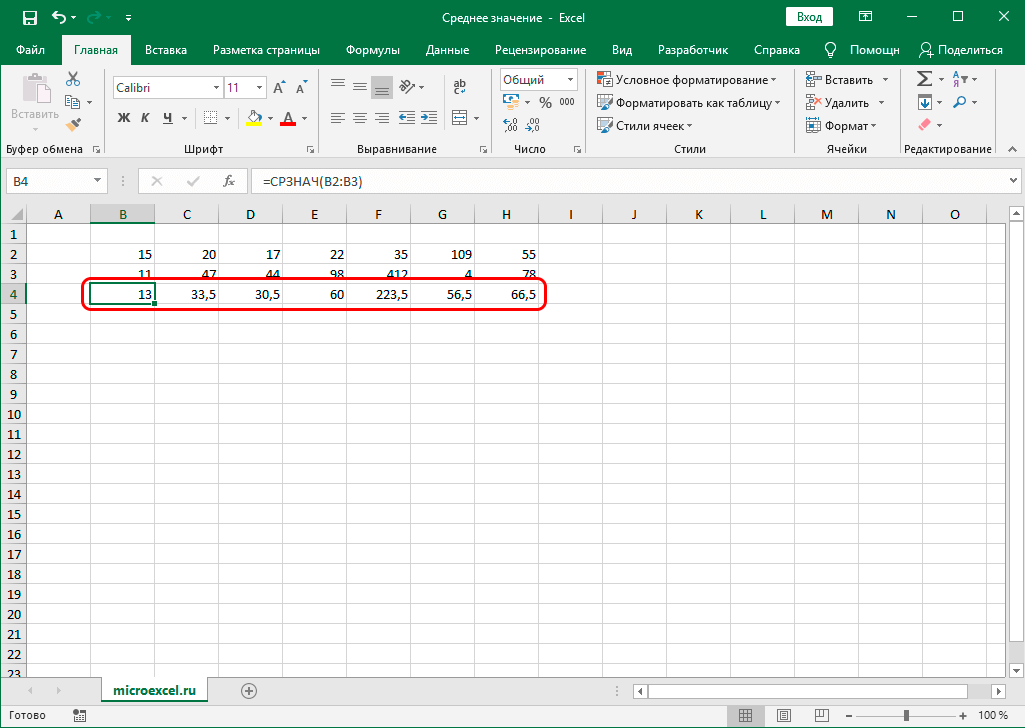
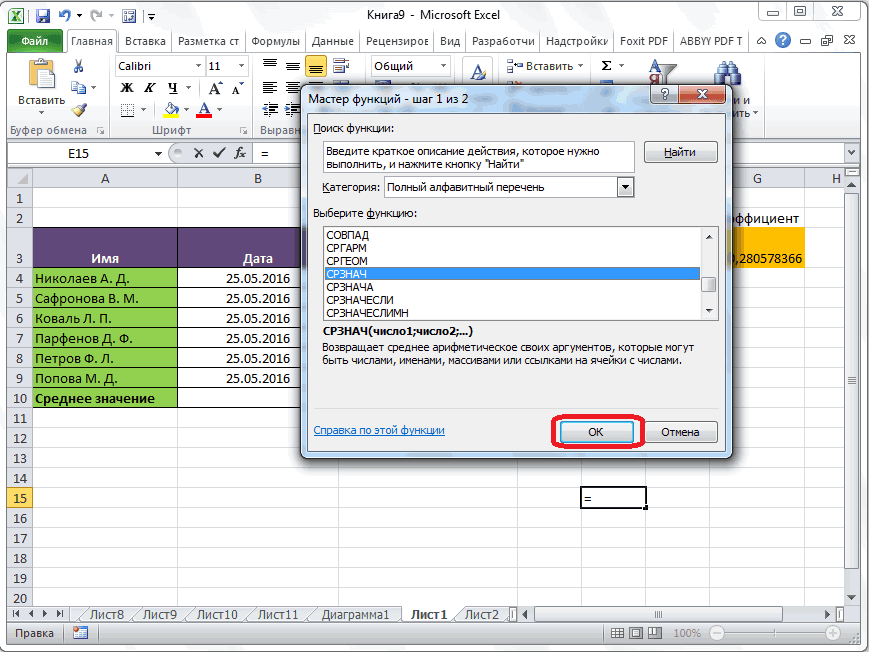
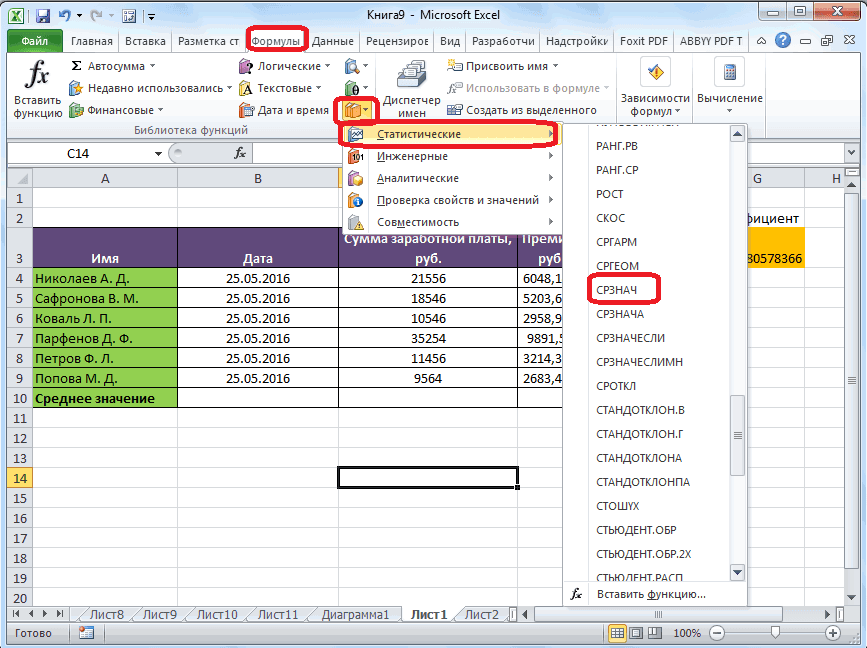
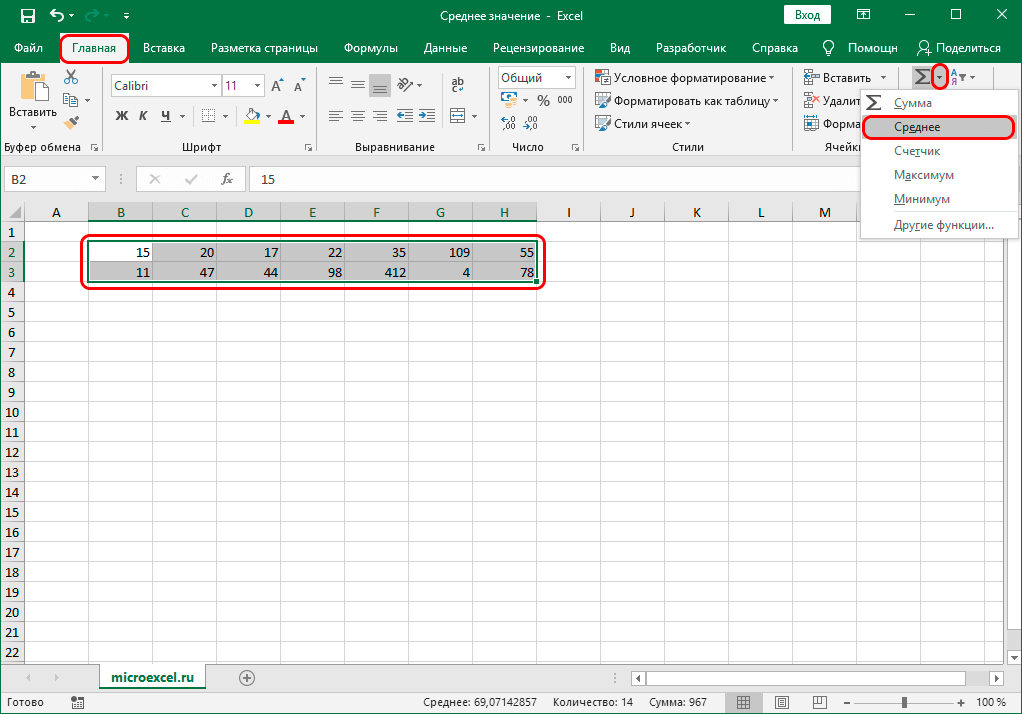
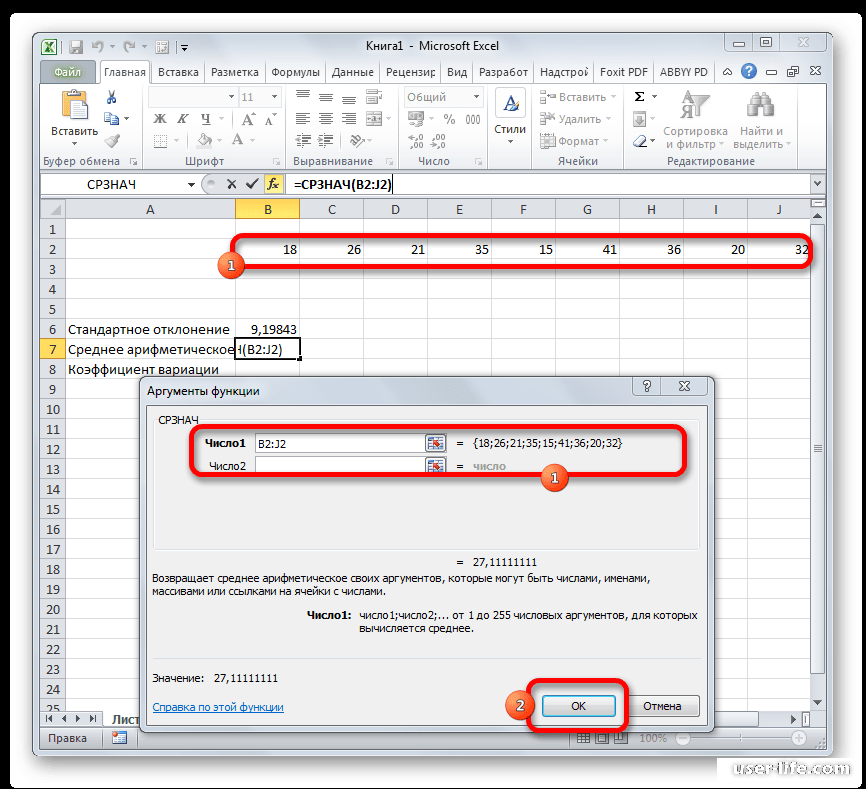
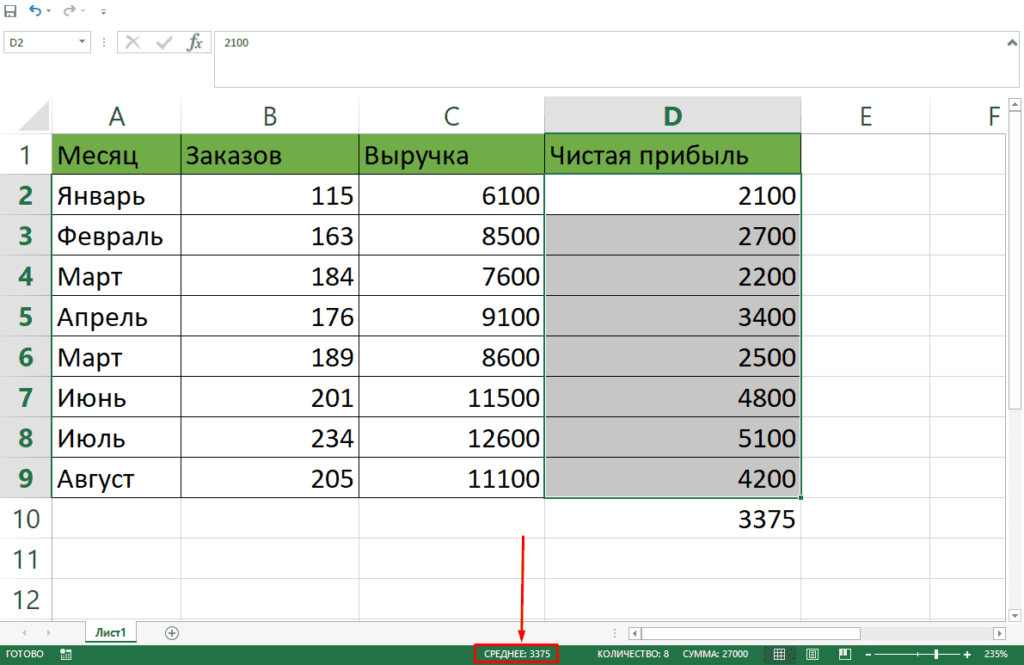
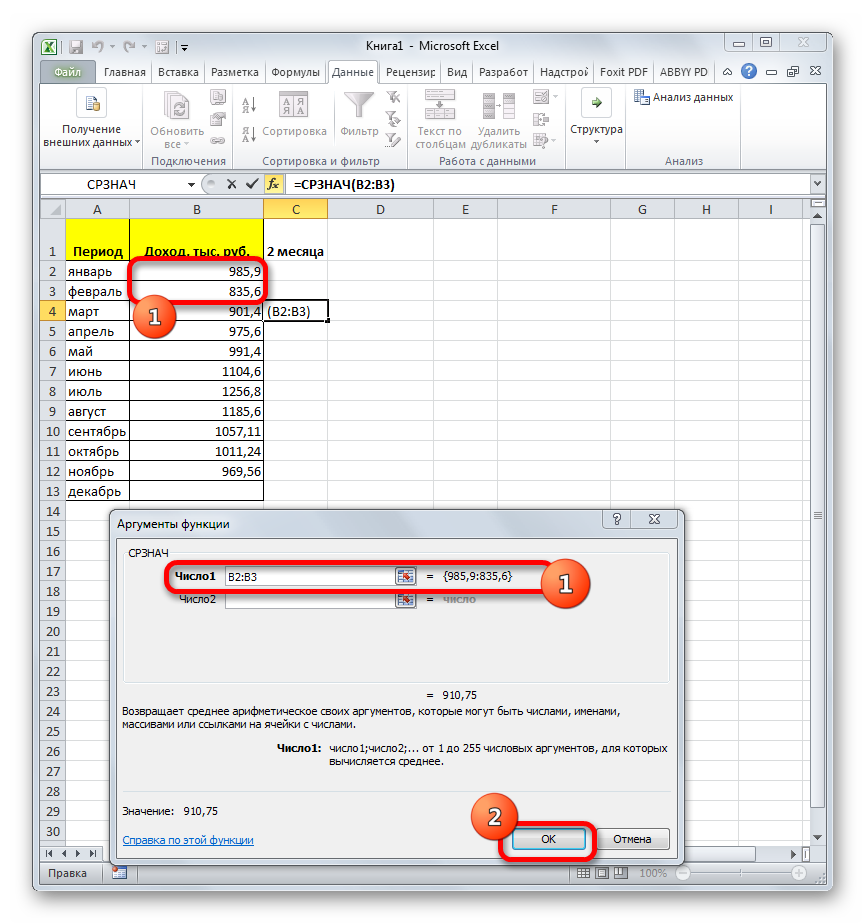
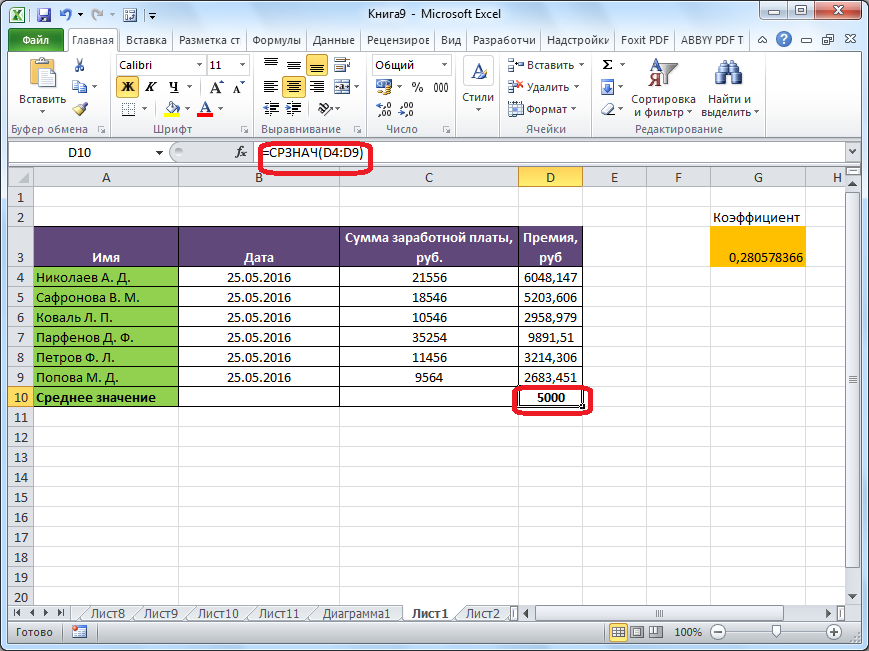
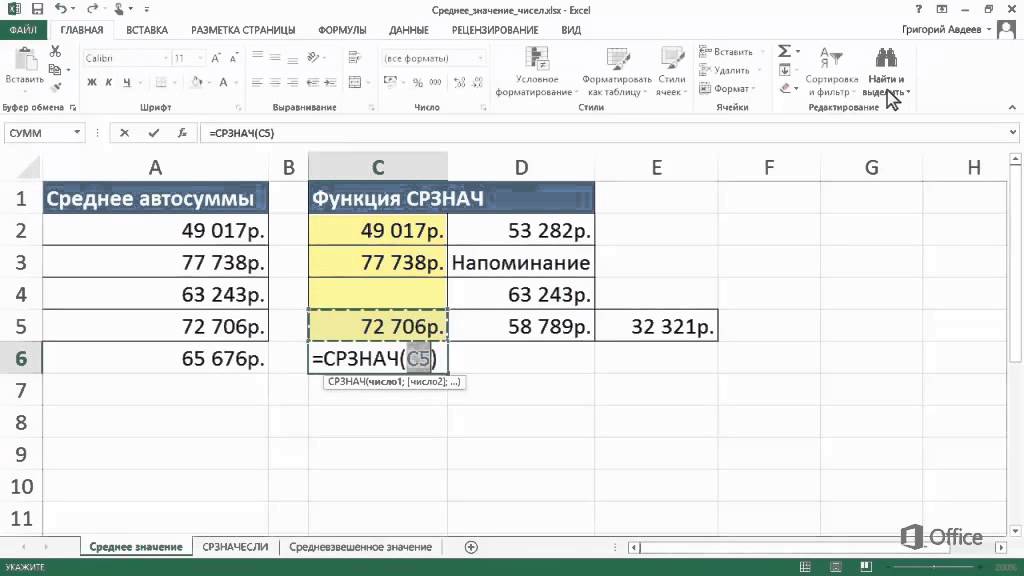
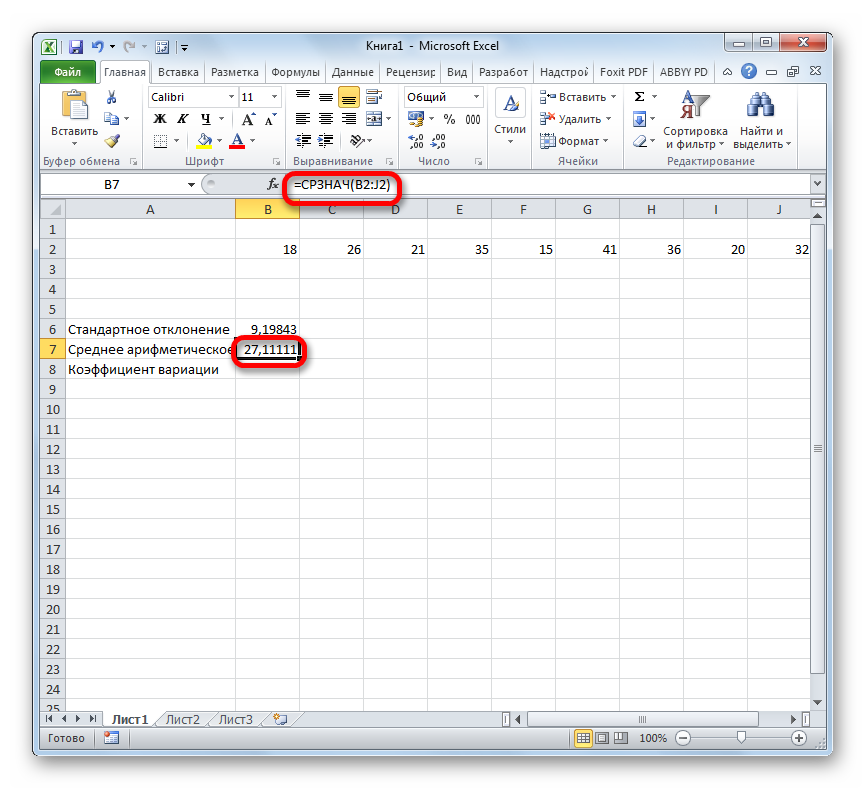
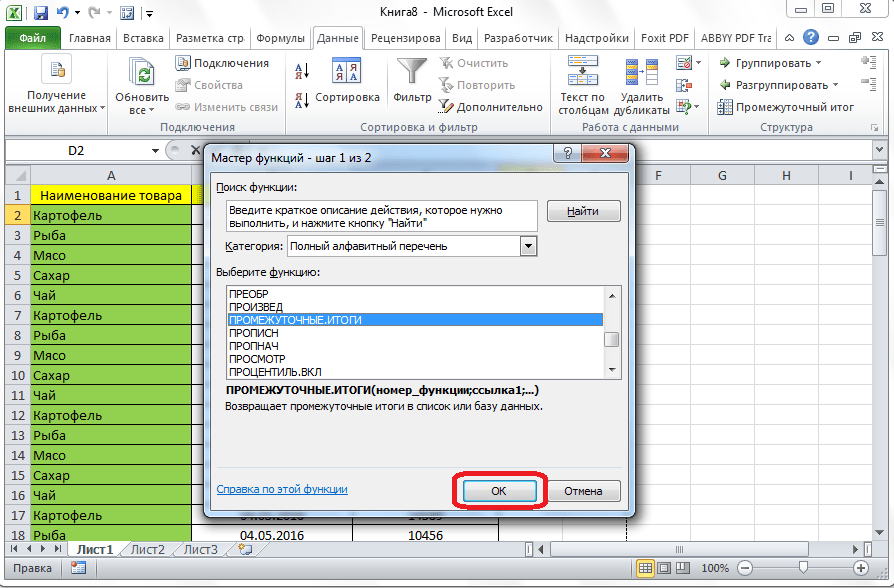
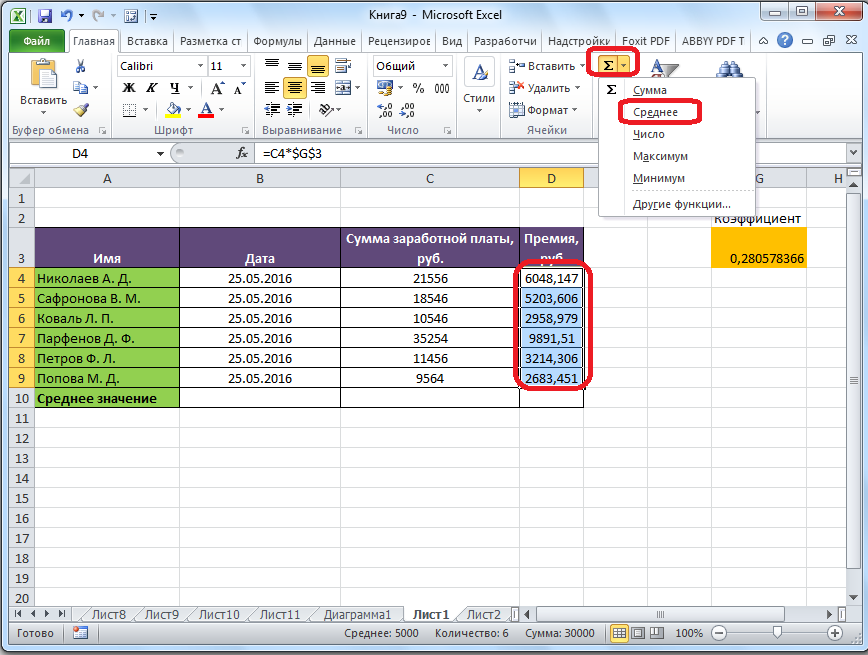
А теперь давайте вернемся к нашему примеру и посчитаем все три варианта среднего при помощи специальных функций Excel:

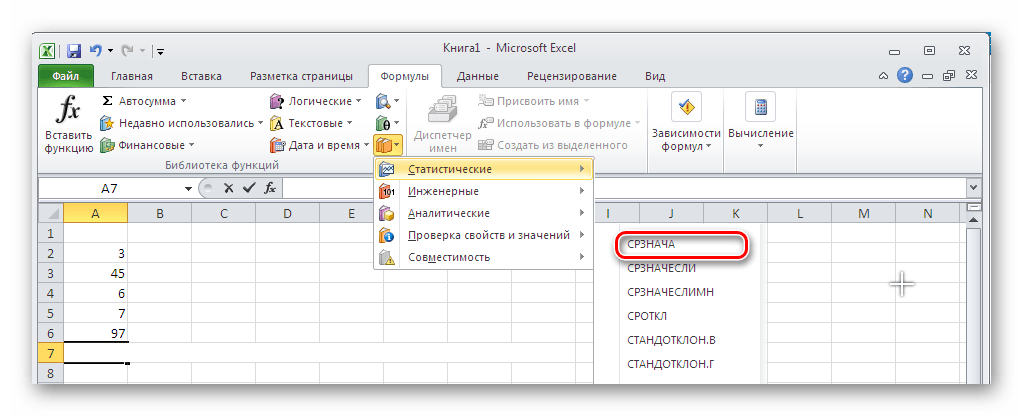
— функция для определения среднего арифметического;
— функция моды (в более старых версиях Excel использовалась );
— функция для поиска медианы.

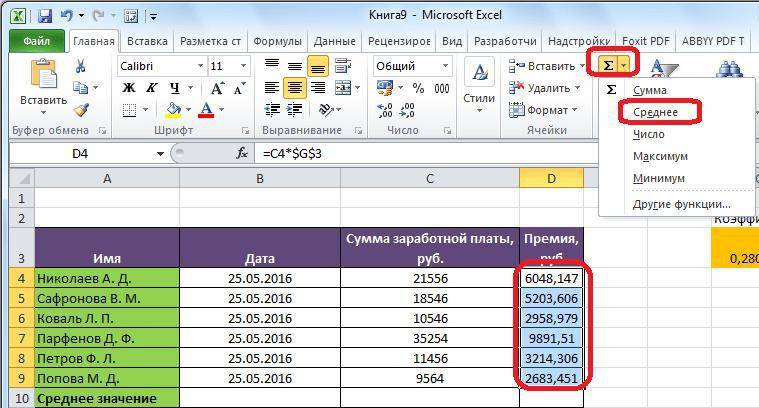
И вот какие значения у нас получились:

В данном случае мода и медиана гораздо лучше характеризуют среднюю зарплату в компании.

Но что делать, когда в выборке не 10 значений, как в примере, а миллионы? В Excel это не посчитать, а вот в базе данных где хранятся ваши данные, без проблем.

Вычисляем среднее арифметическое на SQL

Тут все достаточно просто, так как в SQL предусмотрена специальная агрегатная функция .

И чтобы ее использовать достаточно написать вот такой запрос:

/* Здесь и далее salary - столбец с зарплатами, а employees - таблица сотрудников в нашей базе данных */

SELECT AVG(salary) AS 'Средняя зарплата'
FROM employees

Вычисляем моду на SQL

В SQL нет отдельной функции для нахождения моды, но ее легко и быстро можно написать самостоятельно. Для этого нам необходимо узнать, какая из зарплат чаще всего повторяется и выбрать наиболее популярную.

Напишем запрос:

/* WITH TIES необходимо добавлять к TOP() если множество многомодально, то есть у множества несколько мод */
SELECT TOP(1) WITH TIES salary AS 'Мода зарплаты'
FROM employees
GROUP BY salary
ORDER BY COUNT(*) DESC

Вычисляем медиану на SQL

Как и в случае с модой, в SQL нет встроенной функции для вычисления медианы, зато есть универсальная функция для вычисления процентилей .

Выглядит все это так:

/* В данном случае процентиль 0.5 и будет являться медианой */

SELECT TOP(1) PERCENTILE_CONT(0.5)
       WITHIN GROUP (ORDER BY salary)
       OVER() AS 'Медианная зарплата'
FROM employees

Подробнее о работе функции лучше почитать в справке Microsoft и .

Вычисление среднего арифметического четырёх

Как уже видно по аналогии с предыдущими вариантами вычисление данного значения для количества, равного четырём, будет носить следующий порядок:

Выбираются четыре цифры, для которых надо вычислить среднее арифметическое значение. Далее производится суммирование и нахождение конечного результата этой процедуры.
Теперь чтобы получить окончательный результат, следует взять полученную сумму четырёх и разделить её на четыре. Полученные данные и будут требуемым значением.

Формула

Из описанной выше последовательности действий по нахождению среднего арифметического для четырёх, можно получить следующую формулу:

(А+В+С+Е)/4

В данной формуле переменные имеют следующее значение:

А, В, С и Е – это те, к которым необходимо найти значение среднего арифметического.

Применяя данную формулу, всегда можно будет вычислять требуемое значение для данного количества чисел.

Примеры использования

В физике

Средняя скорость тела

Если тело в течение промежутка времени t1{\displaystyle t_{1}} движется со скоростью v1{\displaystyle v_{1}}, затем в течение следующего промежутка времени t2{\displaystyle t_{2}} — со скоростью v2{\displaystyle v_{2}} и так далее до последнего промежутка времени tn{\displaystyle t_{n}}, в течение которого оно движется со скоростью vn{\displaystyle v_{n}}, то средняя скорость движения тела за суммарный промежуток времени (t1+t2+…+tn{\displaystyle t_{1}+t_{2}+\ldots +t_{n}}) будет равна взвешенному среднему арифметическому скоростей v1,…,vn{\displaystyle v_{1},\ldots ,v_{n}} с набором весов t1,…,tn{\displaystyle t_{1},\ldots ,t_{n}}:

vcp=∑i=1nti⋅vi∑i=1nti{\displaystyle v_{cp}={\frac {\sum \limits _{i=1}^{n}t_{i}\cdot v_{i}}{\sum \limits _{i=1}^{n}t_{i}}}}.

Центр масс

Другим примером использования данного понятия в физике является центр масс системы материальных точек, который задаётся формулой:

r→c=∑imir→i∑imi,{\displaystyle {\vec {r}}_{c}={\frac {\sum \limits _{i}m_{i}{\vec {r}}_{i}}{\sum \limits _{i}m_{i}}},}

где r→c{\displaystyle {\vec {r}}_{c}} — радиус-вектор центра масс,r→i{\displaystyle {\vec {r}}_{i}} — радиус-вектор i-й точки системы,mi{\displaystyle m_{i}} — масса i-й точки.

Температура смеси нескольких порций одной жидкости с разными температурами: tcp=∑i=1nti⋅mi∑i=1nmi{\displaystyle t_{cp}={\frac {\sum \limits _{i=1}^{n}t_{i}\cdot m_{i}}{\sum \limits _{i=1}^{n}m_{i}}}},

где tcp{\displaystyle t_{cp}} — полученная температура смеси,ti{\displaystyle t_{i}} — температура i-й порции,mi{\displaystyle m_{i}} — масса i-й порции.

В экономике

Средневзвешенный курс валюты: Ccp=∑i=1nCi⋅bi∑i=1nbi{\displaystyle C_{cp}={\frac {\sum \limits _{i=1}^{n}C_{i}\cdot b_{i}}{\sum \limits _{i=1}^{n}b_{i}}}},

где Ccp{\displaystyle C_{cp}} — средневзвешенный курс,Ci{\displaystyle C_{i}} — курс оборота по i-му торгу,bi{\displaystyle b_{i}} — размер i-го торга.

Медианта множества дробей (математика) является разновидностью среднего арифметического взвешеннего, где основные числа — это данные дроби, а веса — их знаменатели соответственно. Например, медианта дробей 11/9, 2/1 и медианта дробей 5,5/4,5, 4/2 — разные величины в то время, как 11/9≡5,5/4,5, а 2/1≡4/2.

Использование:

Древо Штерна—Броко

Универсальная формула вычисления

Проводя рассмотрение различных вариантов формул для вычисления среднего арифметического, можно обратить внимание на то, что у них есть общая закономерность. Поэтому практичнее будет применять общую формулу для нахождения среднего арифметического

Ведь бывают ситуации, когда количество и величина расчётов может быть очень большой. Поэтому разумнее будет использовать универсальную формулу и не выводить каждый раз индивидуальную технологию для расчёта данной величины

Поэтому практичнее будет применять общую формулу для нахождения среднего арифметического. Ведь бывают ситуации, когда количество и величина расчётов может быть очень большой. Поэтому разумнее будет использовать универсальную формулу и не выводить каждый раз индивидуальную технологию для расчёта данной величины.

Главным при определении формулы является принцип расчёта среднего арифметического.

Данный принцип как было видно из приведённых примеров, выглядит таким образом:

Производится подсчёт количества чисел, которые заданы для получения требуемого значения. Эта операция может быть проведена как вручную при небольшом количестве чисел, так и при помощи вычислительной техники.
Проводится суммирование выбранных чисел. Эта операция в большинстве ситуаций выполняется при помощи вычислительной техники, так как числа могут состоять из двух, трёх и более цифр.
Сумма, которая получена в результате сложения выбранных чисел, должна быть поделена на их количество. Данная величина определяется на первоначальном этапе расчёта среднего арифметического.

Таким образом, общая формула для расчёта среднего арифметического ряда подобранных чисел будет выглядеть следующим образом:

(А+В+…+N)/N

Данная формула содержит следующие переменные:

А и В – это числа, которые выбраны заранее для расчёта их среднего арифметического.

N – это количество чисел, которые были взяты с целью проведения расчёта требуемого значения.

Подставляя каждый раз в данную формулу выбранные числа, мы всегда сможем получить требуемое значение среднего арифметического.

Как видно, нахождение среднего арифметического является несложной процедурой. Однако надо внимательно относиться к проводимым вычислениям и проводить проверку полученного результата. Такой подход объясняется тем, что даже в самых простых ситуациях существует вероятность получения ошибки, которая может повлиять потом на дальнейшие расчёты. В связи с этим рекомендуется применять вычислительную технику, которая способна произвести подсчёты любой сложности.

Нахождение значения для трёх

Проведение расчёта данной величины в ситуации, когда выбраны три числа, не будет сильно отличаться от предыдущего варианта:

Для этого следует выбрать числа, необходимые в расчёте, и сложить их для получения общей суммы.
После того как данная сумма трёх будет найдена, требуется опять совершить процедуру деления. При этом полученную сумму надо разделить уже на три, что соответствует количеству выбранных чисел.

Формула

Тем самым формула, необходимая при проведении расчётов арифметического трёх, будет выглядеть так:

(А+В+С)/3

В данной формуле принято следующее обозначение:

А, В и С – это числа, к которым необходимо будет находить среднее арифметическое.

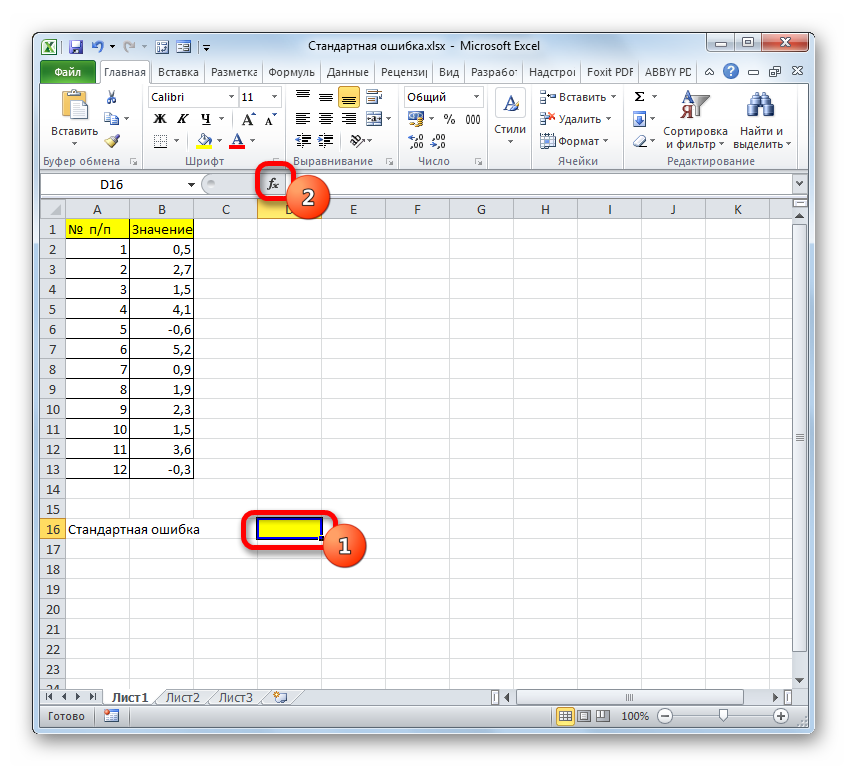
Показатели вариации

Вариация — это различие значений величин X у отдельных единиц статистической совокупности. Для изучения силы вариации рассчитывают следующие показатели вариации: , , , , , .

Размах вариации

Размах вариации – это разность между максимальным и минимальным значениями X из имеющихся в изучаемой статистической совокупности:

Недостатком показателя H является то, что он показывает только максимальное различие значений X и не может измерять силу вариации во всей совокупности.

Cреднее линейное отклонение

Cреднее линейное отклонение — это средний модуль отклонений значений X от среднего арифметического значения. Его можно рассчитывать по формуле средней арифметической простой — получим среднее линейное отклонение простое:

Если исходные данные X сгруппированы (имеются частоты f), то расчет среднего линейного отклонения выполняется по формуле средней арифметической взвешенной — получим среднее линейное отклонение взвешенное:

Линейный коэффициент вариации

Линейный коэффициент вариации — это отношение среднего линейного отклонение к средней арифметической:

С помощью линейного коэффициента вариации можно сравнивать вариацию разных совокупностей, потому что в отличие от среднего линейного отклонения его значение не зависит от единиц измерения X.

Дисперсия

Дисперсия — это средний квадрат отклонений значений X от среднего арифметического значения. Дисперсию можно рассчитывать по формуле средней арифметической простой — получим дисперсию простую:

Если исходные данные X сгруппированы (имеются частоты f), то расчет дисперсии выполняется по формуле средней арифметической взвешенной — получим дисперсию взвешенную:

Если преобразовать формулу дисперсии (раскрыть скобки в числителе, почленно разделить на знаменатель и привести подобные), то можно получить еще одну формулу для ее расчета как разность средней квадратов и квадрата средней:

Если значения X — это , то для расчета дисперсии используют частную формулу дисперсии доли:

Cреднее квадратическое отклонение

Выше уже было рассказано о , которая применяется для оценки вариации путем расчета среднего квадратического отклонения, обозначаемое малой греческой буквой сигма:

Еще проще можно найти среднее квадратическое отклонение, если предварительно рассчитана дисперсия, как корень квадратный из нее:

Квадратический коэффициент вариации

Квадратический коэффициент вариации — это самый популярный относительный показатель вариации:

Критериальным значением квадратического коэффициента вариации V служит 0,333 или 33,3%, то есть если V меньше или равен 0,333 — вариация считает слабой, а если больше 0,333 — сильной. В случае сильной вариации изучаемая статистическая совокупность считается неоднородной, а средняя величина — нетипичной и ее нельзя использовать как обобщающий показатель этой совокупности.

Предыдущая лекция…Следующая лекция…

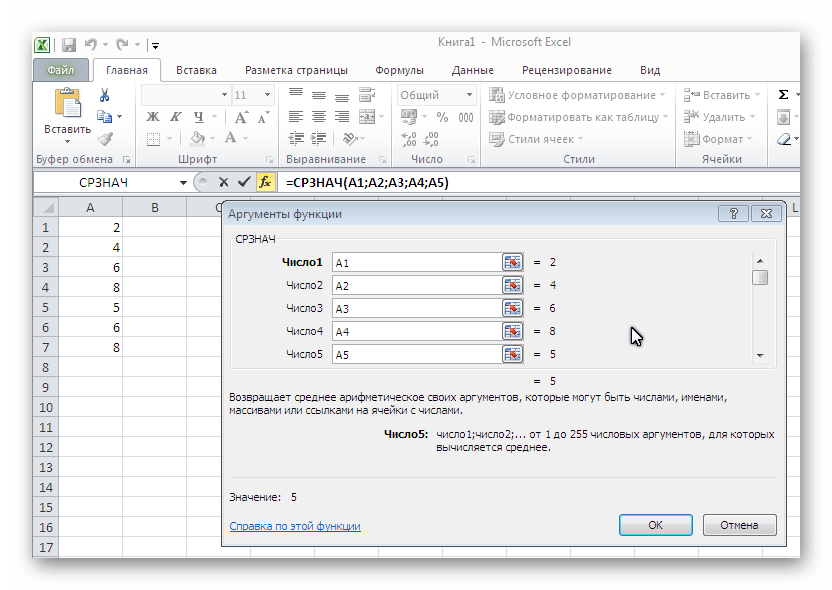
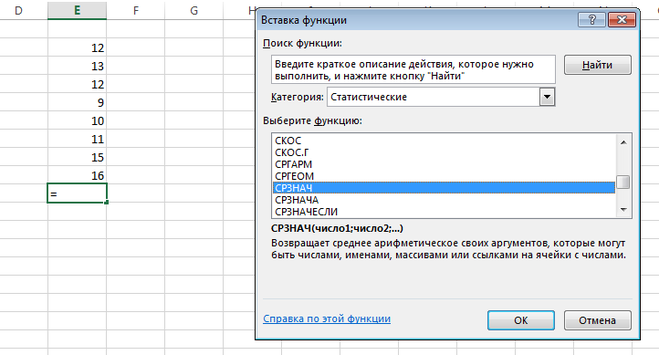
Синтаксис

Аргументы

Обязательный аргумент. Первое число, ссылка на ячейку или диапазон, для которого требуется вычислить среднее значение.

Необязательный аргумент. Дополнительные числа, ссылки на ячейки или диапазоны, для которых требуется вычислить среднее значение. Аргументов может быть не более 255.

Замечания

Аргументы могут быть числами, именами или ссылками на диапазоны или ячейки, содержащие числа.
Учитываются логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов.
Если аргумент является ссылкой на диапазон или ячейку, содержащую текст или логические значения, или ссылкой на пустую ячейку, то такие значения игнорируются; однако ячейки, которые содержат нулевые значения, учитываются.
Аргументы, являющиеся значениями ошибок или текстом, которые не могут быть преобразованы в числа, вызывают ошибки.
Если логические значения и текстовые представления чисел необходимо учитывать в расчетах, используйте функцию СРЗНАЧА.
Если требуется вычислить среднее значение только для тех значений, которые удовлетворяют определенным критериям, используйте функцию СРЗНАЧЕСЛИ или СРЗНАЧЕСЛИМН.
Функция СРЗНАЧ вычисляет среднее значение, то есть центр набора чисел в статистическом распределении. Существует три наиболее распространенных способа определения среднего значения, описанных ниже:
- Среднее значение — это среднее арифметическое, которое вычисляется путем сложения набора чисел с последующим делением полученной суммы на их количество. Например, средним значением для чисел 2, 3, 3, 5, 7 и 10 будет 5, которое является результатом деления их суммы, равной 30, на их количество, равное 6.
- Медиана — это число, которое является серединой множества чисел, то есть половина чисел имеют значения большие, чем медиана, а половина чисел имеют значения меньшие, чем медиана. Например, медианой для чисел 2, 3, 3, 5, 7 и 10 будет 4.
- Мода — это число, наиболее часто встречающееся в данном наборе чисел. Например, модой для чисел 2, 3, 3, 5, 7 и 10 будет 3.
При симметричном распределении множества чисел эти величины оценки степени централизации равны. При ассиметричном распределении множества чисел они могут отличаться.

Расчет процентов в Excel

Эксель умеет выполнять многие математические задачи, в том числе и простейший расчет процентов. Пользователю в зависимости от потребностей не составит труда рассчитать процент от числа и число по проценту, в том числе и в табличных вариантах данных. Для этого следует лишь воспользоваться определенными формулами.

Вариант 1: Расчет процентов от числа

Прежде всего давайте выясним, как рассчитать величину доли в процентах одного числа от другого.

Формула вычисления выглядит следующим образом: .
Чтобы продемонстрировать вычисления на практике, узнаем, сколько процентов составляет число 9 от 17

Выделяем ячейку, куда будет выводиться результат и обязательно обращаем внимание, какой формат указан на вкладке «Главная» в группе инструментов «Число». Если формат отличен от процентного, обязательно устанавливаем в поле параметр «Процентный».
После этого записываем следующее выражение: .

Впрочем, так как мы задали процентный формат ячейки, дописывать значение «*100%» не обязательно. Достаточно ограничиться записью «=9/17».

Чтобы посмотреть результат, жмем на клавишу Enter. В итоге получаем 52,94%.

Теперь взглянем, как можно вычислять проценты, работая с табличными данными в ячейках.

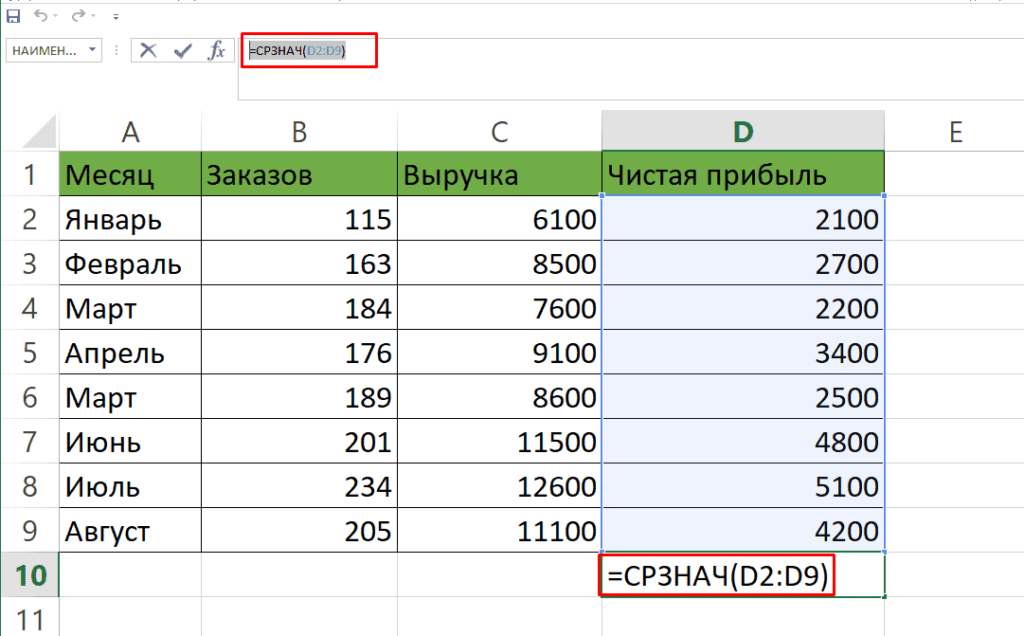
Допустим, нам требуется посчитать, сколько процентов составляет доля реализации конкретного вида товара от общей суммы, указанной в отдельной ячейке. Для этого в строке с наименованием товара кликаем по пустой ячейке и устанавливаем в ней процентный формат. Ставим знак «=». Далее щелкаем по клеточке с указанием величины реализации конкретного вида товара «/». Потом — по ячейке с общей суммой реализации по всем товарам. Таким образом, в ячейке для вывода результата у нас записана формула.

Чтобы посмотреть значение вычислений, нажимаем Enter.

Мы выяснили определение доли в процентах только для одной строки. Неужели для каждой следующей строки нужно будет вводить подобные вычисления? Совсем не обязательно. Нам надо скопировать данную формулу в другие ячейки. Однако поскольку при этом ссылка на ячейку с общей суммой должна быть постоянной, чтобы не происходило смещение, то в формуле перед координатами ее строки и столбца ставим знак «$». После этого ссылка из относительной превращается в абсолютную.

Наводим курсор в нижний правый угол ячейки, значение которой уже рассчитано, и, зажав кнопку мыши, тянем ее вниз до ячейки, где располагается общая сумма включительно. Как видим, формула копируется и на все другие клетки таблицы. Сразу виден результат подсчетов.

Можно посчитать процентную долю отдельных составляющих таблицы, даже если итоговая сумма не выведена в отдельную ячейку. После форматирования ячейки для вывода результата в процентный формат ставим в ней знак «=». Далее кликаем по ячейке, чью долю надо узнать, ставим знак «/» и набираем сумму, от которой рассчитывается процент. Превращать ссылку в абсолютную в этом случае не нужно.

Затем жмем Enter и путем перетягивания копируем формулу в ячейки, которые расположены ниже.

Вариант 2: Расчет числа по проценту

Теперь посмотрим, как рассчитать число от общей суммы по проценту от нее.

Формула для расчета будет иметь следующий вид: . Следовательно, если нам понадобилось посчитать, какое число составляет, например, 7% от 70, то просто вводим в ячейку выражение «=7%*70». Так как в итоге мы получаем число, а не процент, то в этом случае устанавливать процентный формат не надо. Он должен быть или общий, или числовой.

Для просмотра результата нажмите Enter.

Эту модель довольно удобно применять и для работы с таблицами. Например, нам нужно от выручки каждого наименования товара подсчитать сумму величины НДС, которая составляет 18%. Для этого выбираем пустую ячейку в строке с наименованием товара. Она станет одним из составных элементов столбца, в котором будут указаны суммы НДС. Форматируем ее в процентный формат и ставим в ней знак «=». Набираем на клавиатуре число 18% и знак «*». Далее кликаем по ячейке, в которой находится сумма выручки от продажи данного наименования товара. Формула готова. Менять формат ячейки на процентный или делать ссылки абсолютными не следует.

Для просмотра результата вычисления жмем Enter.

Копируем формулу в другие ячейки перетаскиванием вниз. Таблица с данными о сумме НДС готова.

Как видим, программа предоставляет возможность удобно работать с процентными величинами. Пользователь может вычислить как долю от определенного числа в процентах, так и число от общей суммы по проценту. Excel можно использовать для работы с процентами как обычный калькулятор, но также с его помощью легко и автоматизировать работу по вычислению процентов в таблицах.

Опишите, что у вас не получилось.
Наши специалисты постараются ответить максимально быстро.

Средняя арифметическая взвешенная

Рассмотрим следующую простую задачу. Между пунктами А и Б расстояние S, которые автомобиль проехал со скоростью 50 км/ч. В обратную сторону – со скоростью 100 км/ч.

Какова была средняя скорость движения из А в Б и обратно? Большинство людей ответят 75 км/ч (среднее из 50 и 100) и это неправильный ответ. Средняя скорость – это все пройденное расстояние, деленное на все потраченное время. В нашем случае все расстояние – это S + S = 2*S (туда и обратно), все время складывается из времени из А в Б и из Б в А. Зная скорость и расстояние, время найти элементарно. Исходная формула для нахождения средней скорости имеет вид:

Теперь преобразуем формулу до удобного вида.

Подставим значения.

Правильный ответ: средняя скорость автомобиля составила 66,7 км/ч.

Средняя скорость – это на самом деле среднее расстояние в единицу времени. Поэтому для расчета средней скорости (среднего расстояния в единицу времени) используется средняя арифметическая взвешенная по следующей формуле.

где x – анализируемый показатель; f – вес.

Аналогичным образом по формуле средневзвешенной средней рассчитывается средняя цена (средняя стоимость на единицу продукции), средний процент и т.д. То есть если средняя считается по другим усредненным значениям, нужно применить среднюю взвешенную, а не простую.