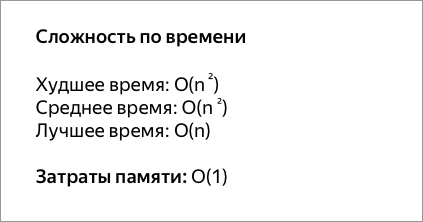Алгоритм сортировки

Примеры реализации

C++

Простой алгоритм.

 1 void counting_sort(int* vec, unsigned int len, int min, int max)
 2 {
 3 	assert(min <= max);
 4 	assert(vec != NULL);
 5 
 6 	int * cnt = new intmax-min+1];
 7 
 8 	for (int i = min; i <= max; ++i)
 9 		cnti - min = ;
10 
11 	for (int i = ; i < len; ++i)
12 		++cntveci - min];
13 
14 	for (int i = min; i <= max; ++i)
15 		for(int j = cnti - min]; j--;)
16 			*vec++ = i;
17 
18 	delete [] cnt;
19 }

Компонентный Паскаль

Простой алгоритм.

PROCEDURE CountingSort (VAR a ARRAY OF INTEGER; min, max INTEGER);
  VAR
    i, j, c INTEGER;
    b POINTER TO ARRAY OF INTEGER;
BEGIN
  ASSERT(min <= max);
  NEW(b, max - min + 1);
  FOR i :=  TO LEN(a) - 1 DO INC(bai - min]) END;
  i := ;
  FOR j := min TO max DO
    c := bj - min;
    WHILE c >  DO
      ai := j; INC(i); DEC(c)
    END
  END
END CountingSort;

Реализация на PascalABC.Net

 1 const
 2   n = 5;
 3   m = 12; // Максимальное значение всех элементов в a.
 4 
 5 var
 6   a array ..n of integer;
 7   c array ..m of integer; // Вспомогательный массив.
 8   i, j integer; // Переменные, играющие роль индексов.
 9   kinteger;
10 begin
11   for i :=  to n do 
12     ai := Random(m); // Заполнение массива.
13   for i :=  to m do
14     ci := ;  //Обнуление вспомогательного массива
15   for i :=  to n do 
16     cai]] := cai]] + 1;
17   j := ; // Обнуление j. Хороший стиль программирования обнулять все переменные изначально, поскольку не все компиляторы это делают автоматически.
18   for i :=  to m do
19     for  k := 1 to ci do 
20     begin 
21         aj := i; 
22         Inc(j); 
23     end;
24   Writeln(a);
25 end.

Алгоритм Кана (1962)

Один из первых алгоритмов, и наиболее приспособленный к исполнению вручную.

Пусть дан бесконтурный ориентированный простой граф G=(V,E){\displaystyle G=(V,E)}. Через A(v),v∈V{\displaystyle A(v),v\in V} обозначим множество вершин таких, что u∈A(v)⇔(u,v)∈E{\displaystyle u\in A(v)\Leftrightarrow (u,v)\in E}. То есть, A(v){\displaystyle A(v)} — множество всех вершин, из которых есть дуга в вершину v{\displaystyle v}. Пусть P{\displaystyle P} — искомая последовательность вершин.

пока |P|<|V|{\displaystyle |P|<|V|}
  выбрать любую вершину v{\displaystyle v} такую, что A(v)=∅{\displaystyle A(v)=\varnothing } и v∉P{\displaystyle v\notin P}
  P←P,v{\displaystyle P\gets P,v}
  удалить v{\displaystyle v} из всех A(u),u≠v{\displaystyle A(u),u\neq v}

Наличие хотя бы одного контура в графе приведёт к тому, что на определённой итерации цикла не удастся выбрать новую вершину v{\displaystyle v}.

Пример работы алгоритма

Пусть задан граф G=({a,b,c,d,e},{(a,b),(a,c),(a,d),(a,e),(b,d),(c,d),(c,e),(d,e)}){\displaystyle G={\Bigl (}{\bigl \{}a,b,c,d,e{\bigr \}},{\bigl \{}(a,b),(a,c),(a,d),(a,e),(b,d),(c,d),(c,e),(d,e){\bigr \}}{\Bigr )}}. В таком случае алгоритм выполнится следующим образом:

шаг	v{\displaystyle v}	A(a){\displaystyle A(a)}	A(b){\displaystyle A(b)}	A(c){\displaystyle A(c)}	A(d){\displaystyle A(d)}	A(e){\displaystyle A(e)}	P{\displaystyle P}
−{\displaystyle -}	∅{\displaystyle \varnothing }	a{\displaystyle a}	a{\displaystyle a}	a,b,c{\displaystyle a,b,c}	a,c,d{\displaystyle a,c,d}	∅{\displaystyle \varnothing }
1	a{\displaystyle a}	∅{\displaystyle \varnothing }	∅{\displaystyle \varnothing }	∅{\displaystyle \varnothing }	b,c{\displaystyle b,c}	c,d{\displaystyle c,d}	a{\displaystyle a}
2	c{\displaystyle c}	∅{\displaystyle \varnothing }	∅{\displaystyle \varnothing }	∅{\displaystyle \varnothing }	b{\displaystyle b}	d{\displaystyle d}	a,c{\displaystyle a,c}
3	b{\displaystyle b}	∅{\displaystyle \varnothing }	∅{\displaystyle \varnothing }	∅{\displaystyle \varnothing }	∅{\displaystyle \varnothing }	d{\displaystyle d}	a,c,b{\displaystyle a,c,b}
4	d{\displaystyle d}	∅{\displaystyle \varnothing }	∅{\displaystyle \varnothing }	∅{\displaystyle \varnothing }	∅{\displaystyle \varnothing }	∅{\displaystyle \varnothing }	a,c,b,d{\displaystyle a,c,b,d}
5	e{\displaystyle e}	∅{\displaystyle \varnothing }	∅{\displaystyle \varnothing }	∅{\displaystyle \varnothing }	∅{\displaystyle \varnothing }	∅{\displaystyle \varnothing }	a,c,b,d,e{\displaystyle a,c,b,d,e}

На втором шаге вместо c{\displaystyle c} может быть выбрана вершина b{\displaystyle b}, поскольку порядок между b{\displaystyle b} и c{\displaystyle c} не задан.

Сложность[править]

Сложность LSD-сортировкиправить

Пусть — количество разрядов, — количество объектов, которые нужно отсортировать, — время работы устойчивой сортировки. Цифровая сортировка выполняет итераций, на каждой из которой выполняется устойчивая сортировка и не более других операций. Следовательно время работы цифровой сортировки — .

Рассмотрим отдельно случай сортировки чисел. Пусть в качестве аргумента сортировке передается массив, в котором содержатся -значных чисел, и каждая цифра может принимать значения от до . Тогда цифровая сортировка позволяет отсортировать данный массив за время , если устойчивая сортировка имеет время работы . Если небольшое, то оптимально выбирать в качестве устойчивой сортировки сортировку подсчетом.

Если количество разрядов — константа, а , то сложность цифровой сортировки составляет , то есть она линейно зависит от количества сортируемых чисел.

Сложность MSD-сортировкиправить

Пусть значения разрядов меньше , а количество разрядов — . При сортировке массива из одинаковых элементов MSD-сортировкой на каждом шаге все элементы будут находится в неубывающей по размеру корзине, а так как цикл идет по всем элементам массива, то получим, что время работы MSD-сортировки оценивается величиной , причем это время нельзя улучшить. Хорошим случаем для данной сортировки будет массив, при котором на каждом шаге каждая корзина будет делиться на частей. Как только размер корзины станет равен , сортировка перестанет рекурсивно запускаться в этой корзине. Таким образом, асимптотика будет . Это хорошо тем, что не зависит от числа разрядов.

Существует также модификация MSD-сортировки, при которой рекурсивный процесс останавливается при небольших размерах текущего кармана, и вызывается более быстрая сортировка, основанная на сравнениях (например, сортировка вставками).

Остаточный правильный вариант алгоритма:

Сигнатура такая же как и в предыдущем варианте

Но следует заметить, что данный вариант предполагает первым параметром указатель, на котором можно вызвать операцию delete[] (почему — мы увидим далее). То-есть когда мы выделяли память, мы именно для этого указателя присваивали адрес начала массива.

Предварительная подготовка

В данном примере так называемый «коэффициент навёрстывания» (catch up coefficient) — это просто константа со значением 8. Она показывает сколько максимум элементов мы попытаемся пройти, чтобы вставить новый «недо-максимум» или «недо-минимум» на своё место.

Теперь, самое главное — правильная выборка элементов из исходного массива

Цикл начинается с localCatchUp (потому что предыдущие элементы уже попали в нашу выборку как значения от которых мы будем отталкиваться). И проходит до конца. Так что после в конце концов все элементы распределятся либо в массив выборки либо в один из массивов недо-выборки.

Для проверки, можем ли мы вставить элемент в выборку, мы просто будем проверять больше (или равен) ли он элементу на 8 позиций левее (right − localCatchUp). Если это так, то мы просто одним проходом по этим элементам вставляем его на нужную позицию. Это было для правой стороны, то-есть для максимальных элементов. Таким же образом делаем с обратной стороны для минимальных. Если не удалось вставить его ни в одну сторону выборки значит кидаем его в один из rest-массивов.

Цикл будет выглядеть примерно так:

Опять же, что здесь происходит? Сначала пытаемся пихнуть элемент в максимумы. Не получается? — Если возможно, кидаем его в минимумы. При невозможности и это сделать — кладём его в restFirst или restSecond.

Самое сложное уже позади. Теперь после цикла у нас есть отсортированный массив с выборкой (элементы начинаются с индекса и оканчиваются в ), а также массивы restFirst и restSecond длиной restFirstLen и restSecondLen соответственно.

Теперь запускаем нашу функцию сортировки рекурсивно для массивов restFirst и restSecond

Для понимания того как оно всё отработает, сначала нужно посмотреть код до конца. Пока что нужно просто поверить что после рекурсивных вызовов массивы restFirst и restSecond будут отсортированными.

И, наконец, нам нужно слить 3 массива в результирующий и назначить его указателю arr.

Можно было бы сначала слить restFirst + restSecond в какой-нибудь массив restFull, а потом уже производить слияние selection + restFull. Но данный алгоритм обладает таким свойством, что скорее всего массив selection будет содержать намного меньше элементов, чем любой из rest-массивов. Припустим в selection содержится 100 элементов, в restFirst — 990, а в restSecond — 1010. Тогда для создания restFull массива нужно произвести 990 + 1010 = 2000 операций копирования. После чего для слияния с selection — ещё 2000 + 100 копирований. Итого при таком подходе всего копирований будет 2000 + 2100 = 4100.

Давайте применим здесь оптимизацию. Сначала сливаем selection и restFirst в массив selection. Операций копирования: 100 + 990 = 1090. Далее сливаем массивы selection и restSecond на что потратим ещё 1090 + 1010 = 2100 копирований. Суммарно выйдет 2100 + 1090 = 3190, что почти на четверть меньше, нежели при предыдущем подходе.

Выводы

Как видим, алгоритм работает, и работает хорошо. По крайней мере всё чего мы хотели, было достигнуто. На счёт стабильности, не уверен, не проверял. Можете сами проверить. Но по-идее она должна достигаться очень легко. Просто в некоторых местах вместо знака > поставить ≥ или что-то того.

Анализ

В первых двух алгоритмах первые два цикла работают за Θ(k){\displaystyle \Theta (k)} и Θ(n){\displaystyle \Theta (n)}, соответственно; двойной цикл за Θ(n+k){\displaystyle \Theta (n+k)}. В третьем алгоритме циклы занимают Θ(k){\displaystyle \Theta (k)}, Θ(n){\displaystyle \Theta (n)}, Θ(k){\displaystyle \Theta (k)} и Θ(n){\displaystyle \Theta (n)}, соответственно. Итого все три алгоритма имеют линейную временную трудоёмкость Θ(n+k){\displaystyle \Theta (n+k)}. Используемая память в первых двух алгоритмах равна Θ(k){\displaystyle \Theta (k)}, а в третьем Θ(n+k){\displaystyle \Theta (n+k)}.

Алгоритм Тарьяна (1976)

На компьютере топологическую сортировку можно выполнить за O(n) времени и памяти, отсортировав вершины по времени выхода в поиске в глубину. А именно:

Изначально все вершины «белые». Из каждой вершины проводим обход в глубину.

• При входе в вершину делаем её «серой», при выходе — «чёрной» и одновременно заносим в окончательный список.
• Если вдруг вошли в серую вершину — найден цикл, топологическая сортировка невозможна.

Пример

Пример будет на том же графе, однако порядок, в котором выбираем вершины для обхода — c, d, e, a, b.

Шаг	Текущая	Белые	Стек (серые)	Выход (чёрные)
—	a, b, c, d, e	—	—
1	c	a, b, d, e	c	—
2	d	a, b, e	c, d	—
3	e	a, b	c, d, e	—
4	d	a, b	c, d	e
5	c	a, b	c	d, e
6	—	a, b	—	c, d, e
7	d	a, b	—	c, d, e
8	e	a, b	—	c, d, e
9	a	b	a	c, d, e
10	b	—	a, b	c, d, e
11	a	—	a	b, c, d, e
12	—	—	—	a, b, c, d, e
13	b	—	—	a, b, c, d, e

Сортировка строк

Одним из наиболее частых приложений алгоритмов сортировки является сортировка строк. Обычно она производится так: сначала множество строк сортируется по первому символу каждой строки, затем каждое подмножество строк, имеющих одинаковый первый символ, сортируется по второму символу, и так до тех пор, пока все строки не будут упорядочены. При этом отсутствующий символ (при сравнении строки длины N со строкой длины N+1) считается меньше любого символа.

Применение данного метода к строкам, представляющим собой числа в естественной записи, выдаёт контринтуитивные результаты: например, «9» оказывается больше, чем «11», так как первый символ первой строки имеет бо́льшее значение, чем первый символ второй. Для исправления этой проблемы алгоритм сортировки может преобразовывать сортируемые строки в числа и сортировать их как числа. Такой алгоритм называется «числовой сортировкой», а описанный ранее — «строковой сортировкой».

Устойчивый алгоритм

В этом варианте помимо входного массива потребуется два вспомогательных массива — для счётчика и для отсортированного массива. Сначала следует заполнить массив нулями, и для каждого увеличить на 1. Далее подсчитывается количество элементов меньших или равных k−1{\displaystyle k-1}. Для этого каждый , начиная с , увеличивают на . Таким образом в последней ячейке будет находиться количество элементов от {\displaystyle 0} до k−1{\displaystyle k-1} существующих во входном массиве. На последнем шаге алгоритма читается входной массив с конца, значение уменьшается на 1 и в каждый записывается . Алгоритм устойчив.

StableCountingSort
    for i = 0 to k - 1
        C = 0;
    for i = 0 to n - 1
        C] = C] + 1;
    for j = 1 to k - 1
        C = C + C;
    for i = n - 1 to 0
        C] = C] - 1;
        B]] = A;

Свойства и классификация

• Устойчивость (англ. stability) — устойчивая сортировка не меняет взаимного расположения элементов с одинаковыми ключами.
• Естественность поведения — эффективность метода при обработке уже упорядоченных или частично упорядоченных данных. Алгоритм ведёт себя естественно, если учитывает эту характеристику входной последовательности и работает лучше.
• Использование операции сравнения. Алгоритмы, использующие для сортировки сравнение элементов между собой, называются основанными на сравнениях. Минимальная трудоемкость худшего случая для этих алгоритмов составляет O{\displaystyle O}(n⋅log⁡n{\displaystyle n\cdot \log n}), но они отличаются гибкостью применения. Для специальных случаев (типов данных) существуют более эффективные алгоритмы.

Ещё одним важным свойством алгоритма является его сфера применения. Здесь основных типов упорядочения два:

• Внутренняя сортировка

  В современных архитектурах персональных компьютеров широко применяется подкачка и кэширование памяти. Алгоритм сортировки должен хорошо сочетаться с применяемыми алгоритмами кэширования и подкачки.

  оперирует массивами, целиком помещающимися в оперативной памяти с произвольным доступом к любой ячейке. Данные обычно упорядочиваются на том же месте без дополнительных затрат.

• Внешняя сортировка оперирует запоминающими устройствами большого объёма, но не с произвольным доступом, а последовательным (упорядочение файлов), то есть в данный момент «виден» только один элемент, а затраты на перемотку по сравнению с памятью неоправданно велики. Это накладывает некоторые дополнительные ограничения на алгоритм и приводит к специальным методам упорядочения, обычно использующим дополнительное дисковое пространство. Кроме того, доступ к данным во внешней памяти производится намного медленнее, чем операции с оперативной памятью.
  • Доступ к носителю осуществляется последовательным образом: в каждый момент времени можно считать или записать только элемент, следующий за текущим.
  • Объём данных не позволяет им разместиться в ОЗУ.

Также алгоритмы классифицируются по:

• потребности в дополнительной памяти или её отсутствию
• потребности в знаниях о структуре данных, выходящих за рамки операции сравнения, или отсутствию таковой

Не спеша, эффективно и правильно – путь разработки. Часть 2. Теория

Черновой вариант книги Никиты Зайцева, a.k.a.WildHare. Разработкой на платформе 1С автор занимается с 1996-го года, специализация — большие и по-хорошему страшные системы. Квалификация “Эксперт”, несколько успешных проектов класса “сверхтяжелая”. Успешные проекты ЦКТП. Четыре года работал в самой “1С”, из них два с половиной архитектором и ведущим разработчиком облачной Технологии 1cFresh. Ну — и так далее. Не хвастовства ради, а понимания для. Текст написан не фантазером-теоретиком, а экспертом, у которого за плечами почти двадцать три года инженерной практики на больших проектах.

Анализ

В первых двух алгоритмах первые два цикла работают за Θ(k){\displaystyle \Theta (k)} и Θ(n){\displaystyle \Theta (n)}, соответственно; двойной цикл за Θ(n+k){\displaystyle \Theta (n+k)}. В третьем алгоритме циклы занимают Θ(k){\displaystyle \Theta (k)}, Θ(n){\displaystyle \Theta (n)}, Θ(k){\displaystyle \Theta (k)} и Θ(n){\displaystyle \Theta (n)}, соответственно. Итого все три алгоритма имеют линейную временную трудоёмкость Θ(n+k){\displaystyle \Theta (n+k)}. Используемая память в первых двух алгоритмах равна Θ(k){\displaystyle \Theta (k)}, а в третьем Θ(n+k){\displaystyle \Theta (n+k)}.

Алгоритм[править]

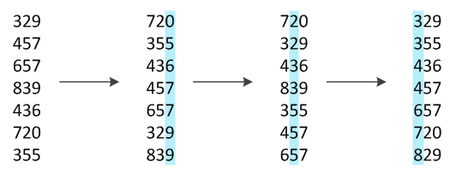
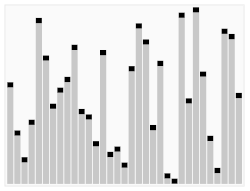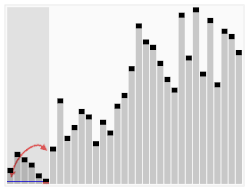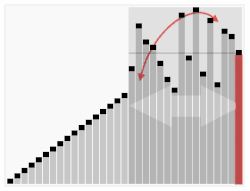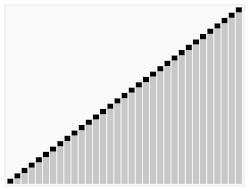
Пример цифровой сортировки трехзначных чисел, начиная с младших разрядов

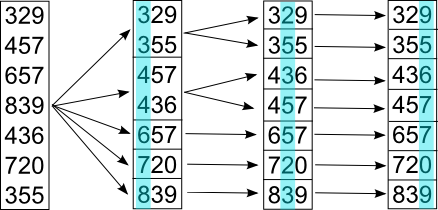
Пример цифровой сортировки трехзначных чисел, начиная со старших разрядов

Имеем множество последовательностей одинаковой длины, состоящих из элементов, на которых задано отношение линейного порядка. Требуется отсортировать эти последовательности в лексикографическом порядке.

По аналогии с разрядами чисел будем называть элементы, из которых состоят сортируемые объекты, разрядами. Сам алгоритм состоит в последовательной сортировке объектов какой-либо устойчивой сортировкой по каждому разряду, в порядке от младшего разряда к старшему, после чего последовательности будут расположены в требуемом порядке.

Примерами объектов, которые удобно разбивать на разряды и сортировать по ним, являются числа и строки.

Для чисел уже существует понятие разряда, поэтому будем представлять числа как последовательности разрядов. Конечно, в разных системах счисления разряды одного и того же числа отличаются, поэтому перед сортировкой представим числа в удобной для нас системе счисления.

Строки представляют из себя последовательности символов, поэтому в качестве разрядов в данном случае выступают отдельные символы, сравнение которых обычно происходит по соответствующим им кодам из таблицы кодировок. Для такого разбиения самый младший разряд — последний символ строки.

Для вышеперечисленных объектов наиболее часто в качестве устойчивой сортировки применяют сортировку подсчетом.

Такой подход к алгоритму называют LSD-сортировкой (Least Significant Digit radix sort). Существует модификация алгоритма цифровой сортировки, анализирующая значения разрядов, начиная слева, с наиболее значащих разрядов. Данный алгоритм известен, как MSD-сортировка (Most Significant Digit radix sort).

Корректность алгоритма LSD-сортировкиправить

Докажем, что данный алгоритм работает верно, используя метод математической индукции по номеру разряда. Пусть — количество разрядов в сортируемых объектах.

База: . Очевидно, что алгоритм работает верно, потому что в таком случае мы просто сортируем младшие разряды какой-то заранее выбранной устойчивой сортировкой.

Переход: Пусть для алгоритм правильно отсортировал последовательности по младшим разрядам. Покажем, что в таком случае, при сортировке по -му разряду, последовательности также будут отсортированы в правильном порядке.

Вспомогательная сортировка разобьет все объекты на группы, в которых -й разряд объектов одинаковый. Рассмотрим такие группы. Для сортировки по отдельным разрядам мы используем устойчивую сортировку, следовательно порядок объектов с одинаковым -м разрядом не изменился. Но по предположению индукции по предыдущим разрядам последовательности были отсортированы правильно, и поэтому в каждой такой группе они будут отсортированы верно. Также верно, что сами группы находятся в правильном относительно друг друга порядке, а, следовательно, и все объекты отсортированы правильно по -м младшим разрядам.

Реализация на VBA

Sub VSort()
    For i = 1 To 10 Step 1
        For j = i + 1 To 10 Step 1
            If ActiveSheet.Cells(i, 1) > ActiveSheet.Cells(j, 1) Then
                ActiveSheet.Cells(i, 1) = ActiveSheet.Cells(i, 1) + ActiveSheet.Cells(j, 1)
                ActiveSheet.Cells(j, 1) = ActiveSheet.Cells(i, 1) - ActiveSheet.Cells(j, 1)
                ActiveSheet.Cells(i, 1) = ActiveSheet.Cells(i, 1) - ActiveSheet.Cells(j, 1)
            End If
        Next j
    Next i
End Sub

' С использованием переменной c.
Sub VSort()
    For i = 1 To 10 Step 1
        For j = i + 1 To 10 Step 1
            If ActiveSheet.Cells(i, 1) > ActiveSheet.Cells(j, 1) Then
                с = ActiveSheet.Cells(i, 1)
                ActiveSheet.Cells(i, 1) = ActiveSheet.Cells(j, 1)
                ActiveSheet.Cells(j, 1) = c
            End If
        Next j
    Next i
End Sub

Здесь сортируются ячейки напрямую. ActiveSheet.Cells(i, 1) — обращение к ячейке с (1, i)

Обратите внимание, что координаты ячеек в VBA задаются как (y, x) — номер колонки и номер ряда, в котором расположена ячейка. Также помните, что ячейки индексируются с 1.

Оценка алгоритма сортировки

Алгоритмы сортировки оцениваются по скорости выполнения и эффективности использования памяти:

• Время — основной параметр, характеризующий быстродействие алгоритма. Называется также вычислительной сложностью. Для упорядочения важны худшее, среднее и лучшее поведение алгоритма в терминах мощности входного множества A. Если на вход алгоритму подаётся множество A, то обозначим n = |A|. Для типичного алгоритма хорошее поведение — это O(n log n) и плохое поведение — это O(n2). Идеальное поведение для упорядочения — O(n). Алгоритмы сортировки, использующие только абстрактную операцию сравнения ключей всегда нуждаются по меньшей мере в сравнениях. Тем не менее, существует алгоритм сортировки Хана (Yijie Han) с вычислительной сложностью O(n log log n log log log n), использующий тот факт, что пространство ключей ограничено (он чрезвычайно сложен, а за О-обозначением скрывается весьма большой коэффициент, что делает невозможным его применение в повседневной практике). Также существует понятие сортирующих сетей. Предполагая, что можно одновременно (например, при параллельном вычислении) проводить несколько сравнений, можно отсортировать n чисел за O(log2n) операций. При этом число n должно быть заранее известно;
• Память — ряд алгоритмов требует выделения дополнительной памяти под временное хранение данных. Как правило, эти алгоритмы требуют O(log n) памяти. При оценке не учитывается место, которое занимает исходный массив и независящие от входной последовательности затраты, например, на хранение кода программы (так как всё это потребляет O(1)). Алгоритмы сортировки, не потребляющие дополнительной памяти, относят к сортировкам на месте.

Оптимальность O(nlog⁡(n)){\displaystyle O(n\log(n))}

Задача сортировки в общем случае предполагает, что единственной обязательно наличествующей операцией для элементов является сравнение. Это делает невозможным реализацию алгоритма Хана, использующего арифметические действия. Рассмотрим схему алгоритма, когда единственным возможным действием над элементами является их сравнение.

Пусть по ходу работы алгоритмом производится k{\displaystyle k} сравнений. Ответом на сравнение двух элементов a{\displaystyle a} и b{\displaystyle b} может быть один из двух вариантов (a<b{\displaystyle a<b} или a>b{\displaystyle a>b}). Значит, всего возможно 2k{\displaystyle 2^{k}} вариантов комбинаций ответов на k{\displaystyle k} вопросов.

Количество перестановок из n{\displaystyle n} элементов равно n!{\displaystyle n!}. Для того, чтобы можно было провести из множества ответов на сравнения на множество перестановок, количество сравнений должно быть не меньше, чем log2⁡n!{\displaystyle \log _{2}{n!}} (это обеспечивается тем, что сравнение — единственная разрешённая операция).

Прологарифмировав формулу Стирлинга, можно обнаружить, что log2⁡n!=log2⁡(2πn(ne)n)=log2⁡2πn+nlog2⁡n−nlog2⁡e∼nlog2⁡n=O(nlog⁡n){\displaystyle \log _{2}{n!}=\log _{2}{\left({\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}\right)}=\log _{2}{\sqrt {2\pi n}}+n\log _{2}{n}-n\log _{2}{e}\sim n\log _{2}{n}=O(n\log {n})}

Достоинства и недостатки

Достоинства:

• Один из самых быстродействующих (на практике) из алгоритмов внутренней сортировки общего назначения.
• Прост в реализации.
• Требует лишь O(log⁡n){\displaystyle O(\log n)} дополнительной памяти для своей работы. (Не улучшенный рекурсивный алгоритм в худшем случае O(n){\displaystyle O(n)} памяти)
• Хорошо сочетается с механизмами кэширования и виртуальной памяти.
• Допускает естественное распараллеливание (сортировка выделенных подмассивов в параллельно выполняющихся подпроцессах).
• Допускает эффективную модификацию для сортировки по нескольким ключам (в частности — алгоритм Седжвика для сортировки строк): благодаря тому, что в процессе разделения автоматически выделяется отрезок элементов, равных опорному, этот отрезок можно сразу же сортировать по следующему ключу.
• Работает на связных списках и других структурах с последовательным доступом, допускающих эффективный проход как от начала к концу, так и от конца к началу.

Недостатки:

• Сильно деградирует по скорости (до O(n2){\displaystyle O(n^{2})}) в худшем или близком к нему случае, что может случиться при неудачных входных данных.
• Прямая реализация в виде функции с двумя рекурсивными вызовами может привести к ошибке переполнения стека, так как в худшем случае ей может потребоваться сделать O(n){\displaystyle O(n)} вложенных рекурсивных вызовов.
• Неустойчив.

Примечания

1. Кормен. Сортировка подсчетом // Алгоритмы: Вводный курс. — Вильямс, 2014. — С. 71. — 208 с. — ISBN 978-5-8459-1868-0.
2. Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L. & Stein, Clifford (2001), «8.2 Counting Sort», Introduction to Algorithms (2nd ed.), MIT Press and McGraw-Hill, сс. 168–170, ISBN 0-262-03293-7.
3. Кнут. Сортировка посредством подсчёта // Искусство программирования. — Т. 3. — С. 77.
4. Knuth, D. E. (1998), «Section 5.2, Sorting by counting», The Art of Computer Programming, Volume 3: Sorting and Searching (2nd ed.), Addison-Wesley, сс. 75-80, ISBN 0-201-89685-0.

Формулировка задачи

Пусть требуется упорядочить N элементов: R1,R2,…,Rn{\displaystyle R_{1},R_{2},\dots ,R_{n}}. Каждый элемент представляет из себя запись Rj{\displaystyle R_{j}}, содержащую некоторую информацию и ключ Kj{\displaystyle K_{j}}, управляющий процессом сортировки. На множестве ключей определено отношение порядка «<» так, чтобы для любых трёх значений ключей a,b,c{\displaystyle a,b,c} выполнялись следующие условия:

• : либо a<b{\displaystyle a<b}, либо a>b{\displaystyle a>b}, либо a=b{\displaystyle a=b};
• закон транзитивности: если a<b{\displaystyle a<b} и b<c{\displaystyle b<c}, то a<c{\displaystyle a<c}.

Данные условия определяют математическое понятие линейного или совершенного упорядочения, а удовлетворяющие им множества поддаются сортировке большинством методов.

Задачей сортировки является нахождение такой перестановки записей p(1)p(2)…p(n){\displaystyle p(1)p(2)\dots p(n)} с индексами {1,2,…,N}{\displaystyle \{1,2,\dots ,N\}}, после которой ключи расположились бы в порядке неубывания:

Kp(1)⩽Kp(2)⩽⋯⩽Kp(n){\displaystyle K_{p(1)}\leqslant K_{p(2)}\leqslant \dots \leqslant K_{p(n)}}

Сортировка называется устойчивой, если не меняет взаимного расположения элементов с одинаковыми ключами:

p(i)<p(j){\displaystyle p(i)<p(j)} для любых Kp(i)=Kp(j){\displaystyle K_{p(i)}=K_{p(j)}} и i<j{\displaystyle i<j}.

Методы сортировки можно разделить на внутренние и внешние. Внутренняя сортировка используется для данных, помещающихся в оперативную память, за счёт чего является более гибкой в плане структур данных. Внешняя сортировка применяется, когда данные в оперативную память не помещаются, и ориентирована на достижение результата в условиях ограниченных ресурсов.

Примечания

1. Кормен. Сортировка подсчетом // Алгоритмы: Вводный курс. — Вильямс, 2014. — С. 71. — 208 с. — ISBN 978-5-8459-1868-0.
2. Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L. & Stein, Clifford (2001), «8.2 Counting Sort», Introduction to Algorithms (2nd ed.), MIT Press and McGraw-Hill, сс. 168–170, ISBN 0-262-03293-7.
3. Кнут. Сортировка посредством подсчёта // Искусство программирования. — Т. 3. — С. 77.
4. Knuth, D. E. (1998), «Section 5.2, Sorting by counting», The Art of Computer Programming, Volume 3: Sorting and Searching (2nd ed.), Addison-Wesley, сс. 75-80, ISBN 0-201-89685-0.