Скалярное произведение

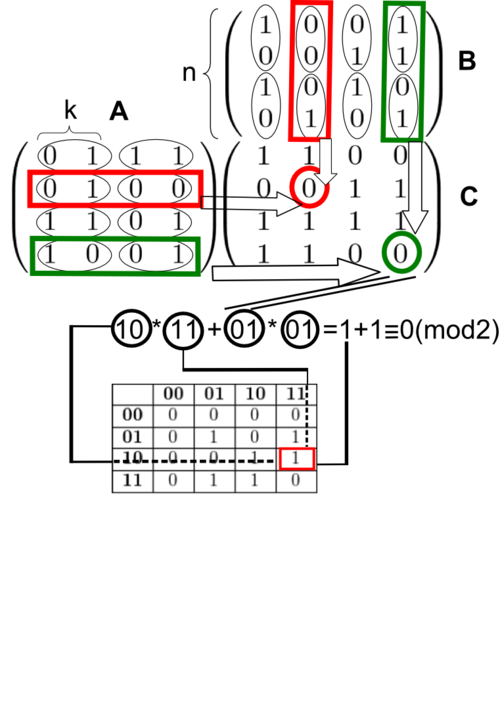
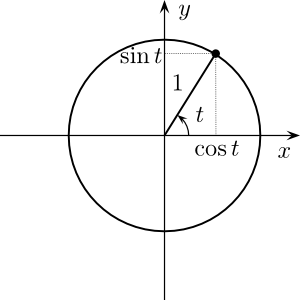
Примеры нахождения скалярного произведения и направления векторов

Зная все необходимые формулы, легко найти не только скалярное произведение вектора, но и длину сторон, косинус угла, площадь, модуль вектора и т. д. Посмотрите, как решаются задачи при помощи основных формул, которые рассмотрены выше.

Пример 1

Задача

Найти скалярное произведение векторов:

=
и
=
.

Решение

Исходя из формулы (3) у нас получается:

x
=

Следующий пример тоже на нахождение скалярного произведения, но решение будет немного другим, хоть и по той же формуле, что и первый пример.

Пример 2

Задача

Даны точки

Найти скалярное произведение векторов
.

Решение

Сначала найдём векторы:

Согласно формуле (3) получается:

Часто попадаются и примеры, где нужно найти площадь, длину сторон, косинус и синус угла. Рассмотрим на примере:

Пример 3

Задача

Даны точки

Для параллелограмма, построенного на векторах

и
вычислить:

1. длину сторон, то есть
   и
   ;
2. косинус и синус угла;
3. площадь.

Решение

Находим векторы

тогда:

1)

=
,

2)

=
=
=
=
(угол
– тупой),
=
=
=

3)

=
=
*
*
=

Пример 4

Задача

Найти модуль вектора  

=
, если  
,
,
, ^
=

Решение

Согласно формуле (4)

=
. Находим
=
=
=

+
=
, тогда
.

Пример 5

Задача

Найти направляющие косинусы вектора

и значения выражения
.

Решение

=

=
=
;
=
;
=
.

=
+
+
=
.

Проверим, что для произвольного вектора

=
.

Направляющие косинусы вектора

полностью определяют направление вектора и они есть координатами единичного вектора
, что совпадает за направлением с
, то есть:

=
=
.

Ответ

.

Примеры

• В трёхмерном вещественном векторном пространстве векторов x=(x1,x2,x3){\displaystyle \mathbf {x} =(x_{1},x_{2},x_{3})} введение скалярного произведения по формуле ⟨x,y⟩=x1y1+x2y2+x3y3{\displaystyle \langle \mathbf {x} ,\mathbf {y} \rangle =x_{1}y_{1}+x_{2}y_{2}+x_{3}y_{3}} превращает это пространство в евклидово пространство

  В любом евклидовом пространстве (размерности n) всегда можно выбратьортонормированный базис e1,e2,…,en{\displaystyle {\mathbf {e} _{1},\mathbf {e} _{2},\dots ,\mathbf {e} _{n}}}

  . Аналогичное утверждение верно для евклидова пространства любой размерности (в сумму тогда входит количество членов, равное размерности пространства).

при разложении векторов по которому:

a=a1e1+a2e2+⋯+anen{\displaystyle \mathbf {a} =a_{1}\mathbf {e} _{1}+a_{2}\mathbf {e} _{2}+\dots +a_{n}\mathbf {e} _{n}},

b=b1e1+b2e2+⋯+bnen{\displaystyle \mathbf {b} =b_{1}\mathbf {e} _{1}+b_{2}\mathbf {e} _{2}+\dots +b_{n}\mathbf {e} _{n}} итд,

скалярное произведение будет выражаться формулой:

⟨a,b⟩=aTb=a1b1+a2b2+⋯+anbn{\displaystyle \langle \mathbf {a} ,\mathbf {b} \rangle =\mathbf {a} ^{T}\mathbf {b} =a_{1}b_{1}+a_{2}b_{2}+\dots +a_{n}b_{n}}.

• В таком же, но комплексном, пространстве, скалярное произведение вводится по несколько другой формуле: ⟨x→,y→⟩=x1y1¯+x2y2¯+x3y3¯{\displaystyle \langle {\vec {x}},{\vec {y}}\rangle =x_{1}{\overline {y_{1}}}+x_{2}{\overline {y_{2}}}+x_{3}{\overline {y_{3}}}}. Здесь через a¯{\displaystyle {\overline {a}}} обозначено число, комплексно сопряжённое к  a{\displaystyle \ a}. При таком определении скалярное произведение становится положительно определённым. Без комплексного сопряжения аксиома эрмитовости скалярного произведения была бы нарушена, а значит, вещественности определённой через него нормы вектора добиться бы не удалось, то есть норма в обычном смысле им бы не порождалась.
• В пространстве измеримых интегрируемых с квадратами на некоторой области Ω вещественных функций можно ввести положительно определённое скалярное произведение:

⟨f,g⟩=∫Ωf(x)g(x)dΩ{\displaystyle \langle f,g\rangle =\int \limits _{\Omega }f(x)g(x)d\Omega }

• В аналогичном случае для комплексных функций, если требуется эрмитовость (и положительная определённость) скалярного произведения, надо добавить комплексное сопряжение к f или g под интегралом.
• При использовании неортонормированных базисов скалярное произведение выражается через компоненты векторов с участием метрического тензора gij{\displaystyle g_{ij}}:

⟨a,b⟩=∑gijaibj{\displaystyle \langle \mathbf {a} ,\mathbf {b} \rangle =\sum g_{ij}a^{i}b^{j}}

при этом сама метрика (говоря точнее, её представление в данном базисе) так связана со скалярными произведениями базисных векторов fi {\displaystyle f_{i}\ }:

gij=⟨fi,fj⟩{\displaystyle g_{ij}=\langle \mathbf {f} _{i},\mathbf {f} _{j}\rangle }

• Аналогичные конструкции скалярного произведения можно вводить и на бесконечномерных пространствах, например, на пространствах функций:

⟨f,g⟩=∫(Ω1×Ω2)K(x1,x2)f(x1)g(x2)d(Ω1×Ω2){\displaystyle \langle f,g\rangle =\int \limits _{(\Omega _{1}\times \Omega _{2})}K(x_{1},x_{2})f(x_{1})g(x_{2})d(\Omega _{1}\times \Omega _{2})}

⟨f,g⟩=∫ΩK(x)f(x)g(x)dΩ{\displaystyle \langle f,g\rangle =\int \limits _{\Omega }K(x)f(x)g(x)d\Omega }

где К — положительно определённая, в первом случае симметричная относительно перестановки аргументов (при комплексных x — эрмитова) функция (если нужно иметь обычное симметричное положительно определённое скалярное произведение).

Угол между двумя векторами

Если
и- ненулевые векторы, то, принимая во
внимание определение вектора и п.4,
получим такое выражение для угламежду векторамиaиb:

.

Отсюда нетрудно получить условие
ортогональности (перпендикулярности)
двух векторов в координатной форме:

Механический смысл скалярного
произведения

Если
— сила, действующая на перемещенииS,
то работаAэтой силы
на указанном перемещении, как известно,
равна,
т.е.(рис. 3.5.1).

Рис. 3.5.1

Пример
1.Даны
три точки

Найти
и направляющие косинусы вектора.

Решение.а);

б)
;;

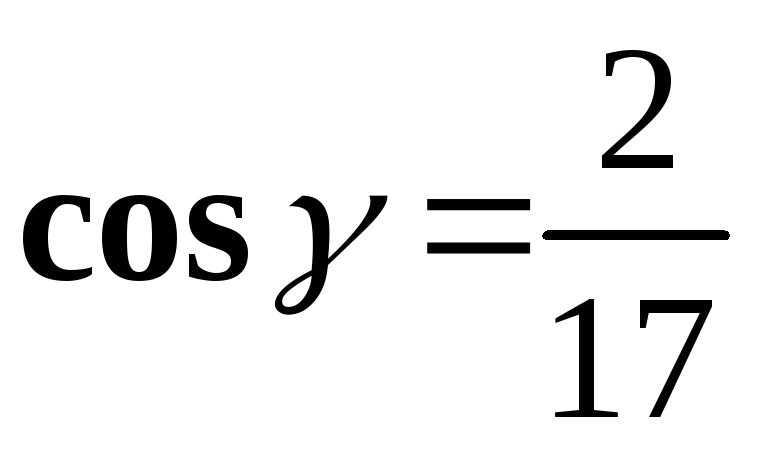
Пример
2. Дан
вектор,,.

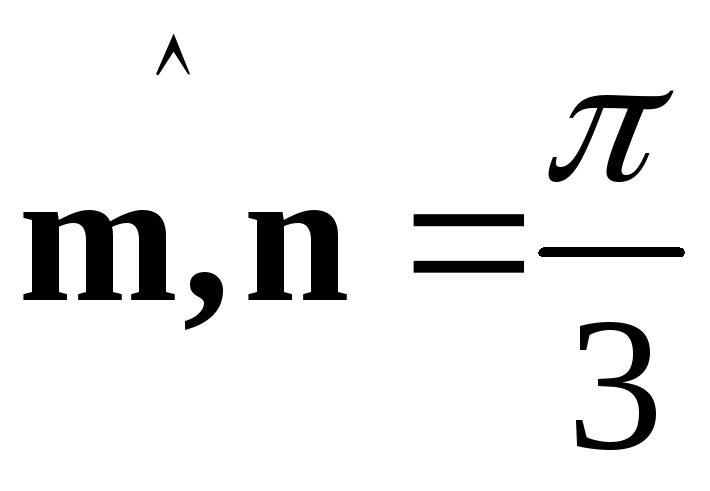Найти
длину вектора
.

Решение.Найдём скалярный квадрат вектора:.
Раскроем скобки, пользуясь свойствами
скалярного произведения:

.

Пример
3. При каком значениивектораиортогональны.

Решение.
Принимая во внимание условие
ортогональности двух векторов,
получим.
Следовательно

Свойства скалярного произведения.

Для любых векторов и справедливы следующие свойства скалярного произведения:

1. свойство коммутативности скалярного произведения ;
2. свойство дистрибутивности или ;
3. сочетательное свойство или , где — произвольное действительное число;
4. скалярный квадрат вектора всегда не отрицателен , причем тогда и только тогда, когда вектор нулевой.

Эти свойства очень легко обосновать, если отталкиваться от определения скалярного произведения в координатной форме и от свойств операций сложения и умножения действительных чисел.

Для примера докажем свойство коммутативности скалярного произведения . По определению и . В силу свойства коммутативности операции умножения действительных чисел, справедливо и , тогда . Следовательно, , что и требовалось доказать.

Аналогично доказываются остальные свойства скалярного произведения.

Следует отметить, что свойство дистрибутивности скалярного произведения справедливо для любого числа слагаемых, то есть, и 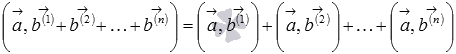, откуда следует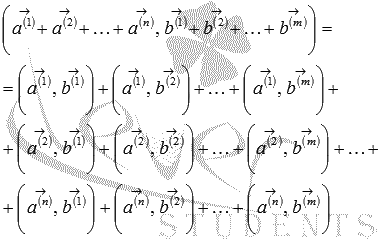

Выражение скалярного произведения вектора через координаты сомножителей. Теорема.

Пусть
в пространстве выбран ортонормированный
базис i,
j,
k.
Наложим на этот базис еще одно
дополнительное условие, а именно: из
конца вектора k
поворот от i
к j
по кратчайшему направлению должен быть
виден против часовой стрелки.

        Определение
10.27
  Упорядоченную тройку некомпланарных
векторов
будем
называть правой тройкой векторов, если
из конца третьего вектораповорот
от первого векторако
второму векторупо
кратчайшему направлению виден против
часовой стрелки. Если поворот виден по
часовой стрелке, то тройку называют
левой тройкой векторов.

Оказывается,
если векторы правой тройки изменять
непрерывно, но так, чтобы в любой момент
времени они были не компланарны, то в
любой момент такой деформации эта тройка
векторов будет правой тройкой. Аналогичным
свойством обладает и левая тройка
векторов.

Отметим
также, что определение векторного
произведения и правой (левой) тройки
вектров связаны с наличием в пространстве
«физических» объектов: часов,
человека и т. п. В абстрактном векторном
пространстве, где такие объекты
отсутствуют, определить, какая тройка —
правая, а какая — левая, невозможно.
Можно только все некомпланарные тройки
векторов разбить на два класса такие,
что при непрерывной деформации тройки
одного класса, при которой в любой момент
векторы тройки не компланарны, тройка
все время остается в своем классе.

Итак,
пусть в трехмерном пространстве задан
ортонормированный базис i,
j,
k,
векторы которого образуют правую тройку
векторов. Такой базис будем называть
правым.

Используя
определение векторного произведения,
легко проверить следующую таблицу
умножения
:

a \ b	i	j	k
i	k	— j
j	— k	i
k	j	— i

Предложение
10.24
  Пусть
,.
Тогда

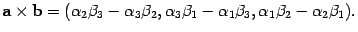
        Доказательство.    
По условию
,.
В силупредложений
10.20
и 10.21
получим

(10.5)

По
тем же правилам

По
таблице умножения
.
Аналогично находим,.
Подставив полученные результаты в
формулу (10.5),
получим

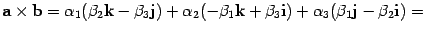
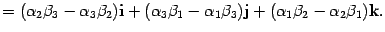
Запомнить
полученную формулу довольно тяжело.
Чтобы облегчить этот процесс, введем
еще два дополнительных объекта —
матрицу и определитель.

Матрицей
второго порядка будем называть таблицу
из четырех чисел, которая обозначается
,
матрицей третьего порядка называется
таблица из 9 чисел —

Определителем
матрицы второго порядка будем называть
число
.
Определитель второго порядка обозначается.

Определителем
матрицы третьего порядка будем называть
число

Сформулируем
словами правило вычисления определителя
третьего порядка.

Берем
первый элемент первой строки. Мысленно
вычеркиваем строку и столбец с этим
элементом. Умножаем этот элемент на
определитель, оставшийся после
вычеркивания. Затем пишем знак «-»
и берем второй элемент первой строки.
Мысленно вычеркиваем строку и столбец
с этим элементом и пишем оставшийся
определитель. Затем пишем знак «+»
и третий элемент первой строки. Снова
вычеркиваем строку и столбец с этим
элементом и пишем оставшийся определитель.

В
дальнейшем мы увидим, что столь сложно
введенное понятие определителя
оказывается очень полезным при решении
систем линейных уравнений, определении
линейной зависимости векторов и во
многих других задачах.

        Пример
10.1
  Вычисление определителей:

1)
.

2)

.
        

Формула
для определителя третьего порядка
позволяет кратко записать формулу для
вычисления векторного произведения.

Предложение
10.25
  Если
в правом ортонормированном базисе
i,j,k
заданы
координаты векторов
,,
то

(10.6)

        Доказательство.    
Достаточно лишь написать формулу
вычисления приведенного в теореме
определителя и сравнить ее с формулой
 предложения
10.24.
    

        Пример
10.2
  Пусть
,.
Тогда

Задача.
Пусть вершины треугольника расположены
в точках
,,.
Найдите площадь треугольника.

Решение.
По  предложению
10.22
.
Находим,,

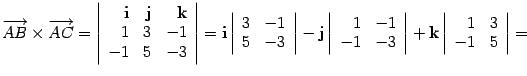
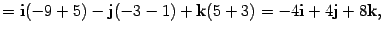
то
есть
.
Тогда

Ответ:
.

Задача.
Найдите такой единичный вектор e,
ортогональный векторам
,,
что тройка векторовa,b,e —
левая.

Решение.
Найдем вектор
:

Вектор
c
ортогонален векторам a
и b.
Найдем его длину:
.
Тогда—
единичный вектор, ортогональный векторамa,b.
Векторы a,b,c,
а следовательно, и векторы a,b,
.
образуют правую тройку векторов. Поэтому.

Ответ:
.

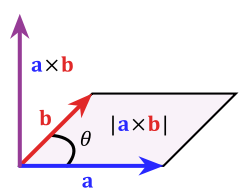
Определение векторного произведения

Определение.Векторным
произведением
ненулевых векторов

и
называется такой вектор,
который удовлетворяет трём условиям:

1.

,
т.е. длина вектора

численно равна площади параллелограмма,
построенного на этих векторах.

2.
Вектор

перпендикулярен плоскости, в которой
лежат векторы

и
.

3.
Тройка
,,— правая(рис.
2.6.1)

Если хотя бы один из векторов
инулевой, то по определению.
Заметим, что иногда векторное произведение
двух векторовиобозначается символом.

Рис. 2.6.1

Свойства
векторного произведения

1.

.

Это очевидно,
так как при перестановке векторов
изменится ориентация тройки.

2.
Свойство сочетательности относительно
скалярного множителя:

.

(без доказательства)

3.
Распределительное свойство относительно
сложения векторов :

.

.

Следствие.
.

То есть скобки можно
раскрывать, как при обыкновенном
умножении, не переставляя местами
множители (без доказательства).

Тройной продукт

Есть две тернарные операции: скалярное произведение и перекрестное произведение .

Смешанное произведение трех векторов определяется как

а⋅(б×c)знак равноб⋅(c×а)знак равноc⋅(а×б).{\ Displaystyle \ mathbf {a} \ cdot (\ mathbf {b} \ times \ mathbf {c}) = \ mathbf {b} \ cdot (\ mathbf {c} \ times \ mathbf {a}) = \ mathbf { c} \ cdot (\ mathbf {a} \ times \ mathbf {b}).}

Его значение является определителем матрицы, столбцы которой являются декартовыми координатами трех векторов. Это объем со знаком параллелепипеда, определяемый тремя векторами.

Вектор тройное произведение определяется

а×(б×c)знак равноб(а⋅c)-c(а⋅б).{\ displaystyle \ mathbf {a} \ times (\ mathbf {b} \ times \ mathbf {c}) = \ mathbf {b} (\ mathbf {a} \ cdot \ mathbf {c}) — \ mathbf {c} (\ mathbf {a} \ cdot \ mathbf {b}).}

Это тождество, также известное как формула Лагранжа , можно запомнить как «BAC минус CAB», имея в виду, какие векторы соединены точками. Эта формула используется для упрощения векторных вычислений в физике .

Геометрический смысл скалярного произведения[править]

Связь с проекциямиправить

Алгебраическое значение проекции вектора a{\displaystyle \mathbf {a} } на вектор b{\displaystyle \mathbf {b} } вдоль прямой, перпендикулярной b{\displaystyle \mathbf {b} }, очевидно, равно

|prba|=|a|cos⁡(a,b^){\displaystyle |\mathrm {pr} _{\mathbf {b} }\mathbf {a} |=|\mathbf {a} |\cos({\widehat {\mathbf {a} ,\mathbf {b} }})}

Аналогично

|prab|=|b|cos⁡(a,b^){\displaystyle |\mathrm {pr} _{\mathbf {a} }\mathbf {b} |=|\mathbf {b} |\cos({\widehat {\mathbf {a} ,\mathbf {b} }})}

Таким образом, скалярное произведение

a⋅b=|a||prab|=|b||prba|{\displaystyle \mathbf {a} \cdot \mathbf {b} =|\mathbf {a} ||\mathrm {pr} _{\mathbf {a} }\mathbf {b} |=|\mathbf {b} ||\mathrm {pr} _{\mathbf {b} }\mathbf {a} |}

Связь с длинамиправить

Рассмотрим скалярное произведение вектора на самого себя.

a⋅a=|a||a|cos⁡(a,a^)=|a|2{\displaystyle \mathbf {a} \cdot \mathbf {a} =|\mathbf {a} ||\mathbf {a} |\cos({\widehat {\mathbf {a} ,\mathbf {a} }})=|\mathbf {a} |^{2}}

Связь с угламиправить

Рассмотрим скалярное произведение единичных векторов. Поскольку их длины равны 1, то

a⋅b=|a||b|cos⁡(a,b^)=cos⁡(a,b^){\displaystyle \mathbf {a} \cdot \mathbf {b} =|\mathbf {a} ||\mathbf {b} |\cos({\widehat {\mathbf {a} ,\mathbf {b} }})=\cos({\widehat {\mathbf {a} ,\mathbf {b} }})}

Примеры

• В трёхмерном вещественном векторном пространстве векторов x=(x1,x2,x3){\displaystyle \mathbf {x} =(x_{1},x_{2},x_{3})} введение скалярного произведения по формуле ⟨x,y⟩=x1y1+x2y2+x3y3{\displaystyle \langle \mathbf {x} ,\mathbf {y} \rangle =x_{1}y_{1}+x_{2}y_{2}+x_{3}y_{3}} превращает это пространство в евклидово пространство

  В любом евклидовом пространстве (размерности n) всегда можно выбратьортонормированный базис e1,e2,…,en{\displaystyle {\mathbf {e} _{1},\mathbf {e} _{2},\dots ,\mathbf {e} _{n}}}

  . Аналогичное утверждение верно для евклидова пространства любой размерности (в сумму тогда входит количество членов, равное размерности пространства).

при разложении векторов по которому:

a=a1e1+a2e2+⋯+anen{\displaystyle \mathbf {a} =a_{1}\mathbf {e} _{1}+a_{2}\mathbf {e} _{2}+\dots +a_{n}\mathbf {e} _{n}},

b=b1e1+b2e2+⋯+bnen{\displaystyle \mathbf {b} =b_{1}\mathbf {e} _{1}+b_{2}\mathbf {e} _{2}+\dots +b_{n}\mathbf {e} _{n}} итд,

скалярное произведение будет выражаться формулой:

⟨a,b⟩=aTb=a1b1+a2b2+⋯+anbn{\displaystyle \langle \mathbf {a} ,\mathbf {b} \rangle =\mathbf {a} ^{T}\mathbf {b} =a_{1}b_{1}+a_{2}b_{2}+\dots +a_{n}b_{n}}.

• В таком же, но комплексном, пространстве, скалярное произведение вводится по несколько другой формуле: ⟨x→,y→⟩=x1y1¯+x2y2¯+x3y3¯{\displaystyle \langle {\vec {x}},{\vec {y}}\rangle =x_{1}{\overline {y_{1}}}+x_{2}{\overline {y_{2}}}+x_{3}{\overline {y_{3}}}}. Здесь через a¯{\displaystyle {\overline {a}}} обозначено число, комплексно сопряжённое к  a{\displaystyle \ a}. При таком определении скалярное произведение становится положительно определённым. Без комплексного сопряжения аксиома эрмитовости скалярного произведения была бы нарушена, а значит, вещественности определённой через него нормы вектора добиться бы не удалось, то есть норма в обычном смысле им бы не порождалась.
• В пространстве измеримых интегрируемых с квадратами на некоторой области Ω вещественных функций можно ввести положительно определённое скалярное произведение:

⟨f,g⟩=∫Ωf(x)g(x)dΩ{\displaystyle \langle f,g\rangle =\int \limits _{\Omega }f(x)g(x)d\Omega }

• В аналогичном случае для комплексных функций, если требуется эрмитовость (и положительная определённость) скалярного произведения, надо добавить комплексное сопряжение к f или g под интегралом.
• При использовании неортонормированных базисов скалярное произведение выражается через компоненты векторов с участием метрического тензора gij{\displaystyle g_{ij}}:

⟨a,b⟩=∑gijaibj{\displaystyle \langle \mathbf {a} ,\mathbf {b} \rangle =\sum g_{ij}a^{i}b^{j}}

при этом сама метрика (говоря точнее, её представление в данном базисе) так связана со скалярными произведениями базисных векторов fi {\displaystyle f_{i}\ }:

gij=⟨fi,fj⟩{\displaystyle g_{ij}=\langle \mathbf {f} _{i},\mathbf {f} _{j}\rangle }

• Аналогичные конструкции скалярного произведения можно вводить и на бесконечномерных пространствах, например, на пространствах функций:

⟨f,g⟩=∫(Ω1×Ω2)K(x1,x2)f(x1)g(x2)d(Ω1×Ω2){\displaystyle \langle f,g\rangle =\int \limits _{(\Omega _{1}\times \Omega _{2})}K(x_{1},x_{2})f(x_{1})g(x_{2})d(\Omega _{1}\times \Omega _{2})}

⟨f,g⟩=∫ΩK(x)f(x)g(x)dΩ{\displaystyle \langle f,g\rangle =\int \limits _{\Omega }K(x)f(x)g(x)d\Omega }

где К — положительно определённая, в первом случае симметричная относительно перестановки аргументов (при комплексных x — эрмитова) функция (если нужно иметь обычное симметричное положительно определённое скалярное произведение).

14.Смешанное произведение векторов

Сме́шанное
произведе́ние
векторов— скалярное произведение векторана векторное произведение векторови:

.

Иногда его
называют тройным скалярным произведением
векторов, по всей видимости из-за того,
что результатом является скаляр (точнее
— псевдоскаляр).

Геометрический
смысл: Модуль смешанного произведения
численно равен объёму параллелепипеда,
образованного векторами
.

Смешанное
произведение кососимметрично по
отношению ко всем своим аргументам:

т. е. перестановка
любых двух сомножителей меняет знак
произведения. Отсюда следует, что

Смешанное
произведение
в правой декартовой системе координат
(в ортонормированном базисе) равно
определителю матрицы, составленной из
векторови:

Смешанное
произведение
в левой декартовой системе координат
(в ортонормированном базисе) равно
определителю матрицы, составленной из
векторови,
взятому со знаком «минус»:

В частности,

Если любые два
вектора параллельны, то с любым третьим
вектором они образуют смешанное
произведение равное нулю.

Если три вектора
линейно зависимы (т. е. компланарны,
лежат в одной плоскости), то их смешанное
произведение равно нулю.

Геометрический
смысл — Смешанное произведение
по абсолютному значению равно объёму
параллелепипеда образованного векторамии;
знак зависит от того, является ли эта
тройка векторов правой или левой.

История

Скалярное произведение было введено У. Гамильтоном в 1846 году одновременно с векторным произведением в связи с кватернионами — соответственно, как скалярная и векторная часть произведения двух кватернионов, скалярная часть которых равна нулю.

15.Прямая линия на плоскости, её общее уравнение и его исследование.

Пусть на
плоскости введена прямоугольная
декартова система координат Оxy.

Теорема.

Всякое уравнение
первой степени вида
,
где А, В и С – некоторые действительные
числа, причем А и В одновременно не равны
нулю, задает прямую линию в прямоугольной
системе координат Oxy на плоскости, и
любая прямая в прямоугольной системе
координат Oxy на плоскости задается
уравнением видапри
некотором наборе значений A, B и C.

Докажемсначала, что уравнение видазадает
прямую на плоскости.

Пусть координаты
точки
удовлетворяют
уравнению,
то есть,.
Вычтем из левой и правой частей уравнениясоответственно
левую и правую части равенства,
при этом получаем уравнение вида,
которое эквивалентно.

Уравнение
представляет
собой необходимое и достаточное условие
перпендикулярности двух векторови.
То есть, множество всех точекопределяет
в прямоугольной системе координат Oxy
прямую линию, перпендикулярную направлению
вектора.
Если бы это было не так, то векторыине
были бы перпендикулярными и равенствоне
выполнялось бы.

Таким образом,
уравнение
задает
прямую линию в прямоугольной декартовой
системе координат Oxy на плоскости,
следовательно, эквивалентное ему
уравнение видазадает
эту же прямую. На этом первая часть
теоремы доказана.

Теперь докажем,
что всякая прямая в прямоугольной
системе координат Oxy на плоскости
определяется уравнением первой степени
вида
.

Пусть в
прямоугольной системе координат Oxy на
плоскости задана прямая a,
проходящая через точку,-
нормальный вектор прямойa, и пусть-
плавающая точка этой прямой. Тогда
векторыиперпендикулярны,
следовательно, их скалярное произведение
равно нулю, то есть,.
Полученное равенство можно переписать
в виде.
Если принять,
то получим уравнение,
которое соответствует прямойa.

На этом
доказательство теоремы завершено.

Вариации и обобщения

Простейшим обобщением конечномерного скалярного произведения в тензорной алгебре является свёртка по повторяющимся индексам. Аналогичное обобщение в принципе нетрудно сделать и в бесконечномерном случае (Для бесконечномерных пространств функций — ).

Свойства скалярного произведения векторов

Для любых трех векторов и действительного числа $k$ справедливо:

1. ${\overrightarrow{a}}^2\ge 0$

   Данное свойство следует из определения скалярного квадрата (определение 2).

2. Переместительный закон: $\overrightarrow{a}\overrightarrow{b}=\overrightarrow{b}\overrightarrow{a}$.

   Данное свойство следует из определения скалярного произведения (определение 1).

3. Распределительный закон:

   $\left(\overrightarrow{a}+\overrightarrow{b}\right)\overrightarrow{c}=\overrightarrow{a}\overrightarrow{c}+\overrightarrow{b}\overrightarrow{c}$.
   \end{enumerate}

   По теореме 1, имеем:

   \

4. Сочетательный закон: $\left(k\overrightarrow{a}\right)\overrightarrow{b}=k(\overrightarrow{a}\overrightarrow{b})$.
   \end{enumerate}

   По теореме 1, имеем:

   \

Определение

Скалярным произведением в векторном пространстве L{\displaystyle \mathbb {L} } над полем C{\displaystyle \mathbb {C} } комплексных (или R{\displaystyle \mathbb {R} } вещественных) чисел называется функция ⟨x,y⟩{\displaystyle \langle x,y\rangle } для элементов x,y∈L{\displaystyle x,y\in \mathbb {L} }, принимающая значения в C{\displaystyle \mathbb {C} } (или R{\displaystyle \mathbb {R} }), определенная для каждой пары элементов и удовлетворяющая следующим условиям:

1. для любых трех элементов x1,x2{\displaystyle x_{1},x_{2}} и y{\displaystyle y} пространства L{\displaystyle \mathbb {L} } и любых чисел α,β{\displaystyle \alpha ,\beta } из C{\displaystyle \mathbb {C} } (или R{\displaystyle \mathbb {R} }) справедливо равенство ⟨αx1+βx2,y⟩=α⟨x1,y⟩+β⟨x2,y⟩{\displaystyle \langle \alpha x_{1}+\beta x_{2},y\rangle =\alpha \langle x_{1},y\rangle +\beta \langle x_{2},y\rangle } (линейность скалярного произведения по первому аргументу);
2. для любых x{\displaystyle x} и y{\displaystyle y} справедливо равенство ⟨y,x⟩=⟨x,y⟩¯{\displaystyle \langle y,x\rangle ={\overline {\langle x,y\rangle }}}, где черта означает комплексное сопряжение (эрмитова симметричность);
3. для любого x{\displaystyle x} имеем ⟨x,x⟩≥{\displaystyle \langle x,x\rangle \geq 0}, причем ⟨x,x⟩={\displaystyle \langle x,x\rangle =0} только при x={\displaystyle x=0} (положительная определенность скалярного произведения).

Заметим, что из п.2 определения следует, что ⟨x,x⟩∈R{\displaystyle \langle x,x\rangle \in \mathbb {R} }. Поэтому п.3 имеет смысл, несмотря на комплексные (в общем случае) значения скалярного произведения.

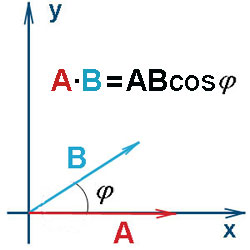
Определение[править]

Пусть a{\displaystyle \mathbf {a} } и b{\displaystyle \mathbf {b} } — два ненулевых вектора.
Если отложить их от одной точки O{\displaystyle O}, получится угол между этими векторами (точнее между несущими их полупрямыми, исходящими из точки O{\displaystyle O}). Этот угол обозначают a,b^{\displaystyle {\widehat {\mathbf {a} ,\mathbf {b} }}}.

Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними:

a⋅b=(a,b)=|a||b|cos⁡(a,b^){\displaystyle \mathbf {a} \cdot \mathbf {b} =(\mathbf {a} ,\mathbf {b} )=|\mathbf {a} ||\mathbf {b} |\cos({\widehat {\mathbf {a} ,\mathbf {b} }})}

Если один из векторов нулевой, то угол не определен, и произведение считают равным нулю.

Свойства скалярного произведения:

1. Коммутативность: a⋅b=b⋅a{\displaystyle \mathbf {a} \cdot \mathbf {b} =\mathbf {b} \cdot \mathbf {a} }
2. Линейность по первому аргументу: (a1+a2)⋅b=a1⋅b+a2⋅b{\displaystyle (\mathbf {a} _{1}+\mathbf {a} _{2})\cdot \mathbf {b} =\mathbf {a} _{1}\cdot \mathbf {b} +\mathbf {a} _{2}\cdot \mathbf {b} } и (αa)⋅b=α(a⋅b){\displaystyle (\alpha \mathbf {a} )\cdot \mathbf {b} =\alpha (\mathbf {a} \cdot \mathbf {b} )}
3. Положительная определенность: a⋅a=|a|2≥{\displaystyle \mathbf {a} \cdot \mathbf {a} =|\mathbf {a} |^{2}\geq 0}, причем a⋅a={\displaystyle \mathbf {a} \cdot \mathbf {a} =0} тогда и только тогда, когда a={\displaystyle \mathbf {a} =\mathbf {0} }

Определение перпендикулярности векторов и прямых

Напомним, что скалярное произведение оказывается нулевым исключительно в случае перпендикулярности векторов. Это позволяет использовать его для проверки перпендикулярности векторов.

Задание. Проверьте, являются ли перпендикулярными вектора:

Решение. В каждом случае мы должны скалярно перемножить пару векторов. Если результат окажется нулевым, то можно сделать вывод о перпендикулярности векторов. В противном случае они не перпендикулярны. Первый вектор будет обозначать буквой а, а второй – буквой b:

Ответ: а) да; б) нет; в) да; г) нет.

Задание. При каком значении переменной х вектора а{4; 5} и b{x; – 6} окажутся перпендикулярными?

Решение. Перемножим скалярно вектора и получим некоторое выражение с переменной x:

Найдем, при каком х это выражение обращается в нуль, то есть вектора становятся перпендикулярными:

Задание. Определите, перпендикулярны ли прямые АВ и CD, если даны координаты точек: А(3; 8), В(4; 10), С(7;12) и D(5;13).

Решение. В этой задаче сначала надорассчитать координаты векторов АВ и CD по координатамих начальной и конечной точки:

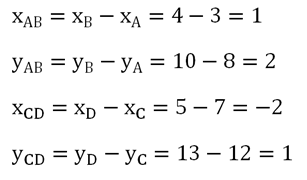
Мы вычислили координаты векторов: АВ{1; 2} и CD{– 2; 1}. Теперь мы можем проверить их перпендикулярность, скалярно перемножив вектора:

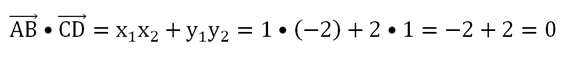
Мы получили ноль. Это означает, что АВ и CD – перпендикулярные вектора. Значит, и прямые, на которых они лежат, также перпендикулярны.

Ответ: перпендикулярны.

Задание. Перпендикулярны ли друг другу прямые, задаваемые уравнениями

Названия точкам в данном примере присвоены произвольно. На следующем шаге по координатам точек мы находим координаты векторов, лежащих на исследуемых прямых:

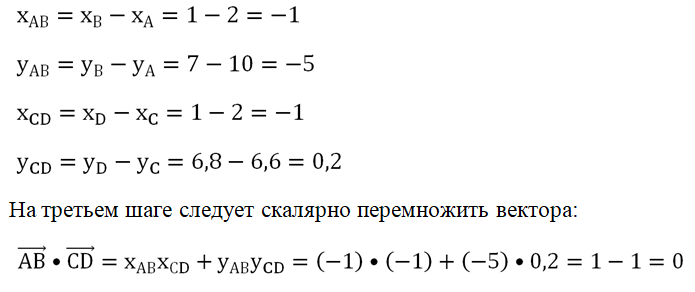
Полученный ноль показывает, что исходные прямые перпендикулярны.

Ответ: перпендикулярны.

В случае, когда прямые заданы уравнениями, необязательно проделывать столь длительные вычисления для определения их перпендикулярности. Есть теорема, сокращающая объем вычислений.

Докажем это утверждение. Пусть две прямые заданы уравнениями

Найдем какие-нибудь точки этих прямых. Для этого подставим в уравнения значения х = 0 и х = 1:

Прямые окажутся перпендикулярными исключительно в том случае, если это выражение будет нулевым. Это условие перпендикулярности можно записать как уравнение:

В результате мы получили доказываемую нами формулу.

Задание. Проверьте, какие из этих пар прямых перпендикулярны:

Решение. В каждом случае надо просто перемножить угловые коэффициенты прямых, то есть числа, стоящие перед переменной х. Другие числа в этих уравнениях (свободные коэффициенты) никак не влияют на перпендикулярность. Если вычисленное произведение окажется равным (– 1), то из этого будет вытекать перпендикулярность прямых.