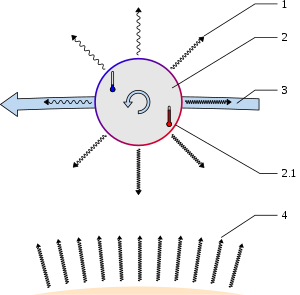
Два тела вращаются друг вокруг друга
В небесной механике , когда необходимо учитывать массы обоих вращающихся тел, орбитальный период T может быть рассчитан следующим образом:
- Тзнак равно2πа3грамм(M1+M2){\ displaystyle T = 2 \ pi {\ sqrt {\ frac {a ^ {3}} {G \ left (M_ {1} + M_ {2} \ right)}}}}
где:
- a — сумма больших полуосей эллипсов, по которым движутся центры тел, или, что то же самое, большая полуось эллипса, по которому движется одно тело, в системе отсчета с другим телом в точке происхождение (что равно их постоянному расстоянию для круговых орбит),
- M 1 + M 2 — это сумма масс двух тел,
- G — гравитационная постоянная .
Обратите внимание, что период обращения не зависит от размера: для масштабной модели он будет таким же при одинаковых плотностях (см. Также ).. По параболической или гиперболической траектории движение не является периодическим, а продолжительность полной траектории бесконечна.
По параболической или гиперболической траектории движение не является периодическим, а продолжительность полной траектории бесконечна.
Синодический и сидерический периоды обращения планет
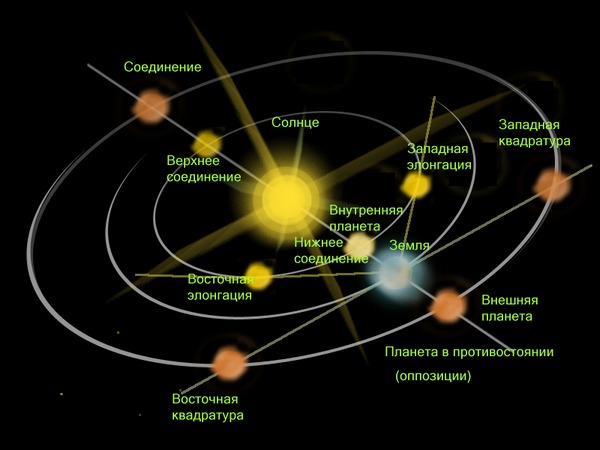
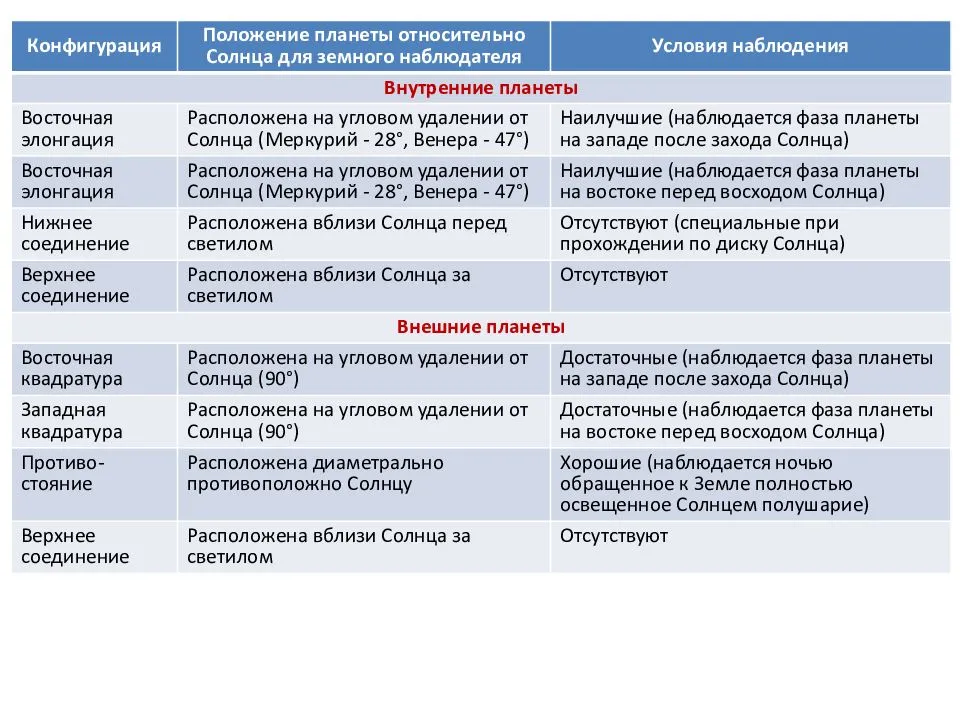
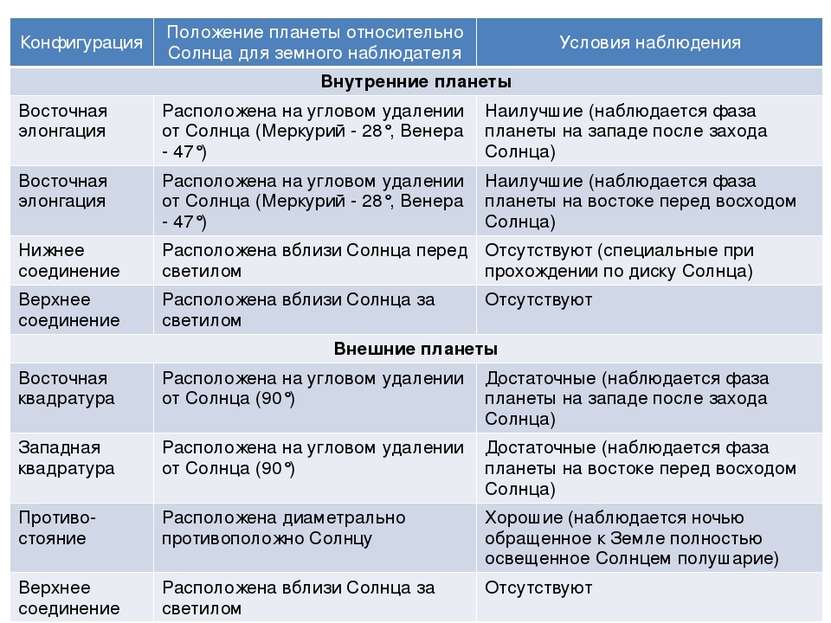
Конфигурации планеты периодически повторяются.
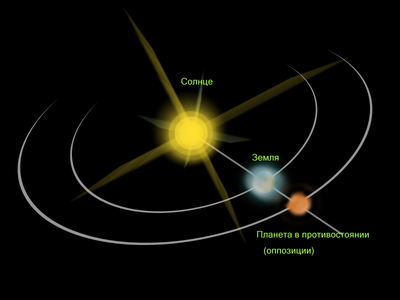
Промежуток времени между двумя последовательными одноимёнными конфигурациями планеты (например, верхними соединениями) называется её синодическим периодом.
Ещё в глубокой древности, когда считалось, что планеты обращаются вокруг Земли, для каждой из них на основе многолетних наблюдении был определен синодический период обращения.
Согласно гелиоцентрической системе, сама Земля обращается вокруг Солнца с периодом, равным году. Это её движение необходимо учитывать, чтобы узнать периоды обращения планет в невращающейся инерциальной системе отсчёта, или, как принято говорить, по отношению к звёздам.
Период обращения планеты вокруг Солнца по отношению к звёздам называется звёздным (или сидерическим) периодом.
Очевидно, что по своей продолжительности синодический период планеты не совпадает ни с её сидерическим периодом, ни с годом, который является звездным периодом обращения Земли.
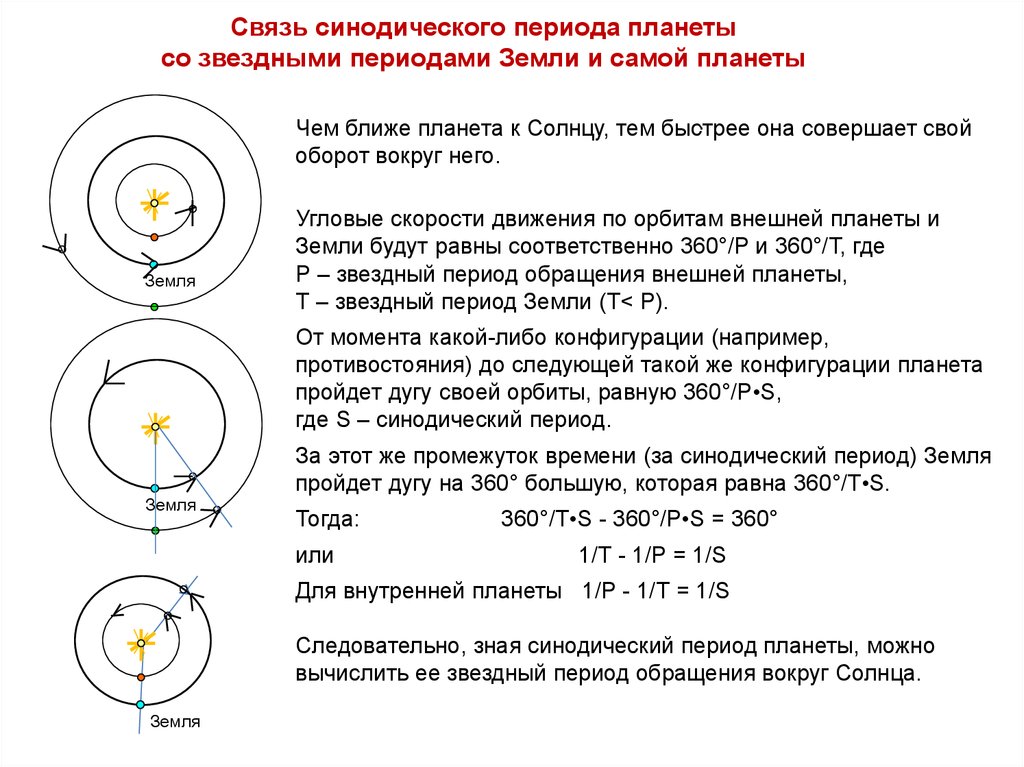
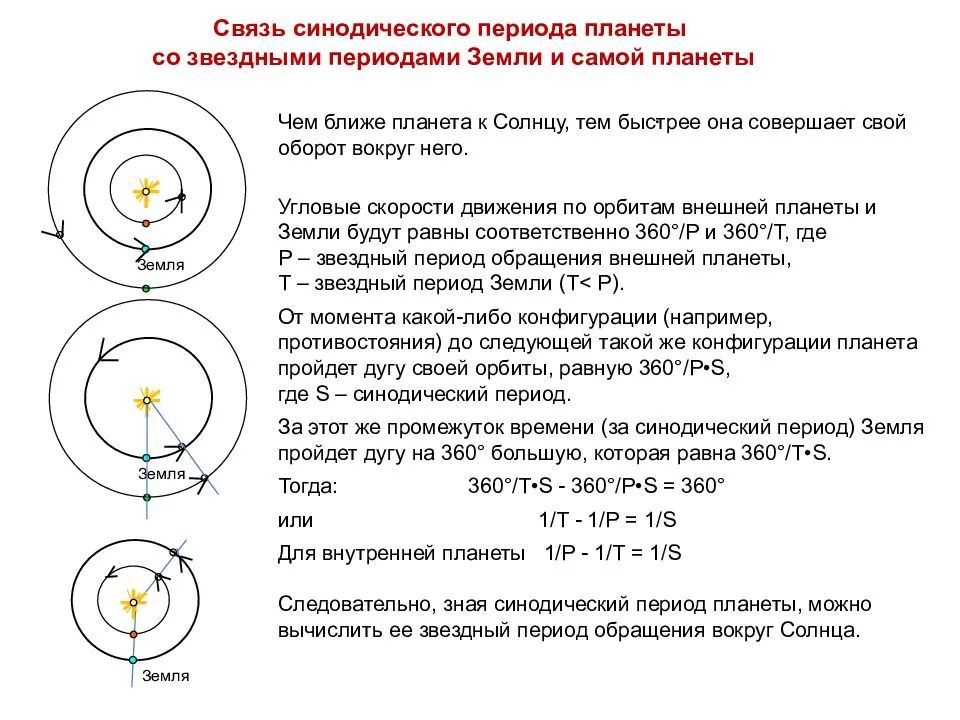
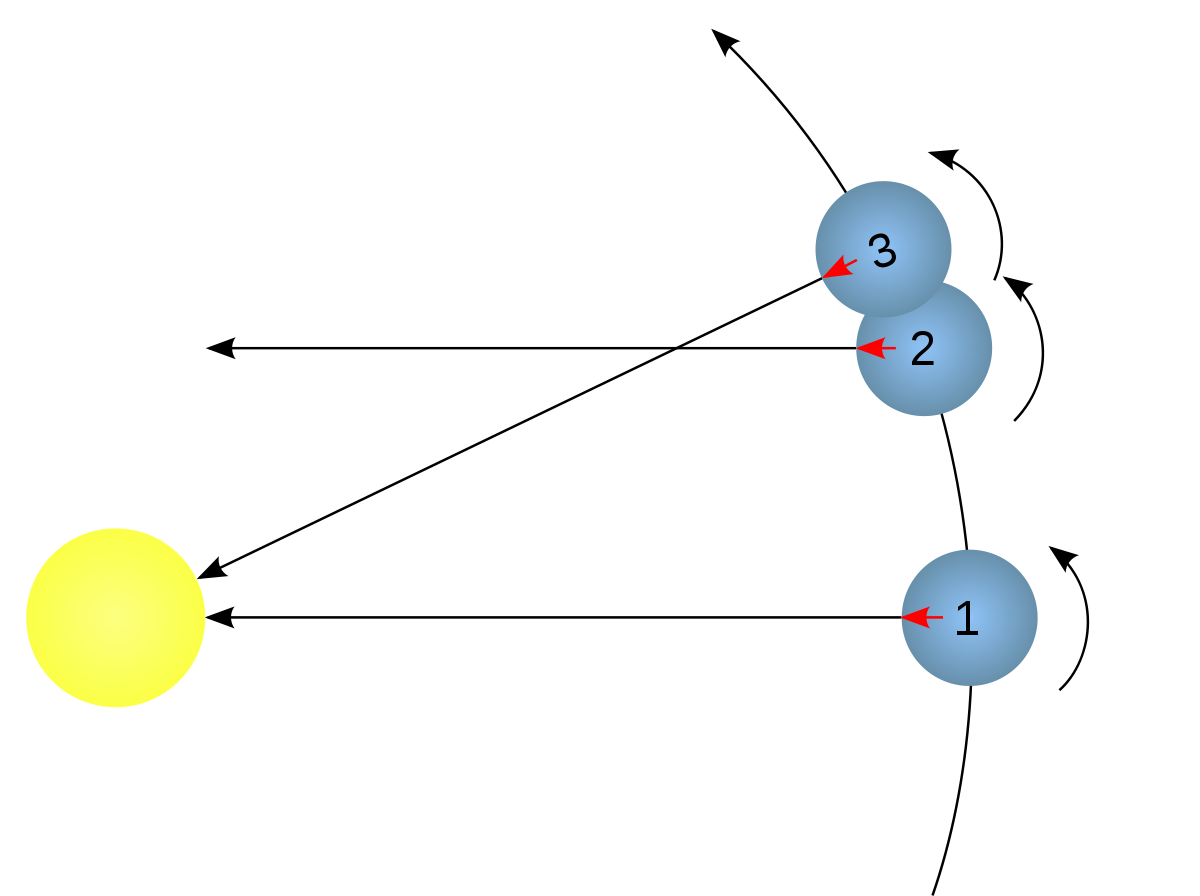
Рассмотрим, как связан синодический период планеты со звёздными периодами Земли и самой планеты. Чем ближе планета к Солнцу, тем быстрее она совершает свой оборот вокруг него. Пусть звёздный период обращения внешней планеты равен Р, звёздный период Земли — T(T < Р), а синодический период — S. Тогда угловые скорости их движения по орбитам будут равны соответственно 360°/P и 360°/T. От момента какой-либо конфигурации (например, противостояния) до следующей такой же конфигурации планета пройдет дугу своей орбиты, равную За этот же промежуток времени (за синодический период) Земля пройдёт дугу на 360° большую, которая равна Тогда:
или
Почти такой же будет формула для внутренней планеты:
Следовательно, зная синодический период планеты, можно вычислить ее звездный период обращения вокруг Солнца.
Вопросы
1. Что называется конфигурацией планеты? 2. Какие планеты считаются внутренними, какие — внешними? 3. В какой конфигурации может находиться любая планета? 4. Какие планеты могут находиться в противостоянии? Какие — не могут? 5. Назовите планеты, которые могут наблюдаться рядом с Луной во время её полнолуния.
Упражнение 9
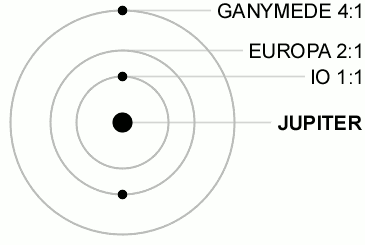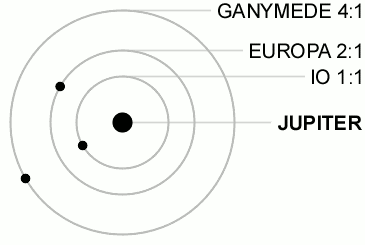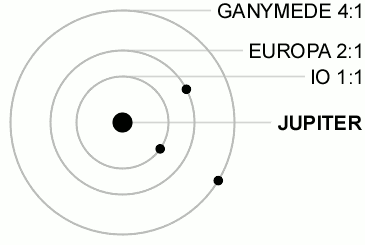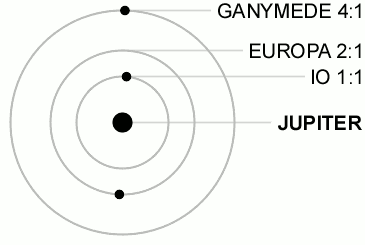
1. Нарисуйте, как будут располагаться на своих орбитах Земля и планета: а) Меркурий — в нижнем соединении; б) Венера — в верхнем соединении; в) Юпитер — в противостоянии; г) Сатурн — в верхнем соединении. 2. В какое время суток (утром или вечером) будет видна Венера, если она расположена так, как показано на рисунке 3.4, г? 3. Сравните условия видимости Марса в положениях, показанных на рисунках 3.4, в и 3.4, а. 4. Оцените, сколько примерно времени и когда (утром или вечером) может наблюдаться Венера, если она удалена к востоку от Солнца на 45°. 5. Через какой промежуток времени встречаются на циферблате часов минутная и часовая стрелки? 6. Звёздный период обращения Юпитера равен 12 годам. Через какой промежуток времени повторяются его противостояния?
Ответы
4. Вечером, около 3 ч.
5. 1 1/11 ч.
6. 584 сут, 1 1/11 года = 398 сут.
Аномалистический месяц
Аномалистический месяц является составляющей одноименного года. Такие периоды связаны с обращением Земли относительно точек ее эллиптической орбиты. Каждые полгода третья планета от Солнца находится максимально удаленно или приближена к нему. Например, 3 января планета находится далеко от Светила, а 4 июля она приближена к нему на предельное расстояние.
Минимум называют перигелием, а максимум — афелием, а год считается временем движения от перигелия к перигелию, т. е. возвращение планеты в точку максимального удаления. Длительность аномалистического периода постоянно изменяется, и ее вычисляют по астрономической формуле, где к 365 земным дням прибавляют 0,00 000 304Т суток (Т — требуемый период). Такой месяц длится почти 28 земных дней.
Ученые установили, что величина любого года со временем меняется. Перемены проходят не сразу, а на протяжении многих сотен и тысяч лет. Также существует понятие високосного года, когда за 48 месяцев накапливается 1 «лишний» день, который и помещают в календарь раз в 4 года.
Маленькое тело, вращающееся вокруг центрального тела
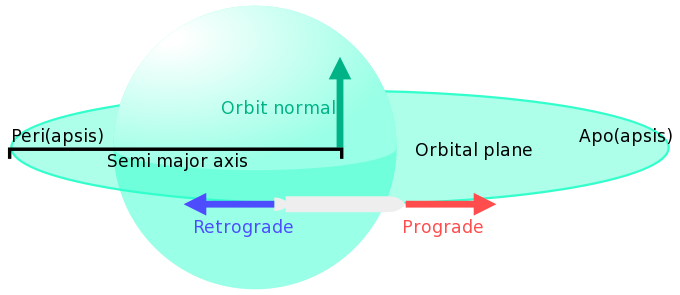
Большая полуось ( а ) и малая полуось ( б ) эллипса
Согласно Третьему закону Кеплера , период обращения T (в секундах) двух точечных масс, вращающихся друг вокруг друга по круговой или эллиптической орбите, равен:
- Тзнак равно2πа3μ{\ displaystyle T = 2 \ pi {\ sqrt {\ frac {a ^ {3}} {\ mu}}}}
где:
-
а — большая полуось орбиты
-
μ = GM — стандартный гравитационный параметр
- G — гравитационная постоянная ,
- M — масса более массивного тела.
Для всех эллипсов с данной большой полуосью период обращения один и тот же, независимо от эксцентриситета.
И наоборот, для расчета расстояния, на котором тело должно вращаться по орбите, чтобы иметь заданный период обращения:
- азнак равнограммMТ24π23{\ displaystyle a = {\ sqrt {\ frac {GMT ^ {2}} {4 \ pi ^ {2}}}}}
где:
- а — большая полуось орбиты в метрах,
- G — гравитационная постоянная,
- M — масса более массивного тела,
- T — период обращения в секундах.
Например, для того, чтобы совершать оборот по орбите каждые 24 часа с массой 100 кг , маленькое тело должно вращаться по орбите на расстоянии 1,08 метра от центра масс центрального тела .
В частном случае идеально круговых орбит орбитальная скорость постоянна и равна (в м / с )
- vознак равнограммMр{\ displaystyle v _ {\ text {o}} = {\ sqrt {\ frac {GM} {r}}}}
где:
- r — радиус круговой орбиты в метрах,
- G — гравитационная постоянная,
- M — масса центрального тела.
Это соответствует 1 / √2 раз (≈ 0,707 раза) на скорости убегания .
Синодический и сидерический периоды обращения планет
Конфигурации планеты периодически повторяются.
Промежуток времени между двумя последовательными одноимёнными конфигурациями планеты (например, верхними соединениями) называется её синодическим периодом.
Ещё в глубокой древности, когда считалось, что планеты обращаются вокруг Земли, для каждой из них на основе многолетних наблюдении был определен синодический период обращения.
Согласно гелиоцентрической системе, сама Земля обращается вокруг Солнца с периодом, равным году. Это её движение необходимо учитывать, чтобы узнать периоды обращения планет в невращающейся инерциальной системе отсчёта, или, как принято говорить, по отношению к звёздам.
Период обращения планеты вокруг Солнца по отношению к звёздам называется звёздным (или сидерическим) периодом.
Очевидно, что по своей продолжительности синодический период планеты не совпадает ни с её сидерическим периодом, ни с годом, который является звездным периодом обращения Земли.
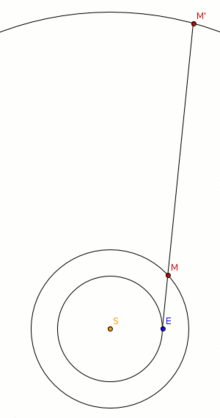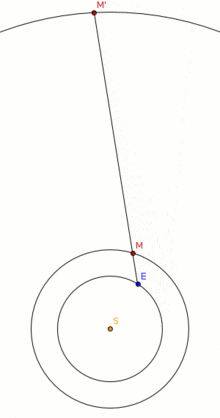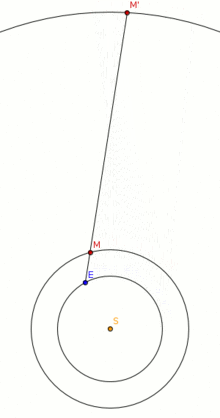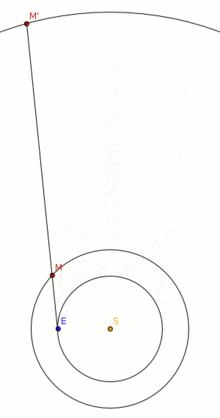
Рассмотрим, как связан синодический период планеты со звёздными периодами Земли и самой планеты. Чем ближе планета к Солнцу, тем быстрее она совершает свой оборот вокруг него. Пусть звёздный период обращения внешней планеты равен Р, звёздный период Земли — T(T < Р), а синодический период — S. Тогда угловые скорости их движения по орбитам будут равны соответственно 360°/P и 360°/T. От момента какой-либо конфигурации (например, противостояния) до следующей такой же конфигурации планета пройдет дугу своей орбиты, равную За этот же промежуток времени (за синодический период) Земля пройдёт дугу на 360° большую, которая равна Тогда:
или
Почти такой же будет формула для внутренней планеты:
Следовательно, зная синодический период планеты, можно вычислить ее звездный период обращения вокруг Солнца.
Вопросы
1. Что называется конфигурацией планеты? 2. Какие планеты считаются внутренними, какие — внешними? 3. В какой конфигурации может находиться любая планета? 4. Какие планеты могут находиться в противостоянии? Какие — не могут? 5. Назовите планеты, которые могут наблюдаться рядом с Луной во время её полнолуния.
Упражнение 9
1. Нарисуйте, как будут располагаться на своих орбитах Земля и планета: а) Меркурий — в нижнем соединении; б) Венера — в верхнем соединении; в) Юпитер — в противостоянии; г) Сатурн — в верхнем соединении. 2. В какое время суток (утром или вечером) будет видна Венера, если она расположена так, как показано на рисунке 3.4, г? 3. Сравните условия видимости Марса в положениях, показанных на рисунках 3.4, в и 3.4, а. 4. Оцените, сколько примерно времени и когда (утром или вечером) может наблюдаться Венера, если она удалена к востоку от Солнца на 45°. 5. Через какой промежуток времени встречаются на циферблате часов минутная и часовая стрелки? 6. Звёздный период обращения Юпитера равен 12 годам. Через какой промежуток времени повторяются его противостояния?
Ответы
4. Вечером, около 3 ч.
5. 1 1/11 ч.
6. 584 сут, 1 1/11 года = 398 сут.
Синодический период
Одной из наблюдаемых характеристик двух тел, которые вращаются вокруг третьего тела по разным орбитам и, следовательно, имеют разные орбитальные периоды, является их синодический период , то есть время между соединениями .
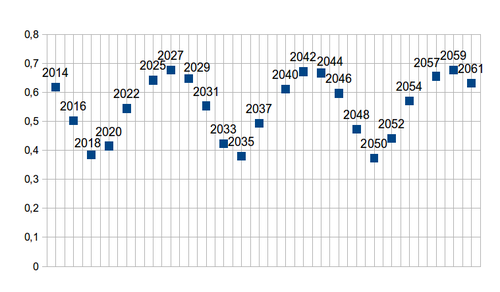
Примером этого описания связанного периода являются повторяющиеся циклы для небесных тел, наблюдаемые с поверхности Земли, так называемый синодический период , применяемый к истекшему времени, когда планеты возвращаются к тому же типу явлений или местоположению. Например, когда любая планета возвращается между своими последовательными наблюдаемыми соединениями с Солнцем или противостояниями с ним. Например, у Юпитера синодический период от Земли составляет 398,8 дня; таким образом, оппозиция Юпитера происходит примерно раз в 13 месяцев.
Если периоды обращения двух тел вокруг третьего называются T 1 и T 2 , так что T 1 < T 2 , их синодический период определяется следующим образом:
- 1Тsyпзнак равно1Т1-1Т2{\ displaystyle {\ frac {1} {T _ {\ mathrm {syn}}}} = {\ frac {1} {T_ {1}}} — {\ frac {1} {T_ {2}}}}
Связанные периоды
Есть много периодов, связанных с орбитами объектов, каждый из которых часто используется в различных областях астрономии и астрофизики . Примеры некоторых из наиболее распространенных:
- Сидерический период является количество времени , которое он принимает объект , чтобы сделать полный оборот, по отношению к звездам . Это период обращения в инерциальной (невращающейся) системе отсчета .
- Синодический период этого количество времени , которое требуется для объекта , чтобы вновь появиться в той же точке , в отношении двух или более других объектов. Обычно эти два объекта — это Земля и Солнце. Время между двумя последовательными противопоставлениями или двумя последовательными соединениями также равно синодическому периоду. Для небесных тел Солнечной системы синодический период (по отношению к Земле и Солнцу) отличается от сидерического периода из-за движения Земли вокруг Солнца. Например, синодический период из Луны орбиты «s , как видно из Земли , по отношению к Солнцу , 29,5 средние солнечные дни, так как фазы и положения относительно Луны к повторам Солнца и Земли после этого периода. Это больше, чем сидерический период его обращения вокруг Земли, который составляет 27,3 средних солнечных дня из-за движения Земли вокруг Солнца.
- Draconitic период (также драконический период или период обращения ), это время , которое проходит между двумя проходами объекта через его восходящий узел , точки его орбиты , где она пересекает эклиптику от южного до северного полушария. Этот период отличается от сидерического периода, потому что как плоскость орбиты объекта, так и плоскость эклиптики прецессируют относительно неподвижных звезд, поэтому их пересечение, линия узлов , также прецессирует относительно неподвижных звезд. Хотя плоскость эклиптики часто фиксируется на том месте, которое она занимала в конкретную эпоху , плоскость орбиты объекта все еще прецессирует, в результате чего драконитовый период отличается от сидерического периода.
- Аномалистический период этого время , которое проходит между двумя проходами объекта на его перицентре (в случае планета в Солнечной системе , называется перигелий ), точка ее ближайшего подход к притягивающему телу. Он отличается от сидерического периода тем, что большая полуось объекта обычно продвигается медленно.
- Кроме того, тропический период Земли ( тропический год ) — это интервал между двумя выравниваниями ее оси вращения с Солнцем, также рассматриваемый как два прохода объекта при прямом восхождении в 0 часов . Один земной год немного короче, чем период, за который Солнце совершит один оборот по эклиптике ( сидерический год ), потому что наклонная ось и экваториальная плоскость медленно прецессируют (вращаются относительно опорных звезд ), выравниваясь с Солнцем до того, как орбита завершится. . Этот цикл осевой прецессии Земли, известный как прецессия равноденствий , повторяется примерно каждые 25 770 лет.
Понятие о синодическом и сидерическом временных периодах

Практически каждый из нас знает, что планеты движутся по эллиптическим орбитам вокруг своих звезд. Звезды, в свою очередь, совершают орбитальные движения вокруг друг друга или вокруг центра Галактики. Иными словами, все массивные объекты космоса имеют определенные траектории движения, включая кометы и астероиды.
Важной характеристикой для всякого космического объекта является время, которое он затрачивает, чтобы совершить один полный оборот по своей траектории. Это время принято называть периодом
Чаще всего в астрономии при изучении Солнечной системы пользуются двумя периодами: синодическим и сидерическим.
Сидерический временной период — это время, которое требуется объекту, чтобы он совершил полный оборот по своей орбите вокруг своей звезды, при этом за точку отчета берется другая удаленная звезда. Этот период также называют реальным, поскольку именно такое значение времени обращения по орбите получит неподвижный наблюдатель, который будет следить за процессом вращения объекта вокруг его звезды.
Синодический период — это время, через которое объект появится в одной и той же точке на небосводе, если смотреть на него с какой-либо планеты. Например, если взять Луну, Землю и Солнце и задаться вопросом о том, через какое время Луна будет находиться в точке на небе, в которой она находится в данный момент, ответом на него будет значение синодического периода Луны. Этот период также называют кажущимся, поскольку от реального орбитального периода он отличается.
Влияние плотности центрального тела
Для идеальной сферы однородной плотности можно переписать первое уравнение без измерения массы как:
- Тзнак равноа3р33πграммρ{\ displaystyle T = {\ sqrt {{\ frac {a ^ {3}} {r ^ {3}}} {\ frac {3 \ pi} {G \ rho}}}}}
где:
- r — радиус сферы
- а — большая полуось орбиты в метрах,
- G — гравитационная постоянная,
- ρ — плотность шара в килограммах на кубический метр.
Например, небольшое тело, вращающееся по круговой орбите на высоте 10,5 см над поверхностью вольфрамовой сферы радиусом полметра, будет двигаться со скоростью чуть более 1 мм / с , совершая один оборот по орбите каждый час. Если бы такая же сфера была сделана из свинца, маленькому телу нужно было бы вращаться на высоте всего 6,7 мм над поверхностью для поддержания того же орбитального периода.
Когда очень маленькое тело находится на круговой орбите чуть выше поверхности сферы любого радиуса и средней плотности ρ (в кг / м 3 ), приведенное выше уравнение упрощается до (поскольку M = Vρ =43π a 3 ρ )
- Тзнак равно3πграммρ{\ displaystyle T = {\ sqrt {\ frac {3 \ pi} {G \ rho}}}}
Таким образом, период обращения на низкой орбите зависит только от плотности центрального тела, независимо от его размера.
Итак, для Земли как центрального тела (или любого другого сферически-симметричного тела с такой же средней плотностью около 5 515 кг / м 3 , например Меркурий с 5 427 кг / м 3 и Венеры с 5 243 кг / м 3 ) получаем:
- T = 1,41 часа
а для тела из воды ( ρ ≈ 1000 кг / м 3 ), соответственно тел с аналогичной плотностью, например, спутник Сатурна Япет с 1088 кг / м 3 и Тетис с 984 кг / м 3, получаем:
- T = 3,30 часа
Таким образом, в качестве альтернативы использованию очень небольшого числа, такого как G , сила всемирной гравитации может быть описана с помощью некоторого справочного материала, такого как вода: период обращения по орбите над поверхностью сферического водоема составляет 3 часа и 18 мин. И наоборот, это можно использовать как своего рода «универсальную» единицу времени, если у нас есть единицы массы, длины и плотности.
Примеры сидерических и синодических периодов
Таблица синодических периодов в Солнечной системе относительно Земли:
| Объект | Сидерический период ( лет ) | Синодический период | |
|---|---|---|---|
| ( год ) | ( г ) | ||
| Меркурий | 0,240846 (87,9691 дней) | 0,317 | 115,88 |
| Венера | 0,615 (225 дней) | 1,599 | 583,9 |
| земной шар | 1 (365,25636 солнечных дней ) | — | |
| Марс | 1,881 | 2,135 | 779,9 |
| Юпитер | 11,86 | 1.092 | 398,9 |
| Сатурн | 29,46 | 1.035 | 378,1 |
| Уран | 84,01 | 1.012 | 369,7 |
| Нептун | 164,8 | 1,006 | 367,5 |
| 134340 Плутон | 248,1 | 1,004 | 366,7 |
| Луна | 0,0748 (27,32 дня) | 0,0809 | 29,5306 |
| 99942 Апофис ( астероид, сближающийся с Землей ) | 0,886 | 7,769 | 2 837,6 |
| 4 Веста | 3,629 | 1,380 | 504,0 |
| 1 Церера | 4,600 | 1,278 | 466,7 |
| 10 Гигея | 5,557 | 1,219 | 445,4 |
| 2060 Хирон | 50,42 | 1.020 | 372,6 |
| 50000 Quaoar | 287,5 | 1,003 | 366,5 |
| 136199 Эрис | 557 | 1,002 | 365,9 |
| 90377 Седна | 12050 | 1.0001 | 365,3 |
В случае с Луной планеты синодический период обычно означает период Солнца-синодика, а именно время, которое требуется Луне, чтобы завершить фазы своего освещения, завершая солнечные фазы для астронома на поверхности планеты. Движение Земли не определяет это значение для других планет, потому что наблюдатель Земли не вращается вокруг рассматриваемых лун. Например, Деймос «ы синодический период составляет 1.2648 дней, 0,18% больше , чем сидерический период Деймоса о 1.2624 г.
Синодические периоды относительно других планет
Концепция синодического периода применима не только к Земле, но также и к другим планетам, и формула для вычисления та же, что и приведенная выше. Вот таблица, в которой перечислены синодические периоды некоторых планет относительно друг друга:
| Относительно | Марс | Юпитер | Сатурн | Хирон | Уран | Нептун | Плутон | Quaoar | Эрис |
|---|---|---|---|---|---|---|---|---|---|
| солнце | 1,881 | 11,86 | 29,46 | 50,42 | 84,01 | 164,8 | 248,1 | 287,5 | 557,0 |
| Марс | 2,236 | 2,009 | 1,954 | 1,924 | 1,903 | 1,895 | 1,893 | 1,887 | |
| Юпитер | 19,85 | 15.51 | 13,81 | 12,78 | 12,46 | 12,37 | 12.12 | ||
| Сатурн | 70,87 | 45,37 | 35,87 | 33,43 | 32,82 | 31.11 | |||
| 2060 Хирон | 126,1 | 72,65 | 63,28 | 61,14 | 55,44 | ||||
| Уран | 171,4 | 127,0 | 118,7 | 98,93 | |||||
| Нептун | 490,8 | 386,1 | 234,0 | ||||||
| 134340 Плутон | 1810,4 | 447,4 | |||||||
| 50000 Quaoar | 594,2 |
Смена лунных фаз во время движения на небесной сфере
Движение Луны на небесной сфере сопровождается непрерывным изменением ее внешнего вида. Происходит так называемая смена лунных фаз. Фазой Луны называется видимая часть лунной поверхности, освещенная солнечными лучами.
Рассмотрим, вследствие чего происходит изменение лунных фаз. Известно, что Луна светит отраженным солнечным светом- Половина ее поверхности всегда освещена Солнцем. Но вследствие различных взаимных положений Солнца, Луны и Земли освещенная поверхность представляется земному наблюдателю в разных видах. Принято различать четыре фазы Луны: новолуние, первая четверть, полнолуние и последняя четверть.

Положения и фазыЛуны (1 – новолуние, 2 – первая четверть, 3 – полнолуние, 4 – последняя четверть)
Во время новолуния Луна проходит между Солнцем и Землей. В этой фазе Луна обращена к Земле неосвещенной стороной, и поэтому она не видна земному наблюдателю.
В фазе первой четверти Луна находится в таком положении, что наблюдатель видит ее в виде половины освещенного диска.
Во время полнолуния Луна находится в направлении, противоположном направлению на Солнце. Поэтому к Земле обращена вся освещенная сторона Луны и она видна в виде полного диска. После полнолуния видимая с Земли освещенная часть Луны постепенно уменьшается.
Когда Луна достигает фазы последней четверти, она снова видна в виде половины освещенного диска. В Северном полушарии в первой четверти освещена правая половина диска Луны, а в последней — левая.
В промежутке между новолунием и первой четвертью и в промежутке между последней четвертью и новолунием к Земле обращена небольшая часть освещенной Луны, которая наблюдается в виде серпа. В промежутках между первой четвертью и полнолунием, полнолунием и последней четвертью Луна видна в виде ущербленного диска.
Полный цикл смены лунных фаз происходит в течение строго определенного периода времени. Его называют периодом фаз. Он равен синодическому месяцу, т. е. 29,53 сут.
Промежуток времени между основными фазами Луны равен примерно 7 сут. Количество дней, прошедших с момента новолуния, принято называть возрастом Луны. С изменением возраста изменяются и точки восхода и захода Луны.
Движение Луны вокруг Земли является причиной лунных и солнечных затмений – затмения происходят только тогда, когда Солнце и Луна одновременно располагаются вблизи узлов лунной орбиты. Солнечное затмение происходит, когда Луна находится между Солнцем и Землей, т. е. в период новолуния, а лунное — когда Земля находится между Солнцем и Луной, т. е. в период полнолуния.
Список источников литературы
Тропический месяц
Кроме перечисленных календарей, астрологи и астрономы используют тропический или солнечный. Главным участником в нем является дневное светило, которое за полный год проходит полный период обращения и возвращается в исходную точку. За новый год по солнечному календарю можно принимать любой день из 365 суток. Предки, например, отмечали новое летоисчисление днями весеннего или летнего солнцестояния.
Солнечный год равен 365,5 дня, и его продолжительность в связи с астрономическими показателями постоянно увеличивается. Месяц тропического года имеет продолжительность в привычные землянам 29-31 день.
Кроме перечисленных календарей, на Земле существует множество других исторических летоисчислений. Предки оставили человечеству неразгаданные послания из прошлого в виде календаря майя или графиков древних ацтеков. Интересным является факт, что в еврейском летоисчислении почти 355 суток, а у последователей Аллаха — 354 дня. Существует также Гауссов год, который равен 365,26 дня и новоюлианский календарь с 365,22 суток за период в 12 месяцев.
На протяжении своего развития и становления люди придумывали разные, удобные для них календари. Если жрец рекомендовал жить по Луне, следили за сменой ее фаз, а когда переключался на Солнце, то календарь вновь менялся. Жители Земли в XXI в. живут по Григорианскому летоисчислению.