Симметрия (биология)

Симметрии в физике

Основная статья: Симметрия (физика)

Симметрия в физике
Преобразование	Соответствующаяинвариантность	Соответствующийзаконсохранения
Трансляции времени	Однородностьвремени	…энергии
⊠ C, P, CP и T-симметрии	Изотропностьвремени	…чётности
Трансляции пространства	Однородностьпространства	…импульса
↺ Вращения пространства	Изотропностьпространства	…моментаимпульса
⇆ Группа Лоренца (бусты)	ОтносительностьЛоренц-ковариантность	…движенияцентра масс
~ Калибровочное преобразование	Калибровочная инвариантность	…заряда

В теоретической физике поведение физической системы описывается некоторыми уравнениями. Если эти уравнения обладают какими-либо симметриями, то часто удаётся упростить их решение путём нахождения сохраняющихся величин (интегралов движения). Так, уже в классической механике формулируется теорема Нётер, которая каждому типу непрерывной симметрии сопоставляет сохраняющуюся величину. Из неё, например, следует, что инвариантность уравнений движения тела с течением времени приводит к закону сохранения энергии; инвариантность относительно сдвигов в пространстве — к закону сохранения импульса; инвариантность относительно вращений — к закону сохранения момента импульса.

Суперсимметрия

Суперсимме́трия или симме́трия Ферми́ — Бозе́ — гипотетическая симметрия, связывающая бозоны и фермионы в природе. Абстрактное преобразование суперсимметрии связывает бозонное и фермионное квантовые поля, так что они могут превращаться друг в друга. Образно можно сказать, что преобразование суперсимметрии может переводить вещество во взаимодействие (или в излучение), и наоборот.

По состоянию на начало 2009 года суперсимметрия является физической гипотезой, не подтверждённой экспериментально. Совершенно точно установлено, что наш мир не является суперсимметричным в смысле точной симметрии, так как в любой суперсимметричной модели фермионы и бозоны, связанные суперсимметричным преобразованием, должны обладать одинаковыми массой, зарядом и другими квантовыми числами (за исключением спина). Данное требование не выполняется для известных в природе частиц. Предполагается, тем не менее, что существует энергетический лимит, за пределами которого поля подчиняются суперсимметричным преобразованиям, а в рамках лимита — нет. В таком случае частицы-суперпартнёры обычных частиц оказываются очень тяжёлыми по сравнению с обычными частицами. Поиск суперпартнёров обычных частиц — одна из основных задач современной физики высоких энергий. Ожидается, что Большой адронный коллайдер сможет открыть и исследовать суперсимметричные частицы, если они существуют, или поставить под большое сомнение суперсимметричные теории, если ничего не будет обнаружено.

Трансляционная симметрия

Трансляционная симметрия — тип симметрии, при которой свойства рассматриваемой системы не изменяются при сдвиге на определённый вектор, который называется вектором трансляции. Например, однородная среда совмещается сама с собой при сдвиге на любой вектор, поэтому для неё свойственна трансляционная симметрия.

Трансляционная симметрия свойственна также для кристаллов. В этом случае векторы трансляции не произвольны, хотя их существует бесконечное число. Среди всех векторов трансляций кристаллической решётки можно выбрать 3 таким образом, что любой другой вектор трансляции был бы целочисленно-линейной комбинацией этих трёх векторов. Эти три вектора составляют базис кристаллической решётки.

Теория групп показывает, что трансляционная симметрия в кристаллах совместима только с поворотами на углы θ=2π/n, где n может принимать значения 1, 2, 3, 4, 6.

При повороте на углы 180, 120, 90, 60 градусов положение атомов в кристалле не меняется. Говорят, что кристаллы имеют ось вращения n-го порядка.[]

Перенос в плоском четырёхмерном пространстве-времени не меняет физических законов. В теории поля трансляционная симметрии, согласно теореме Нётер, соответствует сохранению тензора энергии-импульса. В частности, чисто временные трансляции соответствуют закону сохранения энергии, а чисто пространственные сдвиги — закону сохранения импульса.

О примерах подробнее

Практика многолетнего преподавания математики и геометрии в средней школе показывает, что проще всего с явлением симметрии разобраться, объясняя его на конкретных примерах.

Для начала рассмотрим сферу. Для такого тела одновременно свойственны явления симметричности:

• центральной;
• зеркальной;
• вращательной.

В качестве главной выбирают точку, расположенную точно по центру фигуры. Чтобы подобрать плоскость, определяют большой круг и словно бы «нарезают» его на пласты. О чем говорит математика? Поворот и центральная симметрия в случае шара – понятия взаимосвязанные, при этом диаметр фигуры будет служить осью для рассматриваемого явления.

Еще один наглядный пример – круглый конус. Для этой фигуры свойственна осевая симметрия. В математике и архитектуре это явление нашло широкое теоретическое и практическое применение

Обратите внимание: в качестве оси для явления выступает ось конуса

Наглядно демонстрирует изучаемое явление прямая призма. Этой фигуре свойственна зеркальная симметрия. Плоскостью выбирают «срез», параллельный основаниям фигуры, удаленный от них на равные промежутки. Создавая геометрический, начертательный, архитектурный проект (математике симметрия важна не меньше, чем точным и начертательным наукам), помните о применимости на практике и пользе при планировании несущих элементов явления зеркальности.

А если более интересные фигуры?

О чем нам может рассказать математика (6 класс)? Центральная симметрия есть не только в таком простом и понятном объекте, как шар. Она свойственна и более интересным и сложным фигурам. Например, таков параллелограмм. Для такого объекта центральной точкой становится та, в которой пересекаются его диагонали.

А вот если рассматривать равнобедренную трапецию, то это будет фигура с осевой симметрией. Выявить ее можно в том случае, если правильно выбрать ось. Тело симметрично относительно линии, перпендикулярной основанию и пересекающей его ровно посередине.

Симметрия в математике и архитектуре обязательно учитывает ромб. Эта фигура примечательна тем, что одновременно объединяет в себе два типа симметричности:

• осевой;
• центральный.

В качестве оси необходимо выбрать диагональ объекта. В том месте, где диагонали ромба пересекаются, расположен его центр симметрии.

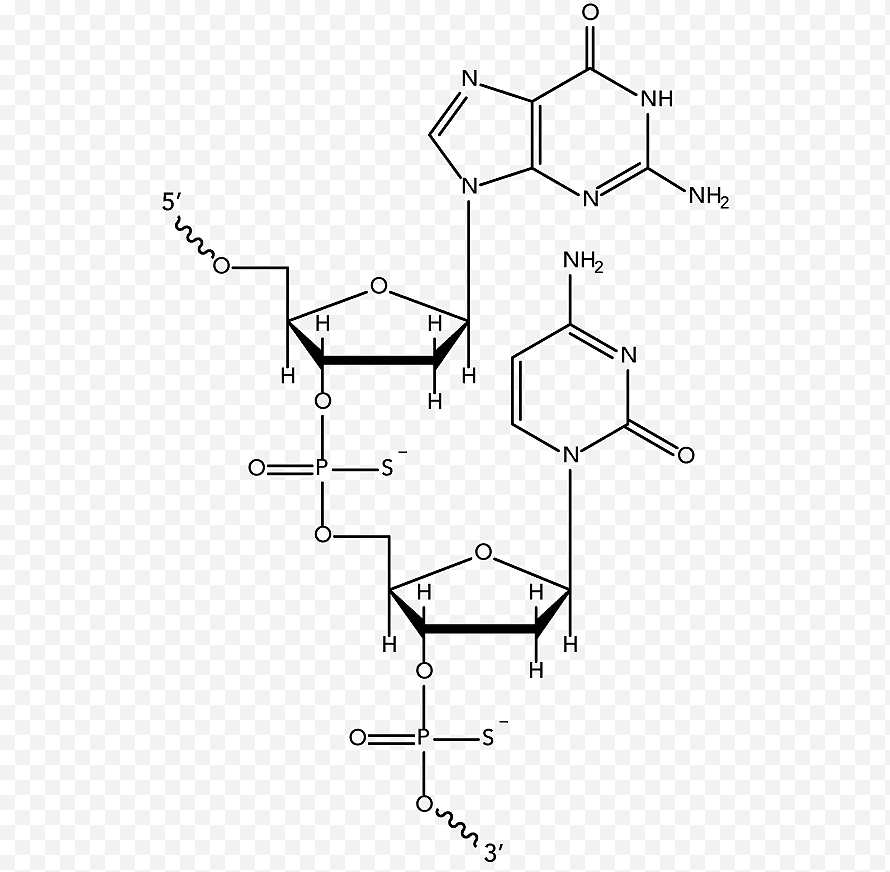
Симметрия в химии

Основная статья: Симметрия молекул

Симметрия важна для химии, так как она объясняет наблюдения в спектроскопии, квантовой химии и кристаллографии.

Кристаллографическая точечная группа симметрии — это точечная группа симметрии, которая описывает макросимметрию кристалла. Поскольку в кристаллах допустимы оси (поворотные и несобственного вращения) только 1, 2, 3, 4 и 6 порядков, из всего бесконечного числа точечных групп симметрии только 32 относятся к кристаллографическим.

Анизотропия (от др.-греч. ἄνισος — неравный и τρόπος — направление) — различие свойств среды (например, физических: упругости, электропроводности, теплопроводности, показателя преломления, скорости звука или и др.) в различных направлениях внутри этой среды; в противоположность изотропии. Причиной анизотропности кристаллов является то, что при упорядоченном расположении атомов, молекул или ионов силы взаимодействия между ними и межатомные расстояния (а также некоторые не связанные с ними прямо величины, например, поляризуемость или электропроводность) оказываются неодинаковыми по различным направлениям. Причиной анизотропии молекулярного кристалла может быть также асимметрия его молекул. Макроскопически эта неодинаковость проявляется, как правило, лишь если кристаллическая структура не слишком симметрична.

Симметрия в религиозных сим­во­лах: ряд 1. христианском, иудейском, даосийском; ряд 2. исламском, буд­дий­ском, синтоистском; ряд 3. сикх­ском, в вере Бахаи, индуистском.

Другие виды симметрий

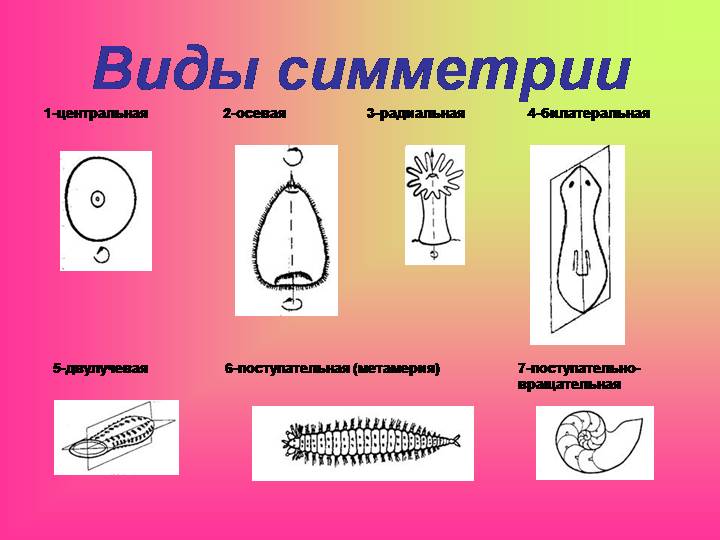
Типы симметрий, встречающиеся в математике и в естественных науках:

• симметрия n-го порядка — симметричность относительно поворотов на угол 360°/n вокруг какой-либо оси. Описывается группой Z_n;
• лоренц-инвариантность — симметричность относительно произвольных вращений в пространстве-времени Минковского;
• калибровочная инвариантность — независимость вида уравнений калибровочных теорий в квантовой теории поля (в частности, теорий Янга — Миллса) при калибровочных преобразованиях;
• высшая симметрия — симметрия в групповом анализе;
• кайносимметрия — явление электронной конфигурации (термин введён С. А. Щукаревым, открывшим его), которым обусловлена (открыта Е. В. Бироном).
• Группа симметрии некоторого объекта (многогранника или множества точек из метрического пространства) ― группа всех движений, для которых данный объект является инвариантом, с композицией в качестве групповой операции.
• Симметрическая группа — группа всех перестановок заданного множества X{\displaystyle X} (то есть биекций X→X{\displaystyle X\to X}) относительно операции композиции.

Краб-скрипач, Uca pugnax

Камбала

Пифагор и симметрия

В период жизни Пифагора и в последующем, когда его учение переживало свой расцвет, явление симметрии удалось четко оформить. Именно тогда симметричность подверглась научному анализу, давшему важные для практического применения результаты.

Согласно полученным выводам:

• Симметрия базируется на понятиях пропорций, однообразности и равенства. При нарушении того или иного понятия фигура становится менее симметричной, постепенно переходя в полностью асимметричную.
• Существует 10 противоположных пар. Согласно учению, симметрия представляет собой явление, сводящее в единое противоположности и тем самым формирующее вселенную в целом. Этот постулат долгие века оказывал сильное влияние на ряд наук как точных, так и философских, а также естественных.

Пифагор и его последователи выделяли «совершенно симметричные тела», к которым причисляли удовлетворяющие условиям:

• каждая грань – многоугольник;
• грани встречаются в углах;
• фигура должна иметь равные стороны и углы.

Именно Пифагор первым сказал, что таковых тел существует всего лишь пять

Это великое открытие положило начало геометрии и исключительно важно для современной архитектуры

А вы хотите своими глазами увидеть самое прекрасное явление симметрии? Поймайте зимой снежинку. Удивительно, но факт – это крошечный кусочек падающего с неба льда имеет не только крайне сложную кристаллическую структуру, но еще и идеально симметричен. Рассмотрите ее внимательно: снежинка действительно прекрасна, а ее сложные линии завораживают.

Симметрия в геометрии

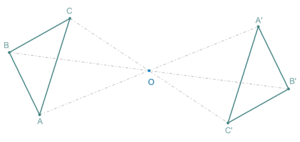
Два треугольника с точечной симметрией отражения в плоскости. Треугольник А’В’С может быть получен из треугольника ABC поворотом на 180 ° вокруг точки O.

Геометрическая симметрия — это наиболее известный тип симметрии для многих людей. Геометрический объект называется симметричным, если после того как он был преобразован геометрически, он сохраняет некоторые исходные свойства. Например, круг, повёрнутый вокруг своего центра, будет иметь ту же форму и размер, что и исходный круг. Поэтому круг называется симметричным относительно вращения (имеет осевую симметрию).
Виды симметрий, возможных для геометрического объекта, зависят от множества доступных геометрических преобразований и того, какие свойства объекта должны оставаться неизменными после преобразования.

Виды геометрических симметрий:

• Зеркальная симметрия
• Осевая симметрия
• Вращательная симметрия
• Центральная симметрия
• Скользящая симметрия
• Винтовая симметрия

Зеркальная симметрия

Зеркальная симметрия или отражение— движение евклидова пространства, множество неподвижных точек которого является гиперплоскостью (в случае трехмерного пространства — просто плоскостью). Термин зеркальная симметрия употребляется также для описания соответствующего типа симметрии объекта, то есть, когда объект при операции отражения переходит в себя. Это математическое понятие в оптике описывает соотношение объектов и их (мнимых) изображений при отражении в плоском зеркале. Проявляется во многих законах природы (в кристаллографии, химии, физике, биологии и т. д., а также в искусстве и искусствоведении).

Осевая симметрия

Фигура называется симметричной относительно прямой А, если для каждой точки фигуры симметричная ей точка относительно прямой А также принадлежит этой фигуре.

Вращательная симметрия

Вращательная симметрия — термин, означающий симметрию объекта относительно всех или некоторых собственных вращений m-мерного евклидова пространства. Собственными вращениями называются разновидности изометрии, сохраняющие ориентацию. Таким образом, группа симметрии, отвечающая вращениям, есть подгруппа группы E+(m) (см. Евклидова группа).

Трансляционная симметрия может рассматриваться как частный случай вращательной — вращение вокруг бесконечно-удалённой точки. При таком обобщении группа вращательной симметрии совпадает с полной E+(m). Такого рода симметрия неприменима к конечным объектам, поскольку делает всё пространство однородным, однако она используется в формулировке физических закономерностей.

Совокупность собственных вращений вокруг фиксированной точки пространства образуют специальную ортогональную группу SO(m) — группу ортогональных матриц m×m с определителем, равным 1. Для частного случая m = 3 группа носит специальное название — группа вращений.

В физике инвариантность относительно группы вращений называется изотропностью пространства (все направления в пространстве равноправны) и выражается в инвариантности физических законов, в частности, уравнений движения, относительно вращений. Теорема Нётер связывает эту инвариантность с наличием сохраняющейся величины (интеграла движения) — углового момента.

Центральная симметрия

Симметрия относительно точки

Центра́льной симме́трией (иногда центра́льной инве́рсией) относительно точки A называют преобразование пространства, переводящее точку X в такую точку X′, что A — середина отрезка XX′. Центральная симметрия с центром в точке A обычно обозначается через ZA{\displaystyle Z_{A}}, в то время как обозначение SA{\displaystyle S_{A}} можно перепутать с осевой симметрией. Фигура называется симметричной относительно точки A, если для каждой точки фигуры симметричная ей точка относительно точки A также принадлежит этой фигуре. Точка A называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией. Другие названия этого преобразования — симметрия с центром A. Центральная симметрия в планиметрии является частным случаем поворота, точнее, является поворотом на 180 градусов.

Скользящая симметрия

Скользящая симметрия — изометрия евклидовой плоскости.
Скользящей симметрией называют композицию симметрии относительно некоторой прямой l{\displaystyle l} и переноса на вектор, параллельный l{\displaystyle l} (этот вектор может быть и нулевым). Скользящую симметрию можно представить в виде композиции 3 осевых симметрий (теорема Шаля).

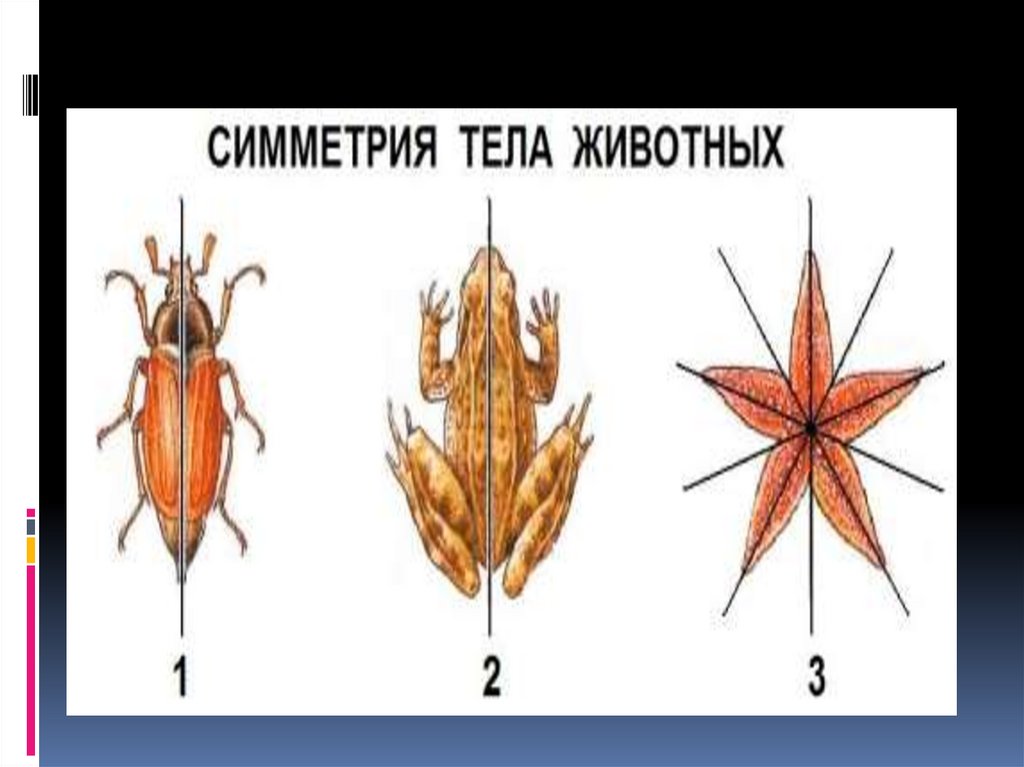
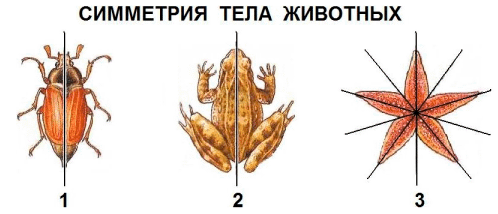
[править] Симметрия в биологии

Симметрия на примере бабочки

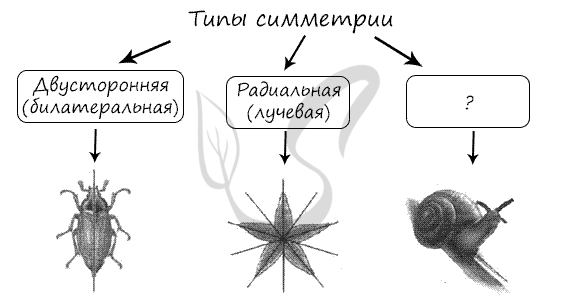
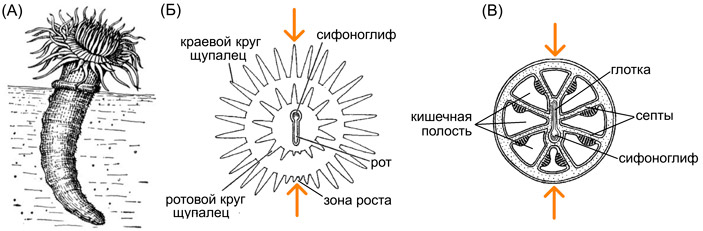
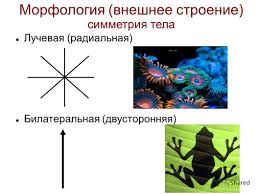
Симметричность — важнейшая характеристика телосложения животных, это свойство организма состоять из частей, которые зеркально повторяются и расположены вдоль воображаемой плоскости, проходящей через тело. Тип симметрии определяет не только общее строение тела, а возможность развития систем органов животного. Если тело животного можно мысленно разделить на две половины, правую и левую, то такое животное называют двустороннесиметричным. Этот тип симметрии присущ подавляющему большинству видов животных, а также человеку. Если тело животного можно мысленно разделить не одной, а несколькими плоскостями симметрии (мнимыми зеркалами) на равные части, то такое животное называют радиально-симметричной. Этот тип симметрии встречается значительно реже. Радиально-симметричные животные имеют простое строение, передвигаются медленно — ползанием. У таких животных отсутствуют высокоразвитые органы чувств и сложные системы органов. Незначительная их подвижность, пассивный образ жизни не способствуют развитию систем органов и совершенствованию нервной регуляции организма.

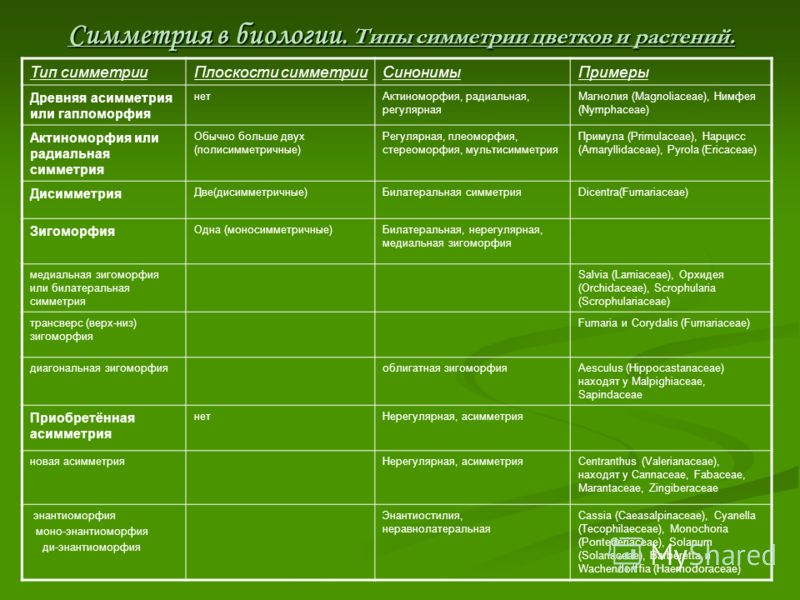
Актиноморфия (от греч. др.-греч ἀκτίς («actis») — луч и μορφή («morphe») — форма, лат. actinomorphia) — явление, когда через орган можно провести не менее двух плоскостей симметрии.

Зигоморфия (от др.-греч ζυγόν («zygon») — ярмо и μορφή («morphe») — форма, лат. zygomorphia) — явление, когда через орган можно провести только одну плоскость симметрии.

Асимметрия (лат. asymmetria) — явление, когда через орган нельзя провести ни одной плоскости симметрии.

См. также: Эволюционная теория асимметрии Геодакяна.

Общая информация

Не только математика, но и естественные науки во многом основаны на понятии симметрии. Более того, оно встречается в повседневной жизни, является одним из базовых для природы нашей Вселенной. Разбираясь, что такое симметрия в математике, необходимо упомянуть, что существует несколько типов этого явления. Принято говорить о таких вариантах:

Двустороннем, то есть такой, когда симметрия зеркальная. Это явление в ученой среде принято именовать «билатеральным».
Эн-ном порядке. Для этого понятия ключевое явление – это угол поворота, вычисляемый разделением 360 градусов на некоторую заданную величину. Кроме того, заранее определяется ось, вокруг которой эти повороты совершаются.
Падиальная, когда явление симметрии наблюдают, если повороты совершатся произвольно на некоторый случайный по величине угол. Ось также выбирается независимым образом. Для описания такого явления применяют группу SO(2).
Сферическая. В этом случае речь идет о трех измерениях, в которых объект вращают, выбирая произвольные углы. Выделяют конкретный случай изотропии, когда явление становится локальным, свойственным среде либо пространству.
Вращательная, соединившая в себе две описанные ранее группы.
Лоренц-инвариативная, когда имеют место произвольные вращения. Для этого типа симметрии ключевым понятием становится «пространство-время Минковского».
Супер, определяемая как замена бозонов фермионами.
Высшая, выявляемая в ходе группового анализа.
Трансляционная, когда имеются сдвиги пространства, для которых ученые выявляют направление, расстояние. На основе полученных данных проводят сравнительный анализ, позволяющий выявить симметрию.
Калибровочная, наблюдаемая в случае независимости калибровочной теории при соответствующих преобразованиях

Здесь особенное внимание обращают на теорию поля, в том числе фокусируются на идеях Янга-Миллса.
Кайно, принадлежащая к классу электронных конфигураций. О том, что представляет собой такая симметрия, математика (6 класс) представления не имеет, ведь это наука высшего порядка

Явление обусловлено вторичной периодичностью. Было открыто в ходе научной работы Е. Бирона. Терминология введена С. Щукаревым.

[править] Симметрия в физике

Ричард Фейнман: Характер физического закона. Лекция #4. Симметрия физических законов

Концепции современного естествознания. Понятие виды и значение симметрии в естествознании // Учебные фильмы

Понятие симметрии играет большую роль в физике. Физические объекты характеризуются без исключения целым рядом пронстранственных симметрий. Здесь следует различать симметрию относительно параллельного переноса, симметрию относительно зеркального отражения, симметрию относительно поворотов, винтовую симметрию и другие. Особый род симметрии есть изотропность — независимость свойств физической системы от направления и траектории, и притом однородность — независимость свойств физической системы от точки пространства-времени. Современная физика не исключает некоторую степень анизотропности сущего: главнейшей из таковых представляется однонаправленное свойство времени, сама история развития событий, «данные» этой истории.

Специфическим для физики видом симметрии является инвариантность физических законов относительно выбора системы отсчета, которая лежит в основе теории относительности. Другим видом симметрии, который встречается в физике есть симметрия относительно замены направлении координатных осей, лежит в основе принципа четности.

Симметрия свойств квантовомеханической системы относительно перестановки частиц местами лежит в основе тождественных частиц.

Для многих физических систем также характерны свои особые, скрытые типы симметрии. В физике элементарных частиц это, в частности, калибровочная инвариантность — симметрия частиц относительно типа преобразований, благодаря которой можно установить внутреннюю структуру в большом количестве открытых физиками элементарных частиц. Существуют гипотезы симметрии между двумя фундаментальными типами частиц: бозонами и фермионами, которые получили название суперсимметрии.

По теореме Нётер каждой симметрии физической системы соответствует интеграл движения. Вследствие этого симметрии Вселенной связаны с законами сохранения.

Несмотря на важность симметрии в физических процессах, мир, в котором мы живем, в определенных аспектах существенно несимметричный. Например, в известной нам Вселенной существует преимущество частиц над античастицами

Эта асимметрия возникла на ранних этапах развития Вселенной при бариогенезисе и лептогенезисе. Ее причины до сих пор не ясны. Слабое взаимодействие несимметрично по хиральности, то есть правозакручености и левозакручености частиц, в частности, нейтрино. Современные физические теории пытаются объяснить возникновение такие явления спонтанным нарушением симметрии.

Другая существенная асимметрия в физике связана с «стрелой времени», то есть с тем, что Вселенная движется от прошлого к будущему. Эта асимметрия по замене направления времени проявляется в втором законе термодинамики, утверждении о неубывания энтропии в изолированных системах.

О терминологии

«Симметрия» – слово, пришедшее в наш язык от древних греков, впервые обративших на это явление пристальное внимание и попытавшихся изучить его. Термин обозначает наличие некоторой системы, а также гармоничное сочетание частей объекта

Переводя слово «симметрия», можно подобрать в качестве синонимов:

• пропорциональность;
• одинаковость;
• соразмерность.

С древних пор симметрия является важным понятием для развития человечества в разных областях и отраслях. Народы с древности имели общие представления об этом явлении, преимущественно рассматривая его в широком смысле. Симметрия обозначала гармоничность и уравновешенность. В наше время терминологию преподают в обычной школе. Например, что такое ось симметрии (2 класс, математика) детям рассказывает учительница на обычном занятии.

Как идея это явление зачастую становится начальным посылом научных гипотез и теорий. Особенно популярно это было в прежние столетия, когда по всему миру властвовала идея математической гармонии, присущей самой системе мироздания. Знатоки тех эпох были убеждены, что симметричность есть проявление божественной гармонии. А вот в Древней Греции философы уверяли, что симметрична вся Вселенная, и все это базировалось по постулате: «Симметрия прекрасна».

Великие греки и симметрия

Симметричность будоражила умы известнейших ученых Древней Греции. До наших дней дошли свидетельства того, что Платон призывал отдельно восхищаться правильными многогранниками. По его мнению, такие фигуры – это олицетворения стихий нашего мира. Существовала следующая классификация:

Стихия	Фигура
Огонь	Тетраэдр, поскольку вершина его стремится ввысь.
Вода	Икосаэдр. Выбор обусловлен «катучестью» фигуры.
Воздух	Октаэдр.
Земля	Самый устойчивый объект, то есть куб.
Вселенная	Додекаэдр.

Во многом именно из-за этой теории принято именовать правильные многогранники платоновыми телами.

А вот терминологию ввели еще раньше, и тут не последнюю роль сыграл скульптор Поликлет.

Литература

• Вигнер Е. Этюды о симметрии. — М., Мир, 1971. — 320 с.
• Нокс Р., Голд А. Симметрия в твердом теле. — М., Наука, 1970. — 424 с.
• Шубников А. В., Копцик В. А. Симметрия в науке и искусстве. — М., Наука, 1972. — 340 с.
• Вернадский В. И. Химическое строение биосферы Земли и её окружения. — М., Наука, 1965. — 373 с.
• Болтянский В. Г., Виленкин Н. Я. Симметрия в алгебре. — М., Наука, 1967. — 284 с.
• Под ред. Сенешаль М., Флека Дж. Узоры симметрии. — М., Мир, 1980. — 269 с.
• А. В. Шубников Симметрия и антисимметрия конечных фигур, Изд-во АН СССР, 1951
• И. Харгиттаи, М. Харгиттаи Симметрия глазами химика. — М., Мир, 1989. — 494 с.

Нюансы

О чем еще интересном можно узнать, разбирая такое явление, как симметрия? Математика (6 класс) рассказывает, что две фигуры, считающиеся симметричными, совсем не обязательно идентичны друг другу. Понятие равности существует в узком и широком смысле. Так вот, симметричные объекты в узком – не одно и то же.

Какой пример из жизни можно привести? Элеметарный! Что скажете насчет наших перчаток, варежек? Мы все привыкли их носить и знаем, что терять нельзя, ведь вторую такую в пару уже не подобрать, а значит, покупать придется обе заново. А все почему? Потому что парные изделия, хотя и симметричны, но рассчитаны на левую и правую руку. Это – типичный пример зеркальной симметрии. Что касается равности, то такие объекты признают «зеркально равными».

Зеркальная

Во время обучения в школе учащихся практически всегда просят сделать работу «Симметрия вокруг нас» (проект по математике). Как правило, ее рекомендуют к выполнению в шестом классе обычной школы с общей программой преподавания предметов. Чтобы справиться с проектом, необходимо сперва ознакомиться с понятием симметрии, в частности, выявить, что представляет собой зеркальный тип как один из базовых и наиболее понятных для детей.

Для выявления явления симметрии рассматривают конкретную геометрическую фигуру, а также выбирают плоскость. Когда говорят о симметричности рассматриваемого объекта? Сперва на нем выбирают некоторую точку, а затем находят для нее отражение. Между ними двумя проводят отрезок и вычисляют, под каким углом к выбранной ранее плоскости он проходит.

Разбираясь, что такое симметрия в математике, помните, что выбранная для выявления этого явления плоскость будет называться именно плоскостью симметрии и никак иначе. Проведенный отрезок должен пересекаться с ней под прямым углом. Расстояние от точки до этой плоскости и от нее до второй точки отрезка должно быть равным.

Как симметрия стала идеей о прекрасном

Удивительно, что на симметричности основано восприятие человеком красоты окружающего его пространства и объектов в нем. Долгие века люди стремятся понять, что же кажется прекрасным, а что отталкивает нелицеприятностью.

Симметричность, пропорции – вот то, что помогает визуально воспринимать некоторый объект и оценивать его положительно. Все элементы, части должны быть сбалансированы и находиться в разумных пропорциях друг с другом. Уже давно выяснили, что асимметричные предметы нравятся людям гораздо меньше. Все это связывают с понятием «гармония»

Над тем, почему это так важно для человека, с древних пор ломали головы мудрецы, артисты, художники

Стоит приглядеться к геометрическим фигурам, и явление симметрии станет очевидным и доступным для понимания. Наиболее типичные симметричные явления в окружающем нас пространстве:

• горные породы;
• цветы и листья растений;
• парные наружные органы, присущие живым организмам.

Описанные явления имеют источником саму природу. А вот что можно увидеть симметричного, приглядевшись к изделиям человеческих рук? Заметно, что люди тяготеют к созданию именно такового, если стремятся сделать нечто красивое или функциональное (или и такое, и такое одновременно):

• узоры и орнаменты, популярные с древних времен;
• строительные элементы;
• элементы конструкций техники;
• рукоделие.