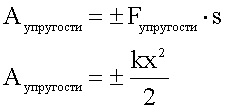Вместо послесловия
Вооружившись некоторыми сведениями о силах упругости и деформациях, мы легко ответим на некоторые вопросы. Скажем, почему крупные кости у человека имеют трубчатое строение?

Изогните металлическую или деревянную линейку. Её выпуклая часть испытает деформацию растяжения, а вогнутая — сжатия. Средняя же часть нагрузки не несет. Природа и воспользовалась этим обстоятельством, снабдив человека и животных трубчатыми костями. В процессе движения кости, мышцы и сухожилья испытывают все виды деформаций. Трубчатое строение костей значительно облегчает их вес, абсолютно не влияя на их прочность.
Стебли злаковых культур имеют такое же строение. Порывы ветра пригибают их до земли, а силы упругости помогают выпрямиться. Кстати, рама у велосипеда тоже изготавливается из трубок, а не из стержней: вес намного меньше и металл экономится.
Закон, установленный Робертом Гуком, послужил основой для создания теории упругости. Расчёты, выполненные по формулам этой теории, позволяют обеспечить долговечность высотных сооружений и других конструкций.
в группе ВКонтакте
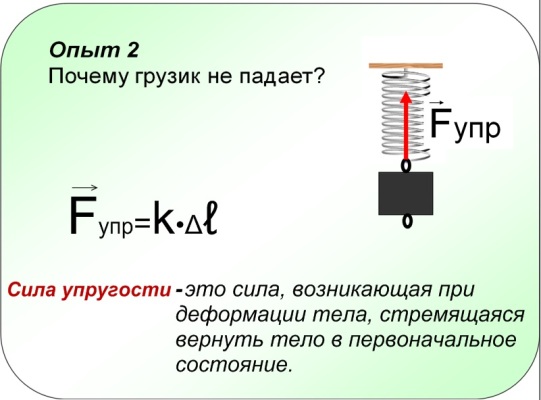
Сила упругости в природе
Сила упругости довольно значимую роль играет и в природе. Ведь только благодаря этой силе, ткани растений, животных и человека способны выдерживать огромные нагрузки и при этом не сломаться и не разрушиться.
Вы, наверное, не раз наблюдали такую картину, как под порывом ветра сгибаются растения или под тяжестью снега прогибаются ветки деревьев, а в результате действия силы упругости возвращаются в свою предыдущую форму.
Также, каждый из вас мог наблюдать, как под натиском сильного ураганного ветра, ломались ветки деревьев. А такой итог мы можем наблюдать тогда, когда действие силы ветра превышает силы упругости самого дерева.
Все находящиеся на Земле тела способны выдерживать силу атмосферного давления только благодаря силе упругости. Обитатели глубоких водоемов способны выдерживать еще большую нагрузку. Поэтому можно прийти к закономерному выводу, что только благодаря силе упругости, все живые организмы в природе имеют возможность не только переносить механические нагрузки, но и сохранить свою форму в целостности.
Сидящие на ветках деревьев стайки птиц, весящие на кустах грозди винограда, огромные шапки снега на еловых лапах – это наглядная демонстрация сил упругости в природе.
Сила упругости
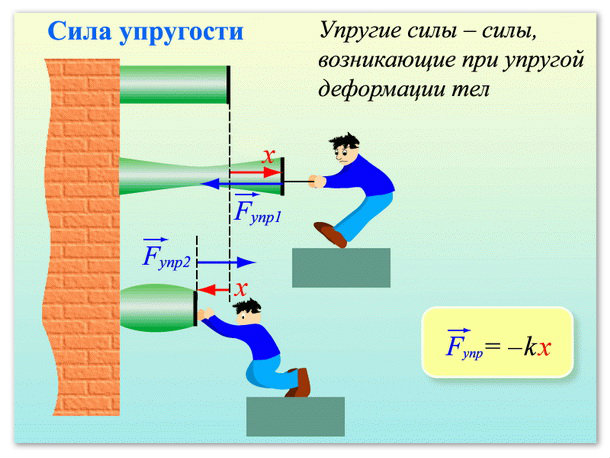
Это сила возникает в результате деформации (изменения первоначального состояния вещества). Например, когда растягиваем пружину, мы увеличиваем расстояние между молекулами материала пружины. Когда сжимаем пружину — уменьшаем. Когда перекручиваем или сдвигаем. Во всех этих примерах возникает сила, которая препятствует деформации — сила упругости.
Закон Гука

Сила упругости направлена противоположно деформации.
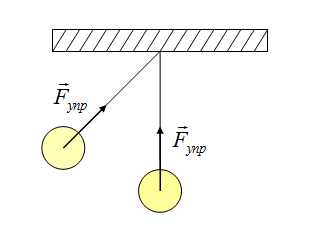
Так как тело представляем в виде материальной точки, силу можно изображать с центра
При последовательном соединении, например, пружин жесткость рассчитывается по формуле
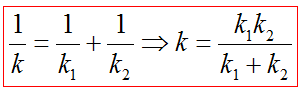
При параллельном соединении жесткость
Жесткость образца. Модуль Юнга.

Модуль Юнга характеризует упругие свойства вещества. Это постоянная величина, зависящая только от материала, его физического состояния. Характеризует способность материала сопротивляться деформации растяжения или сжатия. Значение модуля Юнга табличное.
Подробнее о свойствах твердых тел .
Формула определения жесткости
Изучаемая современными школьниками формула, как найти коэффициент жесткости пружины, представляет собой соотношение силы и величины, показывающей изменение длины пружины в зависимости от величины данного воздействия (или
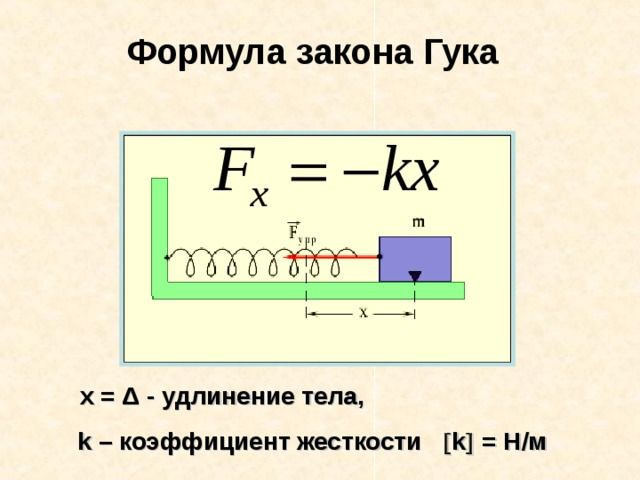
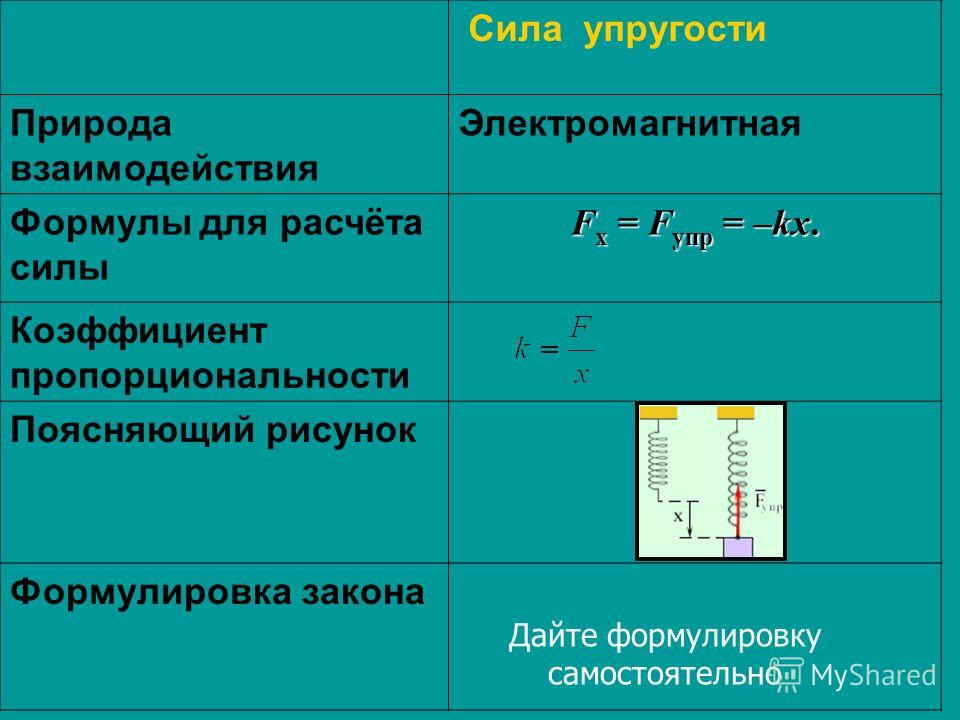
равной ему по модулю силы упругости). Выглядит эта формула так: F = -kx. Из этой формулы коэффициент жесткости упругого элемента равен отношению силы упругости к изменению его длины. В международной системе единиц физических величин СИ он измеряется в ньютонах на метр (Н/м).
Другой вариант записи формулы: коэффициент Юнга
Деформация растяжения/сжатия в физике также может описываться несколько видоизмененным законом Гука. Формула включает значения относительной деформации (отношения изменения длины к ее начальному значению) и напряжения (отношения силы к площади поперечного сечения детали). Относительная деформация и напряжение по этой формуле пропорциональны, а коэффициент пропорциональности — величина, обратная модулю Юнга.
Модуль Юнга интересен тем, что определяется исключительно свойствами материала, и никак не зависит ни от формы детали, ни от ее размеров.
К примеру, модуль Юнга для ста
ли примерно равен единице с одиннадцатью нулями (единица измерения — Н/кв. м).
Смысл понятия коэффициент жесткости
Коэффициент жесткости — коэффициент пропорциональности из закона Гука. Еще он с полным правом называется коэффициентом упругости.
Фактически он показывает величину силы, которая должна быть приложена к упругому элементу, чтобы изменить его длину на единицу (в используемой системе измерений).
Значение этого параметра зависит от нескольких факторов, которыми характеризуется пружина:
- Материала, используемого при ее изготовлении.
- Формы и конструктивных особенностей.
- Геометрических размеров.
По этому показателю можно сд
елать вывод, насколько изделие устойчиво к воздействию нагрузок, то есть каким будет его сопротивление при приложении внешнего воздействия.
Особенности расчета пружин
Показывающая, как найти жесткость пружины, формула, наверное, одна из наиболее используемых современными конструкторами. Ведь применение эти упругие детали находят практически везде, то есть требуется просчитывать их поведение и выбирать те из них, которые будут идеально справляться с возложенными обязанностями.
Закон Гука весьма упрощенно показывает зависимость деформации упругой детали от прилагаемого усилия, инженерами используются более точные формулы расчета коэффициента жесткости, учитывающие все особенности происходящего процесса.
Например:
- Цилиндрическую витую пружину современная инженерия рассматривает как спираль из проволоки с круглым сечением, а ее деформация под воздействием существующих в системе сил представляется совокупностью элементарных сдвигов.
- При деформации изгиба в качестве деформации рассматривается прогиб стержня, расположенного концами на опорах.
Особенности расчета жесткости соединений пружин
Важный моментом является расчет нескольких упругих элементов, соединенных последовательно или параллельно.
При параллельном расположении нескольких деталей общая жесткость этой системы определяется простой суммой коэффициентов отдельных комплектующих. Как нетрудно заметить, жесткость системы больше, чем отдельной детали.
При последовательном расположении формула более сложная: величина, обратная суммарной жесткости, равна сумме величин, обратных к жесткости каждой комплектующей. В этом варианте сумма меньше слагаемых.
Используя эти зависимости, легко определиться с правильным выбором упругих комплектующих для конкретного случая.
Необходимо знать точку приложения и направление каждой силы
Важно уметь определить какие именно силы действуют на тело и в каком направлении. Сила обозначается как , измеряется в Ньютонах
Для того, чтобы различать силы, их обозначают следующим образом
Ниже представлены основные силы, действующие в природе. Придумывать не существующие силы при решении задач нельзя!
Сил в природе много. Здесь рассмотрены силы, которые рассматриваются в школьном курсе физики при изучении динамики. А также упомянуты другие силы, которые будут рассмотрены в других разделах.
Закон Гука и условие его выполнения
В 1660 году известный английский ученый Роберт Гук открыл явление, при помощи которого можно механически описать процесс деформаций.
Для того чтобы понимать при каких условиях выполняется закон Гука, ограничимся двумя параметрами:
- среда,
- сила.
Есть такие среды (например, газы, жидкости, особо вязкие жидкости, близкие к твердым состояниям или, наоборот, очень текучие жидкости) для которых описать процесс механически никак не получится. И наоборот, существуют такие среды, в которых при достаточно больших силах механика перестает срабатывать.
Важно! На вопрос: При каких условиях выполняется закон Гука?, можно дать определенный ответ: При малых деформациях. Закон Гука, определение: деформация, которая возникает в теле, прямо пропорциональна силе, которая вызывает эту деформацию
Закон Гука, определение: деформация, которая возникает в теле, прямо пропорциональна силе, которая вызывает эту деформацию.
Естественно, это определение подразумевает, что:
- сжатия или растяжения невелики,
- предмет упругий,
- он состоит из материала, при котором в результате сжатия или растяжения нет нелинейных процессов.
Бизнес и финансы
БанкиБогатство и благосостояниеКоррупция(Преступность)МаркетингМенеджментИнвестицииЦенные бумагиУправлениеОткрытые акционерные обществаПроектыДокументыЦенные бумаги — контрольЦенные бумаги — оценкиОблигацииДолгиВалютаНедвижимость(Аренда)ПрофессииРаботаТорговляУслугиФинансыСтрахованиеБюджетФинансовые услугиКредитыКомпанииГосударственные предприятияЭкономикаМакроэкономикаМикроэкономикаНалогиАудитМеталлургияНефтьСельское хозяйствоЭнергетикаАрхитектураИнтерьерПолы и перекрытияПроцесс строительстваСтроительные материалыТеплоизоляцияЭкстерьерОрганизация и управление производством
Закон Гука
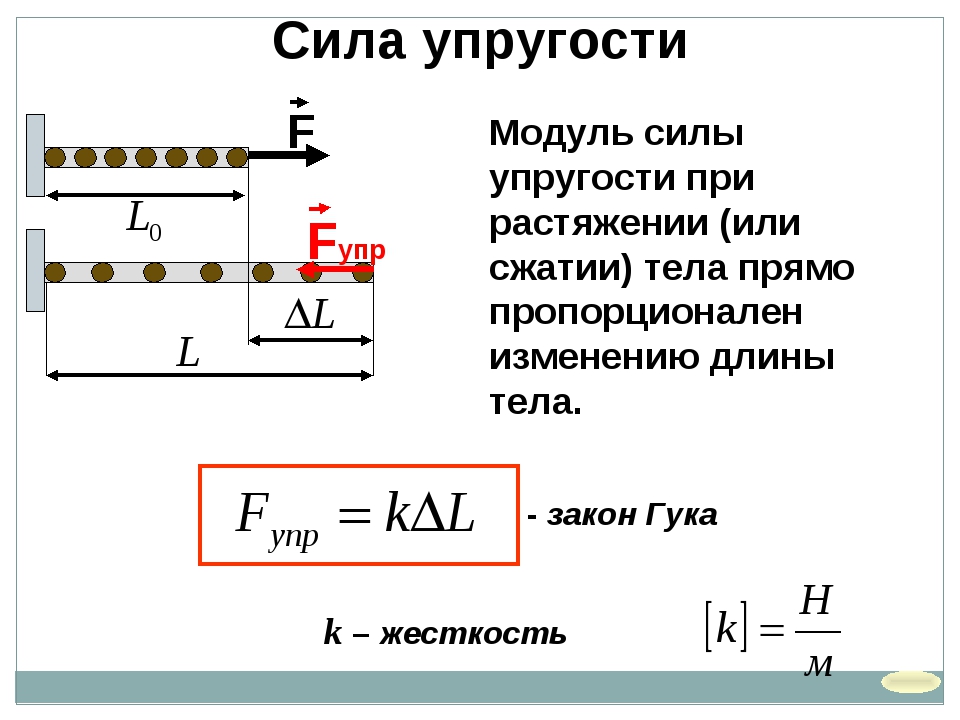
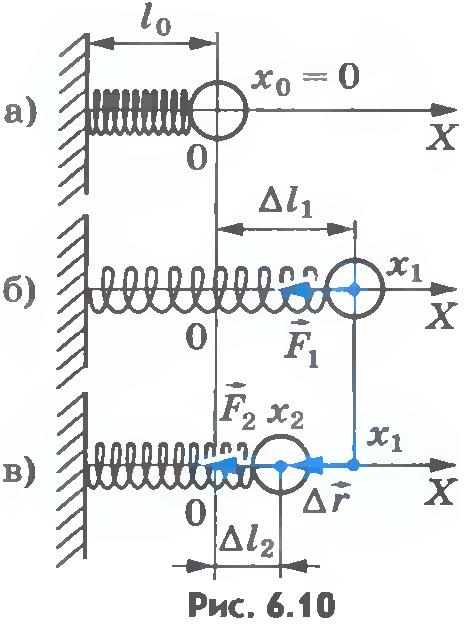
Связь между силой упругости и упругой деформацией тела (при малых деформациях) была экспериментально установлена современником Ньютона английским физиком Гуком. Математическое выражение закона Гука для деформации одностороннего растяжения (сжатия) имеет вид
где Fупр – модуль силы упругости, возникающей в теле при деформации (Н); Δl – абсолютное удлинение тела (м).
Коэффициент k называется жесткостью тела – коэффициент пропорциональности между деформирующей силой и деформацией в законе Гука.
Жесткость пружины численно равна силе, которую надо приложить к упруго деформируемому образцу, чтобы вызвать его единичную деформацию.
В системе СИ жесткость измеряется в ньютонах на метр (Н/м):
Коэффициент жесткости зависит от формы и размеров тела, а также от материала.
Закон Гука для одностороннего растяжения (сжатия) формулируют так:
сила упругости, возникающая при деформации тела, пропорциональна удлинению этого тела.
Диаграмма растяжения
Для исследования деформации растяжения стержень из исследуемого материала при помощи специальных устройств (например, с помощью гидравлического пресса) подвергают растяжению и измеряют удлинение образца и возникающее в нем напряжение. По результатам опытов вычерчивают график зависимости напряжения σ от относительного удлинения ε. Этот график называют диаграммой растяжения (рис. 10).
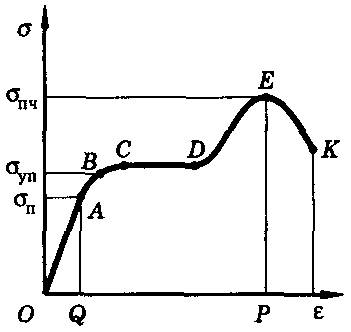
Многочисленные опыты показывают, что при малых деформациях напряжение σ прямо пропорционально относительному удлинению ε (участок ОА диаграммы) – выполняется закон Гука.
Эксперимент показывает, что малые деформации полностью исчезают после снятия нагрузки (наблюдается упругая деформация). При малых деформациях выполняется закон Гука. Максимальное напряжение, при котором еще выполняется закон Гука, называется пределом пропорциональности σп. Он соответствует точки А диаграммы.
Если продолжать увеличивать нагрузку при растяжении и превзойти предел пропорциональности, то деформация становится нелинейной (линия ABCDEK). Тем не менее при небольших нелинейных деформациях после снятия нагрузки форма и размеры тела практически восстанавливаются (участок АВ графика). Максимальное напряжение, при котором еще не возникают заметные остаточные деформации, называется пределом упругости σуп. Он соответствует точке В диаграммы. Предел упругости превышает предел пропорциональности не более чем на 0,33%. В большинстве случаев их можно считать равными.
Если внешняя нагрузка такова, что в теле возникают напряжения, превышающие предел упругости, то характер деформации меняется (участок BCDEK). После снятия нагрузки образец не принимает прежние размеры, а остается деформированным, хотя и с меньшим удлинением, чем при нагрузке (пластическая деформация).
За пределом упругости при некотором значении напряжения, соответствующем точке С диаграммы, удлинение возрастает практически без увеличения нагрузки (участок CD диаграммы почти горизонтален). Это явление называется текучестью материала.
При дальнейшем увеличении нагрузки напряжение повышается (от точки D), после чего в наименее прочной части образца появляется сужение («шейка»). Из-за уменьшения площади сечения (точка Е) для дальнейшего удлинения нужно меньшее напряжение, но, в конце концов, наступает разрушение образца (точка К). Наибольшее напряжение, которое выдерживает образец без разрушения, называется пределом прочности. Обозначим его σпч (оно соответствует точке Е диаграммы). Его значение сильно зависит от природы материала и его обработки.
Чтобы свести к минимуму возможность разрушения сооружения, инженер должен при расчетах допускать в его элементах такие напряжения, которые будут составлять лишь часть предела прочности материала. Их называют допустимыми напряжениями. Число, показывающее, во сколько раз предел прочности больше допустимого напряжения, называют коэффициентом запаса прочности.
Обозначив запас прочности через n, получим:
Запас прочности выбирается в зависимости от многих причин: качества материала, характера нагрузки (статическая или изменяющаяся со временем), степени опасности, возникающей при разрушении, и т.д. На практике запас прочности колеблется от 1,7 до 10. Выбрав правильно запас прочности, инженер может определить допустимое в конструкции напряжение.
1.12. Сила упругости. Закон Гука window.top.document.title = «1.12. Сила упругости. Закон Гука»;
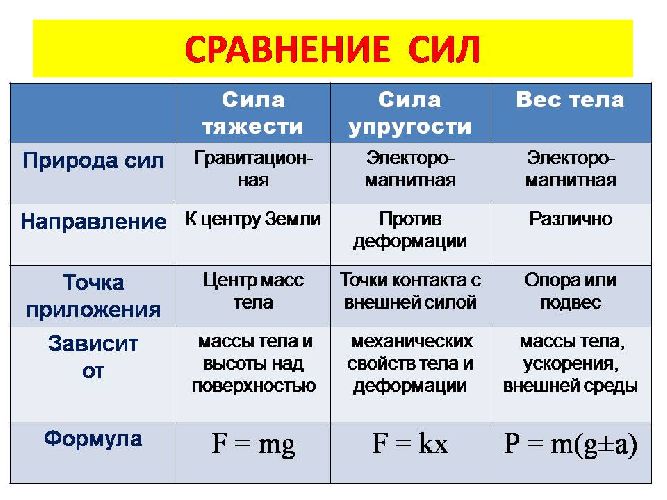
При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Ее называют силой упругости.
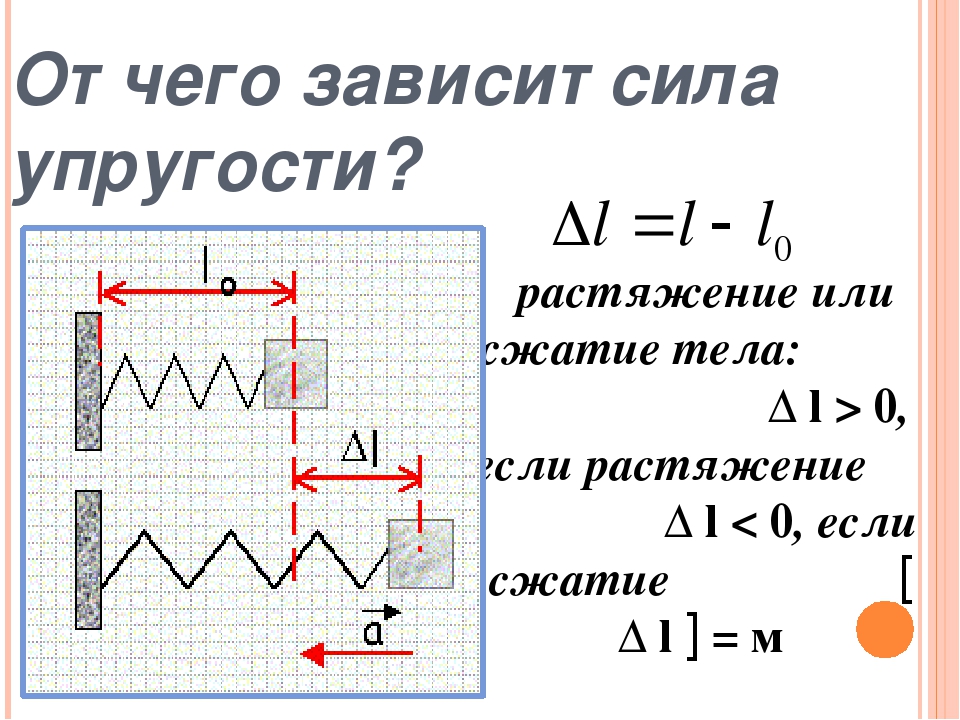
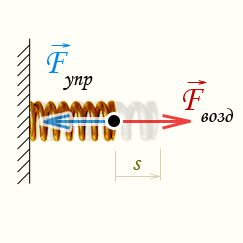
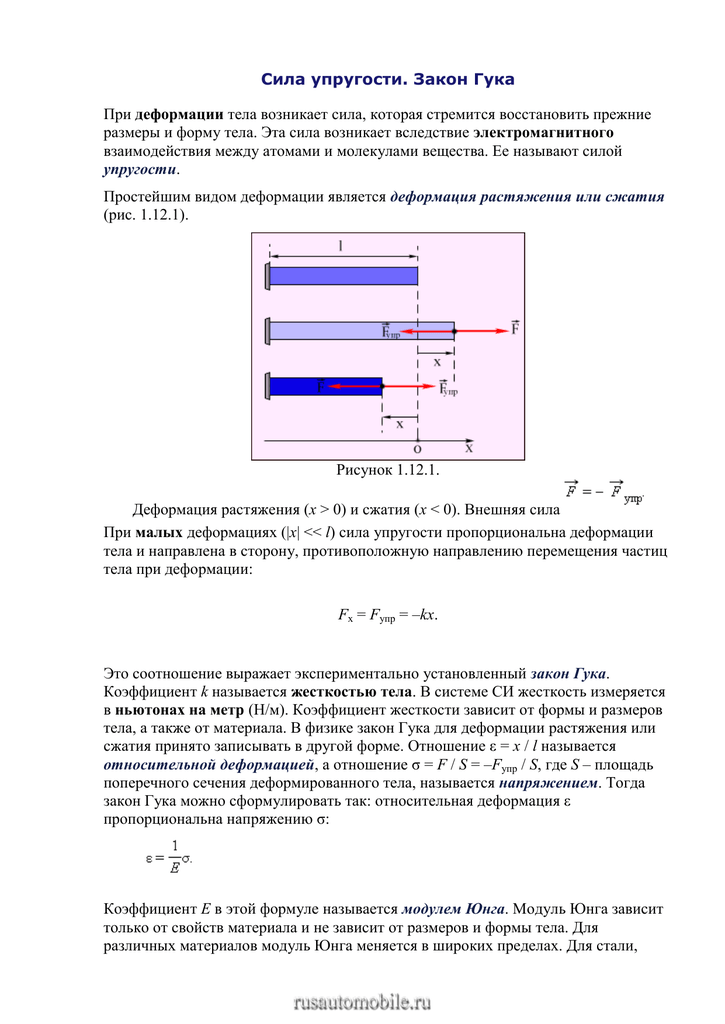
Простейшим видом деформации являются деформации растяжения и сжатия (рис. 1.12.1).
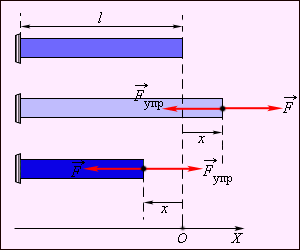 |
| Рисунок 1.12.1.Деформация растяжения (x > 0) и сжатия (x < 0). Внешняя сила |
При малых деформациях (|x| << l) сила упругости пропорциональна деформации тела и направлена в сторону, противоположную направлению перемещения частиц тела при деформации:
Это соотношение выражает экспериментально установленный закон Гука. Коэффициент k называется жесткостью тела. В системе СИ жесткость измеряется в ньютонах на метр (Н/м). Коэффициент жесткости зависит от формы и размеров тела, а также от материала. В физике закон Гука для деформации растяжения или сжатия принято записывать в другой форме. Отношение ε = x / l называется относительной деформацией, а отношение σ = F / S = –Fупр / S, где S – площадь поперечного сечения деформированного тела, называется напряжением. Тогда закон Гука можно сформулировать так: относительная деформация ε пропорциональна напряжению σ:
Коэффициент E в этой формуле называется модулем Юнга. Модуль Юнга зависит только от свойств материала и не зависит от размеров и формы тела. Модуль Юнга различных материалов меняется в широких пределах. Для стали, например, E ≈ 2·1011 Н/м2, а для резины E ≈ 2·106 Н/м2, т. е. на пять порядков меньше.
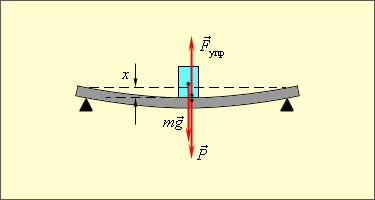
Закон Гука может быть обобщен и на случай более сложных деформаций. Например, при деформации изгиба упругая сила пропорциональна прогибу стержня, концы которого лежат на двух опорах (рис. 1.12.2).
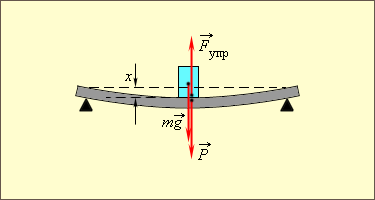 |
| Рисунок 1.12.2.Деформация изгиба. |
Упругую силу действующую на тело со стороны опоры (или подвеса), называют силой реакции опоры. При соприкосновении тел сила реакции опоры направлена перпендикулярно поверхности соприкосновения. Поэтому ее часто называют силой нормального давления. Если тело лежит на горизонтальном неподвижном столе, сила реакции опоры направлена вертикально вверх и уравновешивает силу тяжести: Сила с которой тело действует на стол, называется .
В технике часто применяются спиралеобразные пружины (рис. 1.12.3). При растяжении или сжатии пружин возникают упругие силы, которые также подчиняются закону Гука. Коэффициент k называют жесткостью пружины. В пределах применимости закона Гука пружины способны сильно изменять свою длину. Поэтому их часто используют для измерения сил. Пружину, растяжение которой проградуировано в единицах силы, называют динамометром. Следует иметь в виду, что при растяжении или сжатии пружины в ее витках возникают сложные деформации кручения и изгиба.
| Рисунок 1.12.3.Деформация растяжения пружины. |
В отличие от пружин и некоторых эластичных материалов (резина) деформация растяжения или сжатия упругих стержней (или проволок) подчиняются линейному закону Гука в очень узких пределах. Для металлов относительная деформация ε = x / l не должна превышать 1 %. При больших деформациях возникают необратимые явления (текучесть) и разрушение материала.
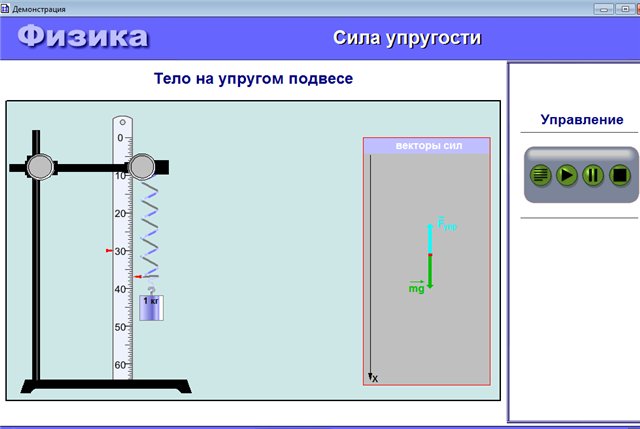
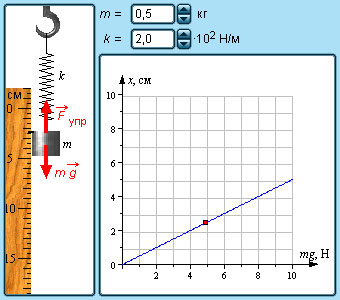 |
|
Модель. Закон Гука |
Закон Гука в математической форме
Формулировка Гука, которую мы привели выше, дает возможность записать его в следующем виде:
,
где изменение длины тела вследствие сжатия или растяжения, F сила, приложенная к телу и вызывающая деформацию (сила упругости), k коэффициент упругости, измеряется в Н/м.
Следует помнить, что закон Гука справедлив только для малых растяжений.
Также отметим, что он при растяжении и сжатии имеет один и тот же вид. Учитывая, что сила величина векторная и имеет направление, то в случае сжатия, более точной будет такая формула:
, но опять-таки, все зависит от того куда будет направлена ось, относительно которой вы проводите измерение .
В чем кардинальная разница между сжатием и растяжением? Ни в чем, если оно незначительно.
Степень применимости можно рассмотреть в таком виде:
Обратим внимание на график. Как видим, при небольших растяжениях (первая четверть координат) долгое время сила с координатой имеет линейную связь (красная прямая), но затем реальная зависимость (пунктир) становится нелинейной, и закон перестает выполняться
На практике это отражается таким сильным растяжением, что пружина перестает возвращаться в исходное положение, теряет свойства. При еще большем растяжении происходит излом, и разрушается структура материала.
При небольших сжатиях (третья четверть координат) долгое время сила с координатой имеет тоже линейную связь (красная прямая), но затем реальная зависимость (пунктир) становится нелинейной, и всё вновь перестает выполняться. На практике это отражается таким сильным сжатием, что начинает выделяться тепло и пружина теряет свойства. При еще большем сжатии происходит слипание витков пружины и она начинает деформироваться по вертикали, а затем и вовсе плавиться.
Как видим формула, выражающая закон, позволяет находить силу, зная изменение длины тела, либо, зная силу упругости, измерить изменение длины:
.
Также, в отдельных случаях можно находить коэффициент упругости. Для того, чтобы понять как это делается, рассмотрим пример задачи:
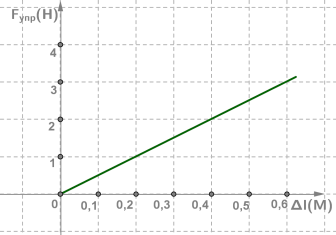
К пружине подсоединен динамометр. Ее растянули, приложив силу в 20 Ньютон, из-за чего она стала иметь длину 1 метр. Затем ее отпустили, подождали пока прекратятся колебания, и она вернулась к своему нормальному состоянию. В нормальном состоянии ее длина составляла 87, 5 сантиметров. Давайте попробуем узнать, из какого материала сделана пружина.
Дано:
Решение:
Найдем численное значение деформации пружины:
Запишем:
.
Отсюда можем выразить значение коэффициента:
Посмотрев таблицу, можем обнаружить, что этот показатель соответствует пружинной стали.
Характеристики сил упругости
Модуль силы упругости, действующий на единицу площади, есть физическая величина, названная напряжением (механическим).
Механическое напряжение, в зависимости от направления приложения силы, может быть:
- нормальным (направленным по нормали к поверхности, $σ$);
- тангенциальным (направленным по касательной к поверхности, $τ$).
Замечание 1
Степень деформации характеризуется количественной мерой – относительной деформацией.
Так, например, относительное изменение длины стержня можно описать формулой:
$ε=\frac{\Delta l}{l}$,
а относительное продольное растяжение (сжатие):
$ε’=\frac{\Delta d}{d}$, где:
$l$ – длина, а $d$ – диаметр стержня.
Деформации $ε$ и $ε’$ протекают одновременно и имеют противоположные знаки, в силу того, что при растяжении изменение длины тела положительно, а изменение диаметра отрицательно; в случаях с сжатием тела знаки меняются на противоположные. Их взаимосвязь описывается формулой:
$ε’=-με$
Здесь $μ$ – коэффициент Пуассона, зависящий от свойств материала.
Закон Гука
По своей природе, упругие силы относятся к электромагнитным, не фундаментальным силам, и, следовательно, они описываются приближенными формулами.
Так, эмпирически установлено, что для малых деформаций относительное удлинение и напряжение пропорциональны, или
$σ=Eε$.
Здесь $E$ – коэффициент пропорциональности, называемый также модулем Юнга. Он принимает такое значение, при котором относительное удлинение равно единице. Модуль Юнга измеряется в ньютонах на квадратный метр (паскалях).
Согласно закону Гука удлинение стержня при упругой деформации пропорционально действующей на стержень силе, или:
$F=\frac{ES}{l}\Delta l=k\Delta l$
Значение $k$ получило название коэффициента упругости.
Деформация твердых тел описывается законом Гука лишь до достижения предела пропорциональности. С повышением напряжения деформация перестает быть линейной, но, вплоть до достижения предела упругости, остаточные деформации не возникают. Таким образом, Закон Гука справедлив исключительно для упругих деформаций.
Сила упругости
Теперь, когда известно, какая формула выражает закон Гука, необходимо разобраться в его основной величине. Основной величиной является сила упругости. Она появляется в определенный момент, когда тело начинает деформироваться, например, когда пружина сжимается или растягивается. Она направлена в обратную сторону от силы тяжести. Когда сила упругости и сила тяжести, действующие на тело, становятся равными, опора и тело останавливаются.
Деформация – это необратимые изменения, происходящие с размерами тела и его формой. Они связанны с перемещением частиц относительно друг друга. Если человек сядет в мягкое кресло, то с креслом произойдет деформация, то есть изменятся его характеристики. Она бывает разных типов: изгиб, растяжение, сжатие, сдвиг, кручение.
Так как сила упругости относится по своему происхождению к электромагнитным силам, следует знать, что возникает она из-за того, что молекулы и атомы – наименьшие частицы, из которых состоят все тела, притягиваются друг другу и отталкиваются друг от друга. Если расстояние между частицами очень мало, значит, на них влияет сила отталкивания. Если же это расстояние увеличить, то на них будет действовать сила притяжения. Таким образом, разность сил притяжения и сил отталкивания проявляется в силах упругости.
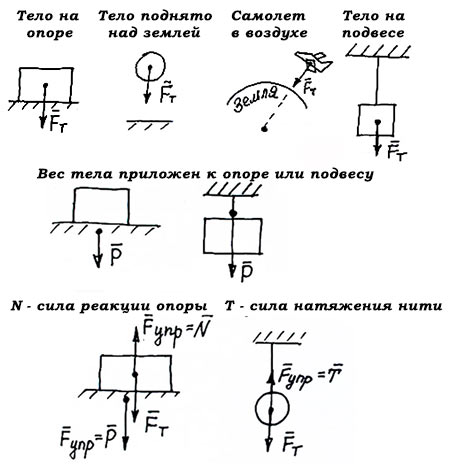
Сила упругости включает в себя силу реакции опоры и вес тела. Сила реакции представляет особый интерес. Это такая сила, которая действует на тело, когда его кладут на какую-либо поверхность. Если же тело подвешено, то силу, действующую на него, называют, силой натяжения нити.
Вес тела
Вес
тела — это сила, с которой предмет
воздействует на опору. Вы скажете, так
это же сила тяжести! Путаница происходит
в следующем: действительно часто вес
тела равен силе тяжести, но это силы
совершенно разные. Сила тяжести — сила,
которая возникает в результате
взаимодействия с Землей. Вес — результат
взаимодействия с опорой. Сила тяжести
приложена в центре тяжести предмета,
вес же — сила, которая приложена на опору
(не на предмет)!
Формулы
определения веса нет. Обозначается эта
силы буквой
.
Сила
реакции опоры или сила упругости
возникает в ответ на воздействие предмета
на подвес или опору, поэтому вес тела
всегда численно одинаков силе упругости,
но имеет противоположное направление.

Сила
реакции опоры и вес — силы одной природы,
согласно 3 закону Ньютона они равны и
противоположно направлены. Вес — это
сила, которая действует на опору, а не
на тело. Сила тяжести действует на тело.
Вес
тела может быть не равен силе тяжести.
Может быть как больше, так и меньше, а
может быть и такое, что вес равен нулю.
Это состояние называется невесомостью.
Невесомость — состояние, когда предмет
не взаимодействует с опорой, например,
состояние полета: сила тяжести есть, а
вес равен нулю!
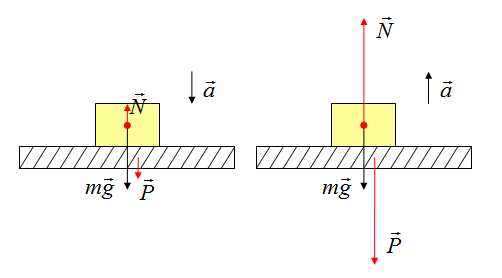
Определить
направление ускорения возможно, если
определить, куда направлена равнодействующая
сила.
Обратите
внимание, вес — сила, измеряется в
Ньютонах. Как верно ответить на вопрос:
«Сколько ты весишь»? Мы отвечаем
50 кг, называя не вес, а свою массу! В этом
примере, наш вес равен силе тяжести, то
есть примерно 500Н!. Перегрузка- отношение веса к силе тяжести
Перегрузка— отношение веса к силе тяжести
Литература
- Кабардин О.Ф. Физика: Справ. материалы: Учеб. пособие для учащих-ся. – М.: Просвещение, 1991. – 367 с.
- Кикоин И.К., Кикоин А.К. Физика: Учеб. для 9 кл. сред. шк. – М.: Про-свещение, 1992. – 191 с.
- Физика: Механика. 10 кл.: Учеб. для углубленного изучения физики / М.М. Балашов, А.И. Гомонова, А.Б. Долицкий и др.; Под ред. Г.Я. Мякишева. – М.: Дрофа, 2002. – 496 с.
- Элементарный учебник физики: Учеб. пособие. В 3 т. / Под ред. Г.С. Ландсберга: т. 1. Механика. Теплота. Молекулярная физика. – М.: Физ-матлит, 2004. – 608 с.
- Яворский Б.М., Селезнев Ю.А. Справочное руководство по физике для поступающих в вузы и самообразования. – М.: Наука, 1983. – 383 с.
Силы вокруг нас (силы тяжести, трения, упругости)
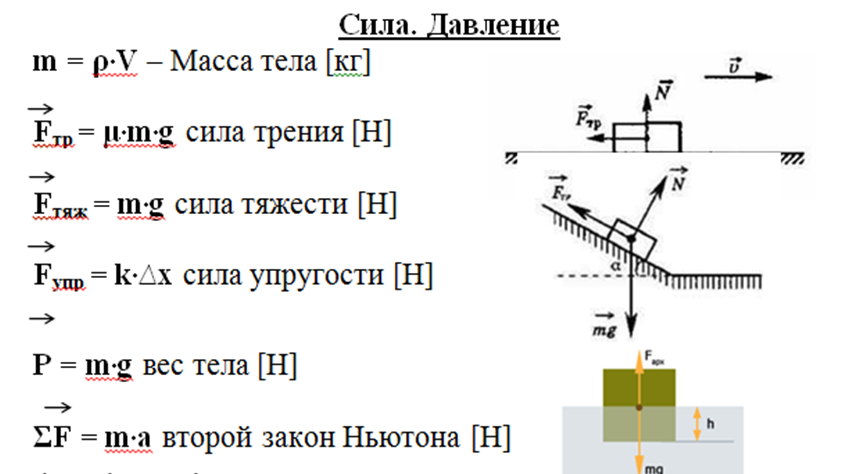
1. Сила – термин, являющийся: а) кратким обозначением действия одного тела на другое; б) названием физической величины, характеризующей действие тел друг на друга (взаимодействие тел).
2. Признаки действия силы: меняется скорость и/или направление движения тела, меняются размеры и/или форма тела.
3. Динамометр – прибор для измерения сил. Единица силы в СИ – 1 Н (один ньютон).
4. На чертежах силу изображают в виде прямой стрелки, называемой вектором силы. Длина вектора символизирует числовое значение силы, а направление вектора указывает направление силы.
5. Если две силы: а) приложены к одному и тому же телу, б) направлены противоположно по одной прямой и в) имеют одинаковую величину, их называют уравновешенными силами.

6. Если на тело действуют только уравновешенные силы, то оно либо покоится, либо движется прямолинейно и равномерно. И наоборот.
7. Силой упругости называют силу, которая возникает при изменении формы и/или размеров тела. Вектор силы упругости всегда противонаправлен вектору той силы, которая вызвала деформацию. Сила упругости обусловлена взаимодействием частиц, из которых состоит тело.
- Силу, действующую на тело со стороны опоры, называют силой нормальной реакции.
- Закон Гука для силы упругости: Fупр = kx, где Fупр — модуль силы упругости, х — удлинение пружины.
- Прибор для измерения силы называют динамометром.
- Равнодействующей двух или нескольких сил называют силу, которая производит на тело такое же действие, как одновременное действие этих сил.
8. Силой трения называют силу, которая возникает при движении (или попытке вызвать движение) одного тела по поверхности другого. Она всегда направлена противоположно направлению скольжения (или направлению возможного скольжения) рассматриваемого тела.
- Основная причина возникновения сил трения скольжения и покоя — зацепление неровностей на поверхностях соприкасающихся тел.
- Модуль силы трения скольжения Fтр= μN, где N — модуль силы нормальной реакции, μ — коэффициент трения.
- Сила трения покоя возникает, когда пытаются сдвинуть одно из соприкасающихся тел относительно другого. Эта сила препятствует движению тел друг относительно друга.
- Сила трения покоя не превышает некоторой предельной величины, которую называют максимальной силой трения покоя. Обычно принимается, что максимальная сила трения покоя равна силе трения скольжения.
- Сила трения качения обычно намного меньше силы трения скольжения — на этом основано использование колеса.
9. Силой тяжести называют силу, с которой тело притягивается к планете. Сила тяжести всегда направлена к центру масс этой планеты. Модуль силы тяжести Fт = gm, где m — масса тела, g = 9,8 Н/кг. Точку приложения силы тяжести называют центром тяжести тела.
10. Весом тела называют силу, с которой это тело действует на свою опору или подвес. Условие равенства веса силе тяжести: тело и его опора (или подвес) должны покоиться или двигаться вместе прямолинейно и равномерно, при этом не должна действовать архимедова сила.
- Вес тела приложен к опоре или подвесу, а сила тяжести — к самому телу.
- Состояние, при котором вес тела равен нулю, называют состоянием невесомости. В состоянии невесомости находятся тела, на которые действует только сила тяжести.
11. Механизмы – устройства для преобразования движения и сил. Простые механизмы – наклонная плоскость (и ее разновидности: клин и винт) и рычаг (и его разновидности: ворот и блоки).
Схемы «Силы вокруг нас (силы тяжести, трения, упругости)».


Конспект по теме «Силы вокруг нас (силы тяжести, трения, упругости)».
Следующая тема: «Задачи на силы тяжести и вес тела»
Вес тела
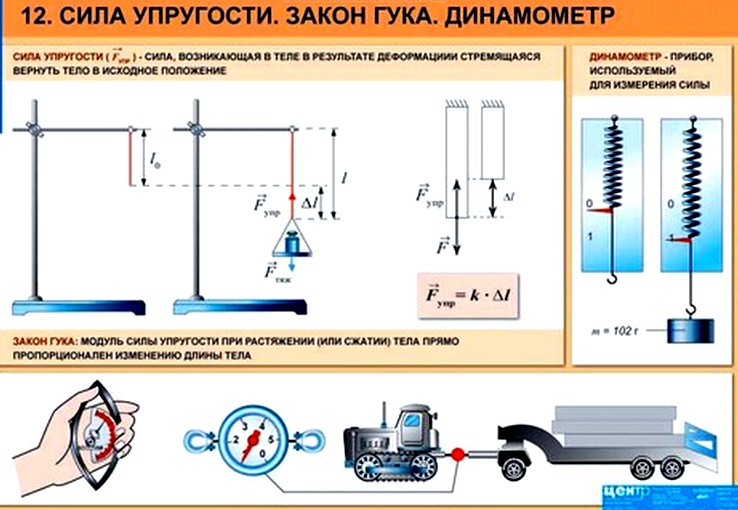
Вес тела — это сила, с которой предмет воздействует на опору. Вы скажете, так это же сила тяжести! Путаница происходит в следующем: действительно часто вес тела равен силе тяжести, но это силы совершенно разные. Сила тяжести — сила, которая возникает в результате взаимодействия с Землей. Вес — результат взаимодействия с опорой. Сила тяжести приложена в центре тяжести предмета, вес же — сила, которая приложена на опору (не на предмет)!
Формулы определения веса нет. Обозначается эта силы буквой .
Сила реакции опоры или сила упругости возникает в ответ на воздействие предмета на подвес или опору, поэтому вес тела всегда численно одинаков силе упругости, но имеет противоположное направление.
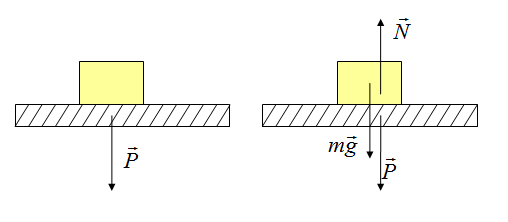
Сила реакции опоры и вес — силы одной природы, согласно 3 закону Ньютона они равны и противоположно направлены. Вес — это сила, которая действует на опору, а не на тело. Сила тяжести действует на тело.
Вес тела может быть не равен силе тяжести. Может быть как больше, так и меньше, а может быть и такое, что вес равен нулю. Это состояние называется невесомостью
. Невесомость — состояние, когда предмет не взаимодействует с опорой, например, состояние полета: сила тяжести есть, а вес равен нулю!
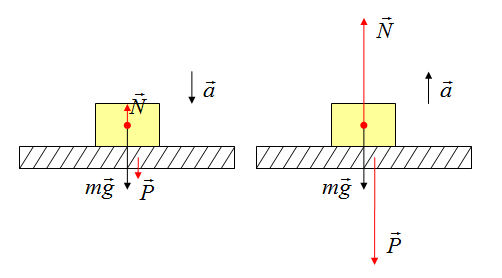
Определить направление ускорения возможно, если определить, куда направлена равнодействующая сила
Обратите внимание, вес — сила, измеряется в Ньютонах. Как верно ответить на вопрос: «Сколько ты весишь»? Мы отвечаем 50 кг, называя не вес, а свою массу! В этом примере, наш вес равен силе тяжести, то есть примерно 500Н!. Перегрузка
— отношение веса к силе тяжести
Перегрузка
— отношение веса к силе тяжести
Что такое сила упругости?
Силой упругости называют такую силу, которая возникает через деформации тела и направленная в сторону, противоположную перемещениям частиц тела при деформации.
Для более наглядного примера, чтобы лучше понять, что такое сила упругости, возьмем яркий пример из повседневной жизни. Представьте, что перед вами обычная бельевая веревка, на которую вы повесили мокрое белье. Если на хорошо натянутую горизонтально веревку мы повесим мокрое белье, то увидим, как под весом вещей эта веревка начинает прогибаться и растягиваться.
Вначале мы с вами вешаем на веревку одну мокрую вещь и видим, как она вместе с веревкой прогибается к земле, а потом останавливается. Затем мы вешаем следующую вещь и видим, что повторяется такое же действие и веревка прогибается еще больше.
В этом случае напрашивается вывод, что при увеличении силы, которая воздействует на веревку, будет происходить деформация, пока силы противодействия этой деформации не будут равны весу всех вещей. И только после этого движение вниз прекратится.
Следует отметить, что работа силы упругости заключается в сохранении целостности предметов, на которые мы воздействуем другими предметами. Если силы
упругости не способны с этим справиться, то тогда тело деформируется безвозвратно, то есть веревка может просто порваться.
И здесь напрашивается риторический вопрос. В какой момент возникла сила упругости? А возникает она тогда, когда мы только начинаем вешать белье, то есть в момент первоначального воздействия на тело. И когда белье высохло, и мы его снимаем, то сила упругости исчезает.
Упругие силы и деформации
Определение 1
Сила, возникающая в теле в результате его деформации и стремящаяся вернуть его в начальное состояние, называется силой упругости.
Все тела материального мира подвержены деформациям различного рода. Деформации возникают в силу перемещения и, как следствие, изменения положения частиц тела друг относительно друга. По степени обратимости можно выделить:
- упругие, или обратимые деформации;
- пластические (остаточные), или необратимые деформации.
В случаях, когда тело по завершении воздействия сил, приводящих к деформации, восстанавливает свои первоначальные параметры, деформация называется упругой.
Стоит отметить, что при упругой деформации воздействие внешней силы на тело не превышает предела упругости. Таким образом, силы упругости компенсируют внешнее воздействие на тело.
В ином случае деформация является пластической или остаточной. Тело, подвергшееся воздействия такого характера не восстанавливает начальные размеры и форму.
Упругие силы, возникающие в телах, не способны полностью уравновесить силы, вызывающие пластическую деформацию.
В целом, различают ряд простых деформаций:
- растяжение (сжатие);
- изгиб;
- сдвиг;
- кручение.
Как правило, деформации нередко представляют собой совокупность нескольких представленных типов воздействия, что позволяет свести все деформации к двум наиболее распространенным типам, а именно к растяжению и сдвигу.