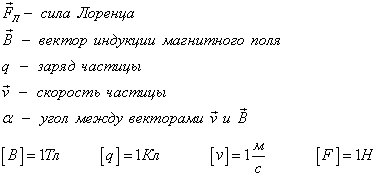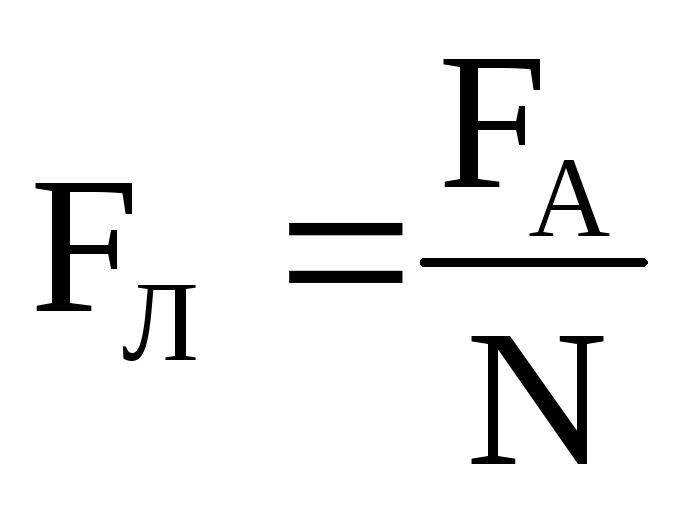Сила лоренца

Введение

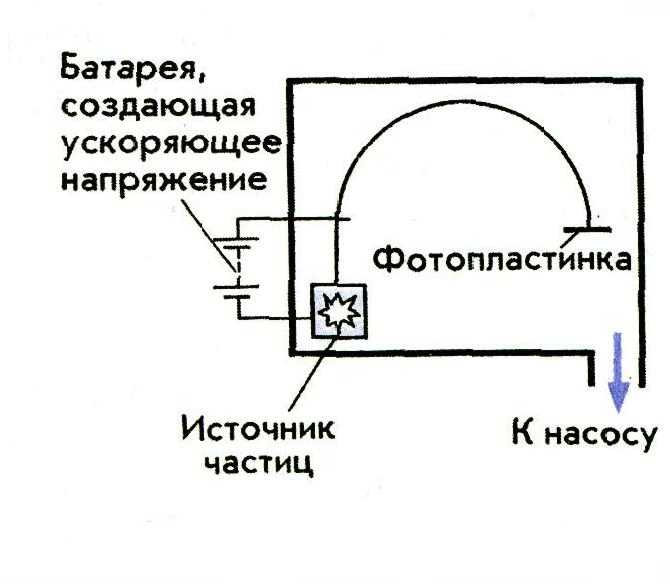
Самое раннее использование магнитного поля для измерения потока жидкости датируется XIX веком, когда в 1832 году Майкл Фарадей пытался определить скорость течения реки Темза. Фарадей применил метод, в котором поток (течение реки) подвергался воздействию магнитного поля (магнитное поле Земли) и возникающая разница потенциалов измерялась при помощи двух электродов, расположенных поперек реки. По этому же принципу работает один из самых коммерчески успешных электромагнитных приборов для изучения потока жидкости — кондукционный расходомер. Теоретическая основа для создания подобных приборов была разработана английским физиком Артуром Шерклифом (Arthur Shercliff) в 50-х годах двадцатого века. Хотя кондукционные расходомеры широко применяются для определения расхода различных жидкостей при комнатной температуре в химической, фармацевтической и пищевой промышленности, они практически не применимы для исследования высокотемпературных и агрессивных сред или для измерения локальной скорости в случае ограниченного доступа к каналу или трубе. Так как использование метода предполагает применение электродов, погруженных в жидкость, кондукционная расходометрия ограничена областью относительно невысоких температур, лежащих значительно ниже точки плавления большинства металлов.

Термин Велосиметрия силой Лоренца был предложен Артуром Шерклифом ещё в середине прошлого века. Но, несмотря на это, практическое применение метода стало возможным лишь с относительно недавнего времени; отправной точкой здесь послужило создание сильных постоянных магнитов на основе редкоземельных материалов, разработка прецизионных методик силовых измерений, появление высокотехнологичного программного обеспечения для моделирования процессов магнитной гидродинамики (МГД). Все это позволило ВСЛ стать конкурентноспособной методикой измерения расхода жидкостей. В данное время метод ВСЛ продолжает своё развитие, как техника измерения расхода в прикладной металлургии и других областях.

Основываясь на предложенной Шерклифом теории были разработаны несколько методов измерения расхода, не требующих какого-либо механического контакта с исследуемой жидкостью. Среди них расходомер на основе действия вихревых токов, который измеряет возбужденные потоком жидкости изменения электрического сопротивления стержней, взаимодействующих с потоком. Существует также бесконтактный расходомер, действие которого основано на измерении деформации приложенного магнитного поля под действием потока жидкости.

Причины дребезга кнопок

Кнопка ардуино – один из самых популярных и простых видов датчиков. В основе работы любой кнопки лежит механический способ смыкания-размыкания контактов. Нажимая на любую, даже самую простую тактовую кнопку, мы формируем определенное давление на внутренние механизмы (пластины или пружины), в результате чего происходит сближение или расхождение металлических пластин.

Мы люди взрослые и хорошо понимаем, что идеального в мире ничего не существует, в том числе идеально гладких поверхностей, контактов без неровностей, сопротивления и паразитной емкости. В нашем неидеальном мире в момент нажатия на кнопку в месте соединения контакты не соприкасаются мгновенно, микро-неровности на поверхности не позволяют пластинам мгновенно соединиться. Из-за этого в короткий промежуток времени на границе пластинок меняется и сопротивление, и взаимная емкость, из-за чего возникают масса разнообразных изменений уровня тока и напряжения. Другими словами, возникают очень интересные, хотя и не очень приятные процессы, которые в электротехнике называют переходными.

Переходные процессы протекают очень быстро и исчезают за доли миллисекунд. Поэтому мы редко их замечаем, например, когда включаем свет в комнате. Лампа накаливания не может менять свою яркость с такой скоростью, и тем более не может реагировать на изменения наш мозг. Но, обрабатывая сигал от кнопки на таком быстром устройстве, как Arduino, мы вполне можем столкнуться с такими переходными эффектами и должны их учитывать при программировании.

В идеальном мире форма сигнала после нажатия на кнопку должна быть строго прямоугольная. В реальных же условиях вместе резкого перехода мы видим множество пиков и спадов.

Классный массаж простаты дома мужу для кайфа поднимает настроение

Массаж простаты дома мужу для кайфа – это один из распространенных способов разнообразить интимную жизнь и одновременно улучшить половое здоровье партнера. Для многих известно, почему это доставляет удовольствие мужчине, а вот как делать массаж правильно знают не все.

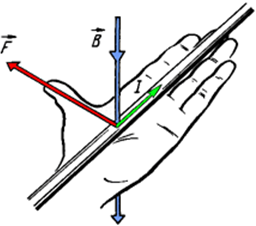
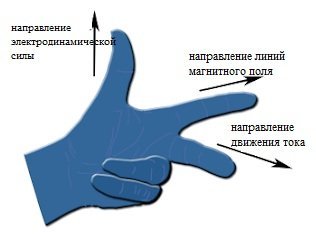
Правило лівої руки

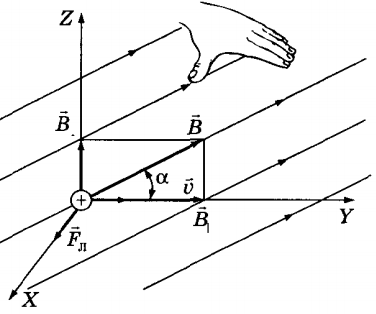
Правило лівої руки дозволяє фізикам визначати напрямок і повернення вектора магнітної (електродинамічної) енергії. Уявіть собі, що наша ліва рука розташована таким чином, що лінії магнітного поля направлені перпендикулярно внутрішньої поверхні руки (так, що вони проникають всередину руки), а всі пальці за винятком великого вказують на напрямок протікання позитивного струму, відхилений великий палець вказує на напрямок електродинамічної сили, що діє на позитивний заряд, поміщений в це поле.

Ось так це буде виглядати схематично.

Є також і другий спосіб визначення напрямку електромагнітної сили. Він полягає в розташуванні великого, вказівного і середнього пальців під прямим кутом. В цьому випадку вказівний палець буде показувати напрямок ліній магнітного поля, середній – напрямок руху струму і великий – напрямок електродинамічної сили.

Примеры из жизни

Насколько вы сильны?

Рассмотрим простейший пример. Ваш ребёнок сел на санки и просит вас его покатать. С какой силой вам нужно тянуть эти санки, чтобы ребёнок остался доволен быстрой ездой ? Пока санки с ребёнком остаются в состоянии покоя, все силы, действующие на них, уравновешены. Состояние покоя — это частный случай инерции. Здесь на санки действуют две силы: тяжести Fт = m•g, направленная вертикально вниз, и нормального давления N, направленная вертикально вверх. Поскольку санки не движутся, то N – m•g = 0. Тогда из этого равенства следует, что N = m•g.

Когда вы решили покатать своего ребёнка, вы прикладываете силу тяги (Fтяги) к санкам с ребёнком. Когда вы начинаете тянуть санки, возникает сопротивление движению, вызванное силой трения (Fтр.), направленной в противоположную сторону. Это так называемая сила трения покоя. Когда тело не движется, она равна нулю. Стоит потянуть за санки — и появляется сила трения покоя, которая меняется от нуля до некоторого максимального значения (Fтр. max). Как только Fтяги превысит Fтр.max, санки с ребёнком придут в движение.

Чтобы найти Fтяги, применим второй закон Ньютона: Fтяги – Fтр.max = m•a, где a – ускорение, с которым вы тянете санки, m – масса санок с ребёнком. Допустим, вы разогнали санки до определённой скорости, которая не изменяется. Тогда a = 0 и вышеприведённое уравнение запишется в виде: Fтяги – Fтр. max = 0, или Fтяги = Fтр.max. Есть известный закон из физики, который устанавливает определённую зависимость для Fтр.max и N. Эта зависимость имеет вид: Fтр.max = fmax • N, где fmax – максимальный коэффициент трения покоя.

Если в эту формулу подставить выражение для N, то мы получим Fтр.max = fmax•m•g. Тогда формула искомой силы тяги примет вид: Fтяги = fmax•m•g = fск•m•g, где fск = fmax – коэффициент трения скольжения, g – ускорение свободного падения. Допустим, fск = 0,7, m = 30 кг, g = 9,81 м/с², тогда Fтяги = 0,7 • 30 кг • 9,81 м/с² = 206,01 Н (Ньютона).

Действие магнитного поля на движущийся заряд. Сила Лоренца

Подробности: Просмотров: 581

«Физика — 11 класс»

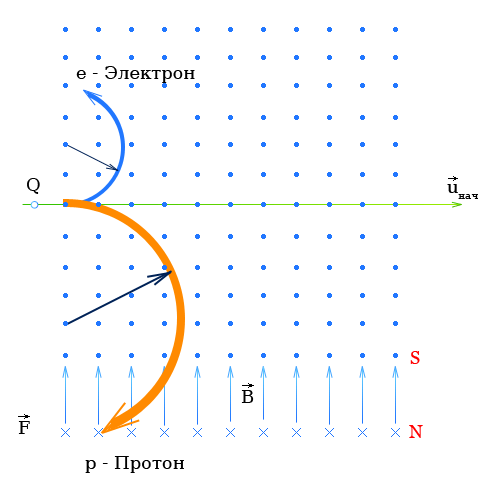
Магнитное поле действует с силой на движущиеся заряженные частицы, в то числе и на проводники с током.
Какова же сила, действующая на одну частицу?

1.
Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца в честь великого голландского физика X. Лоренца, создавшего электронную теорию строения вещества.
Силу Лоренца можно найти с помощью закона Ампера.

Модуль силы Лоренца равен отношению модуля силы F, действующей на участок проводника длиной Δl, к числу N заряженных частиц, упорядоченно движущихся в этом участке проводника:

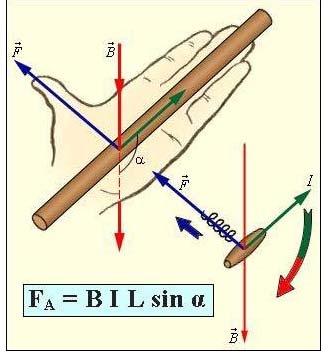
Так как сила (сила Ампера), действующая на участок проводника со стороны магнитного поля
равна F = | I | BΔl sin α,
а сила тока в проводнике равна I = qnvS
где
q — заряд частиц
n — концентрация частиц (т.е. число зарядов в единице объема)
v — скорость движения частиц
S — поперечное сечение проводника.
тогда получаем:
На каждый движущийся заряд со стороны магнитного поля действует сила Лоренца, равная:

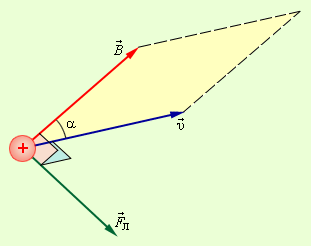
где α — угол между вектором скорости и вектором магнитной индукции.

Сила Лоренца перпендикулярна векторам и .

2.Направление силы Лоренца

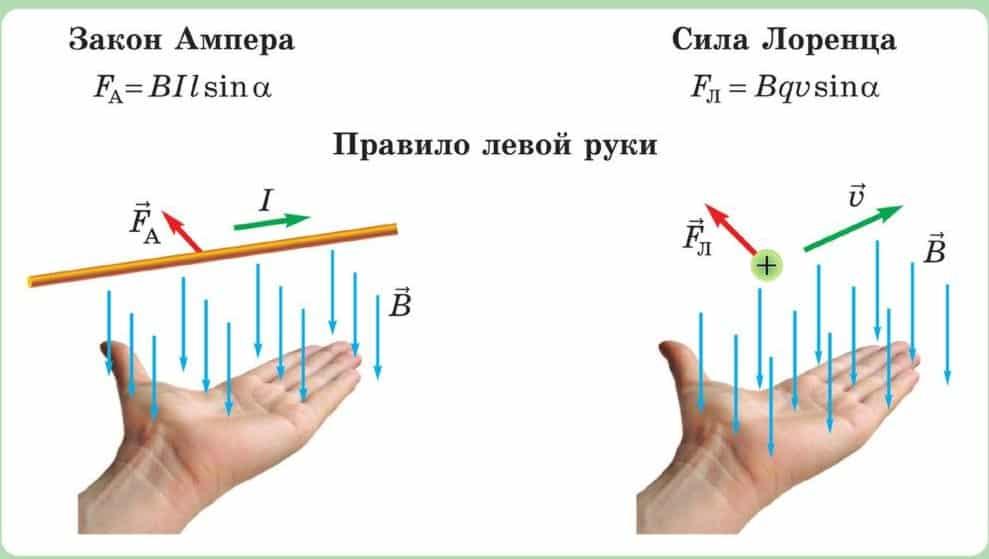
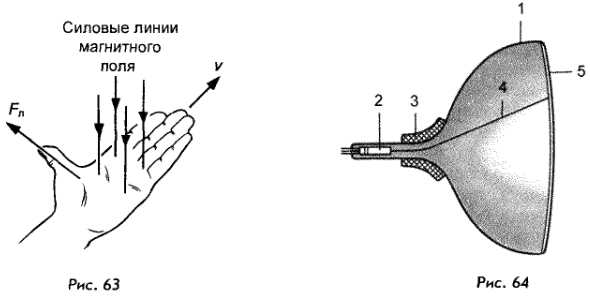
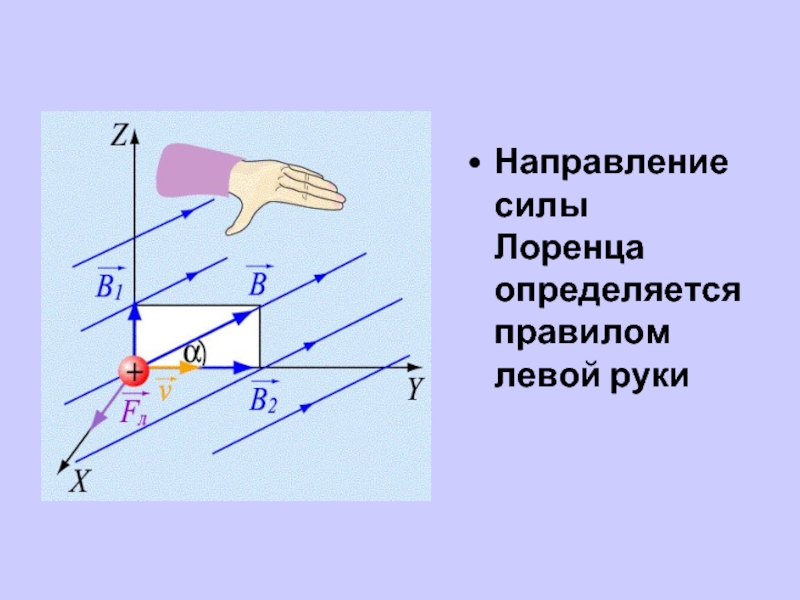
Направление силы Лоренца определяется с помощью того же правила левой руки, что и направление силы Ампера:

Если левую руку расположить так, чтобы составляющая магнитной индукции, перпендикулярная скорости заряда, входила в ладонь, а четыре вытянутых пальца были направлены по движению положительного заряда (против движения отрицательного), то отогнутый на 90° большой палец укажет направление действующей на заряд силы Лоренца F_л.

3.
Если в пространстве, где движется заряженная частица, существует одновременно и электрическое поле, и магнитное поле, то суммарная сила, действующая на заряд, равна:
= _эл + _л
где сила, с которой электрическое поле действует на заряд q, равна F_эл = q.

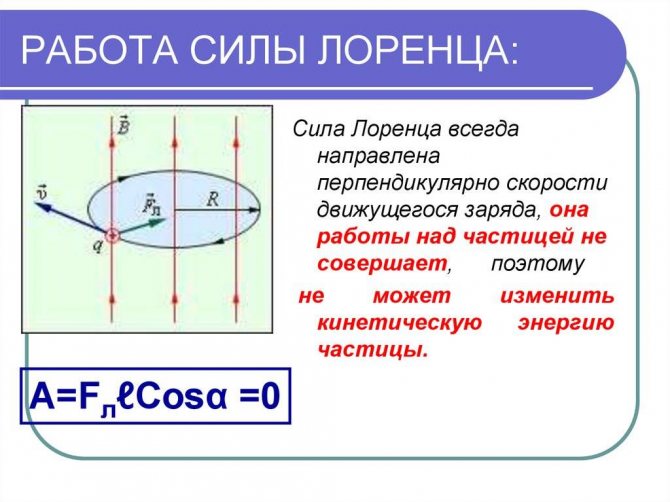
4.Cила Лоренца не совершает работы, т.к. она перпендикулярна вектору скорости частицы.
Значит сила Лоренца не меняет кинетическую энергию частицы и, следовательно, модуль ее скорости.
Под действием силы Лоренца меняется лишь направление скорости частицы.

5.Движение заряженной частицы в однородном магнитном поле

однородное

Сила Лоренца зависит от модулей векторов скорости частицы и индукции магнитного поля.
Магнитное поле не меняет модуль скорости движущейся частицы, значит остается неизменным и модуль силы Лоренца.
Сила Лоренца перпендикулярна скорости и, следовательно, определяет центростремительное ускорение частицы.
Неизменность по модулю центростремительного ускорения частицы, движущейся с постоянной по модулю скоростью, означает, чтоВ однородном магнитном поле заряженная частица равномерно движется по окружности радиусом r.

Согласно второму закону Ньютона

Тогда радиус окружности, по которой движется частица, равен:

Время, за которое частица делает полный оборот (период обращения), равно:

6.Использование действия магнитного поля на движущийся заряд.

Действие магнитного поля на движущийся заряд используют в телевизионных трубках-кинескопах, в которых летящие к экрану электроны отклоняются с помощью магнитного поля, создаваемого особыми катушками.

Сила Лоренца используется в циклотроне — ускорителе заряженных частиц для получения частиц с большими энергиями.

На действии магнитного поля основано также и устройство масс-спектрографов, позволяющих точно определять массы частиц..

Следующая страница «Магнитные свойства вещества»

Назад в раздел «Физика — 11 класс, учебник Мякишев, Буховцев, Чаругин»

Магнитное поле. Физика, учебник для 11 класса — Класс!ная физика

Магнитное поле и взаимодействие токов —
Магнитная индукция. Линии магнитной индукции —
Модуль вектора магнитной индукции. Сила Ампера —
Электроизмерительные приборы. Громкоговоритель —
Действие магнитного поля на движущийся заряд. Сила Лоренца —
Магнитные свойства вещества —
Примеры решения задач —
Краткие итоги главы

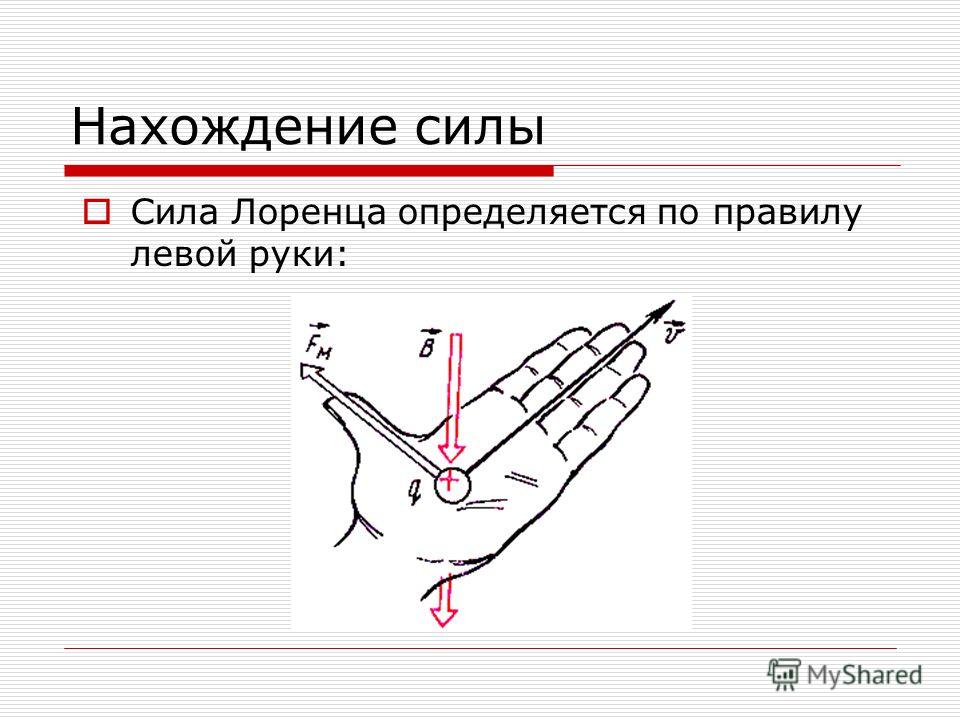
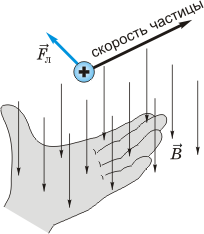
Как направлена сила Лоренца

Чтобы определить направление силы Лоренца, как и с силой Ампера, работает правило левой руки. Это значит, чтобы понять, куда направлено значение Fл нужно раскрыть ладонь левой руки так, чтобы в руку входили линии магнитной индукции, а вытянутые четыре пальца указывали направление вектора скорости. Тогда большой палец, отогнутый под прямым углом к ладони, указывает направление силы Лоренца. На картинке ниже вы видите, как определить направление.

Внимание! Направление Лоренцового действия перпендикулярно движению частицы и линиям магнитной индукции

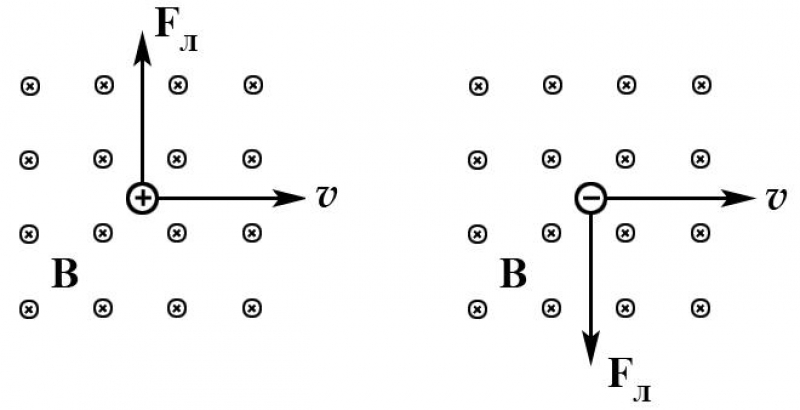
При этом, если быть точнее, для положительно и отрицательно заряженных частиц имеет значение направление четырёх развернутых пальцев. Выше описанное правило левой руки сформулировано для положительной частицы. Если она заряжена отрицательно, то линии магнитной индукции должны быть направлены не в раскрытую ладонь, а в её тыльную сторону, а направление вектора Fл будет противоположным.

Теперь мы расскажем простыми словами, что даёт нам это явление и какое реальное воздействие она оказывает на заряды. Допустим, что электрон движется в плоскости, перпендикулярной направлению линий магнитной индукции. Мы уже упомянули, что Fл не воздействует на скорость, а лишь меняет направление движения частиц. Тогда сила Лоренца будет оказывать центростремительное воздействие. Это отражено на рисунке ниже.

Уравнение (единицы СИ)

Заряженная частица

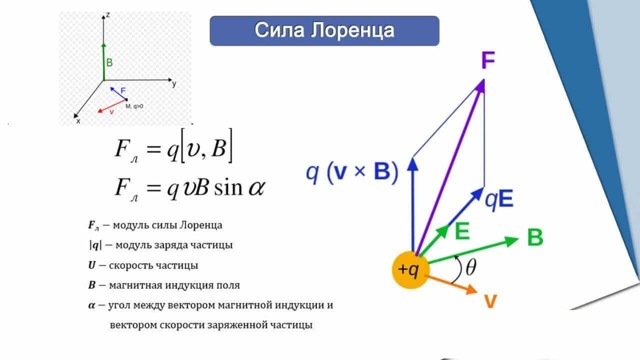
Сила Лоренца f{\displaystyle f} действующая на заряженную частицу (заряда q{\displaystyle q}) при движении (со скоростью v{\displaystyle v}). E{\displaystyle \mathbf {E} } поле и B{\displaystyle B} поле меняются в пространстве и во времени.

Сила F{\displaystyle \mathbf {F} }, действующая на частицу с электрическим зарядом q{\displaystyle q}, движущуюся со скоростью v{\displaystyle \mathbf {v} }, во внешнем электрическом E{\displaystyle \mathbf {E} } и магнитном B{\displaystyle \mathbf {B} } полях, такова:

F=q(E+v×B),{\displaystyle \mathbf {F} =q(\mathbf {E} +\mathbf {v} \times \mathbf {B} ),}

где ×{\displaystyle \times } — векторное произведение. Все величины, выделенные жирным, являются векторами. Более явно:

F(r,t,q)=qE(r,t)+qr˙×B(r,t),{\displaystyle \mathbf {F} (\mathbf {r} ,t,q)=q\mathbf {E} (\mathbf {r} ,t)+q\mathbf {\dot {r}} \times \mathbf {B} (\mathbf {r} ,t),}

где r{\displaystyle \mathbf {r} } — радиус-вектор заряженной частицы, t{\displaystyle t} — время, точкой обозначена производная по времени.

Непрерывное распределение заряда

Сила Лоренца (на единичный 3-объём) f{\displaystyle f} действующая на непрерывное распределение заряда (зарядовая плотность ρ) при движении. 3-плотность потока J{\displaystyle J} соответствует движению заряженного элемента dq{\displaystyle dq} в объеме dV{\displaystyle dV}.

Для непрерывного распределения заряда, сила Лоренца принимает вид:

dF=dq(E+v×B),{\displaystyle d\mathbf {F} =dq\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right),}

где dF{\displaystyle d\mathbf {F} } — сила, действующая на маленький элемент dq{\displaystyle dq}.

Упрощенная схема

Вы уже знаете, что такое диодный мост, поэтому рассмотрим простейший принцип его работы. Когда переменный ток попадает на анод Uвх, оно проходит через положительные полупериоды, тогда как отрицательные полностью удаляются. При этом выходное напряжение, обозначенное с правой стороны под аббревиатурой Uвых, не является выпрямленным, хоть и проходит в одном направлении. Его частота равна тем же 50 Герц, или 50 пикам в секунду.

Чтобы сгладить эти пики к схеме подключается конденсатор высокой емкости. Получается выпрямительный диодный мост –на пике конденсатор заряжается, а на падении отдает заряд в сеть. Это позволяет частично сгладить график частоты и выровнять его, выведя на постоянное значение.

Подобная схема соединения диода и конденсатора носит название однополупериодной и не является достаточной для выравнивания тока в современных устройствах. У нее есть серьезные недостатки:

Нормально выровнять пульсации до настоящей прямой невозможно.
У схемы довольно малый коэффициент полезного действия.
Нерациональное использование трансформатора, чересчур большой вес устройства.

Эти системы сегодня практически не используют или применяют их для маломощных устройств. Более логичные и надежные схемы называются двухполупериодными. Их основное достоинство – возможность инвертировать нижние волны в верхние. Именно подобные системы и называют диодным мостом.

Частные случаи

Направление движения частицы в зависимости от её заряда при векторе магнитной индукции, перпендикулярном вектору скорости (к нам из плоскости рисунка, перпендикулярно ей)

В однородном магнитном поле, направленном перпендикулярно вектору скорости, под действием силы Лоренца заряженная частица будет равномерно двигаться по окружности постоянного радиуса r{\displaystyle r} (называемого также гирорадиусом). Сила Лоренца в этом случае является центростремительной силой:

СГС	СИ
mv2r=\|q\|cvB⇒r=cm\|q\|⋅vB{\displaystyle {mv^{2} \over r}={\|q\| \over c}vB\Rightarrow r={cm \over \|q\|}\cdot {v \over B}}	mv2r=\|q\|vB⇒r=m\|q\|⋅vB{\displaystyle {mv^{2} \over r}=\|q\|vB\Rightarrow r={m \over \|q\|}\cdot {v \over B}}

Работа силы Лоренца будет равна нулю, поскольку векторы силы и скорости всегда ортогональны. При скорости v {\displaystyle v\ }, намного меньшей скорости света, круговая частота ω {\displaystyle \omega \ } не зависит от v {\displaystyle v\ }:

СГС	СИ
ω=\|q\|Bmc{\displaystyle \omega ={\|q\|B \over mc}}	ω=\|q\|Bm{\displaystyle \omega ={\|q\|B \over m}}

Если заряженная частица движется в магнитном поле так, что вектор скорости v {\displaystyle v\ } составляет с вектором магнитной индукции B{\displaystyle \mathbf {B} } угол α {\displaystyle \alpha \ }, то траекторией движения частицы является винтовая линия с радиусом r {\displaystyle r\ } и шагом винта h {\displaystyle h\ }:

СГС	СИ
r=mc\|q\|⋅vsin⁡αB{\displaystyle r={mc \over \|q\|}\cdot {v\sin \alpha \over B}}, h=2πB⋅mc\|q\|⋅vcos⁡α{\displaystyle h={2\pi \over B}\cdot {mc \over \|q\|}\cdot v\cos \alpha }	r=m\|q\|⋅vsin⁡αB{\displaystyle r={m \over \|q\|}\cdot {v\sin \alpha \over B}}, h=2πB⋅m\|q\|⋅vcos⁡α{\displaystyle h={2\pi \over B}\cdot {m \over \|q\|}\cdot v\cos \alpha }

Уравнение (единицы СИ)

Заряженная частица

Силой F действующий на частицу электрического заряда q с мгновенной скоростью v, из-за внешнего электрического поля E и магнитного поля B, дают:

где векторный продукт креста. Все жирные количества — векторы. Более явно заявленный:

в котором r — вектор положения заряженной частицы, t — время, и сверхточка — производная времени.

Положительно заряженная частица будет ускорена в той же самой линейной ориентации как область E, но изогнется перпендикулярно и к мгновенному скоростному вектору v и к области B согласно правому правилу (подробно, если большой палец правых пунктов вдоль v и указательный палец вдоль B, то средний палец указывает вдоль F).

Термин qE называют электрической силой, в то время как термин qv B называют магнитной силой. Согласно некоторым определениям, термин «сила Лоренца» относится определенно к формуле для магнитной силы с полной электромагнитной силой (включая электрическую силу) данный некоторое другое (нестандартное) имя. Эта статья не будет следовать этой номенклатуре: В дальнейшем термин «сила Лоренца» отнесется только к выражению для полной силы.

Магнитный компонент силы силы Лоренца проявляется как сила, которая действует на находящийся под напряжением провод в магнитном поле. В том контексте это также называют лапласовской силой.

Непрерывное распределение обвинения

Для непрерывного распределения обвинения в движении уравнение силы Лоренца становится:

где dF — сила на маленькой части распределения обвинения с обвинением dq. Если обе стороны этого уравнения разделены на объем этой маленькой части распределения обвинения dV, результат:

где f — плотность силы (сила за единичный объем), и ρ — плотность обвинения (обвинение за единичный объем). Затем, плотность тока, соответствующая движению континуума обвинения, является

таким образом, непрерывный аналог уравнению —

Полная сила — интеграл объема по распределению обвинения:

Устраняя ρ и J, используя уравнения Максвелла и управляя использованием теорем векторного исчисления, эта форма уравнения может использоваться, чтобы получить тензор напряжения Максвелла σ, в свою очередь это может быть объединено с вектором Пойнтинга S, чтобы получить электромагнитный тензор энергии напряжения T используемый в Общей теории относительности.

С точки зрения σ и S, другим способом написать силу Лоренца (за единицу 3-й объем) является

где c — скорость света и ∇ · обозначает расхождение области тензора. Вместо суммы обвинения и его скорости в электрических и магнитных полях, это уравнение связывает энергетический поток (поток энергии в единицу времени за расстояние единицы) в областях к силе, проявленной на распределении обвинения. Дополнительную информацию см. в Ковариантной формулировке классического электромагнетизма.

Режим прозвонки

Чтобы проверить работоспособность лампочки, достаточно знать, как прозвонить обычную электроцепь. Для этого переключатель устанавливают в режим «прозвона» – в положение с символом диода.

Затем одним щупом касаются центрального контакта цоколя, вторым – боковой поверхности с резьбой. Сигнал сработает, если сопротивление меньше 50–70 Ом. Это указывает на хорошую электропроводимость цепи и означает, что лампочка исправна.

Связь между силой Ампера и силой Лоренца

Действуя на проводник с током, магнитное поле воздействует на каждую заряженную частицу, создающую этот ток. А сила Ампера действует на весь проводник. Таким образом, сила Ампера равна сумме всех сил Лоренца, действующих на проводник с током.

F_A= F·N

где F– сила Лоренца;

N— число частиц.

Отсюда F= F_AN

I = nqvS

N = nSl

Подставив эти выражения в формулу, получим выражение для силы Лоренца в магнитном поле:

F = qvBˑsinα.

Это выражение позволяет вычислить силу Лоренца в магнитном поле. Но магнитное поле не существует отдельно. Изменяясь, вместе с электрическим полем они порождают друг друга, образуя электромагнитное поле. А оно в каждой точке своего пространства характеризуется напряжённостью электрического поля Еи индукцией магнитного поляВ. И если электрически заряженная частица движется в электромагнитном поле, то на неё одновременно действуют и электрическое, и магнитное поле. Значит, величина силы Лоренца, действующая со стороны электромагнитного поля на частицу с зарядом q, движущуюся со скоростью v, зависит от этих величин:

F = q(E + vxB).

F, E, vиB) – векторные величины.

vxB– векторное произведение скорости движения частицы и индукции магнитного поля.

Направление силы Лоренца, как и силы Ампера, определяют с помощью правила левой руки: «Если расположить ладонь левой руки таким образом, чтобы линии магнитного поля входили в неё перпендикулярно, а 4 пальца направить в сторону движения частицы с положительным зарядом, или против движения частицы с отрицательным зарядом, то отогнутый на 90 большой палец покажет направление силы Лоренца».

Если заряженная частица движется параллельно силовым линиям магнитного поля, то величина силы Лоренца равна нулю, так как в этом случае α = 0, следовательно, sinα = 0

F = qvBˑsinα= 0.

Если же направление движения частицы перпендикулярно силовым линиям, то частица будет двигаться по окружности радиусом r, а сила Лоренца направлена к её центру, то есть является центростремительной силой.

Согласно второму закону Ньютона сила Лоренца равна mv2r.

Отсюда

При движении частицы под углом к силовым линиям её траектория представляет собой винтовую (спиральную) линию, имеющую радиус r и шаг винта h.

Сила Лоренца не совершает работы, так как её направление всегда перпендикулярно направлению движения заряда.

Токовихревая дефектоскопия силой Лоренца (ТДЛ)

Рис. 9 : Принцип работы ТДЛ. Источник

Другая, но физически сходная задача — определение глубокозалегающих каверн и неоднородностей в электропроводящих твердых материалах.

В более традиционной версии токовихревой дефектоскопии для генерирования вихревых токов в исследуемом материале используется переменное магнитное поле. Если материал содержит трещины или каверны, пространственное распределение электропроводности становится неоднородным и траектория вихревых токов подвергается возмущениям, в результате чего изменяется индуктивность катушки, которая создаёт переменное магнитное поле. С помощью измерения индуктивности этой катушки и могут быть обнаружены дефекты. Но исходя из того, что вихревые токи создаются переменным магнитным полем, их проникновение в область материала ограничивается скин-эффектом. В результате этого применимость традиционной версии токовихревой дефектоскопии ограничена анализом области поверхности материала, обычно глубиной порядка одного миллиметра. Попытки обойти эти ограничения с помощью использования низкочастотных катушек и сверхпроводящих датчиков магнитного поля пока не привели к желаемым результатам.

Современная методика, названная вихревой дефектоскопией силой Лоренца, имеет существенное преимущество перед предыдущей за счет применения постоянного магнитного поля и взаимного перемещения материала и источника магнитного поля, что позволяет глубоко и относительно быстро исследовать электропроводящий материал. В принципе, ТДЛ представляет собой модификацию традиционной токовихревой дефектоскопии, из которой можно выделить два аспекта: (1) как генерируются вихревые токи и (2) как регистрируются их возмущения. В ТДЛ вихревые токи генерируются за счет взаимного перемещения исследуемого проводника и постоянного магнита (Рис. 9). Когда магнит проходит над дефектом, сила Лоренца, действующая на него, искажается и обнаружение этого искажения и есть основной принцип измерения ТДЛ. Если исследуемый объект не содержит дефектов, результирующая сила Лоренца остается постоянной.

Частные случаи

СГС	СИ
mv2r=\|q\|cvB⇒r=cm\|q\|⋅vB{\displaystyle {mv^{2} \over r}={\|q\| \over c}vB\Rightarrow r={cm \over \|q\|}\cdot {v \over B}}	mv2r=\|q\|vB⇒r=m\|q\|⋅vB{\displaystyle {mv^{2} \over r}=\|q\|vB\Rightarrow r={m \over \|q\|}\cdot {v \over B}}

СГС	СИ
ω=\|q\|Bmc{\displaystyle \omega ={\|q\|B \over mc}}	ω=\|q\|Bm{\displaystyle \omega ={\|q\|B \over m}}

СГС	СИ
r=mc\|q\|⋅vsin⁡αB{\displaystyle r={mc \over \|q\|}\cdot {v\sin \alpha \over B}}, h=2πB⋅mc\|q\|⋅vcos⁡α{\displaystyle h={2\pi \over B}\cdot {mc \over \|q\|}\cdot v\cos \alpha }	r=m\|q\|⋅vsin⁡αB{\displaystyle r={m \over \|q\|}\cdot {v\sin \alpha \over B}}, h=2πB⋅m\|q\|⋅vcos⁡α{\displaystyle h={2\pi \over B}\cdot {m \over \|q\|}\cdot v\cos \alpha }

Магнетрон

alt=»Магнетрон» src=»radio/magnetron.gif» align=»left» hspace=»20″>

Магнетрон — это мощная электронная лампа, генерирующая микроволны при взаимодействии потока электронов с магнитным полем.

Термин “магнетрон” был предложен А. Халлом (A. Hull), который в 1921 году, впервые опубликовал результаты теоретических и экспериментальных исследований работы прибора в статическом режиме и предложил ряд конструкций магнетрона. Генерирование электромагнитных колебаний в дециметровом диапазоне волн посредством магнетрона открыл и запатентовал в 1924 чехословацкий физик А. Жачек.

В 1940 британские физики Джон Рэндалл (John Randall) и Гарри Бут (Harry Boot) изобрели резонансный магнетрон. Новый магнетрон давал импульсы высокой мощности, что позволило разработать радар сантиметрового диапазона. Радар с короткой длиной волны позволял обнаруживать более мелкие объекты. Кроме того, компактный размер магнетрона привел к резкому уменьшению размеров радарной аппаратуры, что позволило устанавливать ее на самолетах.

Начиная с 1960-х годов, магнетроны получили применение в СВЧ-печах для домашнего использования.

Магнетроны могут работать на различных частотах от 0,5 до 100 ГГц, с мощностями от нескольких Вт до десятков кВт в непрерывном режиме, и от 10 Вт до 5 МВт в импульсном режиме при длительностях импульсов главным образом от долей до десятков микросекунд.

Магнетроны обладают высоким КПД (до 80 %), то есть, способны преобразовывать до 80% подводимой к ним электроэнергии в СВЧ-поле.

Магнетроны бывают как не перестраиваемые, так и перестраиваемые в небольшом диапазоне частот (обычно менее 10 %). Для медленной перестройки частоты применяются механизмы, приводимые в движение рукой, для быстрой (до нескольких тысяч перестроек в секунду) — ротационные и вибрационные механизмы.

Магнетроны как генераторы сверхвысоких частот широко используются в современной радиолокационной технике.

Знаете ли Вы, что в 1965 году два американца Пензиас (эмигрант из Германии) и Вильсон заявили, что они открыли излучение космоса. Через несколько лет им дали Нобелевскую премию, как-будто никто не знал работ Э. Регенера, измерившего температуру космического пространства с помощью запуска болометра в стратосферу в 1933 г.? Подробнее читайте в FAQ по эфирной физике.

Заключение

Подведем итоги и обозначим четыре основных тезиса этой статьи простым языком:

Сила Лоренца действует на заряженные частицы, которые движутся в магнитном поле. Это вытекает из основной формулы.
Она прямо пропорциональна скорости заряженной частицы и магнитной индукции.
Не влияет на скорость частицы.
Влияет на направление частицы.

Её роль достаточно велика в «электрических» сферах. Специалист не должен упускать из вида основные теоретические сведения об основополагающих физических законах. Эти знания пригодятся, как и тем, кто занимается научной работой, проектированием и просто для общего развития.

Напоследок рекомендуем просмотреть полезные видео для закрепления изученного материала:

Материалы по теме:

Правило буравчика простыми словами
Что такое электрический заряд
Как перевести амперы в киловатты
Переходное контактное сопротивление