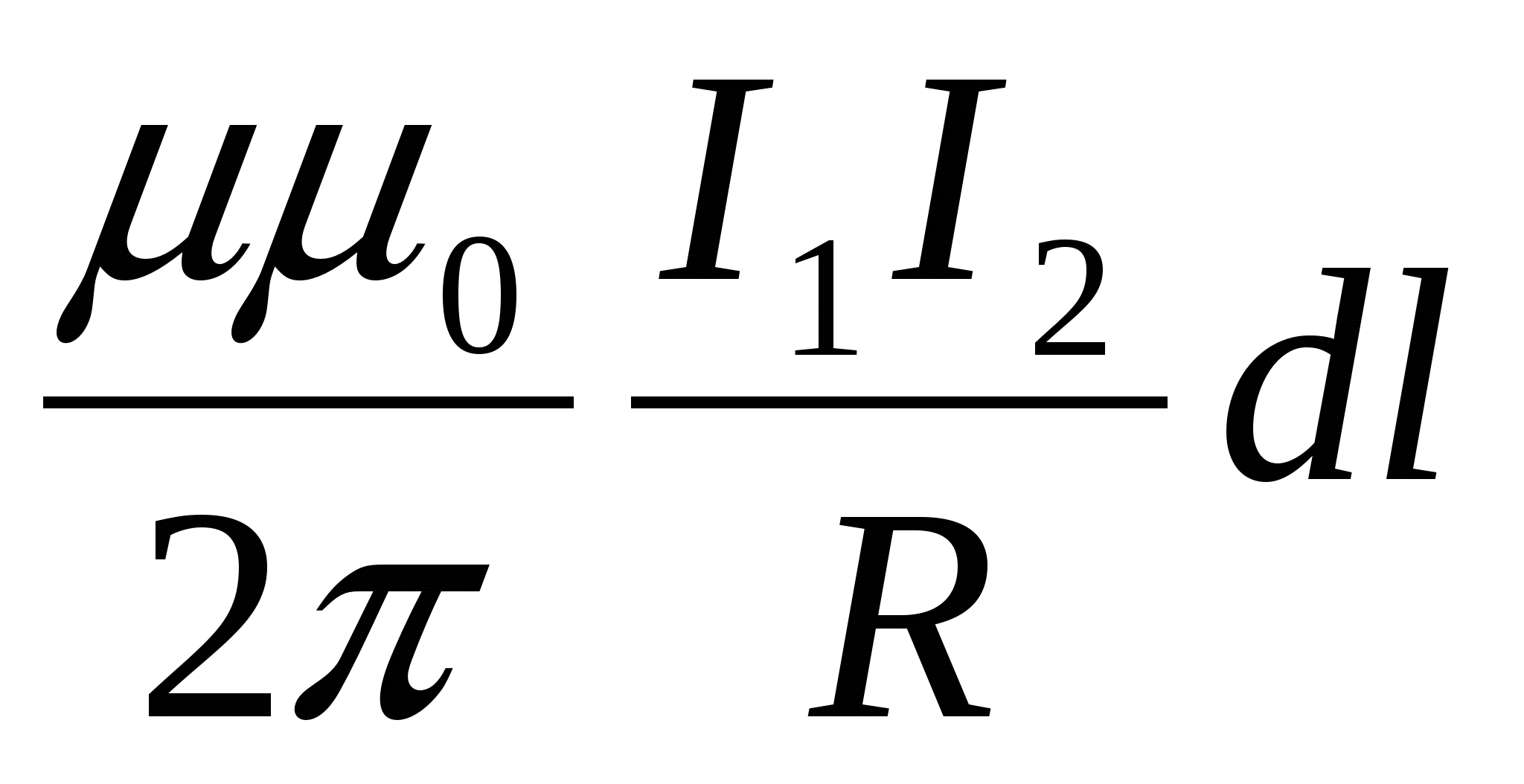Закон ампера

Воздействие на человека

В большинстве случаев электрический ток представляет собой поток электронов. Поскольку ампер является мерой количества заряда, проходящего в секунду, нетрудно будет посчитать количество электронов в перемещённом заряде: 1 Кл = 6,24151·10 18. То есть один ампер равен потоку 6340 квадриллионов частиц в секунду. Это колоссальная цифра, но вряд ли она иллюстративна для сравнительного понимания, когда показатель чего-либо измеряют в амперах. В этом помогут следующие повседневные примеры:

160х10 -19 — один электрон в секунду;
0,7х10 -3 — слуховой аппарат;
5х10 -3 — пучок в кинескопе телевизора;
150х10 -3 — портативный ЖК телевизор;
0,2 — электрический угорь;
0,3 — лампа накаливания;
10 — тостер, чайник;
100 — стартер автомобиля;
30х10 3 — удар молнии;
180х10 3 — дуговая печь для ферросплавов;
5х10 6 — дуга между Юпитером и Ио.

Порог смертельно опасного воздействия на человеческий организм начинается с 18 мА. Ток, превышающий это значение и проходящий через грудную клетку, способен стимулировать мышцы груди таким образом, что их спазмы могут вызвать полную остановку дыхания. Другой опасный эффект при подобном воздействии связан с фибрилляцией желудочков сердца. Основные факторы летальности:

Сила тока. Так как сопротивление между точками входа и выхода — постоянная величина, по закону Ома высокое напряжение делает вероятным высокий ампераж.
Маршрут протекания. Наиболее опасны для сердечной мышцы направления рука-рука и передняя-задняя части грудной клетки.
Индивидуальная чувствительность к воздействию электричества и особенности организма (сопротивление кожи и её влажность, возраст и пол, заболевания, наличие медицинских имплантов).
Продолжительность воздействия.

Вам это будет интересно Разновидности бытовых и промышленных электрических выключателей

Что такое сила ампера

В 1820 году выдающийся французский физик Андре Мари Ампер (именно в его честь названа единица измерения электрического тока) сформулировал один из основополагающих законов всей электротехники. Впоследствии за этим законом закрепилось название сила ампера.

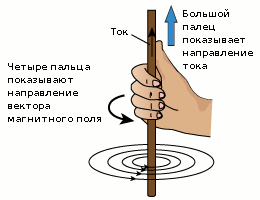
Как известно, при прохождении по проводнику электрического тока вокруг него возникает свое собственное (вторичное) магнитное поле, линии напряженности которого формируют своеобразную вращающуюся оболочку. Направление этих линий магнитной индукции определяют с помощью правила правой руки (второе название «правило буравчика»): мысленно обхватываем правой рукой проводник так, чтобы течение заряженных частиц совпадало с направлением, указываемым отогнутым большим пальцем. В результате другие четыре пальца, обхватывающие провод, укажут на вращение поля.

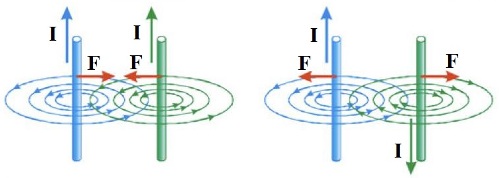
Если расположить параллельно два таких проводника (тонких провода), то на взаимодействие их магнитных полей будет влиять сила ампера. В зависимости от направления тока в каждом проводнике, они могут отталкиваться или притягиваться. При токах, текущих в одном направлении, сила ампера оказывает на них притягивающее действие. Соответственно, противоположное направление токов вызывает отталкивание. В этом нет ничего удивительного: хотя одноименные заряды отталкиваются, в данном примере взаимодействуют не сами заряды, а магнитные поля. Так как направление их вращения совпадает, то итоговое поле представляет собой векторную сумму, а не разность.

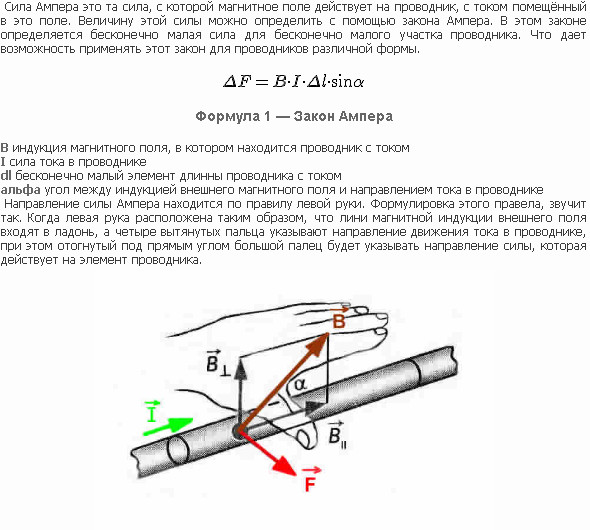
Другими словами, магнитное поле определенным образом воздействует на проводник, пересекающий линии напряженности. Сила ампера (произвольная форма проводника) определяется из формулы закона:

dF=B*I*L*sin a;

где — I — значение силы тока в проводнике; B — индукция магнитного поля, в котором размещается проводящий ток материал; L — взятый для расчетов длины проводника с током (причем, в данном случае считается, что длина проводника и сила стремятся к нулю); альфа (а) — векторный угол между направлением движения заряженных элементарных частиц и линиями напряженности внешнего поля. Следствие следующее: когда угол между векторами составляет 90 градусов его sin = 1, а значение силы максимально.

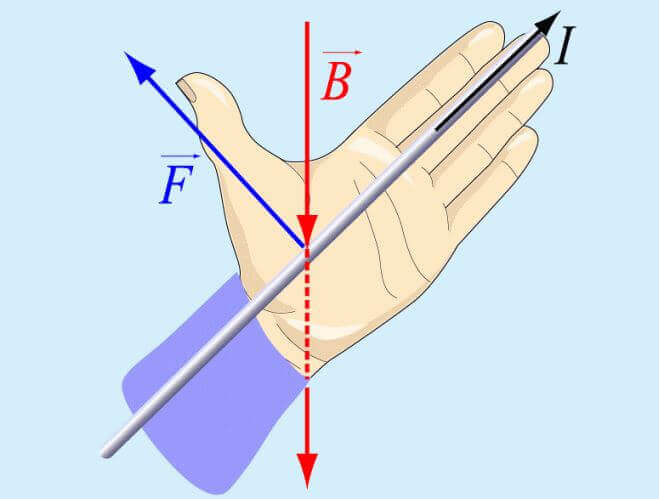
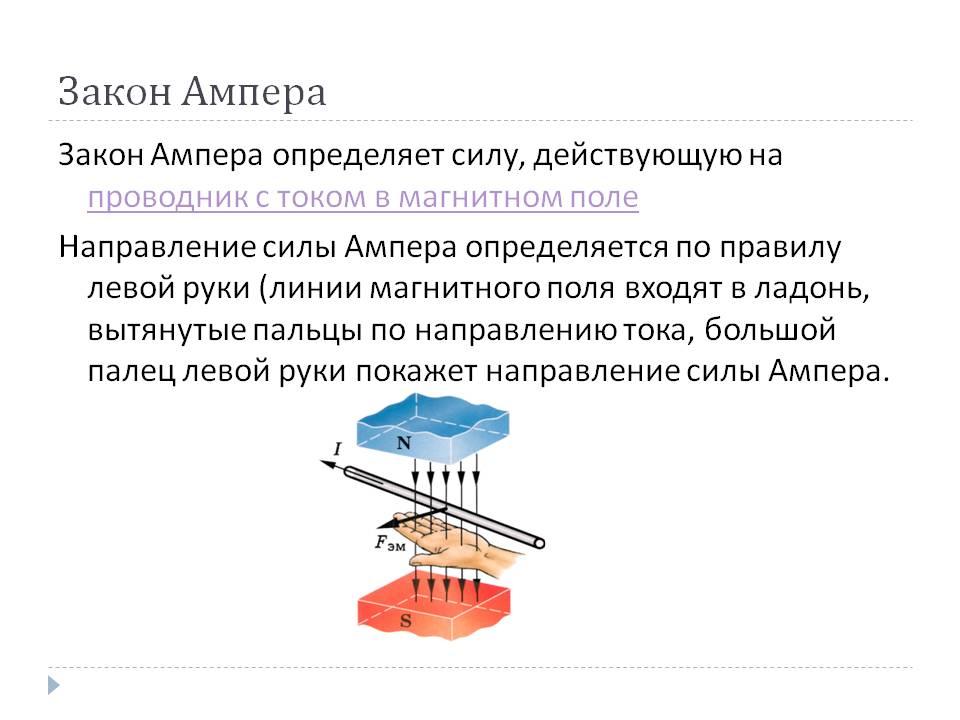
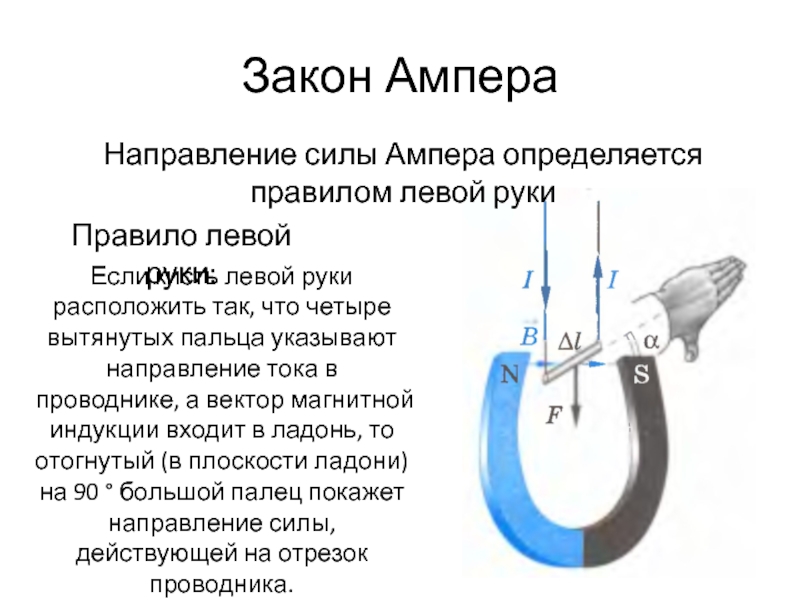
Векторное направление действия силы ампера определяют посредством правила левой руки: мысленно размещаем ладонь левой руки таким образом, чтобы линии (векторы) магнитной индукции внешнего поля входили в раскрытую ладонь, а остальные четыре выпрямленных пальца указывали направление, в котором движется ток в проводнике. Тогда большой палец, отогнутый под углом 90 градусов, покажет направление действующей на проводник силы. Если угол между вектором электрического тока и произвольной линией индукции слишком мал, то для упрощения применения правила в ладонь должен входить не сам вектор индукции, а модуль.

Применение силы ампера дало возможность создать электродвигатели. Все мы привыкли к тому, что достаточно щелкнуть выключателем электрического бытового прибора, оснащенного двигателем, чтобы его исполнительный механизм пришел в действие. А о процессах, происходящих при этом, никто особо не задумывается. Направление силы ампера не только объясняет принцип работы двигателей, но и позволяет определить, куда именно будет направлен вращающий момент.

Для примера представим двигатель постоянного тока: его якорь — это каркас-основа с обмоткой. Внешнее магнитное поле создается специальными полюсами. Так как обмотка, намотанная на якорь, круговая, то с противоположных его сторон направление тока на участках проводника встречно. Следовательно, вектора действия силы ампера также встречны. Так как якорь закреплен на подшипниках, то взаимное действие векторов силы ампера создает вращающий момент. С ростом действующего значения тока увеличивается и сила. Именно поэтому номинальный электрический ток (указан в паспорте на электрооборудование) и вращающий момент непосредственно взаимосвязаны. Увеличение тока ограничивается конструктивными особенностями: сечением использованного для обмотки провода, количеством витков и пр.

fb.ru

Явление электромагнитной индукции. Закон Фарадея. ЭДС индукции в движущихся проводниках. Самоиндукция.

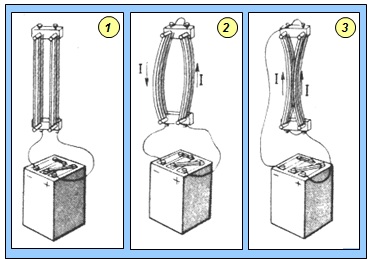
Фарадей предположил, что если вокруг проводника с током существует магнитное поле, то естественно ожидать, что должно происходить и обратное явление – возникновение электрического тока под действием магнитного поля. И вот в 1831 г. Фарадей публикует статью, где сообщает об открытии нового явления – явления электромагнитной индукции.

Опыты Фарадея были чрезвычайно просты. Он присоединял гальванометр G к концам катушки L и приближал к ней магнит. Стрелка гальванометра отклонялась, фиксируя появление тока в цепи. Ток протекал, пока магнит двигался. При отдалении магнита от катушки гальванометр отмечал появление тока противоположного направления. Аналогичный результат отмечался, если магнит заменяли катушкой с током или замкнутым контуром с током.

Движущиеся магнит или проводник с током создают через катушку L переменное магнитное поле. В случае их неподвижности создаваемое ими поле постоянно. Если вблизи замкнутого контура поместить проводник с переменным током, то в замкнутом контуре также возникнет ток. На основе анализа опытных данных Фарадей установил, что ток в проводящих контурах появляется при изменении магнитного потока через площадь, ограниченную этим контуром.

Этот ток был назван индукционным. Открытие Фарадея было названо явлением электромагнитной индукции и легло в дальнейшем в основу работы электрических двигателей, генераторов, трансформаторов и подобных им приборов.

Итак, если магнитный поток через поверхность, ограниченную некоторым контуром, изменяется, то в контуре возникает электрический ток. Известно, что электрический ток в проводнике может возникнуть только под действием сторонних сил, т.е. при наличии э.д.с.. В случае индукционного тока э.д.с., соответствующая сторонним силам, называется электродвижущей силой электромагнитной индукции εi.

Э.д.с. электромагнитной индукции в контуре пропорциональна скорости изменения магнитного потока Фm сквозь поверхность, ограниченную этим контуром:

где к – коэффициент пропорциональности. Данная э.д.с. не зависит от того, чем вызвано изменение магнитного потока – либо перемещением контура в постоянном магнитном поле, либо изменением самого поля.

Итак, направление индукционного тока определяется правилом Ленца: При всяком изменении магнитного потока сквозь поверхность, ограниченную замкнутым проводящим контуром, в последнем возникает индукционный ток такого направления, что его магнитное поле противодействует изменению магнитного потока.

Обобщением закона Фарадея и правила Ленца является закон Фарадея — Ленца: Электродвижущая сила электромагнитной индукции в замкнутом проводящем контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную контуром:

Это выражение представляет собой основной закон электромагнитной индукции.

При скорости изменения магнитного потока 1Вб/с в контуре индуцируется э.д.с. в 1 В.

Пусть контур, в котором индуцируется э.д.с., состоит не из одного, а из N витков, например, представляет собой соленоид. Соленоид – это цилиндрическая катушка с током, состоящая из большого числа витков. Так как витки в соленоиде соединяются последовательно, εi в данном случае будет равна сумме э.д.с., индуцируемых в каждом из витков по отдельности:

Величину Ψ = ΣΦm называют потокосцеплением или полным магнитным потоком. Если

Проверочные задачи по теме: магнитное взаимодействие токов и сила Ампера

Задача 1. Докажите, что два параллельных проводника, в которых текут токи одного направления, притягиваются.

Анализ задачи:

Вокруг любого проводника с током существует магнитное поле, следовательно, каждый из двух проводников находится в магнитном поле другого. На первый проводник действует сила Ампера со стороны магнитного поля, созданного током во втором проводнике, и наоборот. Определив по правилу левой руки направления этих сил, выясним, как вести себя проводники.

Решение:

В ходе решения выполним объяснительные рисунки: изобразим проводники А и В, покажем направление тока в них и др.

Определим направление силы Ампера, действующая на проводник А, находящегося в магнитном поле проводника В.

1) С помощью правила буравчика определим направление линий магнитной индукции магнитного поля, созданного проводником В (рисунок слева). Выясняется, что у проводника А магнитные линии направлены к нам (отметка «•»).

2) Воспользовавшись правилом левой руки, определим направление силы Ампера, действующая на проводник А со стороны магнитного поля проводника В.

3) Приходим к выводу: проводник А привлекается к проводнику В.

Теперь найдем направление силы Ампера, действующая на проводник В, находится в магнитном поле проводника А.

1) Определим направление линий магнитной индукции магнитного поля, созданного проводником А (рисунок справа). Выясняется, что у проводника В магнитные линии направлены от нас (отметка «х»).

2) Определим направление силы Ампера, действующая на проводник В.

3) Приходим к выводу: проводник В привлекается к проводнику А.

Ответ: два параллельных проводника, в которых текут токи одного направления, действительно притягиваются.

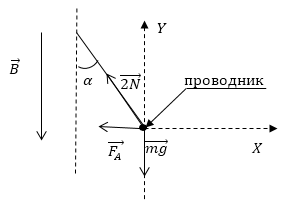
Задача 2. Прямой проводник (стержень) длиной 0,1 м массой 40 г находится в горизонтальном однородном магнитном поле индукцией 0,5 Тл. Стержень расположен перпендикулярно магнитных линий поля). Ток какой силы и в каком направлении следует пропустить в стержне, чтобы он не давил на опору (завис в магнитном поле)?

Анализ задачи:

Стержень не будет давить на опору, если сила Ампера уравновесит силу тяжести. Это произойдет при следующих условиях:

сила Ампера будет направлена противоположно силе тяжести (то есть вертикально вверх)
значение силы Ампера равна значению силы тяжести FA = Fтяж

Направление тока определим, воспользовавшись правилом левой руки.

Решение:

Определим направление тока. Для этого расположим левую руку так, чтобы линии магнитного поля входили в ладонь, а отогнутый на 90 ° большой палец был направлен вертикально вверх. Четыре вытянутые пальцы укажут направление от нас. Итак, ток в проводнике следует направить от нас.

Учитываем, что FA = Fтяж. FA= BIlsinα, где sin α = 1; Fтяж = mg

Из последнего выражения найдем силу тока: I = mg/Bl

Проверим единицу, найдем значение искомой величины.

Ответ: I = 8 А; Ток в направлении от нас.

Подводим итоги

Силу, с которой магнитное поле действует на проводник с током, называют силой Ампера. Значение силы Ампера вычисляют по формуле: FA= BIlsinα, где B — индукция магнитного поля; I — сила тока в проводнике; l — длина активной части проводника; α — угол между направлением вектора магнитной индукции и направлением тока в проводнике.

Для определения направления магнитной силы Ампера используют правило левой руки: если левую руку расположить так, чтобы линии магнитного поля входили в ладонь, а четыре вытянутые пальцы указывали направление тока в проводнике, то отогнутый на 90 ° большой палец укажет направление силы Ампера.

Перспективы единицы силы тока в будущем

Когда определено, что такое амперы, можно рассмотреть перспективы этой единицы в будущем. В 2011 году на международной конференции оговорены условия предстоящей ревизии обозначений единиц в системе СИ.

Предложенные новые эталоны должны повысить точность различных измерений в любом временном, метрическом и географическом векторах без утраты точности. Ампер не потерпит особых изменений, кроме того, что его величина станет обозначаться в зависимости от данного числа.

На сегодняшний день ампер – это результат воображаемого процесса, в котором представляют возникновение силы между двумя проводниками безразмерной длины. Практически это невозможно воспроизвести, потому что нет таких длинных и тонких проводов. На конференции решили применить новую идею. Она будет основываться на физических константах или атомных свойствах. Такой физической константой будет заряд электрона.

Внимание! Современное определение: 1 ампер – это движение электронов соответствующее потоку 1/1,6*10-19 элементарных зарядов в 1 секунду. Практическим инструментом послужит одноэлектронный насос, который позволяет перемещать в течение одного своего цикла фиксированное количество электронов

Практическим инструментом послужит одноэлектронный насос, который позволяет перемещать в течение одного своего цикла фиксированное количество электронов.

В будущем, ампер – это мера силы тока, определение которого перестало описываться вымышленной виртуальной установкой, приобрело прочную, фундаментальную основу.

Сила Лоренца

Сила Лоренца – сила, действующая на движущуюся заряженную частицу со стороны магнитного поля.

Формула для нахождения силы Лоренца:

где \( q \) – заряд частицы, \( v \) – скорость частицы, \( B \) – модуль вектора магнитной индукции, \( \alpha \) – угол между вектором скорости частицы и вектором магнитной индукции.

Направление силы Лоренца определяют по правилу левой руки: если ладонь левой руки расположить так, чтобы перпендикулярная к проводнику составляющая вектора магнитной индукции \( B_\perp \) входила в ладонь, а четыре вытянутых пальца указывали направление скорости положительно заряженной частицы, то отогнутый на 90° большой палец покажет направление силы Лоренца.

Если заряд частицы отрицательный, то направление силы изменяется на противоположное.

Важно!
Если вектор скорости сонаправлен с вектором магнитной индукции, то частица движется равномерно и прямолинейно. В однородном магнитном поле сила Лоренца искривляет траекторию движения частицы

В однородном магнитном поле сила Лоренца искривляет траекторию движения частицы.

Если вектор скорости перпендикулярен вектору магнитной индукции, то частица движется по окружности, радиус которой равен:

где \( m \) – масса частицы, \( v \) – скорость частицы, \( B \) – модуль вектора магнитной индукции, \( q \) – заряд частицы.

В этом случае сила Лоренца играет роль центростремительной и ее работа равна нулю. Период (частота) обращения частицы не зависит от радиуса окружности и скорости частицы. Формула для вычисления периода обращения частицы:

Угловая скорость движения заряженной частицы:

Важно!
Сила Лоренца не меняет кинетическую энергию частицы и модуль ее скорости. Под действием силы Лоренца изменяется направление скорости частицы

Если вектор скорости направлен под углом \( \alpha \) (0° < \( \alpha \) < 90°) к вектору магнитной индукции, то частица движется по винтовой линии.

В этом случае вектор скорости частицы можно представить как сумму двух векторов скорости, один из которых, \( \vec{v}_2 \), параллелен вектору \( \vec{B} \), а другой, \( \vec{v}_1 \), – перпендикулярен ему. Вектор \( \vec{v}_1 \) не меняется ни по модулю, ни по направлению. Вектор \( \vec{v}_2 \) меняется по направлению. Сила Лоренца будет сообщать движущейся частице ускорение, перпендикулярное вектору скорости \( \vec{v}_1 \). Частица будет двигаться по окружности. Период обращения частицы по окружности – \( T \).

Таким образом, на равномерное движение вдоль линии индукции будет накладываться движение по окружности в плоскости, перпендикулярной вектору \( \vec{B} \). Частица движется по винтовой линии с шагом \( h=v_2T \).

Важно!
Если частица движется в электрическом и магнитном полях, то полная сила Лоренца равна:

Особенности движения заряженной частицы в магнитном поле используются в масс-спектрометрах – устройствах для измерения масс заряженных частиц; ускорителях частиц; для термоизоляции плазмы в установках «Токамак».

Алгоритм решения задач о действии магнитного (и электрического) поля на заряженные частицы:

сделать чертеж, указать на нем силовые линии магнитного (и электрического) поля, нарисовать вектор начальной скорости частицы и отметить знак ее заряда;
изобразить силы, действующие на заряженную частицу;
определить вид траектории частицы;
разложить силы, действующие на заряженную частицу, вдоль направления магнитного поля и по направлению, ему перпендикулярному;
составить основное уравнение динамики материальной точки по каждому из направлений разложения сил;
выразить силы через величины, от которых они зависят;
решить полученную систему уравнений относительно неизвестной величины;
решение проверить.

Зачем нужно рассчитывать ток

На большинстве электроприборов указывается мощность потребления. Это необходимо для того, чтобы правильно вести учет потребления электроэнергии. Но для всего остального значение мощности несет мало информации. Параметры автоматов защиты и плавких вставок, сечение электропроводки, требуют знать протекающий ток или, как говорят электрики, ампераж нагрузки.

Вам это будет интересно Как вычисляется резонансная частота колебательного контура

Простой пример: какой паяльник сильнее перегружает электропроводку, 42-х вольтовый на 80 Вт или 220-и вольтовый на 100 Вт? Логичный ответ, что более мощный, является неправильным. Ведь на самом деле, при включении второго паяльника в сети протекает ток около 0.5 А, а при включении первого — почти 2 А. Соответственно, для таких устройств требуется различная электропроводка и номинал защитных устройств. При одинаковой толщине проводов питания нагрев будет сильнее, при работе с низковольтным инструментом.

По этой же причине в линиях электропередач стремятся по максимуму повысить передаваемое напряжение. Поскольку мощность нагрузки остается одинаковой, при более высоком напряжении по проводам протекает меньший ток и поэтому:

Снижаются потери;
Уменьшается нагрев;
Снижается сечение проводов и, как следствие, их масса и нагрузка на опоры линий электропередач.

Высоковольтная опора ЛЭП

Сколько же мы можем «взять» киловатт с С16А?

В первом столбце отношение токов, во втором ток в цепи, протекающий через автоматический выключатель, в третьем время отключения, в четвертом — мощность в однофазной нагрузке без учета коэффициента мощности и гармоник.

Время-Токовая Характеристика С — таблица с мощностью

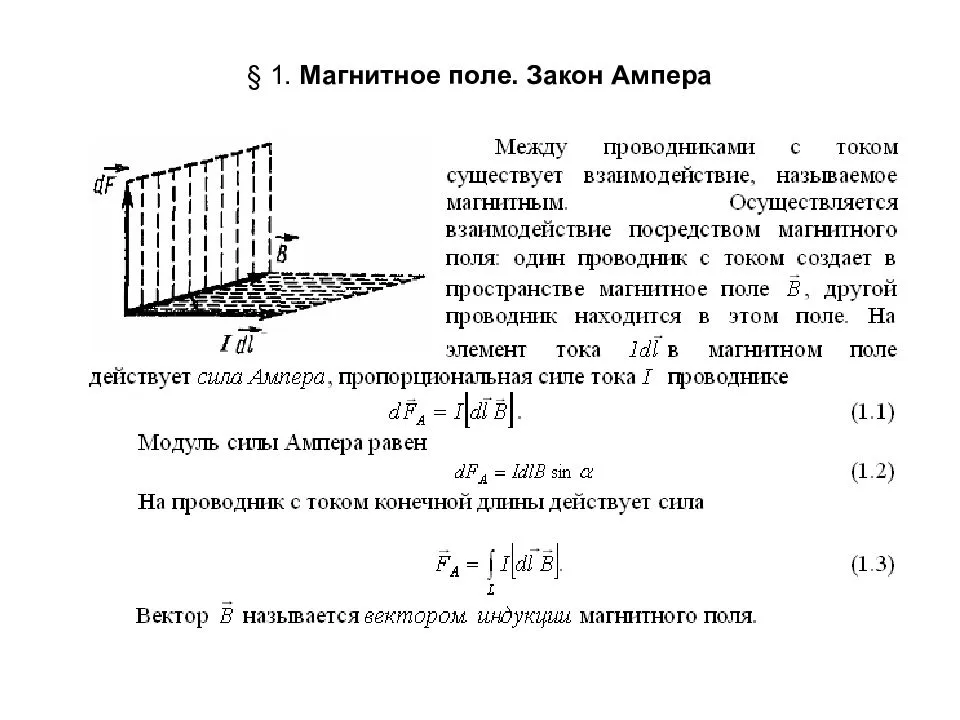
Сила Ампера

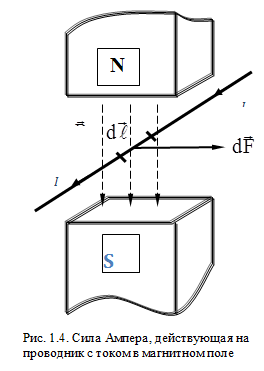
Сила, с которой магнитное поле действует на помещенный в него проводник с током, называется силой Ампера.

Величина этой силы, действующей на элемент Δl проводника с током I в магнитном поле с индукцией \(~\vec B\) , определяется законом Ампера:

\(~\Delta F = B \cdot I \cdot \Delta l \cdot \sin \alpha\) , (1)

где α – угол между направлениями тока и вектора индукции.

Направление силы Ампера можно найти с помощью правила левой руки (рис. 1):

Рис. 1

если левую руку расположить так, чтобы линии магнитной индукции входили в ладонь, а четыре вытянутых пальца совпадали по направлению с направлением тока, то отогнутый на 90° большой палец укажет направление силы, действующей на элемент проводника.

Использование этого правила затруднительно лишь в том случае, когда угол α мал. Поскольку, однако, величина B∙sin α представляет собой модуль перпендикулярной проводнику с током компоненты вектора индукции \(~\vec B_{\perp}\) (рис. 2), то ориентацию ладони можно определять именно этой компонентой – она должна входить в открытую ладонь левой руки.

Рис. 2

Из (1) следует, что сила Ампера равна нулю, если проводник с током расположен вдоль линий магнитной индукции, и максимальна, если проводник перпендикулярен этим линиям.

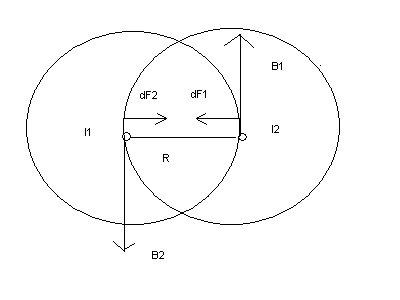
Закон Ампера выполняется для любого магнитного поля. Предположим, что это поле создается длинным линейным проводником с током I₂, параллельным первому проводнику c током I₁ и находящимся на расстоянии r от него. Тогда индукцию магнитного поля в точках расположения первого проводника можно определить (с учетом замены I → I₂) по формуле:

\(~B = \frac{\mu_0 \cdot I}{2 \pi \cdot r} = \frac{\mu_0 \cdot I_2}{2 \pi \cdot r}\) .

Подставляя это выражение в (1) и замечая, что в рассматриваемом случае параллельных проводников α = 90°, находим силу, действующую на линейный элемент Δl первого проводника,

\(~\Delta F = \frac{\mu_0 \cdot I_2}{2 \pi \cdot r} \cdot I_1 \cdot \Delta l = \mu_0 \cdot \frac{I_2 \cdot I_1 \cdot \Delta l}{2 \pi \cdot r} \) . (2)

Совершенно ясно, что точно такое же выражение можно записать для силы, действующей на второй проводник. Используя правило буравчика (для определения магнитной индукции проводника с током) и правило левой руки (для определения силы, действующей на проводник с током), можно убедиться в том, что если токи в проводниках текут в одинаковых направлениях, то эти проводники притягиваются (рис. 3 а, б), а если в разных – отталкиваются (рис. 4, а, б), что и подтверждается опытом.

Рис. 3

Рис. 4

Выражение (2) было положено в основу принципа определения единицы силы тока. Если в (2) считать I₁ = I₂ = 1 А, r = 1 м, Δl = 1 м, то получим F = 2∙10-7 Н/м. Другими словами,

если по двум параллельным, бесконечно длинным линейным проводникам, расположенным на расстоянии 1 м друг от друга, текут одинаковые токи в 1 А, то эти токи взаимодействуют с силой 2∙10-7 Н на каждый метр длины проводников.

Заметим, что единица силы тока – ампер – в СИ принадлежит, наряду с секундой, метром, килограммом, кельвином, молем и канделой, к числу основных единиц измерения физических величин.

Что такое амперы и миллиамперы

Ампер — единица измерения силы тока, физической величины, равной отношению количества заряда к промежутку времени его прохождения через какую-либо поверхность или предмет; одна из 7 основных единиц в Международной системе единиц (СИ).

Амперметр – прибор, измеряющий в амперах.

Дополнительная информация! В качестве единицы измерения ампер был принят в 1881 году на 1-ом Международном конгрессе электриков, проходившем в Париже, и был так назван в честь французского физика, математика и химика Андре-Мари Ампера.

Андре Ампер

В соответствии с изменениями 2018 года, Международный комитет мер и весов приводит следующее определение ампера:

«Величина ампера устанавливается фиксацией численного значения элементарного заряда e равным 1,602 176 634 × 10^−19, когда он выражен в кулонах.»

Эмблема международного комитета мер и весов

Миллиампер — дольная величина, которая в соответствии со своей приставкой, равна одной тысячной доли ампера или же 10^-3. Также часто записывается как «мампер» — это некая усреднённая запись между его обозначением (мА) и названием.

1 микроампер равняется 10^-6 А.

Важно! Запись по типу «миллиА» не рекомендуется, при использовании обозначения единицы измерения лучше сократить и приставку, с которой она употребляется. Таблица приставок и их значений

Таблица приставок и их значений

Открытия Лоренца

Выделим основные открытия Лоренца.

Лоренц установил, что магнитное поле действует на движущуюся в нём частицу, заставляя её двигаться по дуге окружности:

(1.3.)

Поскольку сила Лоренца – центростремительная сила, перпендикулярная направлению скорости. Прежде всего, открытый Лоренцем закон, позволяет определять такую важнейшую характеристику как отношение заряда к массе – удельный заряд.

(1.4.)

Значение удельного заряда – величина уникальная для каждой заряженной частицы, что позволяет их идентифицировать, будь-то электрон, протон или любая другая частица. Таким образом, учёные получили мощный инструмент для исследования. Например, Резерфорд сумел провести анализ радиоактивного излучения и выявил его компоненты, среди которых присутствуют альфа-частицы – ядра атома гелия и бета-частицы – электроны. В ХХ веке появились ускорители, работа которых основана на том, что заряженные частицы ускоряются в магнитном поле. На этом принципе разработан Большой адронный коллайдер. Благодаря открытиям Лоренца наука получила принципиально новый инструмент для физических исследований, открывая дорогу в мир элементарных частиц.

Для того чтобы охарактеризовать влияние учёного на технический прогресс вспомним о том, что из выражения для силы Лоренца вытекает возможность рассчитать радиус кривизны траектории частицы, которая движется в постоянном магнитном поле. При неизменных внешних условиях этот радиус зависит от массы частицы, её скорости и заряда. Таким образом, получаем возможность классифицировать заряжённые частицы по этим параметрам и, следовательно, можем проводить анализ какой-либо смеси. Если смесь веществ в газообразном состоянии ионизировать, разогнать и направить в магнитное поле, то частицы начнут двигаться по дугам окружностей с различными радиусами – частицы будут покидать поле в разных точках и остаётся только зафиксировать эти точки вылета, что реализуется при помощи экрана, покрытого люминофором, который светится при попадании на него заряжённых частиц. Именно по такой схеме работает масс-анализатор. Масс-анализаторы широко применяют в физике и химии для анализа состава смесей.

Это ещё не все технические устройства, которые работают на основе разработок и открытий Ампера и Лоренца, ведь научное знание рано или поздно перестает быть исключительной собственностью учёных и становится достоянием цивилизации, при этом оно воплощается в различных технических устройствах, которые делают нашу жизнь более комфортной.

Вольт — единица измерения напряжения

«Сколько выдает эта батарейка?». — «1.5 вольта». «В этой розетке напряжение 220 вольт?». — «Нет, 110». Напряжение, согласно специальной литературе, это «разность потенциалов между двумя проводниками». На контактах батареек или аккумуляторов оно одно, в розетках — другое, на высоковольтных подстанциях — третье, но все это вольты. Значит, что измеряется в вольтах? Правильно, напряжение. Как и амперы (да и ватты), вольт может иметь десятичную приставку:

1 В = 1000 мВ;
1000 В = 1 кВ;
0.01 В = 10 мВ и т. д.

Вот теперь можно попытаться рассчитать мощность, учитывая ток. Именно рассчитать, а не перевести! Предположим, в вашем распоряжении есть лампа, потребляющая ток 5 А от сети 220 В. Какова ее электрическая мощность? Для ответа на этот вопрос достаточно воспользоваться общеизвестной формулой:

P = I х U,

где P — мощность прибора в ваттах, I — ток, протекающий через прибор в амперах, U — напряжение, подаваемое на прибор в вольтах.

5 А х 220 В = 1100 Вт или 1.1 кВт.

Итак, вы «перевели» амперы в ватты, хотя, как вы понимаете, ни о каком «переводе» речи не шло — обычный расчет, чувствуете разницу? Чтобы «перевести» ватты в амперы, воспользуемся следующей формулой:

I = P/U.

Электроплитка имеет мощность в 1.3 кВт (написано на шильдике). Какой ток она будет потреблять от сети 220 В?

1300 Вт / 220 В = 5.9 А или грубо 6 А.

Взаимодействие проводников с током

Выделим основные открытия Ампера в области электромагнетизма.

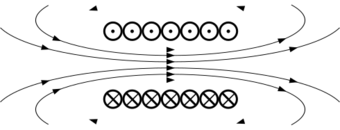
Во-первых, это взаимодействия проводников с током. Два параллельных проводника с токами притягиваются друг к другу, если токи в них сонаправлены, и отталкиваются, если токи в них противонаправлены (рис. 1).

Рис. 1. Проводники с током

Закон Ампера

гласит:

Сила взаимодействия двух параллельных проводников пропорциональна произведению величин токов в проводниках, пропорциональна длине этих проводников и обратно пропорциональна расстоянию между ними.

– сила взаимодействия двух параллельных проводников,

– величины токов в проводниках,

− длина проводников,

– расстояние между проводниками,

– магнитная постоянная.

Открытие этого закона позволило ввести в единицы измерения величину силы тока, которой до того времени не существовало. Так, если исходить из определения силы тока как отношения количества заряда перенесенного через поперечное сечение проводника в единицу времени, то мы получим принципиально не измеряемую величину, а именно количество заряда, переносимое через поперечное сечение проводника. На основании этого определения мы не сможем ввести единицу измерения силы тока. Закон Ампера позволяет установить связь между величинами сил тока в проводниках и величинами, которые можно измерить опытным путем: механической силой и расстоянием. Таким образом, получена возможность ввести в рассмотрение единицу силы тока – 1 А (1 ампер).

Ток в один ампер

– это такой ток, при котором два однородных параллельных проводника, расположенных в вакууме на расстоянии один метрот друга взаимодействуют с силой Ньютона.

Закон взаимодействия токов

– два находящихся в вакууме параллельных проводника, диаметры которых много меньше расстояний между ними, взаимодействуют с силой, прямо пропорциональной произведению токов в этих проводниках и обратно пропорциональной расстоянию между ними.

Два параллельных проводника

Два бесконечных параллельных проводника в вакууме

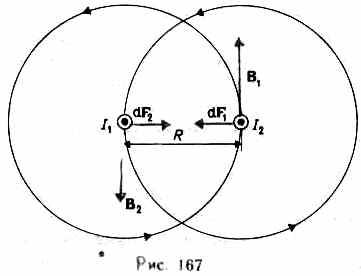
Наиболее известным примером, иллюстрирующим силу Ампера, является следующая задача. В вакууме на расстоянии r{\displaystyle r} друг от друга расположены два бесконечных параллельных проводника, в которых в одном направлении текут токи I1{\displaystyle I_{1}} и I2{\displaystyle I_{2}}. Требуется найти силу, действующую на единицу длины проводника.

В соответствии с законом Био — Савара — Лапласа бесконечный проводник с током I1{\displaystyle I_{1}} в точке на расстоянии r{\displaystyle r} создаёт магнитное поле с индукцией

B1(r)=μ4π2I1r,{\displaystyle B_{1}(r)={\frac {\mu _{0}}{4\pi }}{\frac {2I_{1}}{r}},}

где μ{\displaystyle \mu _{0}} — магнитная постоянная.

Теперь по закону Ампера найдём силу, с которой первый проводник действует на второй:

dF→1−2=I2dl→×B→1(r).{\displaystyle d{\vec {F}}_{1-2}=I_{2}d{\vec {l}}\times {\vec {B}}_{1}(r).}

По правилу буравчика, dF→1−2{\displaystyle d{\vec {F}}_{1-2}} направлена в сторону первого проводника (аналогично и для dF→2−1{\displaystyle d{\vec {F}}_{2-1}}, а значит, проводники притягиваются).

Модуль данной силы (r{\displaystyle r} — расстояние между проводниками):

dF1−2=μ4π2I1I2rdl.{\displaystyle dF_{1-2}={\frac {\mu _{0}}{4\pi }}{\frac {2I_{1}I_{2}}{r}}dl.}

Интегрируем по участку проводника длины L{\displaystyle L} (пределы интегрирования по l{\displaystyle l} от 0 до L{\displaystyle L}):

F1−2=μ4π2I1I2r⋅L.{\displaystyle F_{1-2}={\frac {\mu _{0}}{4\pi }}{\frac {2I_{1}I_{2}}{r}}\cdot L.}

Если L{\displaystyle L} — единичная длина, то это выражение задаёт искомую силу взаимодействия.

Полученная формула используется в СИ для установления численного значения магнитной постоянной μ{\displaystyle \mu _{0}}. Действительно, ампер, являющийся одной из СИ, определяется в ней как «сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения, расположенным в вакууме на расстоянии 1 метр один от другого, вызвал бы на каждом участке проводника длиной 1 метр силу взаимодействия, равную 2⋅10−7ньютона».

Таким образом, из полученной формулы и определения ампера следует, что магнитная постоянная μ{\displaystyle \mu _{0}} равна 4π×10−7{\displaystyle 4\pi \times 10^{-7}} Н/А² или, что то же самое, 4π×10−7{\displaystyle 4\pi \times 10^{-7}} Гн/ м точно.

Применение знаний о силе Ампера

Встретиться с областью применения знания о силе Ампера можно практически на каждом шагу цивилизации. Применение силы Ампера настолько обширно, что среднестатистическому гражданину даже сложно представить себе, что можно делать, зная закон Ампера и особенности применения силы. Так, под действием силы Ампера вращается ротор, на обмотку которого оказывает влияние магнитное поле статора, и ротор приходит в движение. Любое транспортное средство, которое использует электротягу для вращения валов (которые соединяют колеса транспорта), использует силу Ампера (это можно увидеть на трамваях, электровозах, электрических машинах и многих других интересных видах транспорта). Также именно магнитное поле влияет на механизмы, которые являются электрическими приборами, что должны открывать/закрывать что-то (двери лифта, открывающиеся ворота, электрические двери и много других). Другими словами, все устройства, что не могут работать без электричества и имеют движимые узлы, работают благодаря знанию о законе Ампера. Для примера:

Любые узлы в электротехнике. Самый популярный – элементарный электродвигатель.
Различные виды электротехники, которая формирует различные звуковые колебания с использованием постоянного магнита. Механизм действия таков, что на магнит действует электромагнитное поле, что создает расположенный рядом проводник с током, и изменение напряжения приводит к смене звуковой частоты.
На силе Ампера построена работа электромеханических машин, в которых движение обмотки ротора происходит относительно обмотки статора.
С помощью силы Ампера происходит электродинамический процесс сжатия плазмы, что нашло применение в токамаках и потенциально открывает огромные пути развития термоядерной энергии.
Также с помощью электродинамического сжатия применяется электродинамический метод прессования.