Понятие сигнала в радиосвязи

В радиотехнике

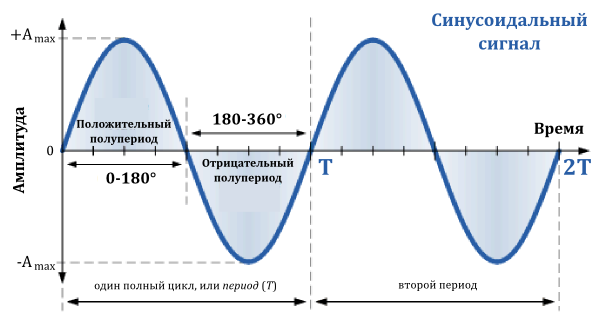
В радиотехнике основным элементом кодирования является модуляция сигнала. При этом обычно рассматривается близкий к гармоническому сигнал вида s(t) = A sin(2πf·t + φ), где амплитуда A, частота f или фаза φ медленно (относительно скорости изменения синуса) изменяются в зависимости от передаваемой информации (амплитудная, частотная или фазовая модуляция, соответственно).

Стохастические модели сигнала, предполагают случайным или сам сигнал, или переносимую им информацию. Стохастическая модель сигнала часто формулируется как уравнение, связывающее сигнал с шумом, который в данном случае имитирует множество возможных информационных сообщений и называется формирующим шумом, в отличие от мешающего шума наблюдения.

Обобщением скалярной модели сигнала являются, например, векторные модели сигналов, представляющие собой упорядоченные наборы отдельных скалярных функций, с определенной взаимосвязью компонентов вектора друг с другом. На практике векторная модель соответствует, в частности, одновременному приёму сигнала несколькими приёмниками с последующей совместной обработкой. Ещё одним расширением понятия сигнала является его обобщение на случай полей.

Сигнал и событие

Событие (получение записки, наблюдение сигнальной ракеты, приём символа по телеграфу) является сигналом только в той системе отношений, в которой сообщение опознается значимым (например, в условиях боевых действий сигнальная ракета — событие, значимое только для того наблюдателя, которому оно адресовано). Очевидно, что сигнал, заданный аналитически, событием не является и не несет информацию, если функция сигнала и её параметры известны наблюдателю.

В технике сигнал всегда является событием. Другими словами, событие — изменение состояния любого компонента технической системы, опознаваемое логикой системы как значимое, является сигналом. Событие, неопознаваемое данной системой логических или технических отношений как значимое, сигналом не является.

Специальные сигналы

Все мы являемся участниками дорожного движения. И хоть раз в своей жизни видели специальный транспорт. Это машины, входящие в парк срочных служб (пожарная и скорая, милиция и военные автомобили). Сюда же можно включить и правительственный кортеж.

Основные значения сигналов, подаваемых данными машинами, заключены в возможности их беспрепятственного проезда сквозь порой огромные городские пробки. Ведь пожарные торопятся спасти людей от огня, а врачи бригады скорой помощи спешат к больному. Для беспрепятственного проезда по городским улицам такие автомобили используют специальные сигналы (СГУ). С их помощью водители уже издалека оповещаются о необходимости уступить дорогу, прижавшись к ближайшей обочине.

Еще одним знаком, которым обладает специальный транспорт, являются мигалки. Эти приспособления могут иметь различную модификацию и способ применения. Мигалки служат для подачи визуального сигнала всем участникам дорожного движения, которые должны очистить дорогу для беспрепятственного проезда специальных автомобилей. Продаются сигналы для такого транспорта специальными службами. Далее подобные знаки проходят соответствующую регистрацию. Необходимо это для того, чтобы сигналы можно было использовать только по назначению.

Особенно актуальными мигалки становятся в ночное и вечернее время суток. В этот период спец. транспорт должен быть более заметен для других водителей.

Динамический диапазон

Динамический диапазон

Важной характеристикой любой системы динамических измерений считается ее динамический диапазон. Четкого определения данного параметра для сигнала пока не существует, поэтому принято считать, что это соотношение наибольшего и наименьшего его значений, измеренных системой в определенный промежуток времени

Для каждого потока важно, чтобы его динамический диапазон максимально соответствовал аналогичной характеристике системы либо устройства, предназначенного для преобразования, передачи и хранения его величин. От правильного подбора зависит, насколько точно будет передана и преобразована информация любого потока

Что такое сигнал

Сигнал – это некоторый физический процесс, параметры которого изменяются в соответствии с передаваемым сообщением. Пример – электрический сигнал, радиосигнал, как частный случай электромагнитного сигнала, акустический сигнал, оптический и т.д. В зависимости от того, в какой среде идет распространение сигнала. Сигнал – это материальный носитель информации.

Обычно сигнал, независимо от его физической природы, представляют, как некоторую функцию времени x(t). Такое представление есть общепринятая математическая абстракция физического сигнала. 

Типы сигналов

Детерминированный, или регулярный – это сигнал, закон изменения которого известен и известны все его параметры. 

Такой сигнал передает информацию? Информация уменьшает неопределенность. В детерминированном сигнале мы знаем все, мы знаем какой он будет через минуту, через год. Детерминированный сигнал информацию в себе никакую не несет. Например, сигнал с гетеродина, мы сами его сформировали, задали частоту, амплитуду, фазу. 

Квазидетерминированный — это сигнал, закон изменения которого известен, но один или несколько параметров является случайной величиной. 

Пример: x(t)=Asin(wt+j), где амплитуда А и j — случайная величина.

Например, мы знаем его частоту, но не знаем амплитуду и фазу — это квазидетерминированный сигнал, “квази”-почти, почти определенный сигнал. Информация вносит некоторую случайность. Если мы знаем амплитуду, частоту и фазу, значит информации там нет. Квазидетерминированный сигнал передает информацию, передача информации идет в тех параметрах, которые случайны, в нашем примере амплитуда и фаза случайные величины. Именно в этих величинах передается информация. Информация всегда несет в себе хаос, случайность. Все модулированные сигналы, ЧМ, ФМ это квазидетерминированные сигналы.       

Случайным называют сигнал, мгновенные значения которого не известны, а могут быть лишь предсказаны с некоторой вероятностью.

Кроме этого все сигналы могут быть непрерывными (аналоговыми) и дискретными (цифровыми или импульсными).

О случайном сигнале мы можем судить о его вероятностных характеристиках. Мы можем знать его плотность вероятности, но какое значение примет сигнал через секунду, минуту мы не знаем. Когда мы работаем со случайным сигналом, мы всегда работаем с вероятностью. 

Параметры сигналов

Какие параметры мы будем использовать? Это энергия за некоторый интервал времени T. X(t) это сам сигнал, чтобы определить энергию мы должны взять по модулю, возвести в квадрат, проинтегрировать на некотором промежутке времени и получим энергию. 

Средняя мощность за некоторое время t. Это энергия деленная на время.

Мгновенная мощность, если средняя мощность измеряется на некотором участке времени, то мгновенная измеряется в один, конкретный момент времени. 

Средняя мощность измеряется на промежутке времени, а мгновенная в точке. 

Спектральная плотность энергии и мощности

Спектральная плотность сигнала характеризует распределение энергии или мощности сигнала по диапазону частот. Спектральная плотность энергии, это как у нас энергия распределяется по частотному диапазону. Вычисляется через преобразование Фурье. 

И соответственно, СПМ это, как у нас распределяется мощность по частотному диапазону. 

В формуле, модуль в квадрате это спектральная плотность энергии, поделили ее на время T и по определению, время T должно стремиться к бесконечности. Но на практике, никто не ждет бесконечности, все оценивают СПМ на некотором интервале времени. 

СПМ это некоторая функция зависящая от частоты. По шкале СПМ возьмем 10 Вт/Гц, и окрестности в 1 Гц по частоте. То в полосе 1 Гц будет заключено 10 Вт мощности. 

Есть два сигнала и представлены их спектральные плотности мощности. ВОПРОС. Мощность какого сигнала больше? 

Мы должны определить площадь под кривой, проинтегрировать. S1=2*10=20 Вт, S2=1*30=30 Вт. В первом случае S1 имеет мощность 20 Вт, а во втором 30 Вт. 

СПМ реального сигнала, отображаемая на спектральном анализаторе.

Современные анализаторы спектра могут считать автоматически площадь, вы включаете определение мощности, задаете частотный интервал в котором он должен измерить эту мощность и он сам вычисляет канальную мощность сигнала. 

Электрический сигнал

Но что же из себя представляет электрический сигнал? Терзают меня смутные сомнения, что где-то здесь замешан электрический ток :-). Чем характеризуется электрический ток? Ну конечно же, напряжением и силой тока. Самое примечательное, что электрический ток очень удобно передавать через пространство с помощью проводов. В этом случае его скорость распространения будет равна скорости света. Хотя и электроны в проводнике движутся со скоростью всего несколько миллиметров в секунду, электрические поле охватывает сразу весь провод со скоростью света! А как вы помните, скорость света равна 300 000 километров в секунду! Поэтому, электрон на другом конце провода практически сразу придет в движение.

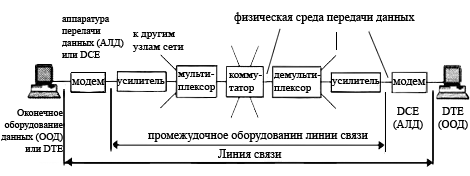
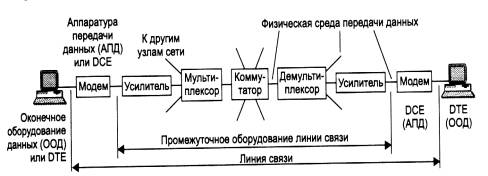
Передача электрических сигналов

Итак, для передачи сигнала через пространство мы будем использовать провода. Чуть выше мы разобрали условия возникновения сигнала. Значит, первым делом, нам нужен генератор этих сигналов! То есть это может быть какая-либо батарея или схемка, которая бы генерировала  электрический ток. Далее, должен быть кто-то, кто бы принимал этот сигнал. Это может быть какая-нибудь нагрузка, типа лампочки, нагревательного элемента или целой схемы, которая бы принимала этот сигнал. Ну и в-третьих, нагрузка должна как-то среагировать на этот сигнал. Лампочка должна источать свет, нагревательный элемент – греться, а схема исполнять какую-либо функцию.

Как вы поняли из всего выше сказанного, главный козырь сигнала – это его генератор. Итак, как мы уже разобрали, по проводам можно передавать два параметра электрического тока – это напряжение и сила тока. То есть мы можем создать  генератор, который бы менял или свое напряжение или силу тока в нагрузке, которая бы цеплялась через провода к этому генератору. В основном в электронике используют именно параметр “напряжение”, так как напряжение легко получить и менять его значение.

Характеристики сигналов [1]

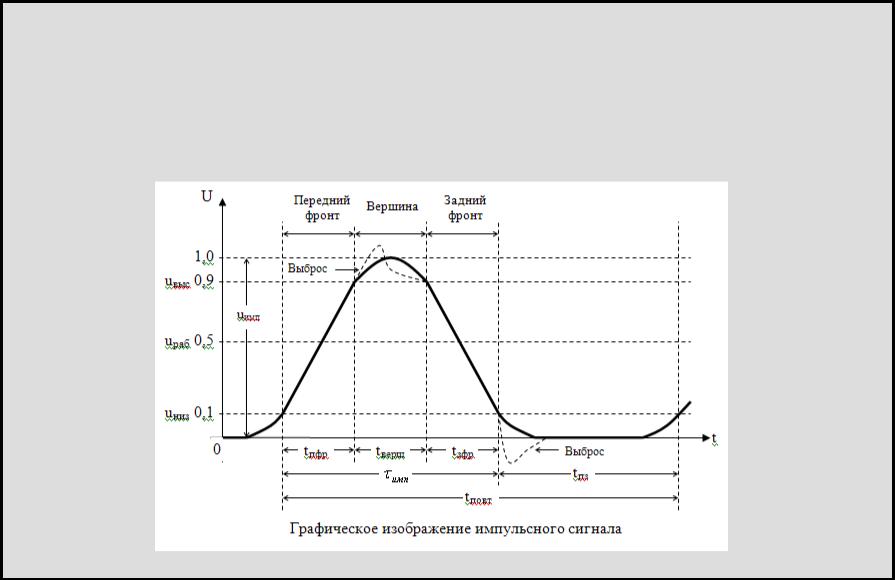
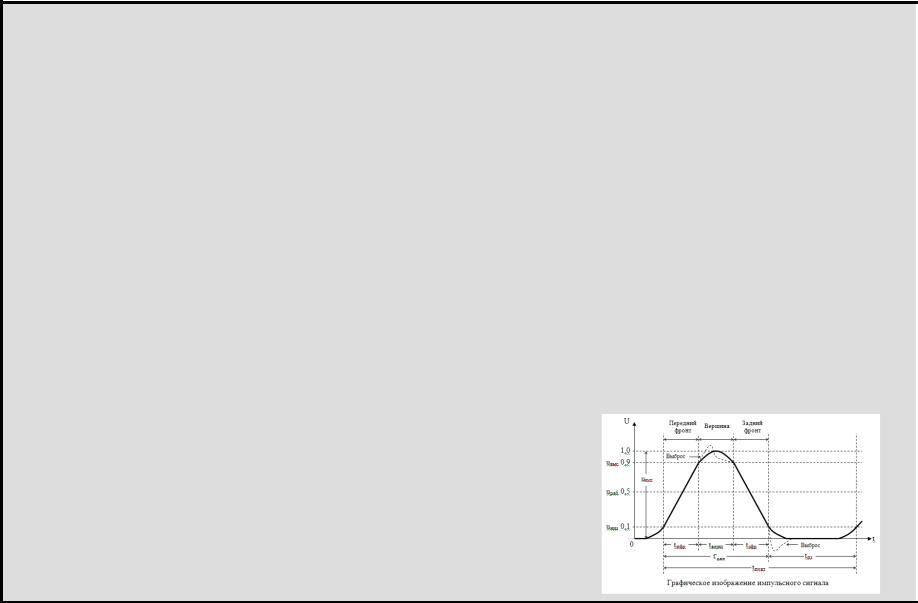
Характеристики импульсов

• Спектральная функция импульса — комплексная функция, представляющая собой преобразование Фурье от импульса.
• Модуль спектральной функции импульса
• Аргумент спектральной функции импульса

Характеристики периодических сигналов

• Период периодического сигнала — параметр, равный наименьшему интервалу времени, через который повторяются мгновенные значения периодического сигнала.
• Частота периодического сигнала — параметр, представляющий собой величину, обратную периоду периодического сигнала.
• Комплексный спектр периодического сигнала — Комплексная функция дискретного аргумента, равного целому числу значений частоты периодического сигнала, представляющая собой значения коэффициентов комплексного ряда Фурье для периодического сигнала.
• Амплитудный спектр периодического сигнала — Функция дискретного аргумента, представляющая собой модуль комплексного спектра периодического сигнала.
• Фазовый спектр периодического сигнала — функция дискретного аргумента, представляющая собой аргумент комплексного спектра периодического сигнала.
• Гармоника — гармонический сигнал с амплитудой и начальной фазой, равными соответственно значениям амплитудного и фазового спектра периодического сигнала при некотором значении аргумента.

Характеристики случайных сигналов

• Одномерная плотность вероятности — функция, равная пределу отношения вероятности пребывания случайного сигнала в некотором интервале значений к ширине этого интервала при стремлении его к нулю, причем ее аргументом является значение, к которому стягивается интервал
• Корреляционная функция — функция, равная среднему значению произведения переменной составляющей случайного сигнала и такой же переменной составляющей, но запаздывающей на заданное время.
• Нормированная корреляционная функция — функция, равная отношению корреляционной функции случайного сигнала к его дисперсии
• Энергетический спектр — функция, представляющая собой преобразование Фурье от корреляционной функции, аргументом которой является частота

Характеристики взаимодействия сигналов

• Отношение сигнал — помеха — отношение величин, характеризующих интенсивности сигнала и помехи.
• Коэффициент модуляции «вверх» — коэффициент, равный отношению пикового отклонения «вверх» закона модуляции к его постоянной составляющей при амплитудной модуляции.
• Коэффициент модуляции «вниз» — коэффициент, равный отношению пикового отклонения «вниз» закона модуляции к его постоянной составляющей при амплитудной модуляции.
• Девиация частоты «вверх» — пиковое отклонение «вверх» закона модуляции при частотной модуляции.
• Девиация частоты «вниз» — пиковое отклонение «вниз» закона модуляции при частотной модуляции.
• Индекс угловой модуляции — пиковое отклонение закона модуляции фазомодулированного сигнала при гармоническом законе модуляции

Характеристики взаимосвязи сигналов

• Взаимокорреляционная функция — функция, равная среднему значению произведения переменной составляющей одного случайного сигнала и запаздывающей на заданное время переменной составляющей другого случайного сигнала.
• Взаимный энергетический спектр — Функция, представляющая собой преобразование Фурье от взаимнокорреляционной функции, аргументом которой является частота
• Время запаздывания — параметр, равный значению временного сдвига одного из сигналов, при котором достигается тождественное равенство его другому сигналу с точностью до постоянного множителя и постоянного слагаемого.
• Фазовый сдвиг — модуль разности начальных фаз двух гармонических сигналов одинаковой частоты.

Характеристики искажений сигналов

• Коэффициент гармоник — коэффициент, характеризующий отличие формы данного периодического сигнала от гармонической, равный отношению среднеквадратического напряжения суммы всех гармоник сигнала, кроме первой, к среднеквадратическому напряжению первой гармоники.
• Относительное отклонение сигнала от линейного закона — коэффициент, равный отношению абсолютного отклонения (40) данного сигнала от прямой линии, соединяющей мгновенные значения сигнала, соответствующие началу и концу заданного интервала времени к максимальному значению сигнала на этом же интервале
• Коэффициент нелинейности сигнала — коэффициент, равный отношению размаха производной сигнала на заданном интервале времени к максимальному значению производной на этом же интервале.
• Абсолютное отклонение сигналов — максимальное значение разности мгновенных значений сигналов, взятых в один и тот же момент времени на протяжении заданного интервала времени.

Какие системы связи используют цифровой сигнал а какие аналоговый

Несмотря на архаичность аналоговая технология ещё используется для телефонной и радио связи. Многие проводные сети до сих пор остаются аналоговыми. В основном это традиционные телефонные линии местных операторов. Но, для магистральной передачи данных связи уже повсеместно используют цифровые каналы. Так же аналоговая технология применяется в простых и дешёвых переносных радиостанциях.

Во всех вновь создаваемых системах используют цифровую технологию обработки сигнала. Это оптоволоконные и проводные линии, сигнализация и телеметрия, военная и гражданская промышленная связь. И конечно же на цифровое вещание переходит телевидение. Аналоговый способ передачи данных исчерпал себя. На смену пришла новая высококачественная и защищенная связь.

Представление сигнала и спектр

Есть два способа представления сигнала в зависимости от области определения: временной и частотный. В первом случае сигнал представляется функцией времени s(t){\displaystyle s(t)} характеризующей изменение его параметра.

Кроме привычного временного представления сигналов и функций при анализе и обработке данных широко используется описание сигналов функциями частоты. Действительно, любой сколь угодно сложный по своей форме сигнал можно представить в виде суммы более простых сигналов, и, в частности, в виде суммы простейших гармонических колебаний, совокупность которых называется частотным спектром сигнала.

Для перехода к частотному способу представления используется преобразование Фурье:

S(ω)=∫−∞+∞s(t)e−jωtdt{\displaystyle S(\omega )=\int \limits _{-\infty }^{+\infty }s(t)e^{-j\omega t}\,dt}.

Функция S(ω){\displaystyle S(\omega )} называется спектральной функцией или спектральной плотностью. Поскольку спектральная функция S(ω){\displaystyle S(\omega )} является комплексной, то можно говорить о спектре амплитуд |S(ω)|{\displaystyle |S(\omega )|} и спектре фаз ϕ(ω)=arg(S(ω)){\displaystyle \phi (\omega )=arg(S(\omega ))}.

Физический смысл спектральной функции: сигнал s(t){\displaystyle s(t)} представляется в виде суммы бесконечного ряда гармонических составляющих (синусоид) с амплитудами |S(ω)|πdω{\displaystyle {\frac {|S(\omega )|}{\pi }}d\omega }, непрерывно заполняющими интервал частот от {\displaystyle 0} до ∞{\displaystyle \infty }, и начальными фазами ϕ(ω){\displaystyle \phi (\omega )}.

Размерность спектральной функции есть размерность сигнала, умноженная на время.

В словаре Ожегова

СИГНАЛ, -а, м. 1. Условный знак для передачи на расстояние каких-н. сведений, сообщений. Звуковой, визуальный, световой с, Дать с. С. 808 (от терпящих бедствие в море; также перен.: призыв о помощи в беде). 2. перен. То, что служит толчком к началу какого-н. действия. Статья послу-жила сигналом к дискуссии, 3. перен. Предупреждение, сообщение о чем-н. нежелательном. Прислушиваться к сигналам с мест. Сигналы общественности. || прил. сигнальный, -ая, -ое (к 1 знач.). Сигнальные огни. Сигнальная связь. С. пистолет (ракетница). С. экземпляр (первый, до тиража, готовый экземпляр произведения печати).

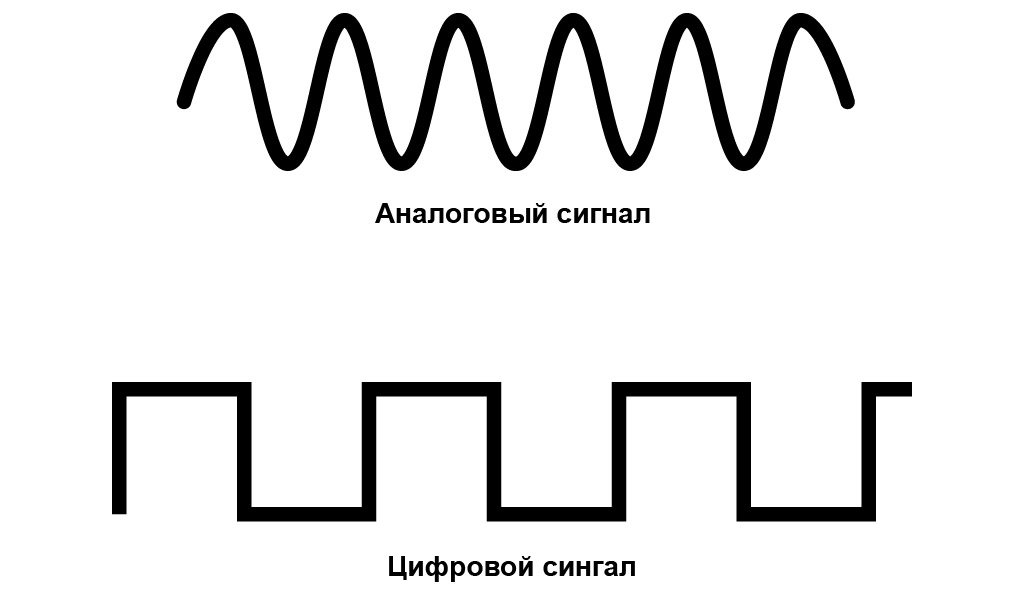
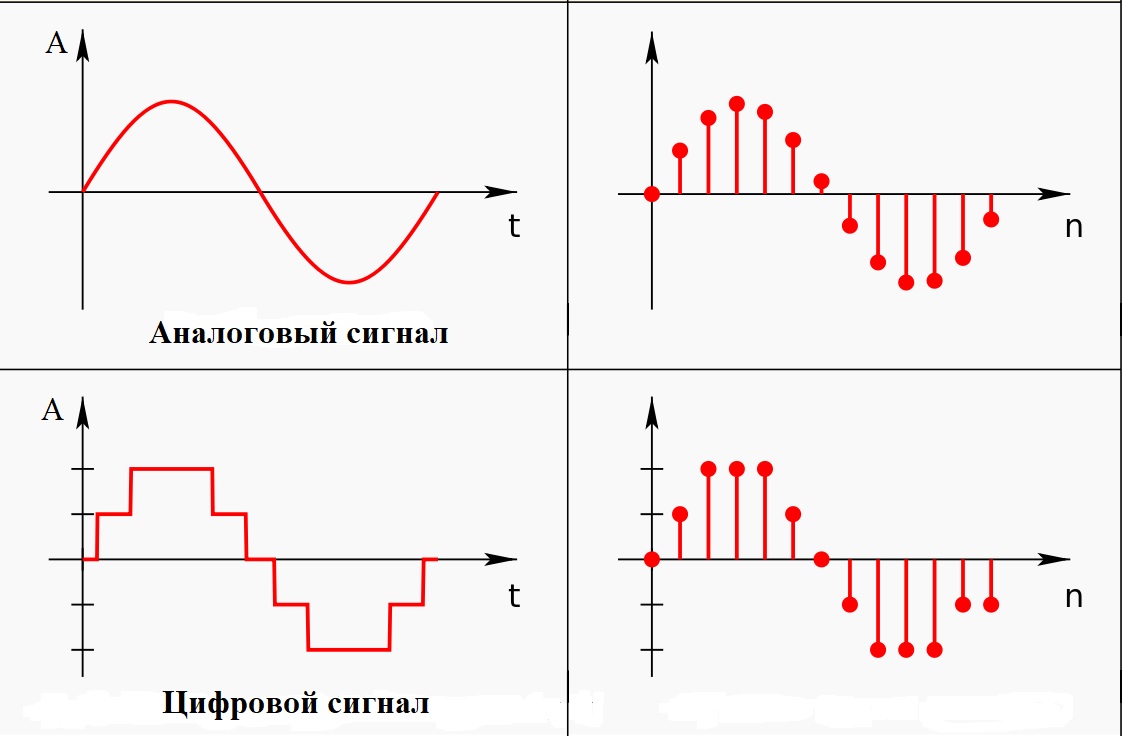
Аналоговый сигнал

Это природный тип сигналов окружает нас повсеместно и постоянно. Звук, изображение, тактильные ощущения, запах, вкус и команды мозга. Все возникающие, во Вселенной без участия человека, сигналы являются аналоговыми.

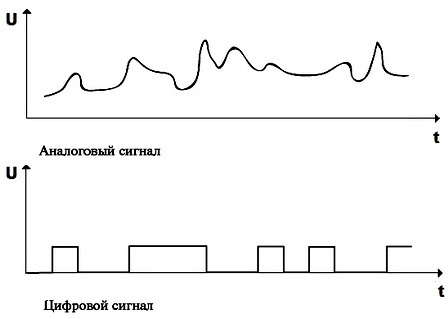
В электронике, электротехнике и системах связи аналоговую передачу данных применяют со времени изобретения электричества. Характерной особенностью является непрерывность и плавность изменения параметров. Графически сеанс аналоговой связи можно описать как непрерывную кривую, соответствующую величине электрического напряжения в определённый момент времени. Линия изменяется плавно, разрывы возникают только при обрыве связи. В природе и электронике аналоговые данные генерируются и распространяются непрерывно. Отсутствие непрерывного сигнала означает тишину или черный экран.

В непрерывных системах связи аналогом звука, изображения и любых других данных является электрические или электромагнитные импульсы. Например, громкость и тембр голоса передаются от микрофона на динамик посредством электрического сигнала. Громкость зависит от величины, а тембр от частоты напряжения. Поэтому при голосовой связи сначала напряжение становится аналогом звука, а потом звук аналогом напряжения. Таким же образом происходит передача любых данных в аналоговых системах связи.

Общая информация

Энергия потока

Так как аналоговый сигнал – это непрерывный поток данных, то энергия его бесконечна. Однако в качестве значения данной характеристики обычно используют усредненную для определенного промежутка времени величину, так, к примеру, переменный электрический ток в телефонной сети, отвечающий за передачу голоса, имеет среднее напряжение 60 В.

Взаимное преобразование различных по природе потоков

Непрерывный поток данных преобразуется в дискретный (прерывистый). Достаточно воспользоваться импульсным блоком питания, который сформирует входное напряжение в виде дискретных ультразвуковых пачек. Преобразование проводится программой либо технически через микросхемы.

Отличия дискретного и цифрового сигналов

Основная разница дискретного и цифрового потоков – ярко выраженная амплитуда у последнего

Один из способов передачи данных, описываемых в данной статье, – дискретный, имеющий сходные характеристики с аналоговым, но отличающийся от него тем, что он является прерывистым.

По сравнению с дискретным и аналоговым, цифровой сигнал, наоборот, характеризуется конкретными параметрами:

• Строго определённой своими характеристиками длительностью;
• Ярко выраженной амплитудой;
• Наличием двух состояний: «0» либо «1».
• Формированием из битов машинных слов, необходимых для дальнейшей обработки информации, ее представлении в доступном и понятном виде для пользователя.

Благодаря этим особенностям, цифровая передача и хранение информации в последнее время находят очень широкое применение в различных отраслях техники, электроники, связи.

Важно! Самое основное, чем отличается аналоговая информация от дискретной, – это прерывистость передачи последней при помощи соответствующего потока данных. Однако, несмотря на данное различие, дискретная информация не является цифровой, так как ее характеристики в процессе существования могут обладать как ограниченным, так и неограниченным диапазоном значений

Как аналоговый сигнал преобразуется в цифровой и наоборот

Первой в цифровую форму преобразовали математическую, физическую и компьютерную информацию. Описать формулы и расчеты не составило труда. А вот для преображения аналоговой действительности в цифровые массивы уже потребовались специальные устройства. Ими стали аналого-цифровые преобразователи или сокращенно АЦП. Они предназначены для преобразования различных физических величин в цифровые коды. Обратное действие совершают устройства ЦАП.

Любые цифровые передатчики и приёмники оснащены такими преобразователями. Например, сотовому телефону, поступивший звук необходимо обработать и передать в оцифрованном виде. В то же время необходимо принять от другого абонента код, преобразовать и передать напряжение на динамик. Так же и с изображением на смартфонах и в телевизорах. В любом случае первоначальной информацией выступает напряжение.

Существует много видов АЦП, но самыми распространёнными являются следующие:

• параллельного преобразования;
• последовательного приближения;
• дельта-сигма, с балансировкой заряда.

Преобразования в АЦП понятийно связаны с измерением и сравнением. Кодировка, это процесс сравнения полученных от источника данных с эталоном. То есть полученная аналоговая величина сравнивается с эталонной (с заданным напряжением). Эталоном выступает информация о конкретном цвете, звуке и т.п. Она соответствует заложенным в устройство представлениям о преобразуемом сигнале. Потом данные эталонной величины кодируются для передачи. Во время аналого-цифровой обработки физических превращений сигнала не происходит. С аналогового делается цифровой матрица (модель).

Упрощенно работу любого АЦП можно представить так:

1. Измерение через определенные интервалы времени амплитуды напряжения.
2. Сравнение с эталоном и формирование данных.
3. Отгрузка оцифрованных сведений об изменениях амплитуды на передатчик.

Качество передаваемой информации зависит от двух параметров — точности и частоты измерений. Чем точнее измеряется и зашифровывается входящее напряжение, тем качественней передаваемая информация. Поэтому, имеет большое значение, сколько бит может зашифровать преобразователь. Чем плотнее информационный поток, тем точней передача данных. Это выражается в красках экрана, контрастности картинки и чистоте звука. Следующим важным показателем является дискретизация, то есть частота измерений. Чем чаще, тем меньше провалов в измерениях и необходимости сглаживания. В совокупности, чем чаще и точнее преобразователь может измерять и обрабатывать полученное напряжение, тем он лучше.

Время и электрический сигнал

Как я уже сказал, сигнал передается во времени и в пространстве. То есть время – важный параметр для электрического сигнала. Сейчас нам придется немного попотеть и вспомнить курс математики и физики за среднюю школу. Вспоминаем декартову систему координат. Как вы помните, по вертикали мы откладывали ось Y, по горизонтали Х:

В электронике и электротехнике по Х мы откладываем время, назовем его буквой t, а по вертикали мы отложим напряжение, обозначим его буквой U. В  результате наша система координат будет выглядеть вот таким образом:

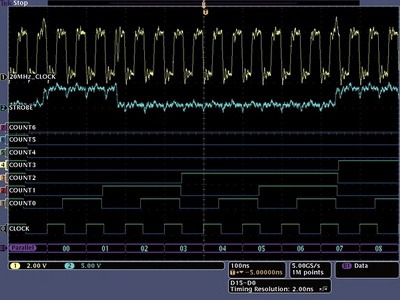
Прибор, который показывает нам изменение напряжения во времени называется осциллографом, а график этого напряжения называется осциллограммой. Осциллограф может быть цифровым:

или аналоговым:

Что такое дискретный сигнал

В цифровой системе хранения и передачи данных, отсутствие сигнала, также является формой обмена информацией. В какой-то момент времени он равен нулю, в другой принимает какое-либо значение. Поэтому дискретным называют сигнал прерывный, отсюда и название discretus или разделённый. Аналоговые данные разбиваются на отдельные блоки, обрабатываются и передаются в виде цифрового кода.

Дискретность не подразумевает разрыв связи. В цифровых системах широко используется двоичная система обработки и обмена информацией. Двоичная подразумевает кодировку данных с помощью единицы и нулей. В доли секунды сигнал прерывисто принимает значение 1 или 0. Вместо непрерывной кривой имеем отдельные дискретные значения. Определенный набор нулей и единичек уже несёт в себе какую либо информацию. Примитивный набор это бит или двоичный разряд. Сам по себе он ничего не значит. Данные могут кодироваться только при объединении восьми битов в следующую по сложности комбинацию – байт. Чем больше объединённых байтов, тем больше и точнее можно описать передаваемую информацию.

На качество генерируемых данных влияет не только количество объединённых битов, но и скорость передачи. Непрерывная аналоговая кривая должна быть разбита на как много больше мини участков прерывного сигнала. Полученный таким образом звук и цвет будут соответствовать оригиналу. Качественный дискретный сигнал формирует точную копию аналогового. Например, звуковая дорожка MP3 закодированная со скоростью 320 000 бит в секунду (320 kbps) значительно лучше кодированной в 128 kbps. Дорожки скоростью меньше 128 слушать вообще невозможно.

Пешеходные светофоры

Этот вид устройств также необходим для безопасности на дорогах. Только ими регулируется не транспортное, а пешеходное движение. Существуют и устройства, которые подают сигналы для велосипедистов.

Линзы подобных светофоров имеют свою особенность. На них наносят изображение силуэта пешехода или велосипедиста. Состоит подобный светофор из двух секций. Верхняя из них имеет красный свет, запрещающий движение. Нижняя подает зеленый знак. Он разрешает движение.

Существуют также Х-образные светофоры. С их помощью регулируется движение по той полосе проезжей части, где поток транспорта может перемещаться то в одном, то в другом направлении.

Классификация сигналов

По физической природе носителя информации:

• электрические;
• электромагнитные;
• оптические;
• акустические

и другие;

По способу задания сигнала:

• регулярные (детерминированные), заданные аналитической функцией;
• нерегулярные (случайные), принимающие произвольные значения в любой момент времени. Для описания таких сигналов используется аппарат теории вероятностей.

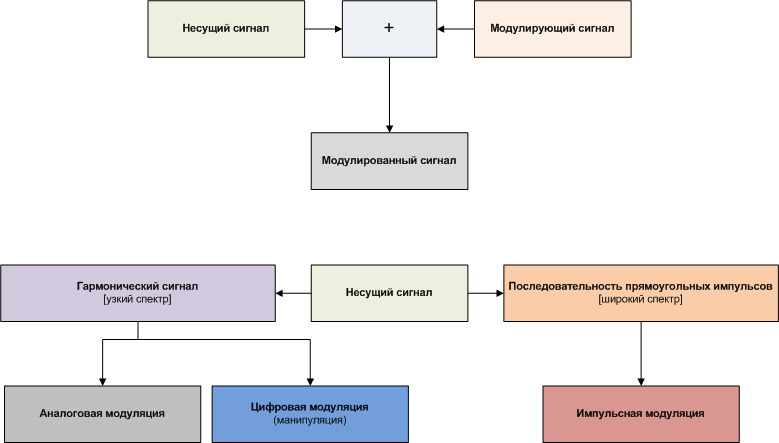
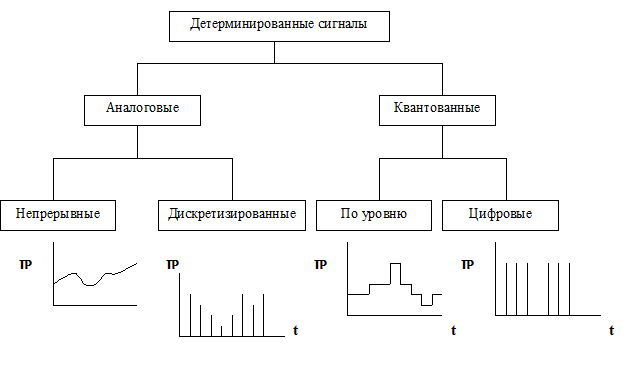
В зависимости от функции, описывающей параметры сигнала, выделяют аналоговые, дискретные, квантованные и цифровые сигналы:

• непрерывные (аналоговые), описываемые непрерывной функцией;
• дискретные, описываемые функцией отсчётов, взятых в определённые моменты времени;
• квантованные по уровню;
• дискретные сигналы, квантованные по уровню (цифровые).

Аналоговый сигнал (АС)

Аналоговый сигнал

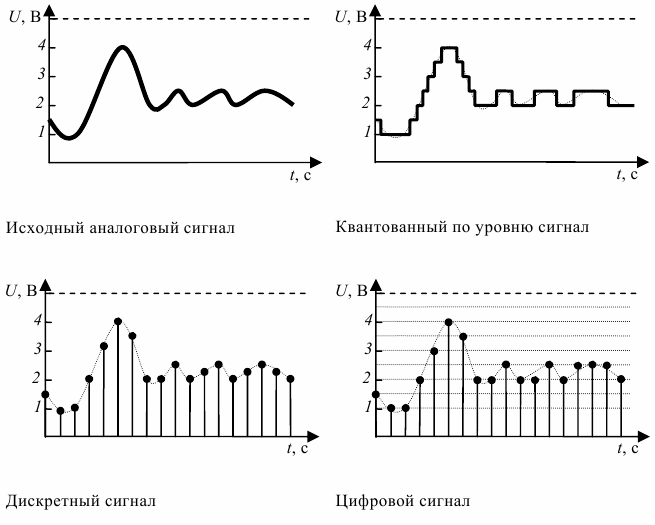
Большинство сигналов имеют аналоговую природу, то есть изменяются непрерывно во времени и могут принимать любые значения на некотором интервале. Аналоговые сигналы описываются некоторой математической функцией времени.

Пример АС — гармонический сигнал: s(t) = A·cos(ω·t + φ).

Аналоговые сигналы используются в телефонии, радиовещании, телевидении. Ввести такой сигнал в цифровую систему для обработки невозможно, так как на любом интервале времени он может иметь бесконечное множество значений, и для точного (без погрешности) представления его значения требуются числа бесконечной разрядности. Поэтому очень часто необходимо преобразовывать аналоговый сигнал так, чтобы можно было представить его последовательностью чисел заданной разрядности.

Дискретный сигнал

Дискретный сигнал

Дискретизация аналогового сигнала состоит в том, что сигнал представляется в виде последовательности значений, взятых в дискретные моменты времени t_i (где i — индекс). Обычно промежутки времени между последовательными отсчётами (Δt_i = t_i − t_i−1) постоянны; в таком случае, Δt называется интервалом дискретизации. Сами же значения сигнала x(t) в моменты измерения, то есть x_i = x(t_i), называются отсчётами.

Квантованный сигнал

Квантованный сигнал

При квантовании вся область значений сигнала разбивается на уровни, количество которых должно быть представлено в числах заданной разрядности. Расстояния между этими уровнями называется шагом квантования Δ. Число этих уровней равно N (от 0 до N−1). Каждому уровню присваивается некоторое число. Отсчёты сигнала сравниваются с уровнями квантования и в качестве сигнала выбирается число, соответствующее некоторому уровню квантования. Каждый уровень квантования кодируется двоичным числом с n разрядами. Число уровней квантования N и число разрядов n двоичных чисел, кодирующих эти уровни, связаны соотношением n ≥ log₂(N).

Цифровой сигнал

Цифровой сигнал

Для того, чтобы представить аналоговый сигнал последовательностью чисел конечной разрядности, его следует сначала превратить в дискретный сигнал, а затем подвергнуть квантованию. Квантование является частным случаем дискретизации, когда дискретизация происходит по одинаковой величине, называемой квантом. В результате сигнал будет представлен таким образом, что на каждом заданном промежутке времени известно приближённое (квантованное) значение сигнала, которое можно записать целым числом. Последовательность таких чисел и будет являться цифровым сигналом.

Что такое сигнал?

Сигнал –  это что-то такое, что можно передать через пространство и время. Итак, какие условия должны быть, чтоб назвать сигнал “сигналом”?

Во-первых, сигнал должен кем-либо создаваться (генерироваться).

Во-вторых, сигнал должен для кого предназначаться.

В-третьих, кто-то должен принять этот сигнал и сделать для себя какие-либо выводы, то есть правильно трактовать сигнал.

Окунемся в Дикий Запад.

Думаю, не секрет, что индейцы разжигали костер, и дым от костра использовался для передачи сигнала. Значит, в нашем случае костер – генератор сигнала. Итак, первый пункт работает). Для кого же был предназначен дым от костра? Для ковбоев? Конечно же нет! Для своих же индейцев. Значит, работает пункт два. Ну ладно, вы увидели два столба дыма, возвышающихся в небо. Вам это что-то говорит? Кто-то, наверное, жарит шашлыки? Может быть. Но если вы подойдете к этим кострам, то шашлык сделают именно из вас). Для индейцев эти два  столба дыма означали, что их отряд благополучно поохотился на ковбоев ;-). Ну вот и выполнилось третье правило ;-).

Параметры сигналов

• Мощность сигнала P(t)=s2(t){\displaystyle P(t)=s^{2}(t)}
• Удельная энергия сигнала Eуд=∫−∞∞s2(t)dt{\displaystyle E_{\text{уд}}=\int \limits _{-\infty }^{\infty }{s^{2}(t)dt}}
• Длительность сигнала T{\displaystyle T} определяет интервал времени, в течение которого сигнал существует (отличен от нуля);
• Динамический диапазон есть отношение наибольшей мгновенной мощности сигнала к наименьшей:

D=10lg⁡PmaxPmin{\displaystyle D=10\lg {\frac {P_{max}}{P_{min}}}}

• Ширина спектра сигнала F{\displaystyle F} — полоса частот, в пределах которой сосредоточена основная энергия сигнала;
• База сигнала есть произведение длительности сигнала на ширину его спектра B=TF{\displaystyle B=TF}. Необходимо отметить, что между шириной спектра и длительностью сигнала существует обратно пропорциональная зависимость: чем короче спектр, тем больше длительность сигнала. Таким образом, величина базы остается практически неизменной;
• Отношение сигнал/шум равно отношению мощности полезного сигнала к мощности шума;
• Объём передаваемой информации характеризует пропускную способность канала связи, необходимую для передачи сигнала. Он определяется как произведение ширины спектра сигнала на его длительность и динамический диапазон:

V=FTD{\displaystyle V=FTD}