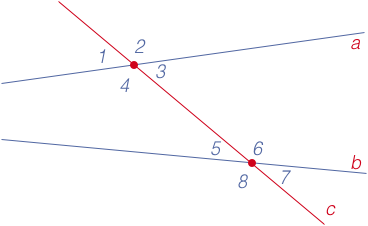
Секущая двух прямых
Секущие двух прямых служат для установления того, являются ли эти две прямые параллельными между собой.
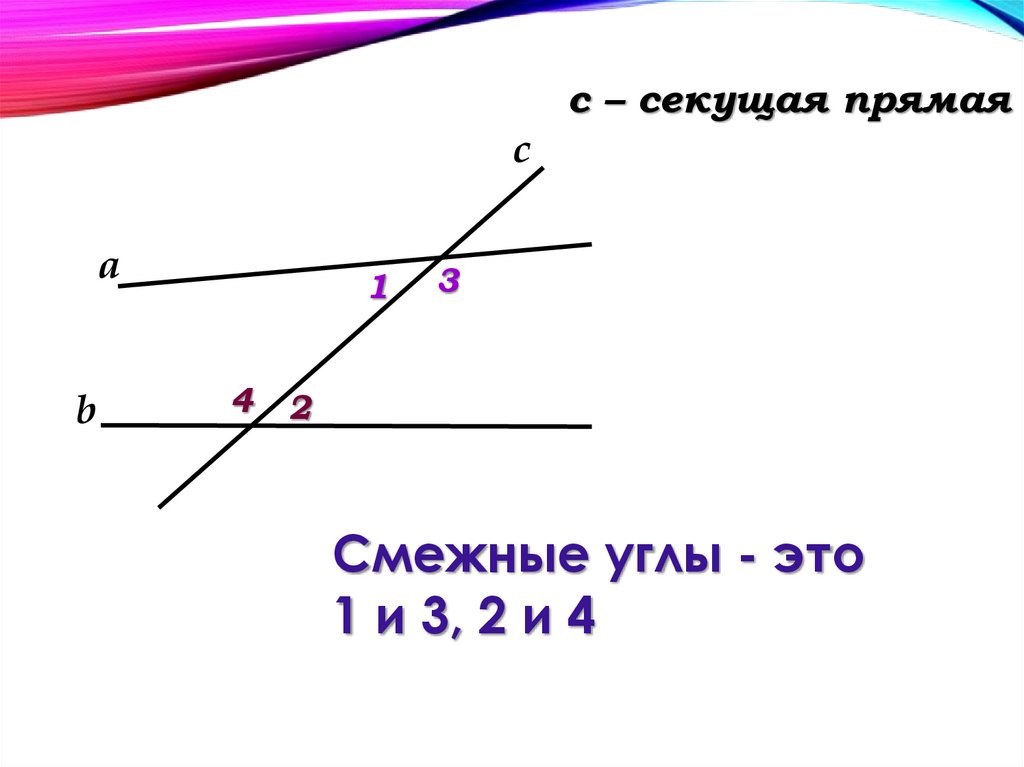
Пересечения этих прямых и секущие образуют различные пары углов: односторонние углы (α{\displaystyle \alpha } и δ1{\displaystyle \delta _{1}}, β{\displaystyle \beta } и γ1{\displaystyle \gamma _{1}} на рисунке), соответственные углы (α{\displaystyle \alpha } и α1{\displaystyle \alpha _{1}}, β{\displaystyle \beta } и β1{\displaystyle \beta _{1}}, γ{\displaystyle \gamma } и γ1{\displaystyle \gamma _{1}}, δ{\displaystyle \delta } и δ1{\displaystyle \delta _{1}}) и накрест лежащие углы (α{\displaystyle \alpha } и γ1{\displaystyle \gamma _{1}}, β{\displaystyle \beta } и δ1{\displaystyle \delta _{1}}, γ{\displaystyle \gamma } и α1{\displaystyle \alpha _{1}}, δ{\displaystyle \delta } и β1{\displaystyle \beta _{1}}).
Согласно пятому постулату Евклида, две прямые параллельны, если:
- сумма односторонних углов равна 180°;
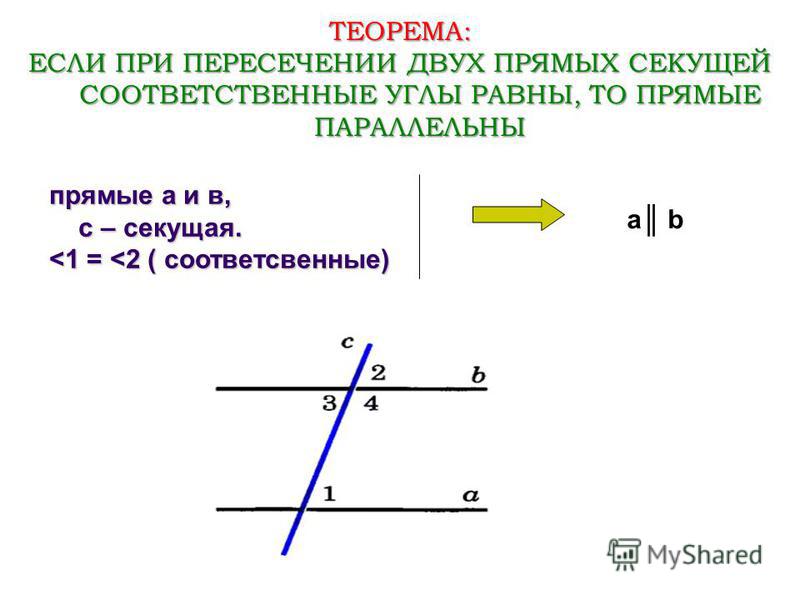
- соответственные углы равны;
- накрест лежащие углы равны.
Любой из этих признаков является необходимым и достаточным условием того, что прямые параллельны.
| Восемь углов трансверсали.(Вертикальные углы такие, как α{\displaystyle \alpha } и γ,{\displaystyle \gamma ,} всегда равны.) | Трансверсаль между непараллельными прямыми. Внутренние не накрест лежащие углы не являются дополнительными (в сумме дающими 180 градусов). | Трансверсаль между параллельными прямыми. Внутренние не накрест лежащие углы являются дополнительными (в сумме дающими 180 градусов). |
Касательные прямые к одной окружности
Касательная прямая t к окружности C пересекает окружность в единственной точке T. Для сравнения, секущие прямые пересекают окружность в двух точках, в то время как некоторые прямые могут не пересекать окружность совсем. Это свойство касательной прямой сохраняется при многих геометрических , таких как подобие, вращение, параллельный перенос, инверсия и картографическая проекция. Говоря техническим языком, эти преобразования не меняют структуру инцидентности касательных прямых и окружностей, даже если сами прямые и окружности деформируются.
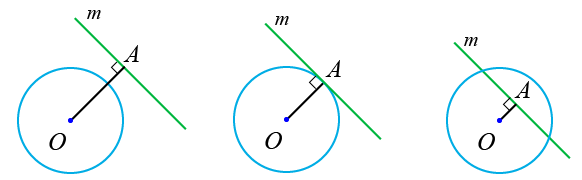
Радиус окружности, проведённый через точку касания, перпендикулярен касательной прямой. И обратно, перпендикуляр к радиусу в конечной точке (на окружности) является касательной прямой. Окружность вместе с касательной прямой имеют осевую симметрию относительно радиуса (к точке касания).
По теореме о степени точки произведение длин PM•PN для любого луча PMN равно квадрату PT, длине отрезка от точки P до точки касания (отрезок показан красным цветом).
Никакая касательная прямая не может проходить через точку внутри окружности, поскольку любая такая прямая должна быть секущей. В то же время для любой точки, лежащей вне круга, можно построить две проходящие через неё касательные прямые. Геометрическая фигура, состоящая из окружности и двух касательных прямых, также обладает осевой симметрией относительно прямой, соединяющей точку P с центром окружности O (см. рисунок справа). В этом случае отрезки от точки P до двух точек касания имеют одинаковую длину. По теореме о степени точки квадрат длины отрезка до точки касания равен степени точки P относительно окружности C. Эта степень равна произведению расстояний от точки P до двух точек пересечения окружности любой секущей линией, проходящей через P.
Угол θ между хордой и касательной равен половине дуги, заключённой между концами хорды.
Касательная прямая t и точка касания T обладают свойством сопряжённости друг другу; это соответствие можно обобщить в идею о полюсе и поляре. Такая же взаимосвязь существует между точкой P вне окружности и секущей линией, соединяющей две точки касания.
Если точка P лежит вне окружности с центром O, и если касательные прямые из P касаются окружности в точках T и S, то углы ∠TPS и ∠TOS дают в сумме 180°.
Если хорда TM проведена из точки касания T прямой P T и ∠PTM ≤ 90°, то ∠PTM = (1/2)∠MOT.
Геометрическое построение
Построение касательной прямой к окружности (выделена красным) перпендикулярно радиусу.
Относительно легко построить прямую t, касательную к окружности в точке T на окружности. Для этого следует провести прямую a через центр окружности O и точку T. Тогда прямая t является перпендикуляром к прямой a. Один из способов построения перпендикуляра следующий (см. рисунок). Проводим тем же радиусом (r) окружность с центром в точке T, получаем вторую точку G на прямой a, а точка T становится серединой отрезка OG. Проводим две окружности радиуса R>r с центрами в точках O и G. Прямая, проходящая через точки пересечения этих окружностей, будет касательной.
Построение касательной прямой к окружности
Для построения касательной прямой через точку P к окружности C можно использовать свойство угла, опирающегося на диаметр окружности. Проводится окружность с центром в точке H, середине отрезка OP, где O — центр окружности C. Пересечения T и T‘ являются точками касания прямых, проходящих через точку P, поскольку углы ∠OTP и ∠OT‘P опираются на диаметр OP окружности с центром в H.
Теорема об описанном четырёхугольнике и вписанные окружности
Описанный четырёхугольник ABCD — это замкнутая фигура с четырьмя сторонами, которые касаются окружности C. Соответственно, C — вписанная в четырёхугольник ABCD окружность. По теореме Пито суммы противоположных сторон любого такого четырёхугольника равны, то есть
- AB¯+CD¯=BC¯+DA¯.{\displaystyle {\overline {AB}}+{\overline {CD}}={\overline {BC}}+{\overline {DA}}.}
Описанный четырёхугольник
Это заключение следует из равенства отрезков касательных от вершин четырёхугольника. Обозначим точки касания как P (на отрезке AB), Q (на отрезке BC), R (на отрезке CD) и S (на отрезке DA). Симметричные отрезки до точек касания от каждой вершины четырёхугольника ABCD равны, то есть BP=BQ=b, CQ=CR=c, DR=DS=d и AS=AP=a.
Но каждая сторона четырёхугольника состоит из двух таких отрезков
- AB¯+CD¯=(a+b)+(c+d)=BC¯+DA¯=(b+c)+(d+a){\displaystyle {\overline {AB}}+{\overline {CD}}=(a+b)+(c+d)={\overline {BC}}+{\overline {DA}}=(b+c)+(d+a)},
что и доказывает утверждение.
Обратное утверждение также верно — окружность можно вписать в любой выпуклый четырёхугольник, у которого суммы длин противоположных сторон равны.
Общие касательные к двум окружностям
| Фигура | Рисунок | Свойства |
| Внешняя касательная к двум окружностям |  |
Прямую называют внешней касательной к двум окружностям, если она каждой из окружностей, а окружности лежат по одну сторону от этой прямой. |
| Внутренняя касательная к двум окружностям | 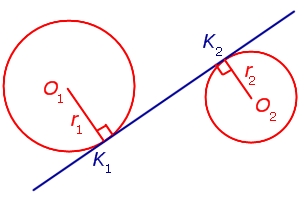 |
Прямую называют внутренней касательной к двум окружностям, если она каждой из окружностей, а окружности лежат по разные стороны от этой прямой. |
| Внутреннее касание двух окружностей |  |
Существует единственная общая внешняя касательная. Других общих касательных нет. |
| Окружности пересекаются в двух точках |  |
Существуют две общих внешних касательных. Других общих касательных нет. |
| Внешнее касание двух окружностей |  |
Существует единственная общая внутренняя касательная, а такжедве общих внешних касательных. Других общих касательных нет. |
 |
||
|
Каждая из окружностей лежит вне другой |
Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет |
|
| Внешняя касательная к двум окружностям | |
|
Прямую называют внешней касательной к двум окружностям, если она каждой из окружностей, а окружности лежат по одну сторону от этой прямой. |
|
| Внутренняя касательная к двум окружностям | |
|
Прямую называют внутренней касательной к двум окружностям, если она каждой из окружностей, а окружности лежат по разные стороны от этой прямой. |
|
| Внутреннее касание двух окружностей | |
|
Существует единственная общая внешняя касательная. Других общих касательных нет. |
|
| Окружности пересекаются в двух точках | |
|
Существуют две общих внешних касательных. Других общих касательных нет. |
|
| Внешнее касание двух окружностей | |
|
Существует единственная общая внутренняя касательная, а также две общих внешних касательных. Других общих касательных нет. |
|
| Каждая из окружностей лежит вне другой | |
|
Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет |
|
| Внешняя касательная к двум окружностям |
|
Прямую называют внешней касательной к двум окружностям, если она каждой из окружностей, а окружности лежат по одну сторону от этой прямой. |
| Внутренняя касательная к двум окружностям |
|
Прямую называют внутренней касательной к двум окружностям, если она каждой из окружностей, а окружности лежат по разные стороны от этой прямой. |
| Внутреннее касание двух окружностей |
|
Существует единственная общая внешняя касательная. Других общих касательных нет. |
| Окружности пересекаются в двух точках |
|
Существуют две общих внешних касательных. Других общих касательных нет. |
| Внешнее касание двух окружностей |
|
Существует единственная общая внутренняя касательная, а также две общих внешних касательных. Других общих касательных нет. |
| Каждая из окружностей лежит вне другой |
|
Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет |
Секущая двух прямых
Секущие двух прямых служат для установления того, являются ли эти две прямые параллельными между собой.
Пересечения этих прямых и секущие образуют различные пары углов: односторонние углы (α{\displaystyle \alpha } и δ1{\displaystyle \delta _{1}}, β{\displaystyle \beta } и γ1{\displaystyle \gamma _{1}} на рисунке), соответственные углы (α{\displaystyle \alpha } и α1{\displaystyle \alpha _{1}}, β{\displaystyle \beta } и β1{\displaystyle \beta _{1}}, γ{\displaystyle \gamma } и γ1{\displaystyle \gamma _{1}}, δ{\displaystyle \delta } и δ1{\displaystyle \delta _{1}}) и накрест лежащие углы (α{\displaystyle \alpha } и γ1{\displaystyle \gamma _{1}}, β{\displaystyle \beta } и δ1{\displaystyle \delta _{1}}, γ{\displaystyle \gamma } и α1{\displaystyle \alpha _{1}}, δ{\displaystyle \delta } и β1{\displaystyle \beta _{1}}).
Согласно пятому постулату Евклида, две прямые параллельны, если:
- сумма односторонних углов равна 180°;
- соответственные углы равны;
- накрест лежащие углы равны.
Любой из этих признаков является необходимым и достаточным условием того, что прямые параллельны.
| Восемь углов трансверсали.(Вертикальные углы такие, как α{\displaystyle \alpha } и γ,{\displaystyle \gamma ,} всегда равны.) | Трансверсаль между непараллельными прямыми. Внутренние не накрест лежащие углы не являются дополнительными (в сумме дающими 180 градусов). | Трансверсаль между параллельными прямыми. Внутренние не накрест лежащие углы являются дополнительными (в сумме дающими 180 градусов). |
Секущая двух прямых
Секущие двух прямых служат для установления того, являются ли эти две прямые параллельными между собой.
Пересечения этих прямых и секущие образуют различные пары углов: односторонние углы (α{\displaystyle \alpha } и δ1{\displaystyle \delta _{1}}, β{\displaystyle \beta } и γ1{\displaystyle \gamma _{1}} на рисунке), соответственные углы (α{\displaystyle \alpha } и α1{\displaystyle \alpha _{1}}, β{\displaystyle \beta } и β1{\displaystyle \beta _{1}}, γ{\displaystyle \gamma } и γ1{\displaystyle \gamma _{1}}, δ{\displaystyle \delta } и δ1{\displaystyle \delta _{1}}) и накрест лежащие углы (α{\displaystyle \alpha } и γ1{\displaystyle \gamma _{1}}, β{\displaystyle \beta } и δ1{\displaystyle \delta _{1}}, γ{\displaystyle \gamma } и α1{\displaystyle \alpha _{1}}, δ{\displaystyle \delta } и β1{\displaystyle \beta _{1}}).
Согласно пятому постулату Евклида, две прямые параллельны, если:
- сумма односторонних углов равна 180°;
- соответственные углы равны;
- накрест лежащие углы равны.
Любой из этих признаков является необходимым и достаточным условием того, что прямые параллельны.
| Восемь углов трансверсали.(Вертикальные углы такие, как α{\displaystyle \alpha } и γ,{\displaystyle \gamma ,} всегда равны.) | Трансверсаль между непараллельными прямыми. Внутренние не накрест лежащие углы не являются дополнительными (в сумме дающими 180 градусов). | Трансверсаль между параллельными прямыми. Внутренние не накрест лежащие углы являются дополнительными (в сумме дающими 180 градусов). |
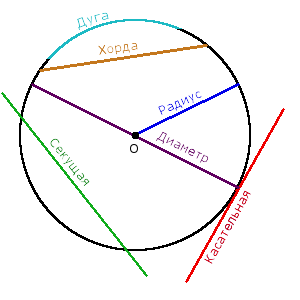
Касательные, секущие, хорды.
Окружность — это фигура, которая состоит из множества точек плоскости, равноудаленных от данной точки (центра).
Отрезок, соединяющий любую точку на окружности с центром окружности, называется радиусом ($R$).
$ОС=OD=OE=R.$
Отрезок, соединяющий любые две точки на окружности, называется хордой, а хорда, проходящая через центр, — диаметром ($d$).
$ВС$ – хорда
$СЕ$ — диаметр
Свойства хорды и диаметра:
1. Диаметр равен двум радиусам $d=2R; СЕ=2СО$
2. Равные хорды стягивают равные дуги
Если $AB=CD$, то $∪AB=∪CD$.
3.Вся окружность составляет $360°$. Диаметр делит окружность на две полуокружности по $180°$.
4. Хорды окружности, удаленные от центра на равные расстояния, равны.
5. Из двух хорд больше та, которая менее отдалена от центра.
Касательные и секущие:
Прямая, имеющая с окружностью только одну общую точку, называется касательной. $АВ$ — касательная
Прямая, имеющая с окружностью две общие точки, называется секущей. $CD$ — секущая
Свойства:
1. Касательная перпендикулярна радиусу, проведенному в точку касания.
$ОА⊥АС; OB⊥BC$
2. Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
$АС=ВС; ОС$ — биссектриса
3. Если хорды $АС$ и $BD$ пересекаются в некоторой точке $N$, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
$AN·NC=BN·ND$
Пример:
Хорды $АВ$ и $CD$ пересекаются в точке $Е$. Найдите $ЕD$, если $АЕ=16, ВЕ=9, СЕ=ED$.
Решение:
Если хорды $АВ$ и $СD$ пересекаются в некоторой точке $Е$, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
$AЕ·ЕВ=СЕ·ЕD$
Так как $СЕ=ED$, данное выражение можно записать в виде:
$ЕD^2=AЕ·ЕВ$
Подставим числовые значения
$ЕD^2=16·9$
$ЕD=√{16·9}=4·3=12$
Ответ: $12$
4. Если из одной точки к одной окружности проведены две секущие, то произведение первой секущей на ее внешнюю часть равно произведению второй секущей на свою внешнюю часть.
$АС·ВС=EC·DC$
5. Если из одной точки к окружности проведены секущая и касательная, то произведение секущей на ее внешнюю часть равно квадрату длины касательной.
$BD·СB=AB^2$
Углы в окружности:
1. Угол, образованный двумя радиусами, называется центральным. Центральный угол равен градусной мере дуги, на которую он опирается
$∠О=∪BmA$
2. Угол, вершина которого лежит на окружности, а стороны являются хордами, называется вписанным. Вписанный угол равен половине градусной меры дуги, на которую он опирается
$∠B={∪AmC}/{2}$
Пример:
Точки $A, B, C$, расположенные на окружности, делят её на три дуги, градусные меры которых относятся как $2:3:7$. Найдите больший угол треугольника $ABC$. Ответ дайте в градусах.
Решение:
Данное условие можно рассмотреть как задачу на части:
1) Найдем общее количество частей, на которые разделили окружность.
$2+3+7=12$ (всего частей)
2) Найдем, сколько градусов приходится на одну часть
$360:12=30°$
3) $∪АВ$ составляет две части, следовательно, $∪АВ=2·30=60°$
$∪АС=3·30=90°$
$∪СВ=7·30=210°$
4) В треугольнике $АВС$ самым большим углом является $∠А$, он вписанный, опирается на дугу $СВ$ и равен ее половине.
$∠А={∪СВ}/{2}={210}/{2}=105°$
Ответ: $105$
3. Угол между хордой и касательной равен половине дуги, отсекаемой хордой .
$∠B={∪BmC}/{2}$
1. Угол между хордами равен полусумме дуг, на которые этот угол опирается
$∠СND={∪CD+∪AB}/{2}$
2. Угол между двумя касательными равен полуразности дуг, заключенных внутри угла.
$∠В={∪АmC-∪AnC}/{2}$
3. Угол между двумя секущими равен полуразности дуг, заключенных внутри угла.
$∠С={∪AE-∪BD}/{2}$
4. Угол между касательной и секущей равен полуразности дуг, заключенных внутри угла.
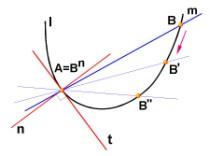
Секущая к кривой
Путём приближения из секущей можно получить касательную в некоторой точке P. Если секущая определяется двумя точками пересечения с данной кривой, P и Q, где положение точки P фиксировано, а положение точки Q может изменяться, то по мере того, как точка Q приближается к точке P вдоль кривой, направление секущей приближается к направлению касательной в точке P (если кривая является гладкой в точке P). Можно сказать, что по мере того, как точка Q приближается к P, наклон (или направление) секущей, в пределе, приближается к наклону касательной. Эта идея является основой для геометрического определения производной.
В случае окружности (или другой гладкой кривой второго порядка) касательные можно также определить как прямые, имеющие с данной кривой ровно одну общую точку.
Хорда — это участок секущей (отрезок), который лежит между двумя точками пересечения с кривой. Диаметр — это хорда окружности, проходящая через её центр.
Секущая к кривой
Путём приближения из секущей можно получить касательную в некоторой точке P. Если секущая определяется двумя точками пересечения с данной кривой, P и Q, где положение точки P фиксировано, а положение точки Q может изменяться, то по мере того, как точка Q приближается к точке P вдоль кривой, направление секущей приближается к направлению касательной в точке P (если кривая является гладкой в точке P). Можно сказать, что по мере того, как точка Q приближается к P, наклон (или направление) секущей, в пределе, приближается к наклону касательной. Эта идея является основой для геометрического определения производной.
В случае окружности (или другой гладкой кривой второго порядка) касательные можно также определить как прямые, имеющие с данной кривой ровно одну общую точку.
Хорда — это участок секущей (отрезок), который лежит между двумя точками пересечения с кривой. Диаметр — это хорда окружности, проходящая через её центр.
Секущая к кривой
Путём приближения из секущей можно получить касательную в некоторой точке P. Если секущая определяется двумя точками пересечения с данной кривой, P и Q, где положение точки P фиксировано, а положение точки Q может изменяться, то по мере того, как точка Q приближается к точке P вдоль кривой, направление секущей приближается к направлению касательной в точке P (если кривая является гладкой в точке P). Можно сказать, что по мере того, как точка Q приближается к P, наклон (или направление) секущей, в пределе, приближается к наклону касательной. Эта идея является основой для геометрического определения производной.
В случае окружности (или другой гладкой кривой второго порядка) касательные можно также определить как прямые, имеющие с данной кривой ровно одну общую точку.
Хорда — это участок секущей (отрезок), который лежит между двумя точками пересечения с кривой. Диаметр — это хорда окружности, проходящая через её центр.