Примечания
- ↑
- Sedgewick, Robert. Algorithms in C++. — Addison-Wesley, 1992. — ISBN 0-201-51059-6., p. 16.
- ↑
- Pritchard, Paul, «Linear prime-number sieves: a family tree,» Sci. Comput. Programming 9:1 (1987), pp. 17–35.
- ↑
- ↑
- Turner, David A. SASL language manual. Tech. rept. CS/75/1. Department of Computational Science, University of St. Andrews 1975. ()
- Crandall & Pomerance, Prime Numbers: A Computational Perspective, second edition, Springer: 2005, pp. 121–24.
- David Gries, Jayadev Misra. A Linear Sieve Algorithm for Finding Prime Numbers
- ↑ Paul Pritchard, A sublinear additive sieve for finding prime numbers, Communications of the ACM 24 (1981), 18–23. MR:
-
↑ Paul Pritchard, Fast compact prime number sieves (among others), Journal of Algorithms 4
(1983), 332–344. MR: - ↑ Paul Pritchard, Explaining the wheel sieve, Acta Informatica 17 (1982), 477–485. MR:
-
Meertens, Lambert. Calculating the Sieve of Eratosthenes // Journal of
functional programming. -
Meertens, Lambert. Calculating the Sieve of Eratosthenes // Journal of
functional programming.
Алгоритм

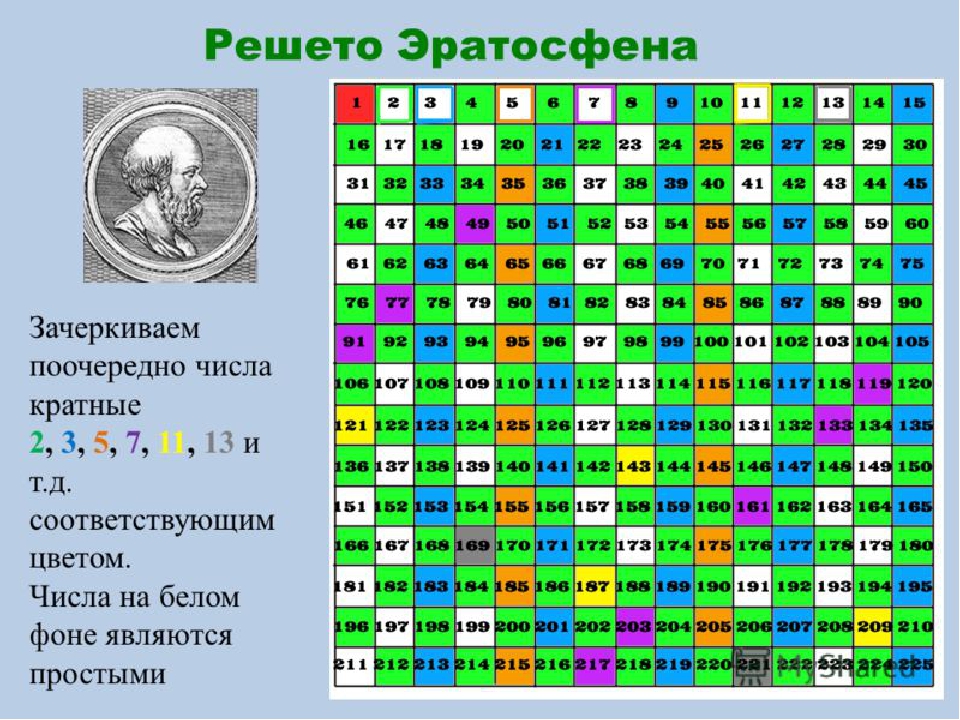
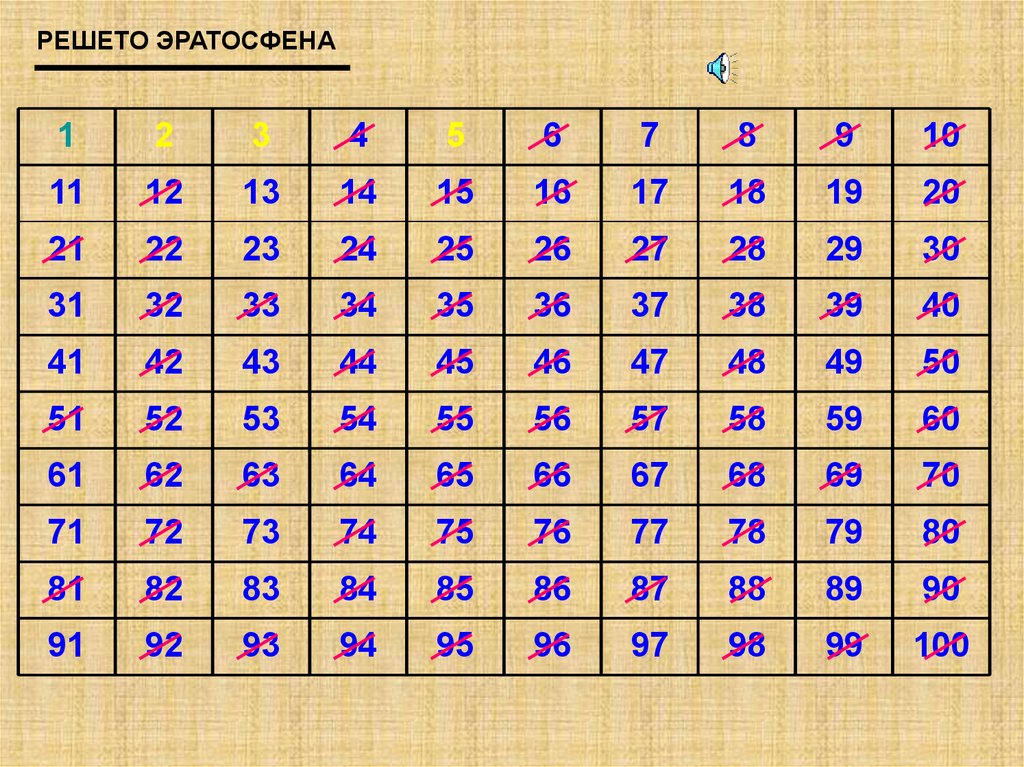
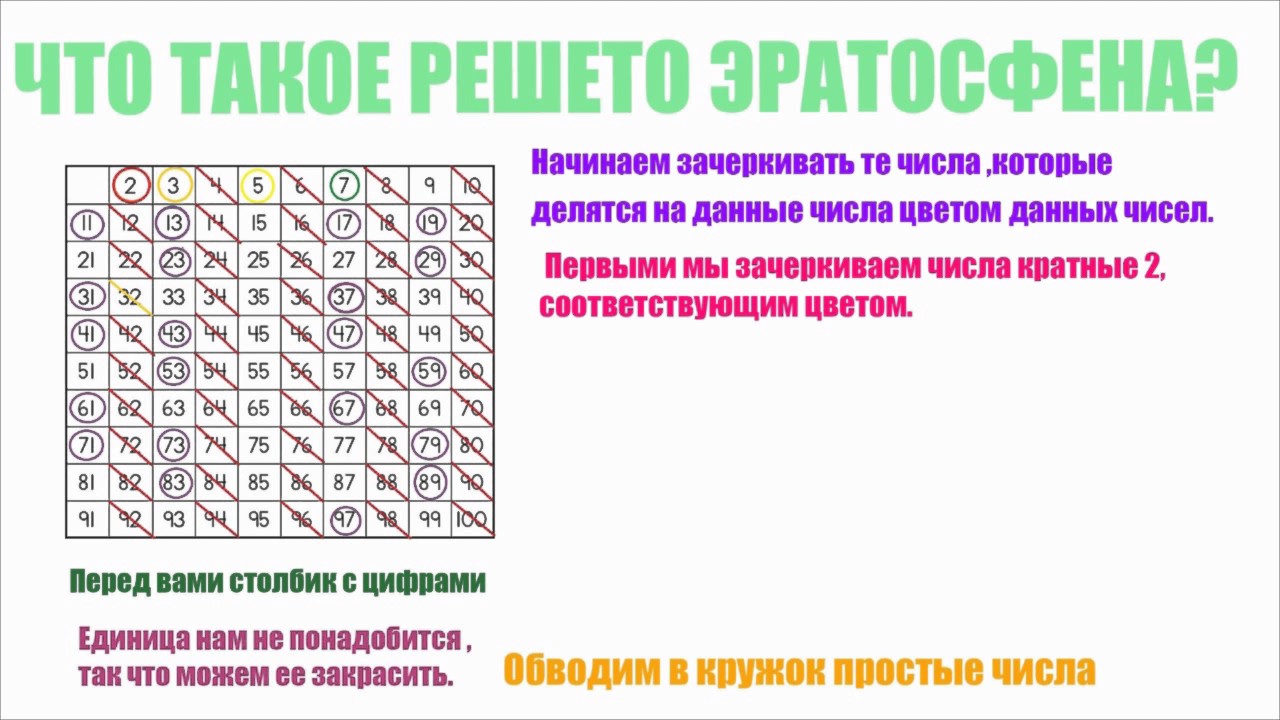
Для нахождения всех простых чисел не больше заданного числа n, следуя методу Эратосфена, нужно выполнить следующие шаги:
- Выписать подряд все целые числа от двух до n (2, 3, 4, …, n).
- Пусть переменная p изначально равна двум — первому простому числу.
- Зачеркнуть в списке числа от 2p до n считая шагами по p (это будут числа кратные p: 2p, 3p, 4p, …).
- Найти первое незачёркнутое число в списке, большее чем p, и присвоить значению переменной p это число.
- Повторять шаги 3 и 4, пока возможно.
Теперь все незачёркнутые числа в списке — это все простые числа от 2 до n.
На практике, алгоритм можно улучшить следующим образом. На шаге № 3 числа можно зачеркивать начиная сразу с числа p2, потому что все составные числа меньше него уже будут зачеркнуты к этому времени. И, соответственно, останавливать алгоритм можно, когда p2 станет больше, чем n. Также, все простые числа (кроме 2) — нечётные числа, и поэтому для них можно считать шагами по 2p, начиная с p2.
Примечания
- ↑
- Sedgewick, Robert. Algorithms in C++. — Addison-Wesley, 1992. — ISBN 0-201-51059-6., p. 16.
- ↑
- Pritchard, Paul, «Linear prime-number sieves: a family tree,» Sci. Comput. Programming 9:1 (1987), pp. 17–35.
- ↑
- ↑
- Turner, David A. SASL language manual. Tech. rept. CS/75/1. Department of Computational Science, University of St. Andrews 1975. ()
- Crandall & Pomerance, Prime Numbers: A Computational Perspective, second edition, Springer: 2005, pp. 121–24.
- David Gries, Jayadev Misra. A Linear Sieve Algorithm for Finding Prime Numbers
- ↑ Paul Pritchard, A sublinear additive sieve for finding prime numbers, Communications of the ACM 24 (1981), 18–23. MR:
-
↑ Paul Pritchard, Fast compact prime number sieves (among others), Journal of Algorithms 4
(1983), 332–344. MR: - ↑ Paul Pritchard, Explaining the wheel sieve, Acta Informatica 17 (1982), 477–485. MR:
-
Meertens, Lambert. Calculating the Sieve of Eratosthenes // Journal of
functional programming. -
Meertens, Lambert. Calculating the Sieve of Eratosthenes // Journal of
functional programming.
Метод
Предположим, что мы пытаемся разложить на множители составное число n. Мы определяем границу B и базу множителей (которую будем обозначать через P), множество всех простых чисел, меньших либо равных B. Затем мы ищем положительное целое z, такое, что как z, так и z+n являются B-гладкими, то есть все их простые делители содержатся в P. Мы можем поэтому записать для подходящих степеней ak{\displaystyle a_{k}}
z=∏pi∈Ppiai{\displaystyle z=\prod _{p_{i}\in P}p_{i}^{a_{i}}},
а также для подходящих bk{\displaystyle b_{k}} мы имеем
z+n=∏pi∈Ppibi{\displaystyle z+n=\prod _{p_{i}\in P}p_{i}^{b_{i}}}.
Но z{\displaystyle z} и z+n{\displaystyle z+n} сравнимы по модулю n{\displaystyle n}, так что любое такое целое число z, которое мы находим, даёт связь по модулю по умножению (mod n) среди всех элементов P, то есть
- ∏pi∈Ppiai≡∏pi∈Ppibi(modn){\displaystyle \prod _{p_{i}\in P}p_{i}^{a_{i}}\equiv \prod _{p_{i}\in P}p_{i}^{b_{i}}\;\operatorname {(mod} \;n\operatorname {)} }
(где ai и bi — неотрицательные целые числа.)
Когда мы сгенерируем достаточно таких соотношений (как правило, достаточно, чтобы число таких отношений было чуть больше размера P), мы можем использовать методы линейной алгебры для умножения этих различных отношений таким образом, чтобы степени всех простых множителей оказались чётными. Это даст нам вида a2≡b2 (mod n), что можно преобразовать в разложение числа n, n = НОД(a—b,n)×НОД(a+b,n). Такое разложение может оказаться тривиальным (то есть n=n×1) и в этом случае нужно попытаться попробовать снова с другой комбинацией отношений. Если посчастливится, мы получим нетривиальную пару делителей числа n, и алгоритм завершится.
Оценка сложности
По оценке авторов алгоритм имеет O(NloglogN){\displaystyle \mathop {O} ({\frac {N}{\log \log N}})} и требует O(N12+o(1)){\displaystyle \mathop {O} (N^{{\frac {1}{2}}+\mathop {o} (1)})} бит памяти. Ранее были известны алгоритмы столь же асимптотически быстрые, но требующие существенно больше памяти.
Теоретически в данном алгоритме сочетается максимальная скорость работы при наименьших требованиях к памяти. Реализация алгоритма, выполненная одним из авторов, показывает достаточно высокую практическую скорость.
В алгоритме используется два вида оптимизации, которые существенно повышают его эффективность (по сравнению с упрощённой версией).
Ниже представлена реализация упрощённой версии на языке программирования C, иллюстрирующая основную идею алгоритма — использование квадратичных форм:
int limit = 1000;
int sqr_lim;
bool is_prime1001];
int x2, y2;
int i, j;
int n;
// Инициализация решета
sqr_lim = (int)sqrt((long double)limit);
for (i = ; i <= limit; i++) is_primei = false;
is_prime2 = true;
is_prime3 = true;
// Предположительно простые — это целые с нечётным числом
// представлений в данных квадратных формах.
// x2 и y2 — это квадраты i и j (оптимизация).
x2 = ;
for (i = 1; i <= sqr_lim; i++) {
x2 += 2 * i - 1;
y2 = ;
for (j = 1; j <= sqr_lim; j++) {
y2 += 2 * j - 1;
n = 4 * x2 + y2;
if ((n <= limit) && (n % 12 == 1 || n % 12 == 5))
is_primen = !is_primen];
// n = 3 * x2 + y2;
n -= x2; // Оптимизация
if ((n <= limit) && (n % 12 == 7))
is_primen = !is_primen];
// n = 3 * x2 - y2;
n -= 2 * y2; // Оптимизация
if ((i > j) && (n <= limit) && (n % 12 == 11))
is_primen = !is_primen];
}
}
// Отсеиваем кратные квадратам простых чисел в интервале .
// (основной этап не может их отсеять)
for (i = 5; i <= sqr_lim; i++) {
if (is_primei]) {
n = i * i;
for (j = n; j <= limit; j += n) {
is_primej = false;
}
}
}
// Вывод списка простых чисел в консоль.
printf("2, 3, 5");
for (i = 6; i <= limit; i++) { // добавлена проверка делимости на 3 и 5. В оригинальной версии алгоритма потребности в ней нет.
if ((is_primei]) && (i % 3 != ) && (i % 5 != )){
printf(", %d", i);
}
}
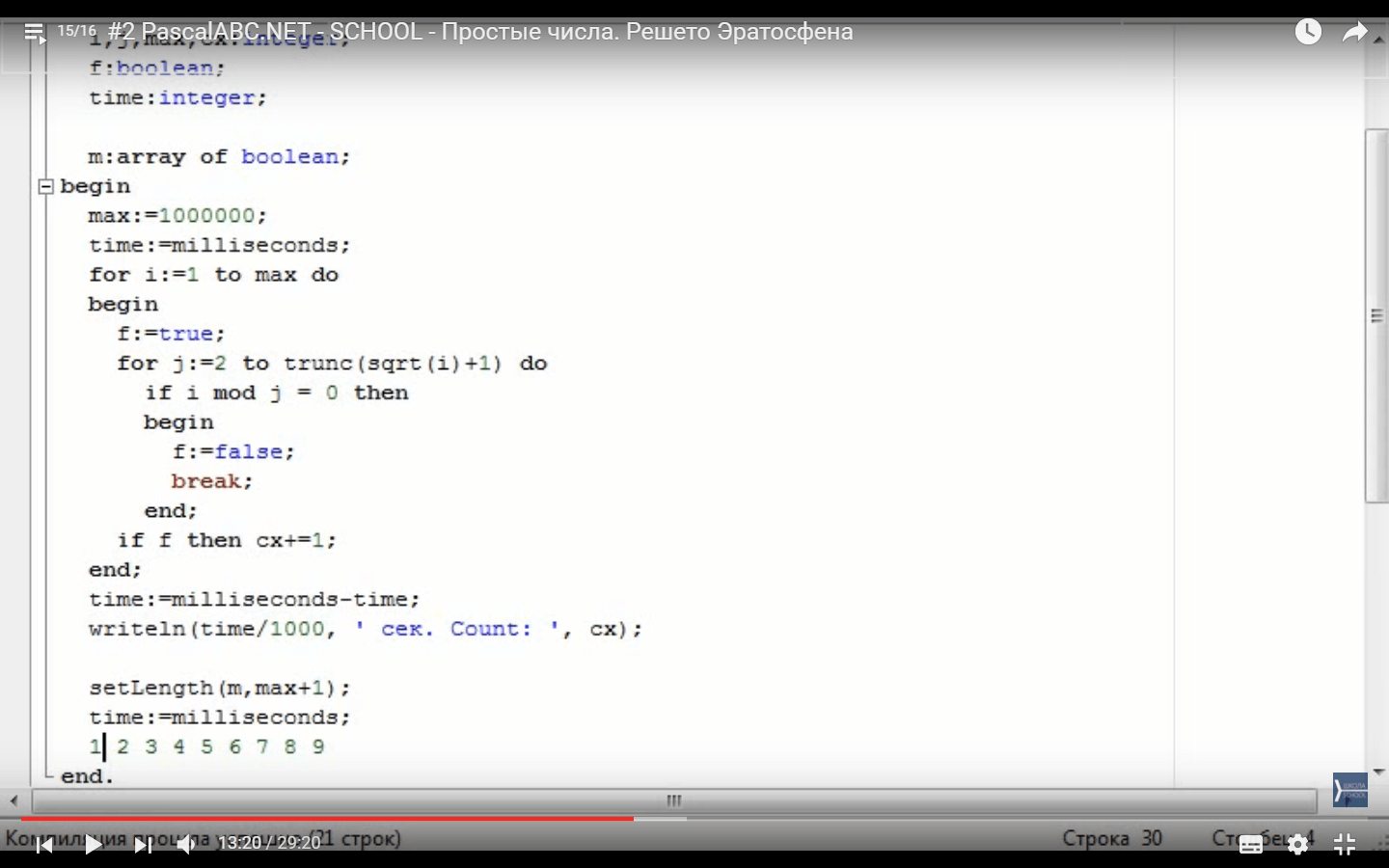
Версия алгоритма на языке Pascal
program atkin;
var is_primearray1..10001 of boolean; jjint64;
procedure dosieve(limitint64);
var i,k,x,yint64; nint64;
begin
for i:=5 to limit do
is_primei:=false;
for x:=1 to trunc(sqrt(limit)) do
for y:=1 to trunc(sqrt(limit)) do
begin
n:=4*sqr(x)+sqr(y);
if (n<=limit) and ((n mod 12 = 1) or (n mod 12 = 5)) then
is_primen:=not is_primen;
n:=n-sqr(x);
if (n<=limit) and (n mod 12 = 7) then
is_primen:=not is_primen;
n:=n-2*sqr(y);
if (x>y) and (n<=limit) and (n mod 12 = 11) then
is_primen:=not is_primen;
end;
for i:=5 to trunc(sqrt(limit)) do
begin
if is_primei then
begin
k:=sqr(i);
n:=k;
while n<=limit do
begin
is_primen:=false;
n:=n+k;
end;
end;
end;
is_prime2:=true;
is_prime3:=true;
end;
begin
dosieve(10000);
for jj:=1 to 10000 do
if is_primejj then
writeln(jj);
end.
Описание
Основная идея алгоритма состоит в использовании неприводимых квадратичных форм (представление чисел в виде ax²+by²). Предыдущие алгоритмы в основном представляли собой различные модификации решета Эратосфена, где использовалось представление чисел в виде редуцированных форм (как правило — в виде произведения xy).
В упрощённом виде алгоритм может быть представлен следующим образом:
- Все числа, равные (по модулю 60) 0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 50, 52, 54, 56 или 58, делятся на два и заведомо не простые. Все числа, равные (по модулю 60) 3, 9, 15, 21, 27, 33, 39, 45, 51 или 57, делятся на три и тоже не являются простыми. Все числа, равные (по модулю 60) 5, 25, 35 или 55, делятся на пять и также не простые. Все эти остатки (по модулю 60) игнорируются.
- Все числа, равные (по модулю 60) 1, 13, 17, 29, 37, 41, 49 или 53, имеют остаток от деления на 4, равный 1. Эти числа являются простыми тогда и только тогда, когда количество решений уравнения 4x² + y² = n нечётно и само число не кратно никакому квадрату простого числа (en:square-free integer).
- Числа, равные (по модулю 60) 7, 19, 31, или 43, имеют остаток от деления на 6, равный 1. Эти числа являются простыми тогда и только тогда, когда количество решений уравнения 3x² + y² = n нечётно и само число не кратно никакому квадрату простого.
- Числа, равные (по модулю 60) 11, 23, 47, или 59, имеют остаток от деления на 12, равный 11. Эти числа являются простыми тогда и только тогда, когда количество решений уравнения 3x² − y² = n (для x > y) нечётно и само число n не кратно никакому квадрату простого.
- Отдельный шаг алгоритма вычеркивает числа, кратные квадратам простых чисел. Так как ни одно из рассматриваемых чисел не делится на 2, 3, или 5, то, соответственно, они не делятся и на их квадраты. Поэтому проверка, что число не кратно квадрату простого числа, не включает 2², 3², и 5².
Сегментация
Для уменьшения требований к памяти «просеивание» производится порциями (сегментами, блоками), размер которых составляет примерно N{\displaystyle {\sqrt {N}}}.
Предпросеивание
Для ускорения работы алгоритм игнорирует все числа, которые кратны одному из нескольких первых простых чисел (2, 3, 5, 7, …). Это делается путём использования стандартных структур данных и алгоритмов их обработки, предложенных ранее Полом Притчардом (англ. Pritchard, Paul). Они известны под названием англ. wheel sieving. Количество первых простых чисел выбирается в зависимости от заданного числа N. Теоретически предлагается брать первые простые примерно до logN{\displaystyle {\sqrt {\log N}}}. Это позволяет улучшить асимптотическую оценку скорости алгоритма на множитель O(1loglogN){\displaystyle \mathop {O} ({\frac {1}{\log \log N}})}. При этом требуется дополнительная память, которая с ростом N ограничена как explogN{\displaystyle \exp {\sqrt {\log N}}}. Увеличение требований к памяти оценивается как O(No(1)){\displaystyle \mathop {O} (N^{\mathop {o} (1)})}.
Версия, представленная на сайте одного из авторов, оптимизирована для поиска всех простых чисел до миллиарда (log109≈log230=3≈5,5{\displaystyle {\sqrt {\log 10^{9}}}\approx {\sqrt {\log 2^{30}}}={\sqrt {3}}0\approx 5,5}), в ней исключаются из вычислений числа, кратные двум, трём, пяти и семи (2 × 3 × 5 × 7 = 210).
В словаре Фасмера Макса
решето́укр. ре́шето, болг. реше́то (Младенов 560), сербохорв. решѐто, словен. rešétọ, чеш. řеšеtо, слвц. rеšеtо, польск. rzeszoto, в.-луж. ŕеšо, род. п. ŕеšеćа «решето», н.-луж. ŕašeśiń ж., ŕašeśina ж. «колючий терновник», полаб. rîsetü.Приемлемое в семантическом отношении сравнение с rědъkъ (см. ре́дкий, ре́дель, ре́день) недостоверно, потому что следует реконструировать праслав. *rеšеtо, а не *rěšeto, вопреки Брюкнеру (476), Преобр. (II, 237), Желтову (ФЗ, 1876, вып. 1, 19). Иначе потребовалось бы принимать чередование гласных в первом слоге. С аналогичными трудностями сопряжено сопоставление с *rěšiti «вязать», откуда «сплетенное» (Потебня, ЖСт., 1891, вып. 3, 123; Младенов 560). Фонетически затруднительно сближение с лит. rezgù, règzti «связывать, плести», rẽkstis «мешок для сена», лтш. rekšis «плетеная вещь, решето», лат. restis «канат» (Маценауэр, LF 16, 183; Махек, LF 55, 148 и сл.; Ильинский, ИОРЯС 23, 2, 181). Махек (там же) возводит š к х, а последнее – к sk, что отнюдь не обязательно. По образованию ср. с тенёто. См. решётка.
Сложность алгоритма
Сложность алгоритма составляет O(nlog(logn)){\displaystyle O(n\log(\log n))} операций при составлении таблицы простых чисел до n{\displaystyle n}.
Доказательство сложности
При выбранном n∈N{\displaystyle n\in \mathbb {N} } для каждого простого p∈Pp≤n{\displaystyle p\in \mathbb {P} \colon p\leq n} будет выполняться внутренний цикл, который совершит np{\displaystyle {\frac {n}{p}}} действий. Сложность алгоритма можно получить из оценки следующей величины:
∑p∈Pp≤nnp=n⋅∑p∈Pp≤n1p{\displaystyle \sum \limits _{p\in \mathbb {P} \colon p\leq n}{\frac {n}{p}}=n\cdot \sum \limits _{p\in \mathbb {P} \colon p\leq n}{\frac {1}{p}}}
Так как количество простых чисел, меньших либо равных n{\displaystyle n}, оценивается как nlnn{\displaystyle {\frac {n}{\ln n}}}, и, как следствие, k{\displaystyle k}-е простое число примерно равно klnk{\displaystyle k\ln k}, то сумму можно преобразовать:
∑p∈Pp≤n1p≈12+∑k=2nlnn1klnk{\displaystyle \sum \limits _{p\in \mathbb {P} \colon p\leq n}{\frac {1}{p}}\approx {\frac {1}{2}}+\sum \limits _{k=2}^{\frac {n}{\ln n}}{\frac {1}{k\ln k}}}
Здесь из суммы выделено слагаемое для первого простого числа, чтобы избежать деления на нуль. Данную сумму можно оценить интегралом
12+∑k=2nlnn1klnk≈∫2nlnn1klnkdk=lnlnk|2nlnn=lnlnnlnn−lnln2=ln(lnn−lnlnn)−lnln2≈lnlnn{\displaystyle {\frac {1}{2}}+\sum _{k=2}^{\frac {n}{\ln n}}{\frac {1}{k\ln k}}\approx \int \limits _{2}^{\frac {n}{\ln n}}{\frac {1}{k\ln k}}\,dk=\ln \ln k{\Bigr |}_{2}^{\frac {n}{\ln n}}=\ln \ln {\frac {n}{\ln n}}-\ln \ln 2=\ln(\ln n-\ln \ln n)-\ln \ln 2\approx \ln \ln n}
В итоге получается для изначальной суммы:
∑p∈Pp≤nnp≈nlnlnn+o(n){\displaystyle \sum \limits _{p\in \mathbb {P} \colon p\leq n}{\frac {n}{p}}\approx n\ln \ln n+o(n)}
Более строгое доказательство (и дающее более точную оценку с точностью до константных множителей) можно найти в книге Hardy и Wright «An Introduction to the Theory of Numbers».
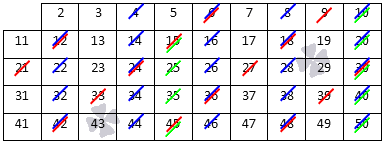
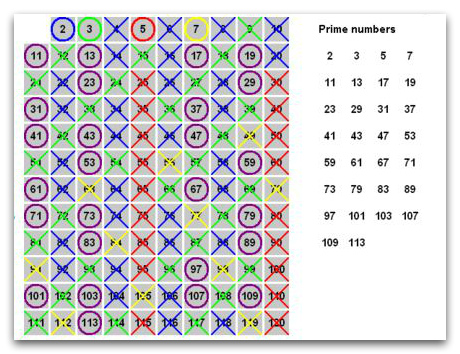
Пример для n = 30
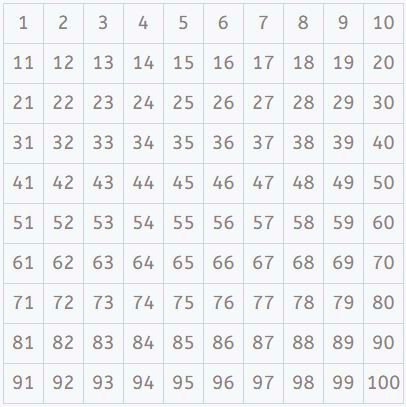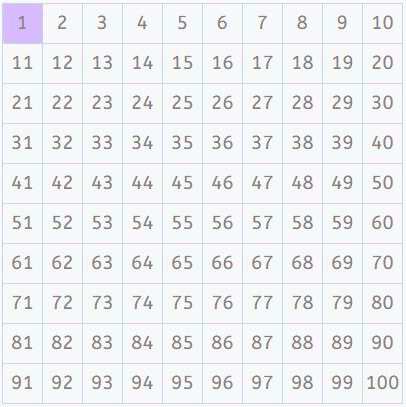
Запишем натуральные числа, начиная от 2, до 30 в ряд:
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
Первое число в списке, 2 — простое. Пройдём по ряду чисел, зачёркивая все числа, кратные 2 (то есть, каждое второе, начиная с 22 = 4):
2 3456789101112131415161718192021222324252627282930
Следующее незачеркнутое число, 3 — простое. Пройдём по ряду чисел, зачёркивая все числа, кратные 3 (то есть, каждое третье, начиная с 32 = 9):
2 3456789101112131415161718192021222324252627282930
Следующее незачеркнутое число, 5 — простое. Пройдём по ряду чисел, зачёркивая все числа, кратные 5 (то есть, каждое пятое, начиная с 52 = 25):
2 3456789101112131415161718192021222324252627282930
Следующее незачеркнутое число — 7. Его квадрат, 49 — больше 30, поэтому на этом работа завершена. Все составные числа уже зачеркнуты:
2 3 5 7 11 13 17 19 23 29
Значение слова Решето по словарю Брокгауза и Ефрона:
Решето — прибор, служащий для проживания различных материалов. Р. состоит из обегайки и дна. Обегайка изготовляется из двух тонких и широких деревянных полос, который лучше всего делать из осины или ивы. Выбирают несучковатое дерево и приготовляют доски длиной в 273 арш., шириной в 3 вершк. и толщиной в 5/8 или 3/4 врш.. такую доску можно распилить на 4—5 тоненьких дощечек, пригодных для обегаек Р.. их гладко обстрагивают, а концы несколько утоняют и потом накладывают один на другой. для придавания дощечкам мягкости и гибкости кладут их на день в воду. Перед сгибанием размоченную дощечку распаривают над огнем, после чего представляется возможность безопасно свернуть ее в кольцо. Чтобы дощечка сохранила кольцеобразную форму, ее кладут в круглую кадку и дают в ней высохнуть. Концы дощечки соединяют склеиванием. для прочности соединения и на случай отсырения клея место склейки скрепляют шпильками, которые загибают с наружной стороны, а на внутренней расклепывают. Для каждого Р. надо иметь два кольца: одно более широкое, в 3 врш., и другое шириною в 1 врш., свободно надевающееся на первое для защиты соединения дна с обегайкою. Дно Р. изготовляется обыкновенно (напр. для просеивания зернового хлеба) из проволочной ткани, ширина которой бывает в 20 дм. Ткань околачивают молотком кругом широкого кольца обегайки и прикрепляют ее маленькими гвоздями на расстоянии 1/2 — 1 врш. один от другого. Когда дно прикреплено, надевают узенькое кольцо, которое соединяют с широким гвоздиками. Вместо проволочной ткани употребляют нередко кожу (овечью), которую предварительно натягивают на обегайку и прикрепляют к ней гвоздиками, а затем уже в коже пробивают дыры круглой высечкой. Пробивание дыр следует начинать с середины. когда все дыры просечены, надевают на обегайку узкое кольцо настолько, чтобы край его отстоял от дна на 1/2 врш.. под дном натягивают три шнура, свитые в сыром виде из остатков кожи, для того чтобы стянуть дно более прочно. концы этих шнуров протягивают через отверстия, просверленные через оба кольца обегайки, и завязывают так, чтобы шнуры соединяли и самые кольца. Приборы для просеивания более мелких материалов называются ситами. они изготовляются так же, как Р., только кольца их обегайки сшивают латунною проволокою. дно сит делают из волосяной или тонкой медной проволочной ткани. А. Пр.