Предельная звёздная величина (m)
Предельная звёздная величина, которая видна в телескоп, в зависимости от апертуры:
m=2.1+5*lg(D), где D – диаметр телескопа в мм., lg — логарифм.
Если возьмётесь расчитывать, то увидите, что предельная звёздная величина,
доступная нашему глазу через самый большой «магазинный» телескоп с апертурой 300мм — около 14,5m.
Более слабые объекты ищутся через фотографирование и последующую компьютерную обработку кадров.
| D, мм | m | D, мм | m | |
|---|---|---|---|---|
| 32 | 9,6 | 132 | 12.7 | |
| 50 | 10,6 | 150 | 13 | |
| 60 | 11 | 200 | 13,6 | |
| 70 | 11,3 | 250 | 14,1 | |
| 80 | 11,6 | 300 | 14,5 | |
| 90 | 11,9 | 350 | 14,8 | |
| 114 | 12,4 | 400 | 15,1 | |
| 125 | 12,6 | 500 | 15,6 |
На деле значения будут немного отличаться из-за разницы световых потерь в разных конструкция телескопов.
При одинаковой апертуре D, выше всего предельная звёздная величина в линзовых телекопах-рефракторах.
В зеркальных рефлекторах потери выше — очень грубо можно отнять 10-15%.
В катадиопртиках потери самые большие, соответственно и предельная звёздная величина самая маленькая.
Также велики потери в биноклях из-за наличия нескольких преломляющих призм — их я имел ввиду, дав диаметры 32 и 50 мм.
То есть, в биноклях предельная звёздная величина будет гораздо меньше табличной. На сколько — зависит от качества марки бинокля, в частности от качества просветляющего покрытия всех поверхностей — это нельзя предсказать для всех моделей.
Сложные и дорогие окуляры тоже задерживают свет за счёт большего количества линз — неизбежная плата за качество изображения
(хотя, их качественные просветляющие покрытия частично снижают этот недостаток).
То есть, при одинаковой апертуре, в линзовый телескоп-рефрактор с самым простеньким окуляром вы увидите максимум возможного при данном D.
Но, поскольку, рефракторы больших диаметров дороги, то за те же деньги можно взять гораздо более апертуристый рефлектор и увидеть значительно больше.
Крупнейшие оптические телескопы
Телескопы-рефракторы
| Обсерватория | Местонахождения | Диаметр, см / дюйм | Год сооружения / демонтажа | Примечания |
|---|---|---|---|---|
| Телескоп всемирной Парижской выставки 1900 года. | Париж | 125 / 49.21″ | 1900 / 1900 | Самый крупный рефрактор в мире, из когда либо построенных. Свет от звёзд направлялся в объектив неподвижного телескопа с помощью сидеростата. |
| Йеркская обсерватория | Уильямс Бэй, Висконсин | 102 / 40″ | 1897 | |
| Обсерватория Лика | гора Гамильтон, Калифорния | 91 / 36″ | 1888 | |
| Парижская обсерватория | Медон, Франция | 83 / 33″ | 1893 | Двойной, визуальный объектив 83 см, фотографический — 62 см. |
| Потсдамский астрофизический институт | Потсдам, Германия | 81 / 32″ | 1899 | Двойной, визуальный 50 см, фотографический 80 см. |
| Обсерватория Ниццы | Франция | 76 / 30″ | 1880 | |
| Пулковская обсерватория | Санкт-Петербург | 76 / 30″ | 1885 | |
| Обсерватория Аллегейни | Питтсбург, Пенсильвания | 76 / 30″ | 1917 | |
| Гринвичская обсерватория | Гринвич, Великобритания | 71 / 28″ | 1893 | |
| Гринвичская обсерватория | Гринвич, Великобритания | 71 / 28″ | 1897 | Двойной, визуальный 71 см, фотографический 66 |
| Обсерватория Архенхольда | Берлин, Германия | 70 / 27″ | 1896 | Самый длинный современный рефрактор |
Солнечные телескопы
| Обсерватория | Местонахождения | Диаметр, м | Год сооружения |
|---|---|---|---|
| Китт-Пик | Тусон, Аризона | 1,60 | 1962 |
| Сакраменто-Пик | Санспот, Нью-Мексико | 1,50 | 1969 |
| Крымская астрофизическая обсерватория | Крым | 1,00 | 1975 |
| Шведский солнечный телескоп | Пальма, Канары | 1,00 | 2002 |
| Китт-Пик, 2 штуки в общем корпусе с 1,6 метра | Тусон, Аризона | 0,9 | 1962 |
| Тейде | Тенерифе, Канары | 0,9 | 2001 |
| Саянская солнечная обсерватория, Россия | Монды, Бурятия | 0,8 | 1975 |
| Китт-Пик | Тусон, Аризона | 0,7 | 1973 |
| Институт физики Солнца, Германия | Тенерифе, Канары | 0,7 | 1988 |
| Митака | Токио, Япония | 0,66 | 1920 |
Камеры Шмидта
| Обсерватория | Местонахождения | Диаметр коррекционной пластины — зеркала, м | Год сооружения |
|---|---|---|---|
| Обсерватория Карла Шварцшильда | Таутенбург, Германия | 1,3-2,0 | 1960 |
| Паломарская обсерватория | гора Паломар, Калифорния | 1,2-1,8 | 1948 |
| Обсерватория Сайдинг-Спринг | Кунабарабран, Австралия | 1,2-1,8 | 1973 |
| Токийская астрономическая обсерватория | Токио, Япония | 1,1-1,5 | 1975 |
| Европейская южная обсерватория | Ла-Силья, Чили | 1,1-1,5 | 1971 |
Телескопы-рефлекторы
| Название | Местонахождения | Диаметр зеркала, м | Год сооружения |
|---|---|---|---|
| Гигантский южно-африканский телескоп, SALT | Сатерленд, ЮАР | 11 | 2005 |
| Большой Канарский телескоп | Пальма, Канарские острова | 10,4 | 2002 |
| Телескопы Кек | Мауна-Кеа, Гавайи | 9,82 × 2 | 1993, 1996 |
| Телескоп Хобби-Эберли, HET | Джефф-Дэвис, Техас | 9,2 | 1997 |
| Большой бинокулярный телескоп, LBT | гора Грэхем (англ.), Аризона | 8,4 × 2 | 2004 |
| Очень большой телескоп, ESO VLT | Серро Параналь, Чили | 8,2 × 4 | 1998, 2001 |
| Телескоп Субару | Мауна-Кеа, Гавайи | 8,2 | 1999 |
| Телескоп Северный Джемини, GNT | Мауна-Кеа, Гавайи | 8,1 | 2000 |
| Телескоп Южный Джемини, GST | Серро Пашон, Чили | 8,1 | 2001 |
| Мультизеркальный телескоп (англ.), MMT | гора Хопкинс (англ.), Аризона | 6,5 | 2000 |
| Магеллановы телескопы | Лас Кампанас, Чили | 6,5 × 2 | 2002 |
| Большой телескоп азимутальный, БТА | гора Пастухова, Россия | 6,0 | 1975 |
| Большой Зенитный телескоп, LZT | Мейпл Ридж, Канада | 6,0 | 2001 |
| Телескоп Хейла, MMT | гора Паломар, Калифорния | 5,08 | 1948 |
Экстремально большие телескопы
Основная статья: ELT
(Экстремально большой телескоп)
| Название | Изображение(рисунок) | Диаметр (м) | Площадь (м²) | Главноезеркало | Высотам | Дата первого света |
|---|---|---|---|---|---|---|
| Европейский чрезвычайно большой телескоп(E-ELT) | 39 | 1116 м² | 798 × 1,45 м шестиугольных сегментов | 3060 | 2024 год | |
| Тридцатиметровый телескоп (TMT) | 30 | 655 м² | 492 × 1,45 м шестиугольных сегментов | 4050 | 2022 год | |
| Гигантский Магелланов телескоп (GMT) | 24,5 | 368 м² | 7 × 8,4 м | 2516 | 2021 год |
Замечание о нормальном увеличении оптических инструментов.
Как в телескопе, так и в микроскопе изображение, полученное с помощью объектива, рассматривается глазом через окуляр. Для того, чтобы реализовать полностью разрешающую способность объектива система окуляр–глаз не должна вносить дополнительных дифракционных искажений. Это достигается целесообразным выбором увеличения оптического инструмента (телескопа или микроскопа). При заданном объективе задача сводится к подбору окуляра. На основании общих соображений волновой теории можно сформулировать следующее условие, при котором будет полностью реализована разрешающая способность объектива: диаметр пучка лучей, выходящих из окуляра не должен превышать диаметра зрачка глаза d3p . Таким образом, окуляр оптического инструмента должен быть достаточно короткофокусным
Поясним это утверждение на примере телескопа. На рис. 2.6 изображен телескопический ход лучей.
Рисунок 2.6.
Телескопический ход лучей
Две близкие звезды, находящиеся на угловом расстоянии min в фокальной плоскости объектива изображаются дифракционными пятнами, центры которых располагаются на расстоянии minF1. Пройдя через окуляр, лучи попадут в глаз под углом minF1/F2 . Этот угол должен быть разрешимым для глаза, зрачок которого имеет диаметр d3p. Таким образом:
Здесь = F1/F2 – угловое увеличение телескопа. Отношение D/ имеет смысл диаметра пучка, выходящего из окуляра. Знак равенства в (4.10) соответствует случаю нормального величения.
(2.11)
В случае нормального увеличения диаметр пучка лучей, выходящих из окуляра, равен диаметру зрачка d3p . При >N в системе телескоп–глаз полностью используется разрешающая способность объектива. Аналогичным образом решается вопрос об увеличении микроскопа. Под увеличением микроскопа понимают отношение углового размера объекта, наблюдаемого через микроскоп, к угловому размеру самого объекта, наблюдаемого невооруженным глазом на расстоянии наилучшего зрения d, которое для нормального глаза полагается равным 25 см. Расчет нормального увеличения микроскопа приводит к выражению:
(2.12)
Вывод формулы (2.12) является полезным упражнением для студентов. Как и в случае телескопа, нормальное увеличение микроскопа есть наименьшее увеличение, при котором может быть полностью использована разрешающая способность объектива. Следует подчеркнуть, что применение увеличений больше нормального не может выявить новые детали объекта. Однако, по причинам физиологического характера при работе на пределе разрешения инструмента целесообразно иногда выбирать увеличение, превосходящее нормальное в 2–3 раза.
Телескопы рефлекторы
Большинство любительских телескопов-рефлекторов имеет фокальные отношения f/6 — f/8; по сравнению с рефракторами они удобнее при наблюдениях, для которых требуются более широкое поле зрения и меньшее увеличение.
Телескопы-рефлекторы бывают разных типов. В практике любительских наблюдений чаще всего используются рефлекторы двух типов: системы Ньютона и системы Кассегрена.
В телескопе системы Ньютона вторичное зеркало плоское, поэтому фокусное расстояние и фокальное отношение объектива постоянны. В телескопе системы Кассегрена вторичное зеркало выпуклое, что значительно увеличивает общее фокусное расстояние телескопа и тем самым изменяет его эффективное фокальное отношение. По этой причине рефлекторы системы Кассегрена находят применение при наблюдениях того же типа, что и телескопы-рефракторы.

Телескоп типа рефлектор
Самое большое преимущество рефлекторов — их низкая стоимость. При той же апертуре они значительно дешевле телескопов любого другого типа. Кроме того, нужное зеркало для объектива рефлектора можно изготовить собственными силами или в крайнем случае — просто купить, а трубу такого телескопа нетрудно собрать в домашних условиях.
Практически все любительские телескопы с большой собирающей поверхностью (диаметры объектива свыше 200 мм) являются рефлекторами. Минимальный диаметр объектива рефлекторов, которые обычно используют для общих наблюдений, составляет около 150 мм; такой рефлектор стоит не дороже рефрактора с объективом диаметром 75 мм. Поскольку рефлектор имеет большую собирающую поверхность, в него можно наблюдать более слабые объекты, однако он не столь компактен, как рефрактор.
Рефлекторы меньших размеров, имеющие малые фокальные отношения, по своим характеристикам занимают промежуточное положение между биноклями и обычными рефлекторами; к тому же они достаточно компактны.
Однако у рефлекторов есть и недостатки. Наиболее существенные из них — необходимость время от времени обновлять отражающие, покрытия и юстировать оптические элементы. При отсутствии дорогостоящего оптического стекла, герметически закрывающего трубу рефлектора, приходится укрывать каждое зеркало телескопа крышкой или чехлом, чтобы воспрепятствовать проникновению пыли.
При наблюдениях окуляр в телескопе системы Ньютона может оказаться в неудобном положении; чтобы избежать этого, следует предусмотреть возможность вращения трубы телескопа.
Если труба рефлектора не закрыта герметически оптическим окном, то холодный наружный воздух, проникая в нее, создает там воздушные потоки, ухудшающие изображение. Весьма эффективным средством борьбы с этим недостатком может быть использование больших теплоизоляционных труб, но чаще для этой цели применяют «трубы» скелетной конструкции.
К сожалению, в последнем случае возникают другие проблемы, связанные с потоками теплого воздуха от самого наблюдателя (так что при наблюдениях старайтесь одевать больше теплоизолирующей одежды!). Кроме того, при этом увеличивается выпадение росы на оптические элементы. Поэтому большое значение приобретает правильная конструкция самой обсерватории.

Катадиоптрический (зеркально-линзовый) телескоп
Разрешающая способность (b)
Разрешающая способность телескопа — наименьший угол между такими двумя близкими звездами, когда они уже видны как две, а не сливаются зрительно в одну.
Проще говоря, под разрешающей способностью можно понимать «чёткость» изображения (да простят меня профессионалы-оптики…).
b=138/D, где D — апертура объектива. Измеряется в секундах (точнее в секундах дуги).
Из-за атмосферы эта величина нечасто бывает меньше 1″ (1 секунды). Например, на Луне 1″ соответствует кратеру диаметром около 2 км.
Для длиннофокусных объективов, со значением светосилы 1:12 и более длинных, формула немного другая: b=116/D (по Данлопу).
Из сказанного выше видно, что в обычных условиях минимальная разрешающая способность в 1″ достигается при апертуре 150мм у рефлекторов
и около 125мм у планетников-рефракторов.
Более апертуристые телескопы дают более чёткое изображение только в теории, ну или высоко в горах, где чистая атмосфера,
либо в те редкие дни, когда «с погодой везёт»…
Однако, не забывайте, что чем больше телескоп, тем ярче изображение, тем виднее более тусклые детали и объекты.
Поэтому, с точки зрения обычного наблюдателя, изображение у больших телескопов всё равно оказывается лучше, чем у маленьких.
Вдобавок, в короткие промежутки времени атмосфера над вами может успокоиться настолько,
что большой телескоп покажет картинку более чёткую, чем при том самом пределе в 1»,
а вот маленький телескоп упрётся в это ограничение и будет очень обидно…
Так что, нет особого смысла ограничиваться 150-ю миллиметрами 😉
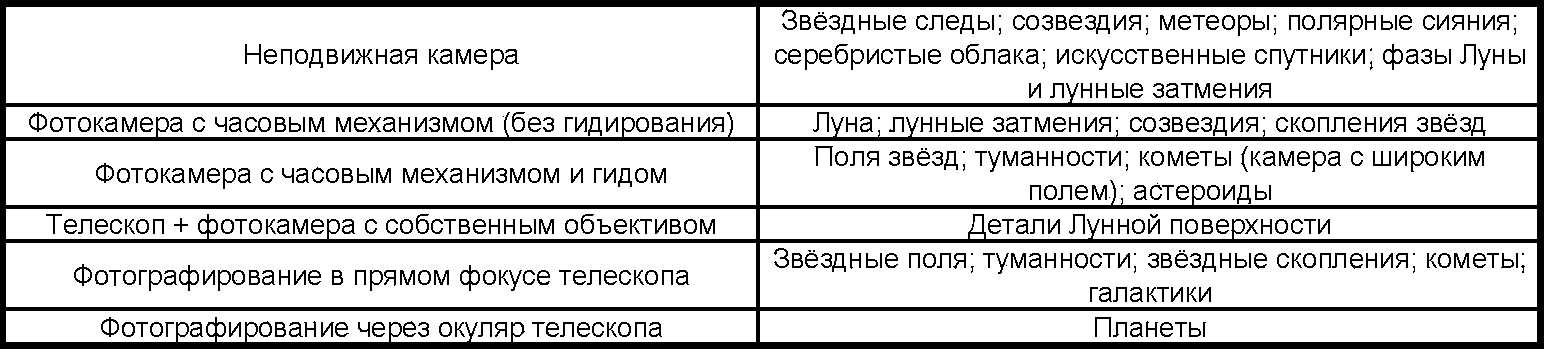
Параметры телескопа:
Типовые увеличения:
| Максимальное (2D) | (с окуляром ) | (?) | ||
|
Максимальное увеличение телескопа рассчитывается как удвоенный диаметр объектива. Обычно нет |
||||
| Разрешающее (1.4D) | (с окуляром ) | (?) | ||
|
При разрешающем увеличении как правило достигается предел по разрешающей способности телескопа. |
||||
| Большое (1D) | (с окуляром ) | (?) | ||
|
Большое увеличение применяют при обзоре диска Луны и Солнца, наблюдении спутников планет, а также |
||||
| Проницающее (0.7D) | (с окуляром ) | (?) | ||
|
Проницающее увеличение является типовым увеличением для наблюдения большинства объектов глубокого |
||||
| Среднее (D/2) | (с окуляром ) | (?) | ||
|
Среднее увеличение обычно применяют при наблюдениях туманностей и ярких галактик. |
||||
| Умеренное (D/3) | (с окуляром ) | (?) | ||
|
Умеренное увеличение обычно применяют при наблюдениях ярких и крупных объектов каталога Мессье. |
||||
| Равнозрачковое (D/6) | (с окуляром ) | (?) | ||
|
Равнозрачковое увеличение является минимальным увеличением телескопа. При равнозрачковом увеличении |
Другие параметры:
| Относительное отверстие | (?) | ||
|
Относительное отверстие определяется как отношение диаметра объектива к фокусному расстоянию телескопа. |
|||
| Разрешающая способность | (?) | ||
|
Разрешающая способность телескопа — это угловой размер объектов и деталей на них, которые можно различить |
|||
| Предельная звездная величина | (?) | ||
|
Предельная величина звезд, которую можно увидеть в этот телескоп при отличных условиях наблюдения. |
|||
| Максимальное поле зрения | (?) | ||
|
Максимальное поле зрения, которое можно получить на этом телескопе. Максимальное поле зрения |
|||
| Размер кратеров на Луне | (?) | ||
|
Кратеры такого размера можно увидеть на Луне в этот телескоп при отличных условиях наблюдения. |
Урок 22 Телескопы и их характеристики. Методы астрофизических исследований. Всеволновая астрономия
Тема. Телескопы и их характеристики. Методы астрофизических исследований. Всеволновая астрономия
Цели урока.
Учащиеся должны знать:
1. Назначение телескопов.
2. Телескопы во всех диапазонах электромагнитных волн.
3. Методы астрофизических исследований.
Основные понятия. Телескопы. Астрофизические исследования.
Демонстрационный материал. Модели телескопы.
Мировоззренческий аспект урока. Формирование научного подхода к изучению Вселенной во всём диапазоне электромагнитных волн.
. Работа с интерактивным моделями
План урока
|
Краткое содержание урока |
Формы использования планетария |
Время, мин |
Приемы и методы |
|
I. Актуализация знаний. Методы астрофизических исследований |
3 |
Сообщение учителя |
|
|
II. Изучение нового материала |
Иллюстрации модель |
15 |
Беседа, объяснение учителя |
|
III. Закрепление материала. |
Иллюстрации, планетарий |
10 |
Объяснение учителя, беседа |
|
IV. Самостоятельная работа с планетарием и подвижной картой. |
Планетарий |
15 |
самостоятельная работа |
|
V. Домашнее задание |
2 |
Запись на доске учителя |
Конспект урока.
I. Методы астрофизических исследований
Астрономия изучает строение Вселенной, движение, физическую природу, происхождение и эволюцию небесных тел и образованных ими систем. Астрономия исследует также фундаментальные свойства окружающей нас Вселенной.
Классические оптические схемы
Схема Галилея

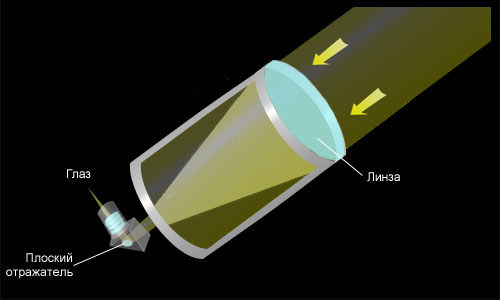
Схема рефрактора Галилея
Телескоп Галилея имел в качестве объектива одну собирающую линзу, а окуляром служила рассеивающая линза. Такая оптическая схема даёт неперевернутое (земное) изображение. Главными недостатками галилеевского телескопа являются очень малое поле зрения и сильная хроматическая аберрация. Такая система все ещё используется в театральных биноклях, и иногда в самодельных любительских телескопах.
Схема Кеплера

Схема рефрактора Кеплера
Иоганн Кеплер в г. усовершенствовал телескоп, заменив рассеивающую линзу в окуляре собирающей. Это позволило увеличить поле зрения и вынос зрачка, однако система Кеплера даёт перевёрнутое изображение. Преимуществом трубы Кеплера является также и то, что в ней имеется действительное промежуточное изображение, в плоскость которого можно поместить измерительную шкалу. По сути, все последующие телескопы-рефракторы являются трубами Кеплера. К недостаткам системы относится сильная хроматическая аберрация, которую до создания ахроматического объектива устраняли путём уменьшения относительного отверстия телескопа.
Схема Ньютона
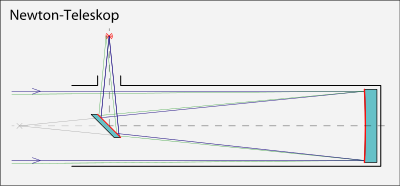
Оптическая схема телескопа Ньютона
Такую схему телескопов предложил Исаак Ньютон в 1667 году. Здесь плоское диагональное зеркало, расположенное вблизи фокуса, отклоняет пучок света за пределы трубы, где изображение рассматривается через окуляр или фотографируется. Главное зеркало параболическое, но если относительное отверстие не слишком большое, оно может быть и сферическим [источник не указан 842 дня].
Схема Грегори

Оптическая схема телескопа Грегори
Эту конструкцию предложил в 1663 году Джеймс Грегори в книге Optica Promota. Главное зеркало в таком телескопе — вогнутое параболическое. Оно отражает свет на меньшее вторичное зеркало (вогнутое эллиптическое). От него свет направляется назад — в отверстие по центру главного зеркала, за которым стоит окуляр. Расстояние между зеркалами больше фокусного расстояния главного зеркала, поэтому изображение получается прямое (в отличие от перевёрнутого в телескопе Ньютона). Вторичное зеркало обеспечивает относительно большое увеличение благодаря удлинению фокусного расстояния.
Схема Кассегрена
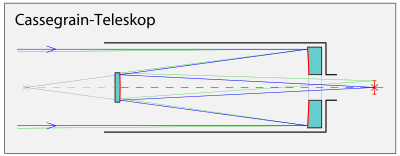
Оптическая схема телескопа Кассегрена
Схема была предложена Лораном Кассегреном в 1672 году. Это вариант двухзеркального объектива телескопа. Главное зеркало вогнутое (в оригинальном варианте параболическое). Оно отбрасывает лучи на меньшее вторичное выпуклое зеркало (обычно гиперболическое). По классификации Максутова схема относится к так называемым предфокальным удлиняющим — то есть вторичное зеркало расположено между главным зеркалом и его фокусом и полное фокусное расстояние объектива больше, чем у главного. Объектив при том же диаметре и фокусном расстоянии имеет почти вдвое меньшую длину трубы и несколько меньшее экранирование, чем у Грегори. Система неапланатична, то есть несвободна от аберрации комы. Имеет много как зеркальных модификаций, включая апланатичный Ричи-Кретьен, со сферической формой поверхности вторичного (Долл-Кирхем) или первичного зеркала, так и зеркально-линзовых.
Отдельно стоит выделить систему Кассегрена, модифицированную советским оптиком Д. Д. Максутовым — , ставшую одной из самых распространённых систем в астрономии, особенно в любительской.
Схема Ричи-Кретьена
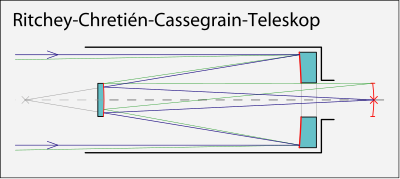
Оптическая схема телескопа Ричи—Кретьена—Кассегрена
Система Ричи — Кретьена — усовершенствованная система Кассегрена. Главное зеркало тут не параболическое, а гиперболическое. Поле зрения этой системы — около 4°.
2.2.2. Характеристики телескопа window.top.document.title = «2.2.2. Характеристики телескопа»;
 |
| Рисунок 2.2.2.1.Устройство телескопа-рефрактора |
К оптическим телескопам относят, прежде всего, рефракторы и рефлекторы.
Главная часть простейшего рефрактора – объектив – двояковыпуклая линза, установленная в передней части телескопа. Объектив собирает излучение. Чем больше размеры объектива D, тем больше собирает излучения телескоп, тем более слабые источники могут быть обнаружены им. Чтобы избежать хроматической аберрации, линзовые объективы делают составными. Однако в случаях, когда требуется свести к минимуму рассеяние в системе, приходится использовать и одиночную линзу. Расстояние от объектива до главного фокуса называется главным фокусным расстоянием F.
Самый большой рефрактор в мире, который находится в Йеркской обсерватории в США, имеет линзу диаметром в 1 м. Линза с большим диаметром была бы слишком тяжела и сложна в изготовлении.
 |
| Рисунок 2.2.2.2.Рефрактор Йеркской обсерватории в США |
 |
| Рисунок 2.2.2.3.Устройство телескопа-рефлектора |
Основным элементом рефлектора является зеркало – отражающая поверхность сферической, параболической или гиперболической формы. Обычно оно делается из стеклянной или кварцевой заготовки круглой формы и затем покрывается отражающим покрытием (тонкий слой серебра или алюминия). Точность изготовления поверхности зеркала, т.е. максимально допустимые отклонения от заданной формы, зависит от длины волны света, на которой будет работать зеркало. Точность должна быть лучше, чем λ/8. К примеру, зеркало, работающее в видимом свете (длина волны λ = 0,5 микрона), должно быть изготовлено с точностью 0,06 мкм (0,00006 мм).
Обращенная к глазу наблюдателя оптическая система называется окуляром. В простейшем случае окуляр может состоять только из одной положительной линзы (в этом случае мы получим сильно искаженное хроматической аберрацией изображение).
Важнейшими характеристиками телескопа (помимо его оптической схемы, диаметра объектива и фокусного расстояния) являются проницающая сила, разрешающая способность, относительное отверстие и угловое увеличение.
Проницающая сила телескопа характеризуется предельной звездной величиной m самой слабой звезды, которую можно увидеть в данный инструмент при наилучших условиях наблюдений. Для таких условий проницающую силу можно определить по формуле:
|
|
где D – диаметр объектива в миллиметрах.
|
||||||||||||
| Таблица 2.2.2.1 |
Разрешающая способность – минимальный угол между двумя звездами, видимыми раздельно. Если невооруженным глазом можно различить две звезды с угловым расстоянием не менее 2′, то телескоп позволяет уменьшить этот предел в Γ раз. Ограничение на предельное увеличение накладывает явление дифракции – огибание световыми волнами краев объектива. Из-за дифракции вместо изображения точки получаются кольца. Угловой размер центрального пятна (теоретическое угловое разрешение)
Разрешающая способность может вычисляться по формуле:
δD
Для видимых длин волн при λ = 550 нм на телескопе с диаметром D = 1 м теоретическое угловое разрешение будет равно δ = 0,1″. Практически угловое разрешение больших телескопов ограничивается атмосферным дрожанием. При фотографических наблюдениях разрешающая способность всегда ограничена земной атмосферой и погрешностями гидирования и не бывает лучше 0,3″. При наблюдениях глазом из-за того, что можно попытаться поймать момент, когда атмосфера относительно спокойна (достаточно нескольких секунд), разрешающая способность у телескопов с диаметром D, большим 2 м, может быть близка к теоретической. Хорошим считается телескоп, собирающий более 50 % излучения в кружке 0,5″.
Относительное отверстие – отношения диаметра D к фокусному расстоянию F:
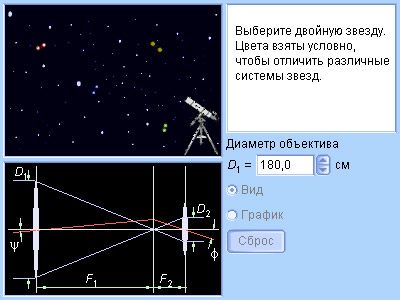 |
|
Модель 2.4. Телескоп |
У телескопов для визуальных наблюдений типичное значение относительного отверстия 1/10 и меньше. У современных телескопов она равна 1/4 и больше.
Часто вместо относительного отверстия используется понятие светосилы, равной (D/F)2. Светосила характеризует освещенность, создаваемую объективом в фокальной плоскости.
Относительным фокусным расстоянием телескопа (обозначается перевернутой буквой А) называется величина, обратная относительному отверстию:
диафрагмой
Угловое увеличение (или просто увеличение) показывает, во сколько раз угол, под которым виден объект при наблюдении в телескоп, больше, чем при наблюдении глазом. Увеличение равно отношению фокусных расстояний объектива и окуляра:
|
|