Классы и разряды. состав числа. сравнение чисел. / числа больше 1000 / справочник по математике для начальной школы

Разряды чисел.

Рассмотрим число 134. У каждой цифры этого числа есть свое место. Такие места, называются, разрядами.

Цифра 4 занимает место или разряд единиц. Так же цифру 4 можно назвать цифрой первого разряда.
Цифра 3 занимает место или разряд десятков. Или цифру 3 можно назвать цифрой второго разряда.
И цифра 1 занимает разряд сотен. По-другому, цифру 1 можно назвать цифрой третьего разряда. Цифра 1 является последней цифрой слава числа 134, поэтому цифру 1 можно назвать, цифрой высшего разряда. Цифра высшего разряда всегда больше 0.

Каждые 10 единиц любого разряда образуют новую единицу более высокого разряда. 10 единиц образуют один разряд десяток, 10 десятков образуют один разряд сотен, десять сотен образуют разряд тысяч и т.д.
Если нет какого-то разряда, то вместо него будет стоять 0.

Например: число 208.
Цифра 8 – первый разряд единиц.
Цифра 0 – второй разряд десятков. 0 означает в математике ничего. Из записи следует, что десятков у данного числа нет.
Цифра 2 – третий разряд сотен.

Такой разбор числа называется разрядным составом числа.

Разряды чисел

Каждая цифра в записи многозначного числа занимает определённое место — позицию. Место (позицию) в записи числа, на котором стоит цифра, называют разрядом.

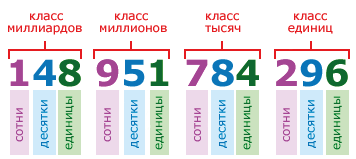
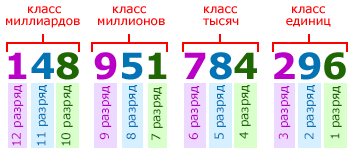
Счёт разрядов идёт справа налево. То есть, первая цифра справа в записи числа называется цифрой первого разряда, вторая цифра справа — цифрой второго разряда и т. д. Например, в первом классе числа 148 951 784 296, цифра 6 является цифрой первого разряда, 9 — цифра второго разряда, 2 — цифра третьего разряда:

Единицы, десятки, сотни, тысячи и т. д. иначе ещё называют разрядными единицами:

Единицы называют единицами первого разряда (или простыми единицами) и пишутся на первом месте справа.
Десятки — единицами второго разряда и пишутся в числе на втором месте справа.
Сотни — единицами третьего разряда и пишутся на третьем месте справа.
Единицы тысяч — единицами четвёртого разряда и пишутся на четвёртом месте справа.
Десятки тысяч — единицами пятого разряда и пишутся на пятом месте справа.
Сотни тысяч — единицами шестого разряда и пишутся в числе на шестом месте справа и так далее.

Каждые три разряда, следующие друг за другом, составляют класс. Первые три разряда: единицы десятки и сотни — образуют класс единиц (первый класс). Следующие три разряда: единицы тысяч, десятки тысяч и сотни тысяч — образуют класс тысяч (второй класс). Третий класс будут составлять единицы, десятки и тысячи миллионов и так далее.

Пример. Запишите цифрами число, которое содержит:

1) 37 единиц второго класса и 565 единиц первого класса;

2) 450 единиц второго класса и 9 единиц первого класса;

3) 8 единиц второго класса и 50 единиц первого класса.

Решение:

1) 37 565;

2) 450 009;

3) 8 050.

Все разрядные единицы, кроме простых единиц, называются составными единицами. Так, десяток, сотня, тысяча и т. д. — составные единицы. Каждые 10 единиц любого разряда составляют одну единицу следующего (более высокого) разряда:

10 единиц	=	1 десяток;
10 десятков	=	1 сотня;
10 сотен	=	1 тысяча;
10 тысяч	=	1 десяток тысяч;
10 десятков тысяч	=	1 сотня тысяч;
10 сотен тысяч	=	1 тысяча тысяч (1 миллион);

и так далее.

Любая составная единица по сравнению с другой единицей, меньшей её называется единицей высшего разряда, а по сравнению с единицей, большей её, называется единицей низшего разряда. Например, сотня является единицей высшего разряда относительно десятка и единицей низшего разряда относительно тысячи.

Чтобы узнать, сколько в числе заключается всех единиц какого-либо разряда, надо отбросить все цифры, означающие единицы низших разрядов и прочитать число, выражаемое оставшимися цифрами.

Например, требуется узнать, сколько всего сотен содержится в числе 6284, т. е. сколько сотен заключается в тысячах и в сотнях данного числа вместе.

В числе 6284 на третьем месте в классе единиц стоит цифра 2, значит в числе есть две простые сотни. Следующая влево цифра — 6, означает тысячи. Так как в каждой тысяче содержится 10 сотен то, в 6 тысячах их заключается 60. Всего, таким образом, в данном числе содержится 62 сотни.

Цифра в каком-нибудь разряде означает отсутствие единиц в данном разряде.

Например, цифра 0 в разряде десятков означает отсутствие десятков, в разряде сотен — отсутствие сотен и т. д. В том разряде, где стоит 0, при чтении числа ничего не произносится:

24 527 — двадцать четыре тысячи пятьсот двадцать семь.

20 507 — двадцать тысяч пятьсот семь.

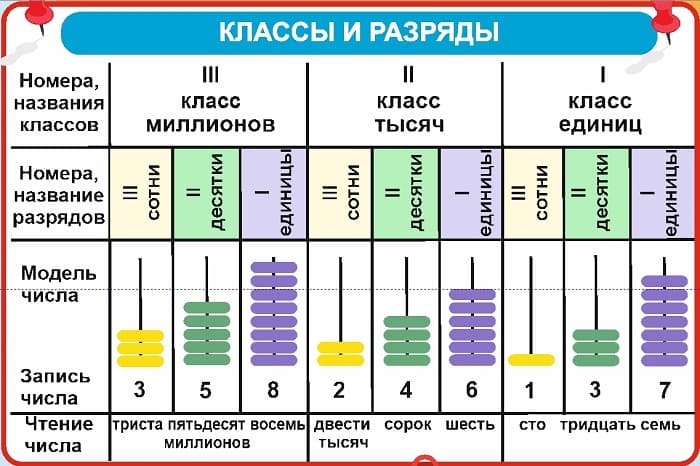
Классы и разряды

Чтобы прочесть многозначное число, его необходимо разбить справа налево на группы по три цифры в каждой. Крайняя левая группа может состоять из одной или двух цифр.

Эти группы называют классами.

Три первые цифры справа ‒ это класс единиц, три следующие — класс тысяч, затем класс миллионов, класс миллиардов и т. д.

Место, занимаемое цифрой в записи числа, называют разрядом.

Если считать справа налево, то первое место в записи числа называют разрядом единиц, второе — разрядом десятков, третье — разрядом сотен и т. д.

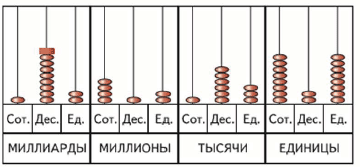
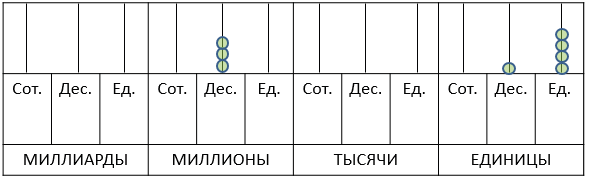
Представленное на рисунке число читают так: 192 миллиарда 412 миллионов 163 тысячи 829. Записывают так: 192 412 163 829.

1) Если в числе отсутствуют единицы какого-либо разряда, то на месте этого разряда в записи числа ставят цифру 0. Например, 4 млрд 130 млн 150 тыс. 405 записывают так:

4 130 150 405

2) Если в числе отсутствуют единицы какого-либо класса, то в записи на месте этого класса будет три нуля. При чтении название этого класса не произносится. Например, число 5 000 430 800 читается так:

5 миллиардов 430 тысяч 800.

Число 30 000 014 читается так: 30 миллионов 14.

Любое число, имеющее разряды, можно разложить на сумму разрядных слагаемых.

Например:

3043 = 3 • 1000 + 0 • 100 + 4 • 10 + 3

43271 = 4 • 10000 + 3 • 1000 + 2 • 100 + 7 • 10 + 1

Разряды местоимений

Что такое разряд местоимения? Русский язык использует местоимения для замены многих частей речи и в зависимости от грамматических признаков различают:

местоимения-существительные – указывают на личность или предмет (я, ты, они, некто, кое-что);
местоимения-прилагательные – указывают на признак предмета (мой, каждый, некоторый);
местоимения-числительные – указывают на количество (несколько, сколько-нибудь);
местоимения-наречия (везде, сюда, никогда).

По лексическому значению существуют следующие разряды местоимений:

личные – указывают на лица (я, ты, его, они);
возвратные – обозначают действия, направленные на самого себя (себе, собою);
притяжательные – указывают на принадлежность предмета (мой, ваш, их);
вопросительные – употребляются в вопросительных предложениях (кто, где, сколько);
относительные – употребляются в качестве союза в придаточных предложениях (чей, который);
неопределенные – указывают на неопределенные предметы, их признаки, количество (кто-либо, откуда-то);
отрицательные – обозначают отсутствие предмета, его признаков (никто, никогда);
указательные – указывают на конкретный предмет, его признаки (тот, там);
определительные – уточняют предмет и его признаки (каждый, всякий).

Математические действия

Существование математики невозможно без выполнения математических действий. Всего существует 4 вида арифметических действий:

Порядок выполнения математических действий в выражениях со скобками и без скобок

Так же имеется определенный порядок математических действий, запомнив который с легкостью можно решать задания любой сложности. Этот порядок зависит от наличия скобок и предложенных действий:

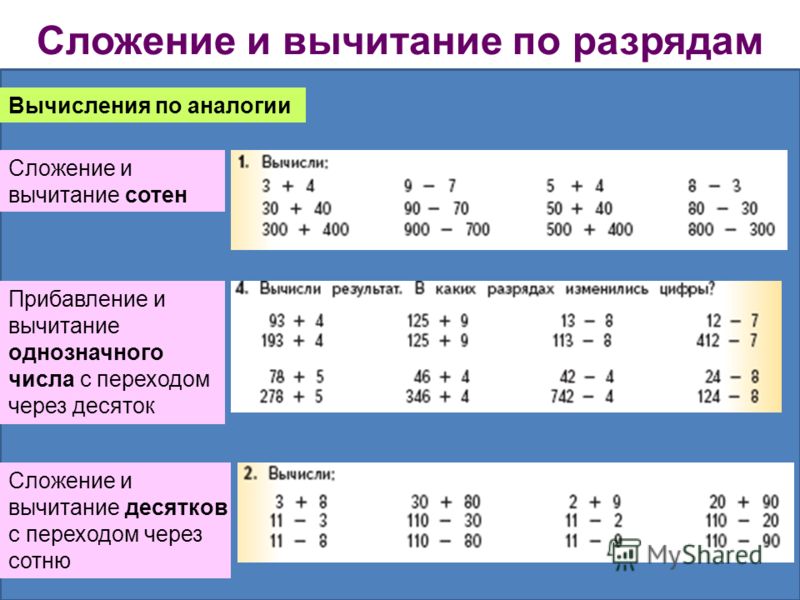
При отсутствии скобок, действия выполняются в обычном порядке. Вот правильный порядок математических действий в примере без скобок:

24+16-5=35

1 действие: 24+16=40

2 действие: 40-5=35

В любом выражении первыми необходимо выполнить умножение или деление в порядке очереди. Вот правильный порядок арифметических действий без скобок:

40-4×5+50=70

1 действие: 4×5=20

2 действие: 40-20=20

3 действие: 20+50=70

Когда выражение содержит скобки, первыми вычисляются действия в скобках, а потом по порядку все остальные. Вот необходимый порядок математических действий в примере со скобками:

5+(20-10):2=10

1действие: 20-10=10

2 действие: 10:2=5

3 действие: 5+5=10

Все очень просто. Если сразу запомнить не получается, то можно пользоваться этим уроком, как шпаргалкой!

Следующий интересный момент заключается в том, что любой компонент математического действия имеет свое название:

Правила нахождения неизвестного компонента при выполнении математических действий

Для того, чтобы максимально упростить решение задач и уравнений, существуют специальные правила нахождения неизвестного компонента:

1) Сложение:

— для нахождения одного из слагаемых необходимо от суммы отнять второе слагаемое:

Например:

?+48=50;

?=50-48=2.

2) Вычитание:

-для нахождения уменьшаемого достаточно найти сумму разности и вычитаемого:

Например:

?-25=50;

?=50+25+75.

-для нахождения вычитаемого, нужно от уменьшаемого отнять разность

Например:

44-?=10;

?=44-10=34.

3) Умножение:

— для нахождения множителя, необходимо найти частное произведения и второго множителя

Например:

?×6=48;

?=48:6=8.

4) Деление:

— для нахождения неизвестного делимого, необходимо найти произведение делителя и частного

Например:

?:11=3;

?=11×3=33.

— для нахождения неизвестного делителя, необходимо делимое разделить на частное

Например:

95:?=19;

?=95:19=5.

Примеры решения задач

Для чего требуется знание числовых разрядов на практике? Для правильного нахождения суммы и разности чисел.

Хотя подобные примеры можно решить онлайн, полезнее уметь просчитывать их самостоятельно. Вычисления проводятся при помощи сложения или вычитания в столбик или

Задача 1

Найти сумму 135 и 241.

Для этого требуется сложить 135 и 241. При этом единицы складываются с единицами и так далее. Поэтому сначала нужно охарактеризовать позицию цифр каждого из слагаемых.

Далее производится сложение – 135 + 241:

друг к другу прибавляются единицы – 1 + 5 = 6;
складываются десятки – 3 + 4 = 7;
складываются сотни – 1 + 2 = 3.

+	1	3	5
2	4	1
	3	7	6

Ответ: 376.

Сходным образом выполняется вычитание.

Задача 2

Найти разность 567 и 254:

сначала вычитаются значения единиц 7 – 4 = 3;
отнимают десятки 6 – 5 = 1;
вычитают сотни 5 – 2 = 3.

–	5	6	7
2	5	4
	3	1	3

Ответ: 313.

Если постоянно упражняться в решении примеров, начиная с самых простых, которые изучаются в 1 классе, и постепенно усложняя, многие арифметические действия можно вычислять устно, тренируя тем самым свой ум, внимание, память и сообразительность. https://www.youtube.com/embed/jykUg0VzFmE

Предыдущая
АлгебраФакториал определение, формула, обозначение, основные свойства и функции, таблица, алгоритмы нахождения, примеры задач с решениями, онлайн-калькулятор
Следующая
АлгебраЭквивалентные функции определение, формулы, основные свойства, доказательство теоремы о замене функций, примеры нахождения пределов, таблица

Разряды чисел

Все натуральные числа записываются с помощью 10 цифр от нуля до девяти. Такая система счисления носит название десятичной.

Кроме того, эта система – позиционная, цифровые символы могут менять положение. Значение каждой следующей позиции больше предыдущей в 10 раз – единицы, десятки, сотни, тысячи и т. д.

Пример 1

Имеются числа 321 и 123. Посмотрим, что они означают, складывая сначала единицы, потом десятки, потом сотни:

321 = 1 * 1 + 2 * 10 + 3 * 100;

123 = 3 * 1 + 2 * 10 + 1 * 100.

Из примера видно, что цифровые символы меняют свое местоположение. Вместе с тем, изменяется числовое значение – в первом случае оно больше.

Место, которое цифра занимает в числе, именуется разрядом. Название каждого элемента соответствует названиям величин счета в десятичной системе. Выделение позиции происходит справа налево, от меньшего к большему.

Важно! Нулем обозначается отсутствие единиц в разрядной позиции. Поэтому он не может стоять на высшей позиции

Например, записывать двадцать три как «023» – некорректно. Правильное написание – 23.

Отнесение цифр к тому или иному месту в числовой записи называется разрядным составом числа.

Пример 2

Разложить на разрядные составляющие число 275.

Решение:

5 располагается на I разрядной позиции (единицы);
7 – на II разрядном месте десятков;
2 – в III разряде сотен.

Правило встречается в следующих упражнениях:

4 класс

Страница 22,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 25,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 26,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 28,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 29,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 61,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 22,
Моро, Волкова, Рабочая тетрадь, часть 1

Страница 46,
Моро, Волкова, Рабочая тетрадь, часть 1

Страница 20. Вариант 1. Тест,
Моро, Волкова, Проверочные работы

Страница 95,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

5 класс

Упражнение 2,
Мерзляк, Полонский, Якир, Учебник

Упражнение 562,
Мерзляк, Полонский, Якир, Учебник

Упражнение 846,
Мерзляк, Полонский, Якир, Учебник

Упражнение 847,
Мерзляк, Полонский, Якир, Учебник

Упражнение 851,
Мерзляк, Полонский, Якир, Учебник

Упражнение 852,
Мерзляк, Полонский, Якир, Учебник

Упражнение 853,
Мерзляк, Полонский, Якир, Учебник

Упражнение 856,
Мерзляк, Полонский, Якир, Учебник

Упражнение 858,
Мерзляк, Полонский, Якир, Учебник

Упражнение 6,
Мерзляк, Полонский, Якир, Учебник

Разряды и классы чисел

Разряды

единиц

1…9,

десятков

10…90,

сотен

100…900.

Отсюда видно, что разрядом числа является его позиция в цифровой записи, причём любое значение можно представлять через разрядные слагаемые в виде nnn = n00 + n0 + n, где n — любая цифра от 0 до 9.

Один десяток является единицей второго разряда, а одна сотня — третьего. Единицы первого разряда называются простыми, все остальные являются составными.

Для удобства записи и передачи применяется группировка разрядов в классы по три в каждом. Между классами для удобства чтения допускается ставить пробел.

Классы

Первый — единиц, содержит до 3 знаков:

200 + 10 +3 = 213.

Двести тринадцать содержит в себе следующие разрядные слагаемые: две сотни, один десяток и три простых единиц.

40 + 5 = 45,

Сорок пять состоит из четырёх десятков и пяти простых единиц.Второй — тысяч, от 4 до 6 знаков:

679 812 = 600 000 + 70 000 + 9 000 + 800 +10 + 2.

Эта сумма состоит из следующих разрядных слагаемых:

шестьсот тысяч,
семьдесят тысяч,
девять тысяч,
восемьсот,
десять,
два,

3 456 = 3000 + 400 +50 +6.

Здесь отсутствуют слагаемые выше четвёртого разряда.

Третий — миллионов, от 7 до 9 цифр:

887 213 644,

Это число содержит девять разрядных слагаемых:

800 миллионов,
80 миллионов,
7 миллионов,
200 тысяч,
10 тысяч,
3 тысячи,
6 сотен,
4 десятка,
4 единицы,

7 891 234.

В этом числе нет слагаемых выше 7 разряда. Четвёртый — миллиардов, от 10 до 12 цифр:

567 892 234 976,

Пятьсот шестьдесят семь миллиардов восемьсот девяносто два миллиона двести тридцать четыре тысячи девятьсот семьдесят шесть.

Разрядные слагаемые 4 класса читаются слева направо:

единицы сотен миллиардов,
единицы десятков миллиардов,
единицы миллиардов,
сотен миллионов,
десятков миллионов,
миллионов,
сотен тысяч,
десятков тысяч,
тысяч,
простые сотни,
простые десятки,
простые единицы.

Нумерация разряда числа производится начиная с меньшего, а чтение — с большего. При отсутствии в числе слагаемых промежуточных значений при записи ставятся нули, при произношении названия отсутствующих разрядов, как и класса единиц не произносится:

400 000 000 004,

Четыреста миллиардов четыре. Здесь не произносятся из-за отсутствия следующие названия разрядов: десятого и одиннадцатого четвёртого класса, девятого, восьмого и седьмого третьего и самого́ третьего класса, также не озвучиваются названия второго класса и его разрядов, а также сотни и десятки единиц.

Пятый — триллионов, от 13 до 15 знаков.

487 789 654 427 241.

Читается слева:

Четыреста восемьдесят семь триллионов семьсот восемьдесят девять миллиардов шестьсот пятьдесят четыре миллиона четыреста двадцать семь двести сорок один.

Шестой — квадриллионов, 16—18 цифр.

321 546 818 492 395 953,

Триста двадцать один квадриллион пятьсот сорок шесть триллионов восемьсот восемнадцать миллиардов четыреста девяносто два миллиона триста девяносто пять тысяч девятьсот пятьдесят три.

Седьмой — квинтиллионов, 19—21 знак.

771 642 962 921 398 634 389.

Семьсот семьдесят один квинтиллион шестьсот сорок два квадриллиона девятьсот шестьдесят два триллиона девятьсот двадцать один миллиард триста девяносто восемь миллионов шестьсот тридцать четыре тысячи триста восемьдесят девять.

Восьмой — секстиллионов, 22—24 цифры.

842 527 342 458 752 468 359 173

Восемьсот сорок два секстиллиона пятьсот двадцать семь квинтиллионов триста сорок два квадриллиона четыреста пятьдесят восемь триллионов семьсот пятьдесят два миллиарда четыреста шестьдесят восемь миллионов триста пятьдесят девять тысяч сто семьдесят три.

Можно просто различать классы по нумерации, к примеру, число 11 класса содержит в себе при написании от 31 до 33 знаков.

Но на практике запись такого количества знаков неудобна и чаще всего приводит к ошибкам. Поэтому при операциях с такими величинами производится сокращение количества нулей путём возведения в степень. Ведь значительно проще написать 10 31, чем приписывать тридцать один ноль к единице.

Многозначные числа в математике

Прежде чем перейти к основному понятию, требуется вспомнить о натуральных числах – тех, что используются при счете.

Их особенность в том, что они имеют наименьшее значение (1), но не имеют наибольшего или конечного. Ведь счет не имеет конца.

Их можно разделить на группы, в зависимости от того, сколько символов входит в их состав:

Однозначные – если для отображения требуется один символ (1, 2, 3 и т. д.).

Двузначные – когда для записи нужно две цифры (10, 11, 12 и т. д.).

Трехзначные – записывают с помощью трех символов (100, 101, 102 и т. д.).

Перечисление можно продолжать дальше – четырехзначные, пятизначные и т. д. Но для простоты обозначения все числа, содержащие в своей структуре более 1 цифры, называют многозначными.

Что такое разрядные слагаемые

Разрядные слагаемые – это сумма чисел с разной разрядностью. Возьмем на примере, число 86. Разложим данное число на десятки и единицы. Получаем: 86 = 80 + 6 = 8 * 10 + 6 * 1. Отсюда видим, что число 86 состоит из 8 десятков и 6 единиц. Это и есть разрядные слагаемые.

Числа 1, 10, 100, 1000 и так далее – это разрядные единицы. Запишем разделение разрядных слагаемых:

Числа от 1 и до 9 – это единицы;
Числа 10, 20, … , 90 – это десятки;
Число 100, 200, … , 900 – это сотни и так далее.

Любое натуральное число можно разделить на разрядные слагаемые и записать в виде суммы. Примеры разрядных слагаемых:

892 = 800 + 90 + 2;
1695 = 1000 + 600 + 90 + 5;
45 = 40 + 5.

Рассмотрим пример определения разрядных слагаемых числа 92586

Сначала, разложим число 92586 на разрядные слагаемые и получим:

92 586 = 90000 + 2000 + 500 + 80 + 6 = 9 * 10 000 + 2 * 1 000 + 5 * 100 + 8 * 10 + 6 * 1.

Запишем, из чего состоит число 92 586:

Из 9 десятков тысяч 9 * 10 000;
Из 2 единиц тысяч 2 * 1000;
Из 5 сотен 5 * 100;
Из 8 десятков 8 * 10;
Из 6 единиц 6 * 1.

Сделаем вывод, что любое число можно разделить на разрядные слагаемые. Разрядные слагаемые помогают при решении более сложных примеров и задач.

Разрядное слагаемое — это любое натуральное многозначное число, которое можно представить в виде суммы разрядных слагаемых. Разложить число на разрядные слагаемые значит разделить число на разряды: единицы, десятки, сотни, тысячи, десятки тысяч и так далее.

Примеры разложения чисел на разрядные слагаемые:123 = 100 + 20 + 3, где 100 — сотни, 20 — десятки, а 3 — единицы.Более сложный пример с большим числом разрядов:16 458 = 10 000 + 6 000 + 400 + 50 + 8, здесь 10 000 — десятки тысяч, 6 000 — тысячи, 400 — сотни, 50 — десятки, 8 — единицы.

Многозначные числа.

Существуют в математике огромное количество натуральных чисел. Они все разные. Например, 2, 67, 354, 1009. Рассмотрим подробно эти числа.Натуральное число 2 состоит из одной цифры, поэтому такое число называют, однозначным числом. Еще пример однозначных чисел: 3, 5, 8.Натуральное число 67 состоит из двух цифр, поэтому такое число называют, двузначным числом. Пример двузначных чисел: 12, 35, 99.Трехзначные числа состоят из трех цифр, например: 354, 444, 780.Четырехзначные числа состоят из четырёх цифр, например: 1009, 2600, 5732.

Двузначные, трехзначные, четырехзначные, пятизначные, шестизначные и т.д. числа, называются, многозначными числами.

Задание 4

Замените суммой разрядных слагаемых числа:

1903

1903: 1 тыс. 9 сот. 3 ед.

407 020

407 020: 4 сот. тыс. 0 дес. тыс. 7 ед. тыс. 0 сот. 2 дес. 0 ед.

300 206

300 206: 3 сот. тыс. 0 дес. тыс. 0 ед. тыс. 2 сот. 0 дес. 6 ед.

164 800

164 800: 1 сот. тыс. 6 дес. тыс. 4 ед. тыс. 8 сот. 0 дес. 0 ед.

Замечание: если в разряде стоит ноль, его можно не писать, так как при прибавлении нуля получается то же число.

Если натуральное число состоит из одного знака – одной цифры, то его называют однозначным, например, числа 3, 5, 9 – однозначные.

сли число состоит из двух знаков – двух цифр, то его называют двузначным. Например, числа 10, 23, 75 — двузначные.

Так же по числу знаков в данном числе дают названия и другим числам. Например: 145, 809 – это трехзначные числа.

Существуют четырехзначные, пятизначные числа и так далее.

Двузначные, трехзначные и так далее числа называют многозначными.

Для чтения многозначное натуральное число разбивают справа налево на группы по три цифры в каждом (самая левая группа может состоять из одной или двух цифр). Эти группы называют классами. Каждая из трех цифр класса обозначает разряд: разряд единиц, разряд десятков, разряд сотен.

Классификация начинается справа. Три первые цифры справа составляют класс единиц, три следующие – класс тысяч, далее идет класс миллионов, затем – миллиардов. (см. Рис.). Так как ряд натуральных чисел бесконечен, то за миллиардами идут триллионы, за триллионами — триллиарды и т.д.

Миллион – это тысяча тысяч, его записывают с помощью единицы и шести нулей.

Миллиард – это тысяча миллионов. Его записывают с помощью единицы и 9 нулей.

Как же правильно прочитать многозначное число? Начинают читать многозначное число слева направо, по очереди называют число единиц каждого класса и добавляют название класса. При этом название класса единиц не называют, как и класса, в котором все три цифры — нули.

Например, вот это число (42 135 308) разбивают на классы так: оно имеет 308 единиц, 135 единиц в классе тысяч, 42 единицы в классе миллионов. Поэтому читают его так: 42 миллиона 135 тысяч 308.

Любое натуральное число можно представить в виде суммы разрядных единиц.

Например:

32 537 = 30 000 + 2 000 + 500 + 30 + 7

Таким образом, в этом уроке Вы познакомились с понятием натурального числа и натурального ряда, научились читать и классифицировать натуральные многозначные числа, а также раскладывать их по разрядам.

Источник конспекта:: http://interneturok.ru/ru/school/matematika/4-klass/tema-3/chtenie-mnogoznachnyh-chisel?konspekt

http://znaika.ru/catalog/5-klass/matematika/Naturalnye-chisla.-Chtenie-i-zapis

Источник видео: https://www.youtube.com/watch?v=frHwo0rvmvM

Классы чисел

Цифры в записи многозначных чисел разбивают справа налево на группы по три цифры в каждой. Эти группы называют классами. В каждом классе цифры справа налево обозначают единицы, десятки и сотни этого класса:

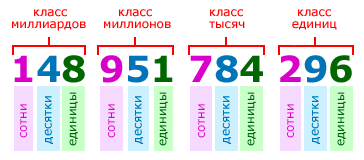
Названия классов многозначных чисел справа налево:

первый — класс единиц,
второй — класс тысяч,
третий — класс миллионов,
четвёртый — класс миллиардов,
пятый — класс триллионов,
шестой — класс квадриллионов,
седьмой — класс квинтиллионов,
восьмой — класс секстиллионов.

Для удобства чтения записи многозначного числа, между классами оставляется небольшой пробел. Например, чтобы прочитать число 148951784296, выделим в нём классы:

148 951 784 296

и прочитаем число единиц каждого класса слева направо:

148 миллиардов 951 миллион 784 тысячи 296.

При чтении класса единиц в конце обычно не добавляют слово единиц.

Задание 2

Запишите цифрами числа:

1. Сто восемь тысяч триста девять

2. Тридцать тысяч семьсот девять

3. Восемь тысяч шестьсот

Решение

Многозначные числа записывают по классам, начиная с высшего. Чтобы записать цифрами число, например «сто восемь тысяч триста девять», сначала записывают, сколько всего единиц второго, высшего, класса в числе – 108, потом записывают, сколько всего единиц первого класса в числе.

Для числа «тридцать тысяч семьсот семьдесят» запишем количество единиц второго высшего класса в числе, их тридцать, и количество единиц первого класса в числе, семьсот семьдесят.

В числе «восемь тысяч шестьсот» 8 единиц второго класса и шестьсот единиц первого класса.

2 класс – класс тысяч	1 класс – класс единиц
Сотни тысяч	Десятки тысяч	Единицы тысяч	Сотни	Десятки	Единицы
1	8	3	9
	3	7	7
		8	6

Что такое разряд в физике

При прохождении электрического тока через газообразное вещество происходит газовый разряд. Различают несколько видов газовых разрядов:

искровой – электрический разряд, сопровождающийся искрением. Примером искрового разряда в природе является молния;
коронный – самостоятельный газовый разряд, возникает при высоком давлении в неоднородных электрических полях;
тлеющий – разряд, который образуется при низком давлении газа и малом токе, например, свечение неоновой лампы;
дуговой разряд или электрическая дуга – физическое явление, представляющее собой ярко светящийся плазменный шнур.

Разряды и классы чисел

Разряды

единиц

1…9;

десятков

10…90;

сотен

100…900.

Классы

Первый — единиц, содержит до 3 знаков:

200 + 10 +3 = 213.

40 + 5 = 45;

Сорок пять состоит из четырёх десятков и пяти простых единиц.
Второй — тысяч, от 4 до 6 знаков:

679 812 = 600 000 + 70 000 + 9 000 + 800 +10 + 2.

шестьсот тысяч;
семьдесят тысяч;
девять тысяч;
восемьсот;
десять;
два;

3 456 = 3000 + 400 +50 +6.

Здесь отсутствуют слагаемые выше четвёртого разряда.

Третий — миллионов, от 7 до 9 цифр:

887 213 644;

Это число содержит девять разрядных слагаемых:

800 миллионов;
80 миллионов;
7 миллионов;
200 тысяч;
10 тысяч;
3 тысячи;
6 сотен;
4 десятка;
4 единицы;

7 891 234.

В этом числе нет слагаемых выше 7 разряда.

Четвёртый — миллиардов, от 10 до 12 цифр:

567 892 234 976;

Разрядные слагаемые 4 класса читаются слева направо:

единицы сотен миллиардов;
единицы десятков миллиардов;
единицы миллиардов;
сотен миллионов;
десятков миллионов;
миллионов;
сотен тысяч;
десятков тысяч;
тысяч;
простые сотни;
простые десятки;
простые единицы.

Нумерация разряда числа производится начиная с меньшего, а чтение — с большего.

При отсутствии в числе слагаемых промежуточных значений при записи ставятся нули, при произношении названия отсутствующих разрядов, как и класса единиц не произносится:

400 000 000 004;

Четыреста миллиардов четыре. Здесь не произносятся из-за отсутствия следующие названия разрядов: десятого и одиннадцатого четвёртого класса; девятого, восьмого и седьмого третьего и самого́ третьего класса; также не озвучиваются названия второго класса и его разрядов, а также сотни и десятки единиц.

Пятый — триллионов, от 13 до 15 знаков.

487 789 654 427 241.

Читается слева:

Шестой — квадриллионов, 16—18 цифр.

321 546 818 492 395 953;

Седьмой — квинтиллионов, 19—21 знак.

771 642 962 921 398 634 389.

Восьмой — секстиллионов, 22—24 цифры.

842 527 342 458 752 468 359 173

Понятие числа. Виды чисел

В понятие числа входит обозначение количественного состава чего-либо.Это одно из главных определений в математике. Каждый вид числа появлялся в результате необходимости выполнения человеком тех или иных расчетов. В связи с необходимостью владеть информацией о количестве предметов, появилось понятие натурального числа и бесконечности ряда натуральных чисел. Необходимость измерения площадей, длин, объемов — породила рациональное число. Для решения сложных уравнений ввели комплексные числа.

Натуральные числа — это числа, получаемые при определении количества 1,2,3. Множество таких чисел принято обозначать буквой N. Например: 1,2,3 …..
Целые числа. Определение понятия формулируется так: множество натуральных, отрицательных чисел и нуль. Их принято обозначать буквой Z. Например: -2,-1,0,1,2,3,4…..
Рациональные числа. В понятие рационального числа входят дроби m/n, где n≠0, при этом m — целое число, а n — натуральное. Обозначаются буквой Q. Например: 2/3, -4/5
Действительные. В понятие действительного числа включены рациональные и иррациональные числа, которые могут записываться в виде обычной и десятичной конечной и бесконечной дробей, а также нуль. Обозначаются буквой R. Например: 1245, 5⅔, -648,35
Простыми называют натуральные числа, которые можно представить в виде двух множителей — единицы и самого этого числа. Обозначается буквой Р. Например: 1,3,7,11….
Также существуют Иррациональные числа – это числа, не являющиеся рациональными, то есть нельзя представить в виде дроби m/n, где n≠0, при этом m — целое число, а n — натуральное. Например, число пи=3,1415926535, число e=2.718281828, квадратный корень из 3 и так далее.

Сумма разрядных слагаемых.

Любое натурально число имеющее различные разряды можно разложить на сумму разрядных слагаемых. Рассмотрим пример:
Число 4062 распишем на разряды.

4 тысяч 0 сотен 6 десятков 2 единиц или по-другому можно записать

4062=4 ⋅1000+0 ⋅100+6 ⋅10+2

Следующий пример:
26490=2 ⋅10000+6 ⋅1000+4 ⋅100+9 ⋅10+0

Вопросы по теме:

Назовите первые четыре класса в записи натуральных чисел?
Ответ: класс единиц, класс тысяч, класс миллионов, класс миллиардов.

Как читают многозначные числа?
Ответ: многозначные числа читают слева направо. Разбивают число по 3 цифры с конца на классы, называют все цифры, кроме нуля. Цифра 0 в записи числа означают отсутствие разряда.

Какие цифры могут стоять в любом разряде числа, кроме высшего?
Ответ: 0, 1, 2, 3, 4. 5, 6, 7, 8, 9.

Какие цифры могут стоять в высшем разряде числа?
Ответ: 1, 2, 3, 4. 5, 6, 7, 8, 9.

Что такое сумма разрядных слагаемых?
Ответ: Это разложение натурального числа на разряды и суммирование их.

Сколько десятков в сотне?
Ответ: в сотне 10 десятков.(10+10+10+10+10+10+10+10+10+10=100)

Сколько сотен в тысячи?
Ответ: в тысячи 10 сотен. (100+100+100+100+100+100+100+100+100+100=1000)

Сколько десятков в тысячи?
Ответ: в тысячи 100 десятков.

Сколько тысяч в миллионе?
Ответ: в миллионе 1000 тысяч.

Примеры на задачи.

Пример №1:
Запишите и прочитайте число: а) пятизначное б) шестизначное.
Ответ: а) 35 100 (тридцать пять тысяч сто) б) 803 273 (восемьсот три тысячи двести семьдесят три)

Пример №2:
Сколько натуральных чисел: а) однозначных б) двузначных?
Ответ: а) однозначных натуральных чисел 10 (0, 1, 2, 3, 4. 5, 6, 7, 8, 9), б) двузначных натуральных чисел 90 (10, 11, 12, …,99)

Пример №3:
В записи числа 10398 назовите цифры разрядов единиц, десятков, сотен, тысяч, десятков тысяч, …
Ответ: 8 – разряд единиц, 9 – разряд десятков, 3 – разряд сотен, 0 – разряд тысяч, 1 – разряд десятков тысяч.

Пример №4:
Напишите наименьшее трехзначное число и наибольшее пятизначное число.
Ответ: 100 и 99999.

Пример №5:
Запишите число 56976 в виде суммы разрядных слагаемых:
Ответ: 56976=50000+6000+900+70+6=5⋅10000+6⋅1000+9⋅100+7⋅10+6