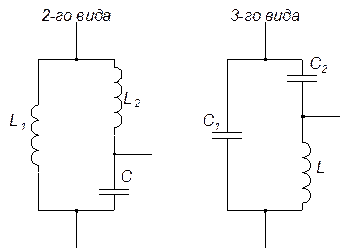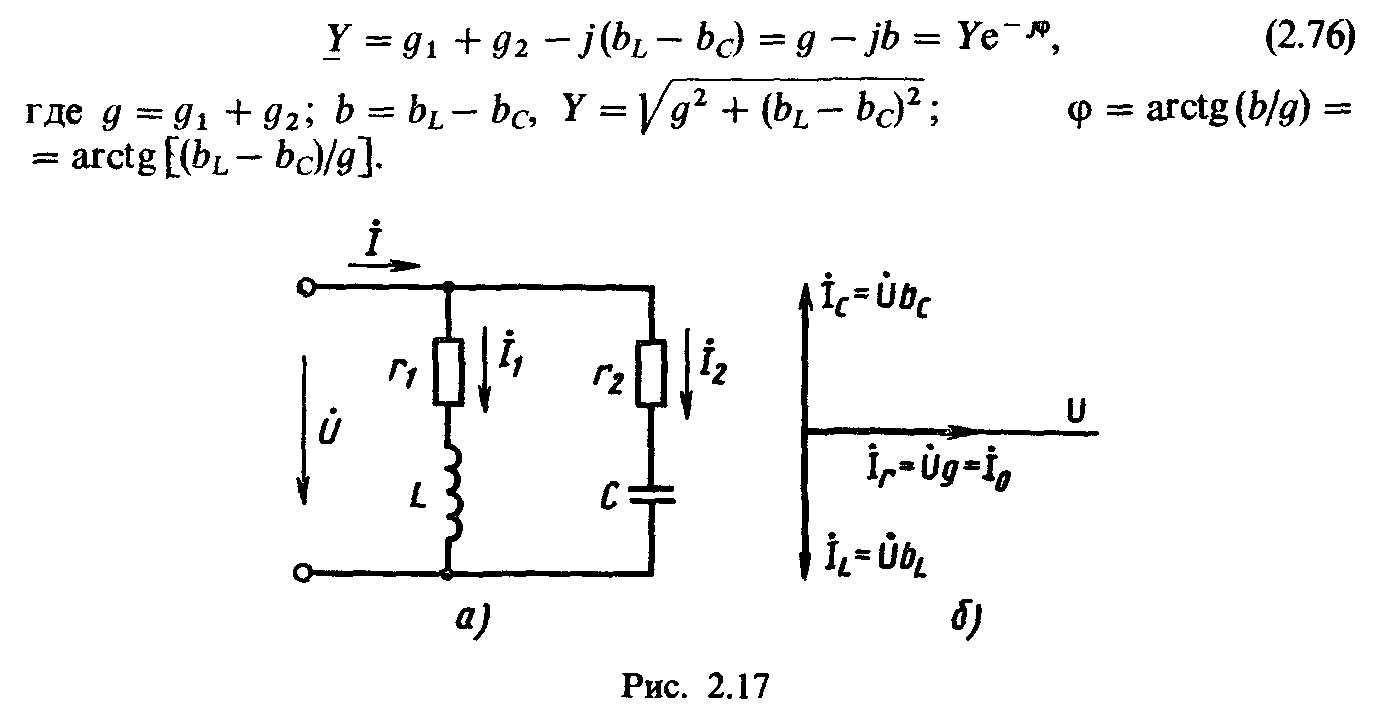Параллельный колебательный контур

Литература

Попов В. П. Основы теории цепей: Учеб. для вузов / В. П. Попов. — 4-е изд., испр. — М.: Высш. шк., 2003. — 575 с.
Скрипников Ю. Ф. Колебательный контур — М.: Энергия, 1970—128 с.: ил. — (МРБ; Вып. 739)
Изюмов Н. М., Линде Д. П. Основы радиотехники. — М.:Радио и связь, 1983

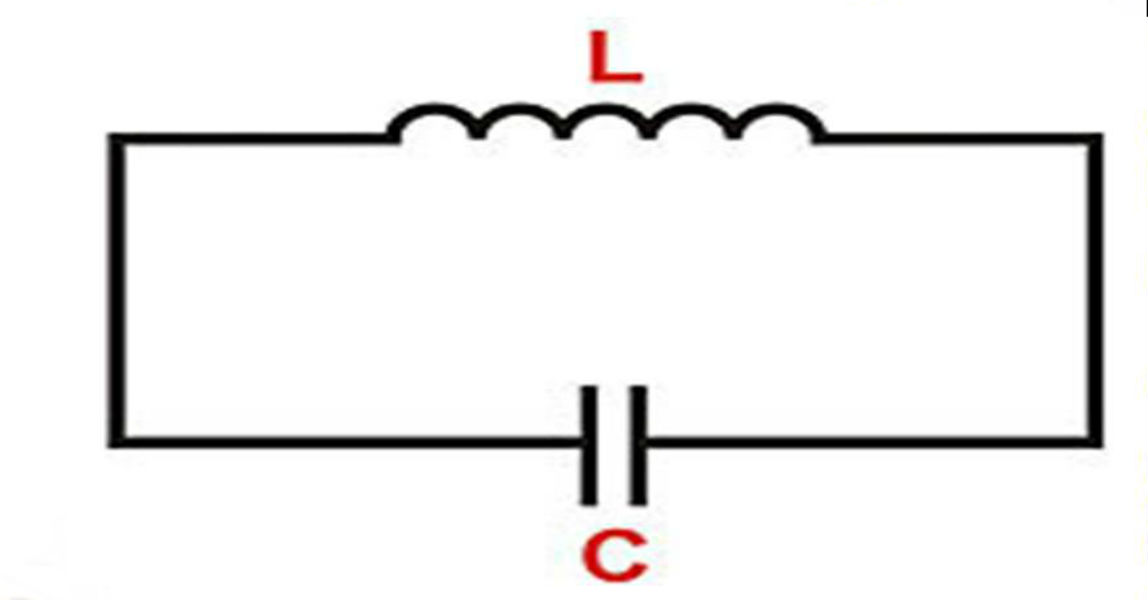
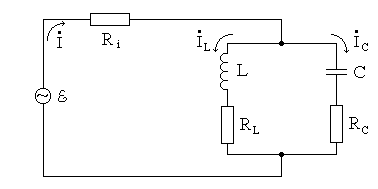
Колебательный контур

Колебательным контуром называется цепь из параллельно соединенных конденсатора и катушки индуктивности.

Рис. 1. Схема колебательного контура.

Разорвем схему, и зарядим конденсатор. На его обкладках появится напряжение. Если теперь соединить выводы конденсатора внешним проводником – возникнет сильный электрический разряд, поскольку сопротивление проводника невелико, ток разряда резко возрастет до больших значений, выделяемая мощность также будет велика.

Однако, если замкнуть контур через катушку индуктивности, ситуация будет иной. Электрическое сопротивление катушки также невелико, однако, резкого броска тока не возникнет. Происходящее дальше будет состоять из двух стадий.

Первая стадия

Конденсатор начнет разряжаться через малое сопротивление катушки. Но, в результате явления самоиндукции, возникающее в катушке магнитное поле будет направлено так, чтобы противодействовать причине, его вызывающей. Поэтому ток будет возрастать гораздо медленнее, чем при коротком замыкании. Напряжение на конденсаторе при этом будет падать. В результате максимальное значение тока не достигнет значений короткого замыкания.

В конце стадии разряда конденсатора ток через обе компоненты контура будет иметь некоторое максимальное значение, а напряжение на конденсаторе уменьшится до нуля.

Вторая стадия

Здесь опять ключевую роль играет явление самоиндукции. Поскольку напряжение на обоих компонентах контура уменьшилось до нуля, ток должен прекратиться. Однако, магнитный поток в катушке индуктивности направлен так, чтобы противодействовать этому. В результате ток исчезает не сразу, а снижается в течение некоторого времени.

Снижающийся ток проходит через разряженный конденсатор, и заряжает его (уже в противоположном направлении). И к моменту полного снижения тока до нуля конденсатор оказывается заряжен снова.

Рис. 2. Переходы энергии в колебательном контуре.

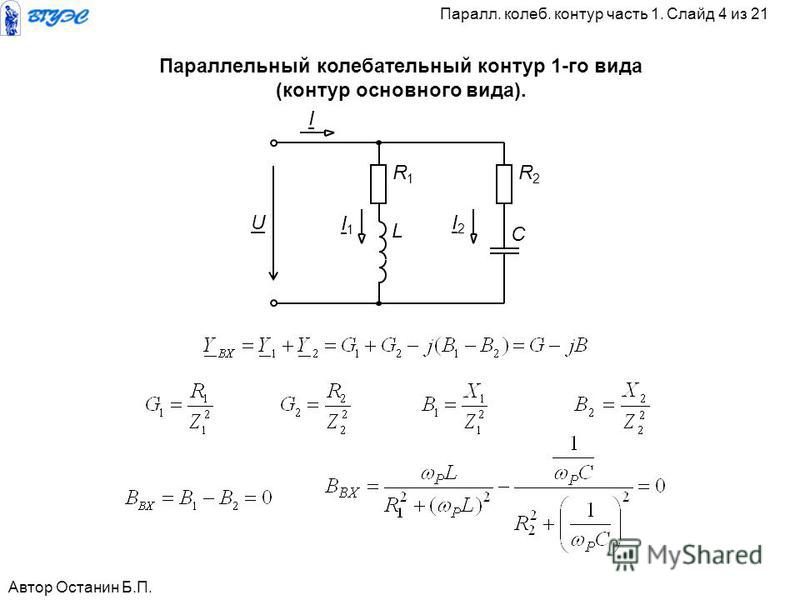
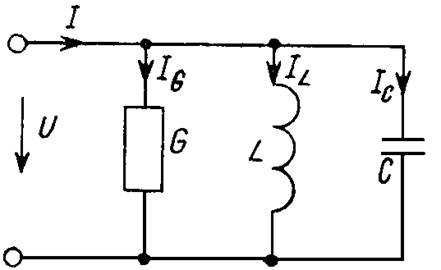
Комплексное сопротивление (импеданс) колебательного контура

Колебательный контур может быть рассмотрен как двухполюсник, представляющий собой параллельное включение конденсатора и катушки индуктивности. Комплексное сопротивление такого двухполюсника можно записать как

z^(iω)=iωL1−ω2LC,{\displaystyle {\hat {z}}(i\omega )\;={\frac {i\omega L}{1-\omega ^{2}LC}},}

где i — мнимая единица.

Для такого двухполюсника может быть определена т. н. характеристическая частота (или резонансная частота), когда импеданс колебательного контура стремится к бесконечности (знаменатель дроби стремится к нулю).

Эта частота равна

ωh=1LC{\displaystyle \omega _{h}={\frac {1}{\sqrt {LC}}}}

и совпадает по значению с собственной частотой колебательного контура.

Из этого уравнения следует, что на одной и той же частоте может работать множество контуров с разными величинами L и C, но с одинаковым произведением LC. Однако выбор соотношения между L и C зачастую не бывает полностью произвольным, так как обуславливается требуемым значением добротности контура.

Для последовательного контура добротность растёт с увеличением L:

Q=1RLC,{\displaystyle Q={\frac {1}{R}}{\sqrt {\frac {L}{C}}},}

где R — активное сопротивление контура.
Для параллельного контура:

Q=ReCL,{\displaystyle Q=R_{e}{\sqrt {\frac {C}{L}}},}

где Re=LCRL+C{\displaystyle R_{e}={\frac {L}{CR_{L+C}}}}, (RL+C{\displaystyle R_{L+C}} — сумма активных сопротивлений в цепи катушки и цепи конденсатора).

Понятие добротности связано с тем, что в реальном контуре существуют потери энергии (на излучение и нагрев проводников). Обычно считают, что все потери сосредоточены в некотором эквивалентном сопротивлении Re{\displaystyle R_{e}}, которое в последовательном контуре включено последовательно с L и C, а в параллельном — параллельно им. Малые потери (то есть высокая добротность) означают, что Re{\displaystyle R_{e}} в последовательном контуре мало, а в параллельном — велико. В низкочастотном последовательном контуре Re{\displaystyle R_{e}} легко обретает физический смысл — это активное сопротивление провода катушки и проводников цепи.

Собственные колебания

Определение 1

Собственными колебаниями называют колебания, которые совершаются за счет энергии, которую сообщили системе в начальный момент времени (т.е. нет постоянно действующего источника ЭДС) и предоставили самой себе.

Если собственные колебания вызваны наличием только квазиупругой силы, то они будут гармоническими.

Допустим, что источник ЭДС в колебательном контуре отсутствует, $\frac{dU}{dt}=0$, тогда уравнение (2) для колебательного контура примет вид:

$L\frac{d^2I}{dt^2}+R\frac{dI}{dt}+\frac{1}{C}I=0\left(5\right)$

Решение уравнения (5) может описывать свободные колебания контура при величине сопротивления, которое входит в состав контура $R

$I=A_0e^{\left(-\beta t\right)}{sin \left(\omega t+{\alpha }_0\right)\left(6\right),\ }$

где $\omega =\sqrt{\frac{1}{LC}-\frac{R^2}{4L^2}}$ — циклическая частота колебаний контура. $\beta =\frac{R}{2L}$ — коэффициент затухания (величина $\tau =\frac{1}{\beta }$ —время релаксации). (В уравнении может быть указан $cos$ вместо синуса — оба случая верны, мы помним, что эти функции имеют сдвиг на $\frac{\pi }{2}$). При $R >2\sqrt{\frac{L}{C}}$ изменение заряда не является колебаниями, разряд конденсатора называют апериодическим.

При $\beta =0$ в цепи осуществляются свободные незатухающие гармонические колебания, описываемые уравнением:

$L\frac{d^2I}{dt^2}+\frac{1}{C}I=0\ или\frac{d^2I}{dt^2}+{{\omega }_0}^2I=0\ \left(7\right),$

где ${\omega }_0=\frac{1}{\sqrt{LC}}$ — частота собственных гармонических колебаний контура.

Используем эту формулу для определения частоты и запишем решение уравнения (7) в виде:

$I(t)=I_0{sin \left({\omega }_0t+{\alpha }_0\right)\left(8\right),\ }$

где $I_0$ — амплитуда силы тока.

Если $\beta >0$, но потери энергии на сопротивлении малы, то колебания считают гармоническими.

В том случае, если в контуре присутствуют $L,R, C$ элементы и реализуется $\beta

Пример 1

Задание: Напишите функцию $U(t)$ для конденсатора, который изображен на схеме (рис.2). В цепи имеются конденсатор, емкость которого равна $C$, резистор с сопротивлением $R$ и генератор тока $I(t)$, который формирует ток вида:

$\left\{ \begin{array}{c} {I\left(t\right)=0\ при\ t0.} \end{array} \right.$

Рисунок 2. Схема цепи. Автор24 — интернет-биржа студенческих работ

Решение:

Суммарный ток в цепи $(I)$ в соответствии с первым правилом Кирхгофа можно записать как:

$I=I_R+I_C\left(1.1\right),$

где $I_R,I_C$ — токи, текущие через сопротивление и конденсатор, $I$ — ток генератора. Сопротивление и конденсатор соединены параллельно, следовательно:

$U_R=U_C=U\ \left(1.2\right).$

Используя формулы:

$I_R=\frac{U}{R},\ I_C=C\frac{dU}{dt}\left(1.3\right),$

подставим в (1.1), получим уравнение:

$C\frac{dU}{dt}+\frac{U}{R}=I\ \to \frac{dU}{dt}+\frac{1}{RC}\left(U-RI\right)=0\left(1.4\right).$

В качестве начального условия используем то, что напряжение на конденсаторе при $t=0$ равно нулю $(U(0)=0)$. Установившееся напряжение на конденсаторе будет равно:

$U’=I_0R\ \left(1.5\right).$

В качестве решения уравнения (1.4) получим выражение:

$U\left(t\right)=U’-\left(U’-U\left(0\right)\right){exp \left(-\frac{t}{RC}\right)\ }=I_0R\left(1-{exp \left(-\frac{t}{RC}\right)\ }\right).$

Ответ: $U\left(t\right)=I_0R\left(1-{exp \left(-\frac{t}{RC}\right)\ }\right).$

Пример 2

Задание: Какова зависимость напряжения на конденсаторе от времени $(U(t))$ после того как замкнули ключ на схеме рис.3? Учесть, что сопротивление резистора равно $R$, конденсатор емкостью $C$ изначально не заряжен, в цепь включен генератор постоянного напряжения ($\mathcal E$).

Рисунок 3. Схема цепи. Автор24 — интернет-биржа студенческих работ

Решение:

По второму правилу Кирхгофа запишем:

$U_C+U_R={\mathcal E}\ \left(2.1\right),$

где $U_C,U_R$ напряжения на конденсаторе и сопротивлении. Еще мы знаем, что:

$U_R=RI_R,\ I_C=C\frac{dU_C}{dt}\left(2.2\right).$

На схеме все элементы цепи соединены последовательно, значит:

$I\left(t\right)=I_R=\ I_C\left(2.3\right).$

В соответствии с избранным направлением обхода контура и уравнениями (2.1)- (2.3) имеем:

$U_C+RC\frac{dU_C}{dt}={\mathcal E}\to \frac{dU_C}{dt}+\frac{1}{RC}\left(U_C-{\mathcal E}\right)\left(2.4\right).$

В соответствии с заданными начальными условиями запишем:

$U_C\left(0\right)=0\ \left(2.5\right).$

Решением уравнения (2.4) будет функция:

$U_C\left(t\right)={\mathcal E}\left(1-e^{-\frac{t}{RC}}\right).$

Ответ: $U_C\left(t\right)={\mathcal E}\left(1-e^{-\frac{t}{RC}}\right).$

Практическое применение

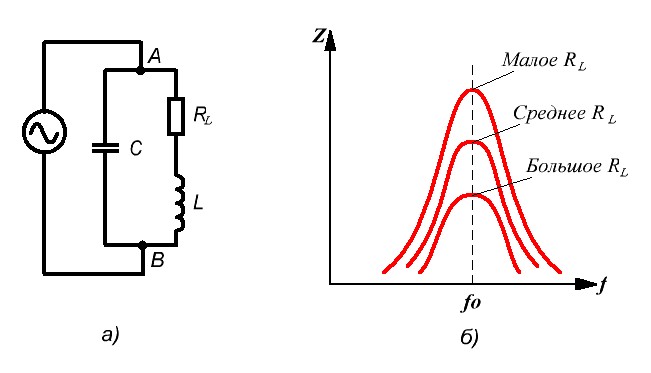
Резонансные контуры широко используются как полосовые и режекторные фильтры — в усилителях, радиоприёмниках, а также в различных устройствах автоматики. Например, на самолётах Ил-62М, Ил-76 и установлены блоки регулирования частоты БРЧ-62БМ, в главном элементе которых — блоке измерения частоты БИЧ-1 — имеются два колебательных контура, настроенных на частоты 760 и 840 Гц. На них поступает напряжение с номинальной частотой 800 Гц от генератора (сам генератор при этом выдаёт 400 Гц). При отклонении частоты от номинальной реактивное сопротивление одного из контуров становится больше, чем другого, и БРЧ выдаёт на привод постоянных оборотов генератора управляющий сигнал для коррекции оборотов генератора. Если частота поднялась выше номинальной — сопротивление второго контура станет меньше, чем первого, и БРЧ выдаст сигнал на уменьшение оборотов генератора, если частота упала — то наоборот. Так поддерживается постоянство частоты напряжения генератора при изменении оборотов двигателя.

Резонанс напряжений

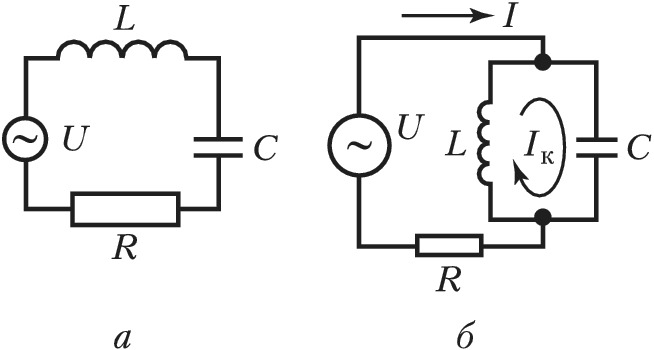
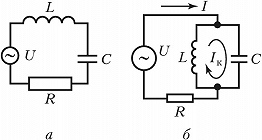
Основы > Задачи и ответы > Одиночные колебательные контуры

Резонанс напряжений

1. Реостат с резистивным сопротивлением R=1Ом, катушка с индуктивностью L=5,05 мГн и конденсатор емкостью С=0,05 мкФ соединены последовательно. Вычислить резонансную частоту, характеристическое сопротивление, затухание контура, напряжения при резонансной частоте. При каких частотах напряжения на конденсаторе и катушке достигнут максимума?Чему они будут равны, если действующее значение напряжения переменной частоты, приложенного к пени, U=10 В?Решение:
Частоты, при которых напряжения на индуктивности и емкости максимальны, и значения этих максимальных напряжений определяют по формулам, известным из теории:2. Электрическая цепь состоит из последовательно соединенных резистора, сопротивление которого R=10Ом, катушки с индуктивностью L=100мкГн и конденсатора с емкостью С=100пФ. Определить резонансную частоту , характеристическое сопротивление r, затухание d и добротность Q. Чему равны ток , расходуемая в цепи мощность , напряжения на индуктивной катушке и конденсаторе при резонансе, если контур включен на напряжение U=1 В? Вычислить абсолютное значение полосы пропускания контура.Решение:

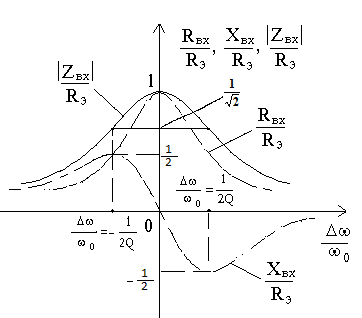
3. К контуру, данные которого приведены в задаче 2, подведено напряжение U=1 В с угловой частотой . Чему при этом равны реактивное и полное сопротивления цепи, ток, мощность, напряжение на конденсаторе, сдвиг фазj между приложенным напряжением и током, сдвиг фаз j’ между приложенным напряжением и напряжением на конденсаторе, коэффициенты передачи по току и по напряжению?Решение:
Прежде всего вычислим абсолютную, относительную и обобщенную расстройки:.Реактивное и полное сопротивления: . Ток и расходуемая в цепи мощность:.Напряжение на конденсаторе:
Сдвиг фаз между напряжением и током:
Найдем сдвиг фаз j’ между . Так как расстройка положительна, то и ток отстает от напряжения на угол j; вектор напряжения на конденсаторе отстает от вектора тока на 90° (рис. 5.11), поэтому отстает от на угол j’= j+ 90°С=111°50′.При заданной расстройке коэффициенты передачи по току и напряжению:

4. Для контура и данных, рассмотренных в задачах 2 и 3, построить ампдитудно- и фазочастотные характеристики тока и напряжения на конденсаторе в зависимости от отношения , от отношения расстройки частоты питающего генератора к резонансной частоте (построение сделать для частот, отличающихся от резонансной на ±10%) и от обобщенной расстройки (в пределах ±4).Решение:
Построение амплитудно- и фазочастотной характеристик тока и напряжения на конденсаторе в зависимости от

На практике обычно приходится иметь дело с небольшими расстройками . В этом случае, учитывая, что
формулы для примут такой вид:
Для удобства расчеты сведены в таблицу 1. При этом следует иметь в виду, что
По данным таблицы 1 на рис. 5.12 начерчены требуемые кривые в зависимости от .Кривые зависимостей от обобщенной расстройки:

Таблица 1


Задаваемые значения	Расчеты по приближенным формулам	Искомые значения, рассчитанные по приближенным формулам

-0,10-0,08-0,06-0,04-0,020,020,040,060,080,10	0,900,920,940,960,981,001,021,041,061,081,10	-0,20-0,16-0,12-0,08-0,040,040,080,120,160,20	-20-16-12-8-4048121620	5,06,28,312,424,310024,312,48,36,25,0	-87°10′-86°25′-85°15′-82°50′-76°076°82°50’85°15’86°25’87°10′	5,06,28,312,424,310024,312,48,36,25,0	2°50’3°35’4°45’7°10’14°90°166°172°50’175°15’176°25’177°10′

Результаты расчетов сведены в таблицу 2, а соответствующие кривые даны на рис. 5.12.Наконец, выясним, каким значениям соответствует некоторая фиксированная величина x. Пусть x=±1. Тогда из выражения находим, что
или , отсюда
Таким образом, значению x=±1 соответствуют или 0,995, т.е. частота генератора напряжения отклоняется от резонансной на ±0,5%. Аналогично найдем, что x=2 соответствует , при; при

Таблица 2



-4-3-2-101234	24,331,644,770,7 100 70,7 44,7 31,6 24,3	-82°50′-71°35′-63°30′-45°045°63°30’71°35’82°50′	24,331,644,770,710070,744,731,624,3	7°10’18°25’26°30’45°90°135°153°30’161°35’172°50′

Смотри полное содержание по представленным решенным задачам на websor.

Принцип действия

Пусть
конденсатор ёмкостью C заряжен
до напряжения . Энергия,
запасённая в конденсаторе составляет

При
соединении конденсатора с катушкой
индуктивности, в цепи потечёт ток ,
что вызовет в катушке электродвижущую
силу (ЭДС) самоиндукции,
направленную на уменьшение тока в цепи.
Ток, вызванный этой ЭДС (при отсутствии
потерь в индуктивности) в начальный
момент будет равен току разряда
конденсатора, то есть результирующий
ток будет равен нулю. Магнитная энергия
катушки в этот (начальный) момент равна
нулю.

Затем
результирующий ток в цепи будет
возрастать, а энергия из конденсатора
будет переходить в катушку до полного
разряда конденсатора. В этот момент
электрическая энергия конденсатора .
Магнитная же энергия, сосредоточенная
в катушке, напротив, максимальна и равна

,
где — индуктивность катушки, —
максимальное значение тока.

После
этого начнётся перезарядка конденсатора,
то есть заряд конденсатора напряжением
другой полярности. Перезарядка будет
проходить до тех пор, пока магнитная
энергия катушки не перейдёт в электрическую
энергию конденсатора. Конденсатор, в
этом случае, снова будет заряжен до
напряжения .

В
результате в цепи возникают колебания,
длительность которых будет обратно
пропорциональна потерям энергии в
контуре.

В
общем, описанные выше процессы в
параллельном колебательном контуре
называются резонанс
токов,
что означает, что
через индуктивность и ёмкость протекают
токи, больше тока проходящего через
весь контур, причем эти токи больше в
определённое число раз, которое
называется добротностью.
Эти большие токи не покидают пределов
контура, так как они противофазны и сами
себя компенсируют. Стоит также заметить,
что сопротивление параллельного
колебательного контура на резонансной
частоте стремится к бесконечности (в
отличие от последовательного колебательного
контура, сопротивление которого на
резонансной частоте стремится к нулю),
а это делает его незаменимым фильтром.

Стоит
заметить, что помимо простого колебательного
контура, есть ещё колебательные контуры
первого, второго и третьего рода, что
учитывают потери и имеют другие
особенности.

Вынужденными
электромагнитными колебаниями называют
периодические изменения силы тока и
напряжения в электрической цепи,
происходящие под действием переменной
ЭДС от внешнего источника. Внешним
источником ЭДС в электрических цепях
являются генераторы переменного тока,
работающие на электростанциях.

Принцип
действия генератора переменного тока
легко показать при рассмотрении
вращающейся рамки провода в магнитном
поле.

В
однородное магнитное поле с индукцией
В помещаем прямоугольную рамку,
образованную проводниками (abсd).

Пусть
плоскость рамки перпендикулярна индукции
магнитного поля В и ее площадь равна S.

Магнитный
поток в момент времени t =
0 будет равен Ф = В*8.

При
равномерном вращении рамки вокруг оси
OO₁ с
угловой скоростью w магнитный поток,
пронизывающий рамку, будет изменяться
с течением времени по закону:

Изменение
магнитного потока возбуждает в рамке
ЭДС индукцию, равную

где
Е=
ВSw — амплитуда ЭДС.

Если
с помощью контактных колец и скользящих
по ним щеток соединить концы рамки с
электрической цепью, то под действием
ЭДС индукции, изменяющейся со временем
по гармоническому закону, в электрической
цепи возникнут вынужденные гармонические
колебания силы тока — переменный
ток.

На
практике синусоидальная ЭДС возбуждается
не путем вращения рамки в магнитном
поле, а путем вращения магнита или
электромагнита (ротора) внутри статора
— неподвижных обмоток, навитых на
сердечники из магнитомягкого материала.
В этих обмотках находится переменная
ЭДС, что позволяет избежать снятия
напряжения с помощью контактных колец.

Явление
резонанса
относится к наиболее важным с практической
точки зрения свойствам электрических
цепей. Оно заключается в том, что
электрическая
цепь, имеющая реактивные элементы
обладает чисто резистивным сопротивлением.

Общее
условие резонанса
для любого двухполюсника можно
сформулировать в виде Im[Z]=0
или Im[Y]=0,
где Z
и Y
комплексное сопротивление и проводимость
двухполюсника. Следовательно, режим
резонанса полностью определяется
параметрами электрической цепи и не
зависит от внешнего воздействия на нее
со стороны источников электрической
энергии.

Комплексное сопротивление (импеданс) колебательного контура

z^(iω)=iωL1−ω2LC,{\displaystyle {\hat {z}}(i\omega )\;={\frac {i\omega L}{1-\omega ^{2}LC}},}

где i — мнимая единица.

Эта частота равна

ωh=1LC{\displaystyle \omega _{h}={\frac {1}{\sqrt {LC}}}}

и совпадает по значению с собственной частотой колебательного контура.

Для последовательного контура добротность растёт с увеличением L:

Q=1RLC,{\displaystyle Q={\frac {1}{R}}{\sqrt {\frac {L}{C}}},}

где R — активное сопротивление контура.
Для параллельного контура:

Q=ReCL,{\displaystyle Q=R_{e}{\sqrt {\frac {C}{L}}},}

Что такое индуктивность?

Индуктивность катушки колебательного контура — это индивидуальный показатель, численно равный электродвижущей силе (в вольтах), которая возникает в цепи при изменении силы тока на 1 А за 1 секунду. Если соленоид подключён к цепи постоянного тока, то её индуктивность описывает энергию магнитного поля, которое создаётся этим током по формуле:

W=(L*I2)/2, где W — энергия магнитного поля.

Коэффициент индуктивности зависит от многих факторов: от геометрии соленоида, от магнитных характеристик сердечника и от количества мотков проволоки. Ещё одно свойство этого показателя в том, что он всегда положителен, потому что переменные, от которых она зависит, не могут быть отрицательными.

Индуктивность также можно определить как свойство проводника с током накапливать энергию в магнитном поле. Она измеряется в Генри (названа в честь американского учёного Джозефа Генри).

Кроме соленоида колебательный контур состоит из конденсатора, о котором пойдёт речь далее.

Колебания в контуре

Из уравнения баланса энергии в контуре можно также вывести уравнение изменения заряда на конденсаторе:

$$q =q_{max}cos(\omega t)$$

А учитывая, что ток в контуре представляет собой производную заряда по времени, можно получить уравнение тока в контуре:

$$I =I_{max}cos(\omega t+{\pi\over2})$$

Из данных формул видно, что и колебания заряда и колебания тока в контуре происходят по гармоническому закону, однако, при этом они смещены друг относительно друга на четверть периода.

Рис. 3. Графики колебаний заряда и тока в контуре.

Колебательный контур во многом аналогичен пружинному маятнику. Заряду соответствует координата, силе тока соответствует мгновенная скорость, индуктивности соответствует масса, емкости соответствует мягкость пружины (большей емкости соответствует более мягкая пружина).

Что мы узнали?

Электрический колебательный контур – это схема, состоящая из параллельных конденсатора и катушки индуктивности. Энергия в колебательном контуре попеременно переходит то в форму заряда в конденсаторе, то в форму магнитного потока в катушке. Возникают колебания напряжения и тока.

Тест по теме

Вопрос 1 из 10

Колебательный контур состоит из …
- катушки индуктивности и источника питания.
- двух резисторов.
- катушки индуктивности и конденсатора.
- нет правильного ответа

Начать тест(новая вкладка)

Математическое описание процессов

Напряжение на идеальной катушке индуктивности при изменении протекающего тока:

uL=LdiLdt.{\displaystyle u_{L}=L{\frac {di_{L}}{dt}}.}

Ток, протекающий через идеальный конденсатор, при изменении напряжения на нём:

iC=CduCdt.{\displaystyle i_{C}=C{\frac {du_{C}}{dt}}.}

Из правил Кирхгофа, для цепи, составленной из параллельно соединённых конденсатора и катушки, следует:

uL+uC=,{\displaystyle u_{L}+u_{C}=0,} — для напряжений,

iC=iL{\displaystyle i_{C}=i_{L}} — для токов.

Совместно решая систему дифференциальных уравнений (дифференцируя одно из уравнений и подставляя результат в другое), получаем:

d2q(t)dt2+1LCq(t)={\displaystyle {\frac {d^{2}q(t)}{dt^{2}}}+{\frac {1}{LC}}q(t)=0.}

Это дифференциальное уравнение гармонического осциллятора с циклической частотой собственных колебаний ω=1LC{\displaystyle \omega ={\frac {1}{\sqrt {LC}}}} (она называется собственной частотой гармонического осциллятора).

Решением этого уравнения 2-го порядка является выражение, зависящее от двух начальных условий:

i(t)=Iasin⁡(ωt+φ),{\displaystyle i(t)=I_{a}\sin({\omega }t+\varphi ),}

где Ia{\displaystyle I_{a}} — некая постоянная, определяемая начальными условиями, называемая амплитудой колебаний, φ{\displaystyle \varphi } — также некоторая постоянная, зависящая от начальных условий, называемая начальной фазой.

Например, при начальных условиях φ={\displaystyle \varphi =0} и амплитуде начального тока Ia{\displaystyle I_{a}}решение сведётся к:

i(t)=Iasin⁡(ωt).{\displaystyle i(t)=I_{a}\sin({\omega }t).}

Решение может быть записано также в виде

i(t)=Ia1sin⁡(ωt)+Ia2cos⁡(ωt),{\displaystyle i(t)=I_{a1}\sin({\omega }t)+I_{a2}\cos({\omega }t),}

где Ia1{\displaystyle I_{a1}} и Ia2{\displaystyle I_{a2}} — некоторые константы, которые связаны с амплитудой Ia{\displaystyle I_{a}} и фазой φ{\displaystyle \varphi } следующими тригонометрическими соотношениями:

Ia1=Iacos⁡(φ),{\displaystyle I_{a1}=I_{a}\cos {(\varphi )},}

Ia2=Iasin⁡(φ).{\displaystyle I_{a2}=I_{a}\sin {(\varphi )}.}

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. На рисунке приведена схема электрической цепи, состоящей из источника тока, ключа и двух параллельно соединённых резисторов. Для измерения напряжения на резисторе $ R_2 $ вольтметр можно включить между точками

1) только Б и В
2) только А и В
3) Б и Г или Б и В
4) А и Г или А и В

2. На рисунке представлена электрическая цепь, состоящая из источника тока, резистора и двух амперметров. Сила тока, показываемая амперметром А₁, равна 0,5 А. Амперметр А₂ покажет силу тока

1) меньше 0,5 А
2) больше 0,5 А
3) 0,5 А
4) 0 А

3. Ученик исследовал зависимость силы тока в электроплитке от приложенного напряжения и получил следующие данные.

Проанализировав полученные значения, он высказал предположения:

А. Закон Ома справедлив для первых трёх измерений.
Б. Закон Ома справедлив для последних трёх измерений.

Какая(-ие) из высказанных учеником гипотез верна(-ы)?

1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б

4. На рисунке изображён график зависимости силы тока в проводнике от напряжения на его концах. Чему равно сопротивление проводника?

1) 0,25 Ом
2) 2 Ом
3) 4 Ом
4) 8 Ом

5. На диаграммах изображены значения силы тока и напряжения на концах двух проводников. Сравните сопротивления этих проводников.

1) $ R_1=R_2 $
2) $ R_1=2R_2 $
3) $ R_1=4R_2 $
4) $ 4R_1=R_2 $

6. На рисунке приведена столбчатая диаграмма. На ней представлены значения мощности тока для двух проводников (1) и (2) одинакового сопротивления. Сравните значения напряжения $ U_1 $ и $ U_2 $ на концах этих проводников.

1) $ U_2=\sqrt{3}U_1 $
2) $ U_1=3U_2 $
3) $ U_2=9U_1 $
4) $ U_2=3U_1 $

7. Необходимо экспериментально обнаружить зависимость электрического сопротивления круглого угольного стержня от его длины. Какую из указанных пар стержней можно использовать для этой цели?

1) А и Г
2) Б и В
3) Б и Г
4) В и Г

8. Два алюминиевых проводника одинаковой длины имеют разную площадь поперечного сечения: площадь поперечного сечения первого проводника 0,5 мм2, а второго проводника 4 мм2. Сопротивление какого из проводников больше и во сколько раз?

1) Сопротивление первого проводника в 64 раза больше, чем второго.
2) Сопротивление первого проводника в 8 раз больше, чем второго.
3) Сопротивление второго проводника в 64 раза больше, чем первого.
4) Сопротивление второго проводника в 8 раз больше, чем первого.

9. В течение 600 с через потребитель электрического тока проходит заряд 12 Кл. Чему равна сила тока в потребителе?

1) 0,02 А
2) 0,2 А
3) 5 А
4) 50 А

10. В таблице приведены результаты экспериментальных измерений площади поперечного сечения $ S $, длины $ L $ и электрического сопротивления $ R $ для трёх проводников, изготовленных из железа или никелина.

На основании проведённых измерений можно утверждать, что электрическое сопротивление проводника

1) зависит от материала проводника
2) не зависит от материала проводника
3) увеличивается при увеличении его длины
4) уменьшается при увеличении его площади поперечного сечения

11. Для изготовления резисторов использовался рулон нихромовой проволоки. Поочередно в цепь (см. рисунок) включали отрезки проволоки длиной 4 м, 8 м и 12 м. Для каждого случая измерялись напряжение и сила тока (см. таблицу).

Какой вывод можно сделать на основании проведённых исследований?

1) сопротивление проводника обратно пропорционально площади его поперечного сечения
2) сопротивление проводника прямо пропорционально его длине
3) сопротивление проводника зависит от силы тока в проводнике
4) сопротивление проводника зависит от напряжения на концах проводника
5) сила тока в проводнике обратно пропорциональна его сопротивлению

12. В справочнике физических свойств различных материалов представлена следующая таблица.

Используя данные таблицы, выберите из предложенного перечня два верных утверждения. Укажите их номера.

1) При равных размерах проводник из алюминия будет иметь меньшую массу и большее электрическое сопротивление по сравнению с проводником из меди.
2) Проводники из нихрома и латуни при одинаковых размерах будут иметь одинаковые электрические сопротивления.
3) Проводники из константана и никелина при одинаковых размерах будут иметь разные массы.
4) При замене никелиновой спирали электроплитки на нихромовую такого же размера электрическое сопротивление спирали уменьшится.
5) При равной площади поперечного сечения проводник из константана длиной 4 м будет иметь такое же электрическое сопротивление, что и проводник из никелина длиной 5 м.

Часть 2

13. Меняя электрическое напряжение на участке цепи, состоящем из никелинового проводника длиной 5 м, ученик полученные данные измерений силы тока и напряжения записал в таблицу. Чему равна площадь поперечного сечения проводника?

Параллельный колебательный контур

Литература

Колебательный контур

Первая стадия

Вторая стадия

Комплексное сопротивление (импеданс) колебательного контура

Собственные колебания

Практическое применение

Резонанс напряжений

Принцип действия

Комплексное сопротивление (импеданс) колебательного контура

Что такое индуктивность?

Колебания в контуре

Что мы узнали?

Тест по теме

Колебательный контур состоит из …

Математическое описание процессов

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

Часть 2