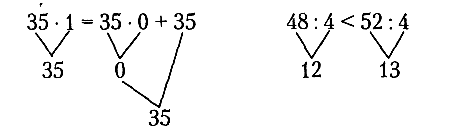
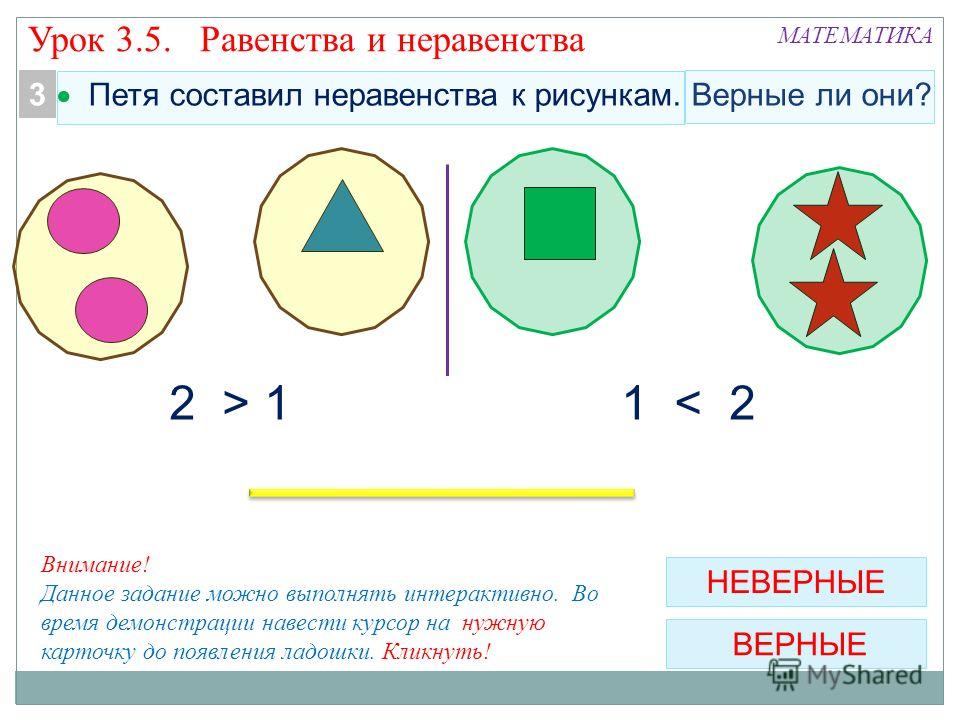
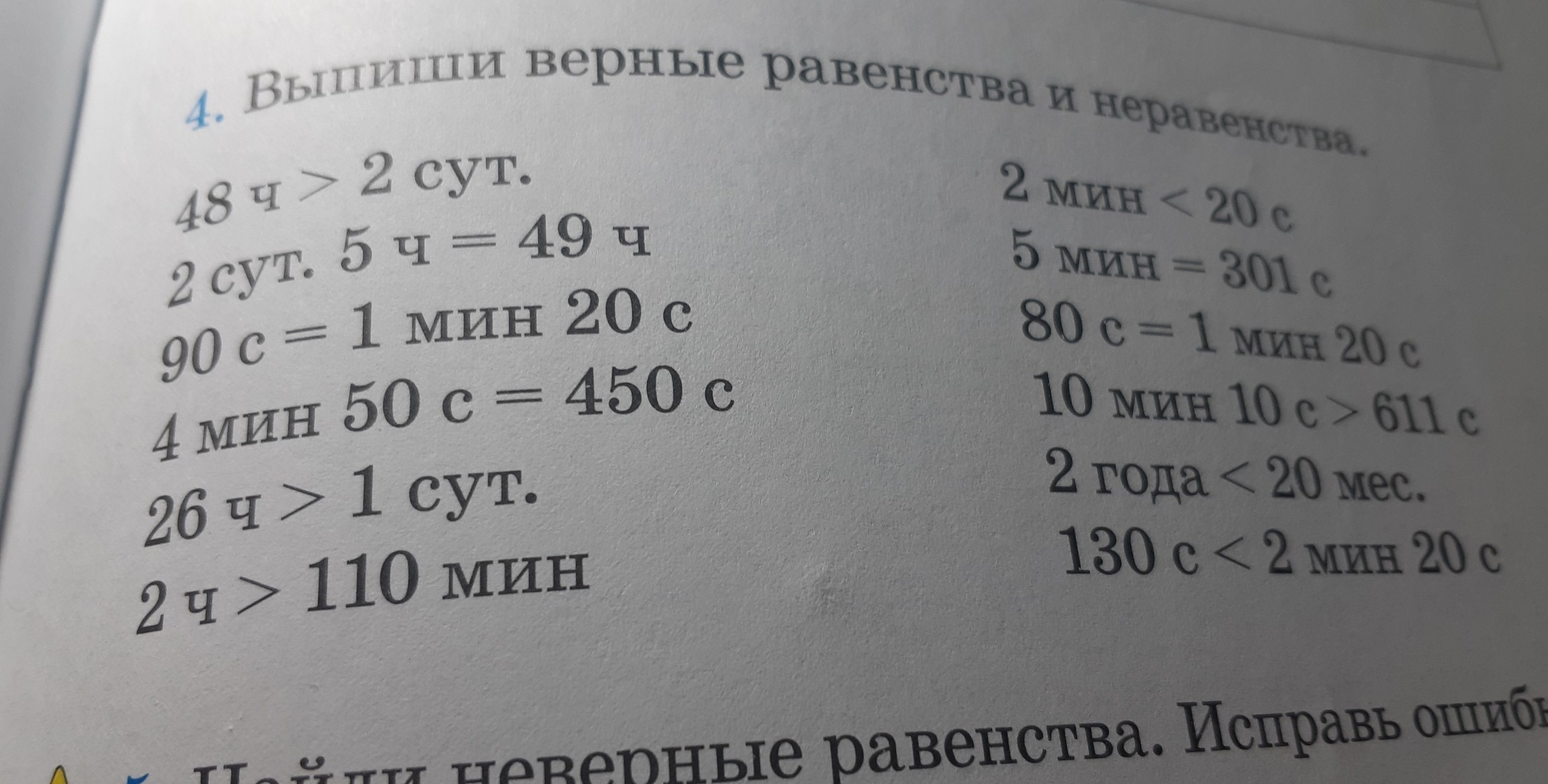Математические знаки
Скорее всего, к первому классу ребенок уже отличает на слух и визуально, что горстка из десяти ягод больше трех штук. Чтобы внедрить в жизнь новые обозначения, посмотрим на знаки «больше», «меньше», «равно» в картинках.
Символ больше (>) — это когда острый нос галочки смотрит направо. Его нужно использовать, когда первое число больше второго:
Символ меньше (<) — это когда острый нос галочки смотрит налево. Его нужно использовать, когда первое число меньше второго:
Символ равенства (=) — это когда два коротких отрезка записаны горизонтально и параллельны друг другу. Используем его при сравнении двух одинаковых чисел:
Чтобы ребенку было легче запомнить схожие между собой знаки, можно применить игровой метод. Для этого нужно сравнить числа и определить в каком порядке они стоят. Далее ставим одну точку у наименьшего числа и две — рядом с наибольшим. Соединяем точки и получаем нужный знак. Вот так просто: 
Равенства и неравенства

Вам понадобятся шесть карточек с арифметическими знаками. Их Вы тоже найдёте в составе 110 карточек цифр и знаков (вторая составляющая часть методики АНАСТА).
Технология показа
Вы решили показать ребёнку такие два неравенства и одно равенство:
8-6<10 −7 11-3= 9 −1 55-12^50 −13
Вы выкладываете их на полу последовательно так, чтобы ребёнок мог видеть сразу каждое из них. При этом Вы всё проговариваете, например: «Восемь минус шесть не равно десять минус семь».
Точно так же Вы проговариваете во время выкладывания оставшиеся равенство и неравенство.
На начальном этапе обучения этой теме выкладываются все карточки.
Затем можно будет показывать только карточки «равно» и «не равно».
В один прекрасный день Вы даёте возможность малышу показать свои знания. Выкладываете карточки с количествами, а ему предлагаете выбрать, карточку с каким знаком надо положить: «равно» или «не равно».
Прежде, чем начать изучать алгебру с малышом,надо познакомить его с понятием переменной величины, представленной буквой.
Обычно в математике используется буква x, но поскольку ее легко спутать со знаком умножения, рекомендуется использовать y.
Вы кладете сначала карточку с пятью бусинками – костяшек, затем знак +плюс ( + ), после него со знаком y, потом знак равенства и, наконец, карточку с семью бусинками- костяшками. Затем вы ставите вопрос: «Что означает здесь у?»
И сами отвечаете на него: “В этом уравнении означает два”
Проверка:
Примерно через одну — полторы недели занятий на данном этапе, Вы можете дать возможность малышу выбрать ответ.
Что такое неравенство?
Понятие неравенства, как и понятие равенства, связано со сравнением двух объектов. И если равенство характеризуется словом «одинаковые», то неравенство, напротив, говорит о различии сравниваемых объектов. Например, объекты и — одинаковые, про них можно сказать, что они равные. А вот два объекта и отличаются, то есть, они не равны или неравные.
Неравенство сравниваемых объектов познается вместе со смыслом таких слов, как выше, ниже (неравенство по высоте), толще, тоньше (неравенство по толщине), дальше, ближе (неравенство по удаленности от чего-либо), длиннее, короче (неравенство по длине), тяжелее, легче (неравенство по весу), ярче, тусклее (неравенство по яркости), теплее, холоднее и т.п.
Как мы уже отмечали при знакомстве с равенствами, можно говорить как о равенстве двух объектов в целом, так и о равенстве их некоторых характеристик. Это же относится и к неравенствам. В качестве примера приведем два объекта и . Очевидно, они не одинаковые, то есть, в целом они неравные. Они не равны по размеру, также они не равны по цвету, однако, можно говорить о равенстве их форм – они оба являются кругами.
В математике общий смысл неравенства сохраняется. Но в ее контексте речь идет о неравенстве математических объектов: чисел, значений выражений, значений каких-либо величин (длин, весов, площадей, температур и т.п.), фигур, векторов и т.п.
Типы неравенств
- Строгие неравенства — используют только знак больше (>) или меньше (<).
- a < b — это значит, что a меньше, чем b.
- a > b — это значит, что a больше, чем b.
- неравенства a > b и b < a означают одно и тоже, то есть равносильны.
- Нестрогие неравенства — используют знаки сравнения ≥ (больше или равно) или ≤ (меньше или равно).
- a ≤ b — это значит, что a меньше либо равно b.
- a ≥ b — это значит, что a больше либо равно b.
- знаки ⩽ и ⩾ являются противоположными.
- Другие типы неравенств.
- a ≠ b — означает, что a не равно b.
- a ≫ b — означает, что a намного больше, чем b.
- a ≪ b — означает, что a намного меньше, чем b.
- знаки >> и << противоположны.
Развивать математическое мышление детей помогут уроки математики в школе Skysmart. Мы подобрали для вашего ребенка тысячи увлекательных заданий — от простых логических загадок до хитрых головоломок, над которыми интересно подумать. Все это поможет легче и быстрее справиться со школьной математикой и влюбиться в числа.
Запишите вашего ребенка на бесплатное пробное занятие в Skysmart: поиграем в цифры вместе с енотом Максом и покажем, что математика — это очень увлекательно!
Понятие равенства
Под этим термином понимают высказывания, в записи которых есть знак «=». Равенства разделяются на верные и неверные. Если в записи вместо = стоит <, >, тогда речь идет о неравенствах. Кстати, первый признак равенства говорит о том, что обе части выражения идентичны по своему результату или записи.

Кроме понятия равенства, в школе изучают также тему «Числовое равенство». Под этим высказыванием понимают два числовых выражения, которые стоят по обе стороны от знака =. К примеру, 2*5+7=17. Обе части записи равны между собой.
В числовых выражениях подобного типа могут использоваться скобки, влияющие на порядок действий. Итак, существует 4 правила, которые следует учесть при вычислении результатов числовых выражений.
- Если в записи нет скобок, тогда действия выполняются с высшей ступени: III→II→I. Если есть несколько действий одной категории, тогда они выполняются слева направо.
- Если в записи есть скобки, тогда действие выполняется в скобках, а затем с учетом ступеней. Возможно, в скобках будет несколько действий.
- Если выражение представлено в виде дроби, тогда вычислять нужно сначала числитель, потом знаменатель, затем числитель делится на знаменатель.
- Если в записи есть вложенные скобки, тогда вычисляется сначала выражение во внутренних скобках.
Итак, теперь понятно, что такое равенство. В дальнейшем будут рассмотрены понятия уравнения, тождества и способы их вычисления.
Последовательности
Последовательности — это те же самые равенства. Опыт работы родителей с этой темой показал, что последовательности детям очень интересны.
Последовательности на плюс — это возрастающие последовательности. Последовательности на минус — убывающие.
Чем разнообразнее будут последовательности, тем они интереснее малышу.
Приведём несколько примеров последовательностей:
3,6,9,12,15,18,2 (+3)
4, 8, 12, 16, 20, 24, 28 (+4)
5,10,15,20,25,30,35 (+5)
100,90,80,70,60,50,40 (-10)
72, 70, 68, 66, 64, 62, 60 (-2)
95,80,65,50,35,20,5 (-15)
Технология показа последовательностей может быть такой. Вы подготовили три последовательности на плюс.
Объявляете малышу тему урока, на полу выкладываете одну за другой карточки первой последовательности, озвучивая их.
Перемещаетесь с ребёнком в другой угол комнаты и точно так же выкладываете вторую последовательность.
В третьем углу комнаты Вы выкладываете третью последовательность, при этом озвучивая её.
Выкладывать последовательности можно и друг под другом, оставляя между ними промежутки.
Старайтесь всегда идти вперёд, двигаясь от простого к сложному. Варьируйте занятия: иногда произнося вслух то, что Вы показываете, а иногда показывайте карточки молча. В любом случае ребёнок видит развёрнутую перед ним последовательность.
Для каждой последовательности нужно использовать не менее шести карточек, иногда больше, для того чтобы ребёнку легче было определить сам принцип последовательности.
Как только Вы увидели блеск в глазах ребёнка, попробуйте добавить к трём последовательностям пример (т.е. проверьте его знания).
Пример показываете так: сначала выкладываете всю последовательность, как Вы обычно это делаете, а в конце поднимаете две карточки (одна карточка — та, которая идёт следующей в последовательности, а другая — случайная) и спрашиваете ребёнка: «Какая следующая?»
На первых порах карточки в последовательностях выкладывайте друг за другом, затем формы выкладывания можно менять: кладите карточки по кругу, по периметру комнаты и т.д.
Когда будет получаться всё лучше и лучше, не бойтесь использовать в последовательностях умножение и деление.
Примеры последовательностей:
4; 6; 8; 10; 12; 14 — в данной последовательности каждое следующее число увеличивается на 2;
2; 4; 7; 14; 17; 34 — в данной последовательности чередуется умножение и сложение (х 2; + 3);
2; 4; 8; 16; 32; 64 — в данной последовательности каждое следующее число увеличивается в 2 раза;
22; 18; 14; 10; 6; 2 — в данной последовательности каждое следующее число уменьшается на 4;
84; 42; 40; 20; 18; 9 — в данной последовательности чередуется деление и вычитание (: 2; — 2);
Знаки «больше», «меньше»
Эти карточки находятся в составе 110 карточек цифр и знаков (вторая составляющая часть методики АНАСТА).
Уроки знакомства малыша с понятиями «больше-меньше» будут очень короткими. Всё, что Вам нужно, — это показать три карточки.
Технология показа
Садитесь на пол и выкладываете каждую карточку перед ребёнком так, чтобы он мог видеть сразу все три карточки. Каждую карточку называете.
Озвучить можно так: «шесть больше трёх» или «шесть больше, чем три».
На каждом занятии Вы показываете ребёнку по три разных варианта неравенств с
карточками «больше» — «меньше». неравенств в день.
Таким образом, Вы демонстрируете девять разных
Как и прежде, Вы показываете каждое неравенство только один раз.
Через несколько дней к трём показам можно добавить пример. Это уже проверка, и проводится она так:
Положите на пол приготовленные заранее карточки, например, карточку с количеством «68» и карточку со знаком «больше». Спросите малыша: «Шестьдесят восемь больше какого числа?» или «Шестьдесят восемь больше пятидесяти или девяносто пяти?». Предложите ребёнку выбрать из двух карточек нужную. Верно указанную малышом карточку, Вы (или он сам) кладёте после знака «больше».
Можно положить перед ребёнком две карточки с количествами и дать ему возможность выбрать знак, который подходит, то есть > или <.
Свойства неравенств
Свойства неравенств — это набор тех правил, которые выполняются при их преобразовании. Ниже представлены свойства неравенств. Подразумевается, что исходные неравенства выполняются при значениях , принадлежащих некоторому, заранее определенному, интервалу.
1) При изменении порядка следования сторон, знак неравенства меняется на противоположный. Если , то . Если , то . Если , то . Если , то .
2) Одно равенство эквивалентно двум нестрогим неравенствам разного знака. Если , то и . Если и , то .
3) Свойство транзитивности Если и , то . Если и , то . Если и , то . Если и , то .
4) К обеим частям неравенства можно прибавить (вычесть) одно и то же число. Если , то . Если , то . Если , то . Если , то .
5) Если есть два или более неравенств со знаком одного направления, то их левые и правые части можно сложить. Если , , то . Если , , то . Если , , то . Если , , то . Аналогичные выражения имеют место для знаков ≥, >. Если в исходных неравенствах имеются знаки не строгих неравенств и хотя бы одно строгое неравенство ( но все знаки имеют одинаковое направление ), то при сложении получается строгое неравенство.
6) Обе части неравенства можно умножить (разделить) на положительное число. Если и , то . Если и , то . Если и , то . Если и , то .
7) Обе части неравенства можно умножить (разделить) на отрицательное число. При этом знак неравенства изменится на противоположный. Если и , то . Если и , то . Если и , то . Если и , то .
8) Если есть два или более неравенств с положительными членами, со знаком одного направления, то их левые и правые части можно умножить друг на друга. Если , , то . Если , , то . Если , , то . Если , , то . Аналогичные выражения имеют место для знаков ≥, >. Если в исходных неравенствах имеются знаки не строгих неравенств и хотя бы одно строгое неравенство ( но все знаки имеют одинаковое направление ), то при умножении получается строгое неравенство.
9) Пусть — монотонно возрастающая функция. То есть при любых , . Тогда к обеим частям неравенства можно применить эту функцию, от чего знак неравенства не изменится. Если , то . Если , то . Если , то . Если , то .
10) Пусть — монотонно убывающая функция, То есть при любых , . Тогда к обеим частям неравенства можно применить эту функцию, от чего знак неравенства изменится на противоположный. Если , то . Если , то . Если , то . Если , то .
Свойства неравенств
Рассмотрим основные свойства числовых неравенств, которые в дальнейшем помогут нам решать некоторые задачи.
Докажем это. Если а >b, то тогда и разность (a –b) является положительным числом:
а – b = c
умножив части равенства на (– 1), получим:
– (а – b) = – с
(b– a) = – с
Так как разность (b– a)оказалась равна отрицательному числу (– с), тоb<a.
Для доказательства этого очевидного факта используем координатную прямую:
Ясно, что если b>a, то оно располагается правее. Аналогично и с располагается правее b, так как с >b. Видно, что тогда сбудет находиться правее а, то есть оно больше.
Данное свойство называют транзитивностью. Им обладает не только отношение «больше — меньше», но и ряд других отношений. Например, из геометрии известно, что если отрезок АВ параллелен отрезку CD, а тот в свою очередь параллелен ещё одному отрезку EF, то и АВ параллельно ЕF.
Свойство транзитивности позволяет использовать так называемые двойные неравенства. Например, нам надо указать, что 25 меньше 48, а 48 меньше 94. Это можно записать в виде одного неравенства:
25 < 48 < 94
Можно использовать и более двух знаков сравнения:
365 <366 < 367 < 368 < 369
Другими словами, к обеим частям верного неравенства можно добавить одинаковое число, и оно всё равно останется верным. Действительно, пусть нам надо сравнить величины (а + с) и (b + c). Для этого найдем их разность:
(а + с) – (b + c) = a + c – b – с = а – b
Так как a<b, то и разность а – b отрицательна. Значит, отрицательна разность величин (а + с) и (b + c), из чего следует, что
а + с <b + c
Проиллюстрируем это на примере неравенства
73 < 86
Добавим к обеим частям число 11 и получим другое верное равенство:
73 + 11 < 86 + 11
84 < 97
Снова рассмотрим разность величин ac и bc:
ac– bc = (a– b)c
Разность (а – b) отрицательна при условии а <b. Если с – положительное число, то всё произведение (a– b)c остается отрицательным, т тогда
ас <bc
Если же c– отрицательное число, то произведение (a– b)c становится положительным, а потому
ас <bc
Пусть есть неравенство
100< 200
Если умножить его на положительное число, например, на 3, то получим верное равенство
300 < 600
Если же умножить его на (– 3), то придется «перевернуть» знак сравнения, поставить вместо «<»знак «>»:
– 300 >– 600
Следующее свойство неравенств позволяет их складывать:
Докажем эту теорему. Найдем разность чисел (а + c) и (b + d):
(а + c) – (b + d) = а + с – b – d = (a– b) + (b– d)
Получили сумму двух слагаемых, (a– b) и (b– d). Каждое из них является отрицательным числом, так как a<bи c<d. Сумма двух отрицательных чисел также отрицательна, а потому можно утверждать, что
а + c<b + d
Покажем, как с помощью этого правила можно складывать неравенства. Пусть есть два верных неравенства:
59<62
69<75
Теперь сложим отдельно их правые и левые части:
59 + 69<62 + 75
128 < 137
Однако если у неравенств разные знаки, то для их сложения надо в одном из них поменять местами правую и левую часть. Например, даны неравенства
63 < 99
26> 25
В одном стоит знак «меньше», а в другом «больше», поэтому сразу их складывать нельзя. Сначала «перевернем» второе неравенство
25 < 26
теперь в обоих неравенствах стоит знак «<», поэтому их можно сложить:
63 + 25 < 99 + 26
88 < 125
Последнее правило позволяет перемножать неравенства:
Для доказательства утверждения найдем разность величин acи bd. При этом добавим к ней слагаемое bc и тут же его вычтем (это необходимо для того, чтобы мы смогли сгруппировать слагаемые):
ac – bd = ac – bd– bc + bc= (ac – bc) + (bc – bd) =
=c(a– b) + b(c– d)
Так как разности (a– b) и (c– d) являются отрицательными числами, c и b – положительными, то и произведения c(a– b) и b(c– d) – это отрицательные величины. Сумма же двух отрицательных величин также отрицательна, поэтому
ac<bd
Покажем на примере использование этого правила. Пусть есть неравенства
7<8
5<6
Перемножив их, получим:
7•5<8•6
35 < 48
Доказательство неравенств
Иногда в неравенствах помимо чисел встречаются переменные величины. При этом некоторые из них верны при любом значении этих переменных
Важно уметь доказывать это. Простейшие случаи связаны с использованием того факта, что квадрат любого числа неотрицателен
Пример. Докажите, что при любом значении d выполняется неравенство
d2+ 11 >5
Решение. Запишем очевидно верное неравенство
d2⩾ 0
Добавим к нему число 11:
d2 + 11 ⩾ 11
Число 11 больше 5, поэтому можно записать:
d2 + 11 ⩾ 11 > 5
d2 + 11 > 5
Пример. Докажите, что неравенство
n2 – 8n + 19> 0
справедливо для любого n.
Решение.
В левой части стоит квадратный трехчлен, попытаемся преобразовать его с помощью формулы :
n2 – 8n + 19 = n2 – 2•4n + 19 = n2 – 2•4n +16 – 16 + 19 =
= (n2 – 2•4n + 42) – 16 + 19 = (n– 4)2 + 3
Величина (n – 4)2 является неотрицательным числом, поэтому сумма (n – 4)2 + 3 никак не меньше трех, то есть положительна.
Иногда для доказательства числового неравенства можно определить знак разности выражений, стоящих в правой и левой части.
Пример. Докажите, что при любом значении переменных выполняется условие
2ut⩽u2 + t2
Решение. Запишем разность выражений, стоящих в неравенстве, а потом преобразуем ее:
2ut – (u2 + t2) = 2ut – u2 – t2 = – (u2 – 2ut + t2) = – (u – t)2
Разность получилась неположительной. Значит, между уменьшаемым и вычитаемым можно поставить знак «⩽»:
2ut⩽u2 + t2
Полученное выражение означает, что удвоенное произведение двух чисел не превосходит сумму их квадратов. Этот факт мы используем при решении следующего задания.
Пример. Докажите, что
d2 + s2 + m2⩾ds + dm + sm
Решение. В предыдущем примере мы установили, что сумма квадратов чисел больше или равна их двойному произведению, поэтому можно записать:
d2 + s2⩾ 2ds
s2 + m2⩾ 2sm
d2 + m2⩾ 2dm
Сложим полученные неравенства:
(d2 + s2) + (s2 + m2) + (d2 + m2) ⩾2ds + 2sm + 2dm
2d2 + 2s2 + 2m2⩾2ds + 2sm + 2dm
Осталось поделить на два это неравенство:
d2 + s2 + 2m2⩾ds + sm + dm
4 способа решить уравнение
Под решением уравнения понимают замену заданного равенства другим, которое равносильно первому. Подобная подмена известна как тождественное преобразование. Чтобы решить уравнение, необходимо воспользоваться одним из способов.
1. Одно выражение заменяется другим, которое в обязательном порядке будет тождественно первому. Пример: (3∙х+3)2=15∙х+10. Это выражение можно преобразовать в 9∙х2+18∙х+9=15∙х+10.
2. Перенесение членов равенства с неизвестным из одной стороны в другую. В таком случае необходимо правильно менять знаки. Малейшая ошибка сгубит всю проделанную работу. В качестве примера возьмем предыдущий «образец».
9∙х2 + 12∙х + 4 = 15∙х + 10
9∙х2 + 12∙х + 4 – 15∙х – 10 = 0
9∙х2 – 3∙х – 6 = 0
Дальше уравнение решается с помощью дискриминанта.
3. Перемножение обеих частей равенства на равное число или выражение, которые не равняются 0. Однако стоит напомнить, что если новое уравнение не будет равносильным равенству до преобразований, тогда количество корней может существенно измениться.
4. Возведение в квадрат обеих частей уравнения. Этот способ просто замечательный, особенно когда в равенстве есть иррациональные выражения, то есть квадратный корень и выражение под ним. Тут есть один нюанс: если возвести уравнение в четную степень, тогда могут появиться посторонние корни, которые исказят суть задания. И если неправильно извлечь корень, тогда смысл вопроса в задаче будет неясен. Пример: │7∙х│=35 → 1) 7∙х = 35 и 2) – 7∙х = 35 → уравнение будет решено верно.
Итак, в этой статье упоминаются такие термины, как то уравнения и тождества. Все они происходят от понятия «равенство». Благодаря различного рода равносильным выражениям решение некоторых задач в значительной мере облегчено.
Запись равенств, знак равно
Пришло время остановиться на правилах записи равенств. Для этого используется знак равно (его также называют знаком равенства), который имеет вид =, то есть, представляет собой две одинаковые черточки, расположенные горизонтально одна над другой. Знак равно = считается общепринятым.
При записи равенств записывают равные объекты и между ними ставят знак равно. Например, запись равных чисел 4 и 4 будет выглядеть следующим образом 4=4, и ее можно прочитать как «четыре равно четырем». Еще пример: равенство площади SABC треугольника ABC семи квадратным метрам запишется как SABC=7 м2. По аналогии можно привести другие примеры записи равенств.
Стоит отметить, что в математике рассмотренные записи равенств часто используют как определение равенства.
Определение.
Записи, в которых используется знак равно, разделяющий два математических объекта (два числа, выражения и т.п.), называют равенствами.
Если письменно требуется обозначить неравенство двух объектов, то используется знак не равно ≠. Мы видим, что он представляет собой перечеркнутый знак равно. В качестве примера приведем запись 1+2≠7. Ее можно прочитать так: «Сумма единицы и двойки не равна семи». Другой пример |AB|≠5 см. – длина отрезка AB не равна пяти сантиметрам.
Ход урока
I. Организационный момент.
II. Подготовительная работа.
Устный счет.
Работа с веером.
– В домике живет цифра 5. Нужно узнать какой цифры не хватает на каждом этаже, чтобы результат был равен 5. (Дети показывают ответ с помощью математического веера.)
– Назовите ответ.
Счет «цепочкой» от 1 до 10 прямой и обратный от 10 до (мячом).
– По очереди посчитайте от 1 до 10.
– Теперь в обратном порядке от 10 до 1.
Работа с математическим набором.
– Откройте математические наборы.
– Положите 4 красных кружка, рядом 1 кружок другого цвета.
– Сколько кружков стало? (5)
– Составьте пример пользуясь цифрами из математического набора. (4+1=5)
– Как записать? (Запись на доске)
– Оставьте цифры 4 и 5.
– Какое число меньше? (4)
– Какую запись записать? (4<5)
– Прочитаем запись. (Четыре меньше пяти.)
– Какое число больше 4? (5)
– Поставьте цифру 5 слева от 4.
– Какой знак между ними поставить? (5>4)
– Прочитайте запись . (Пять больше четырех.)
– Уберите математический набор.
Физминутка.
III. Основная часть.
Работа на доске.
– Поставьте 3 морковки сверху.
– Поставьте 3 репки снизу.
– Что можно сказать о количестве морковок и репок? (Их поровну. Столько же.)
– Какой знак поставим между цифрами? (Равно.)
Учитель записывает на доске 3=3.
– Это равенство – тема урока.
– Кто любит грызть морковку? (Зайчик.)
Учитель ставит зайчика к морковкам.
– Какую сказку узнали по картинкам? («Репка»)
Предлагается драматизация сказки «Репка», раздаются сказочные персонажи:
- репка
- дедка
- бабка
- внучка
- Жучка
- кошка
- мышка
– Встаньте по порядку, как стояли сказочные герои в сказке.
Дети проговаривают последовательность персонажей сказки (кто за кем стоит).
– Сколько репок вытащили герои сказки? (1)
– Что нужно сделать с репками, которые расположены на доске? (Убрать 1.)
– Сколько морковок? (3)
– Сколько репок? (2)
– Как узнали? (3-1=2)
На доске запись 3 2
– Какой знак поставим между цифрами? (>)
– Сколько репок? (2)
– Сколько морковок? (3)
– Какой знак поставим между цифрами? (<)
– Это неравенство.
Физминутка.
IV. Закрепление изученного материала.
Работа в учебнике.
– Прочитайте название темы в учебнике. (Равенство. Неравенство.)
– Посмотрите, с какой стороны написаны равенства? (Слева.) Прочитайте.
– С какой стороны в учебнике написаны неравенства? (Справа.) Прочитайте.
V. Рефлексия.
– С какой темой урока вы сегодня познакомились?
– Какой математический знак используется при записи равенства?
– Какие знаки при записи неравенства?
Формулы основных неравенств
Формулы универсальных неравенств
Универсальные неравенства выполняются при любых значениях входящих в них величин. Ниже перечислены основные виды универсальных неравенств.
1) ; .Доказательство. .
2) .Доказательство. Первое неравенство доказано в пункте 1). Доказываем второе..
3) Равенство имеет место только при .
Доказательство. Докажем, что , где . При имеем:. Применяем метод индукции. Пусть . Тогда.
4) Неравенство Коши — Буняковского Равенство имеет место тогда и только тогда, когда для всех и некоторых .
5) Неравенство Минковского, при
Формулы выполнимых неравенств
Выполнимые неравенства выполняются при определенных значениях входящих в них величин.
1) Неравенство Бернулли:;. В более общем виде:, где , числа одного знака и больше, чем .Лемма Бернулли:. См. «Доказательства неравенств и леммы Бернулли».
2) при .
3) Неравенство Чебышева при и . При и .
4) Обобщенные неравенства Чебышева при и и натуральном. При и .
Тождества
Тождеством называют равенство, которое будет верно при всех допустимых значениях тех переменных, которые входят в задание. Тождества могут быть представлены как буквенные или числовые равенства.
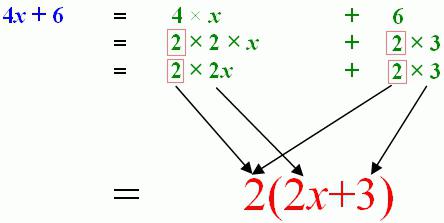
Тождественно равными называются выражения, содержащие в обеих частях равенства неизвестную переменную, которая способна приравнять две части одного целого.
Если проводить замены одного выражения другим, которое будет равно ему, тогда речь идет о тождественном преобразовании. В этом случае можно воспользоваться формулами сокращенного умножения, законами арифметики и прочими тождествами.
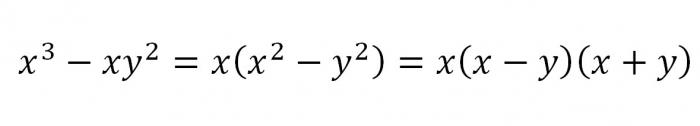
Чтобы сократить дробь, нужно провести тождественные преобразования. К примеру, дана дробь. Чтобы получить результат, следует воспользоваться формулами сокращенного умножения, разложением на множители, упрощением выражений и сокращением дробей.

При этом стоит учесть, что данное выражение будет тождественным тогда, когда знаменатель не будет равен 3.
Коды знаков неравенств
| Символ | Изображение | Юникод | Русское название | HTML | LaTeX | |||
|---|---|---|---|---|---|---|---|---|
| Код | Название | Шестнадцатеричное | Десятеричное | Мнемоника | ||||
| < | <{\displaystyle <} | U+003C | Less-than sign | Меньше | < | < | < | <, \textless |
| > | >{\displaystyle >} | U+003E | Greater-than sign | Больше | > | > | > | >, \textgreater |
| ⩽ | ⩽{\displaystyle \leqslant } | U+2A7D | Less-than or slanted equal to | Меньше либо равно | ⩽ | ⩽ | отсутствует | \leqslant |
| ⩾ | ⩾{\displaystyle \geqslant } | U+2A7E | Greater-than or slanted equal to | Больше либо равно | ⩾ | ⩾ | отсутствует | \geqslant |
| ≤ | ≤{\displaystyle \leq } | U+2264 | Less-than or equal to | Меньше либо равно | ≤ | ≤ | ≤ | \le, \leq |
| ≥ | ≥{\displaystyle \geq } | U+2265 | Greater-than or equal to | Больше либо равно | ≥ | ≥ | ≥ | \ge, \geq |
| ≪ | ≪{\displaystyle \ll } | U+226A | Much less-than | Много меньше | ≪ | ≪ | \ll | |
| ≫ | ≫{\displaystyle \gg } | U+226B | Much greater-than | Много больше | ≫ | ≫ | \gg |
Оценка значений выражений
Если известны пределы, в которых может изменяться переменная, то можно найти оценку значения выражения, в которое оно входит.
Пример. Известно, что 43 <v< 47. Оцените значение выражения 3v + 9.
Решение. Умножим каждую часть исходного неравенства на 3:
43 <v< 47
3•43 < 3•v< 3•47
129 < 3v<141
Далее добавим к неравенству девятку:
129 + 9 < 3v + 9 < 141 + 9
138 < 3v + 9 < 150
Получили оценку выражения 3v + 9, которую и требовалось найти
Ответ: 138 < 3v + 9 < 150.
Пример. Сторона квадрата может принимать значения от 16 до 21 см. Оцените величину площади этого квадрата.
Решение. Обозначим сторону квадрата буквой a. Тогда можно записать двойное неравенство
16⩽ а ⩽ 21
Знак «меньше или равно» используется из-за того, что по условию сторона квадрата может в точности равняться значению 16 или 21 см. Площадь квадрата (обозначим ее как S) равна а2. Запишем неравенство из условия дважды, после чего перемножим эти неравенства:
16⩽ а ⩽21
16⩽ а ⩽21
16•16⩽ а•а⩽21•21
256⩽ а2⩽441
Получили оценку для а2, а значит, и для площади S. Отметим, что при решении задач необязательно два раза писать одно и то же неравенство, чтобы потом их перемножать.
Ответ: 256 ⩽S⩽ 441
Пример. Пете надо купить 2 килограмма бананов и пакет молока. Он точно знает, что пакет молока стоит в разных магазинах от 65 до 80 рублей, а стоимость килограмма бананов колеблется от 54 до 69 рублей. Помогите Пете оценить, сколько денег он потратит в магазине.
Решение. Обозначим буквой h стоимость килограмма бананов, а через k – цену пакета молока. Затраты Пети составят 2h + k, при этом можно написать следующие оценки:
54 <h< 69
65 <k< 80
Оценим величину 2h
2•54 < 2h< 2•69
108 < 2h< 138
Сложим получившееся неравенство с 65 <k< 80:
108 + 65 < 2h + k< 138 + 80
173 < 2h + k< 218
Ответ: Петя потратит от 173 до 218 рублей.