Концепции InfluxDB
В этом разделе будут объяснены ключевые концепции InfluxDB и ключевые запросы, связанные с этими концепциями. InfluxDB встраивает свой собственный язык запросов и это заслуживает отдельного пояснения.
Язык запросов InfluxDB
Прежде чем начать, важно знать, какую версию InfluxDB вы используете в настоящее время. По состоянию на октябрь 2019 года InfluxDB выпускается в двух версиях: v1.7+ и v2.0
InfluxDB v2.0 в настоящее время (на октябрь 2019 года) является альфа-версией и использует язык Flux. InfluxDB v1.7 оснащён языком InfluxQL (а также Flux, если его активировать). Пока лучше использовать InfluxQL, так как Flux не полностью установлен в текущей версии платформы.
InfluxQL — это язык запросов, который очень похож на SQL, и позволяет любому пользователю запрашивать свои данные и фильтровать их. Вот пример запроса InfluxQL:
Дальше будут рассмотрены ключевые концепции InfluxDB, предоставляемые с соответствующими запросами IQL (InfluxQL).
Мода выборки
Иногда важно знать не среднее арифметическое выборки, а то, какая из ее вариант встречается наиболее часто. Так, при управлении магазином одежды менеджеру не важен средний размер продаваемых футболок, а необходима информация о том, какие размеры наиболее популярны
Для этого используется такой показатель, как мода выборки.
В примере с математическим тестом сразу 3 ученика набрали по 13 баллов, а частота всех других вариант не превысила 2, поэтому мода выборки равна 13. Возможна ситуация, когда в ряде есть сразу две или более вариант, которые встречаются одинаково часто и чаще остальных вариант. Например, в ряде
1, 2, 3, 3, 3, 4, 5, 5, 5
варианты 3 и 5 встречаются по три раза. В таком случае ряд имеет сразу две моды – 3 и 5, а всю выборку именуют мультимодальной. Особо выделяется случай, когда в выборке все варианты встречаются с одинаковой частотой:
6, 6, 7, 7, 8, 8.
Здесь числа 6, 7 и 8 встречаются одинаково часто (по два раза), а другие варианты отсутствуют. В таких случаях говорят, что ряд не имеет моды.
Сходимость числовых рядов
Одной из ключевых задач темы является исследование ряда на сходимость. При этом возможны два случая:
1) Ряд расходится. Это значит, что бесконечная сумма равна бесконечности: либо суммы вообще не существует, как, например, у ряда (вот, кстати, и пример ряда с отрицательными членами). Хороший образец расходящегося числового ряда встретился в начале урока: . Здесь совершенно очевидно, что каждый следующий член ряда больше, чем предыдущий, поэтому и, значит, ряд расходится. Ещё более тривиальный пример: .
2) Ряд сходится. Это значит, что бесконечная сумма равна некоторому конечному числу : . Пожалуйста: – этот ряд сходится и его сумма равна нулю. В качестве более содержательного примера можно привести бесконечно убывающую геометрическую прогрессию, известную нам ещё со школы: . Сумма членов бесконечно убывающей геометрической прогрессии рассчитывается по формуле: , где – первый член прогрессии, а – её основание, которое, как правило, записывают в виде правильной дроби. В данном случае: , . Таким образом: Получено конечное число, значит, ряд сходится, что и требовалось доказать.
Однако в подавляющем большинстве случаев найти сумму ряда не так-то просто, и поэтому на практике для исследования сходимости ряда используют специальные признаки, которые доказаны теоретически.
Существует несколько признаков сходимости ряда: необходимый признак сходимости ряда, признаки сравнения, признак Даламбера, признаки Коши, признак Лейбница и некоторые другие признаки. Когда какой признак применять? Это зависит от общего члена ряда , образно говоря – от «начинки» ряда. И очень скоро мы всё разложим по полочкам.
! Для дальнейшего усвоения урока необходимо хорошо понимать, что такое предел и хорошо уметь раскрывать неопределенность вида . Для повторения или изучения материала обратитесь к статье Пределы. Примеры решений.
Размах выборки
Следующий важная характеристика ряда данных – это размах выборки.
Если выборка представлена в виде упорядоченного ряда данных, то достаточно вычесть из последнего числа ряда первое число. Так, размах выборки результатов теста в классе равен:
25 – 12 = 13,
так как самые лучшие ученики смогли решить все 25 заданий, а наихудший учащийся ответил правильно только на 13 вопросов.
Размах выборки характеризует стабильность, однородность исследуемых свойств. Например, пусть два спортсмена-стрелка в ходе соревнований производят по 5 выстрелов по круговой мишени, где за попадание начисляют от 0 до 10 очков. Первый стрелок показал результаты 8, 9, 9, 8, 9 очков. Второй же спортсмен в своих попытках показал результаты 7, 10, 10, 6, 10. Средние арифметические этих рядов равны:
(8+9+9+8+9):5 = 43:5 = 8,6;
(7+10+10+6+10):5 = 43:5 = 8,6.
Получается, что в среднем оба стрелка стреляют одинаково точно, однако первый спортсмен демонстрирует более стабильные результаты. У его выборки размах равен
9 – 8 = 1,
в то время как размах выборки второго спортсмена равен
10 – 6 = 4.
Размах выборки может быть очень важен в метеорологии. Например, в Алма-Ате и Амстердаме средняя температура в течение года почти одинакова и составляет 10°С. Однако в Алма-Ате в январе и феврале иногда фиксируются температуры ниже -30°С, в то время как в Амстердаме за всю историю наблюдений она никогда не падала ниже -20°С.
Ошибки в статистике
Статистика является очень мощным инструментом для исследований во всех областях человеческой деятельности. Однако иногда ее иронично называют самой точной из лженаук. Известно и ещё одно высказывание, приписываемое политику Дизраэли, согласно которому существует просто ложь, наглая ложь и статистика. С чем же связана такая репутация этой дисциплины?
Дело в том, что некоторые люди и организации часто манипулируют данными статистики, чтобы убедить других в своей правоте или преимуществах товара, которые они продают. Требуются определенные навыки, чтобы правильно пользоваться статистикой. Одна из самых распространенных ошибок – это неправильный выбор выборки.
В 1936 году перед президентскими выборами в США был проведен телефонный опрос, который показал, что с большим преимуществом победу должен одержать Альфред Лендон. Однако на выборах Франклин Рузвельт набрал почти вдвое больше голосов. Ошибка была связана с тем, что в те годы телефон могли позволить себе только богатые люди, которые в большинстве своем поддерживали Лендона. Однако бедные люди (а их, конечно же, больше, чем богатых) голосовали за Рузвельта.
Ещё один пример – это агитация в конце XIX века в США к службе на флоте. Пропагандисты в своей рекламе указывали, что, согласно статистике, смертность на флоте во время войны (испано-американской) составляет 0,09%, в то время как среди населения Нью-Йорка она равнялась 0,16%. Получалось, что служить на флоте в военное время безопаснее, чем жить мирной жизнью. Однако на самом деле причина таких цифр заключается в том, что во флот всегда отбирали молодых мужчин с хорошим здоровьем, которые не могли умереть от «старческих» болезней, в то время как в население Нью-Йорка входят больные и старые люди.
При указании среднего значения исследователь может использовать разные характеристики – среднее арифметическое, медиана, мода. При этом почти всегда среднее арифметическое несколько больше медианы. Именно поэтому большинство людей, узнающих о средней зарплате в стране, удивляются, так как они столько не зарабатывают. Правильнее ориентироваться на медианную зарплату.
Ну и наконец, нельзя забывать, что любая статистика может показать только корреляцию между двумя величинами, но это не всегда означает причинно-следственную связь. Так, известно, что чем больше в городе продается мороженого, тем больше в это же время людей тонет на пляжах. Означает ли это, что поедание мороженого увеличивает риск во время плавания? Нет. Дело в том, что оба этих показателя, продажи мороженого и количество утонувших, зависят от третьей величины – температуры в городе. Чем жарче на улице, тем большее количество людей ходят на пляж и тем больше мороженого продается в магазинах.
Создание диаграммы
Созданная в PowerPoint диаграмма используется как медиафайл, который можно динамически изменять в любой момент. Это крайне удобно. Подробности настройки таких объектов будут ниже, а для начала нужно рассмотреть способы, позволяющие создать диаграмму в PowerPoint.
Способ 1: Вставка в область текста
Самый быстрый и простой способ создания диаграммы в новом слайде.
- При создании нового слайда по умолчанию производится стандартная разметка – один заголовок и одна область для текста. Внутри рамки находятся 6 иконок для быстрой вставки разных объектов – таблиц, картинок и так далее. Вторая иконка слева в верхнем ряду как раз и предлагает добавление диаграммы. Остается лишь нажать на нее.
-
Появится стандартное окно создания диаграммы. Здесь все разделяется на три основные зоны.
- Первая – это левая сторона, на которой размещены все виды доступных диаграмм. Здесь потребуется выбрать, что именно требуется создать.
- Вторая – это стиль графического отображения. Это не несет никакого функционального значения, выбор определяется либо регламентом мероприятия, для которого создается презентация, либо собственными предпочтениями автора.
- Третья демонстрирует общий итоговый вид графика перед его вставкой.
- Остается нажать «ОК», чтобы диаграмма была создана.
Стоит отметить, что этот способ позволяет быстро создавать нужные компоненты, однако это занимает всю область текста и после окончания слотов метод уже недоступен.
Способ 2: Классическое создание
График можно добавить и классическим способом, доступным в программе Microsoft PowerPoint с момента ее появления.
- Нужно зайти во вкладку «Вставка», которая расположена в шапке презентации.
Затем понадобится нажать на соответствующую иконку «Диаграмма».
Дальнейшая процедура создания схожа с вышеописанным методом.
Стандартный способ, который позволяет создавать диаграмму без каких-либо других проблем.
Способ 3: Вставка из Excel
Ничто не запрещает вставить этот компонент, если он ранее был создан в Excel. Тем более, если к диаграмме привязана соответствующая таблица значений.
- Там же, во вкладке «Вставка», требуется нажать кнопку «Объект».
В открывшемся окне нужно выбрать слева вариант «Создать из файла», после чего нажать кнопку «Обзор…», либо ввести путь к нужному листу Excel вручную.
Имеющаяся там таблица и диаграммы (либо только один вариант, если второго нет) будет добавлена на слайд.
Здесь важно добавить, что при таком варианте также можно настроить связывание. Это делается перед вставкой – после выбора нужного листа Excel можно поставить под строкой адреса в этом окне галочку в пункте «Связать».
Данный пункт позволит соединить вставленный файл и оригинал. Теперь любые изменения в исходном Excel будут автоматически применяться и для вставленного в PowerPoint компонента. Это касается как внешнего вида и формата, так и значений.
Этот способ удобен тем, что позволяет вставить как таблицу, так и ее диаграмму неотрывно. Также во многих случаях корректировка данных в Excel может оказаться проще.
Вариационный ряд
nnранжированиеx1, x2, …, xnxiвариантойmixiwiminx,xinimax
Таблица 1. Общий вид дискретного вариационного ряда частот
| Значения признака | xi | x1 | x2 | … | xn |
| Частоты | mi | m1 | m2 | … | mn |
Таблица 2. Общий вид интервального вариационного ряда частот
| Интервалы | ai – ai+1 | a1 – a2 | a2 – a3 | … | ak – ak+1 |
| Частоты | mi | m1 | m2 | … | mn |
Таблица 3. Графические изображения вариационного ряда
| Ряд | Полигон или гистограмма | Кумулята | Эмпирическая функция распределения |
| Дискретный | |||
| Интервальный |
ai – ai+1 iximi
В табл. 2.3 (Группировка населения России по размеру среднедушевого дохода в апреле 1994г.) представлен интервальный вариационный ряд.
Удобно ряды распределения анализировать при помощи графического изображения, позволяющего судить и о форме распределения. Наглядное представление о характере изменения частот вариационного ряда дают полигон и гистограмма.
Полигон используется при изображении дискретных вариационных рядов.
Изобразим, например графически распределение жилого фонда по типу квартир, (табл. 2.10).
Таблица 2.10 — Распределение жилого фонда городского района по типу квартир (цифры условные).
| N п/п | Группы квартир по числу комнат | Число квартир, тыс.ед. |
| 1 | 1 | 10 |
| 2 | 2 | 35 |
| 3 | 3 | 30 |
| 4 | 4 | 15 |
| 5 | 5 | 5 |
| ВСЕГО | 95 |
Рис. Полигон распределения жилого фонда
Гистограмма принимается для изображения интервального вариационного ряда
| N п/п | Группы семей по размеру жилой площади, приходящейся на одного человека | Число семей с данным размером жилой площади | Накопленное число семей |
| 1 | 3 – 5 | 10 | 10 |
| 2 | 5 – 7 | 20 | 30 |
| 3 | 7 – 9 | 40 | 70 |
| 4 | 9 – 11 | 30 | 100 |
| 5 | 11 – 13 | 15 | 115 |
| ВСЕГО | 115 | —- |
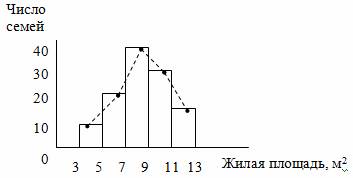Рис. 2.2. Гистограмма распределения семей по размеру жилой площади, приходящейся на одного человека
кумуляту распределения.
Рис. 2.3. Кумулята распределения семей по размеру жилой площади, приходящейся на одного человека
огиву
| N п/п | Группы предприятий по числу занятых, чел. | Число предприятий | Величина интервала, чел. | Плотность распределения |
| А | 1 | 2 | 3=1/2 | |
| 1 | До 20 | 15 | 20 | 0,75 |
| 2 | 20 – 80 | 27 | 60 | 0,25 |
| 3 | 80 – 150 | 35 | 70 | 0,5 |
| 4 | 150 – 300 | 60 | 150 | 0,4 |
| 5 | 300 – 500 | 10 | 200 | 0,05 |
| ВСЕГО | 147 | —- | —- |
Для графического изображения вариационных рядов может также использоваться кумулятивная кривая. При помощи кумуляты (кривой сумм) изображается ряд накопленных частот. Накопленные частоты определяются путём последовательно суммирования частот по группам и показывают, сколько единиц совокупности имеют значения признака не больше, чем рассматриваемое значение.
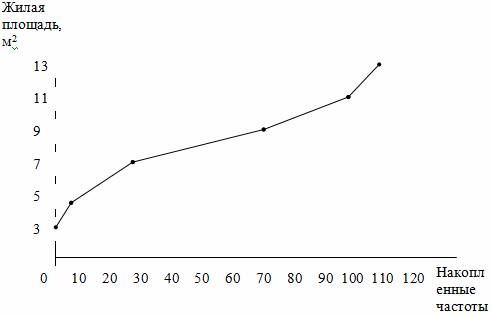Рис. 2.4. Огива распределения семей по размеру жилой площади, приходящейся на одного человека
При построении кумуляты интервального вариационного ряда по оси абсцисс откладываются варианты ряда, а по оси ординат накопленные частоты.
Специфичные концепции баз данных временных рядов
Кроме высокой скорости приёма, базы данных временных рядов вводят специфичные для этих технологий концепции.
Одной из них является организация хранения данных. В традиционной РБД данные хранятся до тех пор, пока вы не решите их удалить. Учитывая сценарии использования БД временных рядов, вы можете не хранить ваши данные слишком долго: это или слишком дорого, или данные со временем теряют актуальность.
Системы вроде InfluxDB могут позаботиться об удалении данных через определённое время, используя концепцию, называемую политикой хранения. Вы также можете выполнять непрерывные запросы к оперативным данным для выполнения определённых операций. В реляционной БД можно найти эквивалентные операции (например «задания» в SQL), которые могут выполняться по заданному расписанию.
Совершенно другая экосистема
Особенности БД временных рядов хорошо видны, когда речь заходит об их экосистемах. Как правило, реляционные базы данных окружены приложениями, которые подключаются к ним для получения информации или добавления новых записей.
Часто база данных ассоциируется с одной системой. Клиенты подключаются к веб-сайту, который обращается к базе данных для получения информации. БД временных рядов созданы под множество клиентов (программ). Здесь нет простого сервера, обращающегося к БД, но есть куча разных сенсоров (к примеру), выполняющих вставку данных одновременно.
Как следствие, её инструменты были разработаны для того, чтобы предоставить эффективные способы потребления или производства данных.
Потребление данных
Потребление данных часто осуществляется с помощью инструментов мониторинга вроде Grafana или Chronograf. Эти клиенты имеют встроенные решения для визуализации данных и даже для создания пользовательских предупреждений.
Эти инструменты часто используются для создания живых панелей мониторинга, которые могут быть представлены графиками, гистограммами, датчиками или картами окружающего мира.
Производство данных
Производство данных осуществляется агентами, которые нацеливаются на специальные элементы в инфраструктуре и извлекают из них метрики. Такие агенты называются «агентами мониторинга». Вы можете легко настроить их для запроса данных за определённый промежуток времени. Примерами являются Telegraf (который является официальным агентом мониторинга), CollectD или StatsD.
Теперь вы лучше понимаете, что такое базы данных временных рядов и чем они отличаются от реляционных. Пришло время углубиться в конкретные концепции InfluxDB.
Понятие числового ряда
В общем виде числовой ряд можно записать так: .
Здесь:– математический значок суммы; – общий член ряда (запомните этот простой термин); – переменная-«счётчик». Запись обозначает, что проводится суммирование от 1 до «плюс бесконечности», то есть, сначала у нас , затем , потом , и так далее – до бесконечности. Вместо переменной иногда используется переменная или . Суммирование не обязательно начинается с единицы, в ряде случаев оно может начинаться с нуля , с двойки либо с любого натурального числа.
В соответствии с переменной-«счётчиком» любой ряд можно расписать развёрнуто: – и так далее, до бесконечности.
Cлагаемые – это ЧИСЛА, которые называются членами ряда. Если все они неотрицательны (больше либо равны нулю), то такой ряд называют положительным числовым рядом.
Пример 1
Записать первые три члена ряда
Это уже, кстати, «боевое» задание – на практике довольно часто требуется записать несколько членов ряда.
Сначала , тогда:
Затем , тогда:
Потом , тогда:
Процесс можно продолжить до бесконечности, но по условию требовалось написать первые три члена ряда, поэтому записываем ответ:
Обратите внимание на принципиальное отличие от числовой последовательности,в которой члены не суммируются, а рассматриваются как таковые. Пример 2
Пример 2
Записать первые три члена ряда
Это пример для самостоятельного решения, ответ в конце урока
Даже для сложного на первый взгляд ряда не составляет трудности расписать его в развернутом виде:
Пример 3
Записать первые три члена ряда
На самом деле задание выполняется устно: мысленно подставляем в общий член ряда сначала , потом и . В итоге:
Ответ оставляем в таком виде, полученные члены ряда лучше не упрощать, то есть не выполнять действия: , , . Почему? Ответ в виде гораздо проще и удобнее проверять преподавателю.
Иногда встречается обратное задание
Пример 4
Записать сумму в свёрнутом виде с общим членом ряда
Здесь нет какого-то четкого алгоритма решения, закономерность нужно просто увидеть.
В данном случае: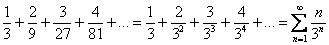
Для проверки полученный ряд можно «расписать обратно» в развернутом виде.
А вот пример чуть сложнее для самостоятельного решения:
Пример 5
Записать сумму в свёрнутом виде с общим членом ряда
Выполнить проверку, снова записав ряд в развернутом виде
5 4 3 2 XI
Обычно
диаграммы в отрезках строят для дискретно
заданных признаков при
небольшом числе вариантов.
Гистограмма
— это график в виде ступенчатой фигуры
из примыкающих друг
к другу прямоугольников, основаниями
которых являются интервалы значений
признаков, а высоты прямоугольников
пропорциональны частоте
или частости ( количеству объектов,
попавших в интервал ). Площади
прямоугольников соответствуют численности
групп, в данном интервале.
Гистограммы
— это графики интервальных рядов. Их
строят преимущественно
для больших объемов совокупностей.
Пример:
Гистограмма нормального распределения
эритроцитов в крови человека.
По горизонтали — диаметр
клеток хi(мк),
по вертикали — частота ni
числа клеток
в интервале.
ni
2
4 6 8 10 12 xi
Полигон
(многоугольник) частот
— график ряда, представленный ломаной
линией
точки — вершины которой соответствуют
серединам интервалов, а высота точки
над горизонталью пропорциональна
частоте или частости.
Полигоны
строят для непрерывных и дискретных
вариационных рядов в тех
случаях, когда в интервалах выделены
средние значения признака. Полигоны
предпочтительнее
гистограмм при
непрерывных рядах распределения
Пример:
полигон
частот на основе гистограммы
распределения эритроцитов
в крови человека.
ni
2
4 6 8 10 12 xi
Вариационная
(частотная) кривая
— график ряда, полученный при условии,
что объем совокупности, стремится к
бесконечности ( N→∞
),
а длина самого
интервала стремится к нулю ( Δх→0
).
Для
практических статистических расчетов
в качестве стандартов выделено четыре
группы частотных распределений:
-
Прямоугольное
распределение. -
Колоколообразное
унимодальное (одновершинное)
распределение. -
Бимодальное
(двухвершинное) распределение. -
Экспоненциальное
распределение:
-
нарастающее,
-
убывающее.
ni
xi
xi
xi
xi
Прямоугольному
распределению подчиняются случайные
равновероятные
события.
Колоколообразному
симметричному распределению
подчиняется широкий класс
явлений ( показатели умственного
и физического развития, рост,
масса, и др ).
На практике наиболее часто встречается
симметричное унимодальное распределение,
поэтому его классическая форма называется
нормальным распределением.
Бимодальному
распределению соответствует, например
успеваемость
студентов имеющих и
не имеющих большого перерыва в учебе.
Экспоненциально
убывающему распределению
соответствует распределение
доходов в капиталистическом
обществе, ( частота
убывает при возрастании дохода
).
Алгебра 9 класс
«Системы уравнений второй степени» — Решение систем, содержащих уравнения второй степени. Закрепление. Тема урока. Повторение. Оборудование. Алгоритм решения системы двух уравнений с двумя переменными методом подстановки. Цели урока. Объяснение нового материала. Алгоритм решения системы двух уравнений с двумя переменными методом алгебраического сложения. План урока. Активизация знаний учащихся.
«Геометрическая вероятность» — Точка. Серия опытов. Решение тренировочных задач. Квадрат. Тетрадный лист. Формулы геометрической вероятности. Стрелка. Оконная решетка. Отрезок. Вероятность. Геометрическая вероятность. Зажмурим глаза. Круг. Мяч. Геометрическое определение вероятности. Понятие вероятности с геометрией.
«Алгоритм решения неравенств» — Алгоритм решения неравенств. Простейшее линейное неравенство. Функция. Ось. Рассмотрим дискриминант. Теперь решим квадратное неравенство. Задача. Решение неравенств. Случай. Множество решений. Неравенства. Решим неравенство методом интервалов. Решение неравенства.
««Графики функций» 9 класс» — Установите соответствие. Тренажер. Цели урока. Заполните пропуски. Выберите уравнение, с помощью которого задана линейная функция. Большему значению аргумента соответствует большее значение функции. Практикум. Нули функции. Обратная пропорциональность. Определение. Выберите уравнение. Функции и их графики. Линейная функция и ее график. Для какой из линейных функций нет соответствующего графика. Укажите области определения.
««Квадратичная функция» 9 класс» — График и свойства функции y=ax2. Функция y=x2. Y=a(x-m)2 + n. Способы построения графика квадратичной функции. Свойства функции. Квадратичная функция. Свойства у = ах2 при а > 0. Схема построения графика квадратичной функции. Сдвиг графика функции y = ax2 вдоль осей координат. Схема построения параболы. График. Функция y=ax2. График функции. Ветви параболы направлены вверх. Свойства у = ах2 при а < 0.
«Прогрессии в жизни» — В верхней строчке написана арифметическая прогрессия с разностью 1. Прогрессии в банковских расчетах. Архимед нашел сумму бесконечной геометрической прогрессии. Прогрессии в банковских расчетах и в промышленности. Два тела движутся навстречу одно другому из двух мест. 100 летучих семян. Разность квадратов двух чисел Фибоначчи. Задачи на применение прогрессий встречаются в старых учебниках. Определения.
«Алгебра 9 класс»
Расчет моды
Теперь посмотрим, как рассчитать моду. Мода – это то значение в анализируемой совокупности данных, которое встречается чаще других, поэтому нужно посмотреть на частоты значений и отыскать максимальное из них. Например, в наборе данных 3, 4, 6, 7, 3, 5, 3, 4 модой будет значение 3 – повторяется чаще остальных. Это в дискретном ряду, и здесь все просто. Если данных много, то моду легче всего найти с помощью соответствующей гистограммы. Бывает так, что совокупность данных имеет бимодальное распределение.
Без диаграммы очень трудно понять, что в данных не один, а два центра. К примеру, на президентских выборах предпочтения сельских и городских жителей могут отличаться. Поэтому распределение доли отданных голосов за конкретного кандидата может быть «двугорбым». Первый «горб» – выбор городского населения, второй – сельского.
Немного сложнее с интервальными данными, когда вместо конкретных значений имеются интервалы. В этом случае говорят о модальном интервале (при анализе доходов населения, например), то есть интервале, частота которого максимальна относительно других интервалов. Однако и здесь можно отыскать конкретное модальное значение, хотя оно будет условным и примерным, так как нет точных исходных данных. Представим, что есть следующая таблица с распределением цен.
Для наглядности изобразим соответствующую диаграмму.
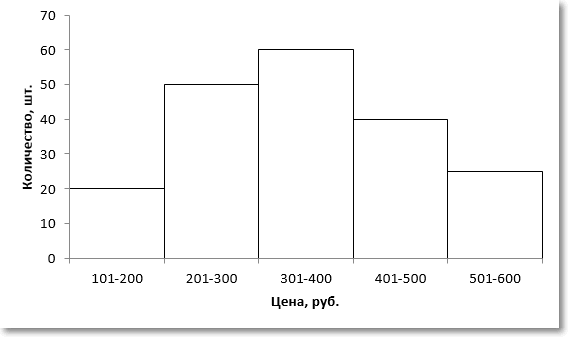
Требуется найти модальное значение цены.
Вначале нужно определить модальный интервал, который соответствует интервалу с наибольшей частотой. Найти его так же легко, как и моду в дискретном ряду. В нашем примере это третий интервал с ценой от 301 до 400 руб. На графике – самый высокий столбец. Теперь нужно определить конкретное значение цены, которое соответствует максимальному количеству. Точно и по факту сделать это невозможно, так как нет индивидуальных значений частот для каждой цены. Поэтому делается допущение о том, что интервалы выше и ниже модального в зависимости от своей частоты имеют разные вес и как бы перетягивают моду в свою сторону. Если частота интервала следующего за модальным больше, чем частота интервала перед модальным, то мода будет правее середины модального интервала и наоборот. Давайте еще раз посмотрим на рисунок, чтобы понять формулу, которую я напишу чуть ниже.
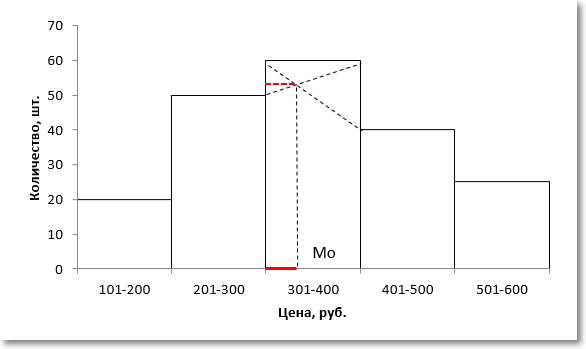
На рисунке отчетливо видно, что соотношение высоты столбцов, расположенных слева и справа от модального определяет близость моды к левому или правому краю модального интервала. Задача по расчету модального значения состоит в том, чтобы найти точку пересечения линий, соединяющих модальный столбец с соседними (как показано на рисунке пунктирными линиями) и нахождении соответствующего значения признака (в нашем примере цены). Зная основы геометрии (7-й класс), по данному рисунку нетрудно вывести формулу расчета моды в интервальном ряду.
Формула моды имеет следующий вид.
Где Мо – мода,
x – значение начала модального интервала,
h – размер модального интервала,
fМо – частота модального интервала,
fМо-1 – частота интервала, находящего перед модальным,
fМо1 – частота интервала, находящего после модального.
Второе слагаемое формулы моды соответствует длине красной линии на рисунке выше.
Рассчитаем моду для нашего примера.
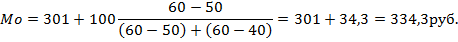
Таким образом, мода интервального ряда представляет собой сумму, состоящую из значения начального уровня модального интервала и отрезка, который определяется соотношением частот ближайших интервалов от модального.
