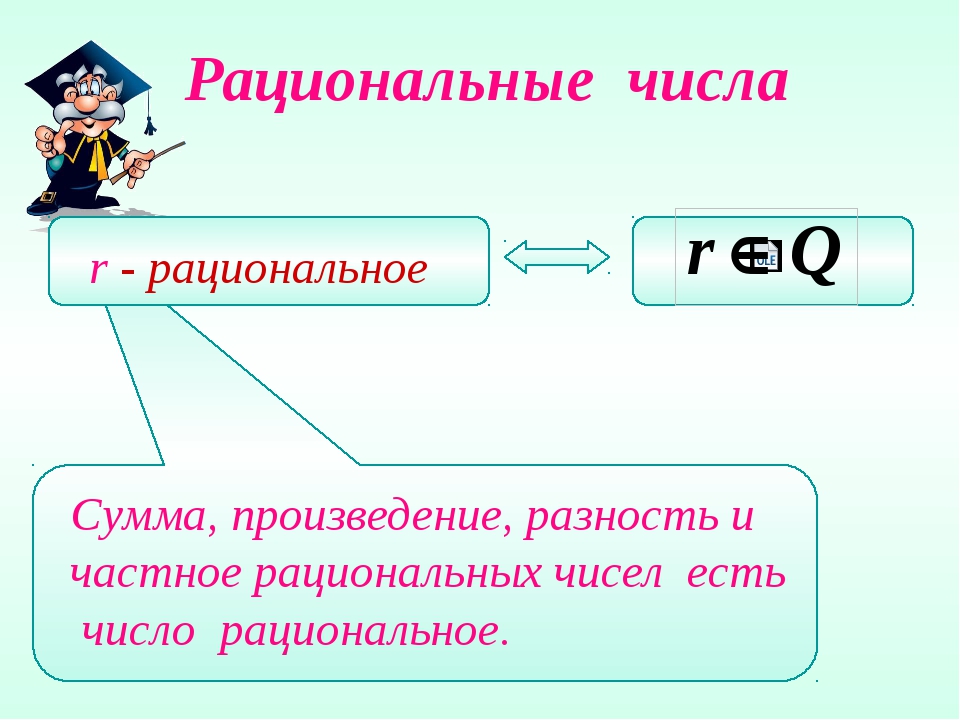
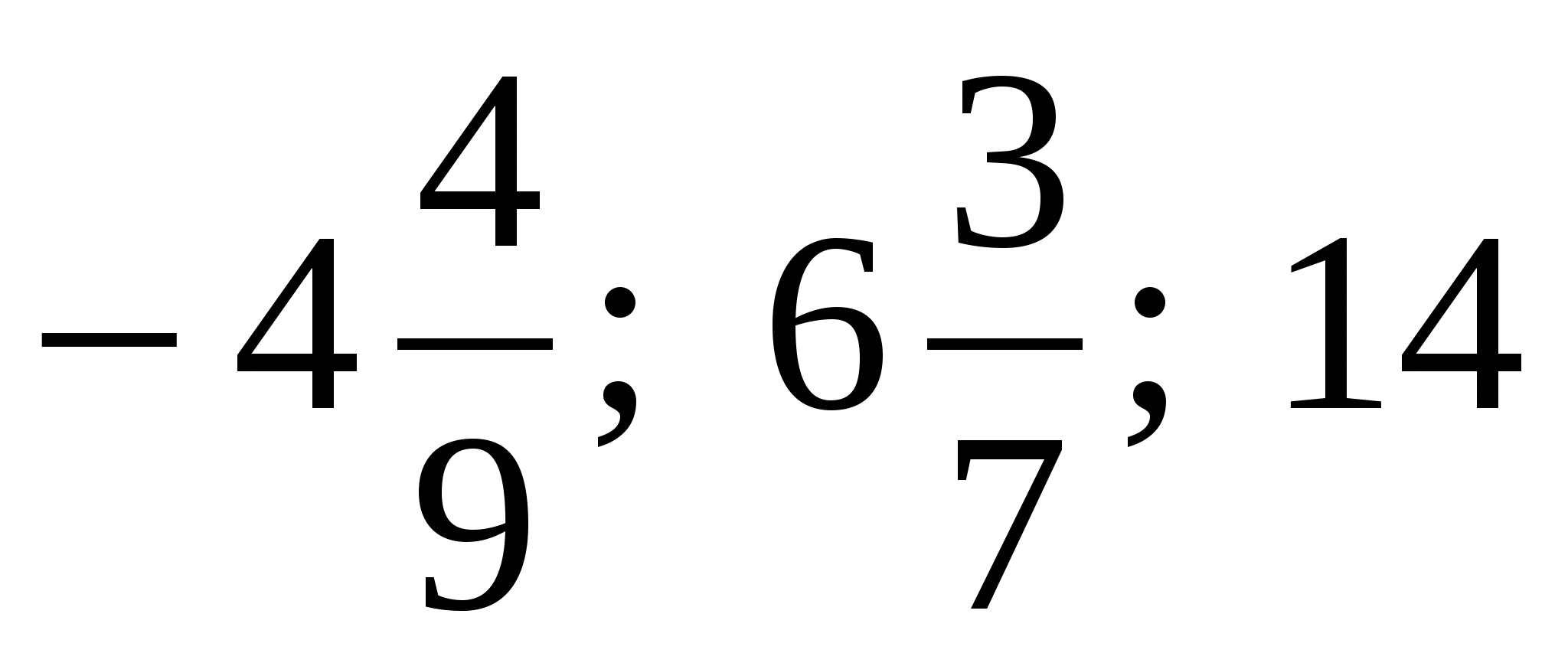Множество рациональных чисел
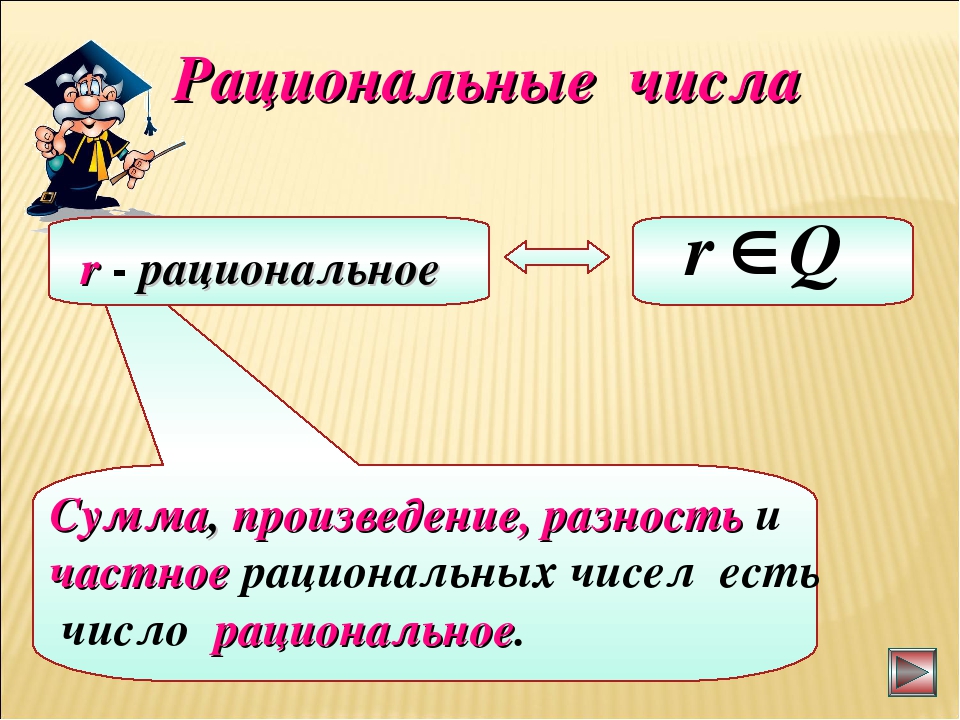
Множество рациональных чисел обозначается Q{\displaystyle \mathbb {Q} } (от лат. quotient, «частное») и может быть записано в таком виде:
- Q={mn∣m∈Z, n∈N}.{\displaystyle \mathbb {Q} =\left\{{\frac {m}{n}}\mid m\in \mathbb {Z} ,\ n\in \mathbb {N} \right\}.}
Другими словами, числитель (m) может иметь знак, а знаменатель (n) должен быть положительным целым числом.
При этом оказывается, что разные записи могут представлять одну и ту же дробь, например, 34{\displaystyle {\frac {3}{4}}} и 912{\displaystyle {\frac {9}{12}}}, (все дроби, которые можно получить друг из друга умножением или делением числителя и знаменателя на одно и то же натуральное число, представляют одно и то же рациональное число). Поскольку делением числителя и знаменателя дроби на их наибольший общий делитель можно получить единственное несократимое представление рационального числа, то можно говорить об их множестве как о множестве несократимых дробей со взаимно простыми целым числителем и натуральным знаменателем:
- Q={mn∣m∈Z, n∈N, gcd(m,n)=1}.{\displaystyle \mathbb {Q} =\left\{{\frac {m}{n}}\mid m\in \mathbb {Z} ,\ n\in \mathbb {N} ,\ \gcd(m,n)=1\right\}.}
Здесь gcd(m,n){\displaystyle \gcd(m,n)} — наибольший общий делитель чисел m{\displaystyle m} и n{\displaystyle n}.
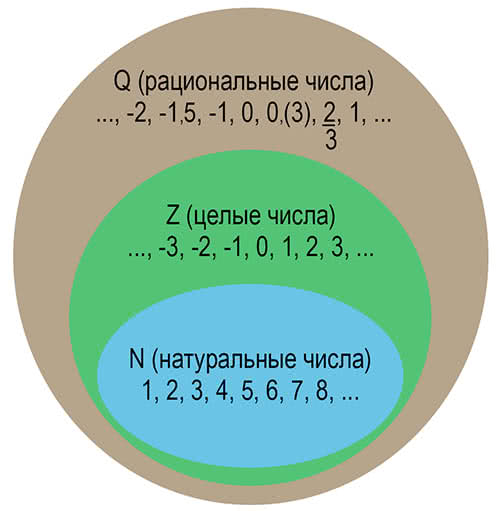
Множество рациональных чисел является естественным обобщением множества целых чисел. Легко видеть, что если у рационального числа a=mn{\displaystyle a={\frac {m}{n}}} знаменатель n=1{\displaystyle n=1}, то a=m{\displaystyle a=m} является целым числом.
Множество рациональных чисел располагается всюду плотно на числовой оси: между любыми двумя различными рациональными числами расположено хотя бы одно рациональное число (а значит, и бесконечное множество рациональных чисел). Тем не менее, оказывается, что множество рациональных чисел имеет счётную мощность (то есть все его элементы можно перенумеровать). Со времён древних греков известно о существовании чисел, не представимых в виде дроби: они доказали, что не существует рационального числа, квадрат которого равен двум. Недостаточность рациональных чисел для выражения всех величин привела в дальнейшем к понятию вещественного числа. В отличие от множества вещественных чисел (которое соответствует одномерному пространству), множество рациональных чисел имеет меру нуль.
Рациональные и иррациональные числа. Понятие о вещественных числах
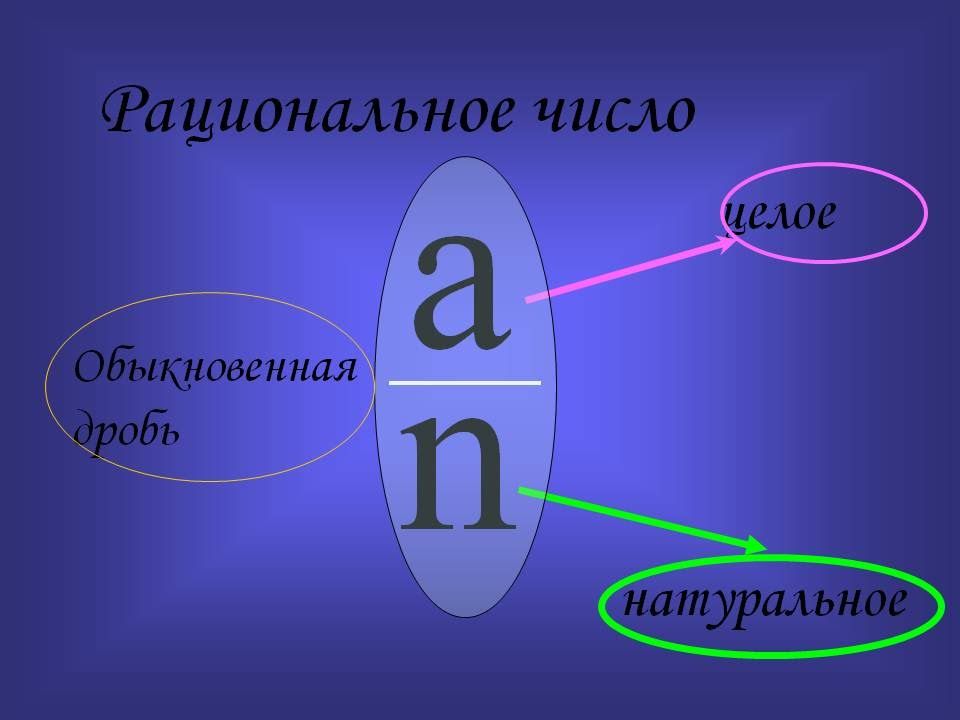
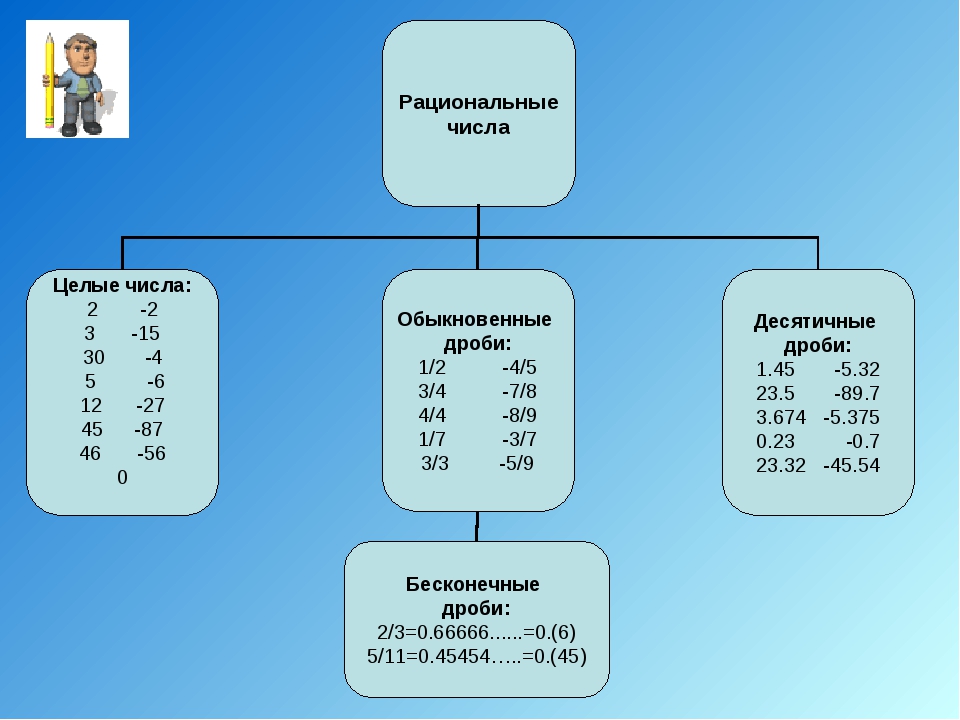
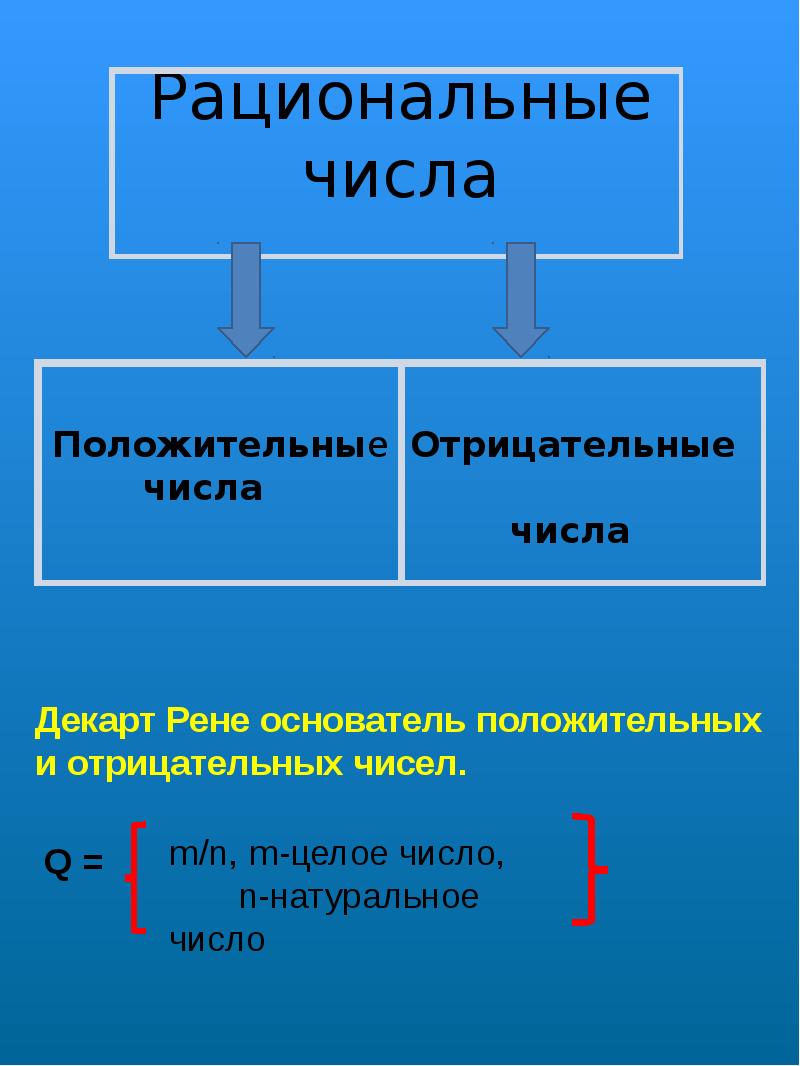
Целые числа и рациональные дроби (простые дроби и смешанные числа) составляют множество рациональных чисел, которое принято обозначать буквой Q .
Каждое из рациональных чисел можно представить в виде
,
где m – целое число, а n – натуральное число.
При получаются и бесконечные периодические десятичные дроби.
Числа

и т.п. являются примерами иррациональных чисел.
Иррациональные числа нельзя представить в виде дроби, числитель которой является целым числом, а знаменатель натуральным числом.
При обращении иррациональных чисел в десятичные дроби получаются бесконечные непериодические десятичные дроби. Множество иррациональных чисел бесконечно.
Множество рациональных и иррациональных чисел составляют множество вещественных (действительных) чисел.
Множество вещественных чисел обозначают буквой R .
Счётность множества

Нумерация положительных рациональных чисел
Чтобы оценить количество рациональных чисел, нужно найти мощность их множества. Легко доказать, что множество рациональных чисел счётно. Для этого достаточно привести алгоритм, который нумерует рациональные числа, то есть устанавливает биекцию между множествами рациональных и натуральных чисел.
Примером такого построения может служить следующий простой алгоритм. Составляется бесконечная таблица обыкновенных дробей, на каждой i{\displaystyle i}-ой строке в каждом j{\displaystyle j}-ом столбце которой располагается дробь ij{\displaystyle {\frac {i}{j}}}. Для определённости считается, что строки и столбцы этой таблицы нумеруются с единицы. Ячейки таблицы обозначаются (i,j){\displaystyle \left(i,j\right)}, где i{\displaystyle i} — номер строки таблицы, в которой располагается ячейка, а j{\displaystyle j} — номер столбца.
Полученная таблица обходится «змейкой» по следующему формальному алгоритму.
- Если текущее положение (i,j){\displaystyle \left(i,j\right)} таково, что i{\displaystyle i} — нечётное, а j=1{\displaystyle j=1}, то следующим положением выбирается (i+1,j){\displaystyle \left(i+1,j\right)}.
- Если текущее положение (i,j){\displaystyle \left(i,j\right)} таково, что i=1{\displaystyle i=1}, а j{\displaystyle j} — чётное, то следующим положением выбирается (i,j+1){\displaystyle \left(i,j+1\right)}.
- Если для текущего положения (i,j){\displaystyle \left(i,j\right)} сумма индексов (i+j){\displaystyle \left(i+j\right)} нечётна, то следующее положение — (i−1,j+1){\displaystyle \left(i-1,j+1\right)}.
- Если для текущего положения (i,j){\displaystyle \left(i,j\right)} сумма индексов (i+j){\displaystyle \left(i+j\right)} чётна, то следующее положение — (i+1,j−1){\displaystyle \left(i+1,j-1\right)}.
Эти правила просматриваются сверху вниз и следующее положение выбирается по первому совпадению.
В процессе такого обхода каждому новому рациональному числу ставится в соответствие очередное натуральное число. То есть дроби 11{\displaystyle 1/1} ставится в соответствие число 1, дроби 21{\displaystyle 2/1} — число 2, и т. д. Нужно отметить, что нумеруются только несократимые дроби. Формальным признаком несократимости является равенство единице наибольшего общего делителя числителя и знаменателя дроби.
Следуя этому алгоритму, можно занумеровать все положительные рациональные числа. Это значит, что множество положительных рациональных чисел Q+{\displaystyle \mathbb {Q} _{+}} счётно. Легко установить биекцию между множествами положительных и отрицательных рациональных чисел, просто поставив в соответствие каждому рациональному числу противоположное ему. Т. о. множество отрицательных рациональных чисел Q−{\displaystyle \mathbb {Q} _{-}} тоже счётно. Их объединение Q+∪Q−{\displaystyle \mathbb {Q} _{+}\cup \mathbb {Q} _{-}} также счётно по свойству счётных множеств. Множество же рациональных чисел Q=Q+∪Q−∪{}{\displaystyle \mathbb {Q} =\mathbb {Q} _{+}\cup \mathbb {Q} _{-}\cup \left\{0\right\}} тоже счётно как объединение счётного множества с конечным.
Разумеется, существуют и другие способы занумеровать рациональные числа. Например, для этого можно воспользоваться такими структурами как дерево Калкина — Уилфа, дерево Штерна — Броко или ряд Фарея.
Утверждение о счётности множества рациональных чисел может вызывать некоторое недоумение, так как на первый взгляд складывается впечатление, что оно гораздо обширнее множества натуральных чисел. На самом деле это не так и натуральных чисел хватает, чтобы занумеровать все рациональные.
Рациональные числа на координатной прямой
Координатную прямую мы рассматривали, когда изучали отрицательные числа. Напомним, что это прямая линия на которой лежат множество чисел. Выглядит следующим образом:

На этом рисунке приведен небольшой фрагмент координатной прямой от −5 до 5.
Отметить на координатной прямой целые числа вида 2, 0, −3 не составляет особого труда.
Намного интереснее дела обстоят с остальными числами: с обыкновенными дробями, смешанными числами, десятичными дробями и т.д. Эти числа лежат между целыми числами и этих чисел бесконечно много.
Например, отметим на координатной прямой рациональное число . Данное число располагается ровно между нулём и единицей

Попробуем понять, почему дробь вдруг расположилась между нулём и единицей.
Как уже говорилось выше, между целыми числами лежат остальные числа — обыкновенные дроби, десятичные дроби, смешанные числа и т.д. К примеру, если увеличить участок координатной прямой от 0 до 1, то можно увидеть следующую картину

Видно, что между целыми числами 0 и 1 лежат уже другие рациональные числа, которые являются знакомыми для нас десятичными дробями. Здесь же видна наша дробь , которая расположилась там же, где и десятичная дробь 0,5. Внимательное рассмотрение этого рисунка даёт ответ на вопрос почему дробь расположилась именно там.
Дробь означает разделить 1 на 2. А если разделить 1 на 2, то мы получим 0,5
Десятичную дробь 0,5 можно замаскировать и под другие дроби. Из основного свойства дроби мы знаем, что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то значение дроби не изменится.
Если числитель и знаменатель дроби умножить на любое число, например на число 4, то мы получим новую дробь , а эта дробь также как и равна 0,5
А значит на координатной прямой дробь можно расположить там же, где и располагалась дробь

Пример 2. Попробуем отметить на координатной рациональное число . Данное число располагается ровно между числами 1 и 2

Значение дроби равно 1,5
Если увеличить участок координатной прямой от 1 до 2, то мы увидим следующую картину:

Видно, что между целыми числами 1 и 2 лежат уже другие рациональные числа, которые являются знакомыми для нас десятичными дробями. Здесь же видна наша дробь , которая расположилась там же, где и десятичная дробь 1,5.
Мы увеличивали определенные отрезки на координатной прямой, чтобы увидеть остальные числа, лежащие на этом отрезке. В результате, мы обнаруживали десятичные дроби, которые имели после запятой одну цифру.
Но это были не единственные числа, лежащие на этих отрезках. Чисел, лежащих на координатной прямой бесконечно много.
Нетрудно догадаться, что между десятичными дробями, имеющими после запятой одну цифру, лежат уже другие десятичные дроби, имеющие после запятой две цифры. Другими словами, сотые части отрезка.
К примеру, попробуем увидеть числа, которые лежат между десятичными дробями 0,1 и 0,2

Ещё пример. Десятичные дроби, имеющие две цифры после запятой и лежащие между нулём и рациональным числом 0,1 выглядят так:

Пример 3. Отметим на координатной прямой рациональное число . Данное рациональное число будет располагаться очень близко к нулю

Значение дроби равно 0,02
Если мы увеличим отрезок от 0 до 0,1 то увидим где точно расположилось рациональное число

Видно, что наше рациональное число расположилось там же, где и десятичная дробь 0,02.
Пример 4. Отметим на координатной прямой рациональное число 0, (3)
Рациональное число 0, (3) является бесконечной периодической дробью. Его дробная часть никогда не заканчивается, она бесконечная
0,33333….и так далее до бесконечности..
И поскольку у числа 0,(3) дробная часть является бесконечной, это означает, что мы не сможем найти точное место на координатной прямой, где это число располагается. Мы можем лишь указать это место приблизительно.
Рациональное число 0,33333… будет располагаться очень близко к обычной десятичной дроби 0,3

Данный рисунок не показывает точное место расположения числа 0,(3). Это лишь иллюстрация, показывающая как близко может располагаться периодическая дробь 0,(3) к обычной десятичной дроби 0,3.
Пример 5. Отметим на координатной прямой рациональное число . Данное рациональное число будет располагаться посередине между числами 2 и 3

это есть 2 (две целых) и (одна вторая). Дробь по другому ещё называют «половиной». Поэтому мы отметили на координатной прямой два целых отрезка и ещё половину отрезка.
Если перевести смешанное число в неправильную дробь, то получим обыкновенную дробь . Эта дробь на координатной прямой будет располагаться там же, где и дробь

Значение дроби равно 2,5
Если увеличить участок координатной прямой от 2 до 3, то мы увидим следующую картину:

Видно, что наше рациональное число расположилось там же, где и десятичная дробь 2,5
Область применения
Итак, тем, кто узнал или вспомнил, что такое рациональные числа, становится ясно, что они используются повсеместно: в бухгалтерии, экономике, статистике, физике, химии и других науках. Естественно, также место им есть в математике. Не всегда зная, что имеем дело с ними, мы постоянно используем рациональные числа. Еще маленькие дети, учась считать предметы, разрезая на части яблоко или выполняя другие простые действия, сталкиваются с ними. Они буквально нас окружают. И все же для решения некоторых задач их недостаточно, в частности, на примере теоремы Пифагора можно понять необходимость введения понятия иррациональных чисел.
Иррациональность числа
Проведем доказательство иррациональности числа методом «от противного». С этой целью предположим, что число является рациональным числом. Тогда существует дробь вида
,
удовлетворяющая равенству
и такая, у которой числитель и знаменатель являются натуральными числами, не имеющими простых общих делителей.
Используя данное равенство, получаем:

Отсюда вытекает, что число m2 является четным числом, а, значит, и число m является четным числом. Действительно, если мы предположим противное, т.е. предположим, что число m является нечетным числом, то найдется такое целое число k , которое удовлетворяет соотношению
m = 2k + 1 .
Следовательно,
m2 = (2k + 1)2 == 4m2 + 4k +1 ,
т.е. m является нечетным числом. Полученное противоречие доказывает, что число m является четным числом. Значит, найдется такое целое число k , которое удовлетворяет соотношению
m = 2k .
Поэтому,

Отсюда вытекает, что число n2 является четным, а, значит, и число n является четным числом.
Итак, число m является четным, и число n является четным, значит, число 2 является общим делителем числителя и знаменателя дроби
.
Полученное противоречие доказывает, что , удовлетворяющей соотношению
не существует. Следовательно, число является иррациональным числом, что и требовалось доказать.
Счётность множества
Нумерация положительных рациональных чисел
Чтобы оценить количество рациональных чисел, нужно найти мощность их множества. Легко доказать, что множество рациональных чисел счётно. Для этого достаточно привести алгоритм, который нумерует рациональные числа, то есть устанавливает биекцию между множествами рациональных и натуральных чисел.
Примером такого построения может служить следующий простой алгоритм. Составляется бесконечная таблица обыкновенных дробей, на каждой i{\displaystyle i}-ой строке в каждом j{\displaystyle j}-ом столбце которой располагается дробь ij{\displaystyle {\frac {i}{j}}}. Для определённости считается, что строки и столбцы этой таблицы нумеруются с единицы. Ячейки таблицы обозначаются (i,j){\displaystyle \left(i,j\right)}, где i{\displaystyle i} — номер строки таблицы, в которой располагается ячейка, а j{\displaystyle j} — номер столбца.
Полученная таблица обходится «змейкой» по следующему формальному алгоритму.
- Если текущее положение (i,j){\displaystyle \left(i,j\right)} таково, что i{\displaystyle i} — нечётное, а j=1{\displaystyle j=1}, то следующим положением выбирается (i+1,j){\displaystyle \left(i+1,j\right)}.
- Если текущее положение (i,j){\displaystyle \left(i,j\right)} таково, что i=1{\displaystyle i=1}, а j{\displaystyle j} — чётное, то следующим положением выбирается (i,j+1){\displaystyle \left(i,j+1\right)}.
- Если для текущего положения (i,j){\displaystyle \left(i,j\right)} сумма индексов (i+j){\displaystyle \left(i+j\right)} нечётна, то следующее положение — (i−1,j+1){\displaystyle \left(i-1,j+1\right)}.
- Если для текущего положения (i,j){\displaystyle \left(i,j\right)} сумма индексов (i+j){\displaystyle \left(i+j\right)} чётна, то следующее положение — (i+1,j−1){\displaystyle \left(i+1,j-1\right)}.
Эти правила просматриваются сверху вниз и следующее положение выбирается по первому совпадению.
В процессе такого обхода каждому новому рациональному числу ставится в соответствие очередное натуральное число. То есть дроби 11{\displaystyle 1/1} ставится в соответствие число 1, дроби 21{\displaystyle 2/1} — число 2, и т. д. Нужно отметить, что нумеруются только несократимые дроби. Формальным признаком несократимости является равенство единице наибольшего общего делителя числителя и знаменателя дроби.
Следуя этому алгоритму, можно занумеровать все положительные рациональные числа. Это значит, что множество положительных рациональных чисел Q+{\displaystyle \mathbb {Q} _{+}} счётно. Легко установить биекцию между множествами положительных и отрицательных рациональных чисел, просто поставив в соответствие каждому рациональному числу противоположное ему. Т. о. множество отрицательных рациональных чисел Q−{\displaystyle \mathbb {Q} _{-}} тоже счётно. Их объединение Q+∪Q−{\displaystyle \mathbb {Q} _{+}\cup \mathbb {Q} _{-}} также счётно по свойству счётных множеств. Множество же рациональных чисел Q=Q+∪Q−∪{}{\displaystyle \mathbb {Q} =\mathbb {Q} _{+}\cup \mathbb {Q} _{-}\cup \left\{0\right\}} тоже счётно как объединение счётного множества с конечным.
Разумеется, существуют и другие способы занумеровать рациональные числа. Например, для этого можно воспользоваться такими структурами как дерево Калкина — Уилфа, дерево Штерна — Броко или ряд Фарея.
Утверждение о счётности множества рациональных чисел может вызывать некоторое недоумение, так как на первый взгляд складывается впечатление, что оно гораздо обширнее множества натуральных чисел. На самом деле это не так и натуральных чисел хватает, чтобы занумеровать все рациональные.
Терминология
Формальное определение
Формально рациональные числа определяются как множество классов эквивалентности пар {(m,n)∣m∈Z,n∈N}{\displaystyle \left\{(m,\;n)\mid m\in \mathbb {Z} ,\;n\in \mathbb {N} \right\}} по отношению эквивалентности (m,n)∼(m′,n′){\displaystyle (m,\;n)\sim (m’,\;n’)}, если m⋅n′=m′⋅n{\displaystyle m\cdot n’=m’\cdot n}. При этом операции сложения и умножения определяются следующим образом:
- (m1,n1)+(m2,n2)=(m1⋅n2+m2⋅n1,n1⋅n2);{\displaystyle \left(m_{1},\;n_{1}\right)+\left(m_{2},\;n_{2}\right)=\left(m_{1}\cdot n_{2}+m_{2}\cdot n_{1},\;n_{1}\cdot n_{2}\right);}
- (m1,n1)⋅(m2,n2)=(m1⋅m2,n1⋅n2).{\displaystyle \left(m_{1},\;n_{1}\right)\cdot \left(m_{2},\;n_{2}\right)=\left(m_{1}\cdot m_{2},\;n_{1}\cdot n_{2}\right).}
Связанные определения
Правильные, неправильные и смешанные дроби
Правильной называется дробь, у которой модуль числителя меньше модуля знаменателя. Правильные дроби представляют рациональные числа, по модулю меньшие единицы. Дробь, не являющаяся правильной, называется неправильной и представляет рациональное число, большее или равное единице по модулю.
Неправильную дробь можно представить в виде суммы целого числа и правильной дроби, называемой смешанной дробью. Например, 237=2+37=147+37=177{\displaystyle 2{\frac {3}{7}}=2+{\frac {3}{7}}={\frac {14}{7}}+{\frac {3}{7}}={\frac {17}{7}}}. Подобная запись (с пропущенным знаком сложения), хотя и употребляется в элементарной арифметике, избегается в строгой математической литературе из-за схожести обозначения смешанной дроби с обозначением произведения целого числа на дробь.
Высота дроби
Высота обыкновенной дроби — это сумма модуля числителя и знаменателя этой дроби.
Высота рационального числа — это сумма модуля числителя и знаменателя несократимой обыкновенной дроби, соответствующей этому числу.
Например, чтобы узнать высоту дроби −156{\displaystyle -{\frac {15}{6}}} нужно сначала из неё получить несократимую дробь. Несократимая дробь будет выглядеть так: −52{\displaystyle -{\frac {5}{2}}}. Потом нужно сложить модуль числителя и знаменатель: 5+2=7{\displaystyle 5+2=7}. Значит высота дроби −156{\displaystyle -{\frac {15}{6}}} равна 7{\displaystyle 7}.
Термин дробное число (дробь) иногда[уточнить] используется как синоним к термину рациональное число, а иногда синоним любого нецелого числа. В последнем случае дробные и рациональные числа являются разными вещами, так как тогда нецелые рациональные числа — всего лишь частный случай дробных.
История рациональных чисел и дробей
Самое раннее известное упоминание иррациональных чисел было между 800 и 500 г. до н. э. в индийской Сулба-Сутре.
Первое доказательство существования иррациональных чисел принадлежит древнегреческому философу-пифагорейцу Гиппасу из Метапонта. Он доказал (вероятнее всего геометрически) иррациональность квадратного корня из 2.
Легенда гласит, что Гиппас из Метапонта открыл иррациональные числа когда попытался представить квадратный корень из 2 в виде дроби. Однако Пифагор верил в абсолютность чисел и не смог принять существование иррациональных чисел.
Считается, что из-за этого между ними получился конфликт, который породил множество легенд. Многие говорят о том, что как раз это открытие убило Гиппаса.
В вавилонских записях по математике часто можно увидеть шестидесятеричную систему счисления, в которой уже использовались дроби. Эти записи были сделаны более 4000 лет назад, система была немного не такой, как у нас, но смысл тот же.
У египтян, которые жили в более поздний период, также был свой способ записи дробей, что-то похожее на: 3⁻¹ или 5⁻¹.
Узнайте больше про Число Пи, Числа Фибоначчи и Экспоненту.
Счётность множества

Нумерация положительных рациональных чисел
Чтобы оценить количество рациональных чисел, нужно найти мощность их множества. Легко доказать, что множество рациональных чисел счётно. Для этого достаточно привести алгоритм, который нумерует рациональные числа, то есть устанавливает биекцию между множествами рациональных и натуральных чисел.
Примером такого построения может служить следующий простой алгоритм. Составляется бесконечная таблица обыкновенных дробей, на каждой i{\displaystyle i}-ой строке в каждом j{\displaystyle j}-ом столбце которой располагается дробь ij{\displaystyle {\frac {i}{j}}}. Для определённости считается, что строки и столбцы этой таблицы нумеруются с единицы. Ячейки таблицы обозначаются (i,j){\displaystyle \left(i,j\right)}, где i{\displaystyle i} — номер строки таблицы, в которой располагается ячейка, а j{\displaystyle j} — номер столбца.
Полученная таблица обходится «змейкой» по следующему формальному алгоритму.
- Если текущее положение (i,j){\displaystyle \left(i,j\right)} таково, что i{\displaystyle i} — нечётное, а j=1{\displaystyle j=1}, то следующим положением выбирается (i+1,j){\displaystyle \left(i+1,j\right)}.
- Если текущее положение (i,j){\displaystyle \left(i,j\right)} таково, что i=1{\displaystyle i=1}, а j{\displaystyle j} — чётное, то следующим положением выбирается (i,j+1){\displaystyle \left(i,j+1\right)}.
- Если для текущего положения (i,j){\displaystyle \left(i,j\right)} сумма индексов (i+j){\displaystyle \left(i+j\right)} нечётна, то следующее положение — (i−1,j+1){\displaystyle \left(i-1,j+1\right)}.
- Если для текущего положения (i,j){\displaystyle \left(i,j\right)} сумма индексов (i+j){\displaystyle \left(i+j\right)} чётна, то следующее положение — (i+1,j−1){\displaystyle \left(i+1,j-1\right)}.
Эти правила просматриваются сверху вниз и следующее положение выбирается по первому совпадению.
В процессе такого обхода каждому новому рациональному числу ставится в соответствие очередное натуральное число. То есть дроби 11{\displaystyle 1/1} ставится в соответствие число 1, дроби 21{\displaystyle 2/1} — число 2, и т. д. Нужно отметить, что нумеруются только несократимые дроби. Формальным признаком несократимости является равенство единице наибольшего общего делителя числителя и знаменателя дроби.
Следуя этому алгоритму, можно занумеровать все положительные рациональные числа. Это значит, что множество положительных рациональных чисел Q+{\displaystyle \mathbb {Q} _{+}} счётно. Легко установить биекцию между множествами положительных и отрицательных рациональных чисел, просто поставив в соответствие каждому рациональному числу противоположное ему. Т. о. множество отрицательных рациональных чисел Q−{\displaystyle \mathbb {Q} _{-}} тоже счётно. Их объединение Q+∪Q−{\displaystyle \mathbb {Q} _{+}\cup \mathbb {Q} _{-}} также счётно по свойству счётных множеств. Множество же рациональных чисел Q=Q+∪Q−∪{}{\displaystyle \mathbb {Q} =\mathbb {Q} _{+}\cup \mathbb {Q} _{-}\cup \left\{0\right\}} тоже счётно как объединение счётного множества с конечным.
Разумеется, существуют и другие способы занумеровать рациональные числа. Например, для этого можно воспользоваться такими структурами как дерево Калкина — Уилфа, дерево Штерна — Броко или ряд Фарея.
Утверждение о счётности множества рациональных чисел может вызывать некоторое недоумение, так как на первый взгляд складывается впечатление, что оно гораздо обширнее множества натуральных чисел. На самом деле это не так и натуральных чисел хватает, чтобы занумеровать все рациональные.
Десятичные приближения иррациональных чисел с недостатком и с избытком
Разберем понятие десятичных приближений иррациональных чисел с недостатком и с избытком на конкретном примере. Для этого рассмотрим иррациональное число
Это число, как и любое другое иррациональное число, изображается бесконечной непериодической десятичной дробью.
Последовательностью десятичных приближений числа с недостатком называют последовательность конечных десятичных дробей, которая получится, если у числа отбросить все десятичные знаки, начиная, сначала с первого десятичного знака, затем со второго десятичного знака, потом с третьего десятичного знака и т.д.
Если последний десятичный знак каждого десятичного приближения числа с недостатком увеличить на 1 , то получится десятичное приближение числа с избытком.
Само число располагается между каждым своим приближением с недостатком и соответствующим ему приближением с избытком.
Для числа возникающая бесконечная последовательность десятичных приближений с недостатком и с избытком, имеет следующий вид:
и т.д.
Точно также можно построить последовательность десятичных приближений с недостатком и с избытком для любого иррационального числа.

На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.